Luis R. Izquierdo and J. Gary Polhill (2006)
Is Your Model Susceptible to Floating-Point Errors?
Journal of Artificial Societies and Social Simulation
vol. 9, no. 4
<https://www.jasss.org/9/4/4.html>
For information about citing this article, click here
Received: 18-Jan-2006 Accepted: 12-Oct-2006 Published: 31-Oct-2006
 Abstract
Abstract
|
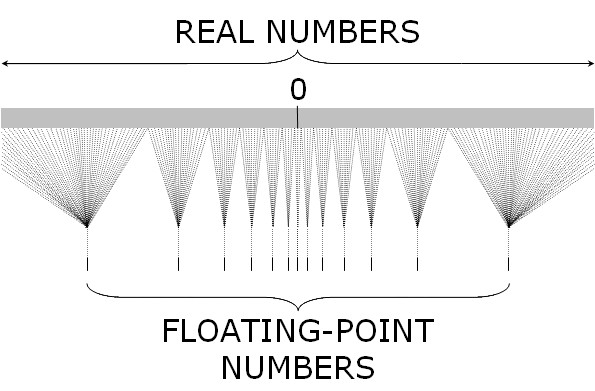
| Figure 1. Schematic illustration of the correspondence between the set of real numbers and their floating-point representation in a computer. The set of real numbers is fully connected and unbounded, whereas the set of floating-point numbers in a computer is sparse and bounded |
|
ENERGY = 0.6; ENERGY = ENERGY – 0.2; ENERGY = ENERGY – 0.4; IF (ENERGY < 0) THEN (AGENT DIES); |
|
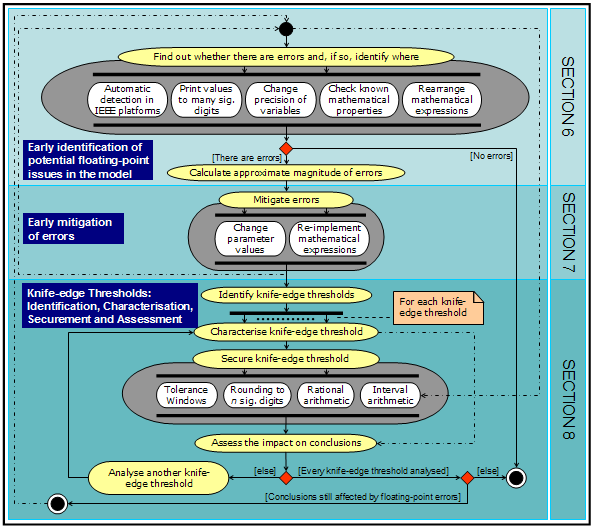
| Figure 2. UML Activity diagram (Booch et al. 1999) of a step-wise methodology to deal with floating-point errors in a model. This methodology is not meant to be prescriptive; it is offered only as a guideline. Many possible variants are possible, some of which are indicated using dotted-dashed arrows. White boxes contained in one single grey box denote actions aimed at achieving one common goal; there is not a fixed execution order for these, and just a few of them may be sufficient to achieve the goal |
|
ENERGY= 0.599999999999999977795539507497 ENERGY= 0.399999999999999966693309261245 ENERGY= -5.55111512312578270211815834045e-17 |
| [ x ⊗ y ]f = ( x ⊗ y ) ·(1 + δ) | |δ| ≤ u |
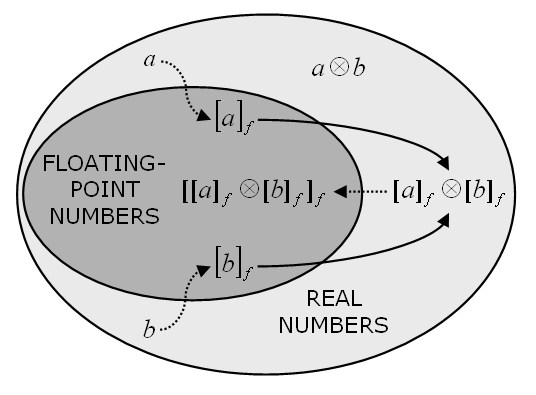
where x and y are two floating point numbers, [z]f denotes the closest representable number to z, ⊗ stands for any arithmetic operation, and δ is the relative error. Note, however, that when performing an arithmetic operation (a ⊗ b) with real numbers a and b in a computer, the result is generally [[a]f ⊗ [b]f]f , which may not coincide with [a ⊗ b]f. This potential discrepancy, illustrated in Figure 3, explains why (0.3 / 0.1) does not equal 3 in IEEE 754 double precision arithmetic, even though [3]f ≡ 3.
|
| Figure 3. Schematic representation of stages in a floating-point calculation with two real operands a and b to the floating-point result [[a]f ⊗ [b]f]f. Dotted lines show conversion from a non-representable to a representable number, and hence a potential source of error, whilst the solid lines indicate the operation |
|
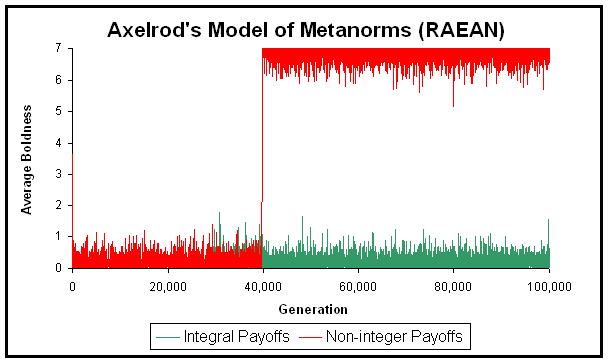
| Figure 4. Population average boldness in two sample runs conducted with RAEAN. The two runs differ only in the magnitude of the payoffs. The green line shows a run in which all the payoffs are integers (T = 3; H = –1; E = –2; P = –9; ME = –2; MP = –9), while the red line shows a run in which all the payoffs have been divided by 10 (T = 0.3; H = –0.1; E = –0.2; P = –0.9; ME = –0.2; MP = –0.9). In real arithmetic, the two runs should give exactly the same output. The program and all the parameters used in this experiment are available in the Supporting Material |
[0.001]f is stored (in binary) as:
1.0000011000100100110111010010111100011010100111111100 · 2–10
9.765625·10–4 ≡ [9.765625·10–4]f is stored as:
1.0000000000000000000000000000000000000000000000000000 · 2–10
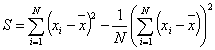
|
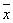 of the set by at least one standard deviation σ:
of the set by at least one standard deviation σ:
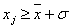
|
(1) |
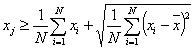
|
(1a) |
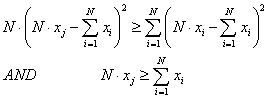
|
(1b) |
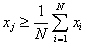
|
(2a) |
should be substituted by
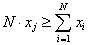
|
(2b) |
if {xi} are integers.
| IF (x < 0.0) THEN (x = –x); |
| IF (randomNumber < probability) THEN action; | (3) |
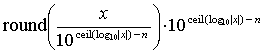
|
where round(z) returns the closest integer to z and ceil(z) denotes the smallest integer greater than or equal to z. An example of this implementation in NetLogo (Wilensky 1999) is provided in Appendix B. In programming languages that allow printing numbers to n significant digits (e.g. C, C++, Objective-C, and Java) a simpler implementation of this technique consists in printing x to a string with the specified precision, and then read the string back as a floating-point value (Polhill et al. 2006; Supporting Material). As an example, printing values to 5 significant decimal digits in the piece of code introduced in section 4 would produce the following results:
|
ENERGY = 0.6; ENERGY-FLOAT-BEFORE-PRINTING-TO-STRING = 0.5999999999999999777955395…; ( ≡ [0.6]f ) ENERGY-STRING = "0.6"; ENERGY-FLOAT-AFTER-READING-STRING = 0.5999999999999999777955395…; ( ≡ [0.6]f ) ENERGY = ENERGY – 0.2; ENERGY-FLOAT-BEFORE-PRINTING-TO-STRING = 0.3999999999999999666933092…; ( ≠ [0.4]f ) ENERGY-STRING = "0.4"; ENERGY-FLOAT-AFTER-READING-STRING = 0.4000000000000000222044604…; ( ≡ [0.4]f ) ENERGY = ENERGY – 0.4; ENERGY-FLOAT-BEFORE-PRINTING-TO-STRING = 0; ( ≡ [0]f ) |
| Table 1: Summary of the most relevant features of every technique | ||||
| Most useful when: | Main advantage(s) | Main disadvantage(s) | Required level of programming expertise | |
| Tolerance windows | In the absence of errors, every possible value xi in the threshold is separated from every other possible value by a substantial minimum distance dmin = min { (xi – xj) ; xi ≠ xj }.[12] | Simplicity | It requires (absolute) error bounds to ensure correct behaviour. | Basic |
| Rounding to n significant digits before comparing | In the absence of errors, every possible value in the threshold has only a few digits in the working base.[12] | Simplicity | It requires (relative) error bounds to ensure correct behaviour. | Basic |
| Rounding to n significant digits after every operation | In the absence of errors, every possible value in the threshold has only a few digits in the working base.[12] | It can prevent accumulation of errors. | It requires (relative) error bounds to ensure correct behaviour. | Intermediate |
| Interval arithmetic | Information about the set of values involved in the threshold in the absence of errors is not readily available and/or the magnitude of the error they may contain is unknown. |
| Weak (i.e. it issues unneccessary warnings) when comparing numbers that should be equal but contain small errors. | Advanced |
| Rational arithmetic | Only rational numbers are used. | It completely solves the problem if only rational numbers are used. | Advanced level of programming expertise required. | Advanced |
|
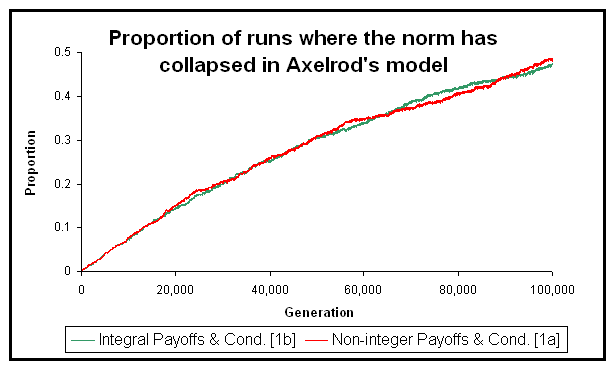
| Figure 5. Proportion of runs (out of 1000 for each line) where the norm collapses in Axelrod's model of metanorms. The green line shows runs in which all the payoffs are integers (T = 3; H = –1; E = –2; P = –9; ME = –2; MP = –9) and condition [1b] was implemented. The red line shows runs where every payoff has been divided by ten (T = 0.3; H = –0.1; E = –0.2; P = –0.9; ME = –0.2; MP = –0.9), and condition [1a] was used. The two programs and all the parameters used in this experiment are available in the Supporting Material |
| IF(rand < pt) THEN [cooperate] ELSE [defect]; |
where rand is a random number in the range [0,1] and pt is the agent's probability to cooperate in time-step t. The probability pt is updated every time-step according to one of two possible formulae. Which formula is used depends on the action (cooperate or defect) undertaken by each of the two agents in the model in the previous time-step. Because of the simple arithmetic form of the two updating formulae (see Macy & Flache 2002), the error in pt+1 will be small given any one particular formula. Thus, assuming the same path has been followed in the floating-point model and in its exact counterpart up to a point, the chances of both implementations keep following the same path will be very high. In the unlikely case that the floating-point model deviates from the 'correct' path at some point, one could always argue that such a deviation could have occurred with extremely similar probability in the correct model anyway. Thus, we would conclude that floating-point errors do not significantly affect the overall statistical behaviour of this model.
|
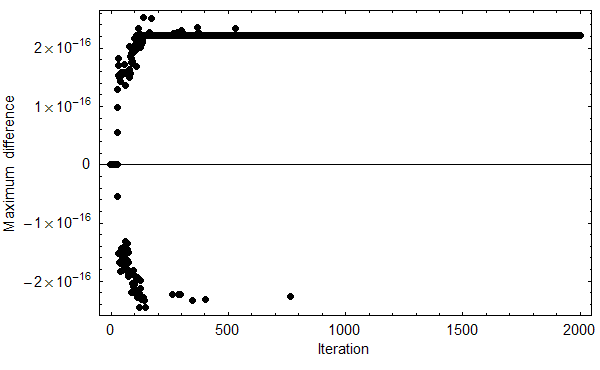
| Figure 6. Maximum difference across 1000 runs between the value of pt in an exact implementation of the BM model (Macy & Flache 2002) and the value of pt in an implementation using IEEE 754 double precision arithmetic. The figure shows data for the Prisoner's Dilemma with parameters [π = (4,3,1,0), A = 2, l = 0.5, h = 0, pC,1 = 0.5] (see Macy & Flache 2002). The program used to conduct this experiment is available in the Supporting Material. |
2Some authors refer to control flow statements, rather than branching statements. By branching statement we mean any point in the code of a program where the flow of control may diverge. Some examples are:
IF(condition)THEN(action), and
DO(action)WHILE(condition).
3It is also assumed that nu < 1.
4RAEAN stands for "Reimplementation of Axelrod's 'Evolutionary Approach to Norms' " (Galán & Izquierdo 2005).
5In the BM model it is necessary to multiply the aspiration level by the same constant too.
6By 'digits of a real number x' in a certain base b we mean the minimum number of digits X necessary to write x in base b, according to the format X·X…X · bexp, and without loss of precision.
7Even if {xi} were large, one could always subtract an integral estimate of the mean of {xi} from every xi, and then apply [1b] to the shifted data.
8Please note that at this stage we are only concerned about the first appearance of floating-point errors, not about the impact of such errors in evaluating the condition. Even if the condition is evaluated correctly in both implementations, implementation [1b] will help us to focus on the relevant errors in the model (e.g when doing an automatic detection of all the errors). The same applies for [2a] and [2b].
9We arrived at this statement using interval arithmetic. Later in the paper we acknowledge interval arithmetic as a useful technique to identify those knife-edge thresholds where the correct branch of the code has been followed for certain, and which therefore do not require any further attention.
10Knuth (1998, p. 233) also suggests a variation on this approach that takes into consideration the magnitude of the operands. A brief investigation using CharityWorld did not find this improved things much (Polhill et al 2006).
11It is also assumed that both numbers lie within the range of normalised floating-point numbers. In double precision that range is: [–1.797…·10308, –2.225…–308] ∪ [2.225…–308, 1.797…·10308].
12If errors are not too large, this means that when the wrong branch is followed, it is because two numbers that should have been equal are detected as different (due to small floating-point errors), which is most often the case.
13In our experiments it turned out that using integral parameters was enough to select the right branch at the knife-edge threshold every time the condition was evaluated: the 1000 runs we conducted with implementation [1b] and integral payoffs produced exactly the same results as the 1000 runs we conducted with implementation [1a] and integral payoffs.
14Interestingly, these tests also showed that the error is somewhat biased.
15The value of pt completely determines the state of the system.
Theorem 1: Let x, y and ε (ε ≥ 0) be three floating-point numbers and assume that summation and subtraction are exactly rounded (as the IEEE 754 standard stipulates). If |x – y| > 2ε, then x and y will be detected as being different using tolerance windows of magnitude ε.
Proof: Assume for now that x > y. Then |x – y| > 2ε implies that x > y + 2ε. Let D(y + ε) be the error in computing [y + ε]f, expressed as D(y + ε) = [y + ε]f – (y + ε). It can be easily shown that |D(y + ε)| ≤ ε. Thus,
x > y + 2ε ⇒ x > y + ε + D(y + ε) ⇒ x > [y + ε]f
The proof for the case where x < y is analogous. The 2ε margin is the smallest needed to guarantee that the two numbers will be detected as different, since there are cases where |x – y| = 2ε and the result of this proposition does not apply. ¤
Theorem 2: Let x, y and ε be three floating-point numbers and assume that summation and subtraction are exactly rounded (as the IEEE 754 standard stipulates). If |x – y| ≤ ε then x and y will be detected as being equal using tolerance windows of magnitude ε.
Proof: |x – y| ≤ ε ⇔ y – ε ≤ x ≤ y + ε
Since subtraction is exactly rounded, we know that [y – ε]f ≤ x. This is because x is a floating point number that is nearer to y – ε than any floating point number greater than x (since y – ε ≤ x ). Similarly, we also know that x ≤ [y + ε]f. Assuming a larger margin for |x – y| would not provide such a guarantee. Thus, if |x – y| ≤ ε, then [y – ε]f ≤ x ≤ [y + ε]f . ¤
In summary, if summation and subtraction are exactly rounded, then using tolerance windows of magnitude ε will enable the model to follow the correct branch if:
It can be easily proved that setting ε = [dmin/3] f– guarantees both (i) and (ii) above as long the absolute error in each number is less than ε/2.
BOOCH G, Rumbaugh J, and Jacobson I (1999) The Unified Modeling Language User Guide. Addison-Wesley, Boston, MA.
CHAN T F, Golub G H, and LeVeque R J (1983) Algorithms for Computing the Sample Variance: Analysis and Recommendations. The American Statistician, 37(3). pp. 242-247.
FLACHE A and Macy M W (2002) Stochastic Collusion and the Power Law of Learning. Journal of Conflict Resolution, 46 (5). pp. 629-653.
GALÁN J M and Izquierdo L R (2005) Appearances Can Be Deceiving: Lessons Learned Reimplementing Axelrod's 'Evolutionary Approach to Norms'. Journal of Artificial Societies and Social Simulation, 8 (3), https://www.jasss.org/8/3/2.html
GOLDBERG D (1991) What every computer scientist should know about floating point arithmetic. ACM Computing Surveys 23 (1). pp. 5-48.
GOTTS N M, Polhill J G, and Law A N R (2003) Aspiration levels in a land use simulation. Cybernetics & Systems 34 (8). pp. 663-683.
HIGHAM N J (2002) Accuracy and Stability of Numerical Algorithms, (second ed.), Philadelphia, USA: SIAM.
IEEE (1985) IEEE Standard for Binary Floating-Point Arithmetic, IEEE 754-1985, New York, NY: Institute of Electrical and Electronics Engineers.
IZQUIERDO L R, Gotts N M, and Polhill J G (2004) Case-Based Reasoning, Social Dilemmas, and a New Equilibrium Concept. Journal of Artificial Societies and Social Simulation, 7 (3), https://www.jasss.org/7/3/1.html
IZQUIERDO L R, Izquierdo S S, Gotts N M, and Polhill J G (2006) Transient and Long-Run Dynamics of Reinforcement Learning in Games. Submitted to Games and Economic Behavior.
JOHNSON P E (2002) Agent-Based Modeling: What I Learned from the Artificial Stock Market. Social Science Computer Review, 20. pp. 174-186.
KAHAN W (1998) "The improbability of probabilistic error analyses for numerical computations". Originally presented at the UCB Statistics Colloquium, 28 February 1996. Revised and updated version (version dated 10 June 1998, 12:36 referred to here) is available for download from http://www.cs.berkeley.edu/~wkahan/improber.pdf
KNUTH D E (1998) The Art of Computer Programming Volume 2: Seminumerical Algorithms. Third Edition. Boston, MA: Addison-Wesley.
LEBARON B, Arthur W B, and Palmer R (1999) Time series properties of an artificial stock market. Journal of Economic Dynamics & Control, 23. pp. 1487-1516.
MACY M W and Flache A (2002) Learning Dynamics in Social Dilemmas. Proceedings of the National Academy of Sciences USA, 99, Suppl. 3, pp. 7229-7236.
POLHILL J G, Gotts N M, and Law A N R (2001) Imitative and nonimitative strategies in a land use simulation. Cybernetics & Systems, 32 (1-2). pp. 285-307.
POLHILL J G and Izquierdo L R (2005) Lessons learned from converting the artificial stock market to interval arithmetic. Journal of Artificial Societies and Social Simulation, 8 (2), https://www.jasss.org/8/2/2.html
POLHILL J G, Izquierdo L R, and Gotts N M (2005) The ghost in the model (and other effects of floating point arithmetic). Journal of Artificial Societies and Social Simulation, 8 (1), https://www.jasss.org/8/1/5.html
POLHILL J G, Izquierdo L R, and Gotts N M (2006) What every agent based modeller should know about floating point arithmetic. Environmental Modelling and Software, 21 (3), March 2006. pp. 283-309.
WILENSKY U (1999) NetLogo. http://ccl.northwestern.edu/netlogo/. Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
SUN MICROSYSTEMS (2000) Numerical Computation Guide. Lincoln, NE: iUniverse Inc. Available from http://docs.sun.com/source/806-3568/.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]