A small Obj-C program was written and compiled with the library containing code for each floating point error mitigation strategy, and an architecture-specific API program (Sun) with a standardised interface to access the proccessor time and process image size. The program uses C macros to select between operations at compile-time, meaning that there are different compiled programs for each operator, each sharing as much of the same code as possible. The user specifies n random numbers (generated using the drand48(3C) standard C library function) in the range [0,1[. The compiled operation is then performed n2 times, each number on the lhs of the operator with each other number on the rhs.
The data below are generated from runs using 64000 random numbers. The techniques tested are:
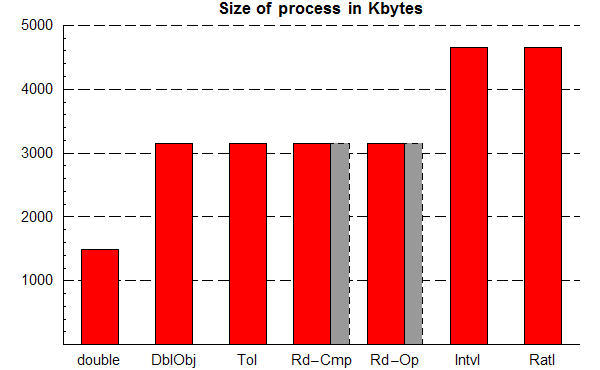
Two bars are given for each of the rounding techniques (Rd-Cmp and Rd-Op) to demonstrate any differences between two approaches to implementing them: mathematically, using the formula in section 8.3 (indicated with the main red bar), or by printing to a string and then converting the string back to a number (indicated with the grey bar). The operator control, for time purposes, was to use no operation at all, and simply compute the time taken to set a variable to the random number n2 times and perform instructions to implement the loop.
The results will depend in part on the speed of any unix API functions involved in the operation of the techniques, which may vary in efficiency from platform to platform. They may also vary depending on the architecture of the Floating Point Unit of the CPU and algorithm used to implement each operator. To that extent, they are merely indicative. In this case, the results are generated on a Sun Fire V240 with 1280 MHz Sparc processors and 4G of RAM, running Solaris 9.
The memory requirements are taken from the size of the process once the array of random numbers has been created; specifically, the value of the pr_size element of the psinfo structure in the Solaris API, see proc(4). As a result, the memory requirements are for comparison purposes only, since they include memory used for other aspects of the program, but also ensure that all memory requirements are captured. As might be expected, those techniques requiring storage of more information about each number (interval and rational) require more memory than those that do not, and using objects rather than doubles to store numbers also requires more memory.

The time requirements were taken by subtracting the elapsed CPU time for the process immediately before the n2 operations are executed from that immediately afterwards. This approach should factor out the influence of competing processes on the recorded time and ensure that the time required for the loop of operations is all that is recorded. In the Solaris API, each time is taken from the pr_time element of the psinfo structure. The figures below may be clicked for a more detailed image, revealing that, in all cases, the use of the standard C datatype is very much faster than applying a mitigation technique using objects. Otherwise, across all the operators, interval arithmetic compares favourably with all the techniques except for tolerance windows.
| No operation | Addition or Subtraction | Multiplication or Division |
|
|
|
The results for No Operation show the overhead involved in simply setting a variable to a value and nested looping through all the numbers. For DblObj, Tol and Rd-Cmp, this overhead is relatively small since these techniques do not involve significant processing activity with each operation, but for Rd-Op, Intvl and Ratl, the processing required to convert the number to be set to the required format (a number with a specified number of significant figures, an interval, and a rational number respectively) inevitably leads to a costly overhead. Interval has the lowest cost here, and for Rd-Op, using the formula rather than strings is also noticeably quicker, as it is in all the other cases. For addition/subtraction and multiplication/division, the relative performance of the techniques is the same, with rational numbers requiring the greatest overhead, particularly for multiplication/division. Rational numbers are more expensive due to the cost of finding the greatest common divisor in each operation, the time requirements of which depend on the values of the operands.
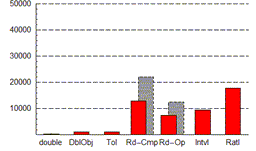
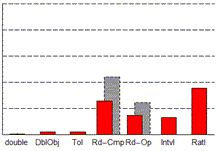
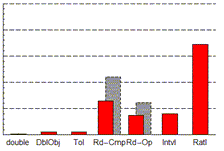
| Equality | Inequality | Comparisons |
|
|
|
For all the comparison operators, Rd-Cmp entails a significant performance overhead, as might be expected, with Rd-Op roughly comparable in performance to the No Operation case since it performs no extra computations at comparison time. Equality takes longer with Intvl because to implement machine interval arithmetic safely (i.e. equality is only true if it is true regardless of floating point errors), the operands must specify equal singleton intervals (i.e. the upper and lower bounds of each interval are equal). This requires more operations to check than the other comparison operators. The directed (<, <=, >=, and >) comparisons in the rightmost graph show Ratl taking longer than it does with equality and inequality. This is because direct comparisons require a series of computations with the numerator and denominator of the operands, whereas the numerators and denominators can be compared directly when checking for equality or inequality if each operand is assumed to have no common factors in its numerator and denominator. Tolerance windows require only a slight loss of performance in comparison with DblObj, suggesting that implementing them without objects (e.g. using macros or inlining) could be a low-cost approach.