Chung-Yuan Huang, Chuen-Tsai Sun, Ji-Lung Hsieh and Holin Lin (2004)
Simulating SARS: Small-World Epidemiological Modeling and Public Health Policy Assessments
Journal of Artificial Societies and Social Simulation
vol. 7, no. 4
<https://www.jasss.org/7/4/2.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 26-May-2032 Accepted: 29-Aug-2004 Published: 31-Oct-2004
 Abstract
Abstract
|
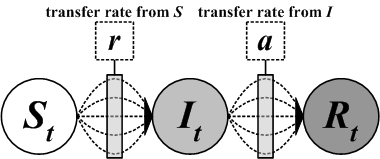
| Figure 1. General transfer diagram for the Compartmental SIR model with susceptible class S, infective class I, and recovered class R |

|
(1) |
|
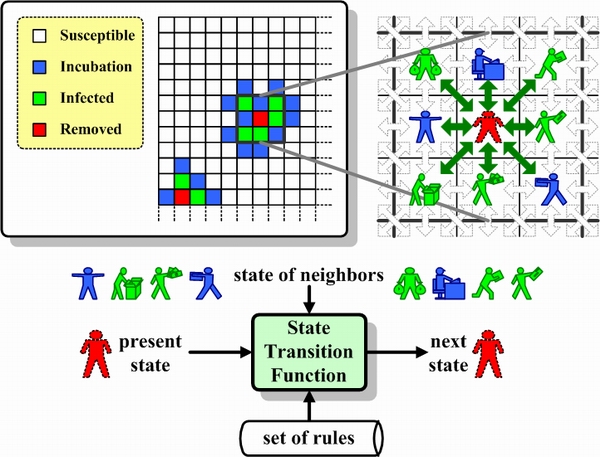
| Figure 2. Cellular Automata, state transition function, and Moore neighborhood concept |
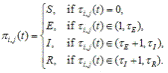
|
(2) |

|
(3) |
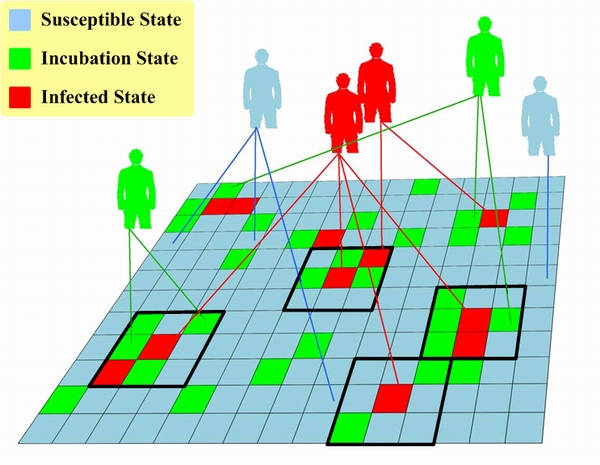
|
| Figure 3. Cellular automata with mirror identity model (CAMIM) |
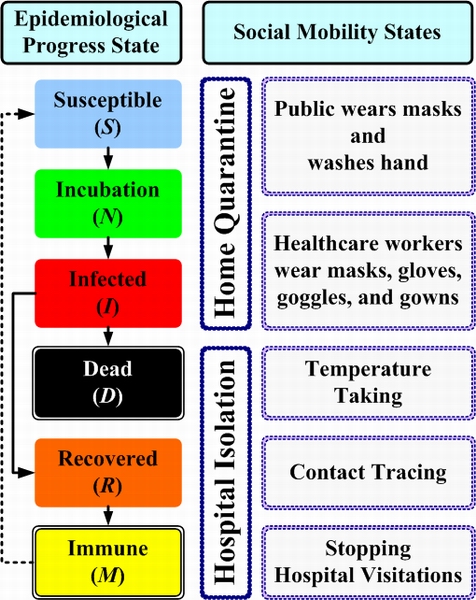
|
| Figure 4. Epidemiological states and two social mobility states |
| Table 1: Agent Attributes | |||
| Attribute | Type | Description | Value |
| ID | Integer | Unique serial number that identifies virtual society agent; sequence not considered critical. | 1~P |
| E | Symbol | When the PopulationAgent parameter is set, the configured RateForeverImmune determines the rate of agents classified as M (Immune) in the epidemiological progress state E - that is, the population of permanently immune agents. All remaining agents are classified as S (Susceptible), meaning “not yet infected but prone to infection.” | Susceptible, Incubation, Infected, Recovered, Immune, Dead |
| Mobility | Symbol | When the PopulationAgent parameter is set, the Mobility status of every agent is preset as “free” - that is, these agents have no restrictions in terms of interacting with the mirror identities of neighboring agents. When an agent is placed under home quarantine or hospital isolation, its Mobility status is respectively changed to Quarantined or Isolated. This means the agent is restricted to its rooted mirror identity (e.g., home, hospital, or dormitory), and the activities of all mirror identities are temporarily suspended. | Free, Quarantined, Isolated |
| Count | Integer | Records the number of an agent's mirror identities; every agent has a minimum of one and a maximum of M. These numbers are normally distributed. | 1~M |
| MirrorIdentity | Set | Data structure for containing mirror identities; each contains at least one. | |
| Age | Symbol | In the proposed model, agents are divided according to three age levels: young (1 to 20), prime (21 to 60); and old (61 and higher). When a simulation system is initiated, agent ages are randomly set based on the RateYoung, RatePrime, and RateOld parameters. | Young, Prime, Old |
| Super | Boolean | Denotes whether an agent is a super-spreader. If yes, set Super to “true”; if no, to “false”. When simulation system is initiated, the RateSuper parameter is used to determine which agents are super-spreaders. | true, false |
| ImmunityPermanent | Boolean | Denotes whether an agent is permanently immune. If yes, set ImmunityPermanenty to “true”; if no, to “false”. When simulation system is initiated, the RatePermanentImmunity parameter is used to determine which agents are permanently immune. | true, false |
| Day | Integer | Number of days for the three epidemiological progress states. If an infected agent has not yet recovered, Day is used to indicate the number of infected days; for recovered agents, Day is used to indicate the number of days since full recovery. If a recovered agent has temporary antibodies, Day is used to indicate the number of immune days. | |
| RateContact | Real | Rate of contact with other agents. For all agents, RateContact is normally distributed. | 0~1 |
| WearingMask | Boolean | Denotes whether agent wears a mask. If yes, set WearingMask to “true”; if no, to “false”. When simulation system is initiated, the WearingMask attribute for all agents is preset to “false”. When a mask wearing policy is enacted (for the general public or healthcare workers), the RateParticipation parameter is used to determine which agents wear masks. | true, false |
| MaskType | Real | Represents average prevention grade of agent masks. The higher the number (close to 1), the greater the efficacy. | 0~1 |
| QuarantinedDay | Integer | Number of home quarantine days, with a range of 0 to Policy.Parameter.DayQuarantined. | |
| Table 2: Mirror Identity Attributes | |||
| Attribute | Type | Description | Value |
| Root | Boolean | Each agent has one mirror identity whose Root = true; for all other mirror identities, Root = false. The root mirror identity is used to mimic special activity locations - e.g., homes, hospitals, and dormitories. | true, false |
| Suspend | Boolean | When the simulation system is initiated, Suspend = false for all agent mirror identities, denoting that all mirror identities are free to move about without any restrictions. Except for its rooted mirror identity, Suspend = true for all of the mirror identities of an agent in home quarantine or hospital isolation. This represents the idea that the agent cannot move about until the end of the home quarantine or recovery period. If the agent dies, Suspend = true for all mirror identities (including the rooted mirror identity), representing the idea that the agent can no longer visit any other locations. | true, false |
| Location | (Integer, Integer) | The first number represents the x-axis coordinate and the second number the y-axis coordinate for the location of a mirror identity in the two-dimensional lattice. Each mirror identity is mapped to a single coordinate location; in other words, each coordinate location contains a single mirror identity of only one agent. | |
| Neighbor | Set | Represents the coordinate locations of an agent's eight mirror identities. Moore or von Neumann neighborhood relationships are used in most simulation systems. Under the Moore system, each mirror identity is defined as having eight neighbor agents; under the von Neumann system the number is four. We adopted the Moore neighborhood definition for our SARS simulation experiments. | |
| Table 3: Simulation System and Epidemic Infection Parameters | ||
| Attribute | Type | Description |
| PopulationAgent | Set | Stores total agent population in the simulation system; maximum capacity is P agents. |
| P | Integer | Total number of agents. |
| M | Integer | Upper limit of an agent's mirror identities. |
| H | Integer | Height of the two-dimensional lattice used in the cellular automata. |
| W | Integer | Width of the two-dimensional lattice used in the cellular automata. |
| N | Integer | Total number of usable lattice H ◊ W in the cellular automata. |
| DayIncubation | Integer | Average number of incubation days. |
| DayInfectious | Integer | Average number of infectious days. |
| DayRecovered | Integer | Average number of recovered days. |
| DayImmune | Integer | Temporarily immune to the disease; average number of incubation days. |
| RateSuper | Real | Percentage of super-spreaders among total population. |
| RateYoung | Real | Percentage of young (0 to 20 years) agents in total population. |
| RatePrime | Real | Percentage of prime (21 to 60 years) agents in total population. |
| RateOld | Real | Percentage of old (60 years and above) agents in total population. |
| RateForeverImmunity | Real | Percentage of permanently immune agents in total population. |
| RateInfection | Real | Average infection rate. |
| RateDeath | Real | Average death rate. |
| Table 4: Public Health Policy Parameters | ||||
| Policy | Attribute | Type | Description | Value |
| WearingMaskInGP | RateParticipation | Real | Policy participation rate. | 0~1 |
| RatePrevention | Real | Infectious disease prevention rate. | 0~1 | |
| WearningMaskInHW | RateParticipation | Real | Policy participation rate. | 0~1 |
| RatePrevention | Real | Infectious disease prevention rate. | 0~1 | |
| TemperatureMeasuring | RateDetection | Real | Fever detection success rate. | 0~1 |
| RateParticipation | Real | Measurement participation rate. | 0~1 | |
| HomeQuarantine | Class | Symbol | A- and B-class quarantines. | A, B |
| DayQuarantined | Integer | Number of home quarantine days. | 0~1 | |
| RateParticipation | Real | Policy participation rate | 0~1 | |
| RestrictingAccessToHospitals | RateParticipation | Real | Policy participation rate. | 0~1 |
| ReducingPublicContact | RateParticipation | Real | Policy participation rate. | 0~1 |
| Table 5: Input Data for Simulating SARS Epidemic Curves in Taiwan, Singapore, and Toronto | ||||
| Category | Attribute | Type | Description | Value |
| Imported Cases | Time Point | Date | Date when the imported case occurred. | |
| Amount | Integer | Number of patients. | 0~999 | |
| Phase | Symbol | Imported during incubation or illness period | Incubation, Infected | |
| Super-spreader | Boolean | Determine whether the imported patient is a super-spreader. | true, false | |
| Public Health Policy | Related Attributes | See Table 4 | ||
| Run | Day | Integer | Number of execution days. | 0~99 |

|

|
|
|

|
|
|

|

|
 
|


|

|
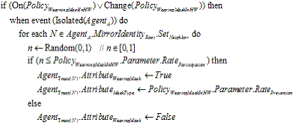
|
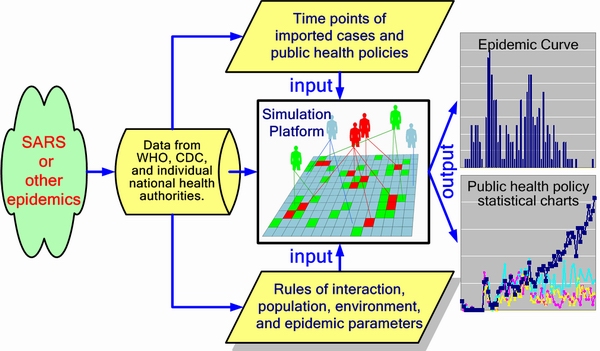
|
| Figure 5. Simulation framework. Data on reported cases came from the World Health Organization (WHO) and health authorities in Singapore, Taiwan, and Toronto. Input data was distributed into three categories: epidemic parameters (e.g., average incubation period, infection rate, distribution among age groups, mortality); imported cases (e.g., time point, amount, imported during incubation or illness period); and public health policies, activated according to data from individual nations (e.g., number of quarantine days, efforts to take body temperatures, restricting access to hospitals). Simulation output includes cellular automata states and various statistical charts |
.jpg)
|
.jpg)
|
.jpg)
|
| Figure 6. Simulation platform for contagious infection |
|
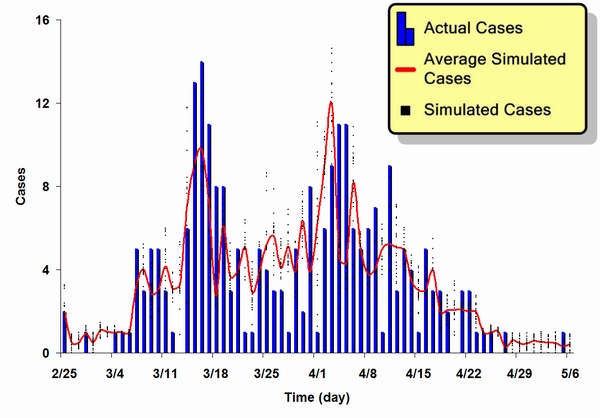
| Figure 7. A Comparison of actual and simulated epidemic results for the SARS outbreak in Singapore. Blue bars represent actual reported cases, red line represents an average of 20 simulation results, and black dots represent 20 simulation results |
|
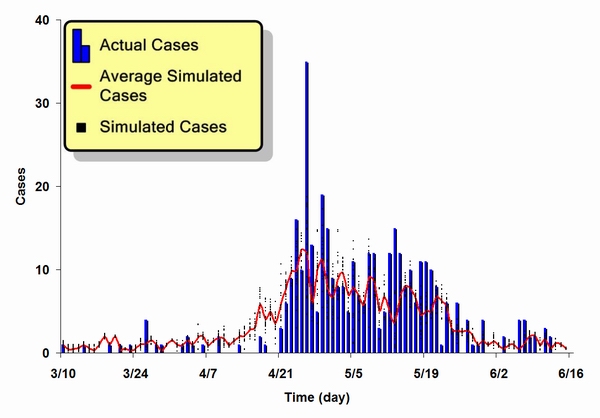
| Figure 8. A comparison of actual and simulated epidemic results for the SARS outbreak in Taipei |
|
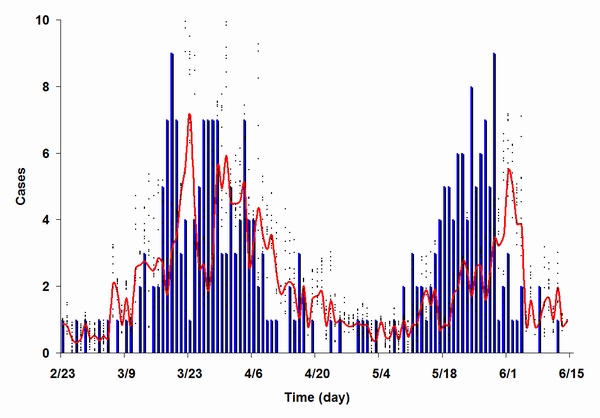
| Figure 9. A comparison of actual and simulated epidemic results for the SARS outbreak in Toronto. We assumed that the second outbreak occurred because preventive policies were relaxed too soon following the first outbreak |
|
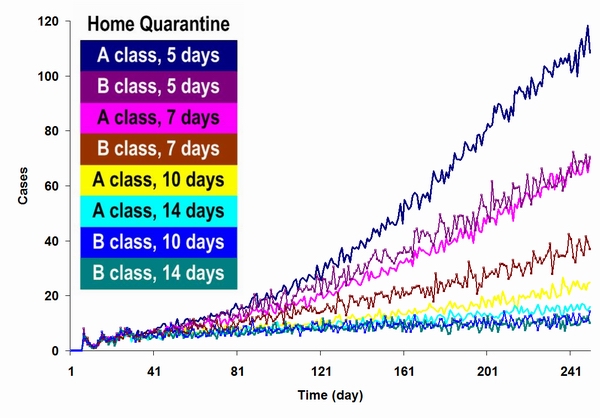
| Figure 10. Results from a simulation based on various home quarantine policies. The time period for the simulation was 250 days, with a default incubation period of 5 days. The results indicate that different home quarantine restriction levels exerted different impacts on the SARS epidemic, and that a home quarantine policy by itself was insufficient for suppressing the epidemic |
|
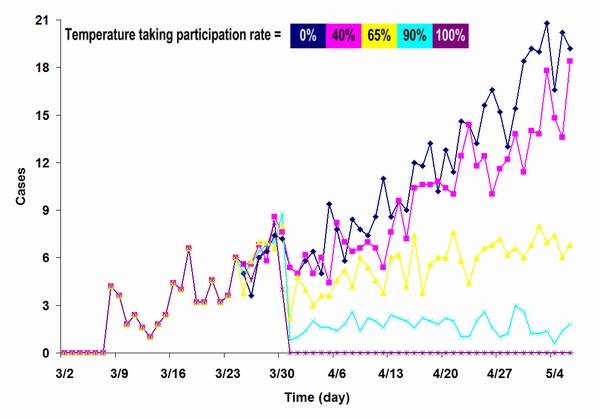
| Figure 11. Results from a simulation focused on temperature measuring policy at different participation levels. We used the 8 imported case reported in Singapore to trigger the simulation. In each 66-day simulation run, the policy was activated on day 24; the goal was to compare impacts at different participation rates |
|
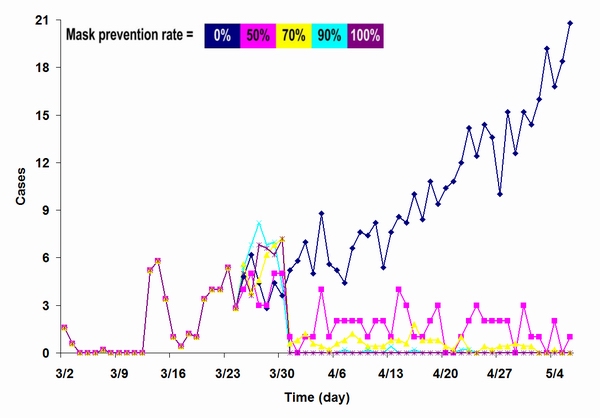
| Figure 12. Results from a simulation focused on the impact of mask-wearing by the general public, comparing different mask protection levels |
|
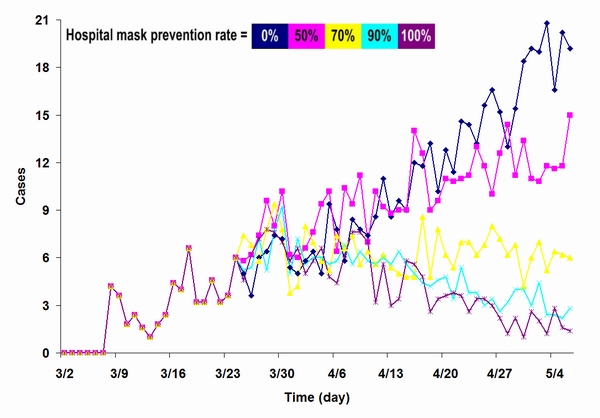
| Figure 13. Results from a simulation focused on the impact of mask-wearing by healthcare workers in healthcare facilities, comparing different mask protection levels |
|
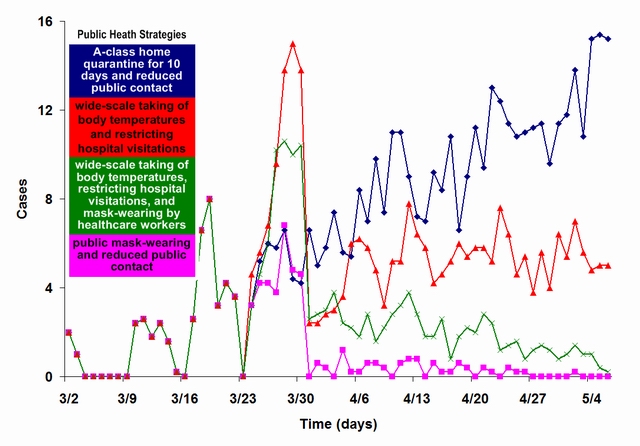
| Figure 14. A comparison of various public health policy suites. We used the 8 imported cases reported in Singapore to trigger the simulation. Policy suites went into effect on day 24 of the 66-day simulation. Suite 1 (cyan): A-class home quarantine for 10 days and reduced public contact; suite 2 (red): wide-scale taking of body temperatures and restricting hospital visitations; suite 3 (green): wide-scale taking of body temperatures, restricting hospital visitations, and mask-wearing by healthcare workers; suite 4 (pink): public mask-wearing and reduced public contact |
AHMED E and Elgazzar A S (2001) On some applications of cellular automata. Physica A, 296, pp. 529-538.
ANAND K, Ziebuhr J, Wadhwani P, Mesters J R, and Hilgenfeld R (2003) Coronavirus Main Proteinase (3CLpro) Structure: Basis for Design of Anti-SARS Drugs. Science, 300(5626), pp. 1763-1767.
ANDERSON R M and May R M (1982) Directly transmitted infectious diseases: control by vaccination. Science 215(4536), pp. 1053-1060.
BENYOUSSEF A, Hafidallah N E, Elkenz A, Ez-Zahraouy H, and Loulidi M (2003) Dynamics of HIV infection on 2D cellular automata. Physica A, 322, pp. 506-520.
BOCCARA N and Cheong K (1992) Automata network SIR models for the spread of infectious disease in populations of moving individuals. Journal of Physics A, 25, pp. 2447-2461.
BOCCARA N and Cheong K (1993) Critical-behavior of a probabilistic-automata network SIS model for the spread of an infectious-disease in a population of moving individuals. Journal of Physics A, 26, pp. 3707-3717.
BOCCARA N, Goles E, Martinez S, and Picco P (1993) Cellular Automata and Cooperative Phenomena. Kluwer Academic Publisher, Boston.
BOCCARA N, Cheong K, and Oram M (1994) A probabilistic automata network epidemic model with births and deaths exhibiting cyclic behavior. Journal of Physics A, 27, pp. 1585-1597.
CDC (CENTERS FOR DISEASE CONTROL) (2003a) SARS: Frequently asked questions, http://www.cdc.gov/ncidod/sars/faq.htm.
CDC (CENTERS FOR DISEASE CONTROL) (2003b) Update: SARS --- Singapore, MMWR, 52(18), pp. 405-411.
CDC (CENTERS FOR DISEASE CONTROL) (2003c) Cluster of SARS Cases Among Protected Health-Care Workers-Toronto, Canada, MMWR, 52(19), pp. 433-436.
CDC (CENTERS FOR DISEASE CONTROL) (2003d) SARS --- Taiwan, MMWR, 52(20), pp. 461-466.
CDC (CENTERS FOR DISEASE CONTROL) (2003e) Update: SARS --- Toronto, Canada, MMWR, 52(23), pp. 547-550.
CDC (CENTERS FOR DISEASE CONTROL) (2003f) Update: SARS --- Worldwide and U.S., MMWR, 52(28), pp. 664-665.
CDC (CENTERS FOR DISEASE CONTROL) (2003g) Use of Quarantine to Prevent Transmission of SARS---Taiwan, MMWR, 52(29), pp. 680-683.
CDC (CENTERS FOR DISEASE CONTROL) (2003h) Revised U.S. Surveillance Case Definition for Severe Acute Respiratory Syndrome (SARS) and Update on SARS Cases --- United States and Worldwide, MMWR, 52(49), pp. 1202-1206.
CHOWELL G, Fenimore P W, Castillo-Garsow M A, and Castillo-Chavez (2003) SARS outbreaks in Ontario, Hong Kong and Singapore: the role of diagnosis and isolation as a control mechanism. Journal of Theoretical Biology, 224(1), pp. 1-8.
DONNELLY C A, Ghani A C, Leung G M, Hedley A J, Fraser C, and Riley S (2003) Epidemiological determinants of spread of causal agent of severe acute respiratory syndrome in Hong Kong. Lancet, 361(9371), pp. 1761-1766.
DYE C and Gay N (2003) EPIDEMIOLOGY: Modeling the SARS Epidemic. Science, 300(5627), pp. 1884-1885.
EDELETEIN-KESHET L (1988) Mathematical Models in Biology. Random House, New York.
EGUILUZ V M and Klemm K (2002) Epidemic threshold in structured scale-free networks. Physical Review Letters, 89(10), 108701.
ENSERINK M (2003) SARS IN CHINA: The Big Question Now: Will It Be Back? Science, 301(5631), pp. 299.
FUENTES M A and Kuperman M N (1999) Cellular automata and epidemiological models with spatial dependence. Physica A, 267, pp. 471-486.
GUAN Y, Zheng B J, He Y Q, Liu X L, Zhuang Z X, Cheung C L, Luo S W, Li P H, Zhang L J, Guan Y J, Butt K M, Wong K L, Chan K W, Lim W, Shortridge K F, Yuen K Y, Peiris J S M and Poon L L M (2003) Isolation and Characterization of Viruses Related to the SARS Coronavirus from Animals in Southern China. Science, 302(5643), pp. 276-278.
KEELING M J (1999) The effects of local spatial structure on epidemiological invasions. Proceedings of the Royal Society of London, 266, pp. 859-867.
KERMACK W O and McKendrick A G (1927) Contributions to the mathematical theory of epidemics. Proceedings of the Royal Society of London, pp. 700-721.
KLECZKOWSKI A and Grenfell B T (1999) Mean-field-type equations for spread of epidemics: the 'small world' model. Physica A, 274, pp. 355-360.
KUPERMAN M and Abramson G (2001) Small World Effect in an Epidemiological Model. Physical Review Letters, 86(13), pp. 2909-2912.
LIPSITCH M, Cohen T, Cooper B, Robins J M, Ma S, James L, Gopalakrishna G, Chew S K, Tan C C, Samore M H, Fisman D, and Murray M (2003) Transmission Dynamics and Control of Severe Acute Respiratory Syndrome. Science, 300(5627), pp. 1966-1970.
MARRA M A, Jones S J M, Astell C R, Holt R A, Brooks-Wilson A, Butterfield Y S N, Khattra J, Asano J K, Barber S A, Chan S Y, Cloutier A, Coughlin S M, Freeman D, Girn N, Griffith O L, Leach S R, Mayo M, Mcdonald H, Montgomery S B, Pandoh P K, Petrescu A S, Robertson A G, Schein J E, Siddiqui A, Smailus D E, Stott J M, Yang G S, Plummer F, Andonov A, Artsob H, Bastien N, Bernard K, Booth T F, Bowness D, Czub M, Drebot M, Fernando L, Flick R, Garbutt M, Gray M, Grolla A, Jones S, Feldmann H, Meyers A, Kabani A, Li Y, Normand S, Stroher U, Tipples G A, Tyler S, Vogrig R, Ward D, Watson B, Brunham R C, Krajden M, Petric M, Skowronski D M, Upton C, and Roper R L (2003) The Genome Sequence of the SARS-Associated Coronavirus. Science, 300(5624), pp. 1399-1404.
MARTINS M L, Ceotto G, Alves S G, Bufon C C B, Silva J M, and Laranjeira F F (2001) A cellular automata model for citrus variegated chlorosis. Physica A, 295, pp. 42-48.
MILGRAM S (1967) The small world problem. Psychology Today, 2, pp. 60-67.
MIRAMONTES O and Luque B (2002) Dynamical small-world behavior in an epidemical model of mobile individuals. Physica D, 168-169, pp. 379-385.
MOORE C and Newman M E J (2000) Epidemics and percolation in small-world networks. Physical Review E, 61(5 Pt B), pp. 5678-5682.
MORENO Y, Pastor-Satorras R, and Vespignani A (2002) Epidemic outbreaks in complex heterogeneous networks. European Physical Journal B, 26(4), pp. 521-529.
NEWMAN M E J (2000) Models of the Small World: A Review. Journal of Statistical Physics, 101, pp. 819-841.
NEWMAN M E J (2002) Spread of epidemic disease on networks. Physical Review E, 66 (1 Pt 2). 016128.
NEWMAN M E J, Jensen I, and Ziff R M (2002) Percolation and epidemics in a two-dimensional small world. Physical Review E, 65 (2 Pt 1), 021904.
NG T W, Turinici G, and Danchin A (2003) A double epidemic model for the SARS propagation. BMC Infectious Disease, 3(19), pp. 1-16.
NISHIURA H, Patanarapelert K, Sriprom M, Sarakorn W, Sriyab S, and Ming T I (2004) Modelling potential responses to severe acute respiratory syndrome in Japan: the role of initial attack size, precaution, and quarantine. Journal of Epidemiology and Community Health, 58(3), pp. 186-191.
PEIRIS J S, Lai S T, Poon L L, Guan Y, Yam L Y, Lim W, Nicholls J, Yee W K, Yan W W, Cheung M T, Cheng V C, Chan K H, Tsang D N, Yung R W, Ng T K, Yuen K Y, and SARS Study Group (2003) Coronavirus as a possible cause of severe acute respiratory syndrome. Lancet, 361(9366), pp. 1319-1325.
RILEY S, Fraser C, Donnelly C A, Ghani A C, Abu-Raddad L J, Hedley A J, Leung G M, Ho L M, Lam T H, Thach T Q, Chau P, Chan K P, Lo S V, Leung P Y, Tsang T, Ho W, Lee K H, Lau E M, Ferguson N M, and Anderson R M (2003) Transmission Dynamics of the Etiological Agent of SARS in Hong Kong: Impact of Public Health Interventions. Science, 300(5627), pp. 1961-1966.
ROTA P A, Oberste M S, Monroe S S, Nix W A, Campagnoli R, Icenogle J P, Penaranda S, Bankamp B, Maher K, Cher M H, Tong S, Tamin A, Lowe L, Frace M, Derisi J L, Chen Q, Wang D, Erdman D D, Peter T C T, Burns C, Ksiazek T G, Rollin P E, Sanchez A, Liffick S, Holloway B, Limor J, Mccaustland K, Olsen-Rasmussen M, Fouchier R, Gunther S, Osterhaus A D M E, Drosten C, Pallansch M A, Anderson L J, and Bellini W J (2003) Characterization of a Novel Coronavirus Associated with Severe Acute Respiratory Syndrome. Science, 300(5624), pp. 1394-1399.
SEBASTIAN B and Hoffmann C (2003) SARS Reference. Flying Publisher.
SIRAKOULIS G C H, Karafyllidis I, and Thanailakis A (2000) A cellular automaton model for the effects of population movement and vaccination on epidemic propagation. Ecological Model, 133, pp. 209-223.
WANG X F and Chen G (2003) Complex Networks: Small-World, Scale-Free and beyond. IEEE Circuits and Systems Magazine, First Quarter, pp. 6-20.
WATTS D J and Strogatz S H (1998a) Collective dynamics of 'small-world' networks. Nature, 393(6684), pp. 440-442.
WATTS D J (1998b) Small Worlds: The Dynamics of Networks between Order and Randomness. Princeton University Press, Princeton, NJ.
WHO (WORLD HEALTH ORGANIZATION) (2003) Consensus document on the epidemiology of severe acute respiratory syndrome (SARS), http://www.who.int/csr/sars/en/WHOconsensus.pdf.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2004]