Abstract

Understanding the relationships between seasonal social networks and diversity in artifact styles, is crucial for examining the production and reproduction of knowledge among complex foraging societies such as those of the Pacific Northwest Coast. This agent-based model examines the impact of seasonal aggregation, dispersion, and learning opportunities on the richness and evenness of artifact styles under random social learning (unbiased transmission). The results of these simulations suggest that the relationship between learning opportunities and innovation rate has more impact on artifact style richness and evenness than seasonal social networks. Seasonal aggregation does appear to result in a higher amount of one-off rare variants, but this effect is not statistically significant. Overall, the restriction of learning opportunities appears more crucial in patterning cultural diversity among complex foragers than the potential impacts from individuals drawing on different seasonal social networks.

Keywords:

Cultural Transmission, Seasonal Mobility, Complex Foragers, Agent-Based Modeling, Social Networks, Cultural Drift

Introduction

1.1

Understanding the linkages between how knowledge was produced and shared in prehistory and the diversity we see in the archaeological record is key to archaeology as an endeavor. There have been considerable efforts to examine what signatures different forms of learning leave in the archaeological record (e.g., Bentley & Shennan 2003; Bentley et al. 2007; Collard et al. 2006; Eerkens et al. 2006; Eerkens & Lipo 2005, 2007; Henrich 2001; Kohler et al. 2004; Lipo et al. 1997; Mesoudi & O'Brien 2008; Neiman 1995; Premo & Kuhn 2010; Premo & Scholnick 2011; Rorabaugh 2014; Shennan & Wilkinson 2001; Steele et al. 2010). One aspect that has been underexplored in the cultural transmission literature, is the impact of different seasonal social networks on learning. There is a high degree of variability in the seasonal movements of hunter-gatherers (Binford 1980, 2001; Chatters 1987; Kelly 1983, 1992, 2007) which impacts the social networks they have and their context of learning.

1.2

Recently, models have been developed that examine the role of space between groups and their mobility on learning (Crema et al. 2014; papers in Kandler et al. 2012; Premo & Scholnick 2011; Perreault & Brantingham 2011). However, reducing these complex relationships to the networks individuals interacted with daily may be a more fruitful approach to examining the impacts of forager seasonal mobility on learning. This paper presents the results of a simulation that examines how different-sized seasonal social networks impact the diversity of artifact styles.

1.3

A second issue that is addressed is the impact of restricting the frequency of learning on stylistic diversity. In past archaeological discussions of stylistic diversity (Bentley et al. 2007; Lipo & Madsen 2001; Neiman 1995) a concept from population genetics, the effective size of a population (Wright 1938; Crow & Kimura 1970) has been a useful heuristic. Effective population size (\(N_{\rm e}\)) is defined as, "...the size of an idealized population that would would have the same amount of inbreeding or of random gene frequency drift as the population under consideration." (Kimura & Crow 1964, p.279–280). Idealized populations are assumed to have constant population sizes, non-overlapping generations, and panmictic mating -assumptions that are often violated in empirical populations.

1.4

As a result of modes of cultural transmission and drift, effective population sizes may be much smaller than the actual, census, population (Neiman 1990, p.206–207). In some scenarios, an empirical population of a given size may demonstrate greater diversity and lower rates of loss of diversity than a theoretically ideal population of a similar size. In these cases the effective population size would be greater than that of the empirical population size. Local-scale unbiased transmission (Premo & Scholnick 2011), and forms of frequency dependent biased transmission that favor rare variants can result in this. In some learning contexts, effective population size is roughly analogous to the potential number of teachers in a population (Neiman 1995; Shennan & Wilkinson 2001; Rorabaugh 2014). Restricting learning opportunities should drastically lower diversity as it lowers the number of teachers or effective population size (Neiman 1995; Wright 1938). In this model I examine the independent effects of social network size, in this case and number of learning opportunities to assess how these factors affect \(N_{\rm e}\). Although the model presented here is intended to examine the impacts of these seasonal groupings on learning in the Pacific Northwest Coast, focusing on the pre-contact Coast Salish, it is broadly applicable to any society where there are seasonal shifts in the size of social networks.

Cultural Transmission Theory

1.5

According to models of gene-culture coevolution, also referred to as dual inheritance or cultural transmission theory (Cavalli-Sforza & Feldman 1981; Boyd & Richerson 1985), cultural activities affect selective pressures and can drive genetic evolution in populations. Unlike genetic inheritance, culture may be acquired from individuals other than biological parents. A key contribution of the gene-culture coevolutionary approach is the attempt to characterize the different pathways by which culture is transmitted. Each pathway of cultural transmission has empirical repercussions for the spatial and temporal patterning of socially learned human behaviors (Boyd & Richerson 1985; Cavalli-Sforza & Feldman 1981; Hewlett et al. 2002).

1.6

Within a given population, individuals will share learned knowledge with others of the same generation or cross-generationally (Boyd & Richerson 1985). This transmission of knowledge can be done through several venues including learning from parents (vertical), peers (horizontal), unrelated older individuals (oblique), key individuals (biased), random individuals (unbiased), or the majority (frequency-dependent and conformist transmission). Individual learning and experimentation (guided variation) are also critical non-social aspects of cultural transmission models that directly relate to modeling the interaction between the mutual selective pressures of culture and environment.

1.7

Population structure is another key factor that patterns cultural variation. Recently the effect population structure has on learning has received more attention in the literature (e.g., Crema et al. 2014; Henrich 2004; Lipo & Madsen 2001; Lipo et al. 1997; Neiman 1995; Premo & Kuhn 2010; Powell et al. 2010; Shennan 2000). Population size and structure impact rates of innovation and the loss of cultural traits due to sampling error, or drift. The role that the spatial distance between populations has on learning has also been examined (Premo & Scholnick 2011).

1.8

The goal of this model is to examine one aspect of population structure, seasonal mobility, on the patterning of the archaeological record. In this model unbiased learning where individuals are allowed to learn randomly from any individual in the population (including their-selves) is used. This was done to focus on how seasonal networks and learning opportunities pattern stylistic diversity since processes such as selection and transmission bias reduce variation and may conflate assessing the impacts of the variables of interest. Selection and environmental constraints are beyond the scope of this paper.

1.9

The assumption of learning randomly from any individual, termed panmixia, is often violated in reality by spatial distance between populations or learners, or in this case, seasonal social networks. As opposed to spatially restricting learning (e.g., Premo & Scholnick 2011) or restricting population size, learning is restricted to a set number of individuals within social networks that have sizes drawn from ethnohistoric data of the seasonal movements of aggregation and dispersal seen among the semi-sedentary hunter-gatherer-fishers of the Pacific Northwest Coast, specifically the pre-contact Coast Salish. Following Neiman (1995), the diversity of non-adaptive or stylistic (sensu, Dunnell 1978; Lipo & Madsen 2001) cultural traits is examined.

Seasonal Mobility among the pre-contact Coast Salish

1.10

Although there is considerable variability among the hunter-gatherer-fishers of the Pacific Northwest Coast, there is a common strategy of seasonal mobility documented among ethnohistoric groups, particularly the Coast Salish of Puget Sound and the Strait of Georgia (Figure 1) (Ames & Maschner 1999; Hill-Tout 1978; Kelly 1983, p.280; Mitchell 1979; Moss 2012; Suttles 1990; Teit 1928). Based on ethnographic accounts, 2-4 residential moves was typical per year for many Northwest Coast groups (Kelly 1983, p.280). During fall and winter months large aggregated villages consisting of multiple households or kin groups were common (Barnett 1955; Hill-Tout 1978; Mitchell 1979; Suttles 1951, 1960, 1990; Teit 1928). These aggregated groups would mass-harvest seasonal resources including roots, terrestrial or marine mammals, shellfish and anadromous fish for winter storage. During spring and summer months these villages dispersed into small household groups to harvest seasonal resources. For the purposes of this model, aggregating for resources and winter villages are combined, due to the brief periodicity of large resource-gathering aggregations of pre-contact Coast Salish communities.

1.11

These seasonally mobile groups would spend some months in small household groups and other parts of the year in larger groups at resource locations, processing camps, or winter villages. As in many parts of the coast resources were owned by extended kin groups (Suttles 1960), the social networks people interacted with could be fundamentally different through the year. Many of the same faces might be seen in a winter village but others might be encountered when gathering certain resources. As such, seasonally based social networks may fundamentally structure learning and the variability seen in the archaeological record.

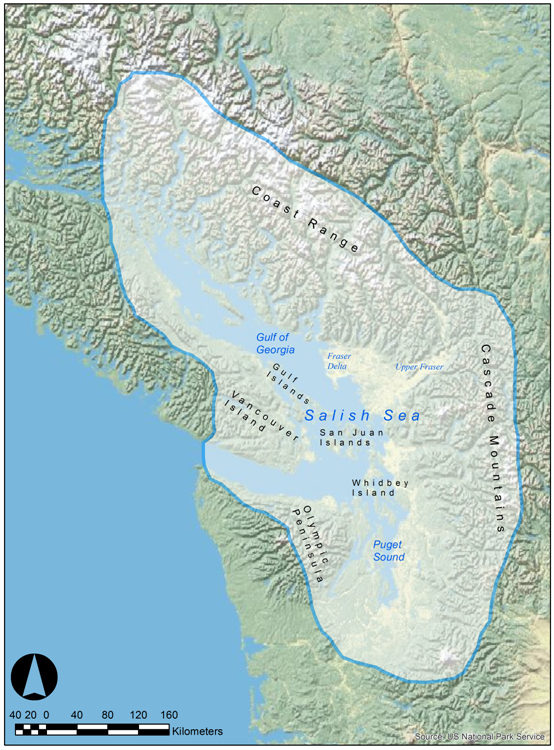
Figure 1. The Salish Sea

1.12

Among the pre-contact Coast Salish, bilateral descent (Suttles 1951, 1960) and use of boats for long-distance travel (Ames 2002) meant that individuals would have highly variable and spatially extensive social networks. I suggest that an appropriate approach for examining the impacts of seasonal movements on learning in the region is an aspatial model that emphasizes differentially sized seasonal social networks while abstracting the considerable spatial variation that an individual's social ties likely had.

Modeling Seasonal Social Networks and Restricted Learning Opportunities

Model Behavior

2.1

This model expands on Neiman's (1995) approach which borrows from neutral theory (Kimura & Crow 1964; Crow & Kimura 1970; Neiman 1990; Wright 1938) which considers the impact of effective population size (number of teachers) and innovation rates on stylistic diversity. Neiman's (1995) model, based on the well-mixed Wright-Fisher infinite alleles (WF-IA) model with neutral variants, has been successfully applied towards examining mechanisms of cultural transmission in ceramic technologies (e.g., Kohler et al. 2004; Shennan & Wilkinson 2001; Steele et al. 2010). I expand on it by restricting learning to differentially sized seasonal social networks.

2.2

In this model, programmed in Netlogo 5.02, each agent represents an individual. Global population size is fixed to 1250 individuals in all runs to hold effects from population size constant. This population size was chosen as an estimate derived from archaeological household population estimates used on the Northwest Coast (e.g., Ames 1996, p.136; Gahr 2006, p.68). For the past 2,000 years in the Salish Sea, population estimates based on Cook and Heizer's (1968) house floor area formula provide a range of 250-500 individuals per house structure. Based on a survey of reported archaeological houses from southern British Columbia and northwest Washington in an unpublished dissertation by Rorabaugh (2015, p.22) over the past 2,500 years Coast Salish villages range from 1-11 substantial house structures but the mean number of house structures in his sample of 22 dated sites is 2.77. The population number provided is based on the population equivalent of 5 structures routinely interacting, which approximates the population of a village and additional affinal ties to members of other houses.

2.3

Interactions between agents are divided into four seasons (each season being a time step), which is to approximate periods of population dispersal and aggregation on the Northwest Coast (Ray 1933; Schalk 1978). The number of seasons that individuals are dispersed or aggregated, and number of seasons individuals can learn are both parameters assessed. These variables are independent as agents can learn during dispersed and aggregated seasons.

2.4

At the outset of the model, each agent is given its own social networks. Each agent has two social networks, one with 200 links for aggregated seasons and another with 10 links for dispersed seasons. Social network sizes are based on archaeological household size estimates for the pre-contact Coast Salish from Gahr (2006). My estimates are based on households dating to the past 2,000 years in the Salish Sea after the emergence of the winter village settlement pattern in the region (e.g., Ames & Maschner 1999; Matson & Coupland 1995). Examining the impact of seasonal mobility on learning prior to this time period is beyond the scope of this model. Presumably the social networks before 2000 BP would be smaller and more spatially bound. The links for each social network are randomly generated, and each agent could have links to itself or multiple links to another agent. Group membership is set for the duration of the model. These social networks are also persistent as agents do not die or reproduce. As I rely on social networks to examine the impacts of seasonality on learning, this model is aspatial.

2.5

The number of dispersed seasons is also a variable (0–4). Dispersed seasons use the dispersed season social network. This enables an examination of learning in fully aggregated groups (0 dispersed seasons) and fully dispersed groups (4 dispersed seasons) in addition to the gamut of seasonal mobility strategies seen on the Northwest Coast.

2.6

At initialization, each agent is assigned a unique, non-adaptive, non-metric cultural variant \(k\) (i.e., \(k=N\)). With each time step, each agent displays a single but not necessarily unique cultural trait. Agents can only copy a cultural trait from other agents in the social network for that season. During an aggregated season an agent can only learn from agents in their aggregated social network while during a dispersed season they can only learn from agents who are in their dispersed social network. Each agent has a probability of transmitting a cultural trait in its active social network per season. This probability is determined by the number of agent learning seasons (1–4). This means that in the model an agent has between a 0.25–1.0 probability of learning each season depending on the value of that parameter (1 learning season yields the 0.25 probability while 4 learning seasons results in a 1.0 probability). After all seasonal learning events are finished, each agent has a 0.001 chance (following Premo & Scholnick 2011) of innovating a novel cultural trait. Each simulation is run for 10,000 time steps.

Assessing Impact of Seasonal Social Networks and Restricted Learning Opportunities

2.7

During each time step richness (number of unique classes) and evenness are reported. Evenness is reported as \(T_{\rm f}\) (Equation 1, Neiman 1995) and as Index of Qualitative Variation (IQV, Equation 2, Madsen 2012; Wilcox 1973) which standardizes \(T_{\rm f}\) between 0–1. An IQV of "0" indicates that all cases belong to a single category, while "1" is when all cases are evenly distributed across all categories. IQV is a useful measure for cultural transmission studies as it enables a comparison of assemblages with different sample sizes and durations of occupation.

\(T_{\rm f}\) Statistic: $$T_{\rm f} = \frac{1}{\sum_{i=1}^k P_i^2} -1$$

(1)

Let \(k\)=total number of variants in the population (richness)
Let \(P_i\)=proportion of \(k\) made up of the \(i\)th variant

Index of Qualitative Variation: $$\mathrm{IQV} = \left( \frac{K}{K-1} \right) \left(1- \sum{i=1}^k P_i^2 \right) $$

(2)

Let \(k\)=total number of variants in the population (richness)
Let \(P_i\)=proportion of \(k\) made up of the \(i\)th variant

2.8

The results of 30 replicates for each possible variant of the examined parameters are reported. Sources of stochasticity include differentially formed social network ties, learning opportunities, and innovation. The first examined parameter is number of dispersed seasons (0–4) where "0" means that individuals engage in their aggregated social networks year round, while "4" means individuals only engage in their dispersed social networks throughout the year. The second parameter is number of learning seasons (1–4) which weights the probability of an agent learning during a season. A value of "1" means that individuals have a 0.25 probability of learning during each season while a value of "4" means that each season agents have a 1.0 probability for learning. This parameter is included to assess how the magnitude of restricting learning opportunities impacts cultural variation compared to social network seasonality and is independent of whether a network is dispersed or aggregated.

2.9

The justification for restricting learning to some seasons is that it provides a rough approximation for certain technical knowledge only being available during certain times. For example, specific types of fishing gear being taught and produced during the timing of specific runs or spawns. Although it is feasible that such knowledge may have been passed on during off-seasons, it is more likely that such cultural information was passed down around the specific times that those seasonal resource procurement technologies would have been utilized.

Results

Comparing Seasonal Social Networks

3.1

The statistical significance of the differences in the richness (Figure 2) and evenness of cultural traits as measured by \(T_{\rm f}\) (Figure 3) and IQV (Figure 4) by number of dispersed and aggregated seasons in the set of simulation runs (\(N=30\)) was assessed using non-parametric Kruskal-Wallis tests (Table 1), broken down by restricted learning opportunities to avoid conflating parameters. The variation in richness and evenness caused by the number of dispersed and aggregated seasons was not found to be statistically significant at a 0.05 level. This suggests that the impacts of seasonal mobility on unbiased learning are weak.

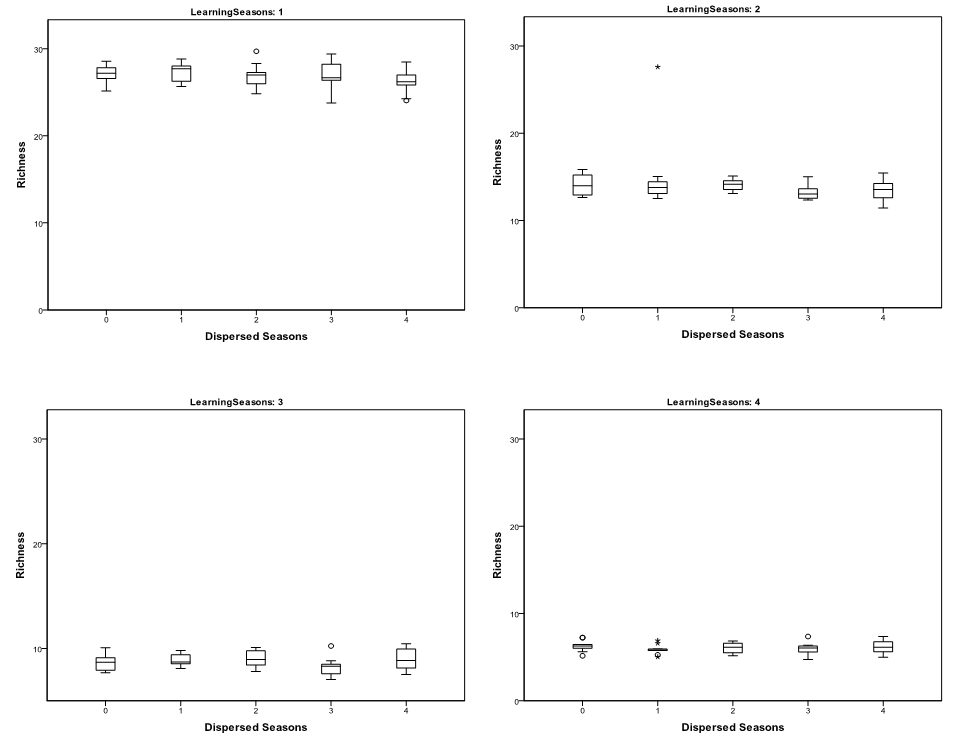
Figure 2. Whiskerplots of Mean Richness of 30 runs by Number of Dispersed Seasons and Seasonal Learning Opportunities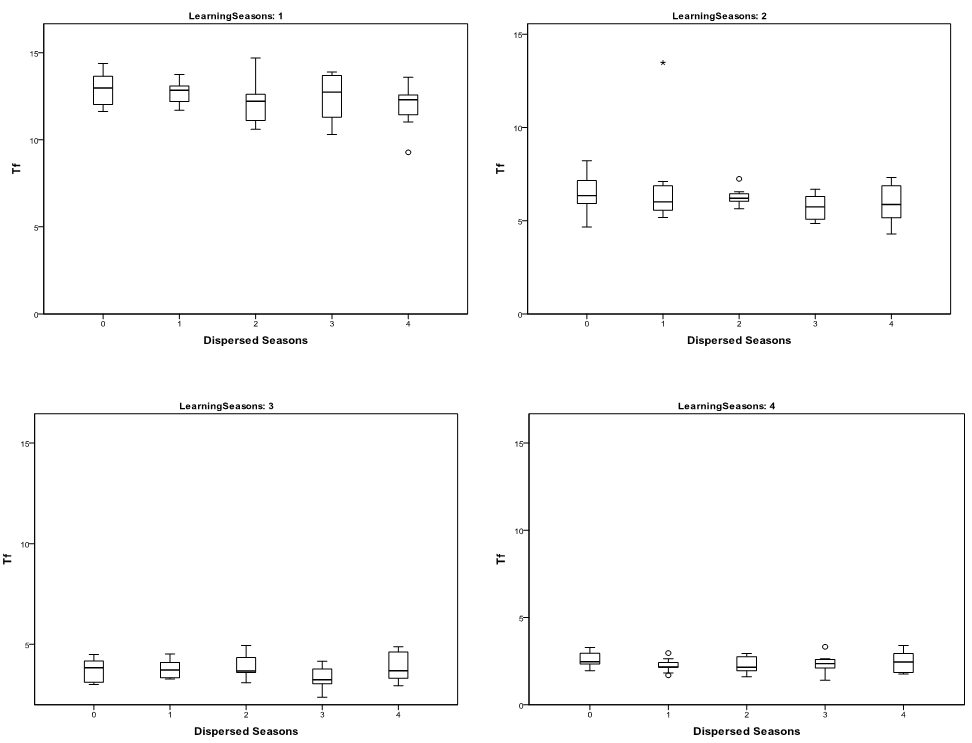

Figure 3. Whiskerplots of Mean \(T_{\rm f}\) of 30 runs by Number of Dispersed Seasons and Seasonal Learning Opportunities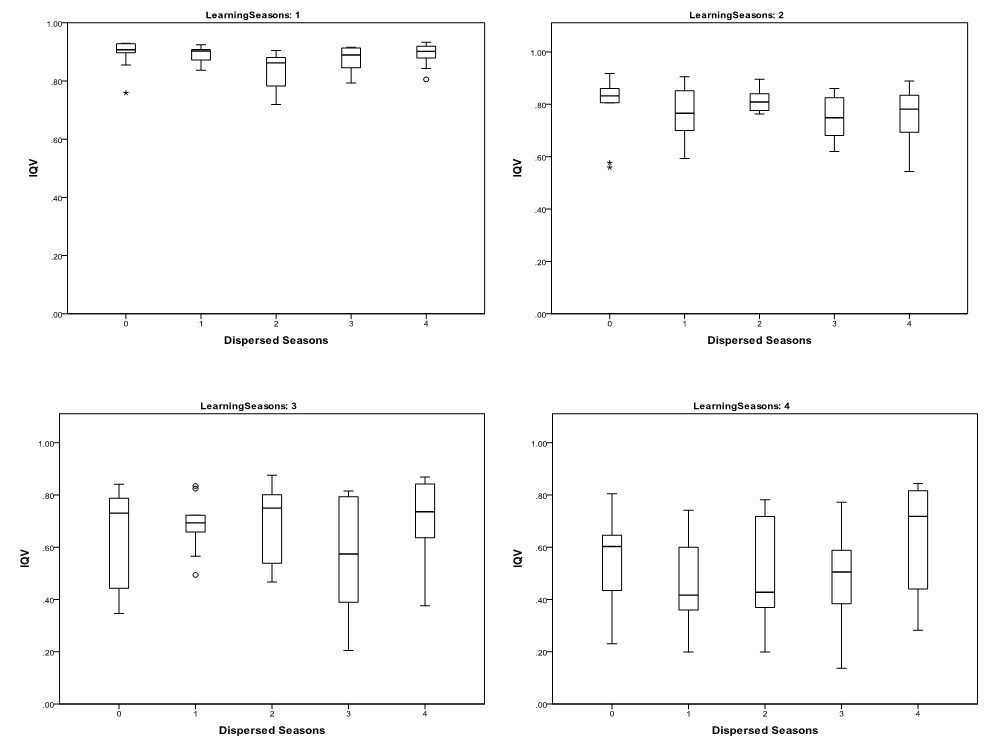

Figure 4. Whiskerplots of Mean IQV of 30 runs by Number of Dispersed Seasons and Seasonal Learning Opportunities

Table 1: Richness and Evenness Measures by # of Dispersed Seasons Kruskal-Wallis Tests
Test	# of Learning Seasons	Sig.	H0(HA) \(p=0.05\)
Richness	1	0.54	H0
\(T_{\rm f}\)	1	0.30	H0
IQV	1	0.08	H0
Richness	2	0.15	H0
\(T_{\rm f}\)	2	0.36	H0
IQV	2	0.47	H0
Richness	3	0.25	H0
\(T_{\rm f}\)	3	0.32	H0
IQV	3	0.55	H0
Richness	4	0.64	H0
\(T_{\rm f}\)	4	0.40	H0
IQV	4	0.26	H0

Table 2: Richness and Evenness Measures by # of Learning Seasons Kruskal-Wallis Tests
Test	# of Dispersed Seasons	Sig.	H0(HA) \(p=0.05\)
Richness	0	0.00	HA
\(T_{\rm f}\)	0	0.00	HA
IQV	0	0.00	HA
Richness	1	0.00	HA
\(T_{\rm f}\)	1	0.00	HA
IQV	1	0.00	HA
Richness	2	0.00	HA
\(T_{\rm f}\)	2	0.00	HA
IQV	2	0.00	HA
Richness	3	0.00	HA
\(T_{\rm f}\)	3	0.00	HA
IQV	3	0.00	HA
Richness	4	0.00	HA
\(T_{\rm f}\)	4	0.00	HA
IQV	4	0.00	HA

Restricting Learning Opportunities

3.2

In contrast, the number of learning opportunities appear to drastically impact trait richness (Figure 2), \(T_{\rm f}\) (Figure 3), and IQV (Figure 4). Increasing the number of learning seasons lowers trait richness and evenness. The significance of this trend was assessed using Kruskal-Wallis tests broken down by number of dispersed seasons (Table 2). The decrease in trait richness and evenness as learning opportunities increased was significant at a 0.05 level. Also of note is that the dispersion in IQV increases dramatically between runs as the number of learning opportunities increases. This is likely the result of variation in the homogenization of cultural traits from learning episodes, impacting richness between different runs.

Discussion

4.1

The model suggests that the impact of differently sized seasonal social networks on the richness and evenness of neutral cultural traits is not significant when dealing with household group sizes similar to those inferred from archaeological and ethnographic data on the Northwest Coast. When thinking of these social networks in terms of effective population size (\(N_{\rm e}\)) which in the case of cultural transmission can be equivalent to the number of teachers in a population (Neiman 1995; Wright 1938), having differently sized seasonal social networks results in an effective population size that is the time-averaged harmonic mean of the largest and smallest seasonal social networks. In the case of the archaeologically and ethnographically informed group sizes used, the differences in trait richness and evenness between the largest seasonal social network (\(N=200\)) and smallest (\(N=20\)) appear to be overwhelmed by other stochastic processes affecting cultural transmission. However, more extreme differences in seasonal social network sizes might have impacts on cultural trait diversity. An examination of these effects is beyond the scope of this paper, which focused on grounding social network sizes on data from the Salish Sea.

4.2

Restricting learning opportunities appears to have more impact on the richness and evenness of cultural traits. A high number of learning opportunities increases transmission episodes and can homogenize cultural traits. My findings suggest that the interactions between learning opportunities and innovation rate likely impact trait diversity more than differentially sized seasonal social networks. More learning opportunities, technologies that would have been used year-round, such as terrestrial mammal hunting tools (darts, spears, arrows), combined with smaller sized social networks led to higher trait richness and evenness. The process driving this appears to be similar to the isolation-by-distance mechanism reported by Premo and Scholnick (2011), but in this case it is isolation by small self-contained social networks. However, in this model the effect is not statistically significant and is overwhelmed by factors such as the number of learning opportunities and innovation rate. The implications of these findings are that the impact of seasonal mobility on trait richness and evenness, at least for social networks with sizes similar to that of the pre-contact Coast Salish, may be easily overwhelmed by other social learning factors such as transmission bias, which was not examined here, since even a small degree of bias can reduce cultural variation (Mesoudi & Lycett 2009), or changes in innovation rate.

4.3

While the model suggests that engagement in different-sized seasonal social networks does not significantly impact the richness and evenness of learned cultural traits, this does not mean that seasonal social networks, and seasonal mobility, have no impact on learning. Alternative approaches such as adding agent mobility to Premo and Scholnick's (2011) spatial restriction model may yield different insights on the interactions between seasonal mobility and learning. Similarly, separately modeling aggregation events such as seasonal resource gathering could reveal whether smaller seasonal movements may have long-term cumulative impacts on learning.

Conclusions

5.1

Although archaeologists have long recognized the importance of seasonal mobility in patterning the archaeological record (e.g., Binford 1980; Kelly 1983, 1992, 2007), particularly for sedentary foragers, the impact of seasonal movements on cultural transmission has had limited treatment. This agent-based model examined the impact of seasonal mobility on the richness and evenness of selectively neutral, stylistic, cultural traits through abstracting mobility as the different sized social networks people engaged with during a year. This aspatial model using social network size estimates from ethnographic data on the Northwest Coast suggests that different sized seasonal social networks have less impact on cultural diversity than does restricting learning opportunities.

5.2

As archaeologists increasingly utilize models that originate from evolutionary biology, we need to examine their assumptions and ways that social learning differs from biological evolution. Agent-based models such as the one presented here, enable an examination of factors unique to social learning and how they pattern the diversity we see in the archaeological record. A modeling approach can also discover emergent dynamics of social phenomena that may not be envisioned in standard anthropological narratives.

Acknowledgements

I thank Dr. Kristin N. Safi, Dr. Patrick Dolan, and Dr. Luke Premo for their comments and feedback on early versions of this paper, this study would not have been possible without their support. I also thank Dr. Timothy A. Kohler and the anonymous reviewers for their insightful comments and feedback.

Appendix

A version of the Netlogo model with full instructions is available through the OpenABMArchive through the following link: https://www.openabm.org/model/4615/version/1

References

AMES, K. (1996). Life in the Big House: Household Labor and Dwelling Size on the Northwest Coast. In G. Coupland & Banning, E. B. (Eds.) People Who Lived in Big Houses: Archaeological Perspectives on Large Domestic Structures. (pp. 131–150) Monographs in World Prehistory Vol. 27. Madison: Prehistory press.

AMES, K. (2002). Going by Boat: The Forager-Collector Continuum at Sea. In B., Fitzhugh & Habu, J. (Eds.) Beyond Foraging and Collecting: Evolutionary Change in Hunter-Gatherer Settlement Systems. (pp. 17–50) New York: Kluwer/Plenum Press.

AMES, K. & Maschner, H. D. G. (1999). Peoples of the Northwest Coast, Their Archaeology and Prehistory. London: Thames and Hudson.

BARNETT, H. G., (1955). The Coast Salish of British Columbia. Studies in Anthropology 4. Eugene: University of Oregon Press.

BENTLEY, A., Lipo, C. P., Herzog, H.A., and Hahn, M. W. (2007). Regular rates of popular culture change reflect random copying. Evolution and Human Behavior, 28, 151–158. [doi:10.1016/j.evolhumbehav.2006.10.002]

BENTLEY, R. A. & Shennan, S. (2003). Cultural transmission and stochastic network growth. American Antiquity, 68, 459–485. [doi:10.2307/3557104]

BINFORD, L. R., (1980). Willow smoke and dogs' tails: hunter-gatherer settlement systems and archaeological site formation. American Antiquity, 45, 4–20. [doi:10.2307/279653]

BINFORD, L. R., (2001). Constructing Frames of Reference: An Analytical Method for Archaeological Theory Building Using Ethnographic and Environmental Data Sets. Berkeley: University of California Press.

BOYD, R., & Richerson, P., (1985). Culture and the Evolutionary Process. London: University of Chicago Press.

CAVALLI-SFORZA, L. & Feldman, M. W., (1981). Cultural Transmission and Evolution: A Quantitative Approach. Princeton: Princeton University Press.

CHATTERS, J. C., (1987). Hunter-gatherer adaptations and assemblage structure. Journal of Anthropological Archaeology, 6, 336–375. [doi:10.1016/0278-4165(87)90005-5]

COLLARD, M., Shennan, S., and Tehrani, J. (2006). Branching, blending, and the evolution of cultural similarities and differences among human populations. Evolution and Human Behavior, 27, 169–184. [doi:10.1016/j.evolhumbehav.2005.07.003]

COOK, S. F. and Heizer, R. F. (1968). Relationships among houses, settlement areas, and population in Aboriginal California. In K. C. Chang (Ed.), Settlement Archaeology (pp. 79–116) Paolo Alto: National Press Books.

CREMA, E. R., Kerig, T., and Shennan, S. (2014). Culture, Space, and Metapopulation: a simulation-based study for evaluating signals of blending and branching. Journal of Archaeological Science, 43, 289-298. [doi:10.1016/j.jas.2014.01.002]

CROW, J. & Kimura, M. (1970). An Introduction to Population Genetics Theory. New York: Harper & Row.

DUNNELL, R. C. (1978). Style and function: A fundamental dichotomy. American Antiquity, 43, 192–202. [doi:10.2307/279244]

EERKENS, J., & Lipo, C., (2005). Cultural transmission, copying errors, and the generation of variation in material culture and the archaeological record. Journal of Anthropological Archaeology, 24, 316–334. [doi:10.1016/j.jaa.2005.08.001]

EERKENS, J. & Lipo, C. P. (2007). Cultural transmission theory and the archaeological record: providing context to understand variation and temporal changes in material culture. Journal of Archaeological Research, 15, 239–274. [doi:10.1007/s10814-007-9013-z]

EERKENS, J. W., Bettinger, R. L., McElreath, R. (2006). Cultural Transmission, Phylogenetics, and the Archaeological Record. In C. P. Lipo, O'Brien, M. J., Collard, M. and Shennan, S. J. (Eds.) Mapping Our Ancestors Phylogenetic Approaches in Anthropology and Prehistory (pp. 169–183.) New York: Aldine.

GAHR, T. D. (2006). Architects to Ancestors: The Lifecycle of a Plankhouse. In E. Sobel, Gahr, T. D., and Ames, K. (Eds.) Household Archaeology on the Northwest Coast. International Monographs in Prehistory Archaeological Series, 16, 57–79.

HENRICH, J. (2001). Cultural transmission and the diffusion of innovations: adoption dynamics indicate that biased cultural transmission is the predominate force in behavioral chance. American Anthropologist, 103, 992–1013. [doi:10.1525/aa.2001.103.4.992]

HENRICH, J. (2004). Demography and cultural evolution: how adaptive cultural processes can produce maladaptive losses: the tasmanian case. American Antiquity, 69, 197–214. [doi:10.2307/4128416]

HEWLETT, B. S., De Silvestri, A., and Guglielmino, C. R. (2002). Semes and Genes in Africa. Current Anthropology, 43, 313–321. [doi:10.1086/339379]

HILL-TOUT, C. (1978). The Salish People Volume III: The Mainland Halkomelem. Vancouver, British Columbia: Talon Books.

KANDLER, A., Perreault, C. and Steele, J. (2012). Editorial - Cultural Evolution In Spatially Structured Populations: A Review Of Alternative Modeling Frameworks. Advances in Complex Systems, 15, 01n02. [doi:10.1142/S0219525912030014]

KELLY, R. L., (1983). Hunter-gatherer mobility strategies. Journal of Anthropological Research, 39, 277–306.

KELLY, R. L., (1992). Mobility/sedentism: concepts, archaeological measures, and effects. Annual Review of Anthropology, 21, 43–66. [doi:10.1146/annurev.an.21.100192.000355]

KELLY, R. L., (2007). The Foraging Spectrum: Diversity in Hunter-Gatherer Lifeways. Clinton Corners, New York: Percheron Press.

KIMURA, M. & Crow, J. (1964). The number of alleles that can be maintained in a finite population. Genetics, 49, 725–738.

KOHLER, T. A., VanBuskirk, S., Ruscavage-Barz, S. (2004). Vessels and villages: evidence for conformist transmission in early village aggregations on the Pajarito Plateau, New Mexico. Journal of Anthropological Archaeology, 23, 100–118. [doi:10.1016/j.jaa.2003.12.003]

LIPO, C. P., Madsen, M. E., Dunnell, R. C., Hunt, T. (1997). Population structure, cultural transmission, and frequency seriation. Journal of Anthropological Archaeology, 16, 301–333. [doi:10.1006/jaar.1997.0314]

LIPO, C. P., Madsen, M. E., (2001). Neutrality, "style," and drift: building models for studying cultural transmission in the archaeological record. In T. D. Hurt & Rakita, G. F. M (Eds.), Style and Function: Conceptual Issues in Evolutionary Archaeology. (pp. 91–118.) Westport, Connecticut: Bergin and Carvey.

MADSEN, M. (2012). Neutral Cultural Transmission in Time Averaged Archaeological Assemblages Paper Presented at the Society for American Archaeology Meetings. Memphis, TN.

MATSON, R. G. & Coupland, G. (1995). The Prehistory of the Northwest Coast. San Diego: Academic Press.

MESOUDI, A. & O'Brien, M. (2008). The cultural transmission of Great Basin Projectile-Point Technology II: an agent-based computer simulation. American Antiquity, 73, 627–644.

MESOUDI, A. & Lycett, S. J. (2009). Random Copying, Frequency-dependent copying, and culture change. Evolution and Human Behavior, 30, 41–48. [doi:10.1016/j.evolhumbehav.2008.07.005]

MITCHELL, D. (1979). Seasonal settlements, village aggregations, and political autonomy on the central Northwest Coast. In E. Tooker, Fried, M. Eds., The Development of Political Organization in Native North America (pp. 97–107). Proceedings of the American Ethnological Society. American Ethnological Society, Philadelphia.

MOSS, M. L. (2012). Northwest Coast: Archaeology as Deep History. Washington, D. C.: The SAA Press.

NEIMAN, F. D. (1990). An Evolutionary Approach to Archaeological Inference: Aspects of Architectural Variation in the 17th Century Chesapeake. Unpublished Ph.D. Dissertation. Department of Anthropology Yale University.

NEIMAN, F. D. (1995). Stylistic variation in evolutionary perspective: inferences from decorative diversity and interassemblage distance in Illinois Woodland ceramic assemblages. American Antiquity, 60, 7–36. [doi:10.2307/282074]

PERREAULT, C. & Brantingham, P. J. (2011). Mobility-driven cultural transmission along the forager collector continuum. Journal of Anthropological Archaeology, 30, 62–68. [doi:10.1016/j.jaa.2010.10.003]

POWELL, A., Shennan, S. J., and Thomas, M. G. (2010). Demography and Variation in the Accumulation of Culturally Inherited Skills. In M. J. O'Brien & Shennan, S. J. (Eds), Innovation in Cultural Systems: Contributions from Evolutionary Anthropology. (pp. 137–161.) Cambridge: The MIT Press.

PREMO, L., & Kuhn S. L. (2010). Modeling Effects of Local Extinctions on Culture Change and Diversity in the Paleolithic PlosOne, 5(12): e15582.

PREMO, L., & Scholnick, J., (2011). The spatial scale of social learning affects cultural diversity. American Antiquity, 76, 163–190. [doi:10.7183/0002-7316.76.1.163]

RAY, V. F., (1933). The Sanpoil and Nespelem: Salishan peoples of Northeastern Washington. Publications in Anthropology No. 5, University of Washington, Seattle.

RORABAUGH, A. N. (2014). Impacts of Drift and Population Bottlenecks on the Cultural Transmission of a Neutral Continuous Trait: An Agent Based Model. Journal of Archaeological Science, 49, 255–264. [doi:10.1016/j.jas.2014.05.016]

RORABAUGH, A. N. (2015) Investigating Restricted Knowledge in Lithic Craft Traditions Among the Pre-Contact Coast Salish. Unpublished PhD Dissertation. Department of Anthropology. Washington State University.

SCHALK, R., (1978). Foragers of the Northwest Coast of North America: The ecology of aboriginal land use systems. Unpublished PhD Dissertation University of New Mexico.

SHENNAN, S. J. (2000). Population, Culture History, and the Dynamics of Culture Change. Current Anthropology, 41, 811–835. [doi:10.1086/317403]

SHENNAN, S. J. & Wilkinson, J. R., (2001). Ceramic style change and neutral evolution: a case study from Neolithic Europe. American Antiquity, 66, 577–593. [doi:10.2307/2694174]

STEELE, J., Glatz, C., & Kandler, A. (2010). Ceramic diversity, random copying, and tests for selectivity in ceramic production. Journal of Archaeological Science, 37, 1348–1358. [doi:10.1016/j.jas.2009.12.039]

SUTTLES, W. (1951). Economic Life of the Coast Salish of Haro and Rosario Straits. Series Coast Salish and Western Washington Indians. New York: Garland Publishers Inc.

SUTTLES, W. (1960). Affinal Ties, Subsistence, and Prestige Among the Coast Salish. American Anthropologist, 62, 296–305. [doi:10.1525/aa.1960.62.2.02a00080]

SUTTLES, W., (1990). Central Coast Salish. In Suttles W. (Ed.), Northwest Coast. Sturtevant, W.C. (General Ed.), Handbook of North American Indians, Vol. 7. (pp. 453–475) Washington D.C.: Smithsonian Institute.

TEIT, J. A., (1928). The Middle Columbia Salish. University of Washington Publications in Anthropology Vol. 2, No. 4. University of Washington Press, Seattle.

WILCOX, A, (1973). Indices of qualitative variation and political measurement. The Western Political Quarterly, 26, 325–343. [doi:10.2307/446831]

WRIGHT, S. (1938). Size of population and breeding structure in relation to evolution. Science, 87, 430–431.