 Abstract
Abstract
- Modelling command and control (C2) is regarded as a difficult task because of the complexity of the decision-making required by individuals in combat. Despite the difficulties, C2 modelling is frequently used for high echelon units, i.e. battalion, division and above. This paper extends these models to the lowest army unit: the infantry company. Previous studies have modelled this particular unit as either an abstract entity or a detailed behaviour model without C2. Our model includes C2 in the models to determine the most critical tasks at company level C2 because this information could direct company commanders to engage in more important operational tasks. Our analysis is based on agent-based modelling and the virtual experiment framework. The overall model includes operational details as discrete event models and soldier behaviour as behavioural models. Our analytical results enable us to identify the key C2 tasks of company commanders and the changes in the importance of various operational environments.
- Keywords:
- Command and Control (C2), Combat Effectiveness, Infantry Company Engagement, Agent-Based Simulation
 Introduction
Introduction
- 1.1
- Tactical decision-making is a complex process that demands consideration of friendly and opposing forces, the situational context and operational environment, and the objectives of military actions within a limited time frame. Command and control (C2) refers to the process and structure of facilitating such tactical decision-making. C2 enables commanders to assess the situation, develop potential courses of action (COA), analyse the COA, and select the appropriate COA based on detailed information, such as the status of enemy and friendly forces, environmental factors including the terrain, weather, and obstacles, the time available, and other considerations, such as civil affairs (U.S. ARMY 2008a). In addition, C2 oversees the structure of the military organisations that support the decision-making processes by assigning tasks to the units and the personnel in the organisations.
- 1.2
- Modern military C2 involves complex hierarchical organisations and the detailed assignment of tasks that have been optimised to control large-scale military forces. Hence, in modern military organisations, the hierarchy of C2 extends from the commander-in-chief to the frontline soldiers. However, this hierarchical and sometimes bureaucratic form of C2 may not be best practice in tactical situations that require rapid decision-making and extensive information sharing. For example, in planning an assault on a hill, multiple units, equipment, and information need to be dynamically assembled, engaged, and operated. In the progress of the assault, a delay in decision-making at a single branch unit (e.g., a delayed request for close-air support) could cause a delayed response from a critical resource (e.g., delayed support fire on the opponent forces) in the assault, which could result in the failure of the operation. Accordingly, we need to consider how to make C2 both procedurally and organisationally robust. When we narrow the scope to the perspective of the commander of an infantry company, C2 can be seen to be a very dynamic process involving limited personnel. In this case, although the commander may not have many officers and sub-commanders, the operational tempo and decision-making processes at the company level are greatly accelerated compared to the C2 of higher ranking units. Therefore, from this perspective, the C2 process is key to optimising the practice of C2.
- 1.3
- The essential C2 functions include the decision-making processes of commanders such as establishing the command intent, allocating missions involving subordinates, and establishing rules, etc (Alberts & Hayes 2006). Thus, numerous methods from various fields have been applied to improve the C2 decision-making process. For example, a decision theoretic method, a heuristic search algorithm based on Markov decision processes, and natural decision-making based on situational awareness have been used to plan military operations(Aberdeen, Thiebaux, & Zhang 2004; Endsley 1997; Klein 2008; Pleban & Salter 2001; Thuve 2001). The speed of commanders' decision-making is also important because the rapid decision-making of commanders ensures subordinates have sufficient preparation time. Thus, commanders and their staff are trained to accomplish troop movement procedures within one third of the total operational preparation time(U.S. ARMY 1997, 2008a, 2011). The C2 process involves 1) the decision-making of commanders and 2) communication down the chain of command. Krausman et al. (2006) suggest a method for alerting and sharing information with subordinates and examine its effects (Krausman et al. 2006).
- 1.4
- In this paper, we use simulation modelling and virtual experiments to examine the importance of tasks in C2 at the infantry company level. The scope of C2 includes the decision-making processes of platoon leaders and a company commander. Their detailed tasks in the C2 process are evaluated by the effects of time-delay on the loss-exchange ratio. To better situate the C2, we also take other combat factors, such as individual soldier's marksmanship and ability to breach obstacles, which reflects their training level, into account. This assumes that C2 is more important for combatants with little training. From the analyses, we pinpoint the key tasks of C2 for low echelon units and provide insights for improving the C2 practice of the units.
 Experimental
Scenario
Experimental
Scenario
- 2.1
- We use an offensive operation by an infantry company
against an opposing unit occupying a hill. For better understanding of
our experimental scenario, we provide the terminology for the operation
as follows.
Terminologies
- An infantry company is a military unit consisting of 80 to 200 soldiers that is usually commanded by a captain or a major. An infantry company is mainly armed with rifles and machine guns, but it can be equipped with 60-mm or 81-mm mortars. An infantry company is composed of three to six infantry platoons (U.S. ARMY 2006a).
- An infantry platoon is a military unit consisting of 15 to 40 soldiers that is usually commanded by a lieutenant. An infantry platoon is equipped with rifles and machine guns. An infantry platoon is composed of two to three squads or sections (U.S. ARMY 2006a).
- An infantry squad is the lowest military unit; it includes seven to twelve soldiers and is usually commanded by a non-commissioned officer. An infantry squad is armed with rifles and a machine gun.
- Combat effectiveness is a quantitative measure of combat power for military units (Hayward 1968). Amongst the various methods used to represent combat effectiveness, we use the loss exchange ratio (LER).
- The loss exchange ratio (LER) is a measure of combat effectiveness that is calculated as 'the number of red soldiers killed' divided by 'the number of blue soldiers killed'.
- An assault is a mission in which an infantry platoon performs a decisive attack during an offensive operation of an infantry company. The assault platoon first enters the position of the opposing force through a passage secured by the breach platoon under cover of the support platoon and mortars (ROK ARMY 2008).
- A breach is a mission in which an infantry platoon secures a passage on the obstacle boundary of the opposing force through which the assault platoon can pass (ROK ARMY 2008).
- Support is a mission in which an infantry platoon occupies a position opposite the assault and breach platoons and suppresses the opposing force by fire to deceive the main attack (ROK ARMY 2008).
- An assault readiness position is an area in which the assault platoon stands by to prepare its attack and wait until a passage is secured (ROK ARMY 2008).
- A fire support position is an area in which the support platoon supports the assault and breach platoons by fire (ROK ARMY 2008).
- A vulnerable point is a specific location at which the breach platoon creates a passage. The infantry company commander designates the location on the obstacle boundary of the opposing force (ROK ARMY 2008).
- A line of departure (LD) is a starting line for an attack on the opposing force's position.
- A release point is a specific location at which platoons are ramified. For example, the breach, assault and support platoons move together from the line of departure and are then ramified at a release point to the vulnerable point for the breach platoon, the assault readiness position for the assault platoon and the fire support position for the support platoon.
- A Bangalore torpedo is an explosive charged within one or more tubes that is used by the breach platoon to clear paths through obstacles (Headquarters 1992).
- METT-TC stands for Mission, Enemy, Terrain, Troops available, Time available and Civil affairs. METT-TC represents the elements that should be considered in military decision-making.
- A theatre-level operation is an operation that takes place in a theatre. A theatre includes air, space, land and sea area. The chairman of the Joint Chiefs of Staff or a full general may command the armed forces during a theatre-level operation.
- An army battalion is a military unit consisting of 300 to 800 soldiers that is usually commanded by a lieutenant colonel. A battalion is divided into many companies (U.S. ARMY 2006b).
- An army brigade is tactical military formation that is usually composed of three to six battalions and is typically commanded by a colonel or brigadier general (U.S. ARMY 1995).
- The DTCO (decision-making time for company commander) is the delay time for the company commander to make decisions.
- The DTPL (decision-making time for platoon leader) is the delay time for the platoon leader to make decisions.
- The FRT (fire request time) is the delay time for the company commander to order fire support to the mortar.
- The OTCO (order time for company commander) is the delay time for the company commander to give orders to the platoon leaders.
- The ORTPL (order/report time for platoon leader) is the delay time for the platoon leaders to give orders to combat entities or report to the company commander.
- The PH (probability of hit) is the probability of hit for individual soldiers, which indicates the soldier's marksmanship.
- The BT (breaching time) is the delay time to breach an obstacle and secure the passage.
Overall mission scenario
- 2.2
- Offensive operations are riskier than defensive operations because the offensive forces may have to pass through open areas to mount an attack while the defensive forces fight from strong hardened positions. Thus, the offensive forces need to demonstrate the greatest efficiency in such operations, and consequently the C2 of the offensive forces needs to be tested under such difficulties.
- 2.3
- The standard procedure of C2 before the operation of assaulting a hill is 1) find the vulnerable points in the enemy positions, 2) allocate the tasks to support, assault, and breach to the platoons in the company, and 3) execute the assigned tasks (U.S. ARMY 2006a, 2006b). Although the tactical planning prior to the actual assault is straight-forward, the dynamic situation after the execution of the plan requires efficient responses through C2. The situation will evolve rapidly and the tasks specified in the planning will need to be adjusted according to the shared situational awareness of the company officers. At this stage, the questions of interest are how to efficiently share the information and how to determine the critical stages and decision paths.
- 2.4
- Figure 1 depicts a
detailed example of the simulated scenario. According to the
hypothetical mission analyses and situational assessments, a company
commander 1) allocates tasks to the platoons and 2) designates routes
to move to and breach the defence line of the opposing forces. When
deployed in the field, the company commander continues to assess the
shared situation and update the task assignments and plans over the
course of the assault operation.

Figure 1. Experiment scenario by phase (a) initial plan, (b) security area operation, (c) main defence area operation, and (d) deep area operation - 2.5
- In Table 1, we
explain the military symbols depicted in Figure 1.
We follow the standard NATO (North Atlantic Treaty Organisation)
military map symbols (Thibault 2005).
Table 1: Explanation of military symbols for Figure 1. Icons / Symbols Name Implication 
Infantry platoon An infantry platoon with a mission. Missions are assault, breach and support, according to the operational scenario of this study. 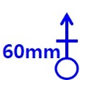
60-mm mortars Three 60-mm mortars that fire high explosive shells upon the commander's order. 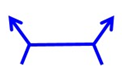
Fire support position A fire support position occupied by the support platoon. The arrows on each side indicate the firing range. 
Release point #1 A release point at which platoons are ramified. The bottom vertex of the inverted triangle indicates the actual point. 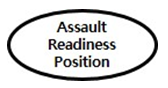
Assault readiness position An assault readiness position is an area in which the assault platoon stands by until the breach platoon clears a path through obstacles. 
Obstacle boundary The obstacle boundary of the opposing force along which barbed wire and mines are established. 
Passage A passage through obstacles cleared by the breach platoon. 
Defensive position of a platoon of the opposing force Strong hardened position of an infantry platoon of the opposing force. 
Defensive position of a squad of the opposing force Strong hardened position of an infantry squad of the opposing force. - 2.6
- Table 2 also
specifies the detailed C2 tasks involved in the assault procedure and
the decision-making by the commanding officer. Platoon leaders are also
key elements in the modelled C2 scenario, as they receive and execute
orders using the platoon resources, and share the execution and
observation results with other C2 elements, such as commanding
officers. The task details at the platoon level, such as route finding,
situation reports, assaults on enemy defence lines, and support fire
requests, are also listed in Table 2.
Table 2: Detailed C2 tasks for the operational scenario Task Name Execution Level Implication Required Resource Decision-making Mission allocation Company Commander allocates missions to platoons (assault, breach, support). Surveillance
Systems
(Soldiers)Designate primary
positionsCompany
Commander designates objectives, breaching point, fire support position, and assault readiness position based on situation assessment. Designate route / release points Company/
PlatoonCommander designates release points for platoons and platoon leaders find routes based on the release points, mission, terrain, and enemy location. Commanders can designate routes for platoons only if it is required for the successful mission. Report Report situation
changePlatoon Platoon leaders report a situation change to the commander in accordance with METT-TC elements. Radio Request fire
supportPlatoon Platoon leaders request fire support from the commander in light of the size of the opposing forces Issue order / Order support
fireCompany Commander orders fire support for the support platoon if support position is secured and breach platoon is ready to breach Radio, Rifles Execution Order mortar
fire
Company Upon fire request from platoons, commander orders mortar fire when the company starts contact with the enemy by breaching, or if the size of the opposing forces assembled is more than squad level Mortars (60mm) Order to breach
Company/
PlatoonCommander gives the order to breach to the breach platoon if the support platoon is ready to support and the assault platoon is in the assault readiness position. Upon receiving the order, the platoon leader executes the command Bangalore torpedo Order to assault Company/
PlatoonCommander orders all platoons to assault if a route in the defence line is secured Radio, Rifles - 2.7
- Our analysis of the combat effectiveness of C2 does not
consider the resources and situation beyond the bounds of the infantry
company level, as these factors are beyond the scope of this paper.
Situational vignette on commander's decision-making
- 2.8
- We provide historical vignettes to illustrate the key
points of a commander's decision-making. We excerpted military history
from the field manual and research report of the US Army (U.S. Army 2003b; Wright 2013) and recast the
situation for the better understanding of the experimental scenario of
this study.
- Vignette #1 – Concentration of
combat power to the weak flank in the Napoleonic war
- Historical vignette: In 1805, Napoleon's army engaged the army of the coalition of Austria and Russia, which numbered 85,000 to Napoleon's 53,000, near the village of Austerlitz. Napoleon enticed the coalition force to attack him by showing weakness on his right flank. He then attacked the coalition's centre, from which the commander of the coalition force had removed forces. Napoleon was able to overcome his numerical inferiority by the use of deception and concentration and win the battle.
- Issue: Creation of a weak flank on the opposing force and concentration on the weak point to overcome numerical inferiority.
- Discussion: The achievement of numerical superiority by means of concentration is a fundamental principle in military tactics. This concept is reflected in the command and control (C2) model of this study. As Figure 1 shows, the support platoon fixes the opposing force by deceiving them with suppressing fire. The infantry company commander finds a vulnerable point and concentrates the assault and breach platoons on it, which creates a numerical advantage at that point. - Vignette #2 – Immediate and correct
decision-making in the Gulf War
- Historical Vignette: At the beginning of the Gulf War in 1991, the 7th Corps commander, Lieutenant General Frederick M. Franks, Jr, received a spot report of 55 Iraqi tanks crossing the Kuwaiti border. He immediately alerted two aviation battalions so that they could respond in 30 minutes and issued a reconnaissance order to the subordinate unit nearest the Iraqi tanks. The entire process was accomplished within seconds. With confidence in the report, immediate decision-making and correct action, the initial operation of the 7th Corps was successful.
- Issue: As described in the previous section, the tasks of C2 are largely divided into 1) reporting, 2) decision-making and 3) issuing orders. Immediate decision-making includes those steps and thus the speed of the commander in reporting, making decisions and issuing orders is the key to the success of the operation.
- Discussion: This historical vignette proves that the immediate C2 process is the key to success in combat. However, C2 is not a single process but the combination of several steps, as mentioned above. To investigate the C2 process, we detail the C2 tasks as described in Table 2 and examine which detailed tasks are important in combat by modelling and simulation. - Vignette #3 – Immediate fire support
to destroy the will to fight in the Vietnam War.
- Historical Vignette: In June 1966, a battalion of the North Vietnamese Army (NVA) attacked an artillery firebase of the US Army. A battalion from the 101st Airborne moved to surround the NVA's position by air infiltration. The battalion commander used a 'checkerboard' technique, in which the battalion was divided into squad-size units to patrol into the NVA's position and then reassembled by company when the heavy opposing force was discovered. A company of the battalion was reassembled after encountering the opposing force but was enveloped by the NVA battalion. The company commander immediately requested an air strike to the battalion. Although only napalm was available for air support, the air strike neutralised the attack from the NVA battalion. The company was in danger, but the quick decision to request fire support saved the company.
- Issue: A commander's use of available assets is also one of the key factors of success in combat. An infantry company has only rifles, machine guns and light mortars, but it can be supported by assets from a higher level of command, such as artillery, engineers, aviation and even air support. With this support, the infantry company can increase its ability to accomplish its mission.
- Discussion: According to the experimental scenario, the infantry company commander can use 60-mm mortars if necessary. Once the company commander receives detection information or a fire request from a subordinate, the commander decides whether to use the fire assets. Because the opposing force continuously moves and attacks the friendly force, the fire request and the decision of how to respond should be immediate. Thus, we also examine the influence of immediate fire support on combat.
- Vignette #1 – Concentration of
combat power to the weak flank in the Napoleonic war
 Literature
Review
Literature
Review
- 3.1
- Historical battles show that the size of a force does not
always determine the winner; rather, the winner is the side that
creates relative superiority at certain points by timely
decision-making (Zsambok &
Klein 2014). Therefore, many studies have been performed to
study military C2.
Classical approach of military decision-making
- 3.2
- Early efforts to study military C2 focused on determination of the best option in uncertain situations (Sokolowski 2012). Military decisions can be divided into two categories: the selection of military actions and the allocation of resources. The purpose of such decisions is to optimise the preferences of decision makers or the possibilities of successful missions. Naturally, an analytical approach is used to solve military command and command issues. Mathematical and analytical theories have been developed and calibrated by comparison with empirical studies (Levis & Athans 1989). The Markov decision process is one of the typical theories applied to military planning (Aberdeen et al. 2004).
- 3.3
- With this classical approach, military commanders have often been trained to develop several courses of action, compare them with analytical methods and select the best course (U.S. ARMY 2003b, 2008a). However, the analytical methods are not fully adopted by the military because 1) they do not reflect command styles in which some factors for successful mission completion are dependent on the commander's intuition based on experience (Van Creveld 1985) and 2) they cannot consider all of the factors that may influence the results of real combat (Zsambok and Klein 2014). Military commanders do not make decisions with quantitative assessments but with their real-world knowledge and experience.
- 3.4
- Moreover, researchers who study military C2 began to doubt
the classical approach to military decision-making problems. Empirical
studies and experiments also showed that the selection of the best
option amongst several alternatives is not more advantageous than
development of a single option (Entin
et al. 1988; Klein 1989,
Klein 1999; Pascual & Henderson 1997).
This trend naturally brought changes of recognition regarding the
interpretation of military C2 problems (U.S.
ARMY 2008a; Zsambok
& Klein 2014).
Considering cognitive processes in military decision-making
- 3.5
- Klein was the one of the first researchers to question the effects of analytically competing decision-making processes (Klein 1989) and suggested a cognitional model to use in deciding military actions during combat. The cognitional model has been developed into naturalistic decision-making (NDM) (Klein et al. 1993), which is not based on an analytical method but on a psychological method that represents the cognitive processes of humans in decision-making.
- 3.6
- According to the NDM theory, a person makes decisions on the basis of his or her knowledge and experience. The NDM theory is different from the classical decision theory in that 1) the decision maker makes greater efforts in situation assessment, 2) the decision maker develops only one option by means of mental simulation of various situations and 3) the decision maker decides on a satisfactory option, not an optimal one (Zsambok & Klein 2014). The theory can be reasonably applied to military commanders, who frequently have to make decisions under time pressure (Pascual & Henderson 1997).
- 3.7
- During the execution of operations, military commanders must often make decisions under uncertain conditions. Obtaining informational superiority is critical, but understanding the correct decision situation can be complicated because of a changing environment and the possibility of imperfect, incorrect or deceitful information.
- 3.8
- The commander makes an effort to obtain insight from the problem context by expending considerable thought. We call the cognitive process situation awareness (SA). Endsley et al. (1997, 2000) found that the most important factor for superior SA is to improve the information-gathering capability of combat entities. They examined the dynamic and complex infantry operational environment. The information should be processed or refined to determine which information is correct by comparing and analysing the information gathered from different sources. Leedom (2004) suggested that the C2 structure perform these functions.
- 3.9
- When making decisions under time pressure and with high stakes, commanders are forced to think of a similar situation they have encountered in their experience. The commanders then match the situation of their experience to the current situation and make decisions on the basis of the results of the original experience. This method was applied in the training of leaders or commanders of small units, i.e., infantry platoons or companies (Pleban et al. 2000; Pleban & Salter 2001).
- 3.10
- Klein (1993) developed a model that reflects the NDM paradigm, which he called the recognition-primed decision (RPD). The RPD describes cognitive decision-making processes according to the NDM theory. The RPD indicates how to 1) assess a situation based on experience, 2) estimate the possible outcomes of the situation and 3) develop and select a competent course of action (Sokolowski 2012).
- 3.11
- Studies have shown the validity of the RPD model in
military C2 (Drillings &
Serfaty 2014). The RPD model has been shown to be a
beneficial means of training naval officers to make decisions under
complex and time-pressured circumstances (Kaemph
et al. 1996). The RPD model has also been applied to
represent battle commanders' decision-making expertise, which is the
commander's ability to make decisions in a timely, efficient and
effective manner (Serfaty et al.
2014).
Modelling command and control in general
- 3.12
- In the past, C2 modelling was not considered essential in wargaming because the C2 processes were carried out by human role players who controlled the combat units in the wargaming models (Tolk 2012). However, C2 modelling is necessary to represent the more complicated C2 processes that are performed by human commanders in constructive simulation settings. The first C2 models described human behaviour based on decision-making in response to the external environment (Sokolowski 2012). However, the modelling and simulation of individual decision-making processes has since developed into modelling the entire C2 process of military units.
- 3.13
- The C2 process does not simply involve commanding and controlling a collection of individual combat entities, but includes processes such as interactions with the environment and between entities (Moon et al. 2013). This broader process encompasses situation assessment, deciding a COA, allocating resources, and ensuring that combat entities behave as ordered, and so on. Naval air defence models are simulation models that include C2 structures and the behaviour of the individuals involved in the decision-making process, such as fleet commanders and radar operators (Calfee 2003; Carley & Lin 1995; Kim et al. 2012; Liebhaber & Smith 2000). They also consider the situation and environment, such as the characteristics of incoming missiles and the physical specifications of ships. The cognitive architecture SOAR, which simulates the decision-making processes of individual agents, has been used to model and simulate C2 to support air operations (Carley et al. 1992; Jones et al. 1999). In these applications, collections of agents are introduced to represent decision-makers and pilots.
- 3.14
- Although numerous defence studies deal with modelling and simulating C2, we limit this literature review to modelling C2 at the army infantry company level. We review the modelling of tactical scenarios for army infantry companies first because scenario technology is used to plan C2 exercises (Burns 1999). Thus, the scenario creation process requires considering the C2 process. Studies on modelling the C2 of army infantry companies are then examined.
- 3.15
- Military scenarios are used at various levels of C2, including the strategic, operational, and tactical levels (U.S. ARMY 2008b). Military tactical scenarios are mainly used for planning C2 exercises. Research on scenario modelling has enabled military planners and the officers conducting exercises to automatically generate exercise scenarios by simply imputing battlefield variables. The scenario development tool, military scenario definition language and coalition battle management services are used to generate exercise scenarios, which are implemented as simulation and exercise environments for training purposes (Blais & Galvin 2005; Hilton & Diallo 2014; SISO 2008).
- 3.16
- For small units at the company-level or below, tactical scenarios are modelled to train soldiers and unit leaders (Pleban et al. 2000). In this case, a scenario model is used to generate events that allow the leaders of small units to encounter various exercise conditions and environments. The scenario model assesses the situation using brain-storming with METT-TC (Mission, Enemy, Terrain and weather, Troops available, Time available, and Civil affairs), which consists of a set of components that yield flexible scenario options (Wampler et al. 2004). The scenario modelling tools are also used to help train the leaders of small units and commanders in tactical decision-making to improve their ability to rapidly perceive a situation and to make the appropriate tactical decisions (Beal 2007).
- 3.17
- Little research has examined the modelling of the C2 of army infantry, whereas numerous studies have explored C2 modelling in various defence areas, such as theatre-level operations and naval and air force applications. The lack of army infantry research is due to the complexity of the environmental factors of land operations. Modelling the C2 of army operations requires perceiving, interpreting, and considering a large amount of information that encompass numerous sporadic combat entities and geographical factors, which greatly exceeds that required for naval or air operations. Thus, studies of army command and control have naturally focused on C2 planning, which is a procedural process conducted by distributed and collaborative C2 staff (Riley et al. 2006).
- 3.18
- Although the research on C2 planning is primarily targeted at modelling C2 for high echelon commanders, i.e. at the army brigade and battalion levels, the army infantry company is a basic combat unit that directly displays the effects of C2. The company commander, who is commander of the smallest unit for which officers can be called commander, commands and controls combatants directly on the battlefield. Thus, it is essential to model the C2 of infantry companies to analyse the more robust and reliable effects of C2 at the upper end of the C2 hierarchy.
- 3.19
- Yun et al. (2013)
develop a C2 model for infantry company-level operations to allow
operators to control a number of combat entities as a unit in a
computer-aided exercise (Yun et al. 2013).
The C2 model, also called commanding agents, observes the operational
environment, orders from operators, and situation reports from combat
entities. The C2 model then makes decisions based on the available
information and issues orders to subordinates and combat entities. To
the best of our knowledge, no existing research has explicitly analysed
the operational delay times during the C2 process at the infantry
company-level, even though the C2 process should be carried out under
high time pressure in most cases (Riley
et al. 2006).
Modelling cognitive processes in military decision-making
- 3.20
- Finite-state machines and rule-based models, also called expert systems, are the traditional modelling methods that are used to model human behaviour and decision-making. However, they have limitations in the modelling of cognitive processes. It is difficult to model a number of possible events and states of cognitive decision-making using finite-state machines. The rule-based models also have difficulties in generating a knowledge base and exactly matching the situations encountered by a decision maker (Gallant 1995).
- 3.21
- In contrast, case-based reasoning, which represents knowledge as a collection of individual cases, is similar to the RPD model in that it makes use of experience in decision-making (Gilboa & Schmeidler 1995). In addition, neural networks have been used for SA and for selection of a course of action, which are processes in the RPD concept (Sokolowski 2012). Fuzzy logic and fuzzy inference systems have also been used to model cognitive decision-making in the commander and the commander behaviour models. It was not an exact application of the RPD, but many parts of the RPD were taken into account (Vakas and Burdick 2001).
- 3.22
- Humans make decisions according to experience and their
understanding of the current decision situation. Multi-agent system
simulation is a bottom-up approach to modelling human decision
processes in ill-structured and uncertain situations (Gilbert 2008). The multi-agent
system simulation is widely used to model cognitive decision-making
processes because of its close match with the concept of cognitive
decision-making processes. A form of multi-agent system simulation
called belief-desire-intent demonstrates the similarity between the
paradigms of multi-agent system simulation and cognitive decision
processes (Poslad 2007).
The 'belief' of agents refers to SA, 'desire' refers to the goal of the
decision makers and 'intent' refers to the actions a decision maker
performs as a result of decision-making (Wooldridge
2009).
Studies on military C2 in terms of cognitive decision processes
- 3.23
- The first task that a commander performs in the cognitive decision-making process is SA and information delivery. To assess the right situation, a commander actively collects information from various intelligence assets. Endsley et al. (1997, 2000) defined the role of SA and used modelling and simulation to show that the information-gathering ability of individual soldiers was the most important in SA.
- 3.24
- Commanders should also compare the collected information with the knowledge obtained from their own experience and doctrines and analyse the information to distinguish which information is correct (Leedom 2004). Leedom also emphasised the design of a C2 structure that enables commanders to analyse the information.
- 3.25
- Information delivery is also one of the most important factors for SA. A commander receives orders including information from the intelligence assets of the higher command. The commander also receives reports from subordinate commanders or combat entities about battlefield situations such as the state of the opposing forces detected. Krausman et al. (2005, 2006) showed the effectiveness of rapid and accurate delivery of information. They concentrated on alerting the initial situation of small units, i.e., squads, platoons and companies.
- 3.26
- In contrast, in other studies on the accurate transmission of the commander's intent, Eriksson and More (2008) studied the representation of the commander's intent by machine, whereas Hieb and Schade (2007) focused on common or unified formats or standards.
- 3.27
- In addition to SA, commanders' decision-making under 1) uncertainty, 2) time pressure and 3) highly complex combat situations have been studied in terms of cognitive decision processes (Thunholm 2005). A series of cognitive simplification processes have been suggested to overcome uncertainty and complex situations in decision-making (Schwenk 1984). Time has also been considered as a crucial factor in military C2 (Van Creveld 1985). Thus, studies on the effects of decision-making under time pressure have always been critical. Lawson (1981) was one of the first researchers to define the role of time in military C2.
- 3.28
- For rapid and timely decision-making, dynamic intuition in military C2 and cognitional decisions with situation assessment and mental simulation were also emphasised (Bakken & Gilljam 2003; Klein 1993).
- 3.29
- Cothier and Levis (1985) integrated the concept of timeliness with the measure of effectiveness analysis. They performed a quantitative comparison of the timeliness factors of response time and operational tempo using the measure of effectiveness. They also yielded useful insights for the design of military C2 systems. According to their assertions, faster C2 does not always mean better; in fact, faster can be worse in trade-off situations, for example, if increasing speed reduces the survivability of the system in terms of development and operational costs.
- 3.30
- Cothier and Levis also applied their method to the C2 of a fire support system and showed that it is possible to improve tactics, training and procedures regarding C2 times (Cothier & Levis 1985).
- 3.31
- Kevin et al. also studied the effects of time delay by investigating the time latency of information in a networked operation. They used a discrete-time Markov chain model that does not deal with cognitive decision processes, and they did not quantify the timeliness. However, they showed means by which to reduce the time latency via training and displayed the importance of timeliness by experiments (Kevin et al. 2008).
- 3.32
- Scott (1993) proposed the use of a formalised timeline for the military decision-making process and showed evidence of its advantages. The steps of decision-making at different echelons were also specified to train commanders to make sound decisions under time pressure (Thunholm 2005).
- 3.33
- Some studies have emphasised tangible combat factors in addition to C2, which is intangible. Studies on the combat effectiveness of the marksmanship of individual soldiers emphasised the importance of improving the individuals soldiers' probability of hit (McGrath 1962; Thompson et al. 1980; White et al. 1991).
- 3.34
- We provide a list of studies of cognitive processes in
military C2 in Table 3. In summary, previous studies have emphasised
the importance of 1) rapid decision-making (HA
in Table 3), 2) rapid SA and
information delivery (HB in Table 3) and 3) a high level of
marksmanship of the individual soldiers (HC in
Table 3).
Table 3: Studies of cognitive processes in military C2. Hypotheses from
previous researchLiteratures Contents HA Time for Lawson, 1981 Defined the role of time in military C2 cognitive Schwenk, 1984 Proposed cognitive simplification processes to shorten decision times decision- Van Creveld, 1985 Time is a crucial factor in military C2, and the C2 should include a command style based on a commander's intuition making Cothier and Levis, 1985 Quantitative comparison of timeliness factors (response time and operation tempo) using the measure of effectiveness in military C2 Entin et al., 1988 Finding the best option amongst several alternatives is not more advantageous than developing a single option has a significant Levis and Athans, 1989 Comparison between analytical theories and empirical studies for military C2 under time pressure effect on
combat
effectivenessKlein, 1989, 1999;
Klein et al., 1993;
Zsambok and Klein, 2014Defined cognitive processes under time pressure in military C2 based on experience (naturalistic decision-making): 1) situation assessment and 2) developing a single course of action via mental simulation Scott, 1993 Suggested a formalised timeline and presented its advantages Klein, 1993; Bakken and Gilljam, 2003 Dynamic intuition is emphasised for rapid and timely decision-making Pascual and Henderson, 1997 Importance of cognitive decision-making processes under time pressure Thumholm, 2005 Defined the conditions faced by a commander in decision-making: 1) uncertainty, 2) time pressure and 3) high complexity Kevin et al., 2008 Investigated effects of time latency of information in networked operation HB Rapid situation Endsley, 1997, 2000 Importance of the information-gathering ability of individual soldiers awareness and Leedom, 2004 Importance of C2 processes and structures that enable commanders to assess situations with refined information information Krausman et al., 2005, 2006 Showed the effectiveness of rapid and accurate information delivery delivery
(order/report)
have significant
effects on
combat
effectivenessEriksson and More, 2008;
Heib and Schade, 2007Importance of accurate transmission of the commander's intent HC Marksmanship has
significant effect on combat effectivenessMcGrath, 1962;
Thompson et al., 1980;
White et al., 1991;Marksmanship of individual infantry soldiers is one of the most critical factors Purpose of this study
- 3.35
- Previous studies have emphasised rapidity in commanders' performance of C2 tasks despite the negative effects on decision-making when decisions are made under time pressure. Many studies have also suggested various methods by which to make sound decisions within a limited time by investigating cognitional decision processes.
- 3.36
- However, few studies have investigated the quantitative combat effectiveness of military C2, which shows the importance of time in military C2, although it is commonly asserted that faster is always better (Cothier & Levis 1985). We have doubts regarding the implicit importance of speed in decision-making. For example, if there is no difference between 5 minutes and 10 minutes in a command process, then 1) we need not pay much attention to speeding up a process that requires more than 5 minutes or 2) we do not need to sacrifice other elements of the command process that should be considered. In addition, to the best of our knowledge, the importance of various command tasks performed in a series of decision-making processes has not been compared.
- 3.37
- This study analyses the combat effectiveness of detailed command tasks on the basis of multi-agent simulation. Our analysis is quantitative and includes hypothesis testing using test statistics. We also show a possible relationship between the intangible and tangible factors of combat. C2 in the military domain is an intangible factor, but it is always regarded as one of the most crucial factors. Tangible combat factors such as the soldiers' marksmanship and the effective range of a weapons system are also frequently investigated and analysed in terms of combat effectiveness. For instance, the marksmanship of individual infantry soldiers was shown to be critical for successful combat missions (McGrath 1962; Thompson et al. 1980; White et al. 1991).
- 3.38
- Modern military doctrines about C2 support mission-oriented C2, especially for small units. In mission-oriented C2, also known as mission-type tactics or mission command, the military commander gives orders that consist only of a clear goal and mission without any details (U.S. ARMY 2003b). The mission-oriented C2 embeds a paradigm in which well-trained commanders and soldiers do not need detailed instructions. This study tries to confirm that the paradigm is dominant for all situations by modelling and simulating the military C2.
- 3.39
- We propose a method to model C2 using discrete-event simulation by building a model of an infantry company engagement. The C2 model encompasses the C2 functions of three platoon leaders and one company commander. We then use the model to analyse the combat effectiveness of C2, particularly with regard to the delay time caused by the C2 process.
 Method
Method
- 4.1
- To ensure the realism of the simulation, we build the model
by following army doctrine (ROK Army
2008; U.S. Army 2003a,
2006a). The C2 model
includes a company commander and three platoon leaders, which are
modelled as state machines following the DEVS formalism. In this
section, we introduce the model structure and the model behaviour in
the formalism. The model code can be found at https://www.openabm.org/model/4361/version/1/view.
DEVS formalism
- 4.2
- Discrete event simulation describe how a system is operated by use of a discrete succession of events (Choi & Kang 2013). Each event occurs discretely in time and changes the states of the models in the system (Robinson 2004). In defence modelling and simulation, each combat entity and operational environment may be modelled as a state machine that receives, processes, and generates discrete events, so the discrete event simulation is a good fit for the scope and characteristics of the model. In addition, agent-based models, which emphasise the decentralisation of event processing, are well-matched to the domain because combat entities often operate through autonomous decision-making and coordination by message exchange.
- 4.3
- We use the discrete event system specification (DEVS)
formalism to describe our models, which is one of the modelling methods
for discrete event simulation (Ziegler
et al. 2000). The DEVS formalism explicitly represents states
and the changes of their models with state transition diagrams,
interactions between models and internal transitions with time advance.
The formal specifications of the discrete event system specification
(DEVS) atomic model (AM) and coupled model (CM) are shown in Figure 2 (Ziegler
et al. 2000).

Figure 2. Formal specification of the DEVS atomic model (AM) and coupled model (CM) - 4.4
- This formalism is able to model complex interactional structures with many interactions due to its hierarchical decomposition and explicit coupling relations. The infantry engagement model requires frequent interaction between the combat entity models, such as sensing the other side, firing upon the other side and communicating with the same side.
- 4.5
- Figure 3 shows the
DEVS diagrams for the AM and CM. In the DEVS AM diagram, input and
output events are represented as filled triangles. Ovals represent the
states of the AM, the state name is written above the centre line of
the oval, and the amount of time advance is represented below the line
with @. For instance, when an input, X, comes in the model and the
model is in 'STATE_A', then the state is changed to 'STATE_B' if
'cond1' is satisfied. In addition, after the defined time, T(STATE_B),
the state is transformed back to 'STATE_A' and an output, Y, is sent to
the outside of the model (Bae et al.
2013).
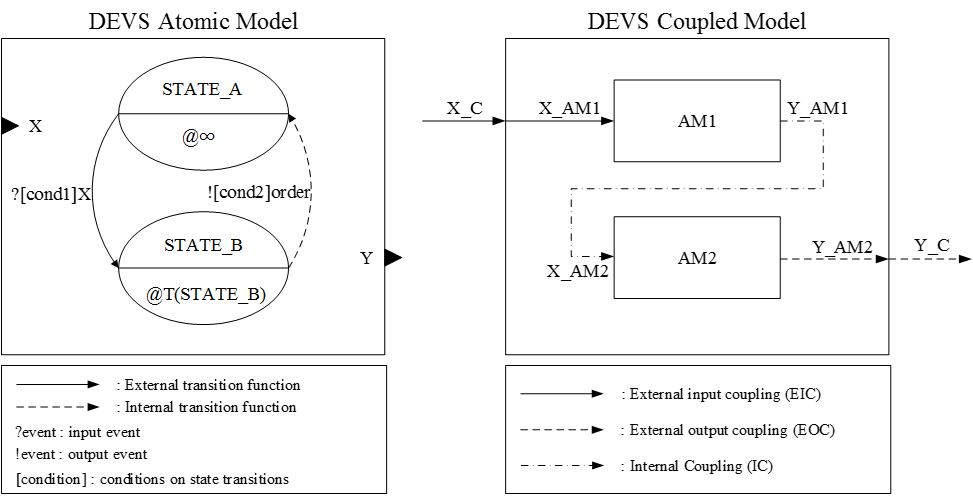
Figure 3. DEVS diagrams for atomic model (left) and coupled model (right) - 4.6
- The DEVS CM diagram depicts the relationships between atomic models. Figure 3 also displays an example diagram for the DEVS CM, which has two AMs. For example, when an input, X_C, comes from outside the CM, the input goes to AM1, which describes an external input coupling relation. An output from AM1, Y_AM1, goes to AM2 and describes an internal coupling relation. Finally, an output from AM1, Y_AM2, becomes an output of the CM, Y_C, which explains an external output coupling relationship (Bae et al. 2013).
- 4.7
- Although we use structural description of the models and
state transitions, we also specify the behaviour of a model at a
certain state with separate descriptions. The separation between the
discrete event level model (DEM) and the behavioural level model (BM)
is applied to flexibly specify the diverse behaviour of the combat
entities (Sung & Kim 2012).
Some details require specification other than the simple state
transition in combat behaviour, and we use pseudo code, formulas, and
flow charts to illustrate such behaviour. The model separation enables
us to exchange the details of our simulated combat entity behaviour. As
the experimental decision-making processes of the C2 model are the
object of interest in this paper, it is important to deliver the
explicit details of the decision-making process. To achieve this, we
use equations, flow charts, and pseudo codes.
Overall structure
- 4.8
- The model is a hierarchy of models representing 1) a
company commander, 2) three platoon leaders, whose missions are
assault, breach, and support, respectively, 3) riflemen for both the
blue and red forces, and 4) mortars for the blue force. Figure 4 shows the hierarchical structure of
the models.

Figure 4. Hierarchical model structure - 4.9
- The infantry company engagement model (EngagementSim) consists of the blue force (BlueForce) and red force (RedForce) models, which are fighting each other. The red force model comprises red soldier (RedSoldier) models that perform detect and fire functions, which are represented BMs. However, there is no detailed C2 process model for the red force because the red force is only included as a baseline of the opponent model and the assault force (the blue force) requires more tactical and C2 effort compared to the defensive force (the red force). The blue force model is more complicated than the red force model because it includes C2 modelling features. The blue force model includes 1) the company commander (Commander), 2) the mortar (BlueMortar), and 3) the platoons by mission (BlueAssault, BlueBreach, and BlueSupport). The commander model includes DEMs and BMs for decision-making (DecisionMaking), ordering (Order), and fire requesting (FireRequest). Each platoon has an identical structure containing models for the platoon leader (PlatoonLeader) and soldiers (BlueSoldier). The platoon leader model includes decision-making and order/report functions that are also described as BMs. The models for the soldiers include their BMs and DEMs of moving (Move), detecting (Detector), and firing (Fire). The DEM of moving also has BMs of moving (Move) and breaching (Breach)
- 4.10
- The model includes environmental factors such as the
terrain, which is modelled as discretised altitude levels and
obstacles. The environmental model interacts with the combat entity
models, i.e., the red and blue forces, to reflect the operating
environment. Table 4 lists
the details of the modelling features and experimental variables. The
input values of the simulation parameters follow those of a standard
infantry company of the US Army.
Table 4: Parameters for the experimental environment, modelling features, and performance measure Type Name Description Scenario parameters Number of blue soldiers Number of blue soldiers (90 for infantry company) Number of red soldiers Number of red soldiers (48 for an augmented red platoon) Cell size Size of one cell (10 m × 10 m) Size for area of
operationSize of area in which the company deploys
(2 km × 3 km; 200 × 300 cells)Model
parametersMovement speed Moving speed of a blue soldier (4 km/h) Probability of kill
given hit (P(K|H))Probability that an enemy is killed given hit
(0.15 for covered position / 0.35 for open area)Probability of kill
for mortars (P(K)m)Probability that an enemy is killed within casualty radius (0.13 / round within 10 m for 60 mm mortars) Mountainous level Information on the mountainous levels that affect the movement delay coefficient and P(K|H) (Low: 1, open; Medium: 1.33, covered, High: 3, covered) Obstacle level Information on level of obstacles (None: 0, Low: 1, High: 2) Level of enemy threat Information of level of enemy threat. Represented as the number of opponents within firing range (squad-level: 1, section-level:2, platoon-level: 3) Command times Delay time to report and make decisions. Specified by decision-making steps and commanding agents; a company commander and platoon leaders
(varies in the experiment design)Probability of hit (P(H)) Probability of hit. The value varies in the experiment design for blue soldiers while the probability of hit for the red soldiers is fixed as 0.6) Breaching time Delay time to breach obstacles and secure a passage (varies in the experiment design) Performance
measureLoss Exchange
Ratio (LER)Loss exchange ratio of blue soldiers to red soldiers (number of red soldiers killed / number of blue soldiers killed) - 4.11
- In addition to the US Army guidelines, we use the calibration data of the JANUS model, which is widely used in engagement simulations. The values originating from JANUS are movement speed, probability of kill given hit for rifle, probability of kill for mortars, and change of movement speed and probability of kill given hit by mountainous level (U.S. TRADOC 2000). We also use Korean Army (ROK Army 2008) guidelines to determine the parameter values of the simulation experiments. The calibration values derived from the Korean Army guidelines are the probability of the hit and the delay time to breach obstacles. The command times are divided into detailed tasks and decision-making points. As the main purpose of this paper is to analyse the combat effectiveness of the C2 process and its delay time, we specify the command times in the subsection on C2 modelling. We use the loss exchange ratio (LER) as the performance measure, which is the number of red soldiers killed divided by the number of blue soldiers killed, with a high LER signifying that the blue soldiers fought well.
- 4.12
- Figure 5
illustrates the coupling structure of the simulation model at a high
level of abstraction. The infantry company engagement simulation model
(EngagementSim) consists of two coupled models, the blue force model
(BlueForce) and red force model (RedForce). The two sides send firing
results to the opposing force. The messages exchanged between the red
and blue forces include position information and firing information.
The sensing and consequences of firing are modelled and simulated by
the blue and red force models.
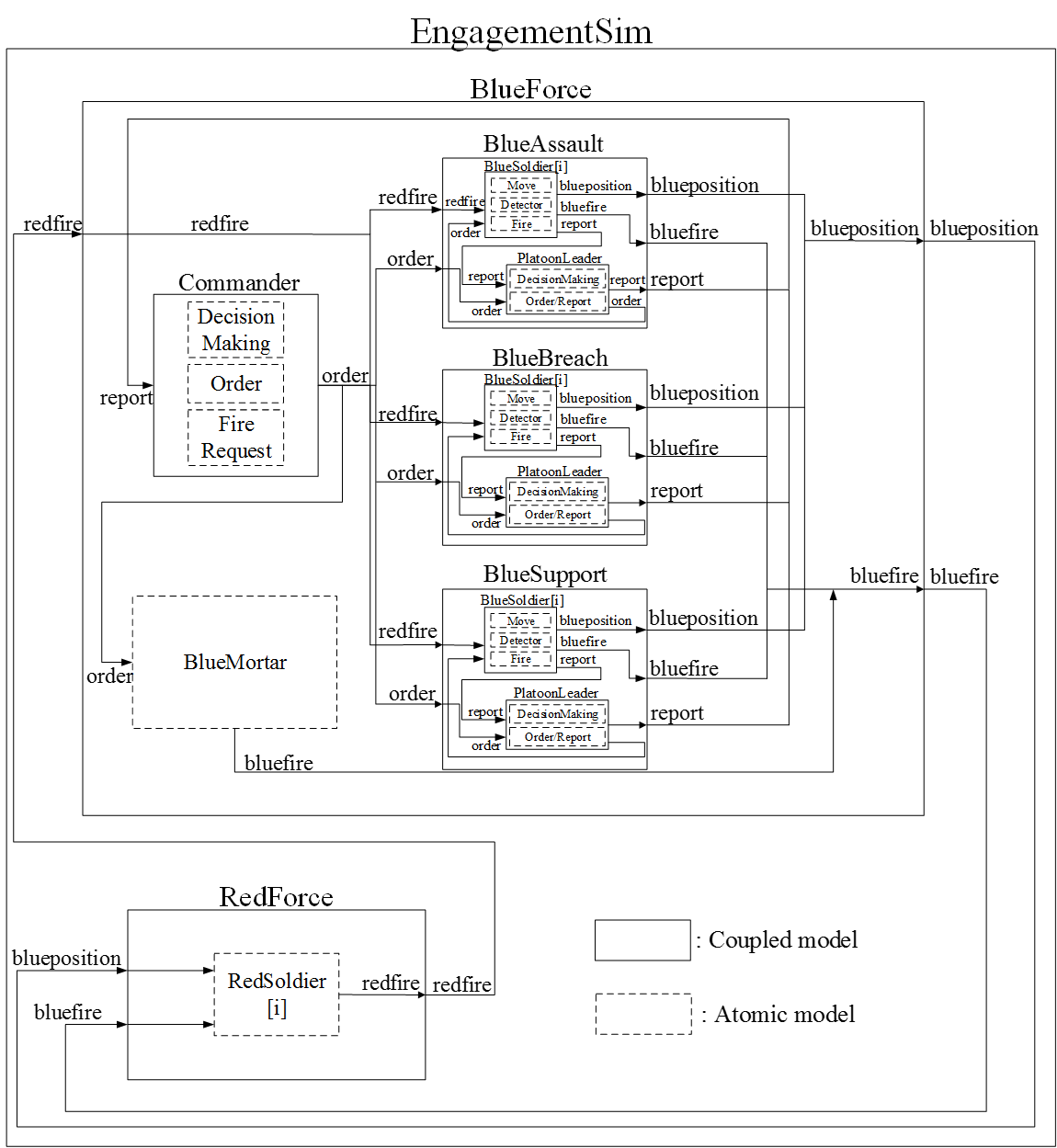
Figure 5. Coupling structure of the infantry company engagement model (EngagementSim) Blue force model with C2 models
- 4.13
- The blue force model includes a set of coupled models that incorporate the combat entities and C2 features As Figure 5 shows, the model includes the company commander, a mortar, and three platoon models: BlueAssault, BlueBreach, and BlueSupport. When the simulation starts, the commander model makes a plan based on the perceived information and issues an order to the platoons through the coupling structure. The commander model continues making decisions and ordering the platoons and the mortar while the operation is in progress. Each platoon model receives orders from the commander model and sends situation reports to its commander, its coordinates to the observing enemy for simulation execution, and weapons fire messages to the opposition through the couplings.
- 4.14
- The platoon models also include a set of coupled models of
blue soldiers and an atomic model of the platoon leader, which is one
of the C2 features. Figure 6
depicts the coupled models of the platoons (nbpl
is the number of soldiers in a platoon). The platoon leader model plays
the same role as the model of the company commander except 1) there is
no planning phase when the simulation starts and 2) the model receives
orders from the commander.
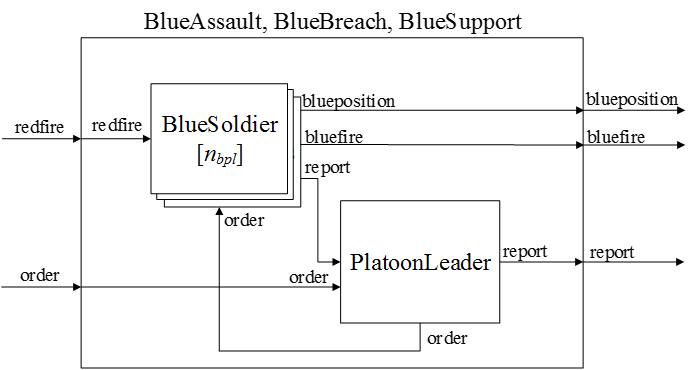
Figure 6. DEVS coupled model of the platoon - 4.15
- Figure 7
illustrates the company commander model, which 1) performs
decision-making with planning, allocates missions and reacts to
situations, 2) issues orders to platoon leaders (npl
is the number of platoon leaders) and 3) sends firing requests to the
mortars. We present the pseudo codes for the commander's
decision-making (see Algorithm 1), orders (see Algorithm 2) and fire
requests (see Algorithm 3) in the Appendix.
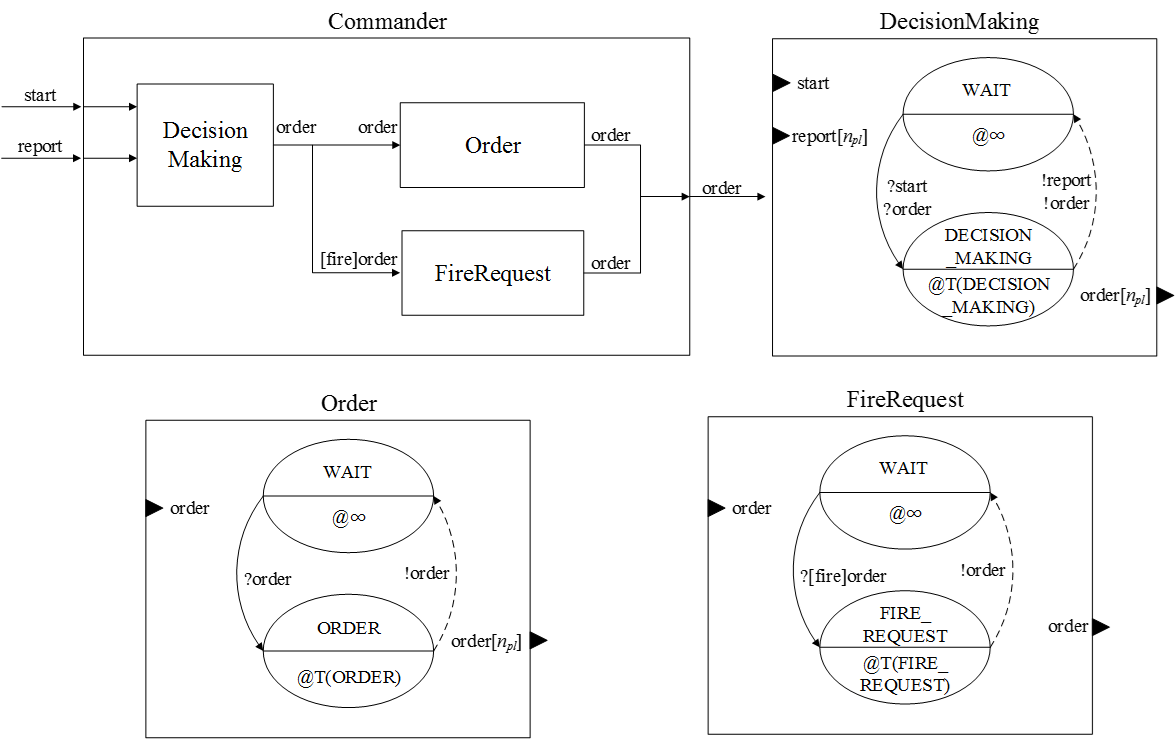
Figure 7. DEVS coupled model and atomic models for the company commander - 4.16
- Figure 8 shows the
platoon leader model with 1) decision-making, 2) reporting to the
company commander and 3) issuing orders to soldiers. We also provide
pseudo codes for the platoon leader's decision-making (see Algorithm 4)
and orders and reporting (see Algorithm 5) in the Appendix.
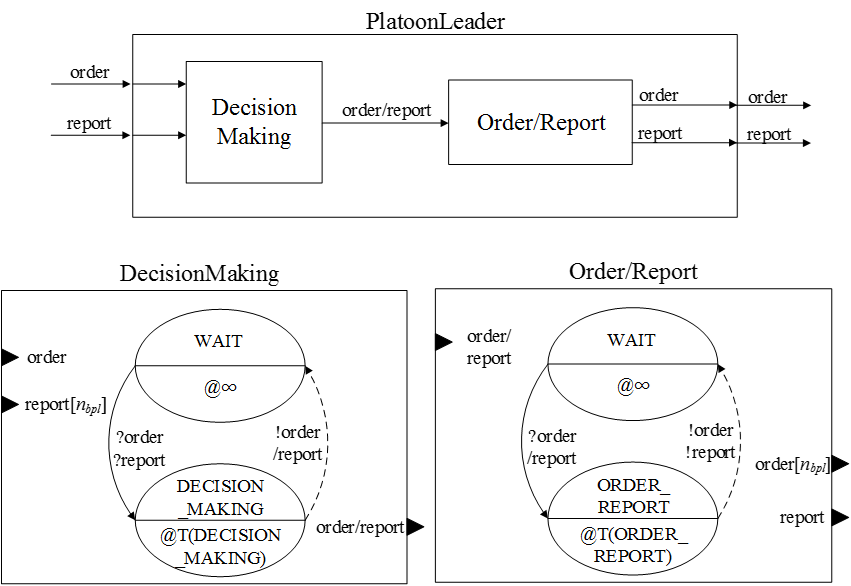
Figure 8. DEVS coupled model and atomic models for the platoon leaders - 4.17
- Figure 9 shows that
the commander model starts planning the operation when the simulation
starts. The operation planning is a sequence of 1) finding a vulnerable
point, 2) allocating missions to the platoons, 3) designating a fire
support position, and 4) determining an assault readiness position.
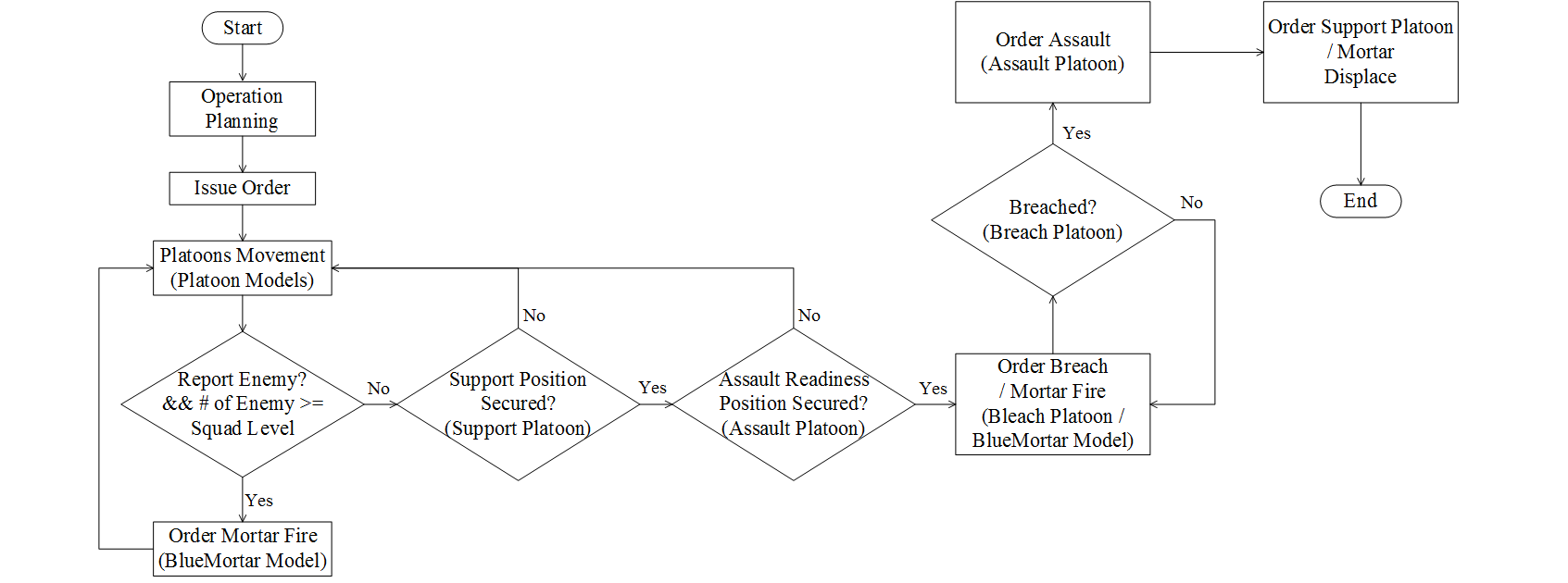
Figure 9. Simulation flow chart of C2: the commander model - 4.18
- Assuming that the \(GP\) is the set of geographical points
in the area of operation, finding a vulnerable point (\(gp_{v}\))
involves locating the weakest point of the obstacle boundary around the
opponent force. The weakest point is the point that has maximum
mountainous level (\(m_{x,y}\), the mountainous level at the
coordinates x, y) that provide cover and concealment while having
minimum obstacle level (\(o_{x,y}\), the obstacle level at the
coordinates \(x, y\)) and enemy threat level (\(t_{x,y}\), the level of
enemy threat at the coordinates \(x, y\)), as in Equation (1).
$$ gp_v = {\mathop{\rm argmax}}_{x,y \in GP_{obs}} (m_{x,y}- o_{x,y}- t_{x,y} ) $$ (1) where \(GP_{obs}\) is the set of geographical points in the obstacle area.
- 4.19
- The company commanders allocate missions based on the combat power of the platoons. Generally, the strongest platoon is charged with the task of assault, whereas the weakest platoon is tasked with support.
- 4.20
- Designating the assault readiness position (\(gp_{arp}\))
and fire support position (\(gp_{fsp}\)) involves finding appropriate
positions that allow 1) the platoons' own missions to be accomplished
and 2) provide enough cover, as in Equations (2) and (3).
$$ gp_{arp} = {\mathop{\rm argmax}}_{x,y \in GP} (m_{x,y}- t_{x,y}) $$ (2) such that \(d(x,y)_{obj} \in [fr_e, 1,000~\mathrm{m}]\), where \(d(x,y)_{obj}\) is the distance from the coordinates \(x, y\) to the objective, and \(fr_e\) is the effective firing range of a rifle.
$$ gp_{fsp} = {\mathop{\rm argmax}}_{x,y \in GP} (m_{x,y}- t_{x,y}) $$ (3) such that \(d(x,y)_{obj} \in [fr_e, fr_m]\) and \(d(x,y)_{gparp} \in [fr_m, d(x,y)_{boundary}]\), where \(fr_m\) is the maximum firing range of a rifle, and \(d(x,y)_{gparp}\) and \(d(x,y)_{boundary}\) are the distances from the coordinates \(x, y\) to the assault readiness position and the boundary of operational area, respectively.
- 4.21
- The tactical decisions during the middle of the operation are another key decision-making process for the company commander. As the situation reports with movement information come in, the commander may decide to stop the advance of the assaulting platoon, provide fire support with the mortar, and resume the assault by the platoon through coordinating messages (see Figure 9).
- 4.22
- Figure 10 depicts
a flowchart of the decision-making processes of the platoon leader
models. The platoons identify their received mission and the mission
directs the next step of the decision-making. The main role of the
platoon leaders is to find routes without being detected by the
opposing forces. The leaders order the coupled soldiers to move along
the found routes.

Figure 10. Simulation flow chart of C2: the platoon leader model - 4.23
- Equation (4) describes the operation of finding the routes
which is a continuous process to find next position (\(gp_{next}\)).
$$ gp_{next} = {\mathop{\rm argmax}}_{x,y \in GP} (m_{x,y}- t_{x,y}) $$ (4) such that \(x \in [c_x- 1, c_x + 1]\) and \(y \in [c_y- 1, c_y + 1]\), where \(c_x\) and \(c_y\) are the current \(x\) and \(y\) position, respectively.
- 4.24
- The soldiers detour around obstacles or the opposing forces if their mission is not to support because neutralising the opposing force is not the mission of the support platoon. The platoons also send situation reports to and receive orders from the company commander.
- 4.25
- Finally, The BlueMortar, which is represented as an atomic
model in Figure 11, sends
mortar fire messages upon orders from the commander (nr
is the number of red soldiers). The fire behaviour
of the BlueMortar is presented as a pseudo code in the Appendix (see
Algorithm 6).
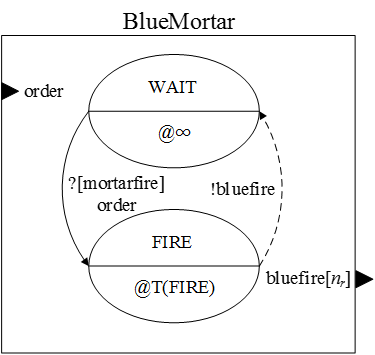
Figure 11. DEVS atomic model of the blue mortar Blue soldier model
- 4.26
- The blue soldier model includes three atomic models, as
depicted in Figure 12, whose roles are move, detect,
and fire. Figure 12
illustrates the coupled model of the blue soldier and the three state
transition diagrams for the three atomic models of the move,
fire, and detect behaviour.
The move model has two behaviours of move
and breach. These models are coupled as separate
models because these actions may be executed simultaneously and we need
to model this concurrency through state combinations.
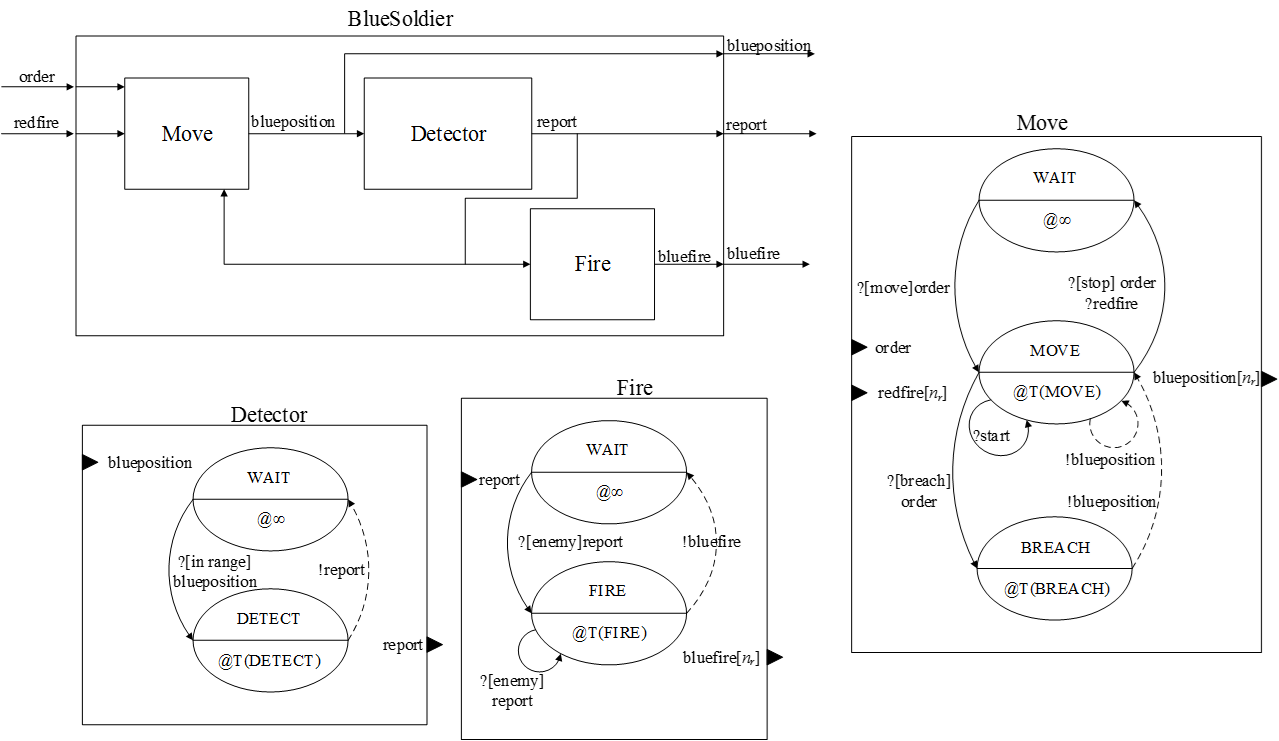
Figure 12. DEVS coupled model and atomic models for the blue soldier - 4.27
- When the simulation starts, the blue soldiers detect red
soldiers and obstacles while they are moving. The blue soldiers breach
obstacles or fire at the detected red soldiers. They also report to
their platoon leader whenever they detect the above entities or change
their states. We also provide pseudo codes in the Appendix for the
behaviour details of 1) move (see Algorithm 7) and breach
(see Algorithm 8) for the move model, 2) detect
(see Algorithm 9) for the detector model and 3) fire
(see Algorithm 10) for the fire model.
Red force model
- 4.28
- As the red force is in a defensive position according to
the simulation scenario, the red force model is the size of an
augmented platoon, as described in Table 4.
The red soldier model observes the distance between the model and an
approaching blue soldier, then the soldier model fires on the blue
soldier when it approaches within firing range. Figure 13 describes the coupled model of
the red force and the atomic model of the red soldier (nb
is the total number of blue soldiers). The algorithms for detect
and fire in the red soldier model are the same as
those in the blue soldier model (see Algorithm 9 and 10).
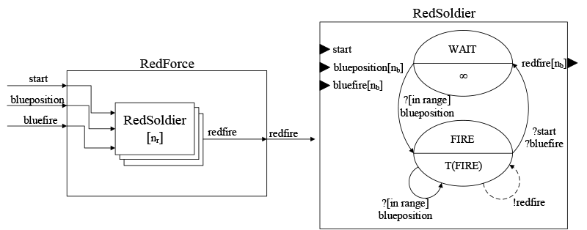
Figure 13. DEVS coupled model and atomic model for the red force Sample simulation execution and face validation
- 4.29
- Model validation in defence modelling and simulation is
particularly difficult because of the lack of a dataset for numerical
validation. Therefore, the practical method used for validation in the
field is qualitative assessment by subject-matter experts (Naylor & Finger 1967).
Subject-matter experts can examine the output metrics and the progress
of the simulations, which is known as face validation.
We perform this validation using an animation of the simulation
progress and statistical analyses of the output variables. Figure 14 and 15
display visualisation captures of the implemented model.
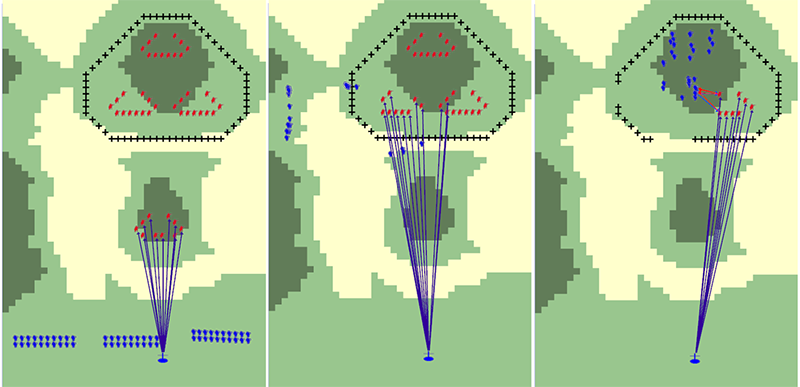
Figure 14. Visualization of the model implementation (model including C2); combat in security area(left), main defense area(middle), and deep area(right) 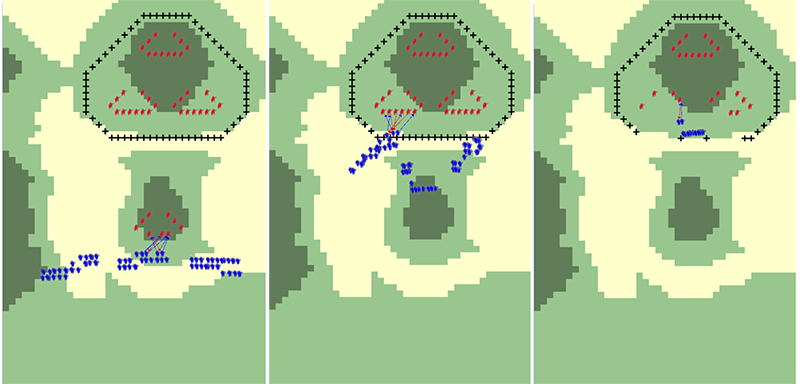
Figure 15. Visualization of the model implementation (model without C2); combat in security area(left), main defense area(middle), and deep area(right) - 4.30
- Figure 14 shows the simulation results of the model with C2 functions and Figure 15 shows the results without C2, which means that there is no planning, no support fire, no coordination between platoons, and no elaborate path-finding algorithm. The subject-matter experts confirm that the operations in Figure 14 follow the Republic of Korea Army doctrine with the given model abstraction. However, Figure 15 is considered unrealistic because there is no such scenario, i.e. combat without C2. Nonetheless, we keep the case of Figure 13 as the baseline of operations for the model validation.
 Experiment
Design
Experiment
Design
-
Hypotheses Generation for Virtual Experiments
- 5.1
- We perform battle experiments to observe how the C2 parameters affected the combat effectiveness of the simulation. We introduce the following independent variables as the combat factors: command time, probability of hit, and breaching time. We then divide the command time of the company commander and the platoon leader into five types. Figure 6 illustrates the three decision-making steps of the company commander: decision-making time (DTCO), order time (OTCO), and fire request time (FRT). Figure 7 shows the two types of command time of the platoon leaders, namely the decision-making time (DTPL), and order/report time (ORTPL). In addition to the division of the command time, we consider the combat factors of training level, reflected by the probability of hit (PH) and breaching time (BT), for the blue soldiers. We use the loss exchange ratio (LER) as the performance measure, as described in Table 4.
- 5.2
- Many researchers have emphasised the importance of speed in
military C2 processes (Cothier
& Levis 1985; Scott
1993; Van Creveld 1985;
Zsambok & Klein 2014),
and the training level of soldiers has always been regarded as a
crucial factor in combat. We generate hypotheses to 1) quantitatively
analyse the importance of detailed C2 tasks, 2) investigate the
possible relationship between detailed C2 tasks and the training levels
of soldiers and 3) test for a synergistic effect between the
decision-making time of the commander and platoon leaders and the
probability of hit, which is a typical factor used to indicate
soldiers' training level. Our hypotheses are listed in Table 5. We use 1) meta-modelling with a
linear regression model, 2) analysis of variance (ANOVA) and 3)
one-tailed t-tests to test the hypotheses.
Table 5: Generated hypotheses regarding the decision-making of commanders. Hypotheses from previous research Hypotheses tested by simulation data Test method HA H1 H1o: Rapid DTCO increases combat effectiveness
H11: Rapid DTCO does not increase combat effectivenessANOVA H2 H2o: Rapid DTPL increases combat effectiveness
H21: Rapid DTPL does not increase combat effectivenessANOVA H3 H3o: Rapid FRT increases combat effectiveness
H31: Rapid FRT does not increase combat effectivenessANOVA HB H4 H4o: Rapid OTCO increases combat effectiveness
H41: Rapid OTCO does not increase combat effectivenessANOVA H5 H5o: Rapid ORTPL increases combat effectiveness
H51: Rapid ORTPL does not increase combat effectivenessANOVA HA,
HCH6 H6o: Synergistic effects exist between DTCO and PH
H61: Synergistic effects do not exist between DTCO and PHMeta-modelling and ANOVA H7 H7o: Synergistic effects exist between DTPL and PH
H71: Synergistic effects do not exist between DTPL and PHMeta-modelling and ANOVA H8 H8o: LER of slow DTCO (10 min) with high training level (PH = 0.8, BT = 2 min) is higher than LER of rapid DTCO (3 min) with medium training level (PH = 0.6, BT = 4 min) (\(\mu_{\rm 0.8,2,10(DTCO)} > \mu_{\rm 0.6,4,3(DTCO)}\))
H81: \(\mu_{\rm 0.8,2,10(DTCO)} \leq \mu_{\rm 0.6,4,3(DTCO)}\)One-tailed
t-testH9 H9o: LER of slow FRT (10 min) with high training level (PH = 0.8, BT = 2 min) is higher than LER of rapid FRT (3 min) with medium training level (PH = 0.6, BT = 4 min) (\(\mu_{\rm 0.8,2,10(FRT)} > \mu_{\rm 0.6,4,3(FRT)}\))
H91: \(\mu_{\rm 0.8,2,10(FRT)} \leq \mu_{\rm 0.6,4,3(FRT)}\)One-tailed
t-testH10 H10o: LER of slow DTPL (10 min) with high training level (PH = 0.8, BT = 2 min) is higher than LER of rapid DTPL (3 min) with medium training level (PH = 0.6, BT = 4 min) (\(\mu_{\rm 0.8,2,10(DTPL)} > \mu_{\rm 0.6,4,3(DTPL)}\))
H101: \(\mu_{\rm 0.8,2,10(DTPL)} \leq \mu_{\rm 0.6,4,3(DTPL)}\)One-tailed
t-test - 5.3
- Hypotheses 1 to 3 (H1 to H3) test whether faster decision-making times in military C2 always show higher combat effectiveness. HA from previous research (see Table 3) is related to H1 to H3. In contrast, hypotheses 4 and 5 (H4 and H5) test the importance of order and report time in military C2, which are related to HB from previous research in Table 3. We use ANOVA to analyse the differences between the means of LER for hypotheses 1 to 5.
- 5.4
- Hypotheses 6 to 10 (H6 to 10) examine the relationships
between the decision-making time and the soldiers' training level.
Previous studies asserted the importance of the decision-making time (HA)
and the soldiers' training level (HC), but did
not discuss their multiplex relationships. Hypotheses 6 and 7 (H6 and
H7) test possible interactions between PH and the decision-making times
of the commander and platoon leaders (DTCO and DTPL). Meta-modelling
and ANOVA are used to test the interactions. Hypotheses 8 to 10 (H8 to
H10) test the relationships between decision-making times and the
soldiers' training levels (PH and BT). The null hypotheses H8 to H10
indicate that faster decision-making cannot overcome the differences in
the soldiers' training level. We use a one-sided t-test to test whether
the null hypotheses are supported.
Experimental Design Table
- 5.5
- We use a full factorial design for the experiments to
examine the possible intervention components according to our
hypotheses. Table 6 shows the
experiment design with the simulation model. The seven variables
correspond to the experimental and independent factors. We assume that
the command times and breaching time follow a Poisson distribution with
the mean of the average delay times (ROK
Army 2008).
Table 6: Experiment design of the infantry company engagement model Experiment variable name Levels Implications Decision-making time for
company commander (DTCO)3, 5, 10 (min) Average delay time for decision-making for company commander (Poisson distribution with mean of the values) Decision-making time for
platoon leader (DTPL)3, 5, 10 (min) Average delay time for decision-making for platoon leader (Poisson distribution with mean of the values) Fire request time (FRT) 3, 5, 10 (min) Average delay time to request mortar fire (Poisson distribution with mean of the values) Order time for
company commander (OTCO)1, 3, 5 (min) Average delay time for company commander to issue orders to platoon leaders (Poisson distribution with mean of the values) Order/report time for
platoon leader (ORTPL)1, 3, 5 (min) Average delay time for platoon leaders to issue orders and report situation (Poisson distribution with mean of the values) Probability of hit (PH) 0.4, 0.6, 0.8 Three levels of blue soldiers' marksmanship Breaching time (BT) 2, 4, 6 (min) Average delay time to breach obstacles (Poisson distribution with mean of the values) Total number of
experiment cells2187 cells 3 × 3 × 3 × 3 × 3 × 3 × 3 cases for C2 models
(Replicated 20 times)
 Simulation
Results
Simulation
Results
-
Overall simulation results
- 6.1
- We analyse the performance measure, the loss exchange ratio
(LER), to find potential areas for improving the C2 practice of the
company unit. Figure 16 shows
the changes in the LER in relation to 1) two training levels of
soldiers, probability of hit and breaching time; and 2) the command
times of the company commander. The results demonstrate that the
company commander's DTCO and FRT are significantly more important than
the OTCO.
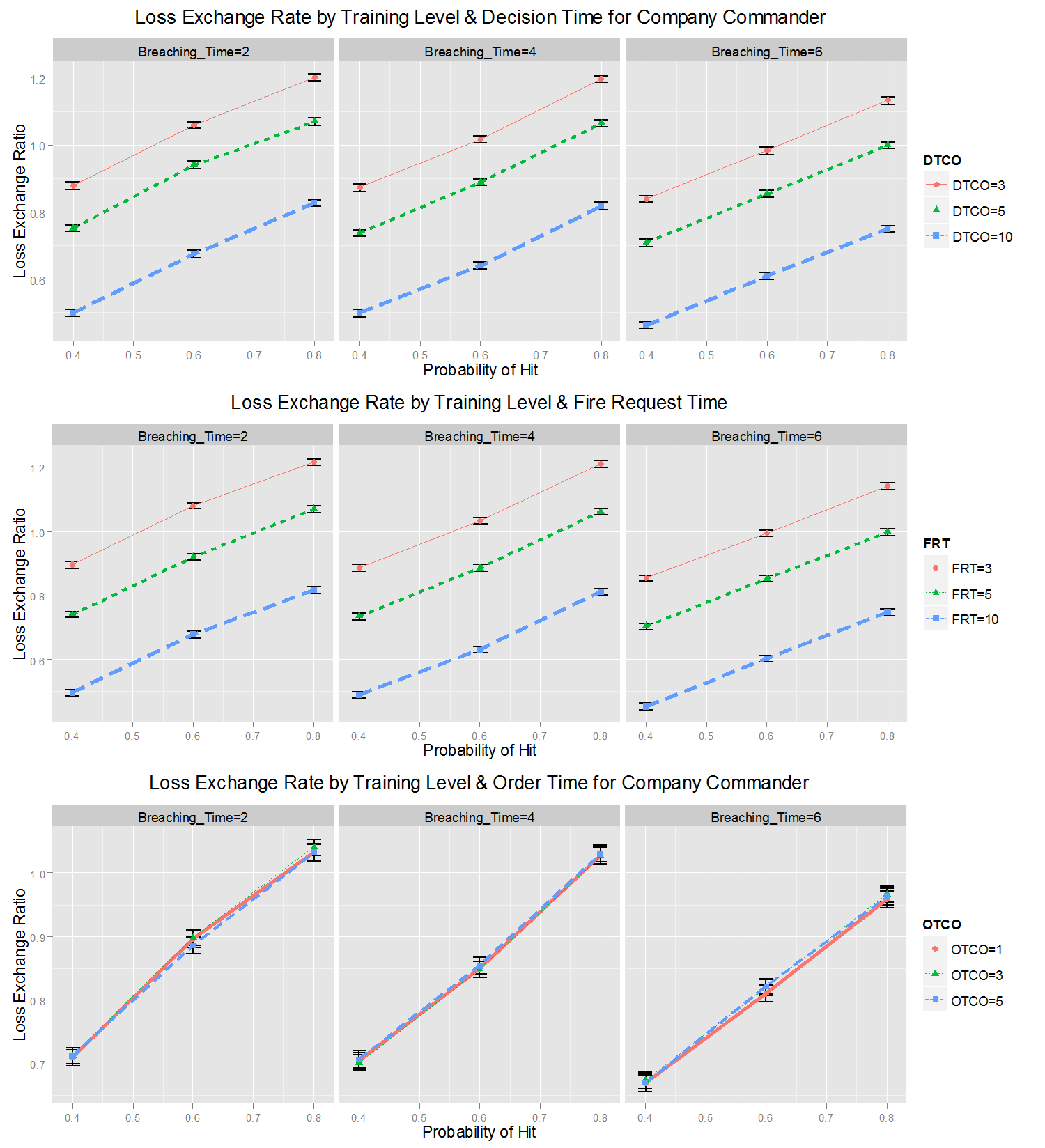
Figure 16. Changes of Loss Exchange Ratio (LER) by Soldiers' Training Level and Commanding Times of the Company Commander. Error bars of 95% confidence intervals - 6.2
- Figure 17 shows
the same correlation between the LER, training levels, and command
times of the platoon leader. When the training level is high, the DTPL
is not critical (see the overlapping confidence interval of the LER for
breaching time (BT) = 2 and probability of hit (PH) = 0.8 of the DTPL
in Figure 15), although the
DTPL becomes a significant factor when the BT and PH become worse.
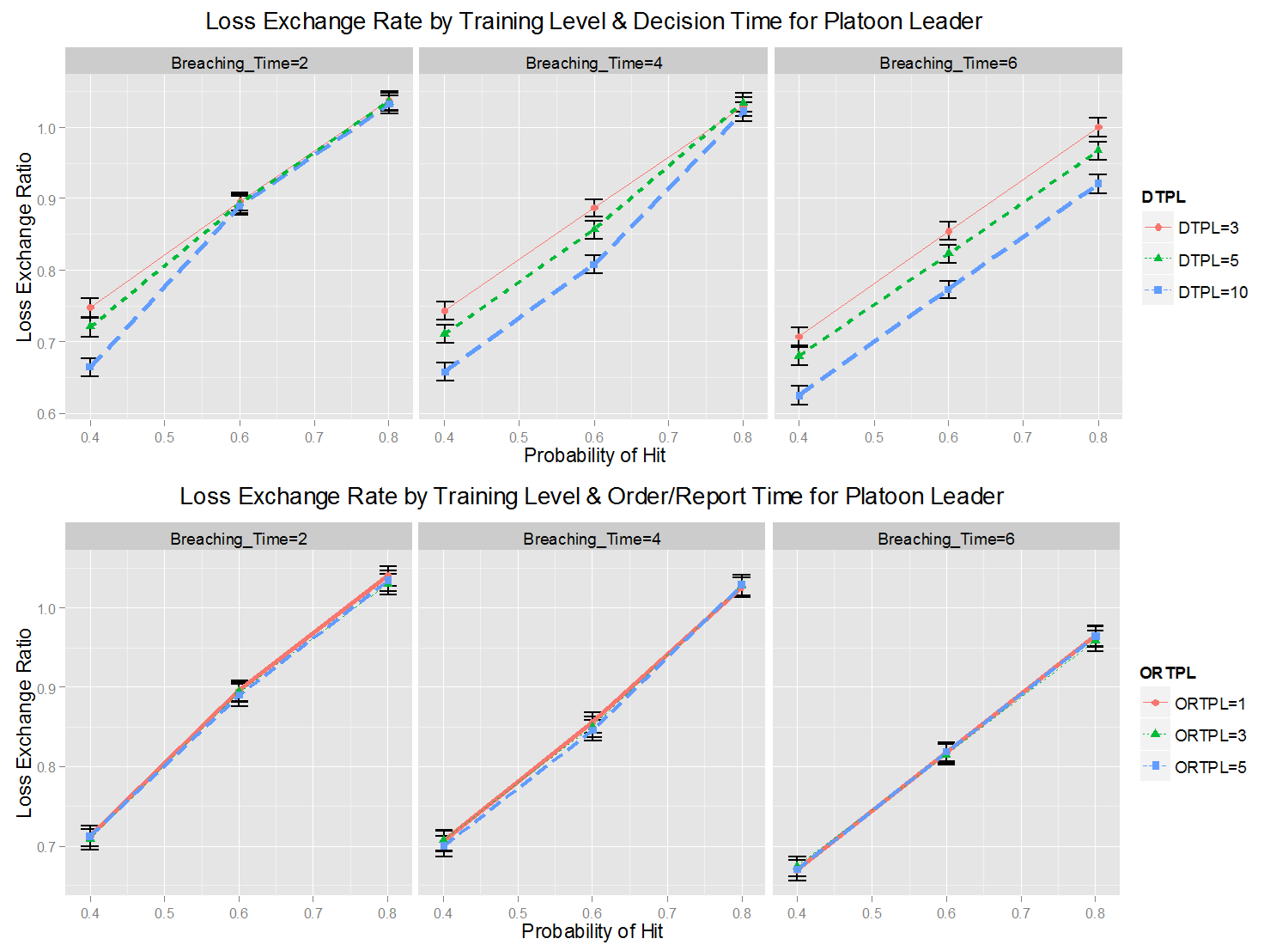
Figure 17. Changes of Loss Exchange Ratio (LER) by Soldiers' Training Level and Commanding Times of the Platoon Leader Hypotheses tests
- 6.3
- Because the chart analysis lacks statistical rigor, we test
our hypotheses using t-tests, meta-modelling and ANOVA. First, the
meta-modelling of the simulation results with the linear regression
model reveals the strength of the factors in determining performance
(Table 7). The analysis
confirms that all of the experimental factors except OTCO and ORTPL
contribute robustly to the model's performance. It also shows an
interaction between DTPL and PH (see the corresponding P values). The
test statistics show the validity of the regression model (F = 18,020;
\(p < 0.001\)).
Table 7: Meta-model analysis on simulation results. Standardized coefficient for sensitivity of factors, and P-value for robustness of factors (*: \(p < 0.01\)) Experiment variable name Standardized coefficient Pr(> |t|) Decision-making time for company commander (DTCO) - 0.5252 <0.001* Decision-making time for platoon leader (DTPL) -0.1896 <0.001* Fire request time (FRT) −0.5525 <0.001* Order time for company commander (OTCO) 0.0027 0.2127 Order/report time for platoon leader (ORTPL) -0.0038 0.0871 Probability of hit (PH) 0.3734 <0.001* Breaching time (BT) −0.0867 <0.001* Interaction between DTCO and PH (DTCO*PH) -0.0081 0.5460 Interaction between DTPL and PH (DTPL*PH) 0.1843 <0.001* Adj. R-square 0.7875 F for change in R-square 18,020 <0.001* - 6.4
- However, the results for the sensitivities in the changes of the experimental factors are different. For instance, FRT and DTCO are by far the most sensitive factors, which indicates the importance of the company commander's C2. The PH is the third-most-significant factor in combat, which suggests that the training of soldiers should not be ignored in the success of a mission. In addition, the sensitivity of DTCO is much greater than that of DTPL, which confirms the importance of the company commander compared to the platoon leaders.
- 6.5
- Second, the ANOVA results in Table 8
show the significance of the factors and their correlations. In
general, the ANOVA results confirm the meta-modelling results with some
additional findings. ANOVA, which focuses on the variance in the
performance, is used to examine the FRT (F = 32438.473), DTCO (F =
29681.555) and PH (F = 19639.133). As shown by the meta-modelling
analysis, FRT and DTCO, which are the C2 times of the company
commander, are important factors with respect to variation in
performance. Here, FRT indicates the C2 time for fire support, which is
also the most important factor in the ANOVA results.
Table 8: ANOVA for significance analysis of experiment factors and their compounding factors (*: \(p < 0.01\)) Source DF SS MS F Pr > F DTPL 2 24.01 12.01 660.198 <0.001* DTCO 2 1079.63 539.81 29681.555 <0.001* BT 2 30.32 15.16 833.559 <0.001* PH 2 714.35 357.17 19639.133 <0.001* FRT 2 1179.90 589.95 32438.473 <0.001* OTCO 2 0.08 0.04 2.170 0.1142 ORTPL 2 0.06 0.03 1.727 0.1778 DTCO*PH 4 0.10 0.03 1.434 0.2196 DTPL*PH 4 3.52 0.88 48.394 <0.001* Error 43717 795.07 0.02 Total 43739 3827.04 - 6.6
- The meta-modelling and ANOVA results indicate that the null hypotheses of H1, H2 and H3 are not rejected and the null hypotheses of H4 and H5 are rejected. These results indicate that we need not spend too much effort on reducing the order and report times in C2 for a small tactical unit.
- 6.7
- Another finding is the compounding effects of DTPL and PH.
When these factors are improved simultaneously, a synergistic effect is
seen to improve the LER, although these factors are not compounded with
the factors relating to the company commander. Thus, the null
hypothesis of H6 is rejected, and the null hypothesis of H7 not
rejected. The platoon leader and the soldiers should be trained
together to simultaneously increase their efficiency, whereas the
company commander can undergo C2 training independently of the
platoon-level training. Although this arrangement may be feasible in
some settings, given that basic infantry operations are initiated at
the company level, this suggestion should be interpreted as an
indication that additional C2 training should be provided for company
commanders in addition to platoon and soldier training. Table 9 shows the results of the
hypothesis tests for hypotheses 1 to 7 (H1 to H7) according to the
meta-modelling and ANOVA.
Table 9: Results of hypothesis tests for hypotheses 1 to 7 (H1 to H7). Null hypotheses Decision H1 H1o: Rapid DTCO increases combat effectiveness Not rejected H2 H2o: Rapid DTPL increases combat effectiveness Not rejected H3 H3o: Rapid FRT increases combat effectiveness Not rejected H4 H4o: Rapid OTCO increases combat effectiveness Reject H5 H5o: Rapid ORTPL increases combat effectiveness Reject H6 H6o: Synergistic effects exist between DTCO and PH Reject H7 H7o: Synergistic effects exist between DTPL and PH Not rejected - 6.8
- Finally, we test hypotheses 8 to 10 (H8 to H10) using a
one-tailed t-test. The hypotheses address the relationships between
command times and soldiers' training level (PH and BT). Table 10 shows the results, which
indicate that rapid decision-making (DTCO) and fire request time (FRT)
by the company commander can overcome an inferior training level of
soldiers.
Table 10: One-tailed t-test results for hypotheses 8 to 10 (H8 to H10) (*: \(p < 0.01\)). Hypotheses n Mean SD t df Pr(>|t|) Decision H8 H80
H811,620
1,6200.8287
1.01900.2132
0.2157-25.2532
3238
1
Reject H9 H90
H911,620
1,6200.8178
1.03400.2011
0.2077-30.1072
3235
1
Reject H10 H100
H1011,620
1,6201.0319
0.88730.2637
0.256315.8293
3235
<0.001*
Not rejected
 Conclusion
Conclusion
- 7.1
- The modelling and simulation of the C2 of the army spear-head, i.e. the infantry company unit, has largely been overlooked compared to studies at the battalion, division, and theatre levels. The models that do exist are often limited to either very small scale models with detailed soldier behaviour, rather than C2 processes, or very abstract models that treat the company as a single entity, both of which misrepresent the operations of infantry units.
- 7.2
- Using agent-based modelling and a set of virtual experiments, we modelled and simulated an infantry company-level engagement that included C2 models and analysed the combat effectiveness of C2 and the C2 delay times. Our results provide a number of insights on C2, in particular that C2 systems are essential, especially for tactical units with low levels of combat training. We also examined the strength and robustness of the experimental factors concerning C2 and the interactions between these C2 factors and soldiers' training level. However, the result should not be interpreted as flawless analyses, and some of the analysed tasks may be more important than others in the real world. These limitations originate from the limited modelled features of the operation and the limited modelling scope in the C2 hierarchy.
- 7.3
- Overall, the results of our virtual experiments demonstrate the importance of detailed C2 analysis of small-scale, front-line echelons. Drilling is not the only solution for improving the performance of such units, although the current practice emphasises repeated drilling at the final stage of C2. Our results indicate that the important tasks in C2 differ according to the training level of the soldiers, the operational progress, and the inherent nature of the task. Therefore, commanders should be trained on the basis of such analytical results, rather than according to a single, static standard that does not distinguish between the differences in the operational environment.
 Acknowledgements
Acknowledgements
- This research was supported by the Defence Acquisition Program Administration and the Agency for Defence Development, under contract UD140022PD, Korea.
 Appendix:
Pseudo codes for atomic model behaviour
Appendix:
Pseudo codes for atomic model behaviour
-
Algorithm 1. Pseudo code for the commander's decision-making (DecisionMaking) 1:\(\hspace{2mm}\) // Find Vulnerable Point 2:\(\hspace{2mm}\) areaXPos ← width of area of operation 3:\(\hspace{2mm}\) areaYPos ← depth of area of operation 4:\(\hspace{2mm}\) vulnerability ← 0 // level of vulnerability of a position 5:\(\hspace{2mm}\) for i, j ←0 to areaXPos, areaYPos 6:\(\hspace{2mm}\) \(\hspace{10mm}\)newVulnerability ← MountaineousLevel(\(i, j\)) − ObstacleLevel(\(i, j\)) 7:\(\hspace{2mm}\) \(\hspace{5mm}\)if \(newVulnerability > vulnerability\) then 8:\(\hspace{2mm}\) \(\hspace{10mm}\)vulnerability ← newVulnerability 9:\(\hspace{2mm}\) \(\hspace{10mm}\) vulnerableXPos ← \(i\) 10:\(\hspace{2mm}\) \(\hspace{10mm}\) vulnerableYPos ← \(j\) 11:\(\hspace{2mm}\) \(\hspace{10mm}\) return vulnerableXPos, vulnerableYPos 12:\(\hspace{2mm}\) \(\hspace{5mm}\) end if 13:\(\hspace{2mm}\) end for 14:\(\hspace{2mm}\) 15:\(\hspace{2mm}\) // Allocate missions 16:\(\hspace{2mm}\) Platoon with largest number of soldiers ← Assault 17:\(\hspace{2mm}\) Platoon second largest ← Breach 18:\(\hspace{2mm}\) Platoon remained ← Support 19:\(\hspace{2mm}\) 20:\(\hspace{2mm}\) //Set assault readiness position 21:\(\hspace{2mm}\) for \(i, j\) ←0 to areaXPos, areaYPos 22:\(\hspace{2mm}\) \(\hspace{5mm}\)if MountaineousLevel(\(i, j\)) is high then 23:\(\hspace{2mm}\) \(\hspace{10mm}\) if 200 ≤ distance to objective ≤ 500 then 24:\(\hspace{2mm}\) \(\hspace{15mm}\) for \(l, k\) ← \(i, j\) to spaceRequired // Check Space 25:\(\hspace{2mm}\) \(\hspace{20mm}\) if MountaineousLevel(\(l, k\)) is high then 26:\(\hspace{2mm}\) \(\hspace{25mm}\) countSpace++ 27:\(\hspace{2mm}\) \(\hspace{30mm}\) if countSpace enough then 28:\(\hspace{2mm}\) \(\hspace{35mm}\) return \(i, j\) 29:\(\hspace{2mm}\) \(\hspace{30mm}\)else countSpace ← 0 30:\(\hspace{2mm}\) \(\hspace{30mm}\) end if 32:\(\hspace{2mm}\) \(\hspace{20mm}\)else countSpace ← 0 33:\(\hspace{2mm}\) \(\hspace{20mm}\)end if 34:\(\hspace{2mm}\) \(\hspace{15mm}\)end for 35:\(\hspace{2mm}\) \(\hspace{10mm}\) end if 36:\(\hspace{2mm}\) \(\hspace{5mm}\)end if 37:\(\hspace{2mm}\) end for 38:\(\hspace{2mm}\) 39:\(\hspace{2mm}\) //Set fire support position 40:\(\hspace{2mm}\) for \(i, j\) ←0 to areaXPos, areaYPos 41:\(\hspace{2mm}\) \(\hspace{5mm}\) if MountaineousLevel(\(i, j\)) is high then 42:\(\hspace{2mm}\) \(\hspace{10mm}\) if 400 ≤ distance to objective ≤ 1,000 then 43:\(\hspace{2mm}\) \(\hspace{15mm}\)for \(l, k\) ← \(i, j\) to spaceRequired // Check Space 44:\(\hspace{2mm}\) \(\hspace{20mm}\) if MountaineousLevel(l, k) is high then 45:\(\hspace{2mm}\) \(\hspace{25mm}\) countSpace++ 46:\(\hspace{2mm}\) \(\hspace{30mm}\) if countSpace enough then 47:\(\hspace{2mm}\) \(\hspace{35mm}\)return \(i, j\) 48:\(\hspace{2mm}\) \(\hspace{30mm}\)else countSpace ← 0 49:\(\hspace{2mm}\) \(\hspace{30mm}\)end if 49:\(\hspace{2mm}\) \(\hspace{20mm}\)else countSpace ← 0 50 \(\hspace{20mm}\) end if 51:\(\hspace{2mm}\) \(\hspace{15mm}\)end for 52:\(\hspace{2mm}\) \(\hspace{10mm}\)end if 53:\(\hspace{2mm}\) \(\hspace{5mm}\) end if 54:\(\hspace{2mm}\) end for 55:\(\hspace{2mm}\) 56:\(\hspace{2mm}\) //Order mortar fire 57:\(\hspace{2mm}\) n ← 0 // Number of Arrays for enemy groups 58:\(\hspace{2mm}\) if enemy report (location) comes in then 59:\(\hspace{2mm}\) \(\hspace{5mm}\)if no Array for enemy groups then 60:\(\hspace{2mm}\) \(\hspace{10mm}\) Add enemy location to Array_n 61:\(\hspace{2mm}\) \(\hspace{5mm}\)else 62:\(\hspace{2mm}\) \(\hspace{10mm}\)for i ← 0 to n 63:\(\hspace{2mm}\) \(\hspace{15mm}\)if |centerOfArray_i − locationOfEnemy| ≤ lethalRange/2 then 64:\(\hspace{2mm}\) \(\hspace{20mm}\) add locationOfEnemy to Array_i 65:\(\hspace{2mm}\) \(\hspace{15mm}\)else 66:\(\hspace{2mm}\) \(\hspace{20mm}\)n++ 67:\(\hspace{2mm}\) \(\hspace{20mm}\)add locationOfEnemy to Array_n 68:\(\hspace{2mm}\) \(\hspace{15mm}\) end if 69:\(\hspace{2mm}\) \(\hspace{15mm}\) if sizeOfArray_i ≥ enemy squad size (6 entities in this simulation model) then 70:\(\hspace{2mm}\) \(\hspace{20mm}\) return centerOfArray_i, sizeOfArray_i (for number of rounds to fire) 71:\(\hspace{2mm}\) \(\hspace{15mm}\)end if 69:\(\hspace{2mm}\) \(\hspace{10mm}\) end for 70:\(\hspace{2mm}\) \(\hspace{5mm}\) end if 71:\(\hspace{2mm}\) end if Algorithm 2. Pseudo code for the commander's order (Order) 1:\(\hspace{2mm}\) if order input from DecisionMaking model comes in then 2:\(\hspace{2mm}\) \(\hspace{5mm}\) orderStartTime ← currentTime 3:\(\hspace{2mm}\) \(\hspace{5mm}\)if (currentTime − orderStartTime) > orderDelayTime then 4:\(\hspace{2mm}\) \(\hspace{10mm}\) if input = mission allocation then 5:\(\hspace{2mm}\) \(\hspace{15mm}\)Allocate mission to platoons 6:\(\hspace{2mm}\) \(\hspace{10mm}\) else if input = vulnerable point then 7:\(\hspace{2mm}\) \(\hspace{15mm}\)Send the vulnerable point to the breach platoon 8:\(\hspace{2mm}\) \(\hspace{10mm}\)else if input = assault readiness position then 9:\(\hspace{2mm}\) \(\hspace{15mm}\) Send the assault readiness position to the assault platoon 10:\(\hspace{2mm}\) \(\hspace{10mm}\)else if input = fire support position then 11:\(\hspace{2mm}\) \(\hspace{15mm}\)Send the fire support position to the support platoon 12:\(\hspace{2mm}\) \(\hspace{10mm}\)else if input = movement order then 13:\(\hspace{2mm}\) \(\hspace{15mm}\)Send the movement order to the platoons 14:\(\hspace{2mm}\) \(\hspace{10mm}\)end if 15:\(\hspace{2mm}\) \(\hspace{5mm}\)end if 16:\(\hspace{2mm}\) end if Algorithm 3. Pseudo code for the commander's fire request (FireRequest) 1:\(\hspace{2mm}\) if fire request input from DecisionMaking model comes in then 2:\(\hspace{2mm}\) \(\hspace{5mm}\) fireRequestStartTime ← currentTime 3:\(\hspace{2mm}\) \(\hspace{5mm}\)if (currentTime − fireRequestStartTime) > fireRequestDelayTime then 4:\(\hspace{2mm}\) \(\hspace{10mm}\)Send position of the enemy and number of rounds to fire to the mortar 5:\(\hspace{2mm}\) \(\hspace{5mm}\) end if 6:\(\hspace{2mm}\) end if Algorithm 4. Pseudo code for the platoon leader's decision-making (DecisionMaking) 1:\(\hspace{2mm}\) While Obstacle > 0 do 2:\(\hspace{2mm}\) \(\hspace{5mm}\) if Mission = Breach then 3:\(\hspace{2mm}\) \(\hspace{10mm}\) Breach obstacles 4:\(\hspace{2mm}\) \(\hspace{5mm}\)else 5:\(\hspace{2mm}\) \(\hspace{10mm}\)Stop ad support fire 6:\(\hspace{2mm}\) for i←0 to Min(areaXPos-CurrentXPos, areaYPos-CurrentYPos) 7:\(\hspace{2mm}\) \(\hspace{5mm}\) if distanceX > distanceY then 8:\(\hspace{2mm}\) \(\hspace{10mm}\)if MountaineousLevel(CurrentXPos+i, CurrentYPos) is medium or high then 9:\(\hspace{2mm}\) \(\hspace{15mm}\) Move position to (CurrentXPos+i, CurrentYPos) 10:\(\hspace{2mm}\) \(\hspace{10mm}\)else if MountaineousLevel(CurrentXPos, CurrentYPos+ j) is medium or high then 11:\(\hspace{2mm}\) \(\hspace{15mm}\)Move position to (CurrentXPos, CurrentYPos +j) 12: \(\hspace{10mm}\)else Move position to (CurrentXPos+i, CurrentYPos) 13:\(\hspace{2mm}\) \(\hspace{10mm}\)end if 13:\(\hspace{2mm}\) \(\hspace{5mm}\)else 14:\(\hspace{2mm}\) \(\hspace{10mm}\)if MountaineousLevel(CurrentXPos, CurrentYPos+i) is medium or high then 15:\(\hspace{2mm}\) \(\hspace{15mm}\)Move position to (CurrentXPos, CurrentYPos+i) 16:\(\hspace{2mm}\) \(\hspace{10mm}\)else if MountaineousLevel(CurrentXPos+i, CurrentYPos) is medium or high then 17:\(\hspace{2mm}\) \(\hspace{15mm}\)Move position to (CurrentXPos+i, CurrentYPos) 18:\(\hspace{2mm}\) \(\hspace{10mm}\) else Move position to (CurrentXPos, CurrentYPos+i) 19: \(\hspace{5mm}\) end if Algorithm 5. Pseudo code for the platoon leader's order/report (Order/Report) 1:\(\hspace{2mm}\) if input from DecisionMaking model comes in then 2:\(\hspace{2mm}\) \(\hspace{5mm}\) orderReportStartTime ← currentTime 3:\(\hspace{2mm}\) \(\hspace{5mm}\) if (currentTime − orderReportStartTime) > orderReportDelayTime then 4:\(\hspace{2mm}\) \(\hspace{10mm}\) if input = order then 5:\(\hspace{2mm}\) \(\hspace{15mm}\)Send order to combat entities 6:\(\hspace{2mm}\) \(\hspace{10mm}\) else if input = report then 7:\(\hspace{2mm}\) \(\hspace{15mm}\)Send report to company commander 8:\(\hspace{2mm}\) \(\hspace{10mm}\) end if 9:\(\hspace{2mm}\) \(\hspace{5mm}\)end if 10:\(\hspace{2mm}\) end if Algorithm 6. Pseudo code for the blue mortar's fire 1:\(\hspace{2mm}\) Count←0 2:\(\hspace{2mm}\) Receive fire request positionOfTheEnemy, NumberOfRound 3:\(\hspace{2mm}\) Count\7#8592; NumberOfRound 2:\(\hspace{2mm}\) while Count > 0 3:\(\hspace{2mm}\) \(\hspace{5mm}\) if randomNumber(0,1) > P(K)m then 4:\(\hspace{2mm}\) \(\hspace{10mm}\)Remove the enemy in the space 5:\(\hspace{2mm}\) \(\hspace{10mm}\)Count = Count-1 5:\(\hspace{2mm}\) \(\hspace{5mm}\) end if 6:\(\hspace{2mm}\) end while Algorithm 7. Pseudo code for the blue soldier's move 1:\(\hspace{2mm}\) if soldierStatus is "Moving" then 2:\(\hspace{2mm}\) \(\hspace{5mm}\)if platoonStatus is "Infiltrating" then 3:\(\hspace{2mm}\) \(\hspace{10mm}\)Move to the release point by 1 step 4:\(\hspace{2mm}\) \(\hspace{5mm}\)end if 5:\(\hspace{2mm}\) \(\hspace{5mm}\) if platoonStatus is "Attacking" then 6:\(\hspace{2mm}\) \(\hspace{10mm}\) Move to the mid-objective by 1 step 7:\(\hspace{2mm}\) \(\hspace{5mm}\)end if 8:\(\hspace{2mm}\) \(\hspace{5mm}\) if platoonStatus is "Sweeping" then 9:\(\hspace{2mm}\) \(\hspace{10mm}\) Move to the final objective by 1 step 10:\(\hspace{2mm}\) \(\hspace{5mm}\)end if 11: end if Algorithm 8. Pseudo code for the blue soldier's breach 1:\(\hspace{2mm}\) if soldierStatus is turned to "Breaching" then 2:\(\hspace{2mm}\) \(\hspace{5mm}\) breachStartTime ← currentTime 3:\(\hspace{2mm}\) end if 4:\(\hspace{2mm}\) if (currentTime − breachStartTime) > breachDelayTime then 5:\(\hspace{2mm}\) \(\hspace{5mm}\)Remove the obstacle from the space 6:\(\hspace{2mm}\) end if Algorithm 9. Pseudo code for the blue soldier's detector 1:\(\hspace{2mm}\) Scan neighbor cells within detecting range 2:\(\hspace{2mm}\) if numberOfEnemyWithinRange > 0 then 3:\(\hspace{2mm}\) \(\hspace{5mm}\)Choose an enemy randomly 4:\(\hspace{2mm}\) \(\hspace{5mm}\)return positionOfTheEnemy 5:\(\hspace{2mm}\) end if Algorithm 10. Pseudo code for the blue soldier's fire 1:\(\hspace{2mm}\) Receive positionOfTheEnemy 2:\(\hspace{2mm}\) while The enemy is not killed 3:\(\hspace{2mm}\) \(\hspace{5mm}\)if randomNumber(0,1) > P(H) then 4:\(\hspace{2mm}\) \(\hspace{10mm}\)Remove the enemy in the space 5:\(\hspace{2mm}\) \(\hspace{5mm}\) end if 6:\(\hspace{2mm}\) end while
 References
References
- ABERDEEN, D., Thiebaux, S.,
& Zhang, L. (2004). Decision-Theoretic Military Operations
Planning. In International Conference on Automated Planning
and Scheduling(ICAPS) (pp. 402–412).
ALBERTS, D. S., & Hayes, R. E. (2006). Understanding command and control. Washington, DC.
BAE, J., Lee, K., Kim, H., Lee, J., Goh, B., Nam, B., … Park, J. (2013). Modeling Combat Entity with POMDP and DEVS. Journal of the Korean Institute of Industrial Engineers, 39(6), 498–516.
BAKKEN, B. T., & Gilljam, M. (2003). Dynamic intuition in military command and control: why it is important, and how it should be developed. Cognition, Technology & Work, 5(3), 197–205. [doi://dx.doi.org/10.1007/s10111-003-0123-1]
BEAL, S. A. (2007). Assessment of Two Desk-Top Computer Simulations Used to Train Tactical Decision Making of Small Unit Infantry Leaders. In Interservice/Industry Training, Simulation, and Education Conference(I/ITSEC). National Training Systems Association.
BLAIS, C., & Galvin, M. K. (2005). Coalition Battle Management Language (C-BML) Study Group Report. In IEEE Fall Simulation Interoperability Workshop. Orlando,FL.
BURNS, C. (1999). Scenario Technology for Planning C2 Exercises. Rome, NY.
CALFEE, S. H. (2003). Autonomous Agent-Based Simulation of an AEGIS Cruiser Combat Information Center Performing Battle Group Air Defense Commander Operations. Naval Postgraduate School.
CARLEY, K., Kjaer-Hansen, J., Newell, A., & Prietula, M. (1992). Plural-Soar: A prolegomenon to artificial agents and organizational behavior. Artificial Intelligence in Organization and Management Theory: Models of Distributed Activity, 87–118.
CARLEY, K. M., & Lin, Z. (1995). Organizational Designs Suited to High Performance Under Stress. IEEE Transactions on Systems, Man and Cybernetics, 25(2), 221–230.
CHOI, B. K., & Kang, D. (2013). Modeling and Simulation of Discrete Event Systems. Hoboken, NJ: John Wiley & Sons.
COTHIER, P. H., & Levis, A. H. (1985). Timeliness and measures of effectiveness in command and control. IEEE Transactions on Systems, Man, and Cybernetics, 16(6), 844–853.
DRILLINGS, M., & Serfaty, D. (2014). Naturalistic decision making in command and control. In Naturalistic Decision Making (pp. 71–80). Psychology Press.
ENDSLEY, M. R. (1997). The role of situation awareness in naturalistic decision making. In Natual Decision Making (pp. 269–283). Mahwah, NJ: Lawrence Erlbaum.
ENDSLEY, M. R., Holder, L. D., Leibrecht, B. C., Garland, D. J., Wampler, R. L., & Matthews, M. D. (2000). Modeling and Measuring Situation Awareness in the Infantry Operational Environment.
ENTIN, E. E., Needalman, A., Mikaelian, D., & Tenny, R. R. (1988). Experiment II report: The effects of option planning and battle workload on command and control. Burlington, MA.
ERIKSSON, P., & More, P. (2008). Machine Interpretable Representation of Commander's Intent. In Proceedings of the 13th International Command and Control Research and Technology Symposium(ICCRTS).
GALLANT, S. I. (1995). Neural Network Learning and Expert Systems. Cambridge, MA: The MIT Press.
GILBERT, N. (2008). Agent-based models (No. 153). Sage.
GILBOA, I., & Schmeidler, D. (1995). Case-Based Decision Theory. The Quarterly Journal of Economics, 110(3), 605–639.
HAYWARD, P. (1968). The Measurement of Combat Effectiveness. Operations Research, 16(2), 314–323. [doi://dx.doi.org/10.1287/opre.16.2.314]
HEADQUARTERS, D. O. T. A. (1992). [FM 5-250] Explosives and Demolitions.
HIEB, M. R., & Schade, U. (2007). Formalizing Command Intent Through Development of a Command and Control Grammar. In Proceedings of the 12h International Command and Control Research and Technology Symposium(ICCRTS).
HILTON, J., & Diallo, S. (2014). The Scenario Development Tool: Enabling Planners to Develop and Refine a Plan at a Rapid Pace. In Proceedings of the 19h International Command and Control Research and Technology Symposium(ICCRTS).
JONES, R. M., Laird, J. E., Nielsen, P. E., Coulter, K. J., Kenny, P., & Koss, F. V. (1999). Pilots for Combat Flight Simulation. AI Magazine, 20(1), 27–42.
KAEMPH, G. L., Klein, G. A., Thordsen, M. L., & Wolf, S. (1996). Decision making in complex naval command-and-control environments. The Journal of the Human Factors and Ergonomics Society, 38(2), 220–231.
KEVIN, Y. K., Mitchell, R., Solomon, M., & Lam, N. (2008). Time Latency of Information in Networked Operations: Effect of "Human in the Loop."
KIM, J., Moon, I. C., & Kim, T. G. (2012). New insight into doctrine via simulation interoperation of heterogeneous levels of models in battle experimentation. Simulation, 88(6), 649–667. [doi://dx.doi.org/10.1177/0037549711414773]
KLEIN, G. (2008). Naturalistic Decision Making. Human Factors: The Journal of the Human Factors and Ergonomics Society, 50(3), 456–460. [doi://dx.doi.org/10.1518/001872008X288385]
KLEIN, G. A. (1989). Strategies Decision Making. Military Review, 64(5), 56–64.
KLEIN, G. A. (1993). A recognition-primed decision (RPD) model of rapid decision making. In Decision Making in Action: Models and Methods (pp. 138–147). [doi://dx.doi.org/10.1002/bdm.3960080307]
KLEIN, G. A. (1999). Sources of power: How people makde decisions. MIT press.
KLEIN, G. A., Orasanu, J., Calderwood, R., & Zsambok, C. E. (1993). Decision Making in Action: Models and Methods. Norwood, NJ: Ablex Publishing Corporation.
KRAUSMAN, A. S., Elliott, L. R., & Pettitt, R. A. (2005). Effects of Visual , Auditory , and Tactile Alerts on Platoon Leader Performance and Decision Making.
KRAUSMAN, A. S., Pettitt, R. A., & Elliott, L. R. (2006). Effects of Alerts on Army Infantry Platoon Leader Decision Making Performance.
LAWSON, J. S. (1981). The role of time in a command control system. In Proceedings of the 4th MIT/ONR Workshop on Distributed Information and Decision Systems Motivated by Command-Control-Communication (C3) Problems. Cambridge, MA.
LEEDOM, D. K. (2004). The Analytic Representation of Sensemaking and Knowledge Management within a Military C2 Organization.
LEVIS, A. H., & Athans, M. (1989). Command and Control Theory. Combridge Lab for information and decision systems, Massachesetts institute of technology.
LIEBHABER, M. J., & Smith, C. A. P. (2000). Naval Air Defense Threat Assessment: Cognitive Factors and Model. San Diego, CA.
MCGRATH, J. E. (1962). The influence of positive interpersonal relations on adjustment and effectiveness in rifle teams. Journal of Abnormal and Social Psychology, 65(6), 365–375.
MOON, I. C., Carley, K. M., & Kim, T. G. (2013). Modeling and Simulating Command and Control For Organizations Under Extreme Situations. Springer.
NAYLOR, T. H., & Finger, J. M. (1967). Verification of computer simulation models. Management Science, 14(2), B–92– B–106.
PASCUAL, R., & Henderson, S. (1997). Evidence of Naturalistic Decision Making in Military Command and Control. In Naturalistic Decision Making (pp. 217–226). Mahwah, NJ: Lawrence Erlbaum Associates.
PLEBAN, R. J., Eakin, D. E., & Salter, M. S. (2000). Analysis of Mission-Based Scenarios for Training Soldiers and Small Unit Leaders in Virtual Environments. Alexandria, VA.
PLEBAN, R. J., & Salter, M. S. (2001). Training and Assessing Decision-Making Skills in a Virtual Environment. In Interservice/Industry Training, Simulation, and Education Conference(I/ITSEC). National Training Systems Association.
POSLAD, S. (2007). Specifying protocols for multi-agent systems interaction. ACM Transactions on Autonomous and Adaptive Systems, 2(4), 15:1–15:24. [doi://dx.doi.org/10.1145/1293731.1293735]
RILEY, J. M., Endsley, M. R., Bolstad, C. A., & Cuevas, H. M. (2006). Collaborative planning and situation awareness in Army command and control. Ergonomics, 49(12-13), 1139–53. [doi://dx.doi.org/10.1080/00140130600612614]
ROBINSON, S. (2004). Simulation: the practice of model development and use. Chichester: John Wiley & Sons.
ROK ARMY. (2008). [RP 1-30-1] Guidance of Combat Skill for Small Rifle Units. Headquarters, Republic of Korea Army.
SCHWENK, C. R. (1984). Cognitive simplification processes in strategic decision-making. Strategic Management Journal, 5, 111–128. [doi://dx.doi.org/10.1002/smj.4250050203]
SCOTT, H. D. J. (1993). Time Management and the Military Decision Making Process. Fort Leavenworth, KS.
SERFATY, D., MacMillan, J., Enton, E. E., & Enton, E. B. (2014). The Decision Making Expertise of Battle Commanders. In Naturalistic Decision Making (pp. 233–246). Psychology Press.
SISO. (2008). [SISO-STD-007-2008] SISO Standard for: Military Scenario Definition Language(MSDL). Simulation Interoperability Standards Organization(SISO).
SOKOLOWSKI, J. A. (2012). Human Behavior Modeling: A Real-World Application. In Handbook of Real-World Applications in Modeling and Simulation (pp. 26–92). Hoboken, NJ: John Wiley & Sons.
SUNG, C., & Kim, T. G. (2012). Collaborative Modeling Process for Development of Domain-Specific Discrete Event Simulation Systems. Systems, Man, and Cybernetics, Part C: Applications and Reviews, IEEE Transactions on, 42(4), 532–546.
THIBAULT, D. U. (2005). APP-6A: Military Symbols for Land Based Systems. Retrieved from http://scholar.google.com/scholar?hl=en&btnG=Search&q=intitle:MILITARY+SYMBOLS+FOR+LAND+BASED+SYSTEMS#4
THOMPSON, J., Smith, S., Morey, J. C., & Osborne, A. D. (1980). Effectiveness of Improved Basic Rifle Marksmanship Training Programs (Research Report 1255).
THUNHOLM, P. (2005). Planning Under Time Pressure: An Attempt Toward a Prescriptive Model of Military Tactical Decision Making. How Professionals Make Decisions, 43–56.
THUVE, H. (2001). TOPFAS(tool for operational planning, force activation and simulation. In Proceedings of the 6h International Command and Control Research and Technology Symposium(ICCRTS). Annapolis, MD.
TOLK, A. (2012). Modeling Communications, Command, and Control. In Engineering Principles of Combat Modeling and Distributed Simulation (pp. 171–183). Hoboken, NJ: John Wiley & Sons.
U.S. ARMY. (1995). [FM7-30] The Infantry Brigade. Washington, DC: Headquarters, Department of Army.
U.S. ARMY. (1997). [FM101-5] Staff Organization and Operations. Washington, DC: Headquarters, Department of Army.
U.S. ARMY. (2003a). [FM 7-1] Battle Focused Training (Vol. 1). Washington, DC: Headquarters, Department of Army.
U.S. ARMY. (2003b). [FM6-0]Mission Command: Command and Control of Army Forces. Washington, DC: Headquarters, Department of Army.
U.S. ARMY. (2006a). [FM3-21.10] The Infantry Rifle Company (Vol. 10). Headquarters, Department of Army.
U.S. ARMY. (2006b). [FM3-21.20] The Infantry Battalion. Washington, DC: Headquarters, Department of Army.
U.S. ARMY. (2008a). [FM 3-0] Operations. Washington, DC: Headquarters, Department of Army.
U.S. ARMY. (2008b). [TRADOC Reguation 71-4] Standard scenarios for capability development. Washington, DC: Headquarters, Department of Army.
U.S. ARMY. (2011). [ATTP 5-0.1] Commander and Staff Officer Guide. Washington, DC: Headquarters, Department of Army.
U.S. TRADOC. (2000). JANUS V7.06D Documentation Software Algorithms. TRADOC Analysis Center – WSMR.
VAKAS, D., & Burdick, C. (2001). Commander Behavior and Course of Action Selection in JWARS. In Proceedings of the 2001 Winter Simulation conference (pp. 697–705).
VAN CREVELD, M. L. (1985). Command in war. Harvard University Press.
WAMPLER, R. L., Blankenbeckler, P. N., & Diubac, M. D. (2004). Scenario-Generation Package for Assessing and Training Leader Skills.
WHITE, C. R., Carson, J. L., & Wilbourn, J. M. (1991). Training Effectiveness of an M-16 Rifle Simulator. Military Psychology, 3(3), 177–184.
WOOLDRIDGE, M. (2009). An Introduction to MultiAgent Systems. Baffins Lane, Chichester: John Wiley & Sons.
WRIGHT, D. P. (2013). 16 Cases of Mission Command. Fort Leavenworth, KS: US Army Combined Arms Center.
YUN, W. S., Moon, I. C., & Lee, T. E. (2013). Entity Level Combat Modeling with Functions of Unit Level Combat. In Interservice/Industry Training, Simulation, and Education Conference(I/ITSEC). National Training Systems Association.
ZIEGLER, B. P., Praehofer, H., & Kim, T. G. (2000). Theory of modeling and simulation: integrating discrete event and continuous complex dynamic systems. Academic press.
ZSAMBOK, C. E., & Klein, G. (2014). Naturalistic decision making. Psychology Press.