 Abstract
Abstract
- Empirical evidences have supported the large heterogeneity in the timing of individuals' activities. Moreover, computational analysis of the agent-based models has shown the importance of the activation regimes. In this paper, we apply four different asynchronous updating schemes including random, uniform, and two state-driven Poisson updating schemes on an agent-based opinion dynamics model. We compare the effect of these activation regimes by measuring the appropriate opinion clustering statistics and also the number of emergent extremists. The results exhibit both qualitative and quantitative difference between different activation regimes which in some cases are counterintuitive. In particular, we find that exposing the radical/moderate agents to more encounters decreases/increases the average number of extremists compared to other types of activation regimes. The results also show that no specific updating scheme can always outperform the others in reaching to consensus.
- Keywords:
- Opinion Dynamics, Activation Regime, Extremism, Opinion Clusters
 Introduction
Introduction
- 1.1
- The term "opinion dynamics" refers to a wide range of models in the social psychology, sociology, physics, and computer science literatures. These models differ in terms of the phenomena of interest, the underlying assumptions and theories, the activation regimes, and updating rules. Usually, the objective of opinion dynamics models is to explore collective behaviors such as reaching to consensus (Huet et al. 2008), emergence of extremists (Deffuant 2006), survival and spreading of minority opinions (Xie et al. 2011), and distributional properties of the opinions (Alizadeh & Cioffi-Revilla 2014).
- 1.2
- Generally, there are two main categories of opinion dynamics models. First are models that are based on statistical physics (Weidlich 1971; Sznajd-Weron 2000; Galam 2005). The underlying concept of these models is a "transition rate" between different states of a social system, and opinion dynamics is considered in terms of order-disorder transitions (Kurmyshev et al. 2011). Castellano et al. (2009) review and summarize the statistical physics models which have been applied in social dynamics problems including the opinion dynamics. The second category of models is agent-based models. Here, the emerging behavior of the social system is studied through the interactions of independent and autonomous agents. That is, no specific goal is set for the agents.
- 1.3
- Agent-based modeling is the fast growing approach to study the collective behavior of large number of people in social science (Cioffi-Revilla 2002). Many agent-based models have been proposed for the dynamics of opinions by capturing the social psychology theories. In any agent-based model, three modeling specifications should be explicitly determined (Page 2005): 1) updating rules, 2) interaction structure, and 3) activation regime. Agent's updating rules can be simple or sophisticated. As Axtell (2001) discusses, one class of agent-based models consists of large number of agents with relatively little cognitive capacity. In this type of models, the agents are very simple meaning they have small number of attributes and methods. But the complexity arises from the huge number of interactions between agents. Conversely, the second class of agent models includes small number of agents with relatively high cognitive ability.
- 1.4
- The interaction structure is the interconnections between agents (Axtell 2001) and can be represented in space or in networks that encode geographic, sociological, or feature based differences (Riolo et al. 2001). Finally, the activation regime (a.k.a. "timing" or "scheduling" or "updating") is the timing of activation. That is, the order on which the agents get called and take their action (Page 2005). Some researchers use "updating scheme" for the same concept, but following Axtell (2001) and Page (2005), we prefer to use "activation regime" as "updating" may get confused with the concept of updating rules in agent-based models which we have discussed above. Moreover, we call it "regime" because it is independent of the agents' opinions and indeed is a parameter of the model (Urbig et al. 2008).
- 1.5
- Studies on cellular automata and agent-based models have shown that different activation regimes produce different results in some models (Axtell 2001; Radax & Rengs 2010; Fates & Chevrier 2010). In general, some of the reported steady-states are artifact of the synchronization of agents' activation. For example, Huberman and Glance (1993) find that by using asynchronous updating, the interesting patterns exhibited in Nowak and May's (1992) work disappears. In another study, Bersini and Detours (1994) show that for modified versions of the game of life and an immune network model, random asynchronous updating leads to stability rather than long transients. Moreover, in the model about the emergence of firms, Axtell (2001) finds that while using random activation show dependence between growth rate and firm size, changing this activation regime to uniform activation exhibits a reverse dependence between the two variables. In addition to computational studies on the effect of activation orders, empirical evidences have also supported the large heterogeneity in the timing of individual activities (Barabási 2005; Oliveira & Barabási 2005; Malmgren et al. 2009; Karsai et al. 2011; Fernández-Gracia et al. 2011).
- 1.6
- Given the potential influence of the activation regime on the qualitative and quantitative properties of the agent-based models, it is surprising that most of the proposed computational opinion dynamics models are based on random or uniform updating. In fact, the impact of applying different activation regimes has received little attention in the opinion dynamics literature. We are aware only of Urbig et al.'s (2008) work on the effect of the number of the agents that interact at each time step. This is a crucial gap in the study of opinion dynamics models because we know that opinion dynamics models usually have large number of simple agents and as Axtell (2001) argues in such models the model specifications (i.e. updating rules, interaction structure, and activation regime) has greater effect on the behavior of the model compared with the model that consists of few sophisticated agents.
- 1.7
- In this paper we want to investigate how applying different agent activation orders may affect the behavior and final output of an opinion dynamics model. In doing so, we apply four different asynchronous activation regimes on the 2-dimensional opinion dynamics model proposed by Huet et al. (2008) and compute the appropriate quantitative measures of opinions. It is important to quantitatively compare the effect of different timing orders because in some cases the qualitative results might be indistinguishable at aggregate level. The number of emergent opinion clusters is a common measure in this sense and have been used by many opinion dynamics researchers (Urbig 2003; Urbig et al. 2008; Huet et al. 2008; Mäs et al. 2014). We also compute and report the maximum cluster size and the number of minority clusters.
- 1.8
- Our forth measure of interest is the phenomenon of drifting toward opinion extremes called Radicalization. A challenging question in radicalization is that why and how extremists become extremists. Several researchers have tried to model the emergence and propagation of extremists in agent-based opinion dynamics models by adding some extremist agents in the population with extreme belief but much lower uncertainty threshold (Deffuant et al. 2002), asymmetric confidence and biased confidence (Hegselmann & Krause 2002), examining the effect of network topology (Amblard & Deffuant 2004), assigning separate uncertainty thresholds for attraction and rejection (Jager & Amblard 2005), incorporating the tendency of adopting the prototypical opinion of a group (Salzarulo 2006), examining the striving for uniqueness among agents (Mäs et al. 2010), and introducing open- and close-minded agents in the population (Lorenz 2010). This paper contributes to the literature of radicalization by examining the heterogeneity of the timing of individuals' interactions.
- 1.9
- The rest of the paper is organized as follows. In section 2, we review the opinion dynamics under bounded confidence and describe our choice for our modeling purposes. In section 3 we introduce four different activation regimes used in the agent-based modeling named uniform, random, and two Poisson activation regimes. Section 4 summarizes simulations that show how the difference in the activation regime influences the qualitative and quantitative properties of the model. Thereby we compare the statistics of opinion clusters and the number of extremists for various values of modeling parameters. Finally, section 5 concludes the paper.
 Agent-based Opinion Dynamics
Models
Agent-based Opinion Dynamics
Models
-
2-1- Opinion Dynamics Models Under Bounded Confidence
- 2.1
- One of the most well-known category of agent-based opinion dynamics model is the Bounded Confidence (BC) model (Krause 1997, 2000). The term "bounded confidence" was coined by Krause (1997) and since after there have been two well-known opinion dynamics under bounded confidence models which have been independently proposed by Deffuant, Weisbuch and others (DW) (2000) and Hegselmann and Krause (HK) (2002). The two models are very much alike, but differ mainly in their communication regimes and slightly in updating mechanisms. While DW model considers random pairwise encounters at each time step in which agents may compromise or not, the HK model allows agents to communicate with all other agents and adopt the average opinion of those who fall in their area of confidence. For a survey of continuous opinion dynamics under bounded confidence models see Lorenz (2007).
- 2.2
- The BC model considers the opinion as a continuous variable representing by a real number. In the BC model, each agent has an opinion and an uncertainty associated with it. Here the uncertainty can be interpreted as the extent to which agents are open to adjust with others' belief during the encounters. When two agents are interacting with each other, if they are close enough in their opinions (i.e. their opinion difference is less than their corresponding uncertainties), they will be attracted by one another and become closer in their opinions. However, if the difference is greater than their associated uncertainties, they will ignore each other and nothing changes.
- 2.3
- Several other extensions of the BC model have been proposed in the literature. Researchers have tried to explore different aspects and applications of the model by changing the initial belief distribution (Jacobmeier 2006), considering multi-dimensional beliefs (Weisbuch et al. 2002; Urbig & Malitz 2005; Lorenz 2006), imposing heterogeneity of uncertainties (Deffuant et al. 2002; Weisbuch et al. 2005), restricting the communications in a social network structure (Fortunato 2005; Lorenz & Urbig 2007), analyzing the effect of convergence parameter (Assmann 2004; Lorenz & Urbig 2007); including the rejection or differentiation mechanisms (Huet et al. 2008; Kurmyshev et al. 2011); considering various ways of averaging (Hegselmann & Krause 2004); implementing different communication regimes (Lorenz & Urbig 2007); differentiating between attitude and opinion (Urbig 2003); and analyzing the effect of intergroup conflict escalation (Alizadeh et al. 2014) .
- 2.4
- In this paper, for our modeling purpose, we choose the
2-dimensional bounded confidence model with rejection mechanism (2D BC)
proposed by Huet et al. (2008).
In an effort to include the rejection mechanism in the DW model, Huet
et al. (2008) propose a
2-dimensional BC model which allows the agents to reject each other's
opinion when they are in a so called "dissonance" situation. This
agent-based model captures the homophily principle and differentiation
mechanism. We will discuss this model and its underlying theories and
assumption in the following sub-section.
Table 1: Summary of Model Components and Parameters Description Abbreviation Value/Range of Values/Equation Reference Agents
Type Individuals Each agent represents an individual – – – Attributes Opinion 1 The opinion of agent on a subject x1 [-1,1] Huet et al. (2008) Opinion 2 The opinion of agent on a subject x2 [-1,1] Huet et al. (2008) Uncertainty 1 Uncertainty related to opinion 1 U1 [0,1] Huet et al. (2008) Uncertainty 2 Uncertainty related to opinion 2 U2 [0,1] Huet et al. (2008) Methods: Attraction Agents get closer in one or two opinion(s) – 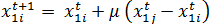
Homophily Differentiation Agents shift away from each other in a given opinion if they are in cognitive dissonance situation. – 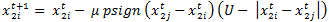
Cognitive Dissonance Ignorance Agents ignore each other and do not make any changes in their opinions if they are far enough in both opinions. – 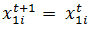
Cognitive Dissonance Parameters Modeling
Parameters
Constriction factor
Used to limit the convergence velocity
μ
0.3
Huet et al. (2008)Intolerance threshold Conceptual threshold in determining the cognitive dissonance situation δ 1, 1.5, 2 (Default = 1) – Global
VariablesPopulation Number of agents in the model – 1,000 – Iterations Number of time steps in each run of the model – 700,000 – Epsilon The minimum distance between agents to be considered in the same opinion cluster ε 0.05 – 2-2- Bounded Confidence Model with Rejection Mechanism
- 2.5
- In this section we present the 2D BC opinion dynamics model (Huet et al. 2008). The model has been developed based on the Cognitive dissonance theory proposed by Festinger (1957). Cognitive dissonance is a psychological conflict that occurs when there is an inconsistency between two or more beliefs which one holds simultaneously. Cognitive Dissonance theory suggests that dissonance is "psychologically uncomfortable" and therefore motivates people to achieve a balanced state. That is, they avoid anything that increases the dissonance and thus change their beliefs in a way that reduces the perceived dissonance. For instance, one plausible way to reduce the dissonance is to shift away from those who possess opposing beliefs. To describe the formal model, let us consider a set of N individuals each having: 1) a 2-dimentional vector containing x1 and x2 representing real numbers ranging from −1 to +1, reflecting the opinion of node over two different issues, and 2) a 2-dimentional vector containing u1 and u2 representing by real numbers between 0 and 1 reflecting uncertainties related to x1 and x2 respectively.
- 2.6
- At each simulation time step, instead of allowing each
agent to interact with all of its neighbors, a pair of individuals is
randomly selected to interact and update their opinions. Here they
condition the updating process based on the values of opinions and
uncertainties. Suppose that agent i has opinions x1i
and x2i with uncertainties u1i
and u2i, and agent j
has beliefs x1j and x2j
with uncertainties u1j and u2j.
For sake of simplicity, the assumption is that all nodes have similar
uncertainties. Also lets assume that x1i(t)
represents the first opinion of agent i at time
step t and μ is a constriction
factor used to limit the convergence velocity. The assumption is that μ
is constant and equal for all agents throughout the simulation.
Finally, let δ represents the "intolerance
threshold", which is a conceptual threshold in determining the
cognitive dissonance situation, and psign(.) be
similar to sign function, except that it returns +1
if the argument is 0. Table 1
summarizes the model's components and parameters.
Table 2: Huet et al's (2008) Opinion Dynamics Model Updating Rules 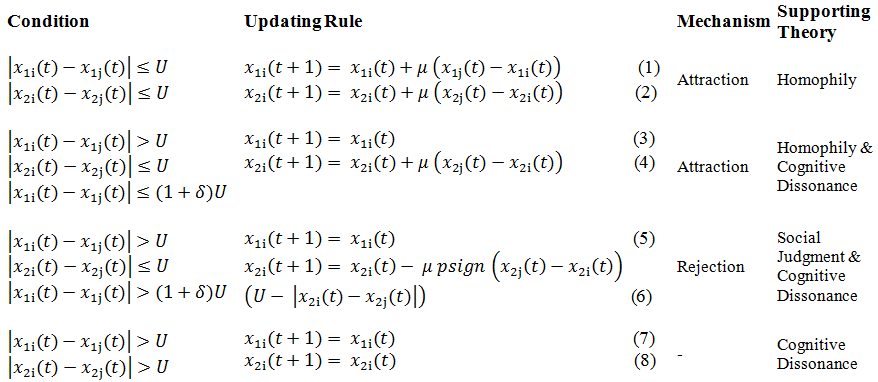
- 2.7
- The entire updating rules are summarized in Table 2. Agent i compares its opinions with those of agent j's and updates its opinions according to updating rules. The general rule is that agents approach each other if they are close enough in both opinions (equations 1 and 2 and 4). Otherwise, they may reject and shift away from one another if the opinion difference is significant enough to trigger the dissonance feeling (equation 6). The movement should be large enough to resolve the dissonance. Since the model has been built on the cognitive dissonance theory, it assumes that for cases in which two agents are far in both opinions, there is no dissonance between them and therefore there is no influence from one to another and they simply ignore each other on both opinions (equations 7 and 8).
 Activation Regimes
Activation Regimes
- 3.1
- There are important differences between the manner social interactions work in real world and the way it is simulated by researchers. These disparities in some cases can be significant enough to cast doubt on the results of the computational models of social interactions (Huberman & Glance 1993). The inter-event time distribution of individuals' activities is one of the influential parameters that needs to be addressed in computational models. In general, activation regimes are categorized to synchronous and asynchronous regimes. While synchronous activation regime assumes that all agents are simultaneously activated and updated at each time step of the simulation, in asynchronous activation regime there is no global clock that causes all agents to update their state at the same time (Huberman & Glance 1993).
- 3.2
- Asynchronous updating schedule could be based on geography in which the order of activation is determined according to agents' spatial characteristics. One example could be that agent located at 12 o'clock activates first and the rest proceeds clockwise. The updating schedule could be state-dependent in which agents having a given state activate first. The activation regime might also depend on the incentives of agents. That is, those agents who benefit the most by activation precede the others (Page 1997). In general, any deterministic or biased activation regimes are plausible. But choosing the activation scheme that fits the best to the system under study remains a modeling challenge. In this following, we describe the four asynchronous updating schemes including uniform, random, and two Poisson activation regimes (Axtell 2001).
- 3.3
- Uniform activation regime creates a sequence of pairs from the population through sampling without replacement. The pairs update their state when they were activated. One turn is defined as activating the entire population (in pairs) exactly once. To avoid spurious correlation between agents, it is crucial to periodically randomize the order of agent activation. That is, given the sequence in which agents are serially activated, some agents should be repositioned so that in the following time step most of the agents have at least one new neighbor. Uniform activation should be applied when activating all agents in a single turn is empirically or behaviorally reasonable (Axtell 2001).
- 3.4
- Random activation involves selecting pairs of agents from the population with replacement. A turn is defined as complete when a full population has been activated, or after n/2 pairs have been selected. Assuming that the activation probability of all agents is equal, the distribution of the inter-activation times of the agents is binomial and called random activation (Axtell 2001).
- 3.5
- In Poisson activation regime, each agent has its own clock
which wakes it up when the agent is to be updated (Schönfisch & de Roos 1999;
Axtell 2001). In this
sense, the activation of each agent is independent of all other agents.
If for every t > 0 the number of
activations in the time interval [0, t] follows the
Poisson distribution with mean λt, then the
sequence of inter-arrival times (i.e. the waiting times of the clocks)
are exponentially distributed with mean 1/λ. To
determine the timing of activations, a random exponential number ti
with parameter λi is
assigned to each agent. The simulation starts with the smallest of
these numbers. After getting updated, the agent calculates its next
activation time according to
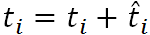 where
where 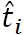 is the new assigned exponential random number with parameter
is the new assigned exponential random number with parameter 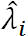 .
Then the model again looks for the smallest activation time and updates
the corresponding agent. Note that the λi
can be constant or dynamic over the simulation period.
.
Then the model again looks for the smallest activation time and updates
the corresponding agent. Note that the λi
can be constant or dynamic over the simulation period.
- 3.6
- Poisson activation regime requires the determination of the activation rate, λi, for each agent. Several ways are possible to determine the value of λi. In this paper, we introduce a state-driven approach in which the agents' timing order depends on their opinions. More specifically, we consider two cases: 1) agents with extreme opinions are more likely to be activated (Poisson-1), and 2) agents with moderate opinions are more likely to be activated (Poisson-2). We choose to make λi proportional to the sum of the absolute values of agents' opinions. Thus, for the former case, those having greater total opinion activate more frequently and those having less total opinion activate at a slower rate. For the latter case, agents having total opinion closer to zero have more activation probability and agents with total opinion closer to 2 have smaller chance of updating. These rates were normalized at the beginning of a turn so that, on average, one population of agents would be activated on each turn.
 Simulation Results
Simulation Results
- 4.1
- In this section, we present and analyze our chosen
agent-based simulation results. First we show the general behavior of
the opinion dynamics model according to four different activation
regimes (i.e. random, uniform, Poisson-1, and Poisson-2). Next, we use
the emergent opinion clusters' statistics and the number of extremists
to compare the output of opinion dynamics model according to different
activation regimes. Then, we run the sensitivity analysis on the
quantitative measures by varying the values of modeling parameters
including the intolerance threshold δ, the opinion
uncertainty U, and the activation regime. Finally,
we use the analysis of variance (ANOVA) test to statistically test the
significance of the modeling specifications.
4-1- General Comparison
- 4.2
- We set the population size as 1000 agents, each having two
opinions x1 and x2.
The initial opinions are randomly assigned to the agents using the
uniform distribution between −1 and 1. The uncertainties u1
and u2 are assumed to have
equal values and held constant throughout the simulation. Figure 1 compares the final configuration of
opinions resulting from different activation regimes. In each of the
figures, the two axes represent the opinions which are bounded between
−1 and 1 and each dot on the figure represents an agent's opinion. All
other variables and parameters among the models are the same including
the initial opinions and uncertainties. Therefore, we can interpret the
results as the effect of applying different activation regimes.
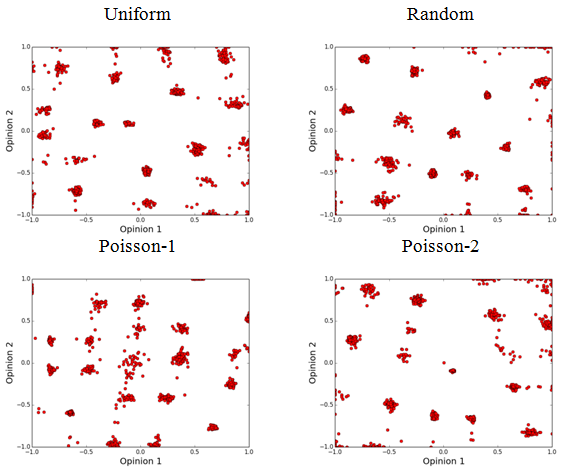
Figure 1. Final opinion configuration for four different activation regimes (U=0.2, μ = 0.3, δ = 1, population = 1000, iteration = 700,000) - 4.3
- Similar to the original DW model with low thresholds (Deffuant et al. 2000), the 2D BC model reaches to pluralism of the opinion where several opinion clusters emerge. The differentiation mechanism gives rise to the emergence of local consensus (i.e. opinion clusters in Figure 1). Huet et al. (2008) argue that after some point, several stable equilibrium points emerge and opinion clusters form around those points. These clusters are predominant opinions and incrementally attract agents toward themselves. Two forces cause the formation of the opinion clusters. On the one hand, those agents which are close in both opinions tend to get closer and form groups. On the other hand, those who feel dissonance are separated and pushed away from each other. As a result, after some steps, some "meta-clusters" emerge in the population (Huet et al. 2008).
- 4.4
- By comparing the final opinion configuration of Figure 1, it seems that applying different
activation regimes qualitatively change the output of the opinion
dynamics model. That is, observational comparison exhibits that not
only the number of opinion clusters may differ, but also the
equilibrium points at which opinion clusters form around differ among
the activation regimes. We can use the number of this local equilibrium
points as a measure to evaluate the degree of consensus in the whole
population. That is, the more the opinion clusters, the less the degree
of consensus.
4-2- Analysis of Opinion Clusters
- 4.5
- In order to compute the number of the clusters, we use the
same algorithm used by Deffuant (2006)
and Huet et al. (2008). That
is, we define a minimum distance ε between the
agents' opinions under which they assign to a same cluster. In practice
we set the minimum distance at ε = 0.05 and
neglected the clusters of size lower than 5 agents and count them as
minority clusters. We run the model for 25 times and report the average
number of clusters. The following pseudo-code can be used to identify
and compute the number of opinion clusters in the final configuration
of opinions.

- 4.6
- From the first column of Figure 2, we can see that the intolerance threshold does not correlate with the number of opinion clusters. However, it has interactions with activation regimes. That is, as we increase δ, different activation regimes exhibit different patterns of increase and decrease. Moreover, no specific pattern can be seen for which activation regime produces the most or least number of opinion clusters. The second column of the Figure 2 shows the effect of different activation orders and intolerance threshold on the maximum cluster size when the uncertainty is fixed. While we cannot explicitly see any regular pattern for the effect of updating schemes and intolerance threshold, we can see that the Poisson activation regime in which the extremists are more likely to become activated (Poisson-1) produces the least maximum cluster size for all combinations except for one case where U = 0.1 and d = 1. Finally, the third column illustrates that except for the U = 0.2 in which the number of minority opinion clusters decreases with intolerance threshold, in other cases no regular pattern can be identified. It should be noted that on average more than 90 percent of theses minority clusters only include one agent.
- 4.7
- A better way to look at the Figure 2,
however, is to go row by row and compare the behavior of each
activation regime with respect to different measures. At U
= 0.2, the uniform updating scheme produces the most number of opinion
clusters with almost least maximum cluster sizes and large number of
minority clusters. The Poisson-2 activation regime leads to the
relatively fewer number of clusters with larger maximum sizes and few
numbers of minorities. At U = 0.3, the Poisson-1
generates large number of opinion clusters with least maximum cluster
sizes and moderate number of minorities. The Poisson-1 results often
show big size opinion clusters and high number of minorities. At U
= 0.4, the Poisson-2 activation regime produces almost largest number
of clusters, maximum size, and minorities. Random updating leads to the
least number of clusters with moderate maximum size and few minorities.
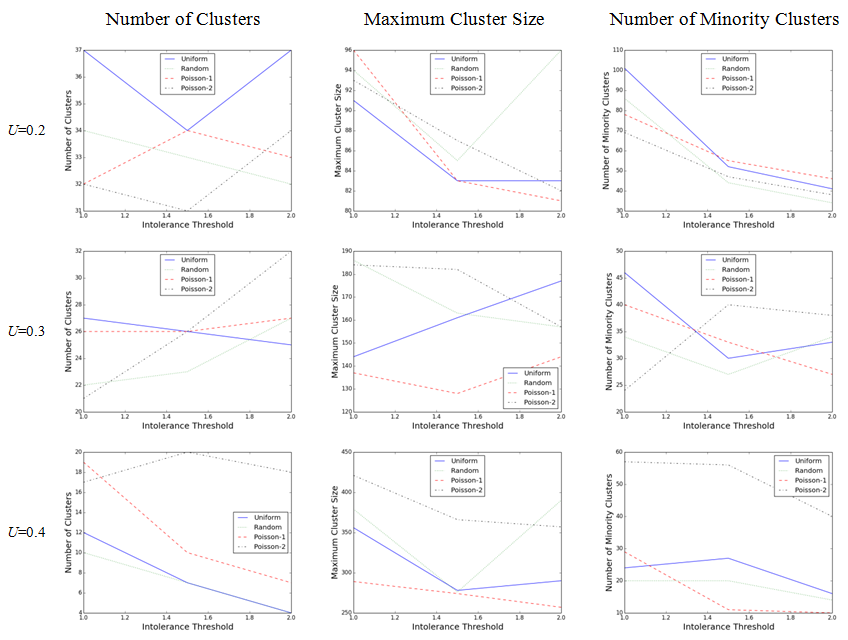
Figure 2. Comparing the effect of applying different activation regimes on the number of clusters, maximum cluster size, and number of minority clusters for three levels of intolerance threshold when opinion uncertainty is fixed ( μ = 0.3, population = 1000, iteration = 700,000) - 4.8
- Figure 3 shows how does the clustering of opinions vary with the updating scheme and opinion uncertainty. The results from the first column exhibit a negative correlation between the number of opinion clusters and opinion uncertainty and a positive correlation between the maximum cluster size and the uncertainty in all activation regimes. However, there is not any general pattern for which timing regime leads to the most or least number of opinion clusters. However, in case of maximum cluster sizes, it seems that the Poisson-2 activation regime almost has the greatest maximum and the Poisson-1 has the least cluster sizes among the others. As for the number of the minority clusters, all updating schemes show decreasing pattern except the Poisson-2 which has a tipping point at U = 0.3.
- 4.9
- A closer look at the behavior of different activation
regimes reveals that when d = 1, the uniform timing
order produces large number of opinion clusters at U
= 0.2 and 0.3 with moderate maximum sizes and relatively high level of
minorities. On the other hand, the Poisson-2 regime generates almost
fewest number of clusters with greatest maximum cluster sizes and often
least minorities. When d = 1.5, applying the
Poisson-2 updating scheme results in large number of clusters with
highest maximum sizes and almost largest minorities. At this level of
intolerance threshold, the behavior of random and uniform regimes is
quite similar. When the intolerance threshold increases to d
= 2, while the Poisson-2 shows pretty similar pattern to that of d
= 1.5, the Poisson-1 produces relatively fewer number of clusters with
the least maximum sizes and almost the least number of minority
clusters.
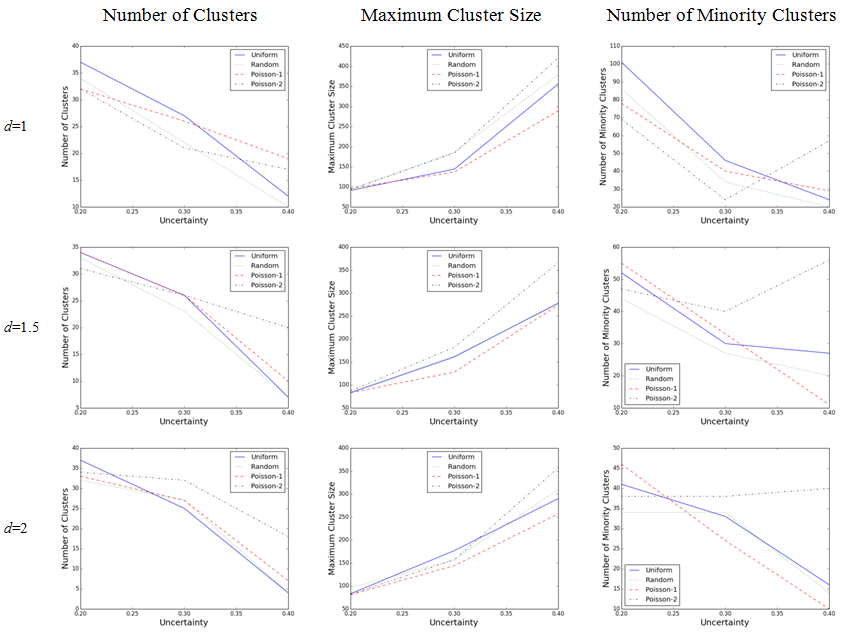
Figure 3. Comparing the effect of activation regimes on the number of clusters, maximum cluster size, and number of minority clusters for three different opinion uncertainty levels when the intolerance threshold is fixed ( μ = 0.3, population = 1000, iteration = 700,000) - 4.10
- The main purpose of analyzing the number of emergent
opinion clusters and its related statistics is to investigate the
process of consensus formation. In this section our main goal is to
explore which activation regime leads to more consensus level in the
population. Ideally, the one that produces the minimum number of
opinion clusters, minimum number of minorities, and largest maximum
cluster size is of interest. However, our results show that these ideal
conditions only occur in 4 out of the 9 combinations of the opinion
uncertainty and intolerance threshold. In other combinations, no
updating scheme has the dominant performance. For example, when U
= 1 and δ = 1.5, the Poisson-2 activation
outperforms the others in the formation of consensus among agents.
Table 3 should be consulted
in order to compare the performance of different activation regimes in
reaching to consensus.
Table 3: Summarizing the Performance of Different Activation Regimes on Consensus Building Opinion Uncertainty Intolerance Threshold Minimum Number of Clusters Largest Maximum Cluster Size Minimum Number of Minorities 0.2 1 Poisson-1 and -2 Poisson-1 Poisson-2 0.2 1.5 Poisson-2 Poisson-2 Poisson-2 0.2 2 Random Random Random 0.3 1 Poisson-2 Poisson-2 & Random Poisson-2 0.3 1.5 Random Poisson-2 Random 0.3 2 Uniform Uniform Poisson-1 0.4 1 Random Poisson-2 Random 0.4 1.5 Random & Uniform Poisson-2 Poisson-1 0.4 2 Random & Uniform Random Random Table 4: ANOVA Test for the Number of Opinion Clusters Source Sum of Squares Degree of Freedom Mean Square F Sig. Corrected Model 88533.070a 35 2529.516 75.750 .000 Intercept 500556.250 1 500556.25 14989.78 .000 D 88.747 2 44.373 1.329 .265 U 76123.087 2 38061.543 1139.801 .000 AR 2208.528 3 736.176 22.046 .000 D * U 2725.427 4 681.357 20.404 .000 D * AR 1719.342 6 286.557 8.581 .000 U * AR 4674.309 6 779.051 23.330 .000 D * U * AR 993.631 12 82.803 2.480 .003 Error 28851.680 864 33.393 Total 617941.000 900 Corrected Total 117384.750 899 a. R Squared = .754 (Adjusted R Squared = .744) Table 5: ANOVA Test for the Maximum Cluster Size Source Sum of Squares Degree of Freedom Mean
SquareF Sig. Corrected Model 9465499.692a 35 270442.84 100.245 .000 Intercept 32471382.668 1 32471382.6 12036.15 .000 AR 282673.639 3 94224.546 34.926 .000 U 8621614.462 2 4310807.2 1597.885 .000 D 113435.829 2 56717.914 21.024 .000 AR * U 239456.018 6 39909.336 14.793 .000 AR * D 29008.944 6 4834.824 1.792 .098 U * D 123051.291 4 30762.823 11.403 .000 AR * U * D 56259.509 12 4688.292 1.738 .055 Error 2330916.640 864 2697.820 Total 44267799.000 900 Corrected Total 11796416.332 899 a. R Squared = .802 (Adjusted R Squared = .794) Table 6: ANOVA Test For the Number of Minority Clusters Source Sum of Squares Degree of Freedom Mean Square F Sig. Corrected Model 359481.422a 35 10270.898 72.174 .000 Intercept 1402487.538 1 1402487.538 9855.3 .000 D 62109.216 2 31054.608 218.22 .000 U 153794.409 2 76897.204 540.36 .000 AR 16062.889 3 5354.296 37.625 .000 D * U 51988.298 4 12997.074 91.331 .000 D * AR 8291.291 6 1381.882 9.711 .000 U * AR 51795.244 6 8632.541 60.661 .000 D * U * AR 15440.076 12 1286.673 9.042 .000 Error 122953.040 864 142.307 Total 1884922.000 900 Corrected Total 482434.462 899 a. R Squared = .745 (Adjusted R Squared = .735) - 4.11
- To better measure the effect of different updating schemes on the properties of opinions, we run a 3×3×4 full-factorial ANOVA test on our results. We consider three levels for intolerance threshold and opinion uncertainty along with four different activation regimes and 25 observations for each combination. The ANOVA table contains the sources of variation, degrees of freedom, sum of squares (SS), mean square (MS), F-ratio test statistics, and the corresponding significance levels (p-values). The results from Table 4 illustrate a significant difference between the different types of activation regimes (p-value = 0.00) and various levels of uncertainty (p-value = 0.00) on the number of opinion clusters. All interactions between factors are significant as well. However, the effect of intolerance threshold does not seem to be statistically significant at 5 percent significance level as the p-value is equal to 0.265. We also run one-way ANOVA test to just measure the significance of the activation regimes on the number of emergent clusters and it turned out to be highly significant (p-value = 0.00).
- 4.12
- Table 5 presents
the ANOVA test results showing the significance level of different
factors and factors interactions on the maximum opinion cluster sizes.
We can see that the difference is significant for all modeling factors
(difference significant at p < 0.05). Table 4 also shows that the interactions
between activation regime and opinion uncertainty and also intolerance
threshold and opinion uncertainty are statistically significant (p-value
= 0.00). The one-way ANOVA test of the effect of updating schemes on
the maximum cluster size supports the significance of activation
regimes (p-value = 0.00). Finally, Table 6 demonstrates the ANOVA test
results for the number of minority clusters. The corresponding p-values
indicate that all modeling factors and their interactions are
significant sources of variation. Similar to previous measures, the
one-way ANOVA shows the significance of the effect of activation regime
on the average number of minority clusters (p-value
= 0.00).
4-3- Number of Extremists
- 4.13
- As mentioned in the introduction part of the paper, our second main interest in this paper is to explore the effect of the activation regimes on the average number of emergent extremists in the population. Here we would like to examine whether any particular activation regime can intensify or moderate the radicalization process. In doing so, we apply different asynchronous updating schemes on the 2D BC opinion dynamics model and test the effect of them along with two other modeling parameters of the 2D BC model (i.e. opinion uncertainty and intolerance threshold). Similar to the analysis of opinion clusters section, we consider three different levels for opinion uncertainty (U = 0.2, 0.3, and 0.4) and intolerance threshold (δ = 1, 1.5, and 2). All other modeling parameters kept constant during the experiment. We run each combination for 25 times and calculate the average number of extremists. We define an agent as an extremist if at least the absolute value of one of its final opinion is equal or greater than 0.9.
- 4.14
- Figure 4 compares
the average number of emergent extremists that resulted from applying
different activation regimes at various opinion uncertainty levels
where the intolerance threshold is fixed at δ = 1,
1.5, and 2. First of all, it appears that in all three levels of
intolerance thresholds, as the opinion uncertainty increases, the
average number of extremists decreases in all activation regimes. The
slope of reduction is usually lower in Poisson-1 activation regime
compared with the others. Moreover, we can see that the uniform and
random activation regimes exhibit similar patterns and produce almost
same number of extremists. On the other hand, the Poisson-1 activation
regime seems to generate relatively fewer number of radical agents at δ
= 1 and δ = 1.5. The Poisson-2 updating scheme
generates the most number of extremists when the intolerance threshold
is fixed at δ = 1 and δ = 1.5.
Indeed, at U = 0.2 level, it always produces the
greatest number of emergent extremists. However, it produces relatively
fewer radicals when δ = 2 and U
= 0.3 or 0.4.
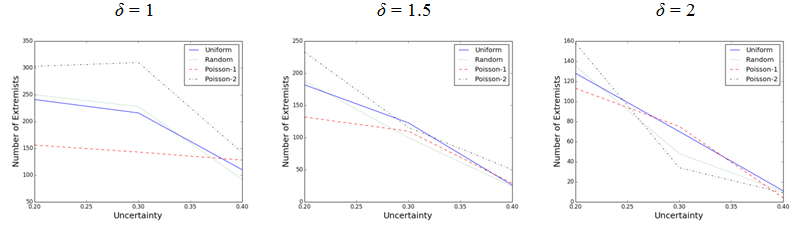
Figure 4. Comparing the number of extremists from four different activation regimes at different opinion uncertainty levels when the intolerance threshold is fixed ( μ = 0.3, population = 1000, iteration = 700,000) 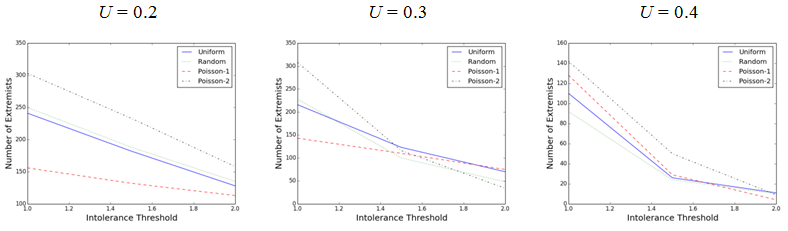
Figure 5. Comparing the number of extremists from four different activation regimes at different intolerance threshold levels when the opinion uncertainty is fixed ( μ = 0.3, population = 1000, iteration = 700,000) - 4.15
- Figure 5 shows how the average number of extremists changes with activation regime when the intolerance threshold is increased and opinion uncertainty is fixed. Two observations should be noticed here. First, in all activation regimes, increasing the level of intolerance threshold decreases the number of radical agents. We should have expected this because higher level of intolerance threshold means that individuals are more likely to tolerate the opinion differences. Therefore, less number of agents decide to differentiate from others which in turn reduces the overall number of differentiating encounters in the simulation. One should also note that the number of extremists usually decreases with lower slope in the Poisson-1 regime compared to other timing schemes.
- 4.16
- Second, it appears that applying uniform and random activation schemes does not significantly change the number of extremists. However, Poisson updating schemes seems to significantly change the number of radical agents compared to other two activation regimes. While the Poisson-1 often leads to the least number of extremists, the Poisson-2 scheme appears to produce the greatest number of radical agents in most combinations. We have seen an almost similar pattern in Figure 4 as well. These observations are quite interesting and somehow counterintuitive because in the Poisson-1 activation regime we have allowed agents with greater total opinions to get activated more frequently. In other words, we let the agents with extreme opinions to involve in more number of encounters compared to moderate ones. As a result, one might expect to see more number of radical agents in the population, but the simulation results actually show an inverse pattern. On the other hand, the Poisson-2 activation regime, in which we let the moderate agents to update more frequently, produces the most number of radical agents compared to other activation regimes. One plausible explanation for this outcome might be that the Poisson-1 updating scheme increases the relative number of "attractive" encounters whereas the Poisson-2 activation regime increases the relative number of "differentiating" or "rejecting" encounters.
- 4.17
- The ANOVA test reveals that all modeling factors including
the activation regime and their interactions have statistically
significant effect on the average number of emergent extremists at the
5 percent significance level (Table 7).
We also ran the one-way ANOVA to only test the effect of using
different activation regimes on the number of extremists and it
supports the significance of it as well (p-value =
0.00). Also, since the interactions are significant, one should be very
cautious in interpreting the main effects. A significant interaction
here means that for example the effect of a given activation regime on
the number of emergent extremists at one opinion uncertainty level is
different from its effect at the other opinion uncertainty level.
Therefore, if one is looking for the lowest or highest number of
extremists, Table 8 should be
consulted to figure out what combinations of fixed factors will
minimize or maximize the average number of radical agents in the
population.
Table 7: ANOVA Tests of Between-Subjects Effects on Number of Extremists Source Sum of Squares Degree of Freedom Mean Square F Sig. Corrected Model 6146316.960a 35 175609.056 132.077 .000 Intercept 13613148.160 1 13613148.16 10238.54 .000 D 2496083.460 2 1248041.730 938.661 .000 U 2638945.680 2 1319472.840 992.385 .000 AR 302714.640 3 100904.880 75.891 .000 D * U 156277.120 4 39069.280 29.384 .000 D * AR 216342.193 6 36057.032 27.119 .000 U * AR 160481.733 6 26746.956 20.117 .000 D * U * AR 175472.133 12 14622.678 10.998 .000 Error 1148772.880 864 1329.598 Total 20908238.000 900 Corrected Total 7295089.840 899 a. R Squared = .843 (Adjusted R Squared = .836) Table 8: Comparing activation regimes with respect to minimum and maximum number of extremists Opinion Uncertainty Intolerance Threshold Minimum Maximum 0.2 1 Poisson-1 Poisson-2 0.2 1.5 Poisson-1 Poisson-2 0.2 2 Poisson-1 Poisson-2 0.3 1 Poisson-1 Poisson-2 0.3 1.5 Random Uniform 0.3 2 Poisson-2 Poisson-1 0.4 1 Random Poisson-2 0.4 1.5 Random Poisson-2 0.4 2 Poisson-1 Uniform
 Discussion and Conclusion
Discussion and Conclusion
- 5.1
- One of the reasons behind the current trend toward the use of computational models in social sciences is to be able to predict and control the collective behavior of people. In order to accomplish these tasks, one should take into account the detailed behavioral aspect of the systems that is intended to be modeled. Agent activation is an important but neglected aspect of agent-based model building and evaluation. It is important to consider multiple activation schemes because, as we have shown here, activation regime has qualitative and quantitative impact on the model output. Without an understanding of the role of activation timing it will be hard to assign causes of variation in a model, as some of this will undoubtedly be due to how agents are turned on.
- 5.2
- This paper contributes to the literature of opinion dynamics in three ways. First we introduce a state-driven activation regime in which agents' timing order depends on their opinions. Second, we show how using different activation regimes can qualitatively change the outcome of a given opinion dynamics model. Third, we discussed various statistics (i.e. number of opinion clusters, maximum cluster size, number of minority clusters, and number of emergent extremists) to show how applying different updating schemes can quantitatively change the results.
- 5.3
- The simulation results showed that none of the activation regime can dominate the others in terms of reaching to consensus. That is, there is no updating scheme that for each combination of opinion uncertainty and intolerance threshold produces the minimum number of opinion clusters, minimum number of opinion cluster minorities, and maximum major cluster size. Out of the nine analyzed combinations of uncertainty and intolerance threshold, only in four of them we could identify an activation regime that has all ideal measures of reaching to consensus. However, even in those four conditions we see different activation regimes. We have provided a table that can be consulted to identify that at each condition which activation regime(s) results in more consensus level. We also performed the one-way and full factorial ANOVA tests to statistically measure the significance of using different activation regimes on the three opinion clusters statistics and the results showed the significance difference at p < 0.05.
- 5.4
- Another fascinating result is the moderating role of Poisson-1 activation regime on the emergent of extremists in the population. This is interesting because in Poisson-1 activation regime we have allowed agents with larger values of opinions to get activated more frequently. In other words, we let the agents with extreme opinions to involve in more number of encounters compared to moderate ones. As a result, one might expect to see more number of extremists in the population, but the simulation results show an inverse pattern. One immediate implication of this finding is that talking and interacting with radical individuals would eventually be effective in reducing the number of people with radical opinions in the society.
- 5.5
- On the other hand, the Poisson-2 updating scheme, in which the moderate agents have more interaction probability and get involved in more encounters, exhibit another counterintuitive result. While we expected to see smaller number of radical agents, the Poisson-2 updating scheme leads to the emergence of maximum number of extremists in all nine combinations of opinion uncertainty and intolerance threshold compared to other three updating regimes. One explanation for this phenomenon might be that allowing moderate agents to get activated more frequently increases the number of differentiating encounters in which agents feel dissonance and reject from each other which eventually leads to the formation of more radical opinions in the population.
- 5.6
- The results of this study support the influential role of activation regime in the collective behavior of individuals' opinions and promote the consideration of activation regime as one of the modeling specifications that should be determined explicitly and appropriately in all agent-based models. Our study has some limitations as well. Since we wanted to only investigate the role of activation regimes, we exactly implemented the original 2D BC model. This model does not include the network structure in its activation and updating mechanisms. Future works can add the social network topology to the current study. To this one might add the analysis and comparison of another computational opinion dynamics models and introducing new state-driven or incentive-based activation regimes as well.
 Acknowledgements
Acknowledgements
- The authors thank two anonymous reviewers for their helpful and detailed reviews. This study was supported in part by the Center for Social Complexity and the Department of Computational Social Science at George Mason University. M. Alizadeh is funded by a GMU Presidential Fellowship and, together with C. Cioffi-Revilla, by ONR-Minerva Grant No. N00014130054. The Python code for the model and supplementary documentation are available from the CoMSES Net Computational Model Library at: https://www.openabm.org/model/4316/version/1/view. CoM-SES is funded by the US National Science Foundation and is an affiliate organization of the Computational Social Science Society of the Americas (CSSSA).
 References
References
- ALIZADEH, M., &
Cioffi-Revilla, C. (2014). Distributions of Opinion and Extremist
Radicalization: Insights from Agent-Based Modeling. In Proceedings
of the 6th International Conference on Social Informatics (SocInfo
2014), Barcelona, Spain, 10–13 November, Heidelberg:
Springer.
ALIZADEH, M., Coman, A., Lewis, M., & Cioffi-Revilla, C. (2014). Intergroup conflict escalation leads to more extremism. Journal of Artificial Societies and Social Simulation, 17(4), 4: https://www.jasss.org/17/4/4.html.
AMBLARD, F., & Deffuant, G. (2004). The role of network topology on extremism propagation with the relative agreement opinion dynamics. Physica A: Statistical Mechanics and its Applications, 343, 725–738. [doi:10.1016/j.physa.2004.06.102]
ASSMANN, P. (2004). Monte Carlo Simulation of Deffuant Opinion Dynamics with Quality Differences. International Journal of Modern Physics C, 15(10), 1439–1447. [doi:10.1142/S0129183104006844]
AXTELL, R. (2001). Effects of interaction topology and activation regime in several multi-agent systems. In: Moss, S. and Davidsson, P. (eds.) Multi-Agent-Based Simulation. pp. 33–48. Springer-Verlag Berlin, Berlin.
BARABÁSI, A.-L. (2005). The origin of bursts and heavy tails in human dynamics. Nature, 435(7039), 207–211.
BERSINI, H., & Detours, V. (1994). Asynchrony induces stability in cellular automata based models. In Artificial Life IV (pp. 382–387). MIT Press, MA.
CASTELLANO, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81, 591–646. [doi:10.1103/RevModPhys.81.591]
CIOFFI-REVILLA, C. (2002). Invariance and universality in social agent-based simulations. Proceedings of the National Academy of Sciences of the United States of America, 99(3), 7314–7316. [doi:10.1073/pnas.082081499]
DEFFUANT, G. (2006). Comparing extremism propagation patterns in continuous opinion models. Journal of Artificial Societies and Social Simulation,9(3), 8: https://www.jasss.org/9/3/8.html.
DEFFUANT, G., Amblard, F., Weisbuch, G., & Faure, T. (2002). How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation, 5(4), 1: https://www.jasss.org/5/4/1.html.
DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3 (1–4), 87–98. [doi:10.1142/S0219525900000078]
FATES, N., & Chevrier, V. (2010). How important are updating schemes in multi-agent systems? An illustration on a multi-turmite model. In van der Hoek, Kaminka, Lesperance, Luck and Sen (eds.) Proceedings of the 9th International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2010)
FERNÁNDEZ-GRACIA, J., Eguíluz, V.M., & San Miguel, M. (2011). Update rules and interevent time distributions: Slow ordering versus no ordering in the voter model. Physical Review E, 84(1), 015103. [doi:10.1103/PhysRevE.84.015103]
FESTINGER, L. A. (1957). Theory of Cognitive Dissonance. Stanford, CA: Stanford University Press.
FORTUNATO, S. (2005). On the Consensus Threshold for the Opinion Dynamics of Krause-Hegselmann. International Journal of Modern Physics C, 16(2), 259–270. [doi:10.1142/S0129183105007078]
GALAM, S. (2005). Heterogeneous beliefs, segregation, and extremism in the making of public opinions. Physical Review E, 71 (4), 046123. [doi:10.1103/PhysRevE.71.046123]
HEGSELMANN, R., & Krause, U. (2002). Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artificial Societies and Social Simulation, 5 (3), 2: https://www.jasss.org/5/3/2.html
HEGSELMANN, R., & Krause, U. (2004). Opinion Dynamics Driven by Various Ways of Averaging. Computational Economics, 25(4), 381–405. [doi:10.1007/s10614-005-6296-3]
HUBERMAN, B., & Glance, N. (1993). Evolutionary Games and Computer-Simulations. Proceedings of the National Academy of Sciences, 90(16), 7716–7718. [doi:10.1073/pnas.90.16.7716]
HUET, S., Deffuant, G., & Jager, W. (2008). Rejection mechanism in 2D bounded confidence provides more conformity. Advances in Complex Systems, 11(4), 529–549. [doi:10.1142/S0219525908001799]
JACOBMEIER, D. (2006). Focusing of Opinions in the Deffuant Model: First Impression counts. International Journal of Modern Physics C, 17(12), 1–8. [doi:10.1142/S0129183106010108]
JAGER, W., & Amblard, F. (2005). Uniformity, bipolarization and pluriformity captured as generic stylized behavior with an agent-based simulation model of attitude change. Computational & Mathematical Organization Theory, 10(4), 295–303. [doi:10.1007/s10588-005-6282-2]
KARSAI, M., Kivelä, M., Pan, R. K., Kaski, K., Kertész, J., Barabási, A.-L., & Saramäki, J. (2011). Small but slow world: How network topology and burstiness slow down spreading. Physical Review E, 83, 025102. [doi:10.1103/PhysRevE.83.025102]
KRAUSE, U. (1997). Soziale Dynamiken mit vielen Interakteuren. Eine Problemskizze. In Krause U and Stöckler M (Eds.) Modellierung und Simulation von Dynamiken mit vielen interagierenden Akteuren, Universität Bremen. pp. 37–51.
KRAUSE, U. (2000). A discrete nonlinear and non-autonomous model of consensus formation. In Elaydi S, Ladas G, Popenda J and Rakowski J (Eds.), Communications in Difference Equations. Proceedings of the fourth International Conference on Difference Equation, Poznan, Poland, August 27–31, 1998. Amsterdam 2000: Gordon and Breach Publ. pp. 227–236.
KURMYSHEV, E., Juárez, H. A., & González-Silva, R. A. (2011). Dynamics of bounded confidence opinion in heterogeneous social networks: Concord against partial antagonism. Physica A: Statistical Mechanics and its Applications, 390< (16), 2945–2955.
LORENZ. J. (2006). Consensus Strikes Back in the Hegselmann-Krause Model of Continuous Opinion Dynamics under Bounded Confidence. Journal of Artificial Societies and Social Simulation, 9(1), 8: https://www.jasss.org/9/1/8.html
LORENZ, J. (2007). Continuous opinion dynamics under bounded confidence: A survey. International Journal of Modern Physics C, 18(12), 1819–1838. [doi:10.1142/S0129183107011789]
LORENZ, J. (2010). Heterogeneous bounds of confidence: Meet, discuss and find consensus!. Complexity, 15(4): 43–52.
LORENZ, J., & Urbig, D. (2007). About the Power to Enforce and Prevent Consensus. Advances in Complex Systems, 10(2), 251–269. [doi:10.1142/S0219525907000982]
MALMGREN, R. D., D. B. Stouffer, Campanharo, A. S. L. O., & Nunes Amaral. L. A (2009). On Universality in Human Correspondence Activity. Science, 325(5948), 1696–1700.
MÄS, M., Flache, A., & Helbing, D. (2010). Individualization as driving force of clustering phenomena in humans. PLoS computational biology, 6<(10), e1000959. [doi:10.1371/journal.pcbi.1000959]
MÄS, M., Flache, A., & Kitts, J. A. (2014). Cultural Integration and Differentiation in Groups and Organizations. In Dignum, V., & Dignum, F. (Eds.) Perspectives on Culture and Agent-based Simulations (pp. 71–90). Springer International Publishing. [doi:10.1007/978-3-319-01952-9_5]
NOWAK, M., & May, R. (1992). Evolutionary Games and Spatial Chaos. Nature, 359, 826–829. [doi:10.1038/359826a0]
OLIVEIRA, J. G., & Barabási, A.-L. (2005) Human dynamics: Darwin and Einstein correspondence patterns. Nature, 437, 1251. [doi:10.1038/4371251a]
PAGE, S. (1997). On Incentives and Updating in Agent Based Models. Computational Economics, 10(1), 67–87. [doi:10.1023/A:1008625524072]
PAGE, S. E. (2005). Agent based models. The New Palgrave Dictionary of Economics. Palgrave MacMillan, New York.
RADAX, W., & Rengs, B. (2010). Timing matters: lessons from the CA literature on updating. arXiv preprint arXiv:1008.0941.
RIOLO, R. L, Cohen, M. D., & Axelrod, R. (2001). Evolution of cooperation without reciprocity. Nature, 414(6862), 441–443.
SALZARULO, L. (2006). A continuous opinion dynamics model based on the principle of meta-contrast. Journal of Artificial Societies and Social Simulation, 9(1)m 13:https://www.jasss.org/9/1/13.html .
SCHÖNFISCH, B., & de Roos, A. (1999). Synchronous and asynchronous updating in cellular automata. BioSystems, 51(3), 123–143. [doi:10.1016/S0303-2647(99)00025-8]
SZNAJD-WERON, K. J. S. (2000). Opinion evolution in closed community. International Journal of Modern Physics C, 11 (6), 1157–1165. [doi:10.1142/S0129183100000936]
URBIG, D. (2003). Attitude Dynamics with Limited Verbalisation Capabilities. Journal of Artificial Societies and Social Simulation, 6(1), 2: https://www.jasss.org/6/1/2.html .
URBIG, D., Lorenz, J., & Herzberg, H. (2008). Opinion Dynamics: the Effect of the Number of Peers Met at Once. Journal of Artificial Societies and Social Simulation, 11(2), 4: https://www.jasss.org/11/2/4.html.
URBIG, D., & Malitz, R. (2005). Dynamics of Structured Attitudes and Opinions. Proceedings of the Third Conference of the European Social Simulation Association (ESSA), September 5–9, Koblenz, German.
WEIDLICH, W. (1971). The statistical description of polarization phenomena in society. British Journal of Mathematical and Statistical Psychology, 24, 251–266. [doi:10.1111/j.2044-8317.1971.tb00470.x]
WEISBUCH, G., Deffuant, G., & Amblard, F. (2005). Persuasion Dynamics. Physica A, 353, 555–575. [doi:10.1016/j.physa.2005.01.054]
WEISBUCH, G., Deffuant, G., Amblard, F. & Nadal, J. P. (2002). Meet, Discuss and Segregate! Complexity, 7 (3), 55–63.
XIE, J., Sreenivasan, S., Korniss, G., Zhang, W., Lim, C., & Szymanski, B. K. (2011). Social consensus through the influence of committed minorities. Physical Review E, 84, 011130. [doi:10.1103/PhysRevE.84.011130]