Abstract
Abstract
- This paper presents an extension to an agent-based model of opinion dynamics built on dialogical logic DIAL. The extended model tackles a pervasive problem in argumentation logics: the difference between linguistic and logical inconsistency. Using fuzzy logic, the linear ordering of opinions, used in DIAL, is replaced by a set of partial orderings leading to a new, nonstandard notion of consistency as convexity of sets of statements. DIAL allows the modelling of the interplay of social structures and individual beliefs, inspired by the interplay between the importance and the evidence of an opinion formulated in the Theory of Reasoned Action, but DIAL was restricted to argumentation about one proposition. FUZZYDIAL allows for a more natural structure of dialogues by allowing argumentation about positions in a multidimensional space.
- Keywords:
- Dialogues, MAS, Fuzzy Logic, Logic-Based
 Introduction
Introduction
- 1.1
- Social systems involve the interaction between large numbers of people, and many of these interactions relate to the shaping and changing of opinions. The dynamics of these opinions elucidate other relevant phenomena such as social polarisation, extremism and pluriformity. It is therefore important to develop models that capture interaction processes in a simple yet realistic manner.
- 1.2
- Traditional opinion dynamics models take into account the
social influence on opinion formation. Hegselmann & Krause
(2002)'s Bounded
Confidence Model explores the influence of a confidence interval
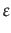 , i.e. an
interval within which opinions are taken into account, on consensus and
polarisation. Deffuant
et al. (2002)'s Relative
Agreement Model extends the Bounded Confidence Model by
interpreting the confidence interval as an uncertainty factor of
agent's regarding their opinion. Rather than a homogenous
, i.e. an
interval within which opinions are taken into account, on consensus and
polarisation. Deffuant
et al. (2002)'s Relative
Agreement Model extends the Bounded Confidence Model by
interpreting the confidence interval as an uncertainty factor of
agent's regarding their opinion. Rather than a homogenous
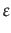 , agents are
heterogeneous in their uncertainties.
, agents are
heterogeneous in their uncertainties.
- 1.3
- These traditional opinion dynamics models have agents engage in opinion formation but do not also model social processes of group formation or segregation. An extension of the traditional opinion dynamics framework is Jager & Amblard (2005) which demonstrates that the attitude structure of agents determines the occurrence of assimilation and contrast effects, which in turn cause a group of agents to reach consensus, to bipolarise, or to develop a number of subgroups sharing the same position. In this model, agents engage in social processes. However, their framework does not have a logic for reasoning about the different agents and opinions.
- 1.4
- Our modelling approach can be seen as a natural extension of these traditional opinion dynamics models. We follow Carley's social construction of knowledge (Carley 1986; Carley et al. 2003), according to which knowledge is determined by communication dependent on an agent's social group while the social group itself is determined by the agent's knowledge. Both DIAL (Dykstra et al. 2013) and FUZZYDIAL are models focusing on the feedback loop of group structuring and opinion formation using a simple argumentation game, reputation levels as payoffs from the game and movement in social space.
- 1.5
- The paper is structured as follows. In Section 2 we discuss the relevant theoretical background to our extended model. In Section 3 we recap the important formal aspects of DIAL that will recur in FUZZYDIAL. In Section 4 we motivate the fuzzy extension by an example and describe FUZZYDIAL. In Section 5 the implemented model is presented. In Section 6 the actual experiments are outlined. We discuss the experimental results in Section 7 and in Section 8 we conclude and point to future work. This paper is a revised and exended version of Dykstra et al. (2010).
 Theoretical
Background
Theoretical
Background
- 2.1
- The theoretical background to our research is formed by theories combining beliefs and attitudes of individuals with the dynamic social environment an individual is situated in. DIAL (Dykstra et al. 2010; Dykstra et al. 2009; Dykstra et al. 2013) was strongly based on the Theory of Reasoned Action (Ajzen & Fishbein 1980; Ajzen 1991). The Theory of Reasoned Action defines an attitude as the sum of beliefs about the outcomes of a particular behaviour, weighted by the evaluations of these outcomes. Next to that, the subjective norm is defined as the perceived beliefs of important other people (normative beliefs) weighted by the motivation to comply to this norm. Whereas in this causal model there is a clear distinction beween the individual attitude and social norm, it is also demonstrated that observing behaviour (descriptive norm) can lead to the development of an expectation of how other people would evaluate a certain behaviour (injunctive norm), and ultimately in personal beliefs (personal norm) (Cialdini et al. 1990). Hence in a causal model such as DIAL, social influences can have an impact on the attitude. Hence in DIAL an attitude is defined a sum of opinions (beliefs), each having its own importance and level of evidence (weight), both importance and evidence being socially constructed.
- 2.2
- DIAL essentially investigates the effects of different parameters on social outcomes such as group segregation and opinion radicalisation. Agent interactions are dialogue games in which agents gain reputation points on winning. Reputation can either be awarded for being in harmony with one's environment (normative redistribution) or by winning arguments (argumentative redistribution). It turns out that the distribution rule for reputation points is the most important factor influencing the simulation outcomes, with normative redistribution favouring segregated configurations and argumentative redistribution resulting in authoritarian societies in which some individuals hold almost all the reputation points.[1] These results are interesting and show how communicative intergroup dynamics influence opinion change as well as social structure.
- 2.3
- However, DIAL has restrictions that are lifted in the fuzzy
extension FUZZYDIAL:
- In DIAL agents only argue about one opinion, in FUZZYDIAL they move in a multidimensional opinion space.
- Agents have a linear ordering of the importance of other agents.
- The concept of 'linguistic consistency' is introduced to define acceptable attitudes, that are sets of opinions that include all opinions which are intermediate between the most extreme opinions that the agents support.
- 2.4
- These extensions go over and above the framework of the
Theory of Reasoned Action. Two psychological theories are the main
source for the formulation of FUZZYDIAL:
1. Social Judgement Theory (Sherif & Hovland 1961) describes the conditions under which a change of attitudes takes place, with the intention to predict the direction and extent of that change. The basic idea of Social Judgment Theory (Sherif & Hovland 1961) is that a change of a person's attitude depends on the position of the persuasive message that is being received. There exists a continuous ordering on statements. If the advocated position is close to the initial position of the receiver, it is assumed that this position falls within the receiver's latitude of acceptance. As a result, the receiver is likely to shift in the direction of the advocated position (assimilation).
- 2.5
- If the advocated position is distant to the initial position of the receiver, it is assumed that this position falls within the latitude of rejection of the receiver. As a result, the receiver is likely to shift away from the advocated position (contrast). If the advocated position falls outside the border of the latitude of acceptance, but is not so distant that it crosses the border of the latitude of rejection, it will fall within the latitude of non-commitment, and the receiver will not shift its initial position.
- 2.6
- Sherif and Hovland speculated that extreme stands, and thus
wide latitudes of rejection,
were a result of high level of ego-involvement. Ego-involvement is the
importance of an issue to a person's life, often expressed by
membership in a group. According to Sherif
& Hovland (1961,
p. 191), the level of
ego-involvement depends upon whether the issue ''arouses an intense
attitude or, rather, whether the individual can regard the issue with
some detachment as primarily a 'factual' matter''. Religion, politics,
and family are typical examples of issues that evoke a high level of
ego-involvement.
2. Social Identity Theory is a social-psychological analysis of group processes, intergroup relations, and the self-concept (Tajfel & Turner 1979):
Norms are shared patterns of thought, feeling, and behaviour, and in groups, what people do and say communicates information about norms and is itself configured by norms and by normative concerns (Hogg & Reid 2006, p. 8).
- 2.7
- Social identity theory focuses on prejudice, discrimination, and conditions that promote different types of intergroup behaviour – for example, conflict, cooperation, social change, and social stasis. An emphasis is placed on intergroup competition over status and prestige, and the motivational role of self-enhancement through positive social identity.
- 2.8
- Social categorisation lies at the core of the social identity approach. It focuses on the basic social cognitive processes, primarily social categorisation, that cause people to identify with groups, construe themselves and others in group terms, and manifest group behaviours.
- 2.9
- Individuals cognitively represent social categories as prototypes. These are fuzzy sets, not checklists, of attributes (e.g., attitudes and behaviours) that define one group and distinguish it from other groups. These category representations capture similarities among people within the same group and differences between groups. In other words, they accentuate intragroup similarities (assimilation) and intergroup differences (contrast) (Tajfel & Turner 1979).
- 2.10
- Group representations are inextricable from intergroup comparisons – they are based on comparisons within and between groups. Specifically, we configure our intra-group representations so that they accentuate differences between a group and the relevant out-groups. For example, our representation of vegetarians will be different if we are comparing them to vegans or to carnivores. In this sense, group prototypes are context-dependent rather than fixed – they vary from context to context as a function of the social comparative frame (situation, goals, and people physically or cognitively present).
- 2.11
- In FUZZYDIAL, the concepts of latitude of acceptance and rejection are used to move the dialogue games from one to two dimensions and to implement linguistic rather than logical inconsistency.
- 2.12
- This paper presents a descriptive study of the influence of normative agents on an artificial society. Agents can be considered as normative because they acquire their opinions in a prescriptive logic-based way. It is assumed that opinions are ordered in an extremeness ordering which is either private to agents (which we call 'own categories') or shared by all agents ('standard categories'). We will show how group norms emerge from private norms under both assumptions.
 Quick DIAL
Quick DIAL
- 3.1
- DIAL has been designed to help understand the social processes of opinion formation and group dynamics by multi-agent simulation, not by implementing group formation behaviour into individuals, but by providing agents with behavioural rules for communication and persuasion and the possibility of movement from an environment with which an agent is in discordance. In this section we briefly recap the formal details of DIAL that are also relevant for FUZZYDIAL.[2]
- 3.2
- Agents are located in a space where they form groups. They try to stay in tune with the opinions of their surrounding agents. Agents assume that the common opinion on a certain location is the accumulation of all utterances in that area that are not defeated in a debate. The real common opinion, however, is determined by the vote of the neighbourhood agents about atomic statements at the end of a debate. Agents want to gather status (operationalised as reputation points), which is possible by winning debates. They like to attack utterances of other agents about which they think that they can win a debate. They also like to make novel, previously unheard, utterances in order to align common opinion with their opinion.
- 3.3
- The dialogue game is played as follows. An announcement consists of a statement S and two numbers p, r between 0 and 1. When an agent announces (S, p, r), it says: I believe in S and I want to argue about it: if I lose the debate I will pay p reputation points, but if I win, I want to receive r reputation points.
- 3.4
- See https://www.jasss.org/16/3/4.html Par 3.16. Example 2, for a detailed example.
- 3.5
- The values p
and r
are designed to be used in the dialogue game,
but they are not very useful when we want to answer the question: ''What will an agent learn from an
announcement made by another agent?''
To answer that question we introduce two more intrinsic concepts: the degree of belief e
(from evidence) an agent has in favour of a
statement and the importance
(i) of
that statement. Evidence is the ratio between pro and con; an evidence
value of 1 means 'absolutely
convinced of S'.
An evidence value of 0 means 'absolutely
convinced of the opposite of S'.
'No clue at all' is
represented by 0.5. An
importance value of 0 means unimportant
and 1 means most important.
Importance is expressed by the sum of both odds divided by 2.
e =
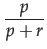 i
=
i
= 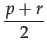
- 3.6
- This means the more important an issue the higher the odds. The (p, r)-values can also be computed from an (e, i)-pair: p = 2 . e . i and r = 2 . i . (1 - e). We call e and i the opinion values.
- 3.7
- Agents learn from other agents by accepting to a degree all
utterances of other agents which are not attacked by some agents and by
accepting all statements of the winner of a dialogue that are uttered
as part of the dialogue. What do agents learn from utterances by other
agents, once they accept those utterances? When an agent believing a
statement with opinion values (e1, i1),
accepts an utterance
of that same statement by another agent with opinion values
(e2,
i2)
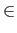 [0, 1]2,
it will acquire new opinion values defined by the functions
AE
:
[0, 1]2
[0, 1]2,
it will acquire new opinion values defined by the functions
AE
:
[0, 1]2  [0, 1] and
AI
:
[0, 1]2×[0, 1]2
[0, 1] and
AI
:
[0, 1]2×[0, 1]2  [0, 1]
and:
[0, 1]
and:AE(e1, e2) = 2e1e2 if e1, e2 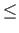 0.5
0.5= 2e1 +2e2 -2e1e2 -1 if e1, e2 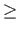 0.5
0.5= e1 + e2 - 0.5 otherwise AI((e1, i1),(e2, i2)) = 0.5(i1 + i2) + 0.125(2e1 -1)(2e2 -1)(2i1i2 - i1 - i2).See https://www.jasss.org/16/3/4.html Appendix B, for the technical details and justification of these formulas. https://www.jasss.org/16/3/4.html Appendix C summarizes the exogenous and endogenous parameters of the simulation and offers a short explanation of their meaning. The next section is devoted to an extension of DIAL with fuzzy logic to enable dialogues about more than one statement.
 FUZZYDIAL
FUZZYDIAL
- 4.1
- In this section we discuss the fuzzy extension to the above
dialogue game model. We first motivate the extension by discussing a
communication scenario the kind of which FUZZYDIAL is supposed to
model.
A Communication Example for FUZZYDIAL
- 4.2
- As an example we consider the following situation:
Example 1 Four friends, Anna, Bob, Chris, and Daphne meet in a bar to celebrate the victory of their football club. When Bob confides to the others that he has lost a considerable amount of money on his Cypriotic bank account, the talk changes to politics and the financial crisis. This is a subject they usually avoid, because all four have very different views on these issues, and they consider talking about such subjects as harmful to their friendship. Their preferred opinions are the following:
- Anna is a socialist with a Keynesian view on economics. She is fully convinced that governments should invest to get out of the current crisis. The state should bail out companies that went bankrupt because of the crisis. And the European Union should invest in national economies that suffer from the crisis.
- Bob has a monetarist view on macro-economics and believes that only a free market for goods and workers can free us from the crisis. The only goal for the European Union and the governments should be, to keep the trust of the investors in the euro as high as possible. He values the EU as the protector of a large free market. National boundaries are bad.
- Chris and Daphne both have anti-European sentiments. Chris, who is a socialist like Anna, believes in the equality of all people and thinks that the richer countries should help the poorer ones, but his fear is that the current European Union is highjacked by a club of multinational companies and that the differences in the labour market are exploited to decrease the workers' power by free exchange of workers.
- Daphne believes in the blessings of the free market economy. And in her opinion the European Union is turning the world into a village and she fears that other people will consider her national idententity sentiments as ridiculous and irrelevant when globalisition progresses.
Daphne says that she feels sorry for Bob and she declares that she does not understand the anger of the Cypriots. They should be happy with the ten billion euros and not bite the hand that feeds them. But in the end Cyprus would have been better off if it still was able to devaluate its own currency. Bob thanks Daphne for her pity, but says that in macro-economics we should not let emotions lead our decisions. And although he himself hates the fact that Cyprus has to be bailed out, he says that we should consider the fact that we would suffer more if we didn't do that, because that would be a very bad signal to the investors all over the world. Thus keeping trust in the euro is worth a lot of money. Anna expresses that she agrees with Bob and the euro group and Dijsselbloem; the small money savers should not become the victims of a disfunctioning banking system. According to her, nationalization would have been the best option. Bob smiles over this last remark and notices that nationalization of banks would definitely destroy the financial safe haven in Cyprus. Chris does understand the anger of the Cypriots; their world is falling apart; it will be very hard for the Cypriots to repay all that money and the interest. And then he utters Daphne's favorite argument: maybe Cyprus would have been better off if it were to conduct its own monetary policy.
Thus ends the first round in the exchange of arguments. The friends are satisfied. The loss of friendship was what they feared, but that did not happen. All persons have strongly opposing opinions, but they don't utter their strongest convictions. On the one hand, they seek the support of one another for their opinion, on the other hand, they want to support one another. By uttering statements which are less extreme than what they really believe, their attitude has been interpreted by all as an attempt to stress what they have in common, and accentuates their friendship.
In another place at another time other players with the same set of opinions could start a debate to find reasons for hating each other. Uttering statements not only serves to inform other people, it also serves to establish a social network (make or break social ties).
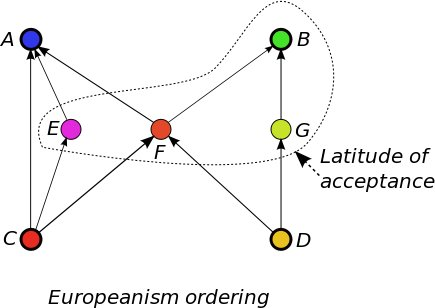
- 4.3
- In Figure 1
the named circles, A,
B, C, and D represent the
first utterances of the four people. Their position signifies their
meaning in an ordering determined by two issues:
pro versus anti the union of Europe, and Keynesian versus monetarist
economics. The circles represent sets of states in which the uttered
statements hold. Their colours symbolise their meanings, endorsing the
idea that utterances can be made that are blends of more extreme
opinions:
blue-green for pro-European statements; red-yellow for anti-Europeans;
red-blue for pro-Keynesians and yellow-green for pro-monetarist
statements. The pink, orange and light-green circles labeled by E, F
and G
respectively represent statements that are not uttered in the debate
yet. They represent a neutral position in the pro-anti-Europe issue,
but they differ in the economics issue. F
is pro-Keynes and H
is pro-Monetarist, while G
is also almost neutral in this issue. Their role will become clear in
the in the examples of Subsection 4.2.
- 4.4
- We want to model this type of exchange of arguments between
agents in a dialogue game similar to DIAL. Whilst DIAL only considers
simulations in which agents argue about one
statement, in this article, we introduce a simulation model with
dialogues about more than one statement.
Conceptual Discussion of FUZZYDIAL
- 4.5
- DIAL only implemented dialogues about one statement. We did not account for a relation between different statements S1 and S2, e.g. in the sense that S1 is more extreme than S2 on some extremeness scale. So in DIAL we cannot describe the change of a multidimensional opinion to a more (or less) extreme position.
- 4.6
- In FUZZYDIAL we allow agents to have opinions about a set of statements. This is more in line with the theoretical notion that an attitude is composed of a set of beliefs (see e.g. Ajzen 1991). For each belief a person can have an opinion that expresses to what extent the belief is accepted or rejected, and the importance and certainty of this belief (see e.g. Visser et al. 2006). In FUZZYDIAL the agent's attitude is formalised in terms of what statements it finds acceptable or not. Another interpretation of an attitude is that it represents a preferred statement, the statement with the highest e-value, of an agent joined with all semantically related statements that the agent consider as acceptable. Therefore sets of statements are referred to as the latitudes of acceptance (LOA), the latitude of rejection (LOR), and the latitude of non-commitment (LON). So (LOA, LOR, LON) is a partition of a set of statements.
- 4.7
- In Fuzzy Logic, the membership of a fuzzy set S is described
by a function
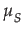 : X
: X  [0, 1],
where X
is the domain space or universe of discourse (see Figure 2).
In FUZZYDIAL the universe of discourse is a possibly infinite set of
statements Stats.
Only atomic sentences and their negations, which are called literals,
will be considered. A linguistic variable V is a function
which takes an element of a set of fuzzy predicates
or linguistic modifiers as value, and produces a
fuzzy set; for example, temperature is a linguistic variable for fuzzy
predicates as cold, moderate, warm, etc. In our first example: the issues
European Unionism and Monetarism are linguistic variables with pro,
anti and moderate as their linguistic
modifiers. For each agent a
and each statement, we define the opinion function
[0, 1],
where X
is the domain space or universe of discourse (see Figure 2).
In FUZZYDIAL the universe of discourse is a possibly infinite set of
statements Stats.
Only atomic sentences and their negations, which are called literals,
will be considered. A linguistic variable V is a function
which takes an element of a set of fuzzy predicates
or linguistic modifiers as value, and produces a
fuzzy set; for example, temperature is a linguistic variable for fuzzy
predicates as cold, moderate, warm, etc. In our first example: the issues
European Unionism and Monetarism are linguistic variables with pro,
anti and moderate as their linguistic
modifiers. For each agent a
and each statement, we define the opinion function 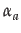 similar
to the membership function. We define the important concepts formally:
Definition 2 (Belief, importance and attitude) Let a
similar
to the membership function. We define the important concepts formally:
Definition 2 (Belief, importance and attitude) Let a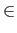 Agents.
We have functions
Bela,
Impa : Stats
Agents.
We have functions
Bela,
Impa : Stats
 [0,
1].
We write
[0,
1].
We write 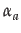 for
(Bela,
Impa).Definition 3 (Issue) An issue iThe minimal and maximal elements are the extreme statements. In our examples we will also attribute our statements with numerically valued issues in the interval [0, 1].
for
(Bela,
Impa).Definition 3 (Issue) An issue iThe minimal and maximal elements are the extreme statements. In our examples we will also attribute our statements with numerically valued issues in the interval [0, 1].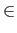 I
is an ordered set (Si,
< i) with
S
I
is an ordered set (Si,
< i) with
S 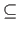 Stats,
S
finite and < i
a connected partial order on Si.[3]
Stats,
S
finite and < i
a connected partial order on Si.[3] - 4.8
- Normally, atomic statements are considered as unordered
sets and in Social Judgement Theory there is a continuous ordering on
statements. We assume a set of partial orderings on statements, one for
each issue. A literal is an atomic statement or its negation. By
s1
< is2
we mean that statement s2
is closer to some positive extreme of issue i
than s1
is. In our experiments, we assume for the sake of simplicity, that the
ordering on statements in an issue is either the same for all agents (standard
categories) or all agents have their own ordering (own
categories) (Sherif
& Hovland 1961).
Definition 4 (Latitude of acceptance, latitude of rejection, latitude of non-commitment) Let 0
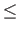 eR
< eA
eR
< eA 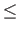 1.
1.
We define:
LOAa, i = {s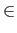 Si | eA
< Bela(s)}
Si | eA
< Bela(s)}
LORa, i = {s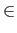 Si | Bela(s)
< eR}
Si | Bela(s)
< eR}
LONa, i = {s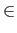 Si | eR
Si | eR
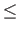 Bela(s)
Bela(s)
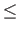 eA}
eA}
- 4.9
- A most preferred statement[4] is one of the statements with the highest e -value of the LOA (see Figure 2).
- 4.10
- The LOA is determined by an interval of a certain size around a preferred statement. This interval is surrounded by the latitudes of non-commitment, which border on their other side to the area with the statements that are rejected (see Figure 2).
- 4.11
- If an agent believes two statements with different
positions on the scale of extremeness, it also has to believe all
intermediate statements. This principle will be called: linguistic
consistency[5].
A logically consistent agent cannot believe a statement and its
negation, but in order to be linguistically consistent, an agent a, who believes
s1
and s3,
also has to believe all the positions s2
that are intermediate between s1
and s3.
So when s1
< is2
< is3
holds for any issue i,
a
also has to believe s2.
- 4.12
- To express this property, the acceptance function A on statements
needs to be extended to a similar function on attitudes. Typical
(fuzzy-) set operations such as union and intersection
can be defined in terms of operations on their elements, e.g. union
in terms of max:
(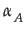
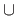
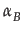 ) = defmax(
) = defmax(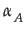 (x),
(x),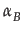 (x)).
In the same way we can extend our concepts for opinion acceptance to
attitudes.
Acceptance of the opinion
(x)).
In the same way we can extend our concepts for opinion acceptance to
attitudes.
Acceptance of the opinion 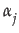 (s)
of agent b
by an agent a
who has opinion
(s)
of agent b
by an agent a
who has opinion 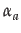 (x)
on x
can be defined as:
(x)
on x
can be defined as:
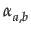 (x)
= defA(
(x)
= defA(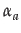 (x),
(x),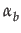 (x))
(x))
- 4.13
- See https://www.jasss.org/16/3/4.html Appendix B for the full definition of acceptance.
- 4.14
- A notion similar to linguistic consistency
in fuzzy logic is known as: convexity. A fuzzy set
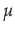 is convex iff for all x
< y < z
holds:
is convex iff for all x
< y < z
holds:
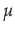 (y)
(y)
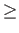 min(
min(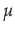 (x),
(x),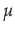 (z))
(Pedrycz & Gomide 1998).
(z))
(Pedrycz & Gomide 1998).
- 4.15
- We call X
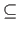 Si
convex with respect to issue i
when we have:
Si
convex with respect to issue i
when we have:
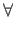 x,
y
x,
y 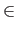 X
X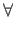 s
s
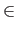 Si(x
< i s < i
y
Si(x
< i s < i
y
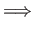 s
s
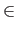 X)
Definition 5 (Linguistic Consistency) An opinion function Bela is linguistically consistent if the following holds:or equivalently:
X)
Definition 5 (Linguistic Consistency) An opinion function Bela is linguistically consistent if the following holds:or equivalently: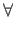 s,
t, u
s,
t, u 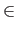 Si(s
< i t < iu
Si(s
< i t < iu
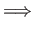 min(Bela(s),
Bela(u))
min(Bela(s),
Bela(u))
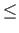 Bela(t))
Bela(s) = min(sup{Bela(t) | t
Bela(t))
Bela(s) = min(sup{Bela(t) | t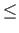 s},
sup{Bela(u) | s
s},
sup{Bela(u) | s
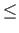 u})
(*)
Proposition 6 if Bela is convex w.r.t. issue i, then LOAa, i is convex.
u})
(*)
Proposition 6 if Bela is convex w.r.t. issue i, then LOAa, i is convex.Proof Let x, y
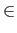 LOAa,
i and s
LOAa,
i and s
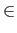 Si
with x
< i s
< iy.
We must show that s
Si
with x
< i s
< iy.
We must show that s 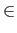 LOAa, i.
We have x, y
LOAa, i.
We have x, y 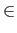 LOAa,
i, so
LOAa,
i, so
(1) Bela(x) > eA and Bela(y) > eA.
By x < i s < iy and linguistic consistency of Bela w.r.t. i, we have
(2) min(Bela(x), Bela(y))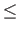 Bela(s).
Bela(s).
Now by (1) and (2) we get Bela(s) > eA. But this is equivalent with s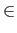 LOAa,
i.
LOAa,
i.
.
- 4.16
- A problem is that the acceptance function as defined in https://www.jasss.org/16/3/4.html Appendix B does not preserve convextity. It will not always be the case that an agent A1 with an opinion function BelA1, who believes statement s1 with opinion values (e1, i1) and accepts the utterance of another agent A2 on s1 with opinion values (e2, i2), will end up with a new opinion function BelA1 that is still linguistically consistent.
- 4.17
- It is however possible to make an opinion function
linguistically consistent by increasing the opinion values of the
statements that violate the linguistic consistency constraint
sufficiently:
Definition 7 (Convexification) The convexification, Belc of an opinion function Bel is:From (*) it follows that: Belc is convex; BelBelc(x) = def min(sup{Belc(y) | y
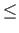 x},
sup{Belc(z) | x
x},
sup{Belc(z) | x
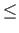 z})
z})
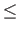 Belc;
if Bel
is convex then Belc
= Bel; from Bel1
is convex and Bel
Belc;
if Bel
is convex then Belc
= Bel; from Bel1
is convex and Bel 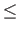 Bel1
follows Belc
Bel1
follows Belc 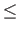 Bel1.
Bel1.
- 4.18
- In Table 1
a list is given with the standard fuzzy logic terminology and its
counterparts in the FUZZYDIAL model.
Figure 3. The result of the acceptance-operator (the circled A) on two opinion functions Bela and Belb. Horizontal axis: statements (s). Vertical axis: [0, 1]. The resulting attitude is in red. (a) Similar opinions enlarge certainty. (b) Two related opinions result in one with a greater tolerance. (c) Unrelated opinions result in one with less certainty and less tolerance. 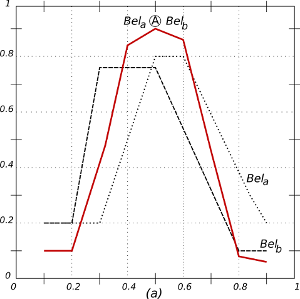
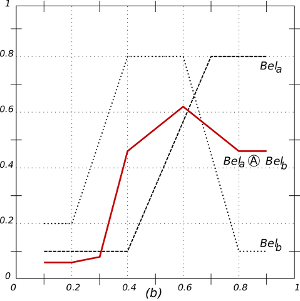
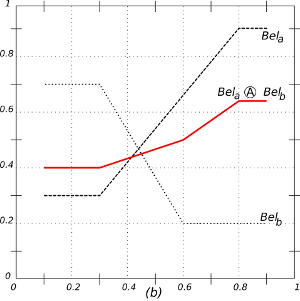
- 4.19
- The examples in Figure 3
show how the acceptance operator
 on opinion
functions produces opinions as predicted in Social Judgement Theory and
the Theory of Reasoned Action. According to Social Judgement Theory (Griffin 2011, p. 194), if an
agent hears opinions that belong to its latitude of acceptance (LOA), a
process of assimilation results in perceiving a
message that is closer to the own opinion than it actually is.
Accepting such misrepresented messages narrows the LOA.
on opinion
functions produces opinions as predicted in Social Judgement Theory and
the Theory of Reasoned Action. According to Social Judgement Theory (Griffin 2011, p. 194), if an
agent hears opinions that belong to its latitude of acceptance (LOA), a
process of assimilation results in perceiving a
message that is closer to the own opinion than it actually is.
Accepting such misrepresented messages narrows the LOA.
- 4.20
- Figure 3a shows that the acceptance of a similar opinion enlarges certainty. The resulting LOA is higher and narrower. Messages in the latitude of non-commitment (LON) have a higher probability of being accepted as desired by the sender, which results in a larger latitude of rejection (LOA).
- 4.21
- In Figure 3b, the acceptance of two related opinions results in one with a greater tolerance with less certain opinions. Finally, Figure 3c shows that the acceptance of more unrelated messages, which fall in the LOR, results in one with less certainty and less tolerance. The effect is reinforced by a contrast-misrepresentation which causes the perception of the message to appear more different from the preferred statement than it really is.
- 4.22
- In social epistemology, the group of agents which tend to
reinforce an agent's opinion is called an 'echo chamber'. The agents which communicate
with each other in FUZZYDIAL function as an echo chamber
(Baumgaertner 2014). 'Echo
chambers' reinforce the agents' opinions when they are echoed
by other agents. Baumgaertner studies the factors which might dismantle
echo chambers (Baumgaertner
2014).[6]
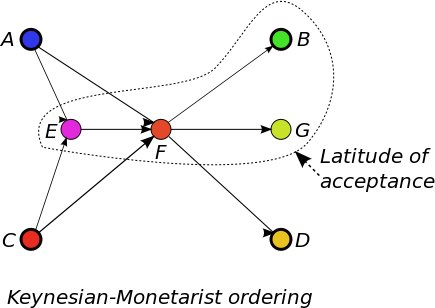
Example 8 In Figure 4, the graphs of the partial ordering of the two issues of Example 1 are represented: the Europeanism issue (left) with the vertical orientation and the Keynesian-Monetarist issue (right) horizontally oriented. The extreme statements in both issues are represented by the thick-lined circles, the statements A, B, C, and D, corresponding to the preferred statements of Anna, Bob, Chris, and Daphne, respectively. The ordering on both issues is not the same:
< Europeanism = { (C, A),(C, E),(E, A),(C, F), (F, A),(F, B),(D, F),(D, G),(G, B)}
and
< KeynesianMonetarist = { (C, E),(A, E),(C, F),(E, F), (F, D),(F, G),(F, B)}.
However in this example, LOABob, Europeanism = LOABob, KeynesianMonetarist because SEuropeanism = SKeynesianMonetarist.This demonstrates that in Example 1 the choices of changes in attitude of agents are nontrivially constrained by convexity.
Suppose Bob's latitude of acceptance consists of the statements contained in the dashed-bordered area. There are four statements accepted by Bob: B, E, F and G. He may drop any statement, except statement F, because that would violate the convexity principle in the Europeanism issue. Bob cannot extend his latitude of acceptance by adding any of the statement A, C or D because they are all complementary to his preferred statement B, which would make his attitude logically inconsistent.
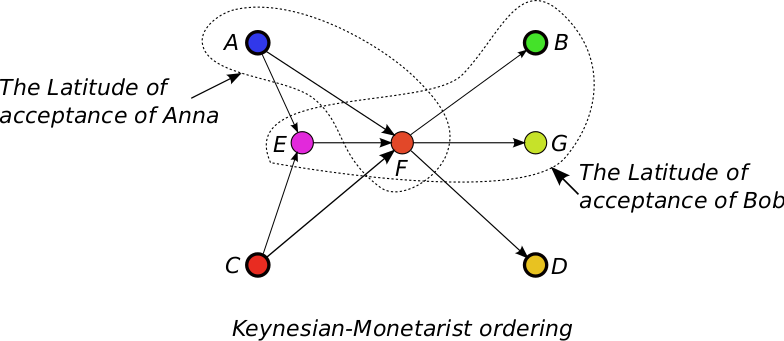
Example 9 In Figure 5, the LOA of Anna and Bob are compared. There are four statements accepted by Bob. The LOA of Bob is convex with respect to both issues. He may drop any statement, except statement F, because that would violate the convexity principle in the Europeanism issue. Bob can extend his latitude only by adding extreme statements.The LOA of Anna is {A, F}, which is not convex because it should contain statement E since A < KeynesianMonetaristE < KeynesianMonetaristF and by Definition 5, BelAnna(E) should be at least as high as BelAnna(A) and BelAnna(F), so E should be in LOAAnna, KeynesianMonetarist.
If all agents share the ordering on the Keynesian-Monetarist issue, as is displayed in Figure 4 and Figure 5 (standard categories), any agent who discovers that Anna does not believe E may attack her because of her linguistic inconsistency.
''Do all agents have the same ordering of statements?'' If agents have to be able to interpret the utterance of another agent to check whether that agent is approaching them or moving away from them in the opinion space, they need a shared or standard ordering of statements.
- 4.23
- When a group of agents shares an ordering of statements,
the next question in that case is: ''How do agents acquire a
shared extremeness ordering?'' If it would be innate, there
could not be any dynamics of opinion. If it is learned by
communication, then it is unlikely that all agents will have the same
extremeness ordering.
Example 10 Suppose that the displayed ordering in Figure 5 is only accepted by Bob and not by Anna, and suppose that LOAAnna, KeynesianMonetarist is the same as LOABob, KeynesianMonetarist, but missing one of the edges (A, E) or (E, F). Now Anna is linguistically consistent according to her own statement ordering, which is fine for her. But how about Bob? How will he know that Anna's statement ordering is not the same as his? Will he accept that other agents adopt a different statement ordering?Example 11 Suppose that in Example 1 in Subsection 1, Bob believes that being monetarist is a position in the Europeanism scale close to the Monetarist extreme, and Bob believes that he shares his statement ordering with the other agents. Suppose furthermore that Bob knows about the pro-European viewpoint on politics of Anna, but he knows nothing about her Keynesian standpoint. Now based on Bob's belief about the shared statement ordering and his assumption about the linguistic consistency of Anna, he might believe that Anna is monetarist. If all agents do have the same (standard) statement ordering, and Anna would utter her Keynesian opinions, Bob might rightfully accuse her of being inconsistent.
- 4.24
- If all agents have their own ordering of statements, Bob will only be able to detect a linguistic inconsistency in another agent's utterances if he knows its private ordering. When agents have no information about one another's statement ordering, they cannot detect any linguistic inconsistency in the utterances of other agents.
- 4.25
- An interesting refinement of this model is to allow agents to have beliefs about the statement orderings of other agents. Learning each other's statement orderings would be a neccessity to acquire information about the attitude of other agents on the basis of announcements. And acquiring a common ordering by alignment would make agent communication simpler. This type of misunderstanding between agents who have incomplete and incorrect beliefs about one another's statement ordering is much harder to resolve than getting an agreement about a particular statement. Robust networks of echo chambers (see Subsection 4.2) are considered hazardous for society as a whole (Sunstein 2003; Bishop 2008) because they inhibit agents to come to a consensus in the context of society as a whole.
- 4.26
- In this article we will not explore this refinement further. It would complicate our communication model seriously because of its higher-order epistemic consequences (What would agent a say if it believes that other agents might not have a correct knowledge of agents a's statement ordering? How would agent a come to believe that other agents have an incorrect view of its statement ordering? See Verbrugge (2009) for the exciting relation between cognition and epistemic logic.).
- 4.27
- For our experiments we introduce two types of linguistic
consistency:
- Standard categories. There exists an extremeness ordering of statements which is the same for all agents. All agents know the statement ordering and are capable of detecting linguistic inconsistency and they will repair their inconsistent attitudes.
- Own categories. Each agent has its own extremeness ordering on the set of statements. Agents do not know the statement ordering of other agents. And having a linguistically inconsistent attitude has no consequence in the social debate.
- 4.28
- In both cases, agents will not utter statements that are linguistically inconsistent, because the acceptance function keeps their attitude linguistically consistent. 'Own categories' are more related to personal choices, which links them to the 'attitudes' in the Theory of Reasoned Action and in contrast 'standard categories' depend more on group opinions and group influence, which they have in common with the 'subjective norms' in the Theory of Reasoned Action (Ajzen & Fishbein, 1980).
 Implementation of
FUZZYDIAL
Implementation of
FUZZYDIAL
- 5.1
- Making an announcement causes a chain of events. An announcement may change the opinion of other agents indirectly in a dialogue game where the direct effect is on the reputation of agents, but there is also a direct effect through learning and assimilation and contrast effects. The way these mechanisms are implemented in the NetLogo simulation program is depicted in the sequence diagram of Figure 14.
- 5.2
- The reputation status of agents can be determined by two
different mechanisms (Dykstra
et al., 2013):
- Force of Norms: The reputation status is determined by similarity with the environment. When an agent is more successful than others in establishing social contacts with similar-minded agents, it will increase its reputation status.
- Force of Arguments: The reputation status is the account of the agent's argumentation score, because reputation points are the currency in which pays and rewards are balanced.
Table 5 Categories of experimental parameters Reputation is the combined parameter which is low when reputation status is determined by high force-of-norms (and low force-of-arguments) and it is high in case resputation status is determind by high force-of-arguments (and low force-of-norms). MOAC Assimilation and Contrast forces. These parameters force opinion changes; agents have to accept or reject the opinions of others. The parameter values are either zero and have no effect at all, or 0.4. SOC Standard verses Own categories. The standard categories option prohibits opinion changes that are linguistically inconsistent.
- 5.3
- Announcements affect the opinions of the listeners
directly. Utterances which agree/disagree sufficiently with the opinion
of the listener (determined by the attraction and rejection
parameters) are considered by the reader for acceptance or rejection,
according to the mechanism of assimilation and contrast (MOAC)
(Jager & Amblard, 2005).
MOAC is implemented by accepting those statements that belong to the latitude
of acceptance (LOA) and rejecting statements (which means:
accepting the negation) that are in the the latitude of
rejection (LOR).
Own / standard categories (SOC) is a test which is performed in case the population imposes standard categories on the agents. If all agents have their own categories, they are free to change the ordering of their opinions. In that case the test is void, because agents can accept or reject whatever they want. If it makes their attitude inconsistent, they just reorder their statements.
- 5.4
- With own categories (OC), the ordering
between the least and most preferred opinion is simply the evidence
ordering. LOA is implemented as the set of statements with an evidence
higher than 1 -
tolerance, LON has evidence between tolerance
and 1 - tolerance.
- 5.5
- When agents have standard categories (SC), all agents know and obey the same ordering between two (or more) extremes. The LOA is the part of the statements that have evidence above 1 - tolerance.
- 5.6
- The details of the flow of consequences of agents' actions, as performed in the procedure act, is explained in Appendix D.
 Simulation experiments
Simulation experiments
- 6.1
- How do announcements affect opinions of other agents? And how do the just named experimental parameters support the propagation of moderate or extreme opinions? Do they affect tolerance or ego-involvement? What is their influence on social networks, and how does the social structure in its turn influence the opinion dynamics? These are the questions we try to answer with our experiments. In Subsection 6.1 we summarise the effects of force-of-norms and force-of-arguments. In Subsection 6.2 we extend the simulation by allowing more statements to the social debate, which forces a choice between two types of extremeness orderings (SOC). We study both own categories and standard categories. And finally in Subsection 6.3, we investigate how a combination of Reputation, SOC and MOAC contributes to the emergence of a latitude of acceptance.
- 6.2
- In simulation runs we studied their effect on a number of parameters that give an impression of the type of opinion and social dynamics. A simulation run is a number of rounds of the simulation. At the start, agents are placed randomly in the world and they are assigned with random opinion- and reputation-values.
- 6.3
- A run of our experiment can be interpreted as a period of
social interaction about an issue.
During a round every agent gets the opportunity to perform one of the
following actions: announce, attack, reply, change their social network
by walking to another place. The actual values of
these exogenous parameters are given in Table 3.
Effects of Norms and Argumentation
- 6.4
- In Dykstra et al. (2013) we studied the effect of norms and argumentation on opinion dynamics and the social structure. Cases concerning only one statement were studied. Typical results of a simulation in which reputation is determined by force-of-norms and force-of-arguments are shown in Appendix B.
- 6.5
- Based on these simulations, we concluded in Dykstra et al. (2013) that argumentation prevents the emergence of extreme opinions and severe segregation. But do these results persist if we extend our simulation to the case where agents debate about more than one statement? We will answer this question in the next subsection.
- 6.6
- The Figures 6
to 8 represent pictures of
the distribution of opinions in the world the agents live in. For the
meaning of the colors of the circles and the background, we refer to
Appendix A.
Effects of Own and Standard Categories
- 6.7
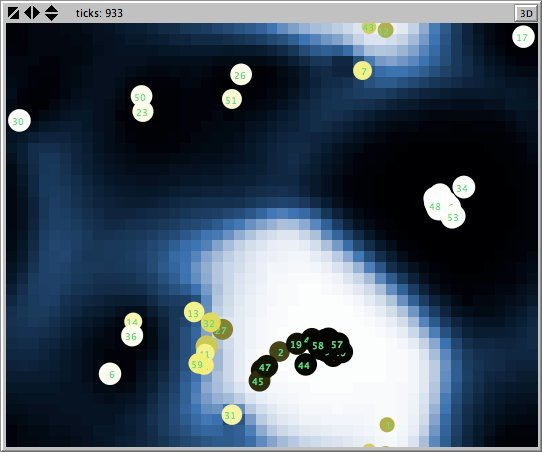
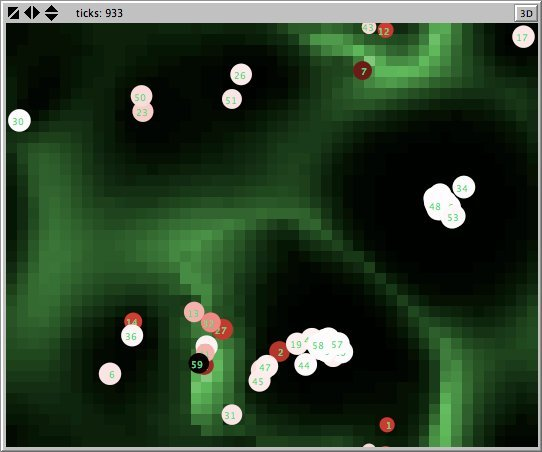
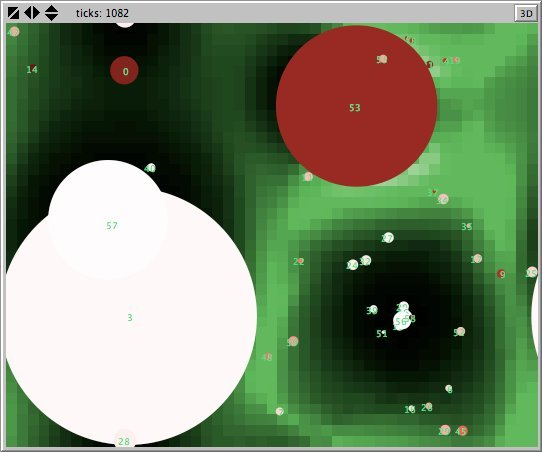
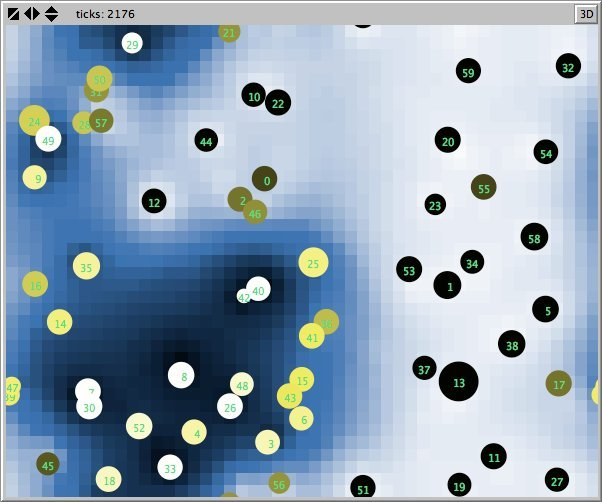
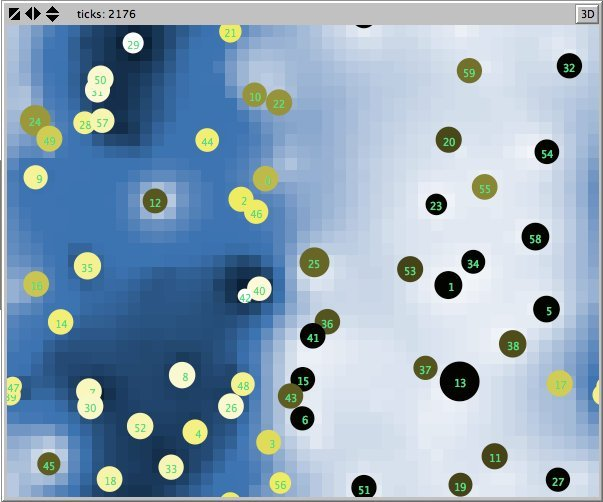
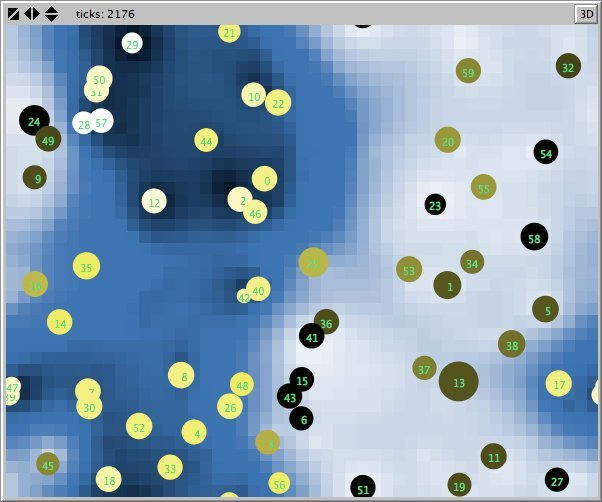
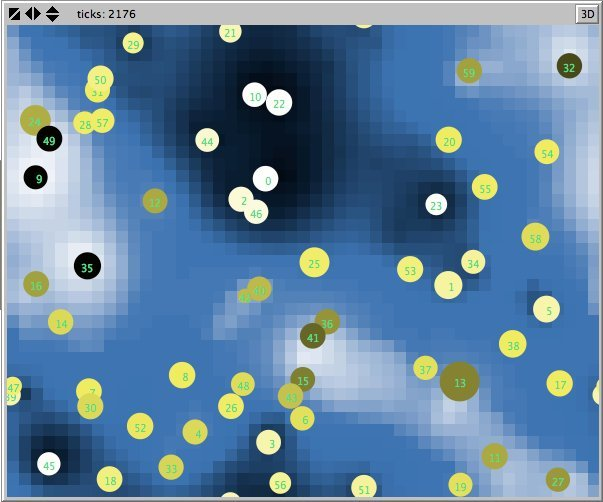
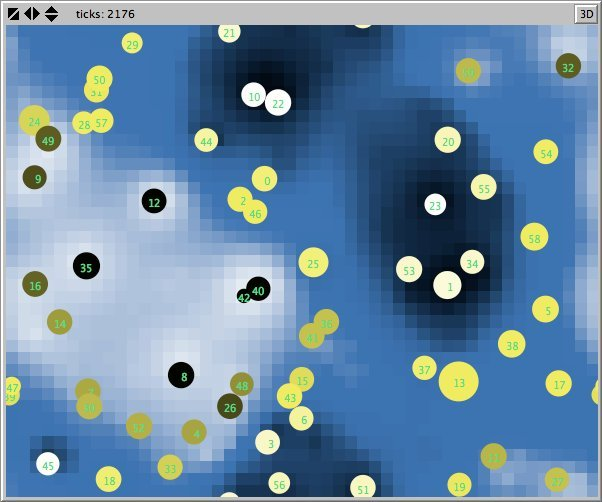
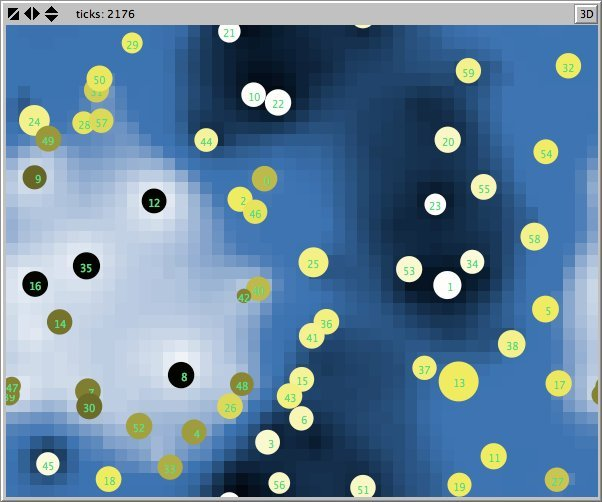
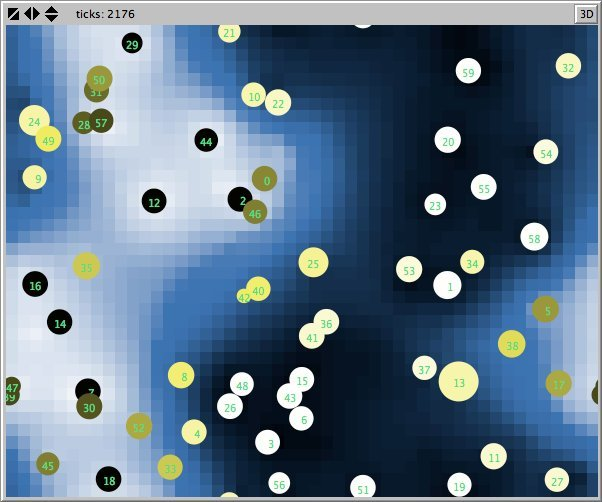
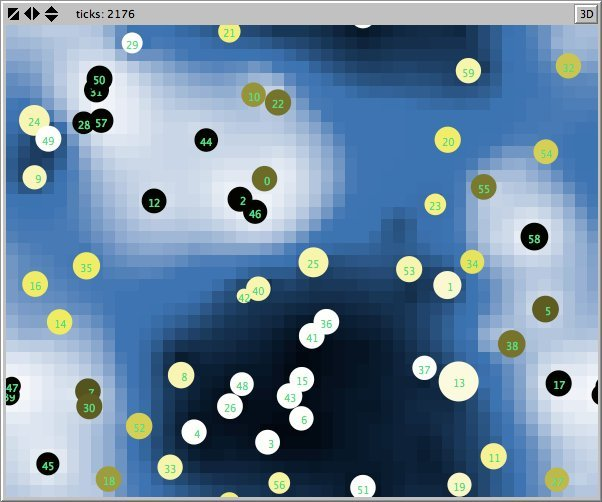
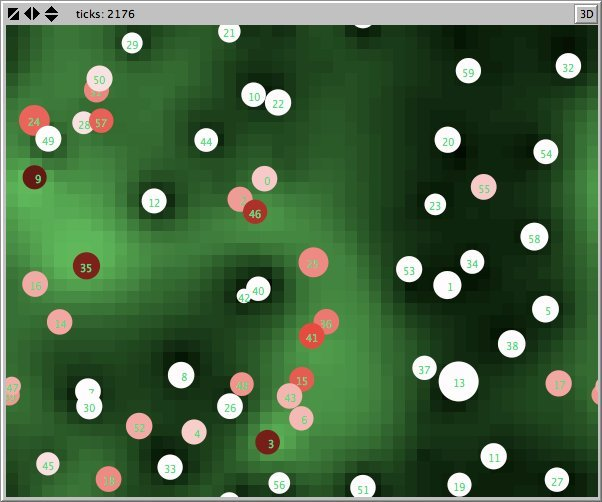
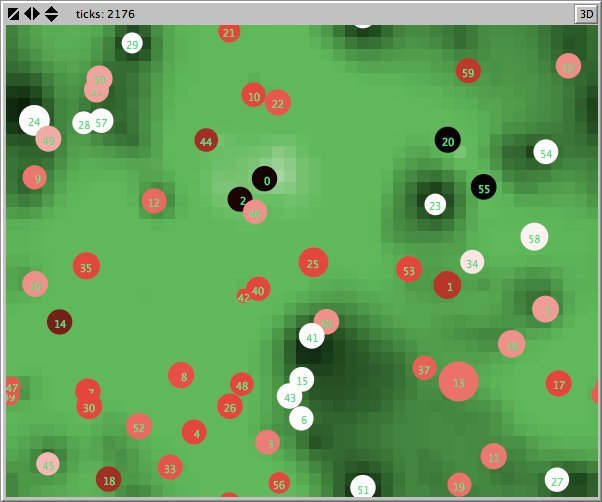
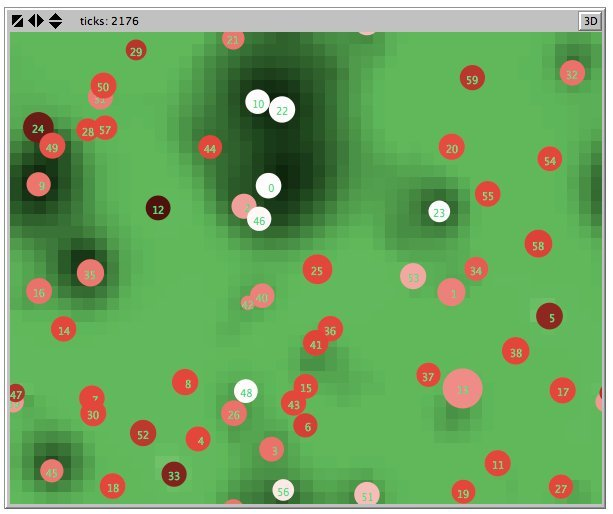
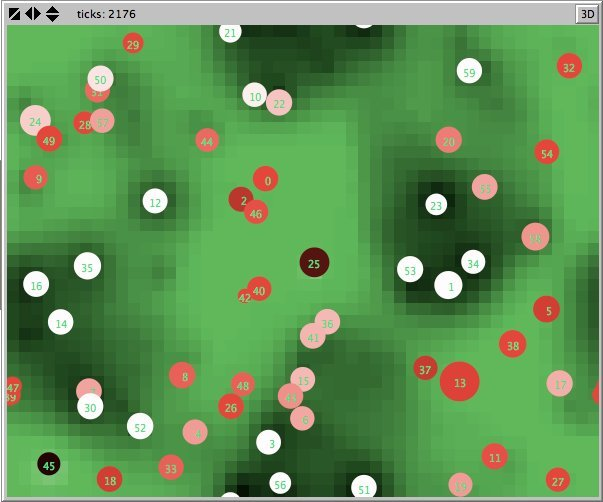
- Figures 6 and 7 show the maps of evidence of ten statements of two simulations after nearly 1700 rounds. The maps are a screenshots of the world window of the FUZZYDIAL simulation program in NetLogo. In each column the same agents occupy the same place, because both columns represent the same stage in a simulation, but they show the belief values for different statements (A to J). For a description of the meaning of the colours we refer to Appendix A . The world has no borders: the world wraps horizonally and vertically, so its shape is toroidal.
- 6.8
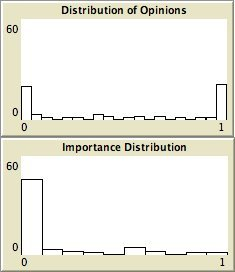
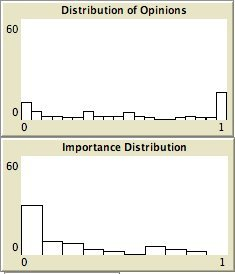
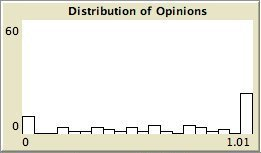
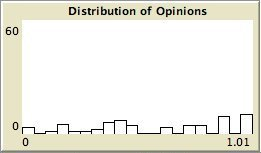
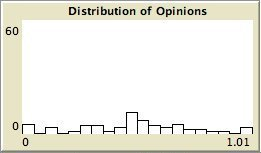
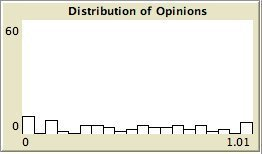
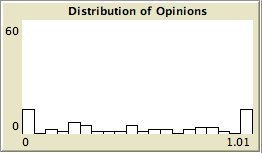
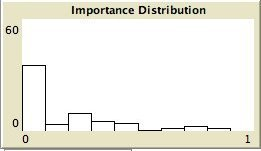
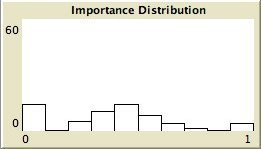
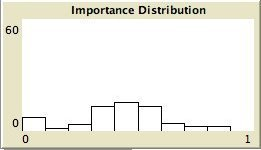
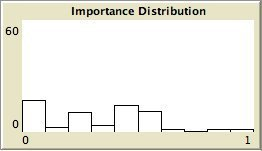
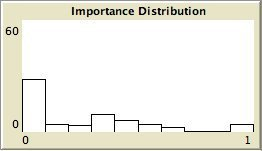
- The left column shows the resulting maps of the simulation with own categories and the right column shows the resulting maps of the standard categories simulation. The reputation of an agent (size) is the same in every map, but their evidence values differ for the different statements. The reputation is only determined by force-of-arguments. So in essence this simulation only differs from the one of which results are shown in Figure 13 by the fact that the number of propostions is 10 instead of 1. Figure 8 shows the importance maps for half of the statements for both simulations. How the degrees of evidence (Figure 9) and importance (Figure 10) are distributed over the agent population is shown in bar charts. Each bar represents a subinterval of the interval [0, 1].
- 6.9
- The most remarkable difference in the Figures 6 to 8 is that the distribution of reputation (size) is more egalitarian in the standard categories column compared to the own categories column. Furthermore the standard categories columns in these figures show a kind of evolving pattern when we compare the maps from statement A to J. In the own categories column the sequential statements appear unrelated. If the statement ordering is private, every agent has its own categories. This explains why no pattern can be found in the evidence and importance values of the agents for the different statements in the left column of the Figures 6 to 8. Neither is there a pattern in the evidence values of the patches.
- 6.10
- The most important difference between both columns is however that the extreme statements in the standard categories simulation (statements A and J) also have the most extreme believers. This can be observed in all Figures 6 to 10. In the maps in Figure 6 and Figure 7 of statements A and J, the agents with the colours black and white (representing the evidence values 0 and 1) are more frequent than in the other maps. The agents also perceive a more extreme environment. The colours black and white are more represented in the background than the colour blue (with evidence values around 0.5).
- 6.11
- The right columns of Figures 6 and 7 reveal an extra property. For each agent we can now actually see what its latitudes of acceptance, non-commitment and rejection are. When we pick an agent and count the number of successive maps where that agent is black, we measure its latitude of acceptance. And similarly, the number of successive maps where an agent is white determines its lattitude of rejection. We can verify that all agents have a convex attitude. As a consequence, the majority of the patches has a convex attitude, although they are not punished for being inconsistent.
- 6.12
- In the right column of Figure 8 the number of white agents is larger for the maps of the statements A and J and the background is darker, meaning that the agents do not want to talk about these statements despite the fact that they have the strongest opinions about it. The left column does not expose any pattern.
- 6.13
- The bar charts of Figure 9 and Figure 10 tell the same story: in the right column the peaks on the left and right side in Figure 9 for statement A and J denote the high number of agents with strong opinions, while for the statements between A and J the moderate opinions dominate. In the right column of Figure 10 the leftmost bar for A and J has a peak (high number of agents who find this statement not important to talk about) and for the statements between A and J the central bars take up most of the agents.
- 6.14
- In the left column there is no difference between the bar charts of A and J and the barcharts of the in-between statements for both Figure 9 and Figure 10.
- 6.15
- In the left columns there is no radicalisation in the evidence values of the agents as in the simulation of Figures 6 to 8. The distribution of evidence is practically random. Importance values converge to 0.5 in all but the fourth statement, which is caused by the forgetting mechanism. This indicates that the dialogue is about other statements.
- 6.16
- The unequality in reputation is lower in the right column,
compared to the left in Figure 6
to Figure 10. This is not
surprising since the agents are more strongly constrained to align to
others compared to the own categories simulation.
When agents talk about more than one statement, while they 'stay on the
same place' in their social network, they have to align to another
agent on some statements. This may lead to different coalitions for
different statements. The consequence of this is twofold: on the one
hand, it prevents the formation of firm and stable groups, on the other
hand, it also prevents the emergence of a few opinion leaders who take
all the reputation points.
Figure 6. The map of evidence of the statements A to E with high force-of-arguments. A 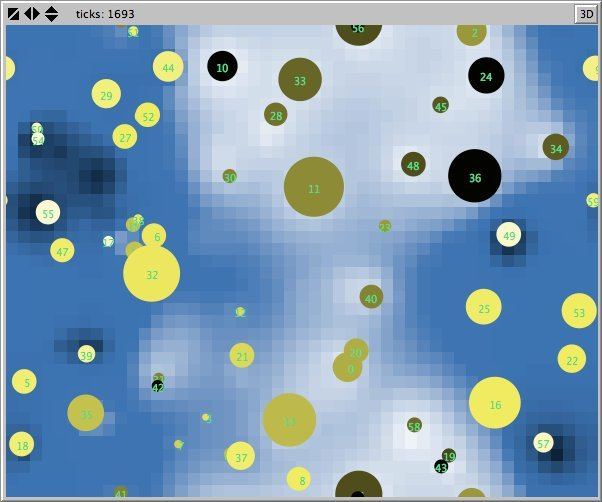
B 
C 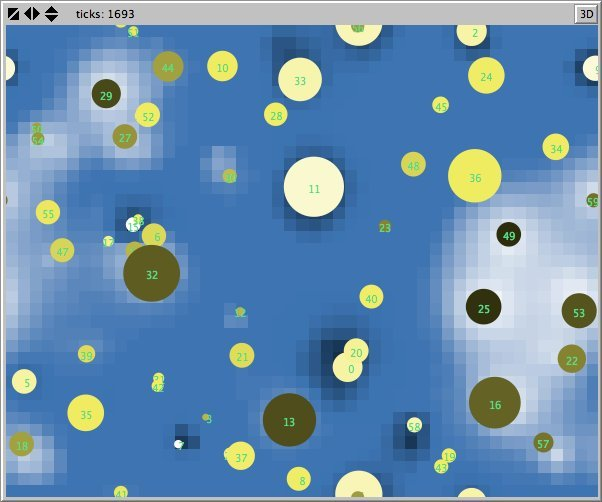
D 

E 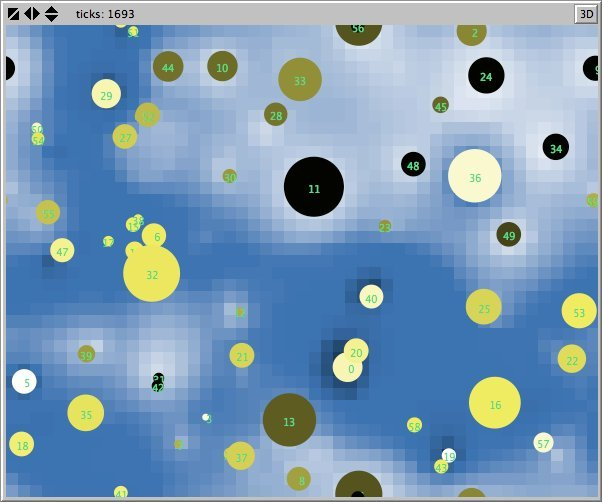
Own categories Standard categories Figure 7. The map of evidence of the statements F to I with high force-of-arguments. F 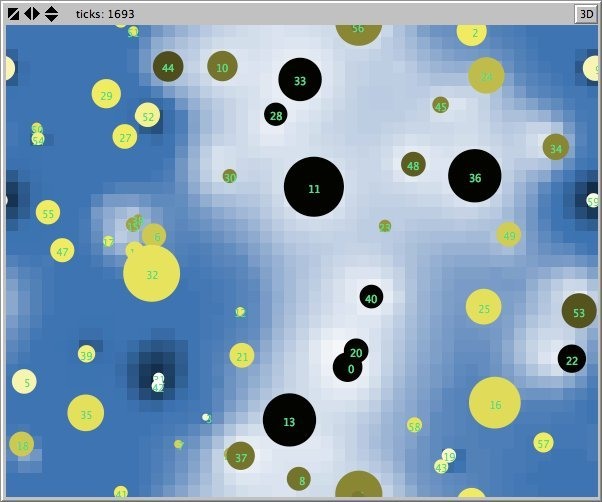
G 
H 

I 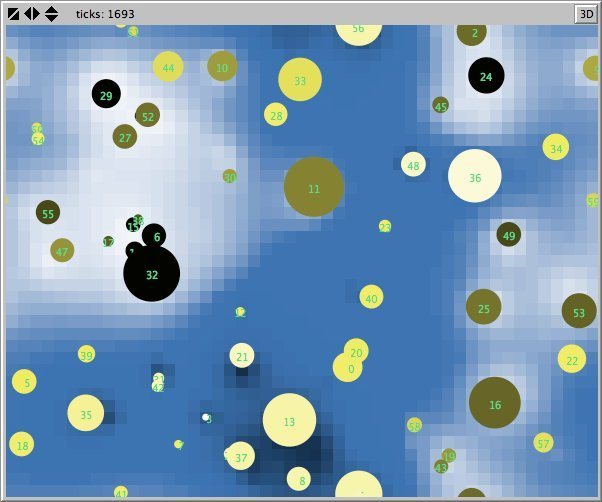
J 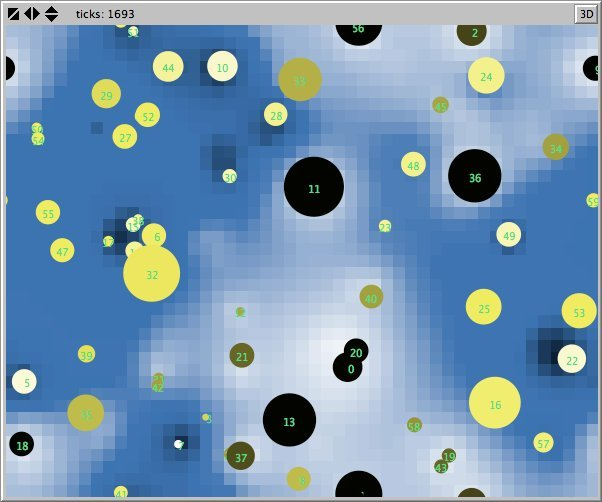
Own categories Standard categories Figure 8. The importance map of the statements A, C, E, H, J with high force-of-arguments. A 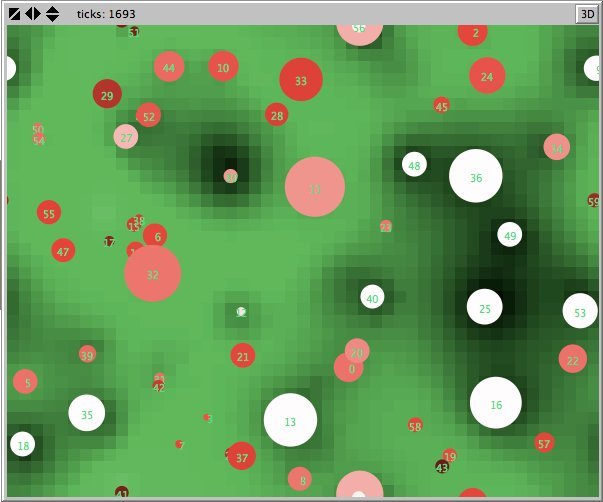
C 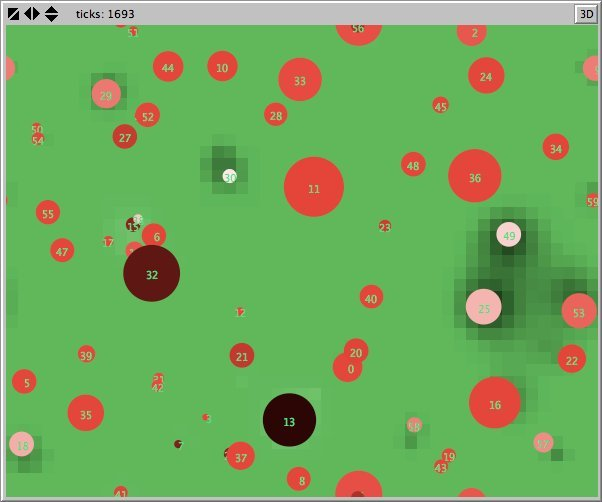
E 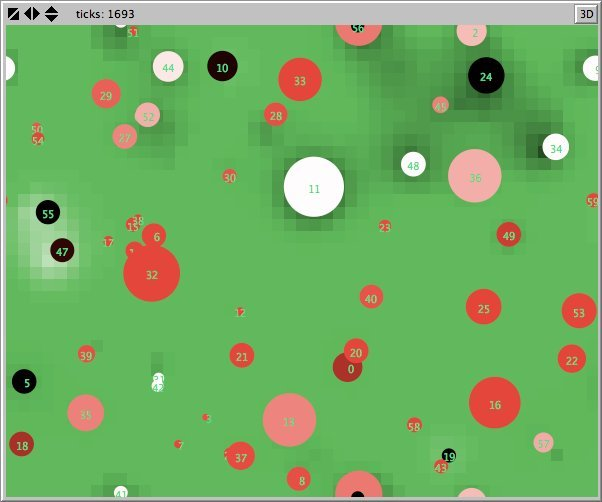
H 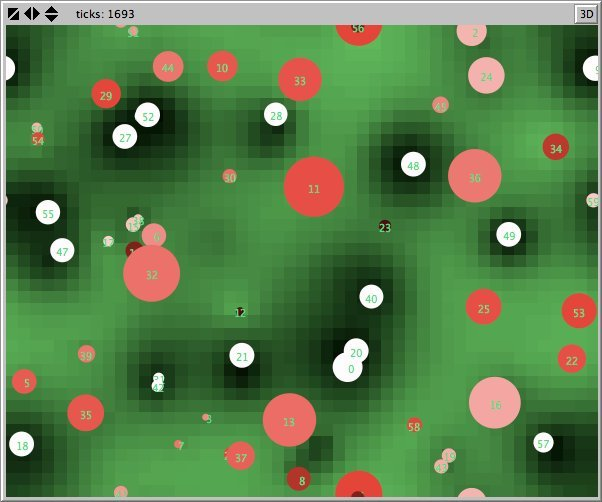
J 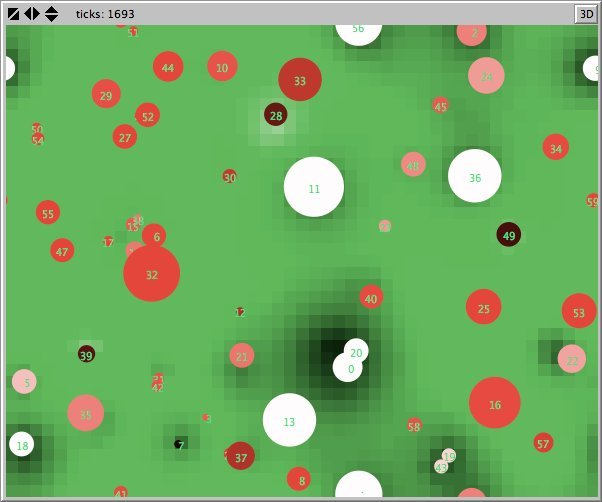

Own categories Standard categories Figure 9. The bar charts and the map of evidence of 5 statements with own categories and high force-of-arguments. For the standard categories A, C, E, H, J are ordered from A to J. A 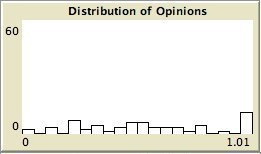
C 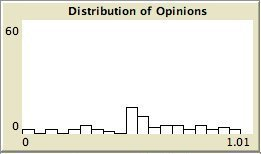
E 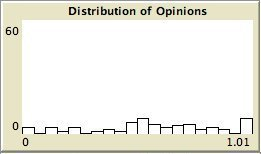
H 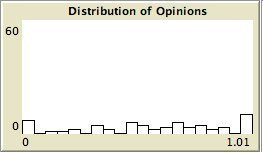
J 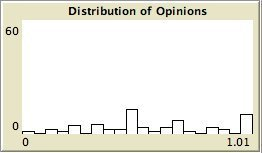
Own categories Standard categories Figure 10. The bar charts and the importance map of 5 statements with standard categories and high force-of-arguments. For the standard categories A, C, E, H, J are ordered from A to J. A 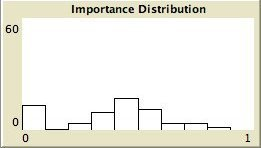
C 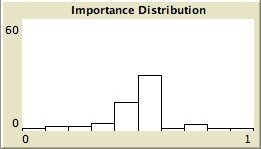
E 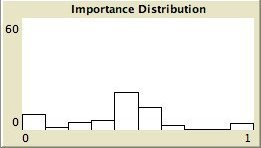
H 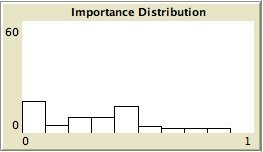
J 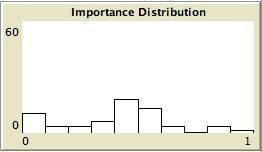
Own categories Standard categories - 6.17
- For the extreme statements A and J only one side has to be considered in the convexity test. That gives them more freedom to change. This can be noticed in the upper and bottom maps and bar charts in the standard categories column of Figure 6 to Figure 10. Agents do not need to talk about A and J anymore; they are certain about their opinion (pro or con).
- 6.18
- This is unlike the other statements, where evidence is randomly distributed and importance converges to 0.5. Agents do want to talk about the moderate statements of which they have moderate importance values. This property makes the dialogue game an effective and goal-oriented communication device. By talking only about statements of which they are uncertain, agents learn to draw a line between what they believe and what they reject in a small number of actions.
- 6.19
- The desire not to talk about their true opinions is also
sometimes the case in real life. People may perceive the fact that
other people do want to talk about those statements as something that
weakens their opinion.
How Latitudes of Acceptance emerge
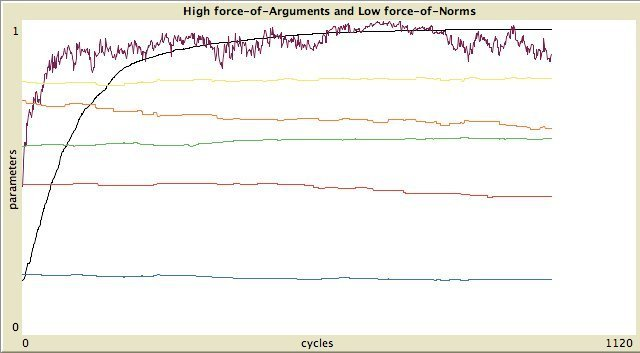
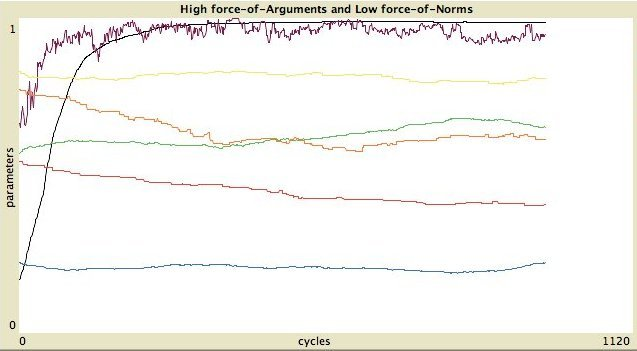
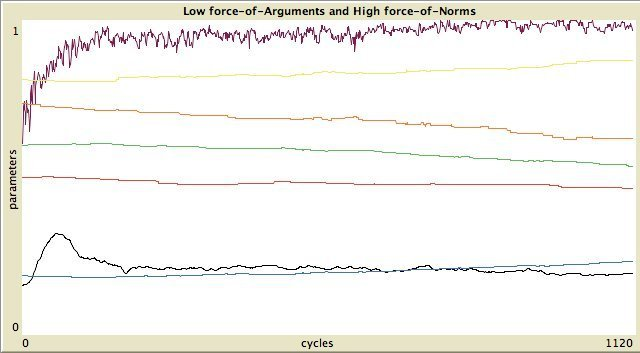
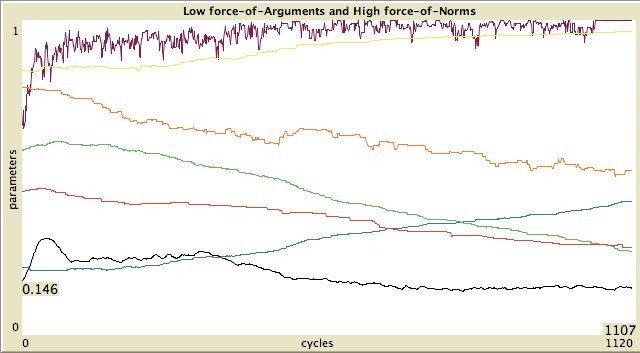
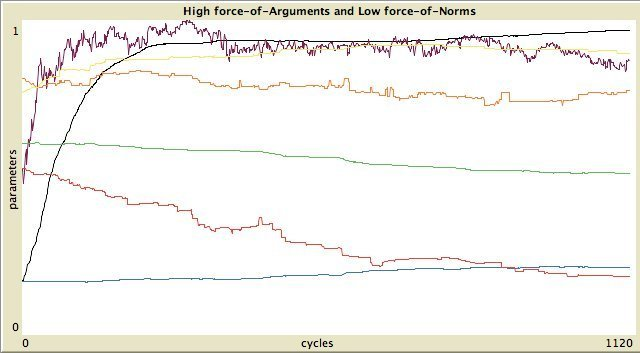
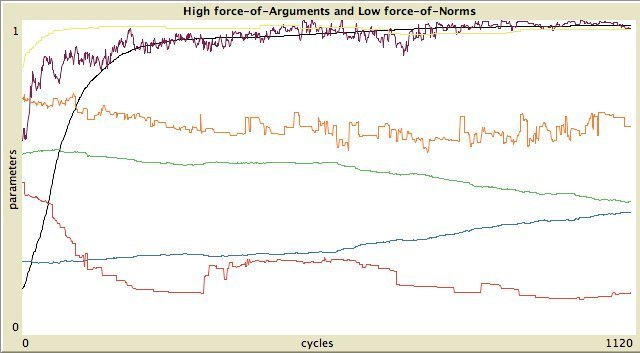
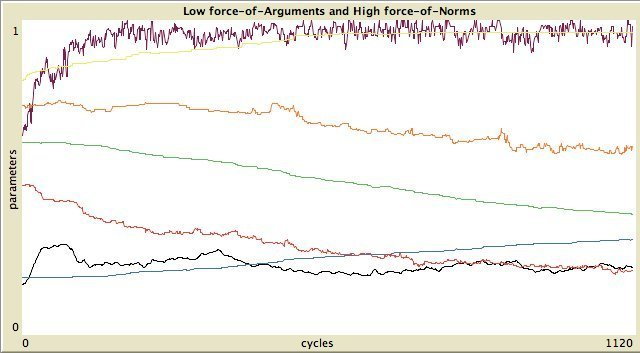
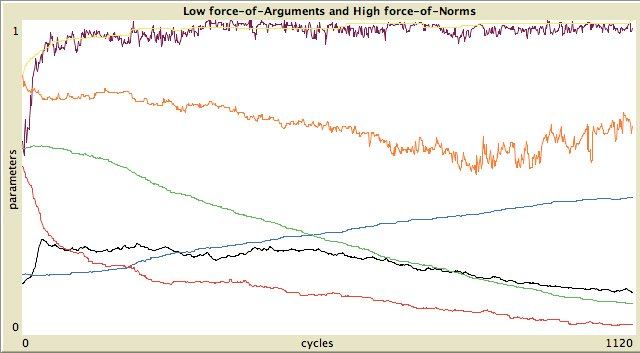
Figure 11. Left column: standard categories, right column: own categories. First and third row: high force-of-arguments. Second and fourth row: high force-of-norms.  Without assimilation and contrast:
Without assimilation and contrast:
Assimilation and contrast .45:
- 6.20
- We compare the simulations of different combinations of the
Reputation, MOAC and SOC parameters (see Table 5). For simplicity
reasons, for all parameters only two values are considered. In a
simulation, reputation is determined either by force-of-norms
or by force-of-arguments.
The attraction and rejection forces are either low or high (0 or 0.47),
and we never considered more than two options for the extremeness
ordering.
The timelines of the 8 possible states are shown in Figure 11.
To express the degree of inequality in the distribution of properties,
as reputation evidence and importance, we use the Gini-coefficient (Deaton, 1997).
The endogenous parameters that are measured to characterise the social
network and the types of opinion dynamics are:
- Reputation Distribution. The Gini-coefficient of the reputation of the agents.
- Spatial Distribution. The clustering coefficient on the relation defined by the agents that are in each other's visiual horizon.
- LOA. Latitude of Acceptance. The average size of the latitude of acceptance of all agents divided by the number of statements.
- LON. Latitude of Noncommitment. The average size of the latitude of non-commitment of all agents divided by the number of statements.
- Opinion Distribution of Preferred Opinions. The Gini coefficient of the evidence of the preferred opinion. Do agents have the same evidence values about their preferred opinion (value = 0) or are there large differences between agents (value > >0)?
- Average Opinion of Preferred Opinion. The mean of the evidence values of the preferred opinion of the agents.
- Average Importance of Preferred Opinion. The mean importance values of the preferred opinion of the agents.
- 6.21
- All experimental parameters have a similar effect on the
endogenous parameters, if we order the dimensions conveniently (see
Table 2). The ordering
of the experimental parameters is:
MOAC same as the ordering of the attraction and rejection parameter SOC standard categories < own categories Reputation force-of-arguments< force-of-norms
- 6.22
- When all parameters have a similar effect, this is because
they influence a common cause. All three parameters contribute to
faster changes of opinion as a result of changes in the agent's
environment.
Table 2: The effect of MOAC, SOC and Reputation on the observable parameters. (Inferred from the correlation matrix. Only the dependence of endogenous parameters from exogenous parameters is considered.)
- 6.23
- An idea of the magnitude of the correlations between the parameters is shown in Table 2. All experimental parameters are positively correlated to Spatial Distribution, LOA and Opinion Distribution (except for MOAC and Spatial Distribution). With the other endogenous parameters the experimental parameters are negatively correlated (except two combinations).
- 6.24
- For an explanation of the results, the LOA is the most important endogenous parameter. LOA represents a complex of attributes; it expresses gain of certainty or the loss of uncertainty, gain in ego-involvement. The other endogenous parameters are strongly correlated with this parameter. force-of-norms promotes extreme opinions, which speeds up the growth of the LOA.
- 6.25
- There is a very strong negative correlation between LOA and LON. This is not very surprising, because LOA behaves very similarly to LOR, which is in fact the LOA of its negation. And since LON + LOA + LOR = 1, the correlation can only be strongly negative.
- 6.26
- Of special interest in the timelines are the points in time where the LOA and LON lines cross (when the certainty about the agent's attitude becomes larger than its unertainty). When all experimental parameters work in cooperation, the combined effect is much stronger and the point where LON and LOA are equal, is reached earlier.
- 6.27
- The mean evidence of the Preferred Opinion (Opinion Distribution) is correlated with the strength of the attraction and rejection forces. So the larger the LOA, the more agents prefer extreme opinions! We already saw in the one statement case of Figure 12 and 13 (see Appendix A) that mean evidence is negatively correlated to importance distribution, similar to the negative correlation between Reputation and Spatial distribution.
 Discussion
Discussion
- 7.1
- In Example 1 on Subsection 1, we suggested that agents could not understand the social implications of the utterances of other agents, if agents do not know the categories of other agents. The experiments show that this is not troublesome for the growth of their latitude of acceptance. When agents are not constrained in changing their opinion, they acquire certainty about statements more quickly than when they have to be linguistically consistent, which is the case when agents share standard categories. Own categories thus helps to gain certainty.
- 7.2
- In Dykstra et al. (2013) we already showed that for a single statement, high certainty and strong social ties (spatial distribution) is correlated with force-of-norms determined reputation. Our new experiment affirms this result also for sets of statements. Argumentation does not help to gain certainty. Similarity with their environment (force-of-norms) is much more effective than winning debates (force-of-arguments).
- 7.3
- Furthermore, own categories stimulates the formation of social clusters, despite the fact that mutual understanding is better under standard categories. Under own categories, agents are not inhibited by consistency constraints when they want to change their opinion. So they can adapt their attitude faster to a socially desirable attitude than agents with standard categories, who have to remain linguistically consistent. A remarkable consequence ist that better understanding does not improve social coherence.
- 7.4
- In Dykstra et al. (2013), it has been shown that in the case of a single statement, clustering of agents leads to radicalisation of opinions. In this article, we conclude that a community of agents who share a statement ordering also enforces the emergence of agents with extreme opinions. In human society both aspects are closely connected. When people form a stable community, they do so because they share a statement ordering or otherwise they will be stimulated to develop such an ordering. This enhances their mutual understanding, which, on its turn, leads to happiness, because it enforces the group stability. But this coin has a downside too: the coming up of actors with nasty ideas is inherent to this situation. In Example 1: once Anna, Bob, Chris and Daphne all agree on one extreme statement, they will be happy about the reached consensus, but they are not anymore inhibited to develop even more extreme statements.
- 7.5
- However in the Examples 8-11 the multi-dimensionality of issues, which is common in real social debates, shows that it is very hard for agents to acquire sufficient information about the statement orderings of other agents. In the presence of multi-dimensional complicated social debates, the construction of standard categories and the establishment of stable communities will be harder. Luckily the upside of this coin is that the inability to really understand each other, also inhibits the radicalisation of opinions.
- 7.6
- The choice of the definition of the experimental and endogenous variables is of great importance to the meaning(fullness) of the simulation. Do the variables cover the ''real'' phenomena? One of the hardest phenomena to catch until now is the clustering of agents and the characterisation of the groups they form as ''open'' or ''closed''. The definition of clustering in social network analysis of Watts & Strogatz (1998) is simple and has a clear meaning. They define the degree of saturation of the social relations in a group as a measure of the degree of clustering. But such a measure does not cover properly what is going on in the model at the level of agent interactions because most of the change in social relations takes place in a very small part of the measuring scale (the (0.95, 1) interval) and an exponential transformation of the measure is of no help because the curve is too noisy.
 Conclusion
Conclusion
- 8.1
- We have extended our dialogical logic-based simulation model DIAL to deal with more than one statement. We introduced fuzzy logic to represent agent attitudes as the sets of statements that are believed by the agent, while the degree of belief is used as the fuzzy membership function. In the resulting model FUZZYDIAL, we introduced a set of a partial orderings on statements, which serves as the domain of the linguistic variables for the corresponding fuzzy sets. The fuzzy set membership function also determines the preferred opinion and the tolerance level (latitude) on which agents decide on the truth of statements. To capture the notion of latitudes in Social Judgement Theory, we introduced the notion of linguistic consistency, which constrains the agent's reasoning. With this extension, changes of opinions can be expressed in accordance with Social Judgement Theory.
- 8.2
- The experimental observations show that in our model, LON and LOA are not only determined by the mechanism of assimilation and contrast, but also by the (lack of) validity of standard categories and most of all the determination of reputation by normative forces. A small LON (and a large LOA) corresponds to high ego-involvement and is the result of strong attraction and rejection forces. So the social interaction in our model leads to a higher degree of ego-involvement. In that respect our dialogical model is in line with the Theory of Social Judgement. In addition to that, it predicts that the stronger the attraction and rejection forces are, the more extreme the preferred opinion is. This result is partly inhibited by the convexity constraint.
- 8.3
- We set out to develop simulation models to understand opinion radicalisation in society. We have shown that the latitudes of acceptance of individual agents can be adjusted by the outcome of their interactions with other agents in dialogue games (downward causation). This architecture allows the social opinion dynamics according to the Theory of Reasoned Action in simulations with reasoning and debating agents to emerge. Future work is the implementation of a fuzzy reasoning engine into the simulation framework. The importance to debate about a statement will also depend on the fact whether that statement is correlated with the statements that are accepted by almost all group members.
- 8.4
- In the description of the results of our experiments, only the existence of correlations between parameters are named without the specification of the statistical details. The reason for this qualitative presentation is that we actually are interested in the causal relations between parameters, and the relation between the statistical information as given in correlation matrices and causality, is too complicated to be treated in this article. We will deal with this subject in a subsequent article by extending our simulation model with instruments that measure directly the forces that change endogeneous parameters.
 Acknowledgements
Acknowledgements
- Authors would like to thank the anonymous referees for their useful comments. Rineke Verbrugge was supported by NWO Vici grant 277-80-001.
 Notes
Notes
-
1We
recap some of the DIAL's formal framework in Section 3.
2A short description of the model can be found in Dykstra et al. (2009) whilst the full description and analysis of DIAL can be found in Dykstra et al. (2013).
3An ordering is connected if and only if its symmetric and transitive closure is the total relation.
4In the Social Judgement theory literature 'most preferred statement' is usually called: 'anchor position' Griffin (2011); Sherif & Hovland (1961).
5The term linguistic consistency is introduced to emphasise the fact that convexity is not the same as logical consistency, but in the dialogical context an agent who utters a linguistically inconsistent statement is treated the same as an agent who utters a logically inconsistent statement.
6In a NetLogo simulation program, a 3-valued logic has been used to demonstrate the effect of impartiality (Baumgaertner 2014).
 Appendix A: Social
configurations resulting from different reputation
functions
Appendix A: Social
configurations resulting from different reputation
functions
-
- A.1
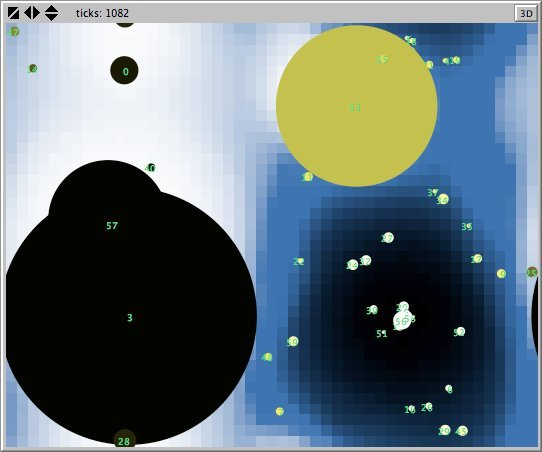
- In both Figures 12 and 13 the bar charts on the left show the distribution of agents over the evidence- (upper chart) and importance-values (lower chart). The parameter values are divided into 20, respectively 10, intervals. In Figure 12 we see that by far the most agents belong to the most extreme evidence value intervals of (0, 0.5) or (0.95, 1). The great majority of the agents belongs to the rank that has importance value in the (0, 0.1) interval. So in a society with strong norms, by far the most agents have extreme opions and they do not want to talk aboutthem.
- A.2
- The two maps of the agents world on right side will provide an explanation for this observation. The upper map shows the height of the accumulated evidence values (with the accepte function) of the utterances regarding a certain statement (current-prop) most recently made in the neigbourhood. The values range from 0 (black) via 0.5 (blue) to 1 (white). The circles represent agents; the diameter represents their reputation and their colour ranges from white (0) via yellow (0.5) to black (1). We see that the agents are clustered in a number of groups. In the centre is a group with high positive opinions. There are four smaller groups with strong negative opinions. But there is also a group with intermediate opinions (yellow agents). The clustering is the cause that agents hear mostly the same opinion as they have themselves, which makes them believe that they have the right opinion. Furthermore under high force-of-norms most agents have about the same reputation.
- A.3
- The lower map represents the accumulation of the importance values of the recent utterances in that neighbourhood. The colours range from black (0) via green (0.5) to white (1). And the agents' colours range from white via red to black over the same interval of their importance values concering the same statement.
- A.4
- This is in strong contrast to Figure 13, where large differences between the reputation values of the agents exist. On the one hand, force-of-arguments enlarges reputation distribution; on the other hand, it prevents the formation of groups (spatial distribution) and the emergence of extreme opinions (opinion distribution and importance distribution - see both bar charts). Explanation: large reputation make global announcements possible. So most of the agents hear different sounds from different directions, which prohibits the formation of niches for agents with extreme opinions, and – according to the bar chart for importance, which shows that almost all ranks except the lowest have more members than in the case of high force-of-norms – agents are inclined to talk about their opinions.
 Appendix B: Exogenous
parameters
Appendix B: Exogenous
parameters
- B.1
- The actual values of these exogenous parameters of all runs
of the simulation program are as shown in the table below.
Table 3: The values of the exogeneous parameters that are kept constant in all simulation runs. Parameter Range Value Description force-of-arguments 0-1 1 Determines the degree in which the agent's reputation is determined by winning and losing debates. force-of-norms 0-1 0 The degree in which the reputation is determined by the similarity with its environment. chance-announce 0-100 49 Utter an announcement. loudness 0-20 2.5 Determines the distance that a message can travel for anonymous communication. Anonymous communication affects the environment (patches) and indirectly its inhabitants through the learn-by-environment action. chance-walk 0-100 16 Movement in the topic space. stepsize 0-2 1.3 Maximum distance traveled during a walk. visual-horizon 0-20 5 Determines the maximum distance to other agents who's messages can be heard (including the sender, which is necessary for attacking. forgetspeed 0-0.005 0.00106 The speed the evidence- and importance-values of the agents' opinion converges to neutral values (typically 0.5). undirectedness 0-45 19 Randomness of the direction of movement. chance-attack 0-100 12 Attack a recently heard announcement. (The most different one from the own opinion with the highest probability) chance-learn-by-neighbour 0-10 0.2 Learn from the nearest neighbour. chance-learn-by-environment 0-10 1 Learn from the average opinion on the agents' location. inconspenalty 0-1 0 Penalty for having inconsistent opinions. attraction 0-1 0.47 The largest distance in the evidence value of an uttered proposition and the evidence value of the same proposition of a receiving agent for which the receiver is inclined to adjust its opinion. rejection 0-1 0.47 The shortest distance in the evidence value of an uttered proposition and the evidence value of the same proposition of a receiving agent for which the receiver is inclined to attack the uttered proposition.
 Appendix C: The Actions of the Agents
Appendix C: The Actions of the Agents
- C.1
- The flow of consequences of agents' actions, as performed
in the procedure act, is shown in an UML sequence
diagram in Figure 14.
The numbers in the enumeration refer to the text labels on the right
side of the sequence diagram.
Figure 14. UML sequence diagram of the influence of opinions. The vertical bars represent the time lines of the relevant objects. The horizontal lines represent the events of sending messages (Synchronous messages are followd by a dashed line with an arrow in the opposite directon, when the receiver returns the control back to the sender). 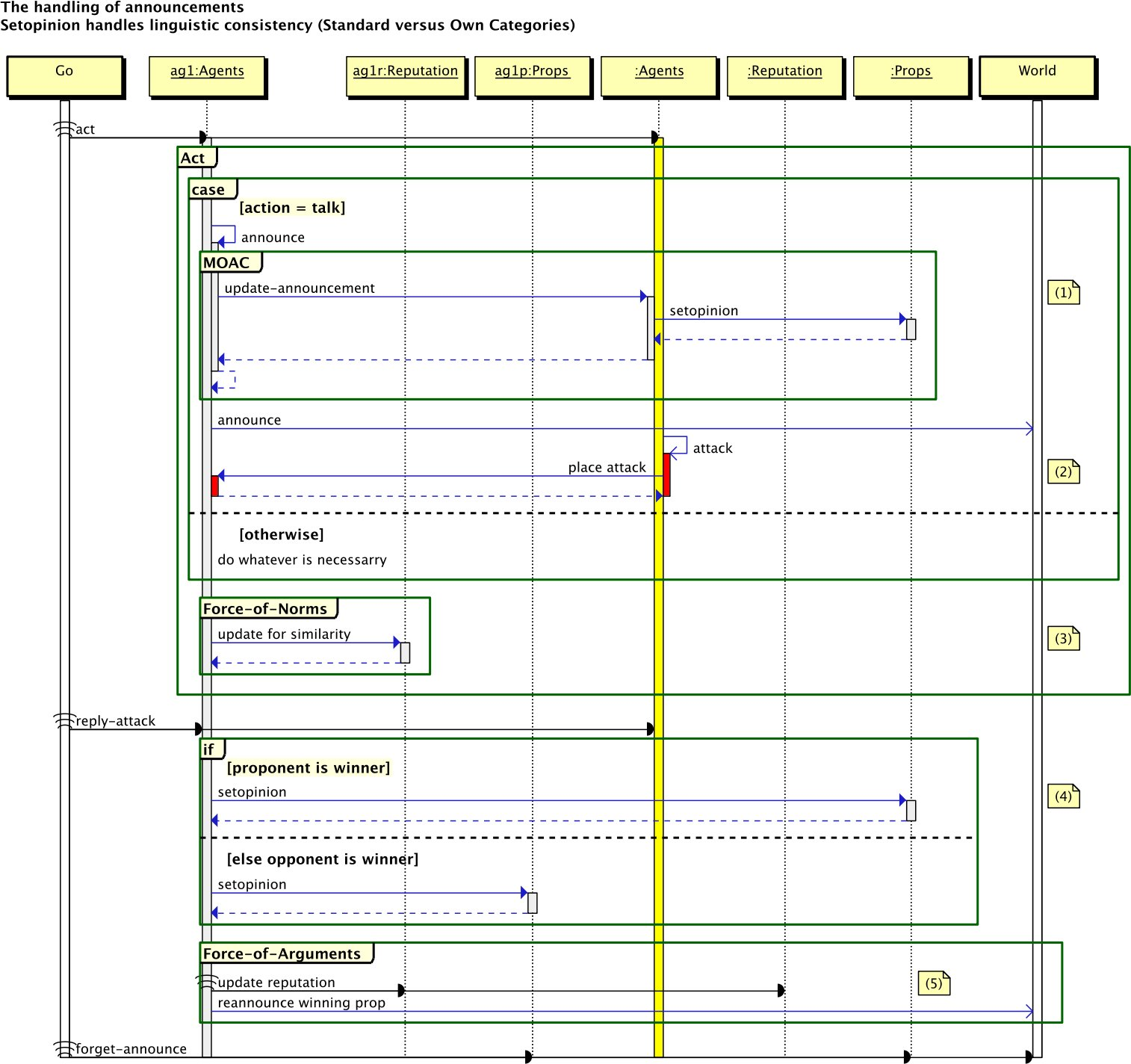
1. Agents utter their most important opinions most frequently. We consider the case that agent ag1, represented by the grey bar (which represents a thread - different threads are denoted by different colours) on the left, announces a statement. That event is communicated to other agents in the neighbourhood by the message update-announcement.
- C.2
- Whether a considered utterance will be accepted/rejected depends on its effect on the agent's attitude. If its attitude remains linguistically consistent after acceptance, then the agent will accept the utterance (or its negation in case of a rejection). In case the agent's attitude will become inconstent, the agent will have to pay a penalty.
- C.3
- There is a possibility that an agent will learn from an utterance. In that case consistency of the resulting attitude determines what will happen with the agent's opinions and reputation.
- C.4
- To form a latitude (interval), the statements have to be ordered in the degree of extremeness and that order is fixed during the simulation, so the evidence assignment to the set of statements needs to be convex at the start. An initial convex set of opinions remains convex by forbidding the acceptance of statements that would result in an non-convex opinion state. Instead of adding acceptance events as in the 'own categories' model to enforce assimilation and contrast, we now decrease the number of acceptance occasions.
- C.5
- This functionality is implemented in the update-announcement
procedure:
if
 agreement >
1 - attraction
agreement >
1 - attraction 
then setopinion announcement
setopinion announcement 
else if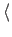 agreement <
rejection -
1
agreement <
rejection -
1 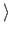
then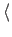 setopinion negation of announcement
setopinion negation of announcement 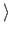
- C.6
- The announcement is communicated to the patches in the
environment (the World) by the message announce.
This message applies the accept-function on the
opinion values of the announcement and the patches.
2. Announcements start a sequence of attacks and defences in the dialogue game. The yellow thread represents another agent who launches an attack on the announcement it just heard. The attack itself is in red. The likeliness of this event is determined by the difference of the agent's opion and the message. The reputation of the agent needs to be high enough to pay the reward in case the attacker loses the dialogue.
3. At the end of a round, the reputation of all agents is adjusted for their similarity with their environment. It will be increased when the similarity is high and otherwise reputation will be decreased. The degree depends on the value of force-of-norms.
4. After the adjustments of the reputation of the agents for similarity, agents, who have been attacked on a recently made utterance, get the opportunity to defend themselves. The verdict comes from the environment patches. If the opinion of the proponent is more similar to the environment than its negation, then the proponent wins: the reward is subtracted from the reputation of the opponent and added to the reputation of the proponent. Otherwise the opponent wins: the reputation of the proponent is subtracted by the pay and the same value is added to the opponent's reputation.
5. The last task in a round is the adjustment of the reputation of the winner and the loser. The winning statement is sent to the environment. And forgetting takes place. - C.7
- The procedure Setopinion. When agents determine an extremeness ordering privately (own categories) they do not have to account for their choice. But when agents share a common extremeness ordering, they can only make opinion adjustments that are linguistically consistent. In the case they cannot change their opinion, they will suffer reputation damage.
- C.8
- The final consistency check is implemented in the procedure
setopinion for the standard categories; for own
categories this procedure does nothing and calls the accept
new opinion code:
if
 newly acquired opinion results in a linguistically
consistent attitude
newly acquired opinion results in a linguistically
consistent attitude 
then accept new opinion
accept new opinion 
else pay inconsistency penalty
pay inconsistency penalty 
 References
References
- AJZEN, I. (1991). The theory of
planned behavior.
Organizational Behavior and Human Decision Processes,
50, 179–211. [doi:10.1016/0749-5978(91)90020-T]
AJZEN, I. & Fishbein, M. (1980). Understanding Attitudes and Predicting Social Behavior. Englewood Cliffs, NJ: Prentice-Hall, 1st ed.
BAUMGAERTNER, B. (2014). Yes, no, maybe so: a veristic approach to echo chambers using a trichotomous belief models. Synthese 191, 2549–2569. [doi:10.1007/s11229-014-0439-9]
BISHOP, B. (2008). The big sort: Why the clustering of like-minded America is tearing us apart. Boston, NY: Houghton Mifflin.
CARLEY, K., Reminga, J. & Kamneva, N. (2003). Destabilizing terrorist networks. In: NAACSOS Conference Proceedings (Penn, O. W., ed.). Pittsburgh, PA.
CARLEY, K. M. (1986). Knowledge acquisition as a social phenomenon. Instructional Science 14(4), 381–438. [doi:10.1007/BF00051829]
CIALDINI, R., Reno, R. & Kallgren, C. (1990). A focus theory of normative conduct: Recycling the concept of norms to reduce littering in public places. Journal of Personality and Social Psychology 58(6), 1015–1026. [doi:10.1037/0022-3514.58.6.1015]
DEATON, A. (1997). Analysis of Household Surveys. Baltimore MD: Johns Hopkins University Press. [doi:10.1596/0-8018-5254-4]
DEFFUANT, G., Neau, D., Amblard, F. & Weisbuch, G. (2002). How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation 5(4) 1: https://www.jasss.org/5/4/1.html
DYKSTRA, P., Elsenbroich, C., Jager, W., Renardel de Lavalette, G. & Verbrugge, R. (2009). A dialogical logic-based simulation architecture for social agents and the emergence of extremist behaviour. In: The 6th Conference of the European Social Simulation Association (Edmonds, B. & Gilbert, N., eds.). Electronic Proceedings 1844690172.
DYKSTRA, P., Elsenbroich, C., Jager, W., Renardel de Lavalette, G. & Verbrugge, R. (2010). A logic-based architecture for opinion dynamics. In: Proceeding of the 3rd World Conongress on Social Simulation WCSS2010 (Ernst, A. & Kuhn, S., eds.). (CD-ROM) Centre for Environmental Systems Research, University of Kassel, Germany.
DYKSTRA, P., Elsenbroich, C., Jager, W., Renardel de Lavalette, G. & Verbrugge, R. (2013). Put your money where your mouth is: DIAL, a dialogical model for opinion dynamics. Journal of Artificial Societies and Social Simulation 16(3)4: https://www.jasss.org/16/3/4.html
GRIFFIN, E. (2011). A First Look at Communication Theory. McGraw-Hill international edition. McGraw-Hill Education.
HEGSELMANN, R. & Krause, U. (2002). Opinion dynamics and bounded confidence: Models, analysis and simulation. Journal of Artificial Societies and Social Simulation 5(3)2: https://www.jasss.org/5/3/2.html
HOGG, M. A. & Reid, S. A. (2006). Social identity, self-categorization, and the communication of group norms. Communication Theory 16(1), 7–30. [doi:10.1111/j.1468-2885.2006.00003.x]
JAGER, W. & Amblard, F. (2005). Uniformity, bipolarization and pluriformity captured as generic stylized behavior with an agent-based simulation model of attitude change. Computational & Mathematical Organization Theory 10(4), 295–303(9). [doi:10.1007/s10588-005-6282-2]
PEDRYCZ, W. & Gomide, F. (1998). An Introduction to Fuzzy Sets. MIT Press.
SHERIF, M. & Hovland, C. (1961). Social Judgment: Assimilation and Contrast Effects in Communication and Attitude Change. New Haven: Yale University Press.
SUNSTEIN, C. (2003). Why societies need dissent. Cambridge, MA: Harvard University Press.
TAJFEL, H. & Turner, J. (1979). An integrative theory of intergroup conflict. In: The Social Psychology of Intergroup Relations (Austin, W. G. & Worchel, S., eds.). Monterey, CA: Brooks/Cole, pp. 33–47.
VERBRUGGE, R. (2009). Logic and social cognition: The facts matter, and so do computational models. Journal of Philosophical Logic 38(6), 649–680. [doi:10.1007/s10992-009-9115-9]
VISSER, P., Bizer, G. & Krosnick, J. A. (2006). Exploring the latent structure of strength-related attitude attributes. Advances in Experimental Social Psychology 38, 1–67. [doi:10.1016/S0065-2601(06)38001-X]
WATTS, D. J. & Strogatz, S. H. (1998). Collective dynamics of 'small-world' networks. Nature 393, 440–443. [doi:10.1038/30918]
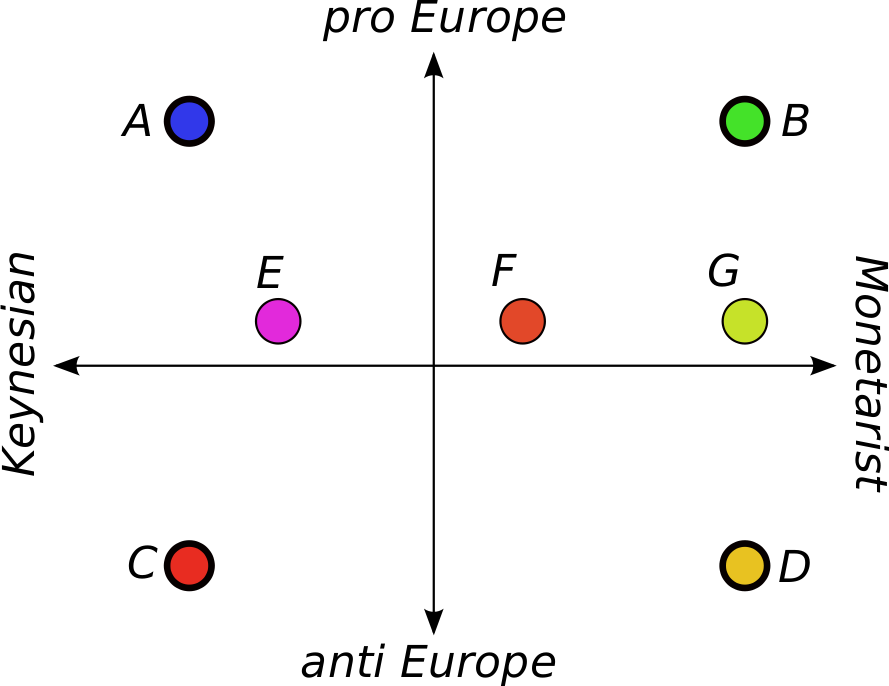
![\includegraphics[width=0.7\textwidth]{framefuzzyset.ps}](3/img20.png)
![\fbox{\begin{minipage}[c]{160pt}\begin{small}\begin{enumerate} \item [e] eviden... ...\item [r] latitude of rejection (LOR) \end{enumerate} \end{small}\end{minipage}}](3/img19.png)