 Abstract
Abstract
- Local opinion heterogeneity (LOH) critically influences an individual's choice of collective behaviors, such as voting and protesting. However, several empirical studies have presented different conclusions on how LOH affects such preference. In the current research, the effect of LOH is considered based on agent-based modeling and the threshold model introduced by Granovetter (1978). A series of simulation experiments and statistical analyses are conducted. Results show that LOH has an inverse U-shape effect on the likelihood of participation (whether an individual decides to participate). By contrast, the findings reveal that LOH has a monotonous effect on participation timing (when a participant makes the decision). Specifically, when LOH is high, an individual opts to participate early. These observations can be explained by the influence of LOH on the structure of social networks and by the moderating effect of the global distribution of opinions within the population.
- Keywords:
- Local Opinion Heterogeneity, Participation Likelihood, Participation Timing, Collective Behavior, Agent-Based Modeling, Threshold Model
 Introduction
Introduction
- 1.1
- Scholars from social and political fields frequently note that individuals have a strong tendency to seek and socialize with people who hold opinions similar to theirs (McPherson et al. 2001). This tendency, which is called homophily[1], is commonly exhibited in various types of social networks, such as friend and political discussion networks. Owing to this tendency, people tend to adopt the same behavior and conform to the group norms (Olson 1965). Scholars have specified that the personal networks of people are not strictly homophilious. For example, Huckfeldt et al. (2004) demonstrated that most Americans have at least one member in their discussion network who disagrees with them. Local opinion heterogeneity (LOH) shapes the social world of people to such a degree that the information they receive and the attitude they form are significantly influenced. Considerable empirical research indicates that LOH is a concern if and when an individual decides to participate in collective behavior such as voting, strike, and protests (e.g., Eveland & Hively 2009; Huckfeldt et al. 2004; Lee 2012; Mutz 2002a, 2002b; Nir & Druckman 2008).
- 1.2
- Nonetheless, exactly how LOH influences people has yet to be clarified. For example, the seminal contributions of Mutz on "cross-cutting discussion" suggest that LOH depresses individual participation because people find themselves at a high level of ambivalence when they are surrounded by heterogeneous opinions (Mutz 2002a, 2002b). Many subsequent studies support the "dark-side" theory (e.g., Belanger & Eagles 2007; Eveland & Hively 2009; Nir & Druckman 2008). Conversely, some scholars have reported that LOH is either positively or insignificantly related to participation (e.g., Nir 2005), whereas others imply that the effect of LOH varies (e.g., Bello 2012; Kwak et al. 2005; McClurg 2006; Nir 2011; Scheufele et al. 2006).
- 1.3
- Why are the extant empirical findings on the effects of LOH inconsistent? A probable reason for such a condition is that these observations may be a relative consequence of varying theoretical predilections. However, this research argues that two problems on databases are likely the culprits for such discrepancy. First, databases contain insufficient information on the structure of a social network. Collective behavior can be fundamentally characterized as a process of diffusion or contagion over a social network because individual behavior depends on the choices of others (Granovetter 1978; Schelling 1978). Many studies claims that the network structure is largely responsible for the scale and speed of participation spreading (e.g., Centola & Macy 2007; Hu, Cui et al. 2014; Hu, Lin et al. 2014; Siegel 2009). Heterogeneity/homophily shapes the structure of a social network. In particular, homophily leads to a high level of transitivity or clustering (Robinson & Balkwell 1995). When an individual selects multiple friends from a group (e.g., political party), these friends are highly likely to become friends with one another. Increasing LOH reduces the clustering level of a network (Kossinets & Watts 2009; Watts & Strogatz 1998) but increases the number of "weak ties"(Granovetter 1973), "cross-cutting ties" (Mutz 2002b), or "long ties" (Centola & Macy 2007). Therefore, the structure of the entire network is potentially consequential to the relationship between LOH and individual participation.
- 1.4
- Furthermore, empirical analyses generally obtain and present inadequate data on global opinion distribution (GOD). Huckfeldt et al. (1995, p. 290) observed that "the [individual's] network can be seen as the end result of efforts made by individuals to impose their own preference upon their social contexts, and the composition of network is subject to the multiple, interdependent, cascading choice of people who are the social space—the people who compose the context." When GOD is meagerly dispersed, LOH among people is expected to be low even if these individuals prefer heterogeneous connections. Moreover, a given value of LOH may reflect extremely different essences in terms of varying combinations of the mean and dispersion of GOD. Many theoretical studies propose that GOD is a critical base for the complicated emergencies of collective behavior (Granovetter 1978; Hu, Cui et al. 2014; Siegel 2009; Watts 2002). Therefore, GOD is assumed to be an important moderator of the effect of LOH on individual participation.
- 1.5
- This study applies the agent-based modeling (ABM) approach to reexamine the role of LOH under different conditions of GOD and network structure. ABM is selected for two reasons. First, this approach is suitable for modeling the nonlinear dynamics of collective behavior (e.g., Centola & Macy 2007; Hu, Cui et al. 2014; Hu, Lin et al. 2014; Siegel 2009). ABM generally focuses on the aggregate outcome caused by the behaviors and interactions of agents (i.e., individuals in this study). ABM also allows for the observation of the micro-level relationship between LOH and behavioral choice. Second and more importantly, ABM does not require considerable empirical data, including the network structure and GOD of a large-scale population. Acquiring these data is a great challenge for empirical studies.
- 1.6
- The model proposed in this research is based on the threshold model of collective behavior introduced by Granovetter (1978). In the model, a population of individuals must select between binary options (i.e., participate or not), in which one will participate if his "threshold" is attained. Threshold can be perceived as the epitome of "goal and preference, and perception of situation" of the individual (Granovetter 1978, p. 1422); it is adopted in this research to represent individual opinion on collective behavior. Granovetter measured threshold as the number of other individuals who are already engaged in that behavior, with an implicit assumption that "each individual is responsive to the behavior of all the others" (1978, p. 1431). However, complete knowledge about what all others are doing is usually unknown to an individual. Following recent literature (e.g., Centola & Macy 2007; Siegel 2009), the current study applies a threshold to the participation rate within individual's personal network as people primarily care about the behaviors of those who are close to them. Therefore, LOH for an individual is measured as the difference in threshold between the individual and the members in his/her personal network. The degree of LOH is determined both by one's propensity to heterogeneous connections and by GOD.
- 1.7
- This study focuses on two dependent variables, namely, participation likelihood (i.e., whether an individual decides to participate) and participation timing (i.e., when a participant makes the decision). The obtained simulation results provide a few important insights.
- 1.8
- The remainder of this paper is organized into five sections. Following the Introduction, the second section presents a review of ABM literature. The third and fourth sections discuss the model and its results, respectively. The fifth section presents the conclusions and theoretical contributions of the study.
 Theoretical
Background
Theoretical
Background
-
Models of Collective Behavior
- 2.1
- For decades, social scientists have been interested in the formal study of "binary–choice dynamics" settings. These settings enable the exploration of a wide variety of collective behavior problems that range from the study of social movements (participating or refusing to participate in a revolution) (e.g., Kuran 1991) to innovation diffusion (purchasing or refusing to purchase a new product) (e.g., Rogers 1995), voting (for a Republican or a Democrat) (e.g., Fowler & Smirnov 2005), and the prevalence of different relevant social opinions (believing or disbelieving a rumor) (Galam 2003).
- 2.2
- Many binary–choice models have been developed thus far. These models can be categorized into three classes. The first class comprises epidemic models (e.g., susceptible–Infection model and its variants); in this class, behavior can spread among individuals like an infectious disease (Dodds & Watts 2005). The second class is called the opinion–dynamics models, such as the voter (Holley & Liggett 1975), majority rule (Galam 2002), social impact (Nowak et al. 1990), and Sznajd models (Sznajd-Weron & Sznajd 2000). In this class of models, individuals hold either one of two conflicting opinions probabilistically depending on what others believe. In particular, opinion–dynamics models assume that the opinions of individuals can be exceedingly volatile overtime and therefore generally focus on the consensus or coexistence of two opinions.
- 2.3
- The third class of models considers the spreading of an innovative behavior over a population. The state of an individual is fixed once he/she has adopted such a behavior. The models that belong to this class are called threshold models, which include the threshold model of Granovetter (1978) and the microbehavior model of Schelling (1978). Threshold models are typically deterministic and characterize the spreading of a behavior as a complex contagion (Centola & Macy 2007). Complex contagion implies that reinforcements from multiple sources are required when a novel behavior is adopted, which is highly different from that of simple contagions (e.g., acquiring an infectious disease or knowing a piece of information) modeled in epidemic models. Moreover, threshold models are employed to analyze the formation of collective behavior. This research refers to the work of Castellano et al. (2009) and Mason et al. (2007) for the sophisticated reviews of the binary-choice models literature.
- 2.4
- As mentioned previously, this research is grounded on the threshold model of Granovetter (1978) for two reasons. First, participating in a collective action is subject to a complex contagion (Centola & Macy 2007); therefore, applying epidemic models is unsuitable. Second, an individual's preference cannot be reverted once s/he has already participated in a collective behavior. For example, one can no longer withdraw his/her vote for a candidate in the presidential elections. In this sense, opinion–dynamics models are also inappropriate.
- 2.5
- In the threshold model of Granovetter (1978), individuals hold varying thresholds for adopting a precise behavior. In particular, a threshold is based on one's personal calculation of costs and benefits in performing a certain behavior. The benefits and risks perceived by an individual may increase or decrease, when that individual observes that other people perform the same action. A collective behavior is initialized by individuals with a non-positive threshold. Once a few people begin participating, others with a relatively low threshold may join in, thus prompting pessimistic persons with a high threshold to participate as well. The structure of this particular threshold model emphasizes the importance of distributing the individual thresholds within the entire population (i.e., GOD).
- 2.6
- This classic model proposes an implicit assumption of
complete connectedness, that is, "each individual is responsive to the
behavior of all the others" (Granovetter
1978, p. 1431). Nevertheless, realizing that complete
information on what other people are doing is usually unknown to an
individual, recent studies assumed that thresholds are applied to the
adoption rate within a local neighborhood rather than in the entire
population (e.g., Centola
& Macy 2007; Siegel
2009; Valente 1996).
This belief has compelled several scholars to explore the effects of
different
social network structures on collective behavior (Goldstone & Janssen 2005).
Related Works Based on ABM
- 2.7
- Recent developments in ABM have enabled scholars to better understand how the synergy of social interaction and threshold distribution may lead to surprising outcomes of collective behavior. For example, Watts (2002) revealed the mechanisms of how the heterogeneity in the distributions of thresholds and connections affects the global cascade of a behavior. In the same vein, Siegel (2009) provided a fuller characterization of the interaction effects of such a component. Watts and Dodds (2007) specified that collective behaviors are driven not by influential groups (those who influence an exceptional number of their peers) but by a critical mass of easily influenced individuals (those with low thresholds).
- 2.8
- LOH (often referred to as "homophily") has attracted considerable attention in the past few years. Several scholars relate this element to the threshold distribution in the personal network of an individual (e.g., Centola 2013; Janssen 2011) or to the structure of a social network (e.g., Yavas & Yucel 2014), whereas others relate it to both of them (e.g., Chiang 2007; DiMaggio & Garip 2011). The results of these recent studies suggest that moderate levels of LOH appear to be significantly effective in promoting individual participation. The reason behind this presumption is the fact that moderate homophily helps participants attain a critical mass faster than heterogeneity; heterogeneity causes collective behaivor to become unlocalized in some clusters. However, all these studies only focused on the aggregate-level outcome of collective behavior and merely provided a few insights into individual-level participation, particularly in terms of participation timing.
 Model
Model
-
Decision Rule and Simulation Procedure
- 3.1
- In our model, an individual
participates in a collective behavior if
(1) where si,t is the participation rate in the personal network of individual i at time t, and τi is the threshold of individual i that remains constant over time. Following earlier studies on collective behavior (Granovetter 1978; Hu, Cui et al. 2014; Hu, Lin et al. 2014; Siegel 2009; Watts 2002; Watts & Dodds 2007), the current research assumes that τi follows a normal distribution, with a mean value (μ) and standard deviation (σ) that represent the mean and dispersion of GOD, respectively.
- 3.2
- The simulations were performed as follows:
- Preparation step: At this stage, all parameter values for the simulation are set up, and each individual is assigned with a threshold and place within the network.
- Period 0: The individuals with τi<0 are the initial participants to initiate the diffusion process, whereas those with τi≥0 remain "inactive" during this period.
- Period t≥1: If any neighbors become "active" (participated) in the last period, the inactive individuals update their decision based on updated information of the local participation rate. The process is repeated until no further participation emerges or until all individuals have participated.
- 3.3
- The pseudo-code for the diffusion dynamics is presented in
Table 1.[2]
Table 1: Pseudo-code for participation dynamics 1. Generate agents (network) 2. Set the states of all agents into inactive (state = 0) 3. Trigger the activity by agents who have τi< 0 4. while there exist new participants at the last step do 5. for each inactive agent who has new participated neighbors do 6. if local participation rate exceeds threshold 7. become active (state = 1) 8. else 9. keep inactive 10. end if 11. end for 12. end while Measures of LOH
- 3.4
- LOH measures the ego-centered difference in a threshold
between the focal individual and his/her direct neighbors. LOH can be
formulated for each individual as follows:
(2) where ki is the size of the personal network of individual i, and ni is the neighbor set of the individual.
Social Network
- 3.5
- The pseudo-code for constructing the social network is
presented in Table 2. The table specifies that such a network is formed
by first endowing the individuals with thresholds and then
incorporating
ties into the network based on the threshold of individuals. For each
tie, an individual is randomly selected
from the population and is then connected to any one with probability q
or to the one who holds the most similar threshold (probability 1-q).
In this case, self-loop and overlapping ties are forbidden.
Table 2: Pseudo-code for network construction % Preparation 1. Generate agents 2. Assign threshold τi to each agent % Creation of Ties 3. for each tie do 4. Randomly select an agent 5. Generate a random number a 6. if a<q 7. Randomly select an agent j; 8. else 9. Select an agent j who has the most similar τi with i; 10. end if % avoid self-loop and overlapping 11. Add a tie between agents i and j 12.end for - 3.6
- The level of individual LOH (hi)
depends on the interaction of q and σ,
as indicated in Figure 1.
Increasing the value of either variable (q or σ)
can linearly enhance the average level of hi.
Figure 1 shows that σ
limits the distribution of LOH. Here, the dispersion
of GOD may play an important role in the relationship of LOH with
individual participation.
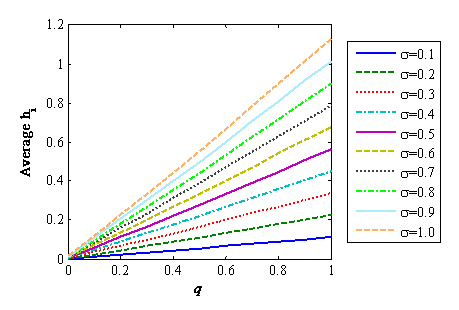
Figure 1. Relationship between hi, q, and σ - 3.7
- Figure 2
illustrates that only the value of q (not σ)
determines the structure of the network. When q =
0, all ties are as local and short as possible[3] (with a large
clustering coefficient and long average path length) and yield a
largely homophilious network. By contrast, when q =
1, individuals may equally interact with one another and yield a
uniform random network (with a small clustering coefficient and short
average path length). Under such a condition, the notion of individual
similarity or dissimilarity is irrelevant.
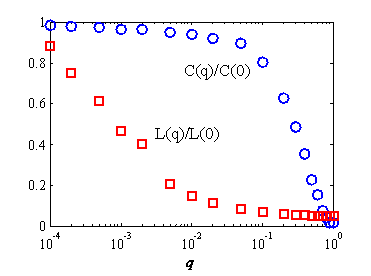
Figure 2. Shortest path length and clustering coefficient corresponding to q - 3.8
- Several points should be
noted in constructing the network. First, the formation of a network in
the proposed model seems to
be structurally similar to that in the small-world network model
developed by Watts and Strogatz (1998).
However, in the newly introduced model, the personal network size
(labeled k) of the individuals always follows a
Poisson distribution[4]
regardless of the value of q. Second, selective
exposure (or social selection) is the underlying mechanism in
constructing the network. This mechanism invokes a long-standing theory
that posits that people require cognitive consistency (Festinger 1957). The most
extreme case is where individuals randomly connect with others
and do not actually seek other people with different thresholds. Third,
the model does not fit several types of networks (e.g., neighboring
networks that are built on physical location) because the model defines
networks depending on similar opinions.
Parameter Settings
- 3.9
- All parameter settings are provided in Table 3. The
simulations were performed with N =
1000 agents. Survey results show that the number of relationships that
can effectively influence individual decision is limited to nearly 10
(e.g.,
Eveland & Hively 2009).
Hence, average network size was set to K =
10. Three values (0.4, 0.5, and 0.6) were adopted for the mean of
threshold distribution (μ), and 10 values (ranging
from 0.1 to 1 in steps of 0.1) were utilized for dispersion σ.
The value of q ranged from 0 to 1 with an interval
of
0.1. Therefore, 330 parameter combinations were gathered for this
research. Each combination was run 100 times.
Table 3: Parameter settings Parameter Value Interpretation N 1000 Population size K 10 Average size of individuals' local network q 0 to 1 in intervals of 0.1 Propensity to heterogeneous exposure μ 0.4, 0.5, or 0.6 Mean value of threshold distribution σ 0.1 to 1 in intervals of 0.1 Standard deviation of threshold distribution - 3.10
- In each simulation, individual-level data on whether and at which simulation period the individual decides to participate (prepared for the analysis on participation likelihood and timing respectively) were gathered. Aggregate-level data on the global participation rate were collected as well.
 Results
Results
-
Preliminary Analysis at the Aggregate Level
- 4.1
- Figure 3 shows the effects of the propensity of individuals
to
heterogeneous ties (q) on aggregate
participation rate, which is associated with the likelihood of
participation. In particular, the figure shows that the effect of q
is remarkably complicated; that is, it can be positively
or negatively monotonous or non-monotonous. The reason for this
condition is that
q is directly related to the network structure.
Siegel (2009) suggested
that the outcome of collective behavior is associated with a trade-off
between the effectiveness of the network in nurturing participation
enclaves and its effectiveness in spreading participation. When
individuals are willing to participate, the ease in spreading
participation is important. In this event, the networks with several
"weak ties" (i.e., a high value of q) are
beneficial. By contrast, when individuals are not inclined to
participate, the networks with a high level of clustering (i.e., a
small q) are suitable because they are effective in
nurturing participation enclaves. The different effects of q
on aggregate participation fundamentally respond to the trade-off.
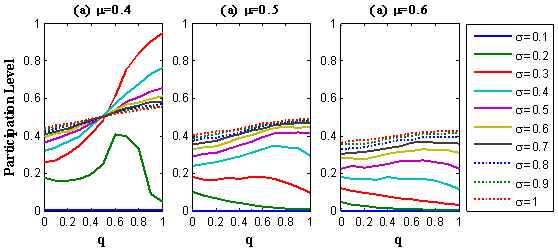
Figure 3. Effect of q on aggregate participation - 4.2
- Nevertheless, as shown in Figure 3,
discerning the relationship between LOH with individual participation
likelihood is difficult because LOH is determined not only by q,
but also by the dispersion of GOD (σ). The same
problem can be observed in participation timing, as indicated in Figure
4, which presents the time
courses of participation under different combinations of q,
μ, and σ. Therefore,
individual-level data must be analyzed.
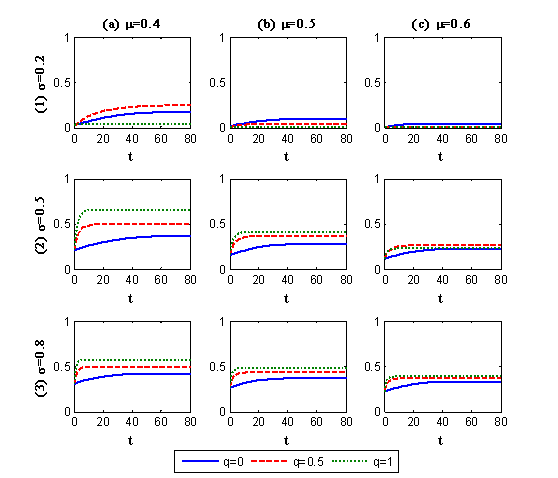
Figure 4. Time courses of participation Analysis on the Participation Likelihood at the Individual Level
- 4.3
- The data for individual-level analysis were filtered first. LOH cannot be meaningfully applied to individuals without any ties. Therefore, records with ki =0 were excluded from the analysis. Iindividuals with τi<0 or τi>1 were also excluded because their decision is independent of LOH. Accordingly, almost one-third of the collected data was dropped, and the remaining data (in which only 23.2% of individuals are participants) were prepared for the analysis of participation likelihood.
- 4.4
- Figure 5
illustrates the relationship between LOH (hi)
and participation likelihood.The initially increasing hi
can significantly increase an individual's participation likelihood.
This
scenario occurs because the personal network of an individual is highly
clustered and therefore extremely closed with regard to
encountering or
accepting a novel behavior. By increasing LOH, the personal network of
an individual can be opened, thereby increasing his/her participation
likelihood. However, when hi is
large, the effect of increasing hi becomes
blurry and is mainly negative, as implied by the fitted curve. The
reason is this condition is that LOH makes people more conflicted and
compels them to
make decisions exhaustingly.
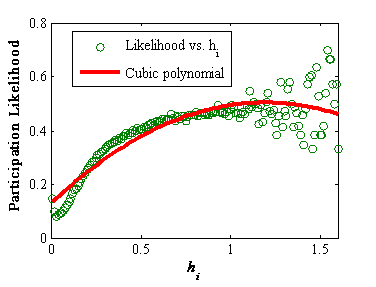
Figure 5. Participation likelihood vs. LOH - 4.5
- Graphical analysis of the subject matter has a serious
problem; that is, it does not control other variables that may
influence the decision of an individual. This study addresses this
issue by using the statistical method to analyze the relationship
between LOH and participation likelihood again. Numerous
statistical controls, including the individual's threshold (τi),
personal network size (ki), mean
(μ) and dispersion (σ)
of GOD, and propensity to heterogeneous ties (q),
were incorporated into the model of binary logistic regression. Table 4
shows the statistical results that verify the quadratic (inverted
U-shaped) relationship between LOH and participation likelihood. The
findings indicate that the coefficient for LOH is
positive and significant (β = 6.038, p<0.001),
whereas the coefficient for squared LOH is negative and significant (β
= -5.353, p<0.001). This is
consistent with the observation of Bello (2012)
on voting for the national elections in America; that is, the
relationship between LOH and voting is nonlinear.
Table 4: Binary logistic regression for participation likelihood Variable Test 1 Test 2 Test 3 Test 4 Constant 7.495*** 6.939*** 5.143*** 6.939*** ki 0.116 0.079 0.119 0.079 τi -13.458*** -13.208*** -13.998*** -13.208*** q -1.716*** -1.350*** -1.661*** -1.350*** μ -11.115*** -11.581*** -5.782*** -11.581*** σ 3.986*** 4.753*** 3.730*** 4.752*** hi 1.802*** 6.038*** 13.257*** 6.038*** hi2 -5.353*** hi×μ -22.602*** hi×σ -5.352*** *p<0.1, ** p<0.01, *** p<0.001 - 4.6
- This study also tested how μ and σ moderate the effect of LOH on the likelihood of participation. Increasing μ reduces the number of individuals who are willing to participate and thus suppresses the spread of participation. Therefore, LOH exerts a weak effect on participation at a high μ. Meanwehile σ positively relates to the value of LOH and positively affects participation. Therefore, σ has a negative moderating effect on LOH. The findings shown in Figure 3 confirm some empirical conclusions claiming that the influence of LOH is variable and is subject to the broader social context in which it occurs (McClurg 2006).
- 4.7
- Table 4 shows
that the relationship between the size of a personal network and the
likelihood of participation is insignificant. This finding counters
empirical
observations that specify that the two factors are positively related
(e.g., Eveland & Hively
2009). We believe this experimental finding is credible.
Individuals with a large network can encounter more participants, but
the percentage of participants in their networks may not increase.
Analysis on Participation Timing at the Individual Level
- 4.8
- This subsection shows the results on participation timing.
Figure 6
shows the
average value of participation timing corresponding to
LOH. LOH
has a monotonously negative effect on participation
timing, although the effect appears to be weak when LOH is large.
Specifically, when LOH is large, individuals participate earlier.
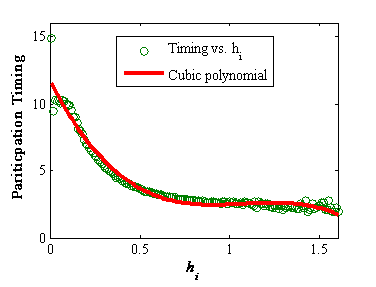
Figure 6. Participation timing vs. LOH - 4.9
- The statistical results obtained using negative binomial
regression are shown in Table 5.
These findings indicate that the monotonous effect of LOH is robust. In
this case, the coefficient for LOH is negative and significant (β =
-0.919, p<0.001), whereas the coefficient
for squared LOH is insignificant (β = -0.022, p>0.1).
The empirical conclusions posit that LOH can delay one's participation
because the ambivalence caused by LOH prompts individuals to wait and
see the outcome of events before they make their final decisions (Nir & Druckman 2008). As
previously discussed, increasing LOH may increase the "weak ties"
within the network. This finding implies that participation can spread
more easily and quickly according to the theory of "weak ties." The
negative effect of personal network size (ki)
on participation timing supports the argument of this research from
another perspective; that is, a larger personal network means that
an individual can hold more weak ties.
Table 5: Negative binomial regression for participation timing Variable Test 1 Test 2 Test 3 Test 4 Constant 0.134* 0.135* 0.133* 0.135* ki -0.071** -0.071** -0.071** -0.071** τi 4.377*** 4.377*** 4.377*** 4.376*** q 1.827*** 1.827*** 1.827*** 1.827*** μ 0.791*** 0.791*** 0.791*** 0.791*** σ -1.338*** -1.338*** -1.338*** -1.338*** hi -0.919*** -0.919*** -0.919*** -0.919*** hi2 -0.022 hi×μ 0.007 hi×σ -0.011 *p<0.1, ** p<0.01, *** p<0.001 - 4.10
- Moreover, the empirical findings reveal that GOD insignificantly moderates the relationship between LOH and participation timing. All these observations strongly suggest that participation timing mainly depends on network structure.
 Discussion
and Conclusion
Discussion
and Conclusion
- 5.1
- The relationship between LOH and individual participation in collective behavior remains to be a continuously and extensively explored topic. In this research, this issue was reconsidered with ABM. A series of simulation experiments were conducted to determine if and when individuals decide to participate under various conditions of network structure and GOD. The results demonstrate that the effect of LOH on participation likelihood exhibits an asymmetric inverse U-shape. The mean and dispersion of GOD can negatively moderate such an effect. However, the effect of LOH on participation timing is monotonous. When LOH is large, individuals participate early in collective behavior. The analytical results indicate that GOD functions as an insignificant moderator between the relationship of LOH and participation timing. LOH affects participation timing based on its influence on network structure.
- 5.2
- The above findings differ strongly from the results presented by empirical studies that suggest the existence of a linear relationship between LOH and participation in collective behavior (e.g., Eveland & Hively 2009; Huckfeldt et al. 2004; Mutz 2002a, 2002b; Nir & Druckman 2008). Empirical studies often utilize random or snow sampling method to gather data (Eveland & Hively 2009). However, this approach cannot acquire sufficient information on network structure and GOD, which can significantly influence one's participation and moderate the role of LOH. Many empirical studies have attempted to examine the role of LOH in a broader context, such as neighborhoods (e.g., McClurg 2006; Scheufele et al. 2004). The observations of these studies provide preliminary supporting evidence to the results of the current research.
- 5.3
- One of the important contributions of this study is that it provides a setting for examining the social effects of LOH on individuals in the process of participating in a collective behavior. With the growing reliance of the public on various forms of social media, examining collective behavior and modeling possible interactions that may occur among individuals are important. The framework of diffusion over the network used in this research facilitates such analysis. Another contribution of this research is that it verifies the importance of GOD in collective behavior and focuses on participation at the individual level.
- 5.4
- Moreover, this study shows that ABM provides extensive flexibility and power in exploring the diffusion process of collective behavior at the individual level. This methodology opens new opportunities by overcoming the limitations of other methodologies. For example, empirical studies should avoid some important control variables because of difficulties in gathering data. Quantitative studies that employ closed-form solutions should over-solidify their model because of computational limitations.
- 5.5
- The findings of this study are robust because the simulation methodology has a high degree of internal validity, and its assumptions are based on previous empirical and conceptual studies. However, the authors acknowledge several limitations and provide future research directions. First, this study focuses on direct social effects (i.e., individuals only care about the behaviors of their direct network neighbors). However, the results may differ for other types of collective behavior. Second, in the model of this research, the opinion of individuals (threshold) remains constant during simulation. This limitation may be extremely parsimonious in modeling long-term collective behavior. Future research can address the outcomes of individual decision for collective behavior with indirect social effects or dynamic threshold. Third, the simulation model examines the research question in the network defined only by opinion similarity and does not capture other network characteristics, such as status homophily or scale-free degree distribution. Examining how these factors affect the results could be interesting.
 Acknowledgements
Acknowledgements
- This research was supported by the Fundamental Research Funds for the Central Universities (Program Nos. 2662014BQ049 and sk2014043) and the National Natural Science Foundation of China (Nos. 71001084, 71371149 and 71472146). The authors also thank the anonymous reviewers and the editor for their valuable comments.
 Notes
Notes
-
1Homophily
has two types: (1) status homophily, in which similarity is based on
informal, formal, or ascribed status; and (2) value homophily, which is
based on values, attitudes, and beliefs. This research focuses on the
latter.
2The program is implemented in Matlab (2009a) and available at http://www.openabm.org/model/3969/version/1/view.
3As suggested by McPherson et al. (2001, p. 419), value traits "often prove to be derivative of social positions themselves," If two individuals have similar threshold, we can expect that they are close in social space, or that they belong to the same social circle with a high probability.
4Such a setting is to emphasize the heterogeneity in personal network size, which is irrelevant to tau. A scale-free (power-law) distribution is another viable option, which can be seen in many physical networks such as the Web. However, as Urry (2004) suggested, there is a major difference between social networks and the networks of the Web. In the former the network size of individuals across the world are approximately normally distributed. To guarantee that the number of connections is always positive, we use poison distribution to describe the number of links that each person possesses.
 References
References
- BELANGER, P., &
Eagles, M. (2007). Partisan cross-pressure and voter turnout: The
influence of micro and macro environments. Social Science
Quarterly, 88(3), 850–867. [doi:10.1111/j.1540-6237.2007.00486.x]
BELLO, J. (2012). The dark side of disagreement? Revisiting the effect of disagreement on political participation. Electoral Studies, 31(4), 782–795. [doi:10.1016/j.electstud.2012.06.004]
CASTELLANO, C., Fortunato, S., & Loreto, V. (2009). Statistical physics of social dynamics. Reviews of Modern Physics, 81(2), 591–646. [doi:10.1103/RevModPhys.81.591]
CENTOLA, D. (2013). Homophily, networks, and critical mass: Solving the start-up problem in large group collective action. Rationality and Society, 25(1), 3–40. [doi:10.1177/1043463112473734]
CENTOLA, D., & Macy, M. (2007). Complex contagions and the weakness of long ties. American Journal of Sociology, 113(3), 702–734. [doi:10.1086/521848]
CHIANG, Y.-S. (2007). Birds of moderately different feathers: Bandwagon dynamics and the threshold heterogeneity of network neighbors. Journal of Mathematical Sociology, 31(1), 47–69. [doi:10.1080/00222500601013536]
DIMAGGIO, P., & Garip, F. (2011). How network externalities can exacerbate intergroup inequality. American Journal of Sociology, 116(6), 1887–1933. [doi:10.1086/659653]
DODDS, P. S., & Watts, D. J. (2005). A generalized model of social and biological contagion. Journal of Theoretical Biology, 232(4), 587–604. [doi:10.1016/j.jtbi.2004.09.006]
EVELAND, W. P., & Hively, M. H. (2009). Political Discussion Frequency, Network Size, and "Heterogeneity" of Discussion as Predictors of Political Knowledge and Participation. Journal of Communication, 59(2), 205–224. [doi:10.1111/j.1460-2466.2009.01412.x]
FESTINGER, L. (1957). A theory of cognitive dissonance: Evanston, IL: Row & Peterson.
FOWLER, J. H., & Smirnov, O. (2005). Dynamic parties and social turnout: An agent-based model. American Journal of Sociology, 110(4), 1070–1094. [doi:10.1086/426554]
GALAM, S. (2002). Minority opinion spreading in random geometry. European Physical Journal B, 25(4), 403–406. [doi:10.1140/epjb/e20020045]
GALAM, S. (2003). Modelling rumors: the no plane Pentagon French hoax case. Physica a-Statistical Mechanics and Its Applications, 320, 571–580. [doi:10.1016/S0378-4371(02)01582-0]
GOLDSTONE, R. L., & Janssen, M. A. (2005). Computational models of collective behavior. Trends in Cognitive Sciences, 9(9), 424–430. [doi:10.1016/j.tics.2005.07.009]
GRANOVETTER, M. (1973). The strength of weak ties. American Journal of Sociology, 78(6), 1360–1380. [doi:10.1086/225469]
GRANOVETTER, M. (1978). Threshold models of collective behavior. American Journal of Sociology, 83(6), 1420–1443. [doi:10.1086/226707]
HOLLEY, R. A., & Liggett, T. M. (1975). Ergodic Theorems for Weakly Interacting Infinite Systems and the Voter Model. The Annals of Probability, 3(4), 643–663. [doi:10.1214/aop/1176996306]
HU, H., Cui, W., Lin, J., & Qian, Y. (2014). ICTs, Social Connectivity, and Collective Action: A Cultural-Political Perspective. Journal of Artificial Societies and Social Simulation, 17 (2) 7: https://www.jasss.org/17/2/7.html.
HU, H., Lin, J., & Cui, W. (2014). Cultural Differences and Collective Action: A Social Network Perspective. Complexity, In press.
HUCKFELDT, R. R., Beck, P. A., Dalton, R. J., & Levine, J. (1995). Political environments, cohesive social-groups, and the communication of public-opinion. American Journal of Political Science, 39(4), 1025–1054. [doi:10.2307/2111668]
HUCKFELDT, R. R., Mendez, J. M., & Osborn, T. (2004). Disagreement, ambivalence, and engagement: The political consequences of heterogeneous networks. Political Psychology, 25(1), 65–95. [doi:10.1111/j.1467-9221.2004.00357.x]
JANSSEN, M. A. (2011). Targeting Individuals to Catalyze Collective Action in Social Networks. Paper presented at the annual conference of the Computational Social Science Society of America, Santa Fe, NM.
KOSSINETS, G., & Watts, D. J. (2009). Origins of Homophily in an Evolving Social Network. American Journal of Sociology, 115(2), 405–450. [doi:10.1086/599247]
KURAN, T. (1991). Now out of never: The element of surprise in the East European revolution of 1989. World Politics, 44(1), 7–48. [doi:10.2307/2010422]
KWAK, N., Willlams, A. E., Wang, X. R., & Lee, H. (2005). Talking politics and engaging politics: An examination of the interactive relationships between structural features of political talk and discussion engagement. Communication Research, 32(1), 87–111. [doi:10.1177/0093650204271400]
LEE, F. L. F. (2012). Does Discussion With Disagreement Discourage All Types of Political Participation? Survey Evidence From Hong Kong. Communication Research, 39(4), 543–562. [doi:10.1177/0093650211398356]
MASON, W. A., Conrey, F. R., & Smith, E. R. (2007). Situating social influence processes: Dynamic, multidirectional flows of influence within social networks. Personality and Social Psychology Review, 11(3), 279–300. [doi:10.1177/1088868307301032]
MCCLURG, S. D. (2006). Political disagreement in context: The conditional effect of neighborhood context, disagreement and political talk on electoral participation. Political Behavior, 28(4), 349–366. [doi:10.1007/s11109-006-9015-4]
MCPHERSON, M., Smith-Lovin, L., & Cook, J. M. (2001). Birds of a feather: Homophily in social networks. Annual Review of Sociology, 27, 415–444. [doi:10.1146/annurev.soc.27.1.415]
MUTZ, D. C. (2002a). The consequences of cross-cutting networks for political participation. American Journal of Political Science, 46(4), 838–855.
MUTZ, D. C. (2002b). Cross-cutting social networks: Testing democratic theory in practice. American Political Science Review, 96(1), 111–126.
NIR, L. (2005). Ambivalent social networks and their consequences for participation. International Journal of Public Opinion Research, 17(4), 422–442. [doi:10.1093/ijpor/edh069]
NIR, L. (2011). Disagreement and Opposition in Social Networks: Does Disagreement Discourage Turnout? Political Studies, 59(3), 674–692.
NIR, L., & Druckman, J. N. (2008). Campaign mixed-message flows and timing of vote decision. International Journal of Public Opinion Research, 20(3), 326–346. [doi:10.1093/ijpor/edn035]
NOWAK, A., Szamrej, J., & Latané, B. (1990). From private attitude to public opinion: A dynamic theory of social impact. Psychological Review, 97(3), 362–376. [doi:10.1037/0033-295X.97.3.362]
OLSON, M. (1965). The Logic of Collective Action: Public Goods and the Theory of Groups (Vol. 124): Harvard University Press.
ROBINSON, D. T., & Balkwell, J. W. (1995). Density, transitivity, and diffuse status in task-oriented groups. Social Psychology Quarterly, 58(4), 241–254. [doi:10.2307/2787126]
ROGERS, E. M. (1995). Diffusion of innovations. New York: Free Press.
SCHELLING, T. C. (1978). Micromotives and Macrobehavior. New York: Norton.
SCHEUFELE, D. A., Hardy, B. W., Brossard, D., Waismel-Manor, I. S., & Nisbet, E. (2006). Democracy based on difference: Examining the links between structural heterogeneity, heterogeneity of discussion networks, and democratic citizenship. Journal of Communication, 56(4), 728–753. [doi:10.1111/j.1460-2466.2006.00317.x]
SCHEUFELE, D. A., Nisbet, M. C., Brossard, D., & Nisbet, E. C. (2004). Social structure and citizenship: Examining the impacts of social setting, network heterogeneity, and informational variables on political participation. Political Communication, 21(3), 315–338. [doi:10.1080/10584600490481389]
SIEGEL, D. A. (2009). Social Networks and Collective Action. American Journal of Political Science, 53(1), 122–138. [doi:10.1111/j.1540-5907.2008.00361.x]
SZNAJD-WERON, K., & Sznajd, J. (2000). Opinion evolution in closed community. International Journal of Modern Physics C, 11, 1157–1165. [doi:10.1142/S0129183100000936]
URRI, J. (2004). Small worlds and the new 'social physics'. Global Networks, 4(2)(1), 109-130. [doi:10.1111/j.1471-0374.2004.00083.x]
VALENTE, T. W. (1996). Social network thresholds in the diffusion of innovations. Social Networks, 18(1), 69–89. [doi:10.1016/0378-8733(95)00256-1]
WATTS, D. J. (2002). A simple model of global cascades on random networks. Proceedings of the National Academy of Sciences of the United States of America, 99(9), 5766–5771. [doi:10.1073/pnas.082090499]
WATTS, D. J., & Dodds, P. S. (2007). Influentials, networks, and public opinion formation. Journal of Consumer Research, 34(4), 441–458. [doi:10.1086/518527]
WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of 'small-world' networks. Nature, 393(6684), 440–442. [doi:doi:10.1038/30918]
YAVAS, M., & Yucel, G. (2014). Impact of homophily on diffusion dynamics over social networks. Social Science Computer Review, Inpress, 1–19. [doi:doi:10.1177/0894439313512464]