 Abstract
Abstract
- The rapid changes occurring in the higher education domain are placing increasing pressure on the actors in this space to focus efforts on identifying and adopting strategies for success. One particular group of interest are academics or scientists, and the ways that these individuals, or collectives as institutional or discipline-based science systems, make decisions about how best to achieve success in their chosen field. The agent-based model and simulation that we present draws on the hypothetical "strategic publication model" proposed by Mölders, Fink and Weyer (2011), and extends this work by defining experimental settings to implement a prototype ABMS in NetLogo. While considerable work remains to fully resolve theoretical issues relating to the scope, calibration and validation of the model, this work goes some way toward resolving some of the details associated with defining appropriate experimental settings. Also presented are the results of four experiments that focus on exploring the emergent effects of the system that result from varying the strategic mix of actors in the system.
- Keywords:
- Academic Science, Lotka's Law, Strategic Publication Model, Agent-Based Model
 Introduction
Introduction
- 1.1
- Since the publication in 2003 of the Shanghai Jiao Tong University Academic Ranking of World Universities (ARWU), university rankings continue to have a pervasive effect on the ways in which individual institutions compete in the global higher education market. Numerous global university ranking schemes have swiftly evolved, and major media organisations, top universities, research organisations, and even governments, are involved in developing 'better' methods that can be used for the global ranking of universities. In 2013, there are 10 main global rankings (Hazelkorn 2013). Fundamentally global university rankings are used to compare educational performance and productivity nationally and internationally, and measure educational quality and excellence (Hazelkorn 2009, 2013). Also, global university rankings are often used as an indication of a nation's global competitiveness, given the importance of higher education to social and economic growth and innovation (Hazelkorn 2009; Marginson & Van der Wende 2007).
- 1.2
- Giving rise to differing perspectives on the appropriateness and methodology for constructing global university rankings, each ranking scheme has its own specific indicators and calculation formulas. For example, based on ARWU, higher education is about scientific research and Nobel Prizes (Marginson & Van der Wende 2007); based on Times Higher Education (THE), higher education is primarily about building reputation and international marketing (Marginson 2007); and based on US News and World Report (USNWR) and Quacquarelli Symonds (QS), higher education is about research productivity with 60 per cent of the final score attributed to research outputs (Hazelkorn 2009). Although rankings can be capricious, research output, as an indicator, weights the highest among all the ranking schemes. Regardless the ranking scheme count, research output is primarily measured by the quality (proxy measure based on citations) and quantity (number) of publications (Marginson 2007).
- 1.3
- The importance of academic publication in university rankings has led some universities set annual publication performance criteria for their academics (Sullivan 1996). In addition to the pressure from universities, academics are motivated to publish. Via academic publication, academics can receive recognition and esteem from the scholarly community, obtain career promotion, and secure funding opportunities for future research (Fox 1983; Sullivan 1996). However the most significant reason for academic publications is for knowledge dissemination and advancement (Fox 1983; Jacot 1937; McGrail, Rickard & Jones 2006; Sullivan 1996). This reason persistently remains.
- 1.4
- Gerard Piel said, "Without publication, science is dead" (Day & Gastel 2012, p. 18).
This research is motivated by the importance of academic publications,
and the aim of this research is to analyse how the academic publication
system works. In broad terms, we consider strategies for academic
success, where success is considered as producing the journal outputs
necessary for academic survival (Frey
2003).
The conceptual model
- 1.5
- Agent-based modelling and simulation (ABMS) is one of the techniques that can used to observe and understand individuals, their behaviours, and the interactions among them in complex systems (Macal & North 2009). In 2011, Mölders, Fink, and Weyer considered ABMS as a tool and proposed a hypothetical conceptual 'strategic publication model'. Although the authors referred to the publication system as the 'science system', our study adopts the more generic term of 'academic' to explicitly capture a broader notion covering both science and non-science based publications. The conceptual model was not implemented. Our goal is to implement their hypothetical conceptual model to better understand the competitive dynamics in academic publication system, before we carry out further work on the model including calibration and validation. This paper presents the first step in this process.
- 1.6
- In the conceptual model, actors were categorised as either
a "Careerist", "Orthodox Scientist",
or "Mass Producer", and journals
were characterised by the criteria of impact factor (IF), acceptance
rate (AR), and topical fitting factor (TFF). Scientists in each of the
three categories have a specific order of preferences for the different
journal criteria (Figure 1). In
this hypothetical model, the decision making of a scientist agent
involves a simple choice regarding where to submit a paper on a given
topic, to one of the various types of journal. Since productivity
varies among different disciplines (Fox
1983), our study will simplify this complexity, so is based
on a single, arbitrary discipline in each simulation.

Figure 1. Preference Rules for Academic Strategy Types (Mölders, Fink, & Weyer 2011)
 The
Agent-Based Strategic Publication Model
The
Agent-Based Strategic Publication Model
- 2.1
- Based on the hypothetical conceptual strategic publication
model (Mölders et al. 2011),
the design of our Agent-Based Strategic Publication Model (ABSPM) is
described in Figure 2.
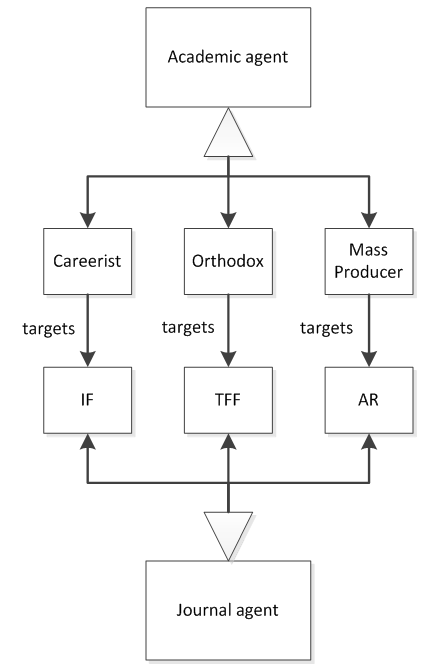
Figure 2. ABSPM framework with academic agents' behaviour rules of publication strategy. - 2.2
- The ABSPM comprises two agent types: journal agents and academic agents. Based on an academic agent's publication strategy, academic agents are categorised as Careerist, Orthodox, or Mass Producer. The agents are aged between 30 and 65. The academic agents retire at 65 and newly recruited academic agents are aged 30. Journal agents are categorised as being oriented to one of the three factors: impact factor (IF), topical fitting factor (TFF), and acceptance rate (AR). Academics submit papers to journals based on the preferences denoted by their strategic type. Journals accept papers from academics based on the acceptance rate, their total monthly published paper, and the Zipf distribution of scientific publication. Each of these is discussed in detail in following sections.
- 2.3
- To describe the model in detail, we adopt the Overview,
Design concepts, and Details (ODD) protocol (Grimm
et al. 2006), which is the standard protocol used to describe
agent-based models (Polhill,
Parker, Brown, & Grimm 2008). This protocol consists
of three blocks (Overview, Design concepts, and Details), which are
subdivided into seven elements: purpose, state variables and scales,
process overview and scheduling, design concepts, initialisation,
input, and submodels (Grimm et al.
2006). Each of these seven elements is discussed in the
following sections.
Purpose
- 2.4
- The end purpose of the ABSPM is to explore the emergent
phenomena associated with scientific publication, including quantity
and quality, from different types of academics based on their
publication strategies in an academic system. A further purpose of this
work is to develop a theoretical framework to understand the impacts of
academic publishing strategies on the higher education system. The
purpose of this initial implementation is to identify relevant
variables for calibration and validation.
State Variables and Scales
- 2.5
- Journal agents are characterised by the state variables of
journal-type, impact-factor, topical-fitting-factor, acceptance-rate,
monthly-published-paper, and academics-with-publication. Except
academics-with-publication, the other values are assigned to the
journal agents and stay the same when the simulation starts. Brief
descriptions and data values of these variables are shown in Table 1.
Given that we are implementing a hypothetical model, the data values
are randomly selected.
Table 1: State variables of journal agents Variable name Brief description Data Value journal-type Three types of Journals: (1) impact factor oriented (2) topical fitting factor oriented (3) acceptance rate oriented "IF", "TFF", or "AR" impact-factor Value of impact factor (IF) is assigned when a journal agent is created. IF value is a float with 1 decimal place, between 0 and 1. Different types of journal agents have their own range of IF values. See Submodel 1. Range [0,1] topical-fitting-factor Value of topical fitting factor (TFF) is assigned when a journal agent is created. TFF value is a float with 1 decimal place, between 0 and 1. Different types of journal agents have their own range of TFF values. See Submodel 1. Range [0,1] acceptance-rate Value of acceptance rate (AR) is assigned when a journal agent is created. AR value is a float with 1 decimal place, between 0 and 1. Different types of journal agents have their own range of AR values. See Submodel 1. Range [0,1] monthly-published-paper
Total published paper count per month is assigned when a journal agent is created. Monthly-published-paper value is an integer between 3 and 20. In this model, once this value is assigned to the journal agent, this value stays the same. Monthly-published-paper is the maximum number of acceptable papers from academic agents for the journal agent during each time tick. Different types of journal agents have their own range of monthly-published-paper values. In this hypothetical model, journals with higher impact (IF journals) publish less papers than average each month, journals with higher acceptance rate (AR journals) publish more papers than average each month, and journals focusing on topical fitting factor (TFF journals) publish average amount of papers each month. See Submodel 1. The range of 3 to 20 is arbitrary. These values can be changed to higher or lower accordingly within reasonable bounds for similar simulation experiment results. However, the values need to be calibrated and validated. Range [3, 20] academics-with-publication List of academics with published papers. When the simulation starts, the list is empty. When the journal agent publishes a paper, the ID of the academic agent gets recorded in the list. - 2.6
- Academic agents are characterised by the state variables of
academic-type, start-age, start-tick, total-publication, total-if, and
journals-with-publication. The brief descriptions and data values of
these variables are shown in Table 2.
Again, given that we are implementing a hypothetical model, the data
values are randomly selected.
Table 2: State variables of academic agents Variable name Brief description Data Value academic-type Three types of Academics: (1) Careerist: targeting IF journals (2) Orthodox: targeting TFF journals (3) Mass Producers: targeting AR journals "careerist", "orthodox", or "mass-producer" start-age It is the start age of an academic agent. The minimum start age is 30.0. Academic agents retire at the age of 65. When an academic agent is created, the start age is assigned stochastically. The range is arbitrary within hypothetical reasonable bounds, which needs calibration. Range [30.0, 64.9] start-tick It is the tick when an academic agent is created. A new academic agent can be created at any time during the simulation, possibly on the last tick. This is used to calculate the age of the academic agent. Range [0, global-total-ticks] total-publication It is used to count the published papers of the academic agent. It is an incremental data field. When an academic agent publishes a paper, total-publication increases by 1. The academic agent can have 0 papers published or n papers published. n is an unlimited integer. Range [0, n] total-impact It is used to store the sum of impact factor of the agent. This value is the sum of the impact factors from the journals where the agent published papers. When an academic agent publishes a paper, the impact factor of the journal will be added to the total-impact data field. The impact factor of the agent can be either 0 or n. n is an unlimited integer. Range [0, n] journals-with-publication This is a list of journals where the agent published papers. It is stored in an array. When the simulation starts, the list is empty. When an academic agent publishes a paper, the ID of the journal agent that accepts the paper is added to the list. The length of the array is between 0 and n. n is an unlimited integer. Length Range [0, n] - 2.7
- The scales addressed by the ABSPM include simulation environment (size of habitat cells, global-total-ticks), number of academics (num-aca-careerist, num-aca-orthodox, num-aca-producer), and number of journals (num-journal-if, num-journal-tff, and num-journal-ar). Except the value for 'size of habitat cells', the other values of defining the scales of ABSPM are changeable parameters in NetLogo.
- 2.8
- At each time tick, academic agents move around randomly in a radius of 1 to maximum 20 grid cells (global-academic-move-limit). After an academic agent moves to a new location, the agent will look for a journal in the neighbourhood using a radius of 10 grid cells for paper submission (global-academic-journal-in-radius). Without implying any decision making process, these two values are absolutely arbitrary. Real-world data is required for the frequency of submission and publication counts for different academic types. The experiment results with different settings for global-academic-move-limit and global-academic-journal-in-radius reflect similar phenomena, although having different publication results.
- 2.9
- In this hypothetical model, before a simulation starts, the
number of academic and journal agents can be changed. Once it is set
up, the number of academic agents (num-aca-careerist, num-aca-orthodox,
num-aca-producer) and the number of journal agents (num-journal-if,
num-journal-tff, and num-journal-ar) stay the same throughout the
simulation experiment. The experiment results with difference number of
agents reflect similar phenomena. As the baseline, 20 is specified for
number of journal agents for all types and 200 is specified for number
of academic agents for all types. Although in the real world, number of
academics and journals always changes, this model needs to be improved
to reflect this dynamic phenomena and it also needs calibration. Brief
explanations and default data values of the scales are shown in Table 3.
Table 3: Scales of ABSPM Scale Brief explanation Data Value global-total-ticks Each time tick in ABSPM denotes one month. 420 time ticks mean 35 years, the equivalent of a single academic life cycle (30-65 years). Therefore, each simulation experiment of ABSPM runs for 420 time ticks. 420 size of habitat cells All agents are randomly distributed using grid-based locations. Location on the grid does not imply or involve any decision-making process and thus is arbitrary.
The total number of patches in the grid are determined using the following parameters: Max-pxcor: 26 and max-pycor: 16
This habitat cell size 53x33 is sufficient to distribute 60 journal agents and 600 academic agents without overlapping. The requirement for the grid size is that there is enough space to populate all agents without overlapping. For this initial implementation, the grid size has no meaning in terms of decision making processes.53x33 global-academic-journal-in-radius After an academic agent moves to a new location, the agent identifies a suitable journal in the neighbourhood using a radius of 10 grid cells for paper submission. Sufficient number of academic agents is located within the 10 grid cells spatial radius to perform paper submission process on a 53*33 grid. 10 global-academic-move-limit At the beginning of each time tick, each academic agent physically moves randomly in a radius of 1 to 20 grid cells in the NetLogo simulation space, where the value is randomly selected. It is possibly higher or lower than global-academic-journal-in-radius. It allows academic agents to potentially explore the full simulation space. Range [1, 20] num-aca-careerist As the base line, number of Careerist academic agents is set to 200. 200 num-aca-orthodox As the base line, number of Orthodox academic agents is set to 200. 200 num-aca-producer As the base line, number of Mass Producer academic agents is set to 200. 200 num-journal-if As the base line, number of IF journal agents is set to 20. 20 num-journal-tff As the base line, number of TFF journal agents is set to 20. 20 num-journal-ar As the base line, number of AR journal agents is set to 20. 20 Process overview and scheduling
- 2.10
- When the simulation initiates, the ABSPM runs two
submodels: 'create journals', and 'create academics'. These two
submodels run only once. During the simulation, time is progressed in
monthly time ticks. Within each monthly time tick, four submodels are
processed in the following order: 'academics move around', 'academics
submit papers', 'journal publish papers', and 'retire & recruit
academics'. No action is executed in a random order. The details of
these four submodels will be explained in the section 'Submodels'.
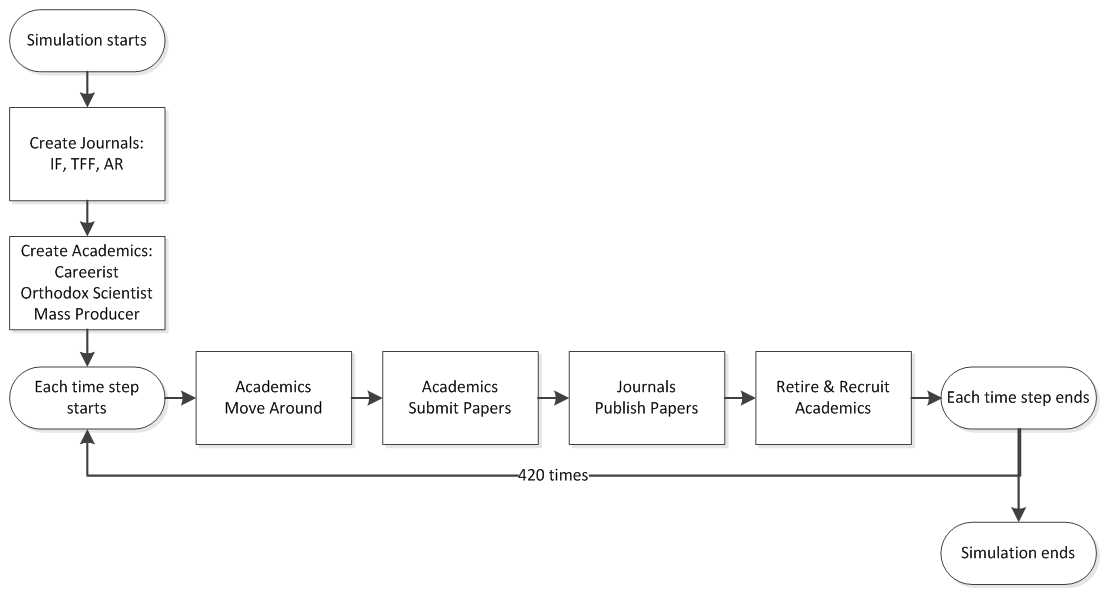
Figure 3. Process overview of ABSPM Design concepts
-
Emergence
- 2.11
- The ABSPM was designed to explore the two emergent
phenomena of publication quantity and publication quality as they arise
from the different types of academic agents.
Interaction
- 2.12
- Two types of interactions are modelled implicitly. Academic agents directly interact with their neighbour journal agents when submitting papers. Journal agents publish papers from academic agents based on the publication rule of including 41% of new authors and 59% of seasoned authors (Gilbert 1997; Simon 1957).
- 2.13
- Lotka's Law (Lotka 1926)
has been shown to specify the frequency distribution of scientific
productivity. It means that a proportion of published papers are
submitted by new authors, and the rest are from seasoned authors (Gilbert 1997), and the portion
of all authors with just a single paper should be just over 60 percent (Lotka 1926). Simon (1957) further validated the
scientific publication distribution proposed by Lotka in his study of
five Zipf skew distribution functions. For the probability that the
paper is from a new, not previously published author in any particular
journal (Simon 1957).
Therefore, we adopt 41% in our study as used in the agent-based
Academic Science Model by Gilbert (1997).
Stochasticity
- 2.14
- The ABSPM uses stochasticity to represent (1) the
distribution of the journal and academic agents, (2) IF, TFF, and AR
values for each journal agent, which are generated within its specific
range based on the journal type, (3) the distance and direction of each
move of academic agents, (4) the selection of the submitted paper for
publishing by the journal agents, and (5) the age of the academic
agents (between 30.0 and 64.9) when the simulation starts.
Collectives
- 2.15
- The agents in ABSPM are individual decision-makers. No
collectives, or collective decision-makings, are considered in this
model.
Observation
- 2.16
- Various observations are available in the ABSPM. However
for model analysis, the key observations include: the academic type of
the academic agents; the publication count of each academic agent; and
the impact factor sum of all the publications from each academic agent.
Other design concepts
- 2.17
- Other design concepts, such as adaptation, fitness,
prediction, and sensing, were omitted in order to preserve the
simplicity and transparency of the model.
Initialisation
- 2.18
- To initialise the simulation environment of the ABSPM, the
journal and academic agents are created and randomly distributed within
the grid-based environment based on the settings in Table 3. Additional parameters
controlling the dynamics of the models are specified at the beginning
of a simulation run. The additional parameters for ABSPM are
publication rate, academic age values, and journal settings, as shown
in Table 4. Publication rate (global-new-author-publication-rate) and
academic age values (global-academics-start-age-min,
global-academics-start-age-max, and global-academics-retire-age) are
fixed in the ABSPM. Settings for IF journals
(if-journal-if-min, if-journal-if-max, if-journal-tff-min,
if-journal-tff-max, if-journal-ar-min, if-journal-ar-max,
if-journal-monthly-paper-min, if-journal-monthly-paper-max), TFF
journals (tff-journal-if-min, tff-journal-if-max,
tff-journal-tff-min, tff-journal-tff-max, tff-journal-ar-min,
tff-journal-ar-max, tff-journal-monthly-paper-min,
tff-journal-monthly-paper-max), and AR journals (ar-journal-if-min,
ar-journal-if-max, ar-journal-tff-min, ar-journal-tff-max,
ar-journal-ar-min, ar-journal-ar-max, ar-journal-monthly-paper-min,
ar-journal-monthly-paper-max) are parameterised in NetLogo. The maximum
values for these parameters are set to 1 and the minimum values are set
to 0. The baseline data values for journal settings are specified in
Table 4, however these values for the journals settings are arbitrary
and need calibrating. Based on the hypothetical conceptual model, we
assume that IF journals have the highest impact
factor, an average topical fitting factor, and lowest acceptance rates,
TFF journals have an average impact factor, the
highest topical fitting factor, and an average acceptance rates, and AR
journals have lowest impact factor, an average topical
fitting factor, and the highest acceptance rates.
Table 4: Parameter settings at initialisation of ABSPM simulation Parameter Brief explanation Data Value global-new-author-publication-rate 41% (Gilbert 1997; Simon 1957) of the papers to be published by a journal each time tick are from new authors.
This is the only fixed parameter value in the initialisation of ABSPM simulation in NetLogo.0.41 global-academics-start-age-min The minimum start age of an academic agent is 30.0. 30.0 global-academics-start-age-max The maximum start age of an academic agent is 30.9 30.9 global-academics-retire-age The retirement age of an academic agent is 65.0. 65.0 if-journal-if-min This is the minimum value of impact factor for an IF journal. 0.8 if-journal-if-max This is the maximum value of impact factor for an IF journal. 0.9 if-journal-tff-min This is the minimum value of topical fitting factor for an IF journal. 0.1 if-journal-tff-max This is the maximum value of topical fitting factor for an IF journal. 0.6 if-journal-ar-min This is the minimum value of acceptance rate for an IF journal. 0.2 if-journal-ar-max This is the maximum value of acceptance rate for an IF journal. 0.3 if-journal-monthly-paper-min This is the minimum value of average published paper per month for an IF journal. 3 if-journal-monthly-paper-max This is the maximum value of average published paper per month for an IF journal. 10 tff-journal-if-min This is the minimum value of impact factor for a TFF journal. 0.3 tff-journal-if-max This is the maximum value of impact factor for a TFF journal. 0.5 tff-journal-tff-min This is the minimum value of topical fitting factor for a TFF journal. 0.7 tff-journal-tff-max This is the maximum value of topical fitting factor for a TFF journal. 0.9 tff-journal-ar-min This is the minimum value of acceptance rate for a TFF journal. 0.3 tff-journal-ar-max This is the maximum value of acceptance rate for a TFF journal. 0.5 tff-journal-monthly-paper-min This is the minimum value of average published paper per month for a TFF journal. 8 tff-journal-monthly-paper-max This is the maximum value of average published paper per month for a TFF journal. 15 ar-journal-if-min This is the minimum value of impact factor for an AR journal. 0.1 ar-journal-if-max This is the maximum value of impact factor for an AR journal. 0.2 ar-journal-tff-min This is the minimum value of topical fitting factor for an AR journal. 0.1 ar-journal-tff-max This is the maximum value of topical fitting factor for an AR journal. 0.6 ar-journal-ar-min This is the minimum value of acceptance rate for an AR journal. 0.7 ar-journal-ar-max This is the maximum value of acceptance rate for an AR journal. 0.8 ar-journal-monthly-paper-min This is the minimum value of average published paper per month for an AR journal. 12 ar-journal-monthly-paper-max This is the maximum value of average published paper per month for an AR journal. 20 Input
- 2.19
- There is no further input required for the ABSPM.
Submodels
- 2.20
- As shown in Figure 3,
there are six submodels in total, namely: create journals; create
academics; academics move around; academics submit papers; journals
publish papers; and retire & recruit academics. The submodels
explain in detail all the processes outlined in the 'Process overview
and scheduling' subsection of 'Overview', however this does not include
describing how parameter values are chosen, or calibration of the
submodels. The conceptual model that ABSPM is built on, and the
parameters used in the model, are hypothetical. Therefore, the
pre-initial values are arbitrary and serve to identify the key
components of the model that require calibration. Each of the submodels
are described below.
Submodel 1: Create Journals
- 2.21
- This submodel runs only once when the simulation starts.
a. Create num-journal-if number of IF journal agents (20 as base line)
- Set journal-type to "IF"
- Set impact-factor to a random value between if-journal-if-min and if-journal-if-max
- Set topical-fitting-factor to a random value between if-journal-tff-min and if-journal-tff-max
- Set acceptance-rate to a random value between if-journal-ar-min and if-journal-ar-max
- Set monthly-published-paper to a random value between if-journal-monthly-paper-min and if-journal-monthly-paper-max
b. Create num-journal-tff number of TFF journal agents (20 as base line)
- Set journal-type to "TFF"
- Set impact-factor to a random value between tff-journal-if-min and tff-journal-if-max
- Set topical-fitting-factor to a random value between tff-journal-tff-min and tff-journal-tff-max
- Set acceptance-rate to a random value between tff-journal-ar-min and tff-journal-ar-max
- Set monthly-published-paper to a random value between tff-journal-monthly-paper-min and tff-journal-monthly-paper-max
c. Create num-journal-ar number of AR journal agents (20 as base line)
- Set journal-type to "AR"
- Set impact-factor to a random value between ar-journal-if-min and ar-journal-if-max
- Set topical-fitting-factor to a random value between ar-journal-tff-min and ar-journal-tff-max
- Set acceptance-rate to a random value between ar-journal-ar-min and ar-journal-ar-max
- Set monthly-published-paper to a random value between ar-journal-monthly-paper-min and ar-journal-monthly-paper-max
d. Set properties of all journal agents
- Set visual icon to house
- Set colour to white
- Set academics-with-publication to empty
- Distribute the journal agents randomly in a radius of 1 to maximum 20 grid cells
Submodel 2: Create Academics
- 2.22
- As with the Create Journals submodel, this submodel also
runs only once when the simulation starts.
a. Create num-aca-careerist number of Careerist academic agents (200 as base line)
- Set academic-type to "Careerist"
- Set colour to red
b. Create num-aca-orthodox number of Orthodox academic agents (200 as base line)
- Set academic-type to "Orthodox"
- Set colour to green
c. Create num-aca-producer number of Mass Producer academic agents (200 as base line)
- Set academic-type to "Mass Producer"
- Set colour to yellow
d. Set properties to all academic agents
- Set visual icon to person
- Set start-age to a random float number between 30.0 and 65.0
- Set start-tick to 0
- Set total-publication to 0
- Set total-impact to 0
- Set journals-with-publication to empty
- Set the current journal where the academic submit a paper and waits for submission result to -1, which means this academic currently has no relationships to any journals
- Distribute the academic agents randomly in a radius of 1 to maximum 20 grid cells on the grid
Submodel 3: Academics Move Around
- Every time when the academic agents move around, the links between academics and journals are cleared. Therefore, their current journal ids are set to -1
- All academic agents physically move forward between 1 to maximum 20 random grid cells
- All academic agents physically move right between 1 to maximum 20 random grid cells
- All academic agents physically move left between 1 to maximum 20 random grid cells
Submodel 4: Academics Submit Papers
a. Determine the journal for submission based on the academic type
- Find all the IF journals within a 10 grid cell neighbourhood of the academic
- Find all the TFF journals within a 10 grid cell neighbourhood of the academic
- Find all the AR journals within a 10 grid cell neighbourhood of the academic
- Submit paper to IF journal in Step 4.b, if this academic is Careerist and there is at least one IF journal in the neighbourhood
- Submit paper to TFF journal in Step 4.c, if this academic is Orthodox and there is at least one TFF journal in the neighbourhood
- Submit paper to AR journal in Step 4.d, if this academic is Mass Producer and there is at least one AR journal in the neighbourhood
b. Submit paper to IF journal
- Determine the particular IF journal for submission based on the IF journals found in Step 4.a
- If no IF journals are found, the academic agent will have no submission in this time tick.
- If one IF journal is found, set the journal for submission to this particular journal.
- If the number of IF journals is more than 1, find IF journals with the maximum impact factor
- If the number of IF journals with the maximum impact factor is 1, set the journal for submission to this particular journal
- Else find journals with maximum acceptance rate among these IF journals with maximum impact factor
- If the number of IF journals with maximum impact factor and maximum acceptance rate is 1, set the journal for submission to this particular journal
- Else find journals with maximum topical fitting factor among these IF journals with maximum impact factor and maximum acceptance rate
- If only one journal matches the criteria, set the journal for submission to this particular journal
- If more than one journal matches the criteria, randomly choose one of the matching IF journals with the maximum impact factor, maximum acceptance rate, and maximum topical fitting factor.
- Submit paper from this academic to the journal for submission
c. Submit paper to TFF journal
- Determine the particular TFF journal for submission based on the TFF journals found in Step 4.a
- If no TFF journals are found, the academic agent will have no submission in this time tick.
- If one TFF journal is found, set the journal for submission to this particular journal.
- If the number of TFF journals is more than 1, find TFF journals with the maximum topical fitting factor
- If the number of TFF journals with the maximum topical fitting factor is 1, set the journal for submission to this particular journal
- Else find journals with maximum acceptance rate among these TFF journals with maximum topical fitting factor
- If the number of TFF journals with maximum topical fitting factor and maximum acceptance rate is 1, set the journal for submission to this particular journal
- Else find journals with maximum impact factor among these TFF journals with maximum topical fitting factor and maximum acceptance rate
- If only one journal matches the criteria, set the journal for submission to this particular journal
- If more than one journal matches the criteria, randomly choose one of the matching TFF journals with the maximum topical fitting factor, maximum acceptance rate, and maximum impact factor
- Submit paper from this academic to the journal for submission
d. Submit paper to AR journal
- Determine the particular AR journal for submission based on the AR journals found in Step 4.a
- If no AR journals are found, the academic agent will have no submission in this time tick.
- If one AR journal is found, set the journal for submission to this particular journal.
- If the number of AR journals is more than 1, find AR journals with the maximum acceptance rate
- If the number of AR journals with the maximum acceptance rate is 1, set the journal for submission to this particular journal
- Else find journals with maximum impact factor among these AR journals with maximum acceptance rate
- If the number of AR journals with maximum acceptance rate and maximum impact factor is 1, set the journal for submission to this particular journal
- Else find journals with maximum topical fitting factor among these AR journals with maximum acceptance rate and maximum impact factor
- If only one journal matches the criteria, set the journal for submission to this particular journal
- If more than one journal matches the criteria, randomly choose one of the matching AR journals with the maximum acceptance rate, maximum impact factor, and maximum topical fitting factor
- Submit paper from this academic to the journal for submission
e. Submit paper
- Create link from academic to the journal where a paper is submitted
- Set the current journal of the academic to the journal where the paper is submitted
Submodel 5: Journals Publish Papers
a. Determine the acceptance for each journal
- Calculate all the submissions from academics from each particular journal
- Calculate the number of acceptable papers based on the
acceptance rate of each journal and the total submission. The formula
is as below:
Total acceptable paper count = (AR * Total-submission) - Set total acceptable paper count to monthly published paper count, if total acceptable paper count is greater than monthly published paper count. This parameter sets a maximum limit for the number of individual papers that a journal will publish per month (i.e. time tick).
- Determine the number of papers from new authors (new-author-pool), and the number of papers from seasoned authors (seasoned-author-pool)
- Set two local variables, new-author-count and seasoned-author-count to 0
- Find the academics who have submitted papers to this journal that are within 10 grid cell neighbourhood radius.
- If this academic has not published any papers before
Determine if new author pool is not full by checking new-author-count < new-author-pool
• Add 1 to the local variable new-author-count
• Proceed Publish paper - Else if this academic has published papers before
Determine if the seasoned author pool is not full by checking seasoned-author-count < seasoned-author-pool
• Add 1 to the local variable seasoned-author-count
• Proceed Publish paper
b. Publish paper
- Journal
- Create a link to the academic from the journal
- Add this academic to the list of academics who have published papers at this journal
- Set the value of the impact factor of the journal to a local variable: this-if
- Academic
- Add 1 to the total-publication count
- Add the local this-if value to the total-if of the academic
- Add this journal to the list of journals where this academic has published
Submodel 6: Retire & Recruit Academics
a. Determine the retiring academics
- Calculate the age of each academic agent. The current age is the start age plus total years of academic life.
- The formula is shown as below:
- Current-age = Start-age + (Current-tick − Start-tick) / 12 months)
b. Recruit a new academic if the academic is older than retirement age - 65
- Create a new academic agent
- Set start age between 30.0 and 30.9
- Set the start tick to the current tick
- Set the total publication to 0
- Set the total impact to 0
- Set the list of the journals where the academic will publish to empty
- Set the current journal where the academic submits a paper and waits for submission result to -1
c. Retire this original academic agent and remove the agent from the simulation
 Implementation
Implementation
- 3.1
- We implemented the ABSPM in NetLogo (Wilensky 1999). This is a cross-platform multi-agent modelling environment for simulating natural and social phenomena, and it is particularly suitable for modelling complex systems developing over time. The flowchart in Figure 3 shows the process and sequence of execution that takes place in our NetLogo model.
- 3.2
- Our simulation space is partitioned into the global
parameter section, simulation environment, graphs, and command centre,
as shown in Figure 4.
Figure 4. NetLogo interface of ABSPM simulation - 3.3
- In the NetLogo model, the agent icons are explained in the submodels in Section 3.
- 3.4
- The model code can be found at http://www.openabm.org/model/4169/version/4/view
 Simulation Experiments
Simulation Experiments
- 4.1
- In this section, we present the results of four types of computational simulation scenarios conducted in the NetLogo model that has been described in the previous sections.
- 4.2
- The simulation scenarios consider environments populated
with varying proportions of each academic strategy type as specified in
Table 5. We initialise a
baseline simulation with equally distributed numbers of academic types
(Simulation A). The second experimental design considers an environment
that is dominated by the Careerists with less Orthodox
academics and Mass Producers
(Simulation B). The third experimental design considers an environment
dominated by the Orthodox types, and with less Careerists
and Mass Producers (Simulation
C). Finally, the fourth experimental design involves an environment
dominated by Mass Producers with less Careerists
and Orthodox academics (Simulation D). In the rest
of the paper, we name the Simulation A type as 'Simulation-A
200-200-200', as the simulation includes 200 Careerists,
200 Orthodox, and 200 Mass Producers.
The other three types of simulation scenarios are named in a similar
way: 'Simulation-B 400-100-100', 'Simulation-C 100-400-100', and
'Simulation-D 100-100-400'.
Table 5: Four types of simulation scenarios with various academic type counts Simulation A Simulation B Simulation C Simulation D Careerist 200 400 100 100 Orthodox 200 100 400 100 Mass Producer 200 100 100 400 - 4.3
- We conduct 10 experiments for each of the simulation
scenarios. From the experiments, the average number of papers published
per agent and the average impact delivered per agent in each of the
four different environments is calculated. The experiment results are
shown in Table 6.
Table 6: 10 simulation experiment results Simulation Environment Careerist Orthodox Mass Producer Paper
per AgentImpact
per AgentPaper
per AgentImpact
per AgentPaper
per AgentImpact
per AgentSimulation-A
200-200-200Mean 54.70 48.79 93.13 38.07 155.59 24.92 S.D. 2.80 2.48 4.37 2.08 5.53 1.74 Simulation-B
400-100-100Mean 39.37 34.54 110.09 46.00 198.26 33.04 S.D. 2.57 2.35 4.66 2.44 8.82 2.65 Simulation-C
100-400-100Mean 65.99 58.77 64.24 26.36 198.30 34.14 S.D. 3.31 2.51 2.66 1.41 7.47 1.89 Simulation-D
100-100-400Mean 67.79 59.84 108.86 44.22 100.33 14.97 S.D. 3.36 2.89 6.05 3.15 4.18 0.58 - 4.4
- Compared with the baseline 'Simulation-A 200-200-200', Careerists deliver the least number of papers and the lowest impact for these papers in 'Simulation-B 400-100-100', the Careerist dominated environment. This pattern ensues for the other three simulations; the lowest agent performance for any type occurs in the environment where that agent type dominates.
- 4.5
- Standard deviation values from the 10 simulation experiments show minimal variation across all simulation scenarios. However, Orthodox types exhibit larger variation in the average number of papers per agent in environments dominated by Mass Producers. In general, across all scenarios, Mass Producers show higher variation in the average number of papers and lower variation in average impact than the other strategy types.
- 4.6
- Figure 5 and Figure 6 show four types of simulation scenarios including 'Simulation-A 200-200-200', 'Simulation-B 400-100-100', 'Simulation-C 100-400-100', and 'Simulation-D 100-100-400'. Each graph shows the average of 10 runs for each type of simulation scenarios. In each graph, there are four series: red for Careerists, green for Orthodox, yellow for Mass Producers, and grey for the average of these three academic types. The X-axis, the horizontal axis, identifies the time tick in both Figure 5 and Figure 6. The Y-axis, the vertical axis, identifies for the quantity of papers in Figure 5, and the impact of papers in Figure 6.
- 4.7
- The plots of productivity by academic type in Figure 5 show that the specific agents
deliver fewer publications in the specific academic type dominated
environments, while the other types deliver more. For example, the
baseline simulation ('Simulation-A 200-200-200') shows each Mass
producer agent delivers close to 80 papers at tick 420. In
the Mass Producer dominated environment
'Simulation-D 100-100-400', each Mass Producer
agent delivers close to 50 papers at tick 420.
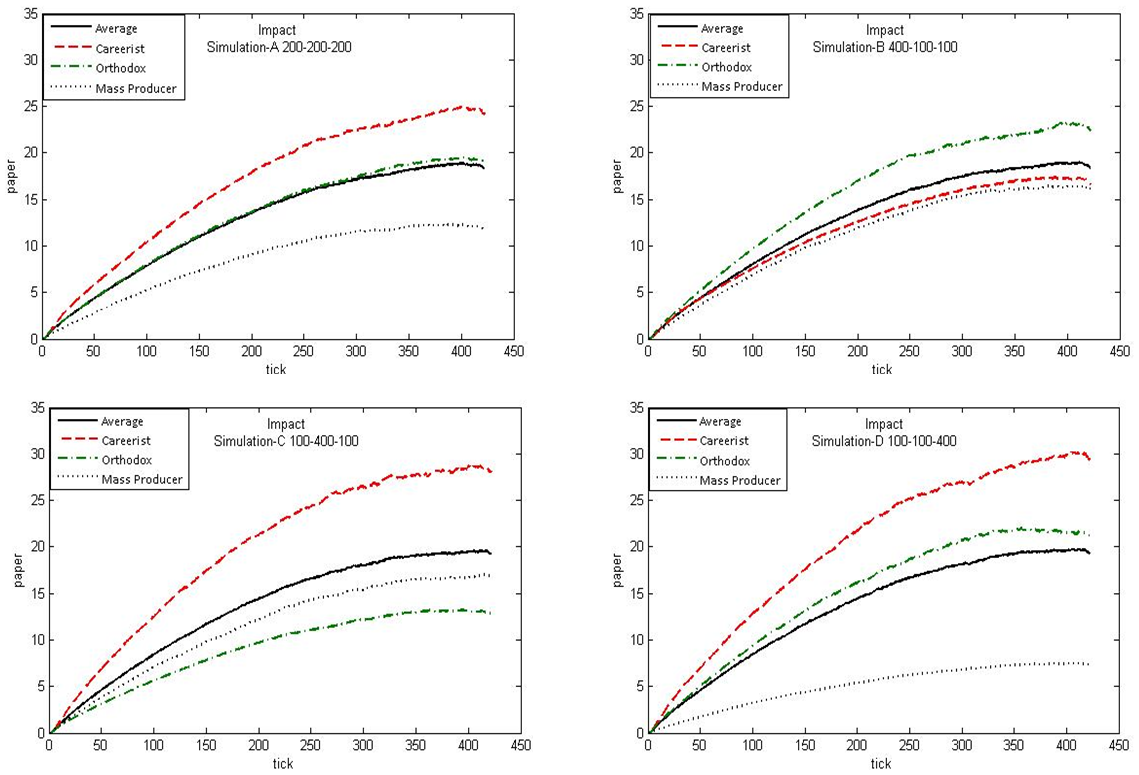
Figure 5. Publication count of each academic type in four simulation environments - 4.8
- The plots of the total impact by academic type in Figure 6 also show that the specific agents
contribute less impact in the specific academic type dominated
environment, while the other types will contribute more. For example,
the baseline simulation ('Simulation-A 200-200-200') shows the impact
of each Careerist agent is close to 25 at tick 420.
In the Careerist dominated environment
'Simulation-B 400-100-100', the impact of each Careerist
agent is close to 50 at tick 420.
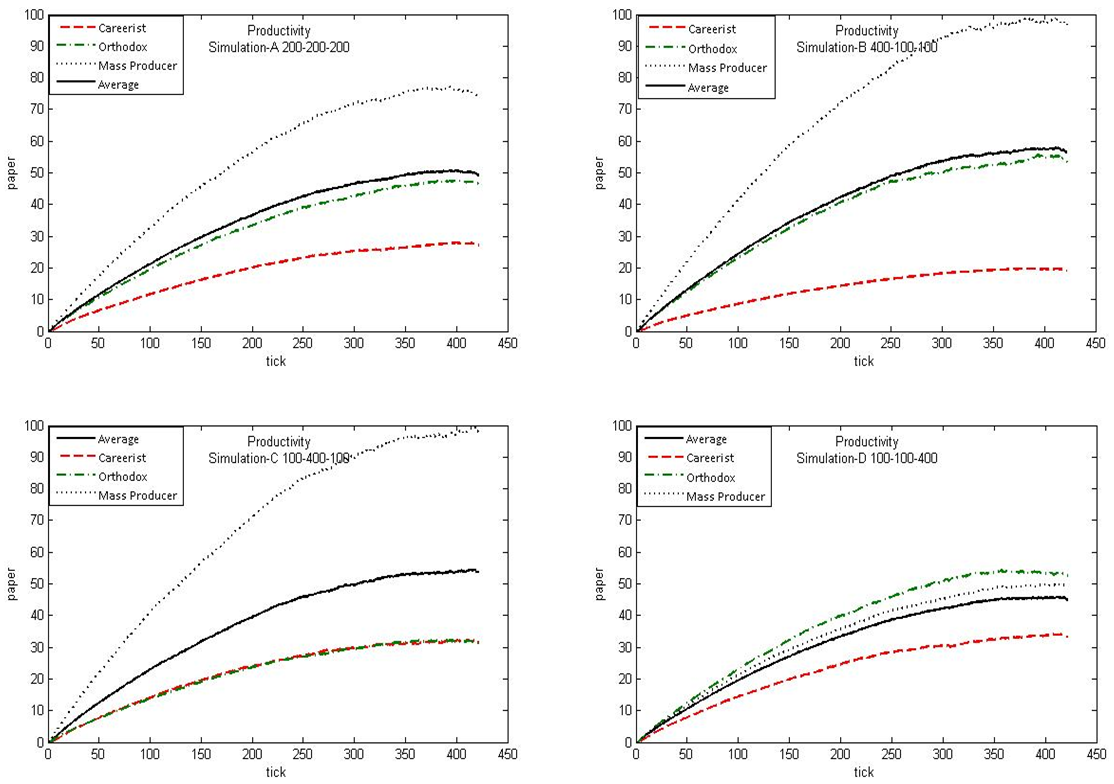
Figure 6. Total impact of each academic type in four simulation environments - 4.9
- Generally, Orthodox appears as the most consistent academic type under different environmental conditions, obtaining the closest to average performance, from both an impact and productivity perspective, in all experiements. An interesting observation relates to the impact of a Mass Producer dominated environment on this agent type, again in terms of both impact and productivity. Mass Producers are severely affected when this type dominates the environment, and while this ABMS is yet to be calibrated, these results suggest that there may be optimal strategy types for different environmental conditions.
 Conclusions and Further Opportunities
Conclusions and Further Opportunities
- 5.1
- The agent-based strategic publication model presented in this paper is based on the hypothetical conceptual model proposed by Mölders et al. (2011), and implemented in NetLogo (Wilensky 1999). In the model, actors were categorised as either a "Careerist", "Orthodox", or "Mass Producer", and journals were characterised by the criteria of impact factor (IF), acceptance rate (AR), and topical fitting factor (TFF). Scientists in each of the three categories have a specific order of preferences for the different type of journals. Careerists prefer IF journals, mass producers prefer AR journals, and the Orthodox prefer TFF journals. In the context of the simulation model, the type and number of the academic and journal agents are hypothesised. Although there are arbitrary values, the simulation results reveal interesting competitive dynamic phenomena. Dominance by any given academic type reduces the productivity, both in terms of the number and impact of papers published, of that academic type. The number of journals and the total number of acceptable papers stays the same throughout all simulation scenarios, thus the specific academic type agents suffer from higher levels of competition. This dynamic is an artefact that arises from the model where each academic strategy type has a specific set of unique preferences for journals, and where the number of available "publication spaces" in the model does not increase in response. Increasing the level of competition restricts the "journal outlets" available to an academic type and thus reduces the quantity of publications that any given agent of that type can achieve. For academics, it may be worth staying as Orthodox, as Orthodox appears as the most consistent academic type under different environmental conditions, obtaining the closest to average performance, from both an impact and productivity perspective, in all simulation experiements.
- 5.2
- The growing global demand for data on the quality of higher education institutions, such as that provided by global university rankings, fuels institutional strategies to deliver better outcomes. Subsequently, there is increasing pressure on actors in the academic publication space to increase publication rates, and improve the quality of these publications (Van Dalen & Hendrik 2012). The model reveals a potential for these activities to effectively stifle the ability of academics to achieve these desired goals. This is particularly true if these activities result in an increase in the number of academics following a particular publication strategy type.
- 5.3
- Although interesting, these results remain the product of a hypothetical model, albeit more rigorously explored in this research. In order to adequately develop the model, calibration and validation using data obtained from the real world system is required. However, our implementation of the conceptual "strategic publication model" proposed by Mölders et al. (2011) in the Netlogo environment has allowed for a more detailed exploration of key aspects of the model and the academic publication system.
- 5.4
- In order to move forward, we propose to further develop the underlying theoretical model using a combination of publically available publication data and data obtained through targeted surveys of the publishers of scholarly works. A significant amount of data on the academic publication system can be freely accessed through online resources such as Google Scholar, Thomson Reuters' ResearcherID, Scopus Author ID and ORCID. Each of these sources provides information on the publications, the publishers of these publications, and institutional details of individual academics over time.
- 5.5
- Significant data extraction and cleaning processes are required to further this work, and our initial investigation of these data sources has identified a set of key parameters relevant to the development of the theoretical model. Initial analysis tasks will involve exploration of the data using clustering techniques to determine the appropriate number of academic strategy types in the system, at both the total system and individual discipline levels. The data extends from 1940 to present, thus allowing for consideration of the possibility of changes in strategy types for individual academics that may occur over time. We identify this temporal factor as an important consideration missing from the original conceptual model.
- 5.6
- Although a vast amount of data on the publication history of individual academics is available, the same is not true for data relating to the activities of publishers of scholarly works. A targeted survey is planned to obtain data on journal level impact factors and acceptance rates for publishers within the academic publication system. We aim to obtain sufficient data to calibrate this component of the model at a discipline level. Additionally, data on the number of academics in the system, and the number of publishers of scholarly works, will be used to determine changes in supply (by academics) and demand (by journal publishers) over time.
- 5.7
- The strategic publication model that we seek to develop aims to explore the academic publishing system using a typology based approach. Typologies are used to identify a set of 'ideal types' that provide a parsimonious, high-level description of complex behaviours and/or mechanisms (Doty & Glick 1994). The importance of exploring not only the variables, but also the processes that characterise agents, was highlighted in the study of differing computational models of the peer review process (Paolucci & Grimaldo 2014). This approach is eluded to by Baier (2012), who proposes three individual dispositions followed by utility-driven scientist agents. While the approach that we take may ultimately provide only approximations of local processes such as peer review, high-level system models such as the one we are developing are useful tools for policy and management decision-making (Baier 2012; Payette 2011).
- 5.8
- Despite a considerable program of research still required to develop and implement a calibrated strategic publication model, this initial implementation represents a valuable step toward this goal. The model allows for preliminary exploration of the system, and also helps to clarify many of the finer level details required. This is a positive step toward the development of a model that we aim to use to explore the implications of institutional policies on the traditional academic publication system.
 References
References
- BAIER, M. (2012). A
simulation model of scientists as utility-driven agents. Proceedings
of the 26th European Conference on Modelling and
Simulation. K. G. Troitzsch, M. Möhring, U. Lotzmann (eds.), Koblenz,
Germany, pp. 683-689: http://www.scs-europe.net/conf/ecms2012/ecms2012%20accepted%20papers/sdcb_ECMS_0104.pdf.
DAY, R., & Gastel, B. (2012). How to write and publish a scientific paper: Cambridge, MA: Cambridge University Press.
DOTY, D. H., & Glick, W. H. (1994). Typologies as a unique form of theory building: Toward improved understanding and modeling. Academy of Management Review, 19(2), 230–251.
FOX, M. F. (1983). Publication productivity among scientists: A critical review. Social Studies of Science, 13(2), 285–305. [doi:10.1177/030631283013002005]
FREY, B. S. (2003). Publishing as prostitution?–choosing between one's own ideas and academic success. Public Choice, 116(1–2), 205–223. [doi:10.1023/A:1024208701874]
GILBERT, N. (1997). A simulation of the structure of academic science. Sociological Research Online, 2(2): http://www.socresonline.org.uk/2/2/3.html.
GRIMM, V., Berger, U., Bastiansen, F., Eliassen, S., Ginot, V., Giske, J., et al. (2006). A standard protocol for describing individual-based and agent-based models. Ecological Modelling, 198(1–2), 115–126: http://www.sciencedirect.com/science/article/pii/S0304380006002043.
HAZELKORN, E. (2009). Impact of global rankings on higher education research and the production of knowledge. Articles, 4.
HAZELKORN, E. (2013). How rankings are reshaping higher education? Paper presented at the IAU 13th General Conference, Utrecht, The Netherlands.
JACOT, A. P. (1937). Principles of scientific publication. Journal of the New York Entomological Society, 127–129.
LOTKA, A. J. (1926). The frequency distribution of scientific productivity. Journal of Washington Academy Sciences, 16, 317–323.
MACAL, C. M., & North, M. J. (2009). Agent-based modeling and simulation. Paper presented at the 2009 Winter Simulation Conference, Austin, TX, USA. [doi:10.1109/WSC.2009.5429318]
MARGINSON, S. (2007). Global university rankings: Where to from here. Centre for the Study of Higher Education, University of Melbourne, Australia.
MARGINSON, S., & Van der Wende, M. (2007). To rank or to be ranked: The impact of global rankings in higher education. Journal of studies in international education, 11(3-4), 306–329. [doi:10.1177/1028315307303544]
MCGRAIL, M. R., Rickard, C. M., & Jones, R. (2006). Publish or perish: A systematic review of to increase academic publication rates. Higher Education Research & Development, 25(1), 19–35. [doi:10.1080/07294360500453053]
MÖLDERS, M., Fink, R. D., & Weyer, J. (2011). Modeling scientists as agents. How scientists cope with the challenges of the new public management of science. Journal of Artificial Societies and Social Simulation, 14(4), 6. https://www.jasss.org/14/4/6.html.
PAOLUCCI, M., & Grimaldo, F. (2014). Mechanism change in a simulation of peer review: From junk support to elitism. Scientometrics, 99(3), 663–688. [doi:10.1007/s11192-014-1239-1]
PAYETTE, N. (2011). For an integrated approach to agent-based modeling of science. Journal of Artificial Societies and Social Simulation, 14(4), 9: https://www.jasss.org/14/4/9.html.
POLHILL, J. G., Parker, D., Brown, D., & Grimm, V. (2008). Using the ODD protocol for describing three agent-based social simulation models of land-use change. Journal of Artificial Societies and Social Simulation, 11(2), 3: https://www.jasss.org/11/2/3.html.
SIMON, H. A. (1957). On a class of skew distribution functions Models of man; social and rational. New York: John Wiley & Sons, Inc.
SULLIVAN, S. (1996). Scholarly publishing: Trash or treasure? Australian Academic & Research Libraries, 27(1), 40–46: .