 Abstract
Abstract
- Pluralistic ignorance, a well-documented socio-psychological conformity phenomenon, involves discrepancies between private attitude and public opinion in certain social contexts. However, continuous opinion dynamics models based on a bounded confidence assumption fail to accurately model pluralistic ignorance because they do not address scenarios in which non-conformists do not need to worry about holding and expressing conflicting opinions. Such scenarios reduce the power of continuous opinion dynamics models to explain why certain groups doubt or change their opinions in response to minority views. To simulate the effects of (a) private acceptance of informational social influence and (b) public compliance with normative social influence on pluralistic ignorance and minority influences, we have created an agent-based simulation model in which attitude and opinion respectively represent an agent's private and expressed thoughts. Results from a series of simulation experiments indicate model validity equal to or exceeding those of existing opinion dynamics models that are also based on the bounded confidence assumption, but with different dynamics and outcomes in terms of collective opinion and attitude. The results also support the use of our proposed model for computational social psychology applications.
- Keywords:
- Social Influence, Private Acceptance, Public Compliance, Theory of Reasoned Action, Cognitive Dissonance Theory, Agent-Based Simulation
 Introduction
Introduction
- 1.1
- As in the fable of "The Emperor's New Clothes", individual opinions and behaviors often clash with internal attitudes, values, beliefs, and morals (Sekiguchi & Nakamaru 2011). A common reason is that people are structurally embedded in tight social networks in which they influence one another (Putnam 2000). In simple language, whenever someone does something, others believe they should follow suit, and when we respond to the actions of people we know, we tend to adjust our behaviors to meet their expectations and/or those of the greater society (Cialdini & Goldstein 2004). There is a large social psychology literature on the tendency to alter one's opinions and behaviors due to real or imagined influences in order to conform to group behavior patterns or expectations (Aronson et al. 2007; Baron & Byrne 1991; Kiesler & Kiesler 1969).
- 1.2
- The social influences underlying conformity motivation can be categorized as informational or normative (Cialdini & Goldstein 2004; Deutsch & Gerard 1955). A simple example of informational social influence is a foreign traveler or immigrant carefully watching others to gather data on how to act properly in social situations. Informational social influence often leads to private acceptance – that is, belief in the accuracy of others' opinions and behaviors so that one's own internal attitudes and beliefs are altered (Allen 1965). Normative social influence is associated with the desire to be accepted by others and to avoid exclusion (Deutsch & Gerard 1955). Thus, even when individuals have preexisting views on certain issues, they are likely to adjust their opinions and behaviors based on the statements of other members of a group to avoid being labeled as dissidents. Many examples of normative social influence can be observed in daily life: teenagers are known to speak and act in ways that they would never do on their own or among strangers in order to comply with the perceived norms of their peers. Unlike informational social influence (which leads to private acceptance), normative social influence often results in public compliance involving simple changes in behaviors and opinions to fit with the perspectives of one's community, without changing one's internal attitudes or beliefs (Allen 1965).
- 1.3
- Two core conformity studies illustrating the power of informational and normative social influences are Sherif's (1935, 1936) autokinetic experiments and Asch's (1955, 1956) line experiment. Sherif demonstrated that in environments with high degrees of ambiguity, people tend to infer facts by referring to each other's judgments, resulting in private acceptance. Two decades later, Asch demonstrated that even in situations marked by clear differences in two opinions, individuals still tend to accept opinions that, on their own, they would consider wrong. As he observed,
The tendency to conform in our society is so strong that reasonably intelligent and well-meaning young people are willing to call white black. This is a matter of concern. It raises questions about our ways of education and about the values that guide our conduct. (1955)
It is important to emphasize that Asch's experiments demonstrate that normative social influence leads to public compliance with a group's social norms, but not necessarily to private acceptance. - 1.4
- Ajzen and Fishbein's (1980) reasoned action and Festinger's (1957) cognitive dissonance are central theories in this area of research. Ajzen and Fishbein provide additional support for Asch's assertions regarding the significance of normative social influences. They found that predictions of overt behaviors are often determined by a combination of one's actual views and subjective social norms; accordingly, opinions and behaviors cannot be automatically assumed as reflecting an individual's actual views. Festinger observed that conflicting attitudes and behaviors produce significant psychological distress. To eliminate cognitive dissonance, individuals frequently change their internal attitudes to match their external behaviors. Behaviors are seldom modified to mitigate or eliminate cognitive dissonance because doing so implies the admission of mistakes – an action frequently perceived as intolerable.
- 1.5
- Group norms exert strong influences on collective opinions regarding specific issues – influences that cannot be neglected even when the actual views of individuals remain unchanged (Janis 1982). Pluralistic ignorance,[1] which occurs in groups dominated by powerful normative social influences, is an example of this phenomenon (Miller & McFarland 1987, 1991; O'Gorman 1975, 1986; Prentice & Miller 1993). In the absence of public opposition, individuals who do not support or are undecided about a majority opinion may falsely assume that they are the only dissenters in their groups (O'Gorman 1975). Under the influence of superficial consistency, they may choose or be coerced into conforming to their groups' opinions without realizing that many other group members also disagree with the majority opinion. In other words, their actual views are not affected by their groups' majority opinions. Radical changes to group opinion dynamics occur when opposing individuals assert their personal positions, thus creating competitive scenarios.
- 1.6
- Pluralistic ignorance can be broken by minority influence[2] (Miller & McFarland 1987; Moscovici 1980; Sampson 1991). For example, employees may complain internally about their employers' policies for many years, but never express their complaints publicly. When they do speak out, the accumulation of grievances can result in overly strong statements. Another example is a car accident scenario in which all witnesses fail to take action to rescue the victims; however, when the witnesses are uncertain about how to act, that is more an example of pluralistic ignorance than indifference. Such situations can immediately change when a single individual (known as the "expresser") takes action, giving the majority the courage to express their own true thoughts or the willingness to act.
- 1.7
- Two examples of continuous opinion dynamics models[3] based on the bounded confidence assumption that fail to accurately model the pluralistic ignorance phenomenon are from Hegselmann-Krause (Hegselmann & Krause 2002) and Deffuant-Weisbuch (Deffuant et al. 2000). Certain individuals use their personal opinions to decide whether or not to accept the views of others and to modify their own opinions accordingly. In such cases, opposing individuals in the same group may disregard the discrepancy between personal and majority opinions and maintain their own original opinions. This inhibits the development of superficial consistency in pluralistic ignorance. Further, a continuous opinion dynamics model with a bounded confidence assumption cannot simulate (a) the confusion of collective opinion dynamics, or (b) competition among diverse opinions resulting from a minority of opposing individuals asserting their personal opinions.
- 1.8
- For this project we used attitudes and opinions as they are commonly applied in social simulation and psychology studies to represent the private and expressed thoughts of agents (Petty et al. 1997; Urbig 2003). Attitude is defined as an agent's internal evaluation of events or objects that are not directly observed or perceived. Opinion refers to forms of agent expression, including utterances, emotions, and body language. To simulate the potential effects of informational and normative social influence on conformity, a single opinion attribute within a traditional continuous opinion dynamics model with a bounded confidence assumption was expanded to two attributes – attitude and opinion – to reflect more complex and realistic collective attitude and opinion dynamics. We designed a series of simulation experiments to verify consistency between our proposed model and earlier continuous opinion dynamics models based on the bounded confidence assumption, as well as to reconfirm that group opinions and attitudes have different macro-level dynamics and outcomes. After reviewing the basic properties of our simulation model and discussing sensitivity analyses of two micro-level factors, we will review two issues considered important by sociologists to demonstrate our proposed model's value: pluralistic ignorance and minority influence. These applications demonstrate the model's potential utility for social simulations.
 Attitude and Opinion Dynamics Model
Attitude and Opinion Dynamics Model
- 2.1
- Based on existing conformity research, we used a mix of reasoned action theory, cognitive dissonance theory, and commonly used bounded confidence assumptions to develop a novel continuous attitude and opinion dynamics model.[4] We believe this model is appropriate for use with single issues to explore ways that the private acceptance of informational social influence, and public compliance with normative social influence, affect opinion and attitude dynamics, as well as mutual influences between opinions and attitudes. By "single issues" we mean questions with quantifiable answers – for example, "Do you agree that the death penalty should be abolished?" "Do you agree that a new nuclear power plant should be built?" "What is your level of support for the current President?" or "How likely are you to purchase an iPad Mini or Samsung Note 8.0?"
- 2.2
- As part of the first simulation stage, we constructed a two-dimensional N-by-N cellular automata[5] with Moore neighborhood and periodic boundary conditions to ensure that all cells had equal numbers of neighboring cells (Table 1). Each cell in a cellular automata corresponds to one agent in a social network, and is connected to eight surrounding cells (neighboring agents) to form a small and tightly clustered group; 4–6 cells may overlap. A social network consists of N2 cells and 4N2 links between cells.
Table 1: Simulation parameters for our proposed attitude and opinion dynamics model. Scope Attribute Type Default Description System G constant 2 Normative social influence threshold. U 0.8 Attitude-lacking agent threshold. N 24 Number of cells in cellular automata length and width. RED 0.6 Opinion spectrum constant for public compliance. Agent op variable Agent's expressed opinion on a specific issue as shown by external behaviors. att Agent's private views on the same issue. u constant 0.6 Uncertainty. red Refer to Eq. 3 Opinion spectrum threshold for public compliance. green Refer to Eq. 2 Opinion spectrum threshold for private acceptance. - 2.3
- As shown in Table 1, agents have three attributes: opinion op, attitude att, and uncertainty u – all expressed as real numbers between 0 and 1. Attitude att and opinion op both refer to an agent's view about a specific issue, with att representing the agent's actual view, and op the agent's view as expressed in the form of issue-related behaviors. If an agent's op or att value is very close to 1, then it is said to either possess a strongly positive internal attitude, or to express strong external behaviors regarding the issue. During the initialization stage of a simulation, an agent's op and att are set to the same random real number – that is, 0≤agenti.op=agenti.att=random(0,1)≤1, indicating that the agent's exhibited opinion and internal attitude are consistent. Uncertainty u adheres to the definition of a bounded confidence assumption in terms of the degree of affirmation regarding a particular issue. The closer u is to 0, the clearer and more affirmative the agent attitude regarding the issue, and the less likely the agent will be affected by others' opinions. In contrast, the closer u is to 1, the less clear the agent's attitude regarding the issue, and the more likely it will broadly adopt an external opinion. To meet the requirements of individual experiments, initial uncertainty u values can be identical for all agents, set as random numbers in the interval [0, 1], or initialized via random sampling from a given statistical distribution.
- 2.4
- During each time step, all agents decide whether or not they will exchange opinions with neighboring agents based on surrounding public opinions, and then adjust their opinions and attitudes accordingly. As shown in the following pseudo-code, the process for updating an agent's opinion and attitude consists of four steps:

- 2.5
- In Step 1, individual agents use a K-means clustering algorithm (Hartigan & Wong 1979) to partition their neighbors into k groups (minimum 1, maximum 4). Since a K-means clustering algorithm requires the assignment of a group number k prior to execution, we used the mean square difference to identify the most appropriate g number of surrounding groups (Eq. 1).
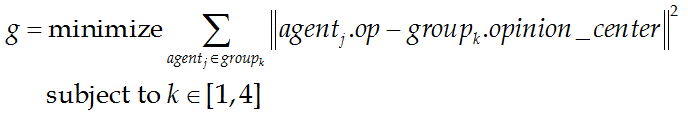
(1) - 2.6
- Next, individual agents use g to determine the existence/non-existence of normative social influences within a group. Overly scattered neighboring agent opinions (g > G) indicate that a mainstream group opinion has not yet been formed. Thus, an agent can freely exchange opinions with its neighbors within a scope based on the bounded confidence assumption (Step 4). However, if neighboring agents have already formed opinion subgroups (g ≤ G), that is an indication of concentrated opinion and public opinion pressure.
- 2.7
- A G group threshold value of 1 indicates that unless a single dominant public opinion subgroup emerges around an agent (i.e., g ≤ 1), it can continue to freely exchange opinions with neighboring agents within the scope based on the bounded confidence assumption. A G value of 2 indicates that such opinions cannot be exchanged freely because one or two opinion subgroups have formed (i.e., g ≤ 2), therefore the agent must select one subgroup to serve as a reference for calculating public opinion magnitude.[6] In other words, a society with a smaller G value is considered more open to multiple opinions, with individuals freely choosing whether or not to exchange opinions with others. A society with a larger G value is considered more authoritarian.
- 2.8
- We assumed that agents with high uncertainty levels (u > U) lack firm attitudes on specific issues, and therefore simply join the largest opinion subgroup (Step 2). Agents with lower uncertainty levels (u ≤ U) are assumed to have firm attitudes on issues, and therefore must be concurrently sensitive to their internal attitudes and external group norms when expressing their opinions. They must carefully select an opinion subgroup that is closest to their own attitudes when calculating public opinion magnitude and executing a corresponding strategy (Step 3).
- 2.9
- In Step 3, three factors (each expressed as a real number between 0 and 1) must be considered when calculating the public opinion magnitude of any subgroup: (a) the number of people in the opinion group, with larger numbers indicating higher public opinion magnitudes (Figure 1a); (b) the consistency of opinions within a group, with greater consistency indicating higher public opinion magnitude (Figure 1b); and (c) the difference between an agent's attitude and public opinion, with larger differences indicating higher public opinion magnitude (Figure 1c). Public opinion magnitude O is calculated as the arithmetic mean of these three factors. The closer public opinion magnitude O is to 1, the greater the pressure on an agent to accept the group's opinion. After calculating O, agents decide whether or not to conform based on their uncertainty levels. Conformation determines whether or not this decision represents simple public compliance, or concurrent public and private acceptance.
- 2.10
- A description of our proposed public opinion spectrum is given in Figure 2a. To simulate psychological mechanisms based on cognitive dissonance and self-perception theories, our model uses a public opinion spectrum with two thresholds, red and green, each expressed as a real number between 0 and 1, and with green ≤ red. The model determines both the potential for change in an agent's opinion and attitude, and the change mechanism based on relationships between public opinion magnitude O and the two spectrum thresholds. The public opinion spectrum is divided into three cases denoted by color: green (Case C), yellow (Case B), and red (Case A). The first case indicates a situation where public opinion magnitude O < green, in which the magnitude is too small to make an agent conform to the majority view in terms of either attitude or opinion. The second category indicates a case where green ≤ O < red, in which a medium public opinion magnitude is sufficient to make an agent change its opinion to follow that of the larger group. After changing its opinion, the agent also changes its attitude to match its new opinion in order to eliminate cognitive dissonance. In other words, the agent's opinion and attitude both move closer to public opinion – an example of the "private acceptance" concept in social psychology. The third (red) category indicates a case where red ≤ O, indicating an extremely large public opinion magnitude and sufficient external reasons for an agent to change its opinion but not its attitude – an example of the "public compliance" concept in social psychology.
(a) (b) (c) 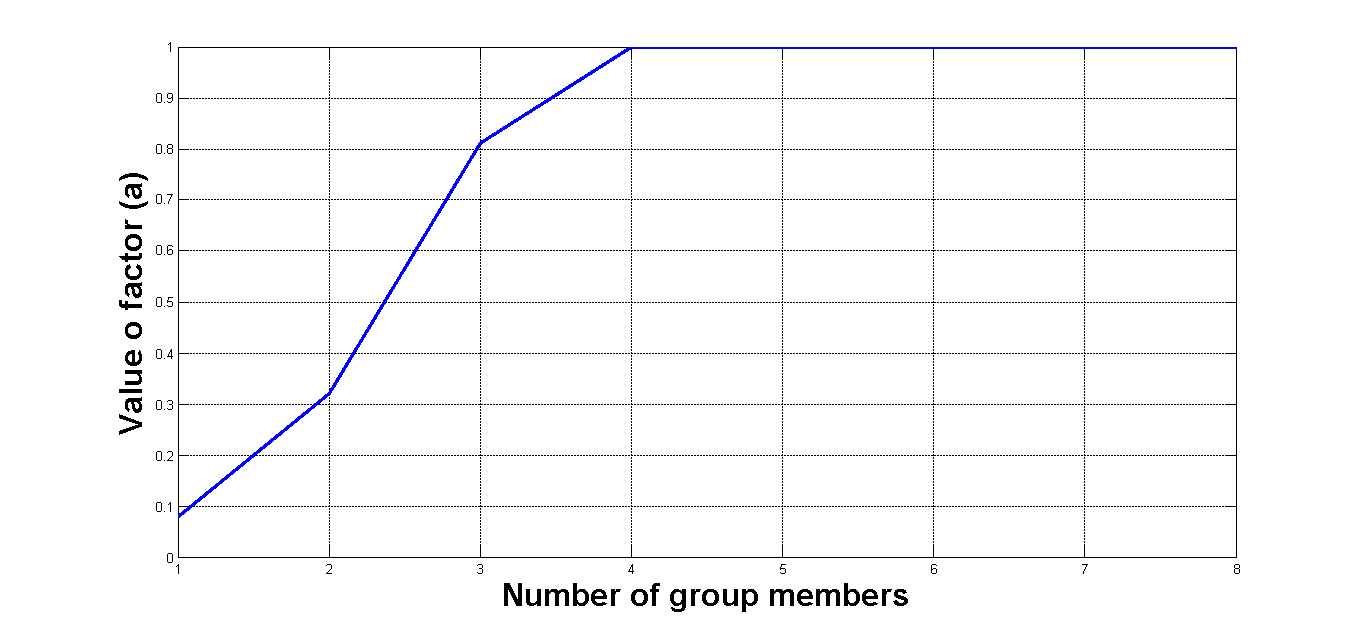

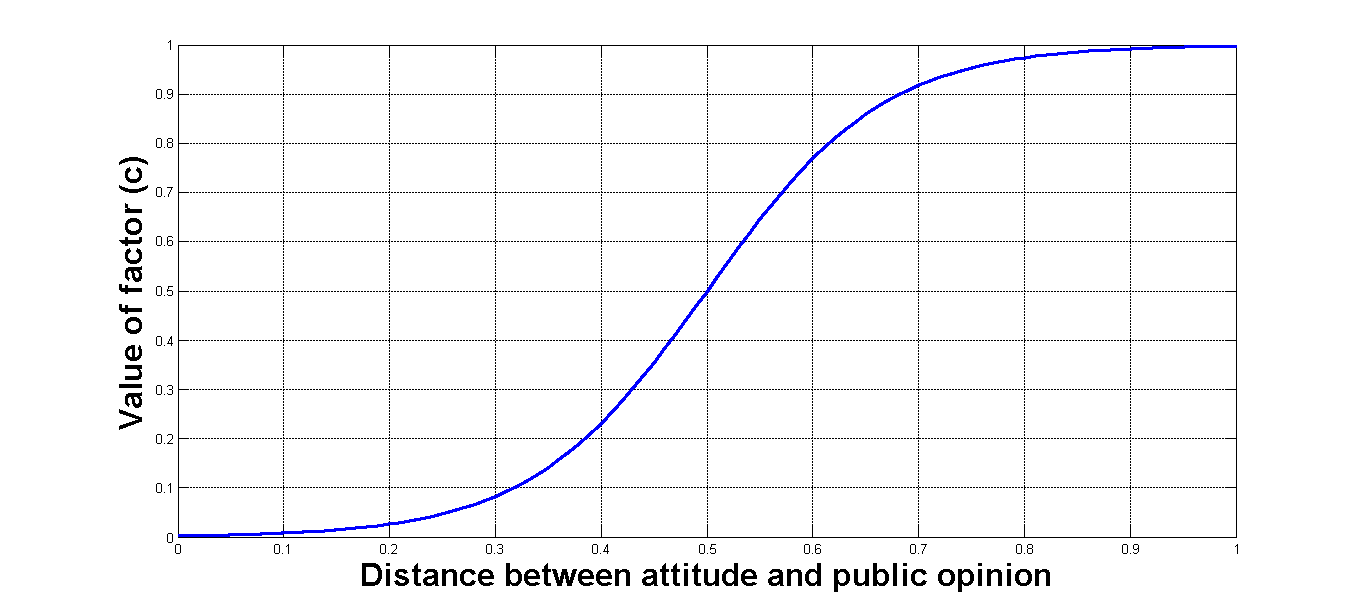
Figure 1. Functions for calculating the strengths of three factors associated with the public opinion magnitude of an opinion subgroup. (a) Opinion group size (number of members); (b) standard deviation of group members' opinions (internal opinion homogeneity); (c) distance (discrepancy) between an agent's private attitude and public opinion. 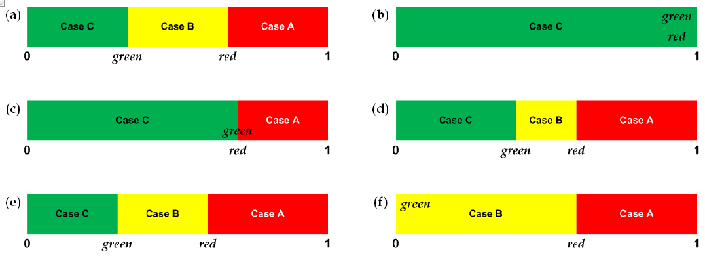
Figure 2. Public opinion spectrum and variations according to different uncertainty values. - 2.11
- Public opinion spectrums for each agent are determined by their uncertainty (u) values (Eq. 2). The green value is higher for agents with lower u, indicating that they are relatively certain of their views regarding the issue in question, and that their opinions will only change if public opinion magnitude experiences a significant increase. Regarding Case A scenarios, the red threshold for each agent is established as a fixed constant RED (Eq. 3). Calculations for the green and red thresholds are as follows:
green = 1 − u (2) 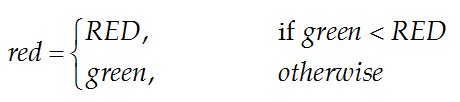
(3) - 2.12
- As shown, when u = 0, then green=red=1 (Figure 2b), indicating that the agent is very certain and insistent on maintaining its attitude – that is, its opinion and attitude will stay the same regardless of the size of the public opinion magnitude O. When 0 < u ≤ 1 − RED, then green=red=(1 − u) (Figure 2c), indicating high agent certainty and strong insistence on maintaining its own attitude. In Step 3, this type of agent has only two possible results: not change at all, or choose public compliance due to normative social influences. When 1 − RED < u ≤ RED, then 1 − RED ≤ green < RED and red = RED (Figure 2d), indicating agreement between an agent's opinion and that held by the majority of all agents. Even if the agent insists on retaining its attitude to some degree, there is great potential for it to be affected by public opinion and to change its attitude. When the influence of public opinion is significantly strong, there is also more potential for the agent to choose public compliance. When RED < u < 1, then 0 < green < 1 − RED and red = RED (Figure 2e), indicating a high level of agent uncertainty, lack of insistence on keeping its original attitude, and greater potential to be affected by public opinion and to change as a result. However, in cases where public opinion is extremely high, the result is that the agent fails to change its attitude, and fails to choose public compliance. When u = 1, then green = 0 and red = RED (Figure 2f), indicating extreme agent uncertainty and the absence of any view regarding the issue being discussed. In such cases, any magnitude of public opinion will result in a complete change in agent attitude and opinion.
 Comparison and Sensitivity Analysis
Comparison and Sensitivity Analysis
- 3.1
- There are two situations in which it is unnecessary to distinguish between opinion and attitude attributes, or to compare opinion dynamics between our model and Hegselmann and Krause's (2002) HK model by manipulating threshold G: when informational social influence is the only factor under consideration, and when an agent's opinion exchange process completely conforms to a bounded confidence assumption. According to our model, normative social influence will not occur as long as G = 0, since surrounding neighbors form at least one group. As shown in Figure 3, the opinion dynamics of our simplified model[7] (with a well-mixed agent population instead of the default and pre-established underlying cellular automata) are consistent with those of the HK model. In both, uncertainty is not assigned a fixed value, but gradually increases over simulation time steps (u=t/100). Also in both models, initial agent opinion values are evenly and randomly distributed between 0 and 1 when time step t = 0. As t increases, agent opinions gradually move toward the center and two extremes. However, when t = 20 or higher, agent opinions at the two extremes move toward the center as uncertainty u increases (u ≈ 0.2). When t = 40, all agent opinions become concentrated near the center of the opinion spectrum, thus forming a normal distribution of consistent opinions.
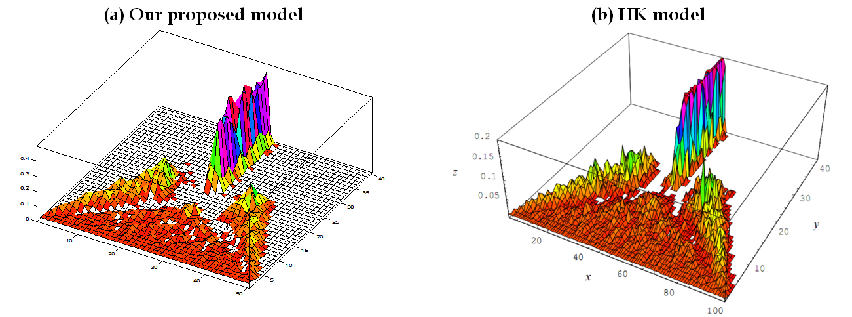
Figure 3. A comparison of simulation results generated by our proposed model and Hegselmann and Krause's (2002) HK model. X-axes represent opinion value. In our proposed model, the x-axis opinion spectrum is divided into 50 intervals between 0 and 1 (i.e., each interval has a value of 0.02). The HK model spectrum is divided into 100 intervals (i.e., 0.01 each). Y-axes denote time steps from 0 to 40, z-axes the probability distribution of opinions. - 3.2
- To determine the influences of uncertainty factor u, we assigned G a value of 2. This is the equivalent of a real-life scenario in which an agent chooses between two opinion groups on a specific issue. In Eq. 3, the default RED value for the red threshold of the opinion spectrum is 0.6 – that is, a public opinion value exceeding 0.6 gives an agent sufficient external justification to comply with that opinion (Table 1). To compare differences between attitude and opinion, the initial values for both micro-level attributes are considered equal (i.e., cognitively consistent).
- 3.3
- We observed three types of attitude and opinion dynamics based on three uncertainty scenarios: low (0 ≤ u ≤ 0.4), medium (0.4 < u ≤ 0.8), and high (0.8 < u ≤ 1). For the sake of simplicity, but without loss of generality of sensitivity, the uncertainty u values of all agents were initialized with very similar or identical values for later sensitivity analysis experiments. In the first scenario, the red and green thresholds are assigned the same 1 − u value (Eqs. 2 and 3) – the smaller the u, the longer the green section and the shorter the red section in the public opinion spectrum (Figures 2b and 2c). Since an agent's public compliance requires a high public opinion magnitude, we assumed that the attitude and opinion dynamics simulated by our proposed model would not produce large discrepancies at low uncertainty levels. As shown in Figure 4a, we observed less than 10 (1.6%) instances of public compliance out of 576 (N2) agent opinion update processes during each time step; those we observed occurred at higher u values. Using our proposed model, we found that this scarcity of public compliance resulted in zero gaps between opinion and attitude dynamics. As shown in Figure 4b, few discrepancies were found between the standard deviations of the two types.
- 3.4
- According to the results shown in Figure 4, if policymakers were to adopt our proposed model to simulate opinion and attitude dynamics for an issue in which people have low degrees of uncertainty, they would observe that the vast majority were affected by informational social influences to change their expressed opinions and inner attitudes (i.e., private acceptance). A handful would be affected by normative social influences to change their expressed opinions, but would not change their inner attitudes (i.e., public compliance) (Figure 4a). Furthermore, the final simulation results would indicate only slight differences in the agents' inner attitudes and expressed opinions – that is, they would be virtually identical (Figure 4b). Thus, for a specific issue in which individuals have low degrees of uncertainty, policymakers could assume that the opinion dynamics of all agents in our proposed model were consistent with their attitude dynamics.
(a) (b) 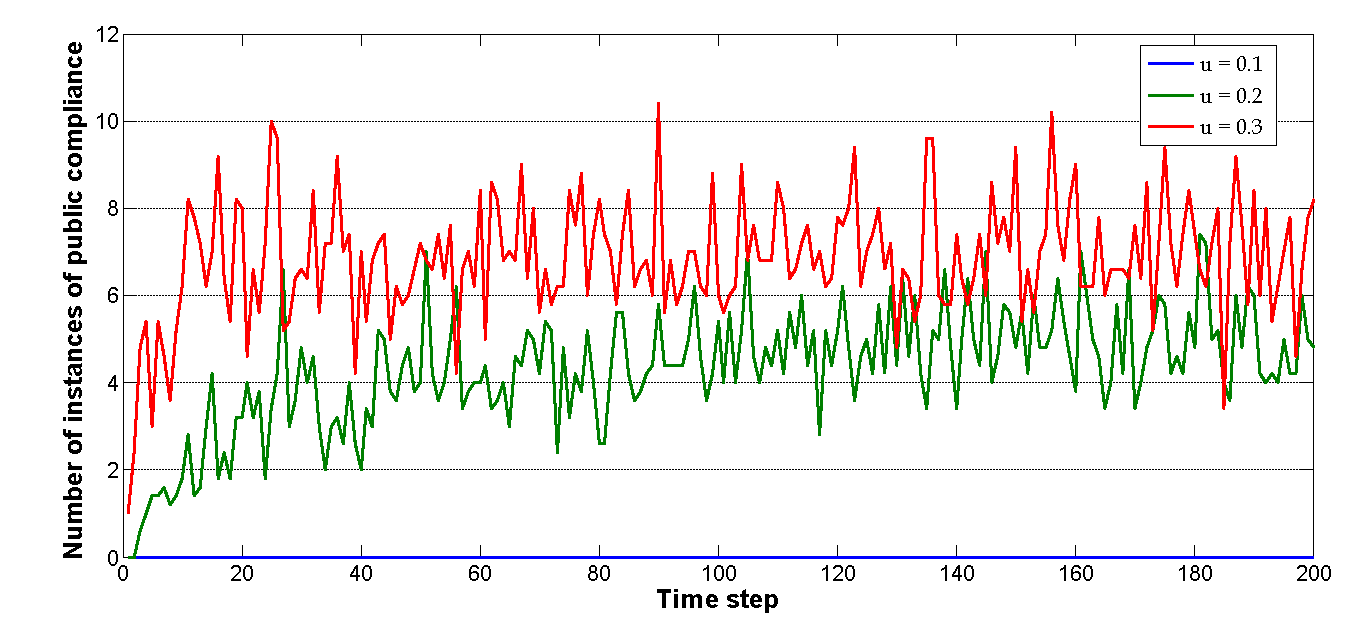
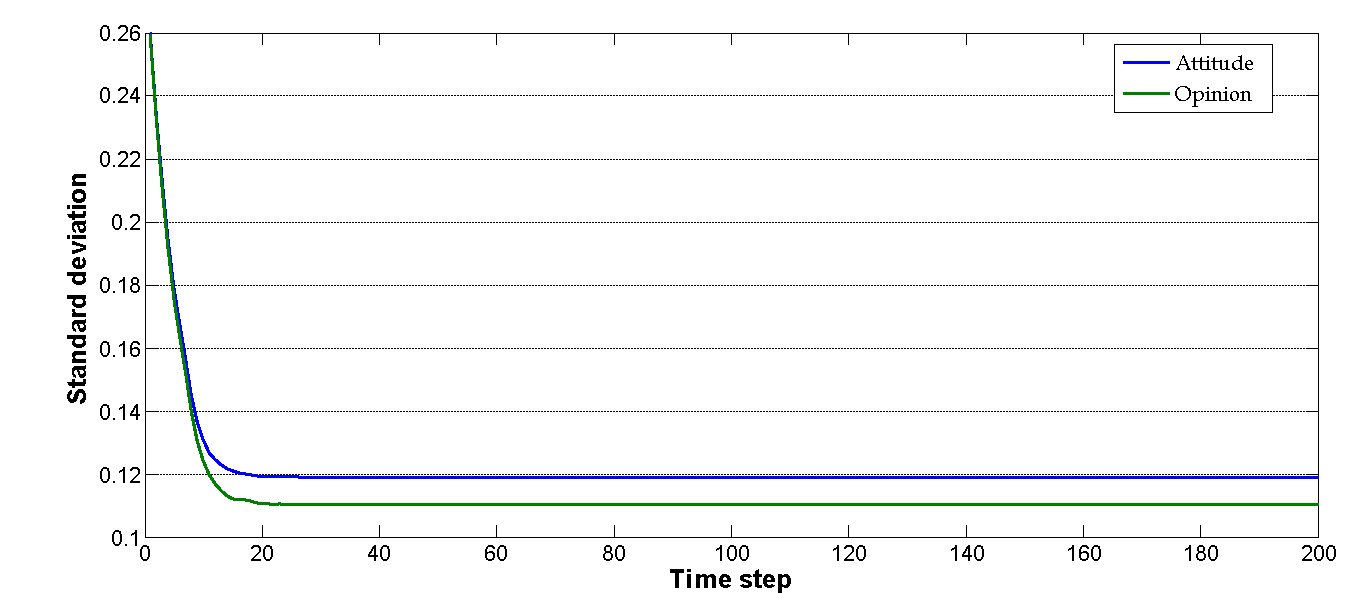
Figure 4. Simulation results under various low uncertainty levels. (a) Comparison of public compliance instances at low uncertainty levels. (b) Comparison of standard deviations of opinion and attitude dynamics when all agent uncertainty u values are assigned a uniform value of 0.3. After time step 20, the average values for both dynamics are the same, with standard deviations within a very narrow range. Note that under the lowest uncertainty level in the left sub-figure (blue curve, all agent u values uniform at 0.1), public compliance is zero for all 576 agent opinion update processes. - 3.5
- At a medium uncertainty level, the green threshold is assigned a value of 1 − u (Eq. 2) and the red threshold a RED default value (Eq. 3). This means that each agent's opinion spectrum contains its own red, yellow, and green sections, with the yellow sections lengthening and green sections shortening as uncertainty u increases (Figures 2d and 2e). In short, the higher the level of uncertainty, the more likely an agent will engage in private acceptance, but when public opinion magnitude exceeds the red threshold, the agent will always choose public compliance. The likelihoods of both public compliance and private acceptance are high in cases of medium uncertainty. Discrepancies between opinion and attitude dynamics are easily observed in these environments.
- 3.6
- The results shown in Figures 5 and 6 indicate that even if all agents have the same initial attitude and opinion settings, during the simulation process they will have different dynamics and outcomes. The main similarity between opinion and attitude dynamics is that both are initially concentrated toward the middle of the opinion spectrum when time step t is between 1 and 10 (Figure 5); the biggest difference occurs during the later stages, when opinion clearly becomes more concentrated than attitude (Figure 6). We applied a standard deviation equation to quantify the range of opinion and attitude dynamics at each time step. As shown in Figure 7a, when the u uncertainty values of all agents were assigned a uniform value of 0.5 during the initialization stage, the standard deviations of opinion and attitude dynamics were 0.0867 and 0.1304, respectively, during the final simulation stage (time step t ≥ 10) – that is, opinion dynamics were more concentrated than attitude dynamics.
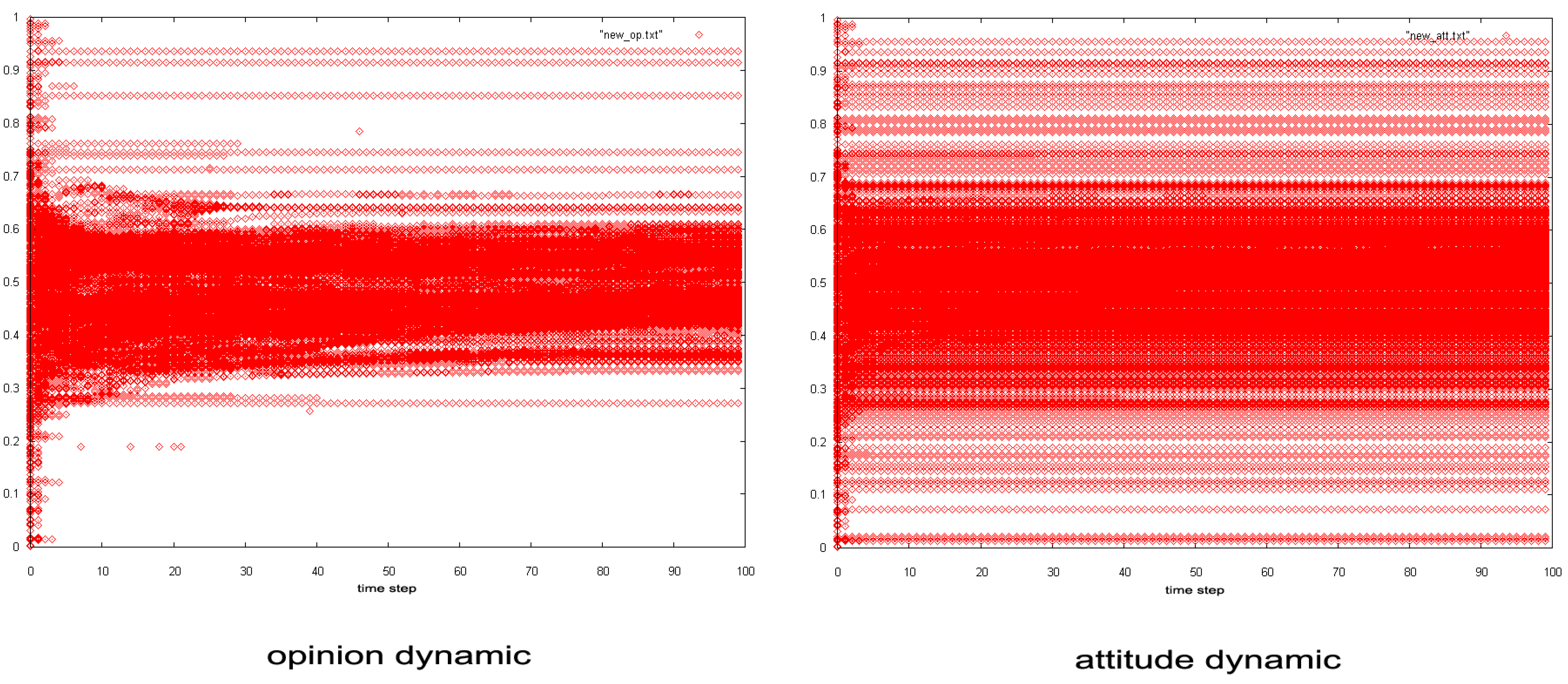
Figure 5. Comparison of opinion and attitude dynamics when all agent uncertainty u values are assigned a uniform value of 0.5. (a) Opinion distribution (b) Attitude distribution 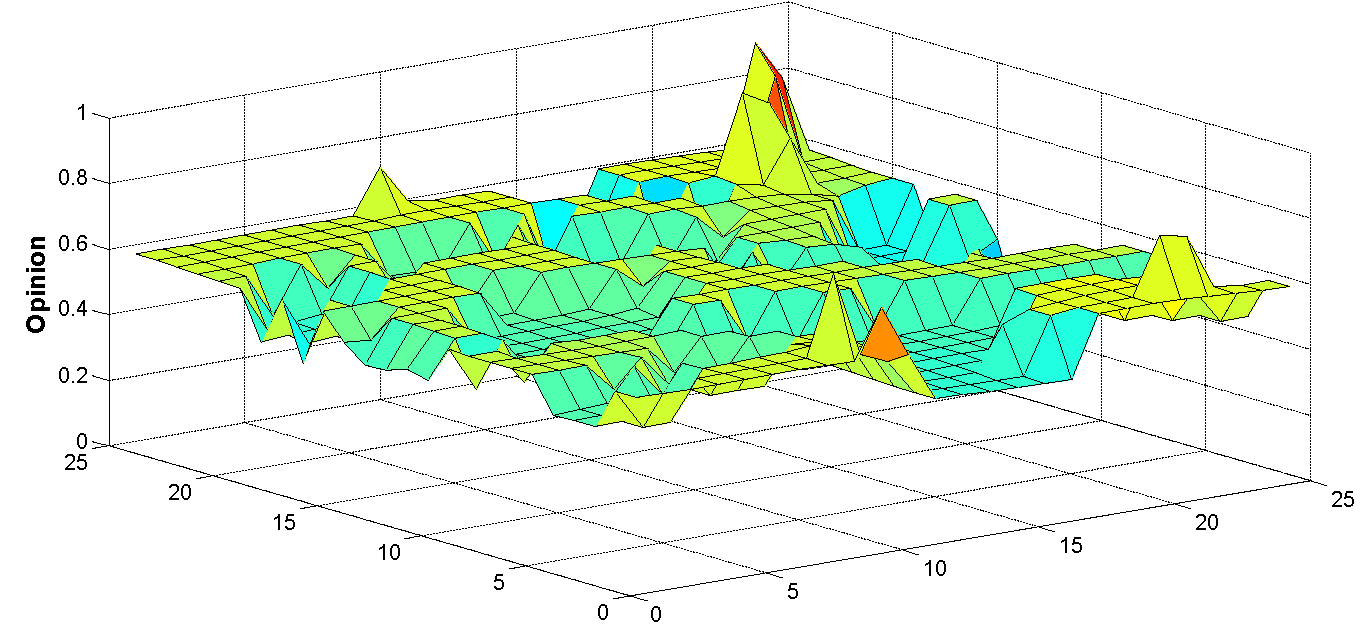
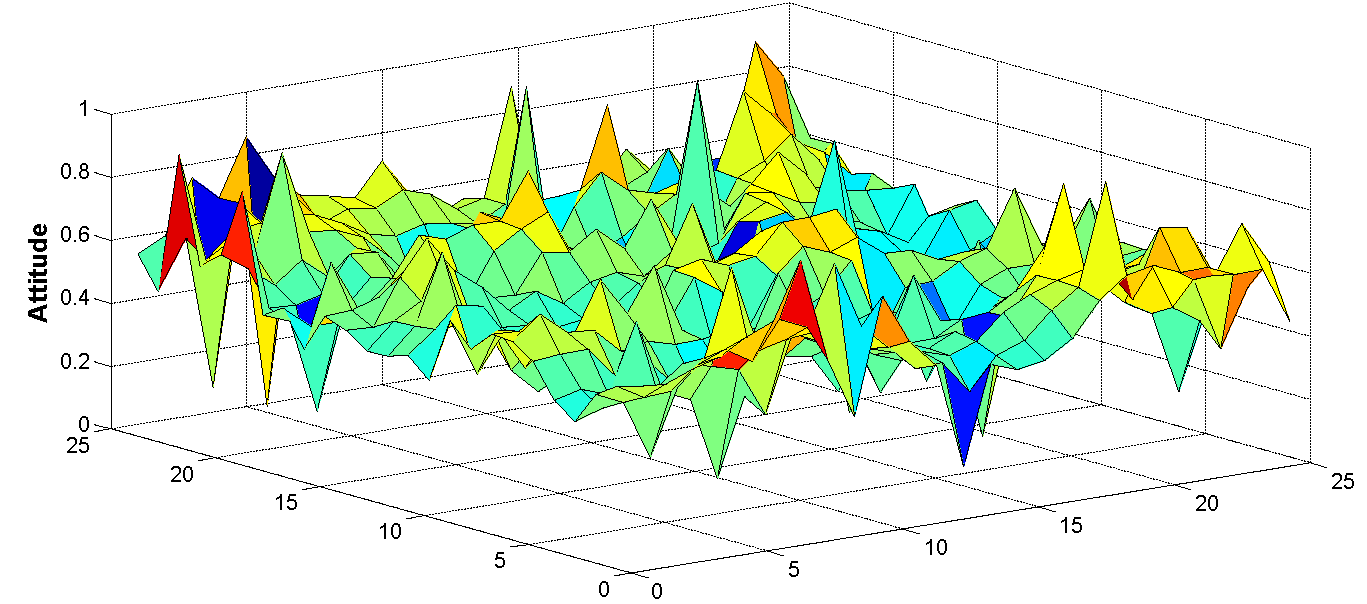
Figure 6. (a) Opinion and (b) attitude values for all agents (all cellular automata cells) in the final stage of a simulation. A coordinate plane consisting of horizontal x- and y-axes denotes a cellular automata. Spikes in the vertical z-axis indicate opinion (left) and attitude (right) values. Attitude values are clearly more dispersed when the uncertainty u values of all agents are assigned a uniform value of 0.5. - 3.7
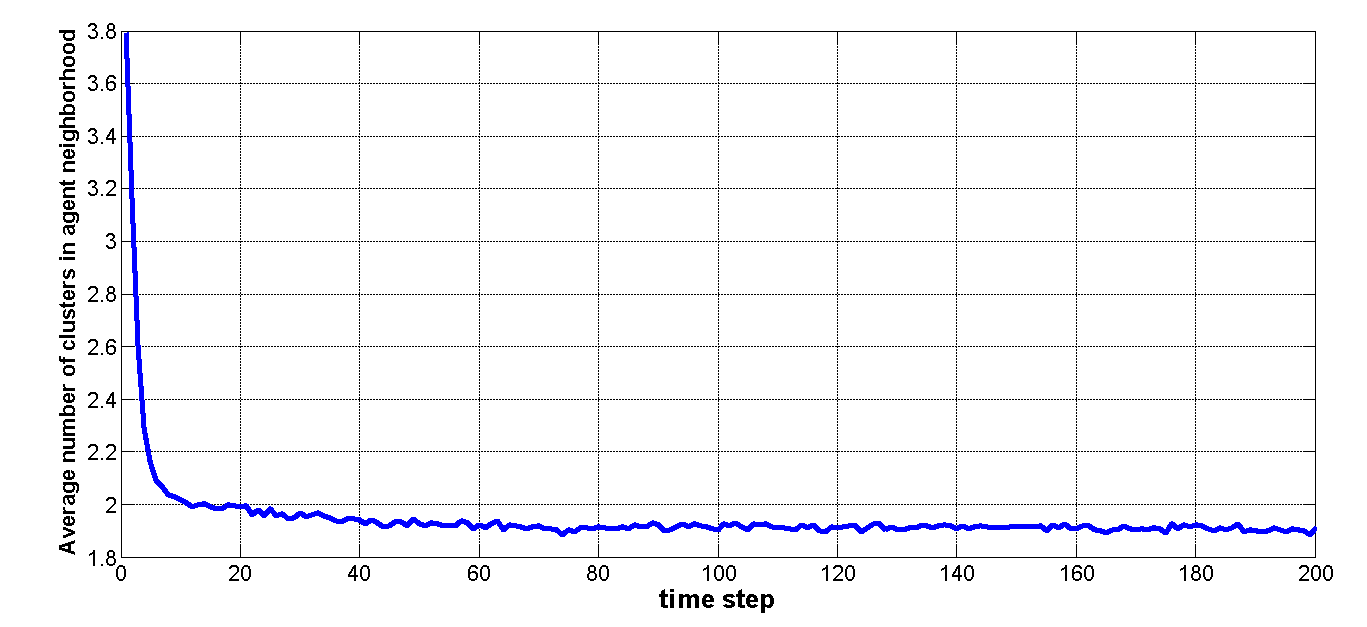
- Opinion dynamics show dispersed distributions prior to the tenth time step, indicating that agents are likely to be surrounded by more than two opinion groups (Figure 7b). In such cases, informational social influence prevails and opinions can be exchanged freely. Over ongoing exchanges, group opinions sharply converge after the tenth time step, and the number of opinion groups sharply decreases. In most cases, when the number of surrounding opinion groups falls to 2 or 1, the amount of normative social influence sharply increases (Figure 7c).
- 3.8
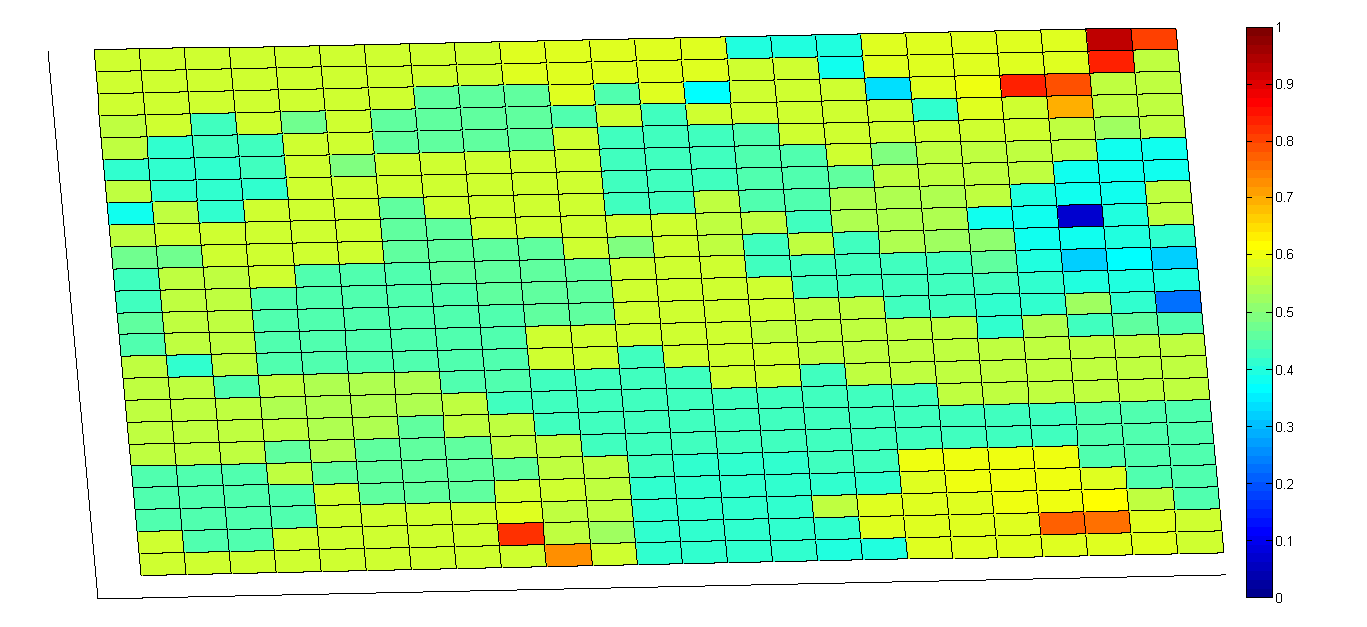
- When opinions move toward the center of opinion spaces and only two clusters (g = 2) remain, normative social influence starts to force group members toward the center. However, clusters stop moving toward each other, resulting in coexistence between formerly competing clusters. Note that the two cluster centers in Figures 7d and 7e are slightly closer to 0 and 1.
- 3.9
- Our simulation results are similar to real-life scenarios in which individuals hold customary views on specific issues that have been discussed over a period of time. When they express opinions in a group setting, they often take social norms into consideration, even if they are not in complete agreement. For most people, no major differences exist between the two, therefore their opinions gravitate toward public opinion. For example, in many elections the majority of centrist voters do not take strong political stances, which is similar to the discussion and simulation experiments we discussed in an earlier section. To a certain degree our simulation results demonstrate pluralistic ignorance – that is, even though group members appear to express consistent opinions or behaviors, they may not necessarily share the same private attitudes (Figures 5 and 6).
(a) (b) 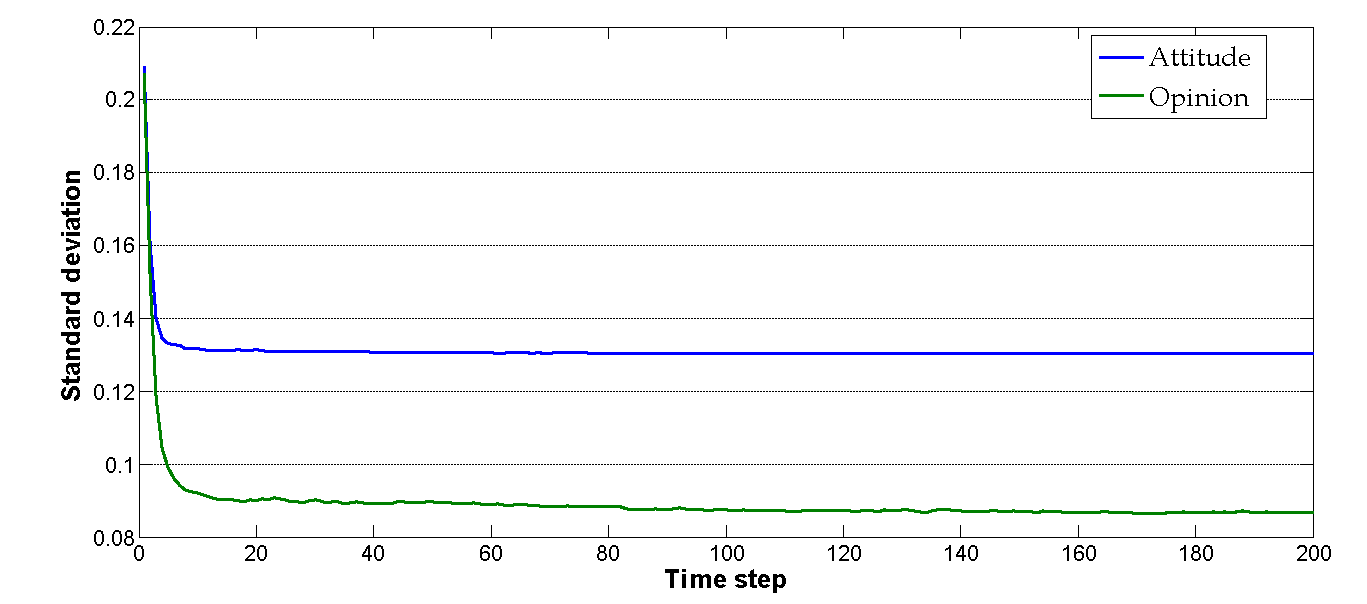
(c) (d) 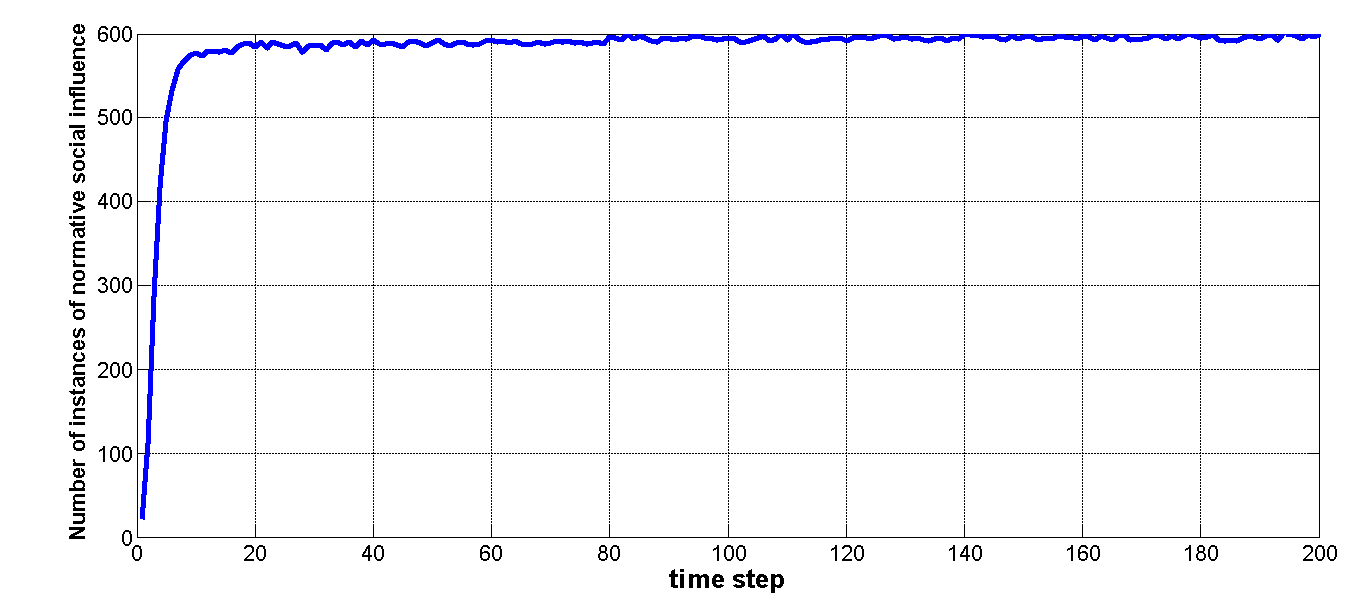
(e) 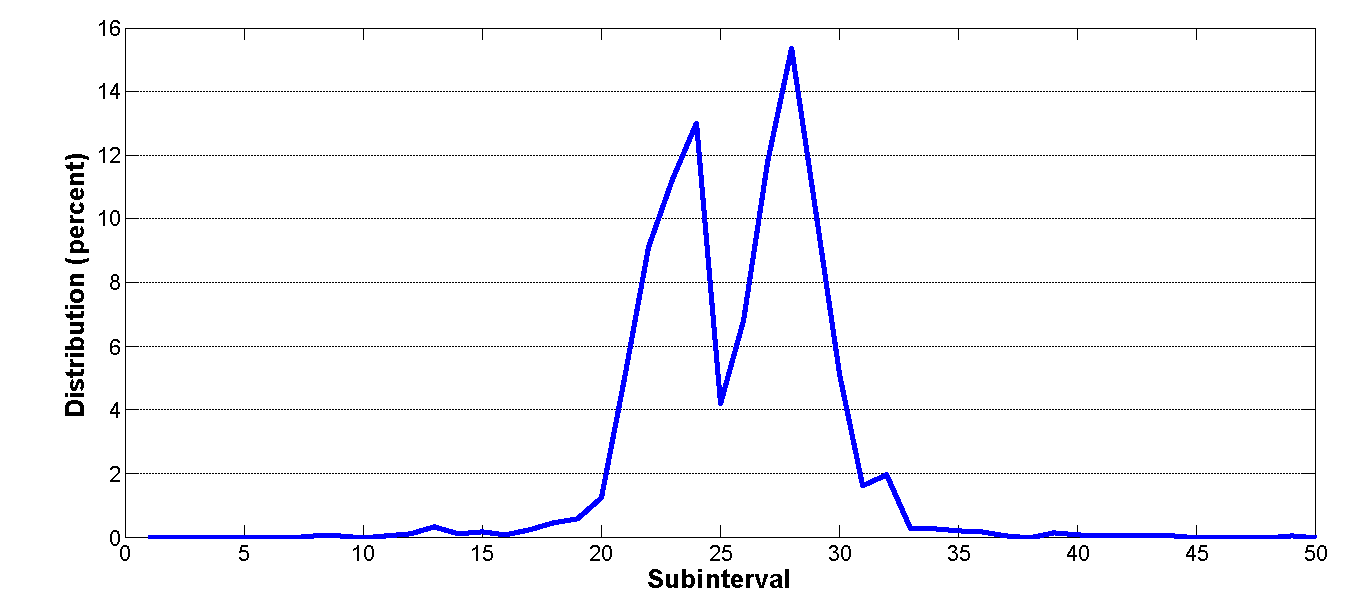
Figure 7. Simulation results when the uncertainty u values of all agents are assigned a uniform value of 0.5. (a) Comparison of standard deviations of opinion and attitude dynamics. After time step 10, the average values for both dynamics are the same, but their standard deviations are significantly different. (b) Number of clusters surrounding an agent plotted against time. (c) Instances of normative social influence plotted against time. (d) Birds-eye view of overall final stage opinions after stability is achieved at time step 199. Most individuals are slightly for or slightly against the issue in question. Note that individuals holding extreme views form several small clusters. (e) At time step 199, all individuals are divided into two similar clusters. - 3.10
- When facing public opinion pressure, agents with high degrees of uncertainty do not calculate public opinion magnitude (i.e., agenti.u > U), but follow the opinion that has the largest number of supporters (Step 2) – in other words, attitudes and opinions move in the same direction with no discrepancies. According to these three uncertainty levels, the greatest discrepancy between attitude dynamics and opinion dynamics occurs when the population in question has a medium level of uncertainty.
- 3.11
- Our simulation results are consistent with real-life scenarios. Imagine a society of individuals with no personal opinions who believe whatever they hear – in other words, their only rule is to follow the actions of others, therefore no discrepancies exist between their attitudes and opinions. In contrast, it would be difficult to formulate public opinion in a society where most individuals do not follow others' opinions, since any localized public opinion would be insufficiently strong to encourage self-confident individuals to comply, as opposed to expressing their attitudes openly and directly. Societies often exist at a medium level of uncertainty, with minorities capable of comprehending complex issues or handling ambiguity. The majority have their own ideas, but are neither certain nor confident about them. When there is no obvious pressure to follow public opinion, individuals in societies marked by medium levels of uncertainty may voluntarily exchange ideas with others and determine how much they want to integrate others' opinions into their own. However, when strong pressure exists to follow public opinion, most people choose public compliance over private acceptance – a common occurrence in daily life.
 Pluralistic Ignorance and Minority Influence in Sociological Simulations
Pluralistic Ignorance and Minority Influence in Sociological Simulations
- 4.1
- In this section we will discuss the potential value and applications of our proposed model in terms of pluralistic ignorance and minority influence. Real-world newcomers tend to comply with existing norms and group consensus, even though they do not fully agree with them. To observe the effects of a small number of newcomers on an opinion group that has already achieved consensus on a specific issue, we randomly selected 7 (≈1%) agents from a two-dimensional cellular automata and reset them so that their opinions and attitudes were assigned the same random real number. Uncertainties were assigned according to random sampling from a normal distribution with a mean of 0.5 and standard deviation of 0.025. The opinion exchange process was then restarted (time step t = 0) (Figures 8a and 8b).
- 4.2
- Newcomers in such scenarios were likely to comply with public opinion, since they were dealing with group norms that had already been established. When the model regained stability, the opinion dispersal level did not change (Figure 8a), and the attitude dispersal level increased slightly (Figure 8b). After multiple iterations, opinion dispersal increased slightly and then stopped (Figure 9a), while attitude dispersal continued to increase over time (Figure 9b). In other words, a growing number of group members were identified as holding different opinions from what they expressed publicly. However, in light of their neighbors' expressions of support, these individuals still maintained public conformity, meaning that the degree of pluralistic ignorance remained unchanged. In the previous simulation experiment, it was important to ensure that two newcomers with similar views were never situated as neighbors, since that might increase the potential for resisting compliance with public opinion, for establishing small opinion clusters, and for increasing opinion dispersal.
- 4.3
- In societies marked by pluralistic ignorance, individuals may decide to tolerate the status quo because they do not see others taking action. The appearance of only one individual who is willing to speak out has the potential to create a viable structure for public complaints. These initiators disrupt group homogeneity, thus supporting the decisions of others to overcome pluralistic ignorance. Results from a simulation of this type of scenario are shown in Figure 10. We initially assumed that most agents had an opinion value of 0.9 and attitude value of 0.5, and that approximately 1% of all agents ("pioneers") had 0.5 opinion and 0.5 attitude values. We expected that in the absence of these pioneers, all newcomer agents would be surrounded by neighbors with 0.9 opinion values, and therefore continue to conform to public opinion; this would result in ongoing discrepancies between opinion and attitude. However, if a small number of pioneers start to express their shared opinion, their surrounding neighbors are likely to follow them because the opinions of the pioneers and their neighbors are similar. Such a chain reaction supports the overturning of group opinion within a short time period. As shown, it only takes one individual to break group homogeneity and to exert disproportionate influence. This phenomenon is difficult to explain when observations are limited to expressed opinions and behaviors.
- 4.4
- There are many real life examples of minority influence that do not involve pluralistic ignorance, including environmental, human rights, and women's rights activism. To demonstrate how a minority view can influence the majority, we conducted a what-if experiment[8] in which the opinion group's threshold G = 0 – that is, members of a society are completely free to discuss ideas because no normative social influence exists. In such cases, all opinions can be considered as long as they sit within the public's confidence bounds; as ideas are exchanged, the public is gradually influenced by extremist views. In contrast, the presence of a two-dimensional cellular automata means that minority viewpoints must be disseminated one-by-one, resulting in a slow change process (Figure 11a) and increasing the importance of minority access to media (Figure 11b). In the extreme example shown in Figure 11b, a dictator or small number of politicians can control public opinion by controlling the media (Figure 12) – that is, by disseminating ideas beneficial to their regimes, and banning all public discussion of sensitive issues in an effort to prevent the formation of a collective opinion.
(a) Opinion distribution 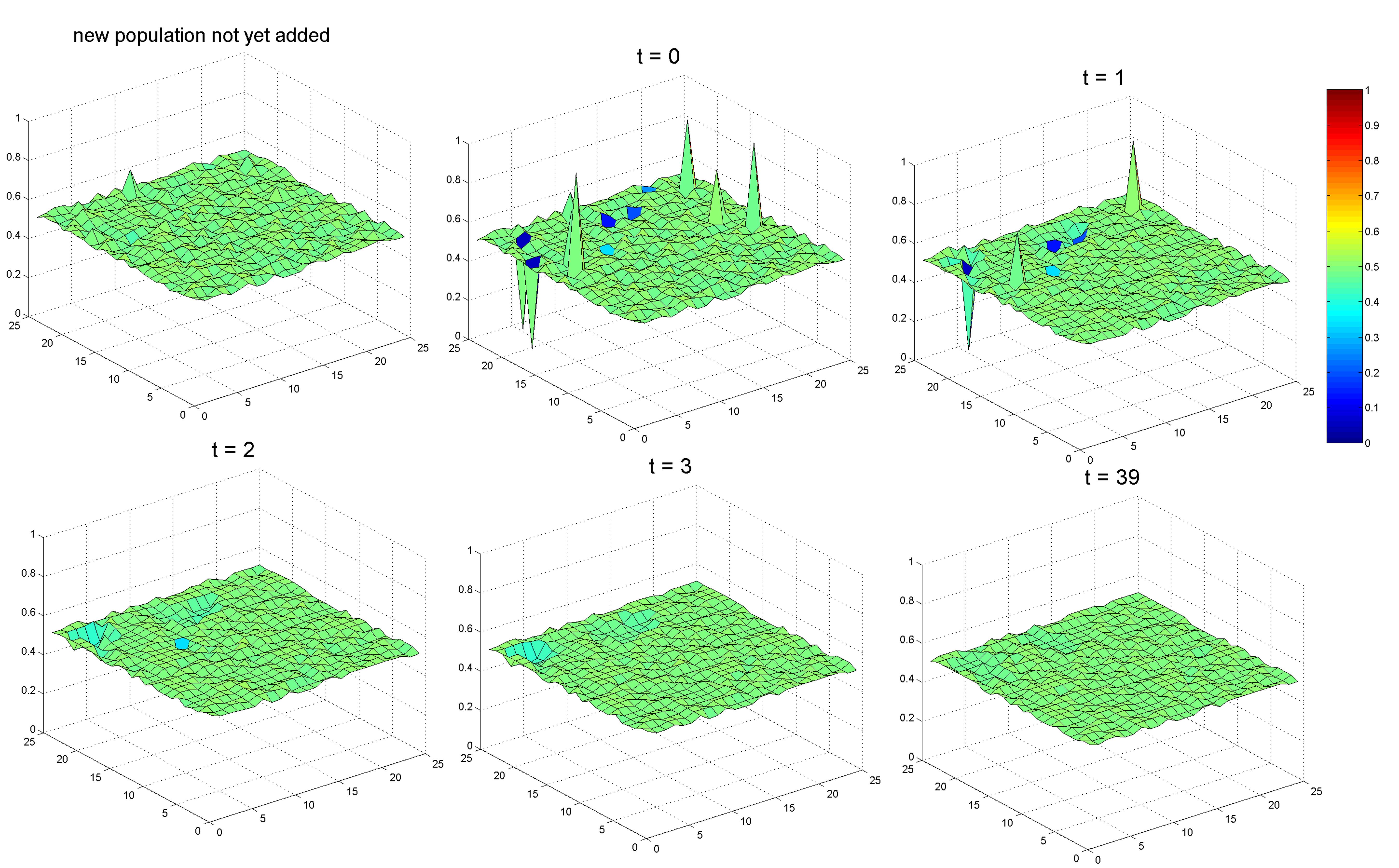
(b) Attitude distribution 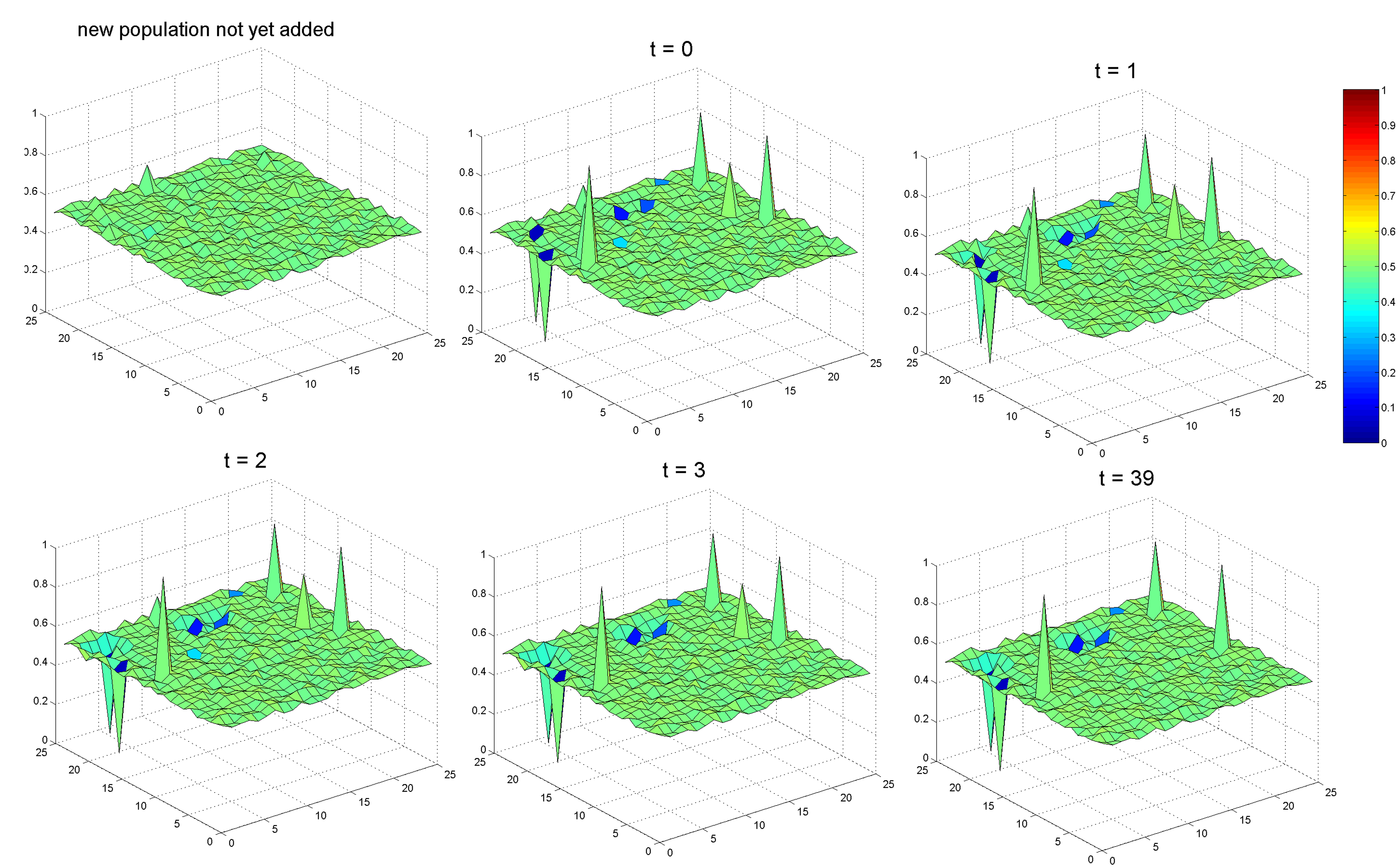
Figure 8. (a) Opinion distributions before and after a small number of newcomers are added to the original population. In this case, opinion returns to consensus. (b) Attitude distributions before and after a small number of newcomers are added to the original population. In this case, attitude dispersal increases slightly. (a) (b) 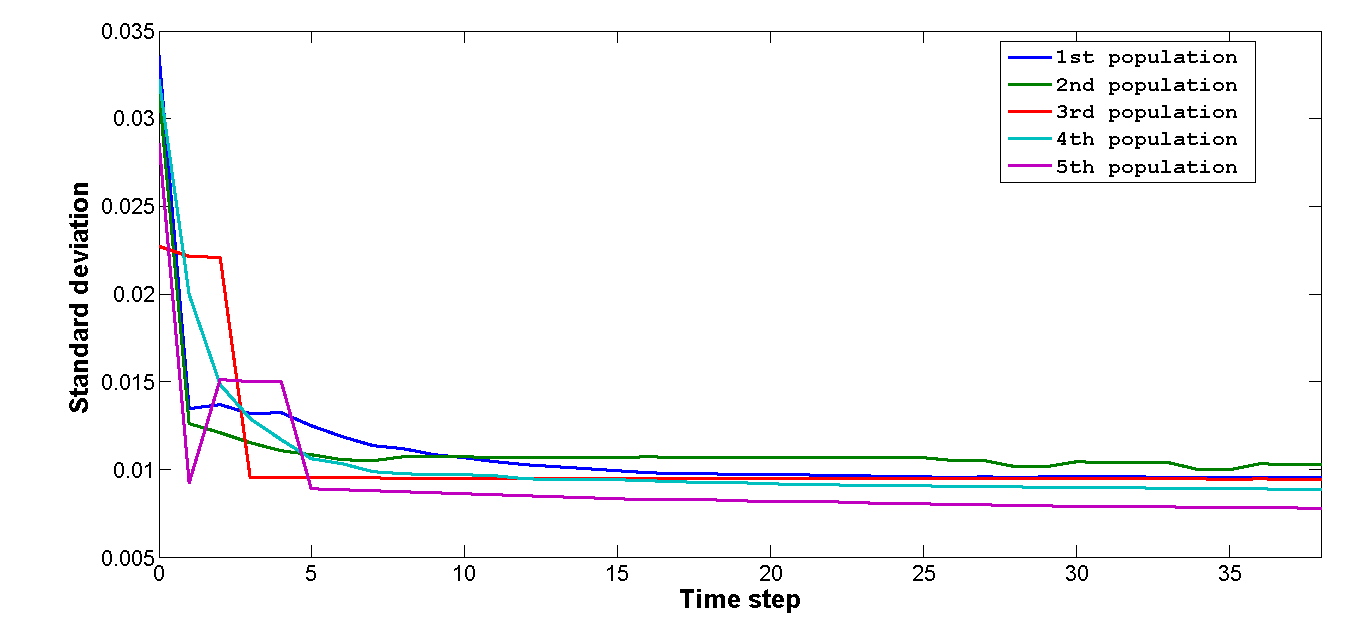
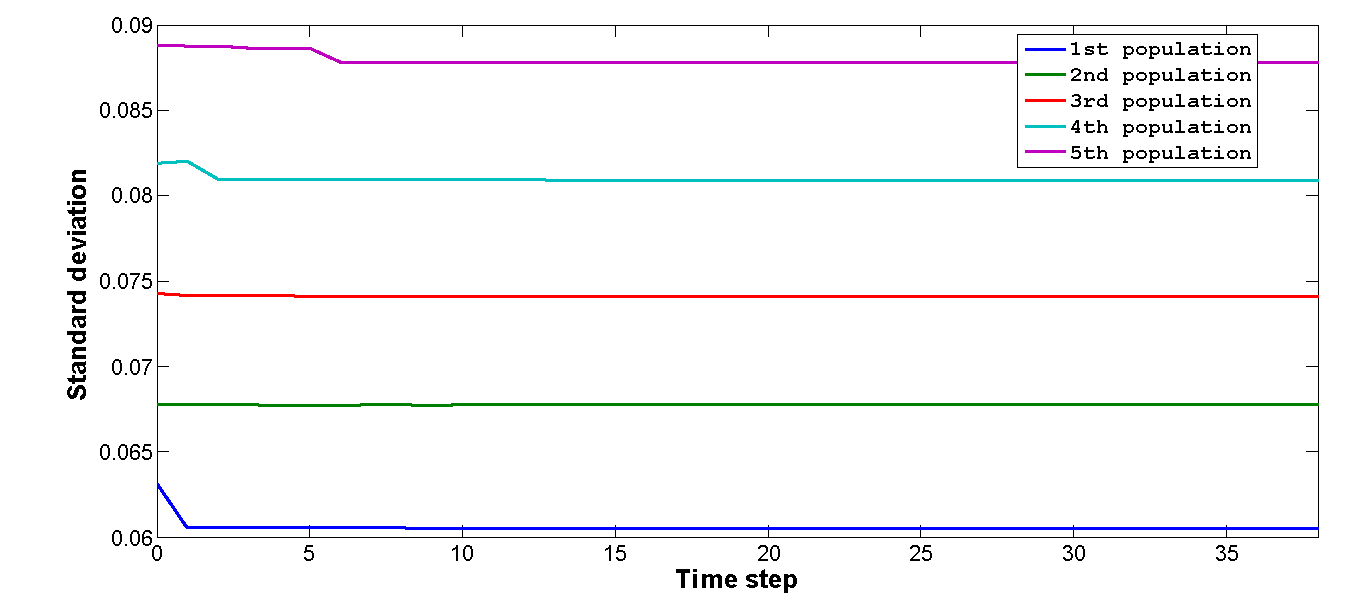
Figure 9. (a) Change in the standard deviation of opinion dynamics following the addition of five new agents – a slight increase. (b) Change in the standard deviation of attitude dynamics following the addition of five new agents – a gradual increase. 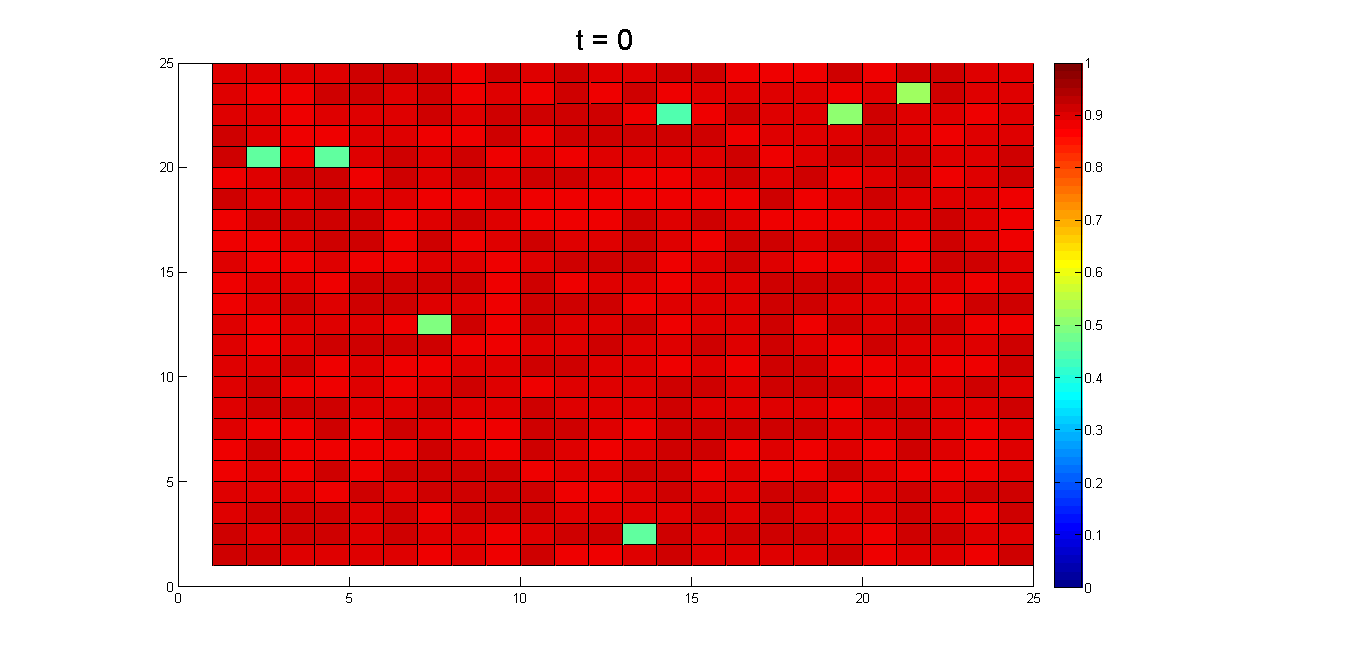
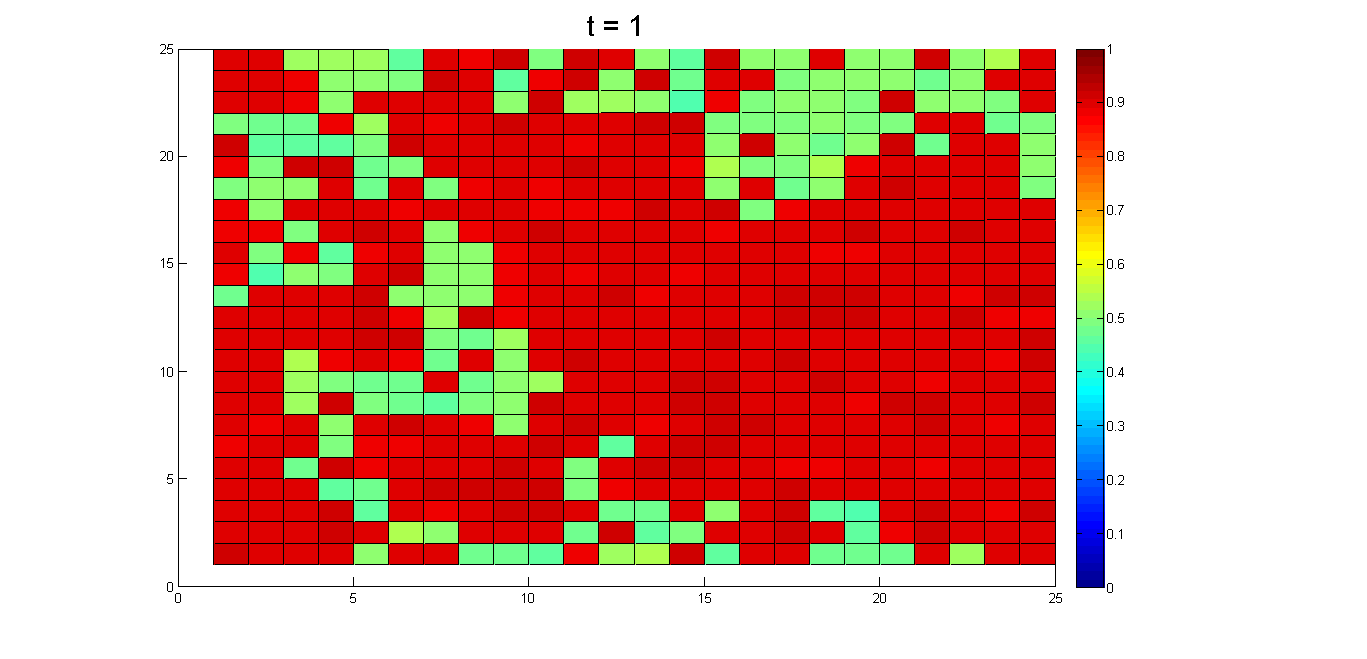
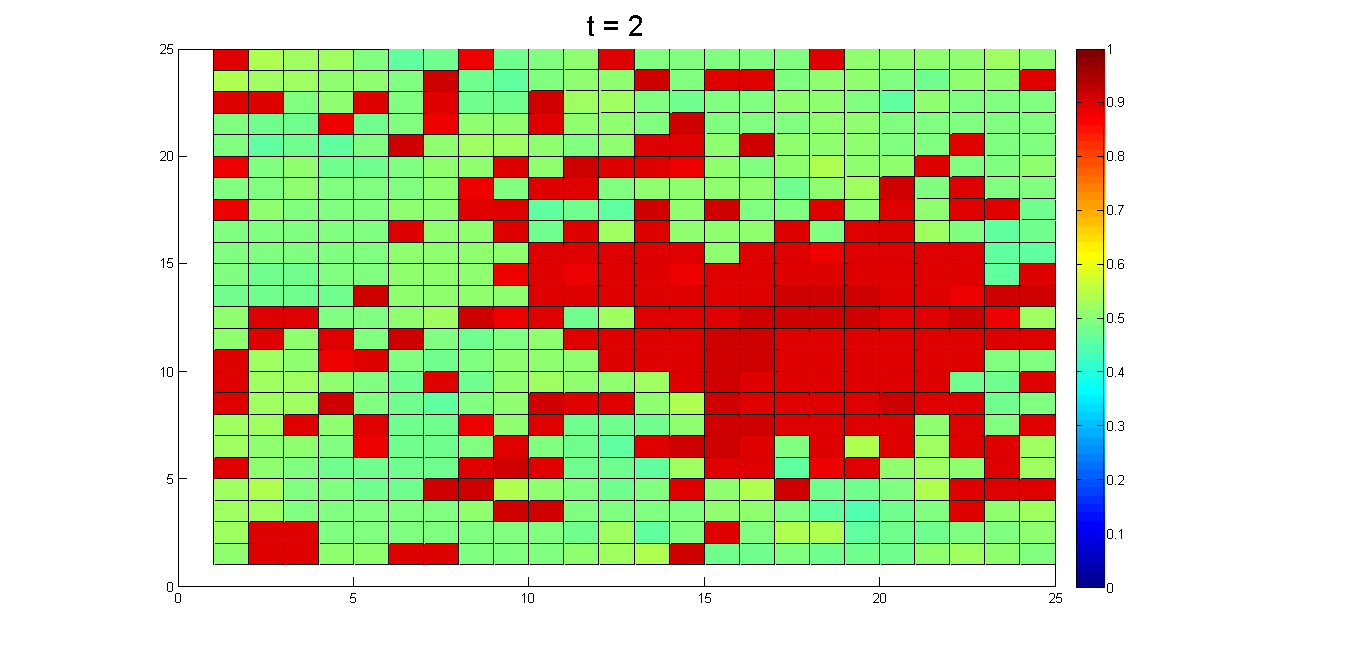
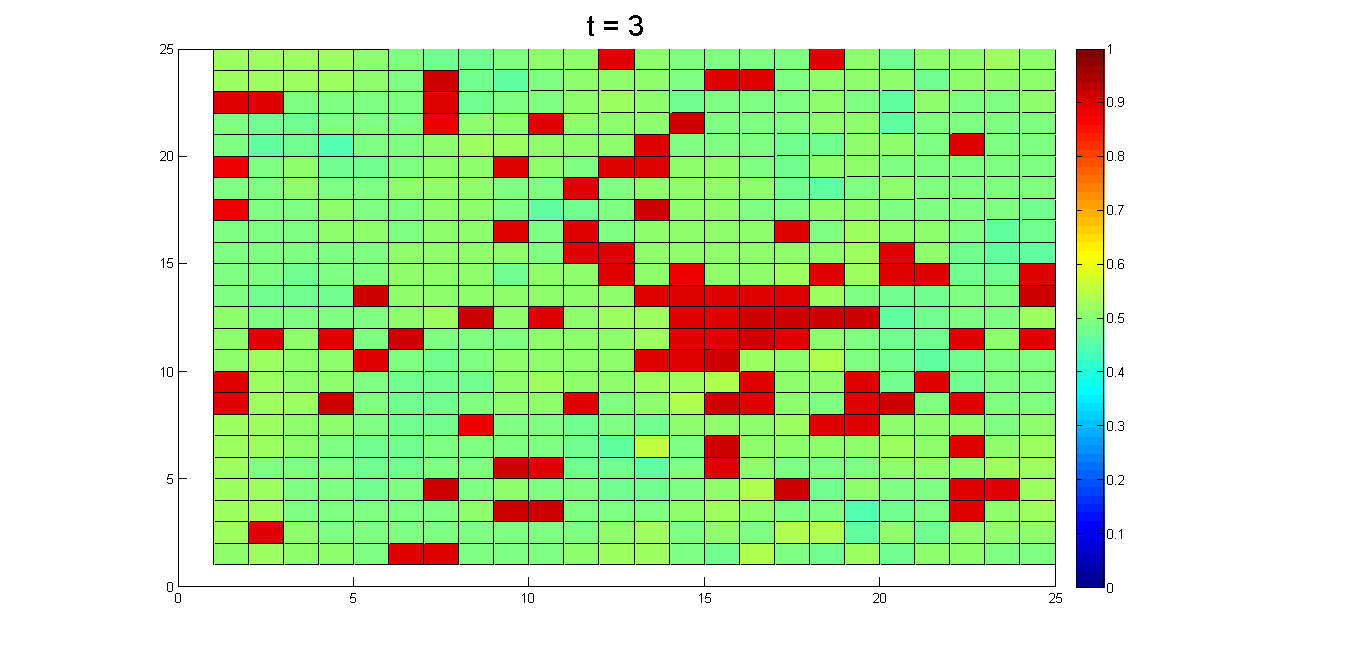
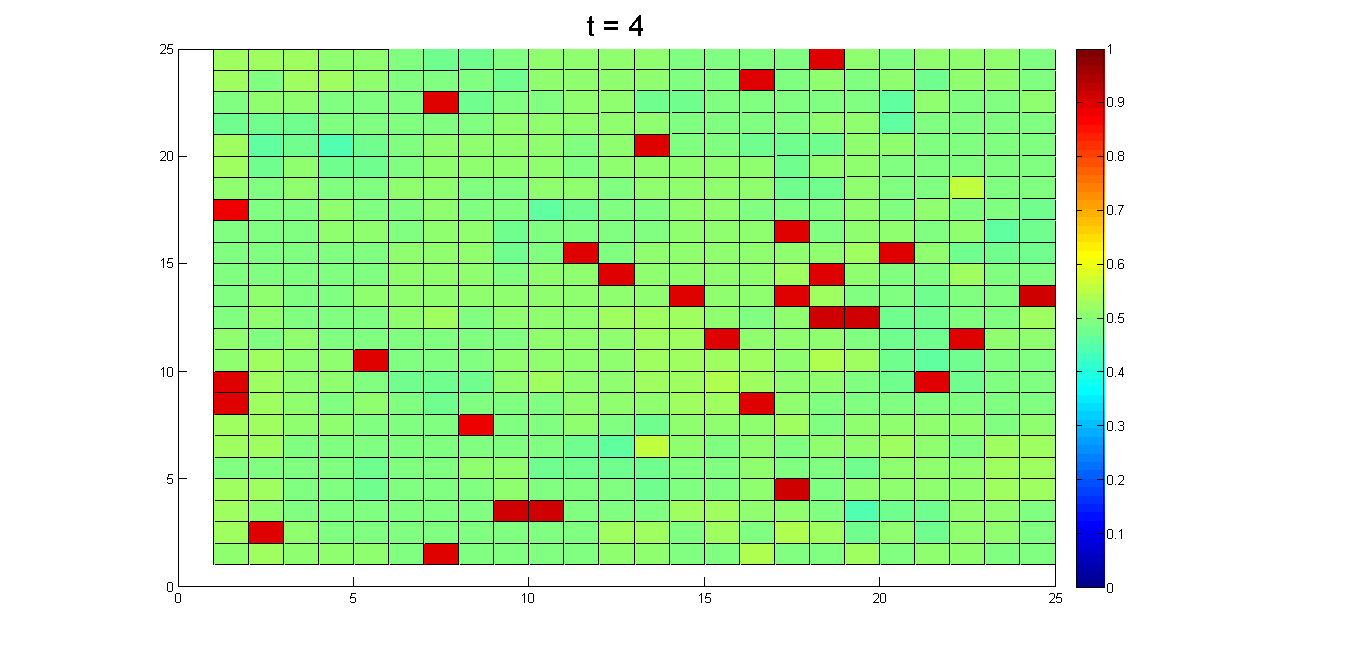
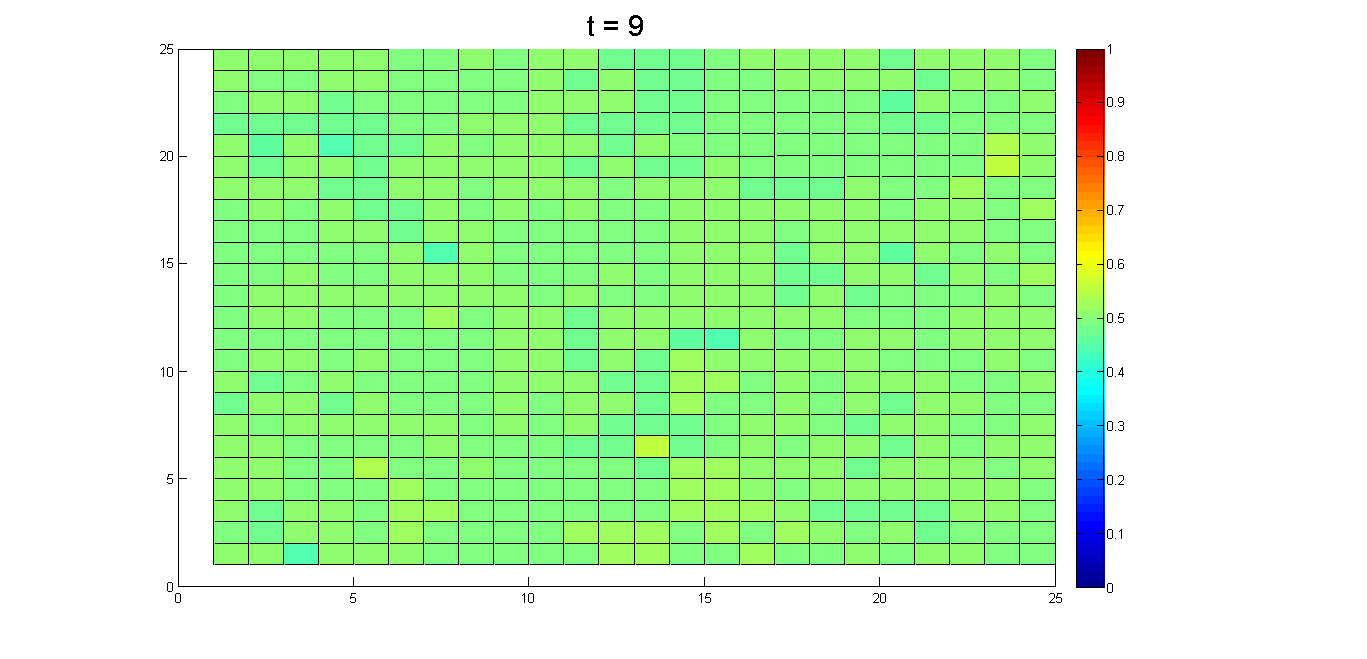
Figure 10. Pluralistic ignorance elimination process. (a) 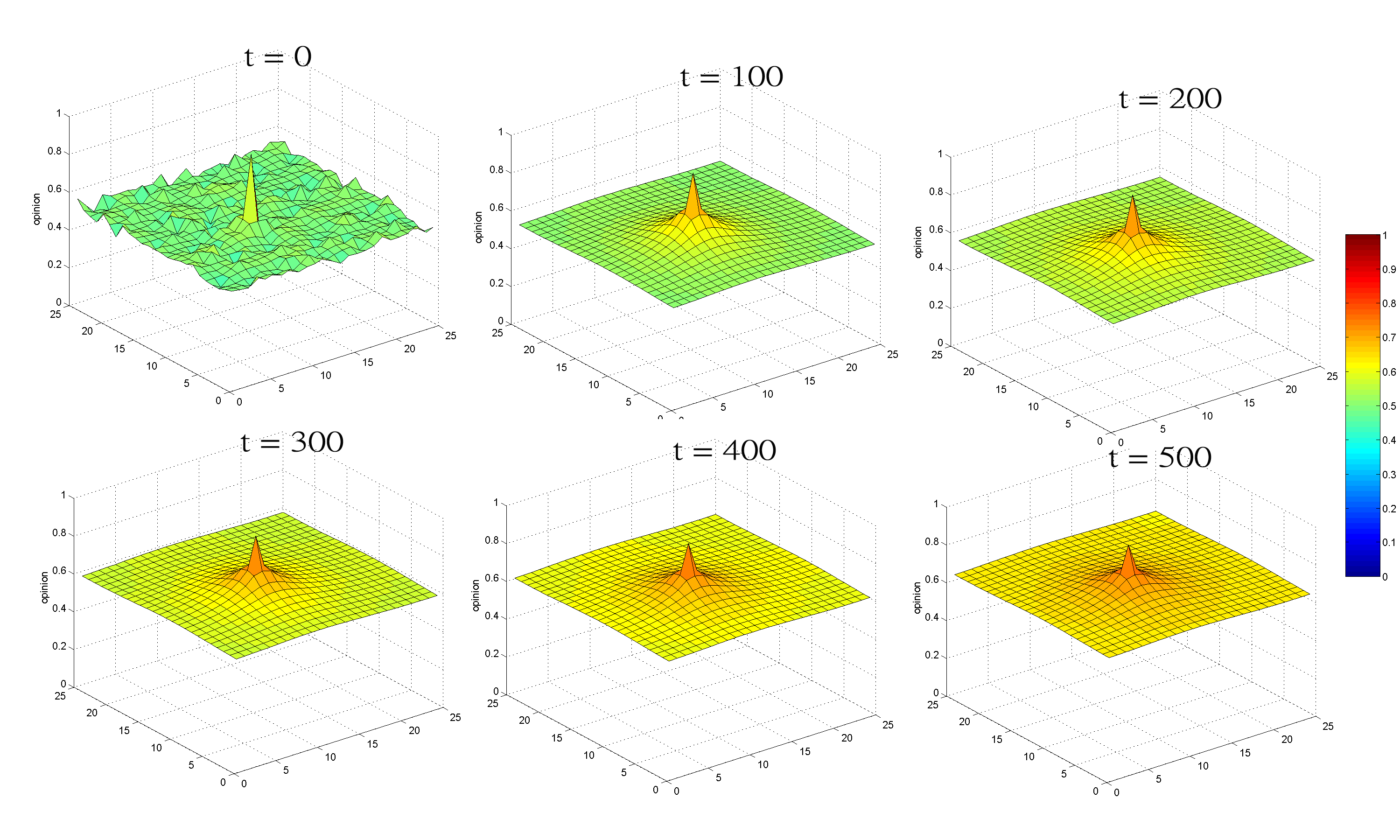
(b) 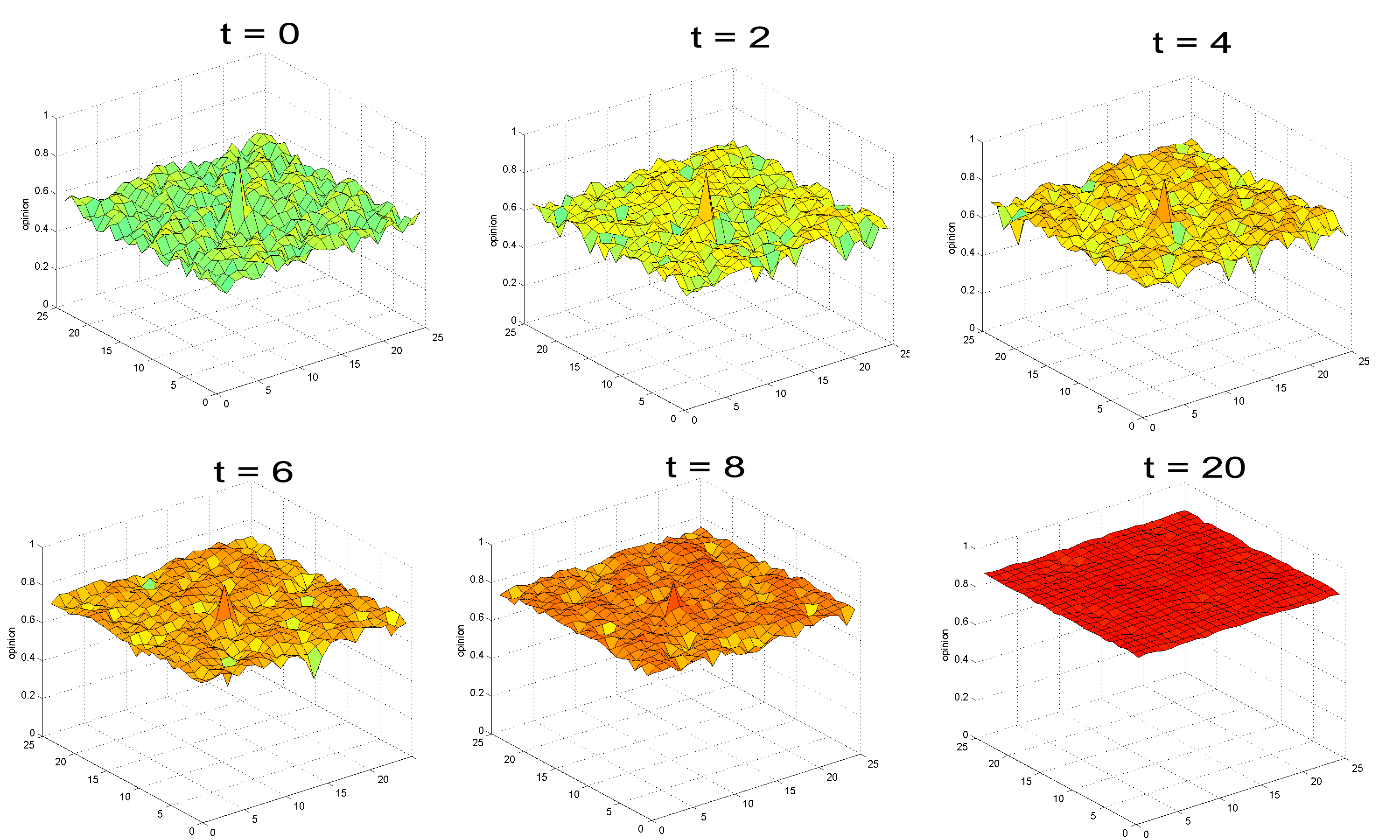
Figure 11. (a) Opinion distribution when members of a society are completely free to discuss ideas. We initially assumed that the minority would consist of single agents only. Bulge represents minority time step 0. (b) Opinion distribution when individuals in a society are free to discuss ideas, and when the minority has access to the media for idea dissemination. 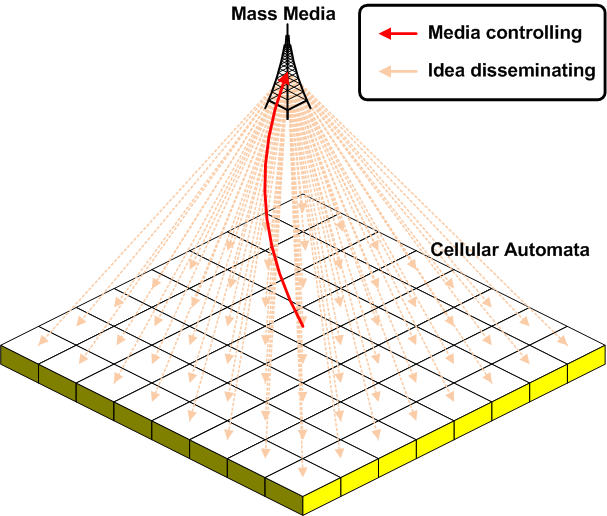
Figure 12. A concept model of the mass media controlled by a dictator or small number of politicians.
 Conclusion
Conclusion
- 5.1
- We incorporated public compliance with normative social influence into a continuous opinion dynamics model with a bounded confidence assumption to explore collective opinion and attitude dynamics. According to our simulation results, if a small number of newcomers are added to a group in which a consensus has already been achieved, and the newcomers' initial opinions and attitudes are randomly distributed, most of the newcomers will choose public compliance due to the magnitude of public opinion. Consequently, all group members will express identical opinions, but their attitudes may not be identical. Attitudes will become more scattered as the process is repeated, even if opinion homogeneity remains stable – that is, the degree of pluralistic ignorance will remain unchanged. If most people have the same attitude, a small number of individuals whose opinions are the same as the general public's may cause group opinion to be overturned.
- 5.2
- In our proposed simulation model, when normative social influence exists and when opinion and attitude values are equal, it is very difficult for individuals with a minority view to change public opinion. However, we acknowledge that in the real world there are many examples in which a small number of individuals have successfully influenced public opinion, therefore we conducted a what-if experiment that allowed for public opinion to be affected by a minority viewpoint – that is, permitting all individuals to openly discuss their opinions, and controlling the media so as to disseminate ideas beneficial to the minority.
- 5.3
- Future researchers may be interested in assessing the effects of different topologies of underlying interaction networks on our proposed attitude and opinion dynamics model for simulating the more advanced phenomena of normative social influence and public compliance. Cellular automata, which represent the spatial and temporal structure of society as well as high degree of clustering, provide a solid foundation as the underlying interaction network of our proposed model. However, in recent years, many social network scientists have argued that real-world human interaction networks are similar to scale-free networks, with the small-world characteristics of low degree of separation, high degree of clustering, and power-law connectivity distribution, rather than network models based on a well-mixed population assumption. Therefore, assessing the effects of different theoretical social network topologies on our proposed model is an important task requiring a detailed review of the literature.
 Acknowledgements
Acknowledgements
- This work was supported in part by a grant from the Republic of China National Science Council (NSC-102-2221-E-182-052). This work was supported in part by the High Speed Intelligent Communication (HSIC) research center, Chang Gung University, Taiwan, R.O.C.
 Notes
Notes
-
1 According to Katz and Allport (1931), pluralistic ignorance is the state of affairs wherein nearly all members of a group privately refute what is considered to be the majority outlook and belief. Each member falsely believes that those principles are approved by all other group members. In terms of carnal behavior, they suggest that obviously abrupt modifications in cultural norms can be credited to the gradual acknowledgement by multiple individuals that other people in the group think the same way they do.
2 Minority influence is defined as the pressure exerted by a small minority that can lead to changes in group opinion.
3 The designers of continuous opinion dynamics models utilize the bounded confidence assumption when proposing opinion exchange processes. Opinion exchange processes based on the bounded confidence assumption are viewed as one type of informational social influence. According to the assumption, agents only exchange opinions with other agents who hold similar opinions. Accordingly, opinion exchanges only occur when the difference in opinion value is smaller than the "bounded confidence" (also referred to as uncertainty). Since the bounded confidence assumption is considered both simple and reasonable, some researchers are currently using it with well-known continuous opinion dynamics models for various applications (Salzarulo 2006; Stauffer et al. 2004; Suo & Chen 2008; Urbig et al. 2008).
4 We used the ANSI C++ programming language to implement a general-purpose and extendable continuous attitude and opinion dynamics model. All output data generated from our proposed model were organized and processed using MathWorks MATLAB to plot statistical charts. The simulation system can be run on almost all operating systems, including Linux, Macintosh, and Windows. For source code matching specific research requirements, please contact the corresponding author.
5 Cellular automata have been widely used in studies of computational social science for investigating the large-scale outcomes of millions of individual small-scale events, and for achieving visually impressive patterns. In our study, cellular automata represent a temporal-spatial simulation and visualization platform for exploring ways that private acceptance of informational social influence, and public compliance with normative social influence, affect opinion and attitude dynamics, as well as mutual influences between opinions and attitudes.
6 We assumed that people's opinions must be close to each other and consistent in order for the pressure of public opinion to be formed – in other words, a few opinions have already been formed, and individuals have generated normative social influence affecting certain group members so that they follow the claims of a particular subgroup. The more concentrated the opinions within a subgroup or the larger the number of subgroup members, the greater the pressure such a subgroup imposes on other group members. We label this type of pressure as public opinion magnitude.
7 We assumed that the agent population in our simplified model is homogeneous and uniformly mixed, with no explicit spatial or social structure. However, this assumption is implausible because real-world interactions occur within structures. Accordingly, many researchers consider interaction structures in their opinion dynamics models as foundations for emerging social-scale outcomes. A typical interaction structure is cellular automata, in which each cell (agent) interacts with its closest neighbors. Thus, a fundamental difference between our original model and the simplified model used for comparison purposes is the number of communicating agents (described by Lorenz [2007] and Urbig et al. [2008] as "the communication regime"). In each time step in our original model, each agent communicates with eight surrounding agents (i.e., cells in a cellular automata with Moore neighborhood and periodic boundary conditions). In the simplified version, all agents can communicate with all other agents.
8 In this experiment, (a) the uncertainty u values of most agents were assigned by random sampling from a normal distribution with mean of 0.75 and standard deviation of 0.05, with a single extremist agent's uncertainty u value assigned as 0.1; (b) the op opinion values of most agents were also assigned by random sampling from a normal distribution with a mean of 0.5 and a standard deviation of 0.0168, but with the extremist agent having an opinion value of 0.9; and (c) agent op and att values were set at the same random real number, indicating consistent external opinion and internal attitude.
 References
References
-
AJZEN, I. & Fishbein, M. (1980). Understanding Attitudes and Predicting Social Behavior. Englewood Cliffs, NJ: Prentice Hall.
ALLEN, V. L. (1965). Situational factors in conformity. In Berkowitz L (ed.) Advances in Experimental Social Psychology. New York: Academic Press. [doi:10.1016/s0065-2601(08)60105-7]
ARONSON, E., Wilson, T. D., & Akert, R. M. (2007). Social Psychology (6th ed.). Upper Saddle River, NJ: Pearson Prentice Hall.
ASCH, S. E. (1955). Opinion and Social Pressure. Scientific American, 193(5): 33–35. [doi:10.1038/scientificamerican1155-31]
ASCH, S. E. (1956). Studies of Independence and Conformity: A Minority of One against a Unanimous Majority. Psychological Monographs, 70, (9): 1–70. [doi:10.1037/h0093718]
BARON, R. A. & Byrne, D. E. (1991). Social Psychology: Understanding Human Interaction (6th ed.). Boston, MA: Allyn and Bacon.
CIALDINI, R. B. & Goldstein, N. J. (2004). Social influence: compliance and conformity. Annual Review of Psychology, 55, 591–621. [doi:10.1146/annurev.psych.55.090902.142015]
DEFFUANT, G., Neau, D., Amblard, F., & Weisbuch, G. (2000). Mixing beliefs among interacting agents. Advances in Complex Systems, 3, 87–98. [doi:10.1142/S0219525900000078]
DEUTSCH, M. & Gerard, H. B. (1955). A study of normative and informative social influences upon individual judgment Journal of Abnormal Social Psychology, 51, 629–636. [doi:10.1037/h0046408]
FESTINGER, L. (1957). A Theory of Cognitive Dissonance. Stanford, CA: Stanford University Press.
HARTIGAN, J. A. & Wong, M. A. (1979). A K-Means clustering algorithm. Applied Statistics, 28(1), 100–108. [doi:10.2307/2346830]
HEGSELMANN, R. & Krause, U. (2002). Opinion dynamics and bounded confidence: models, analysis and simulation. Journal of Artificial Societies and Social Simulation, 5(3), 2 https://www.jasss.org/5/3/2.html.
JANIS, I. L. (1982). Groupthink: Psychological Studies of Policy Decisions and Fiascoes. Boston: Houghton Mifflin.
KATZ, D. & Allport, F. H. (1931). Student Attitudes: A Report from the Syracuse University Research Study. Syracuse, NY: Craftsman Press.
KIESLER, C. A. & Kiesler, S. B. (1969). Conformity. Reading, MA: Addison-Wesley.
LORENZ, J. (2007). Continuous opinion dynamics under bounded confidence: a survey. International Journal of Modern Physics C, 18(12), 1819–1838. [doi:10.1142/S0129183107011789]
MILLER, D. T. & McFarland, C. (1987). Pluralistic ignorance: when similarity is interpreted as dissimilarity. Journal of Personality and Social Psychology, 53(2), 298–305. [doi:10.1037/0022-3514.53.2.298]
MILLER, D. T. & McFarland, C. (1991). When social comparison goes awry: the case of pluralistic ignorance. In Suls J and Wills TA (Eds.), Social comparison: Contemporary Theory and Research (pp. 287–313). Hillsdale, NJ: Erlbaum Press.
MOSCOVICI, S. (1980). Toward a theory of conversion behavior. In Berkowitz L (Ed.) Advances in Experimental Social Psychology (vol. 13, pp. 287–313). Hillsdale, NJ: Erlbaum Press.13, 209–239. New York: Academic Press. [doi:10.1016/s0065-2601(08)60133-1]
O'GORMAN, H. J. (1975). Pluralistic ignorance and white estimates of white support for racial segregation. Public Opinion Quarterly, 39(3), 313–330. [doi:10.1086/268231]
O'GORMAN, H. J. (1986). The discovery of pluralistic ignorance: An ironic lesson. Journal of the History of the Behavioral Sciences, 22, 333–347. [doi:10.1002/1520-6696(198610)22:4<333::AID-JHBS2300220405>3.0.CO;2-X]
PETTY, R. E., Wegener, D. T., & Fabrigar, L. R. (1997). Attitudes and attitude change. Annual Review of Psychology, 48(1), 609–647. [doi:10.1146/annurev.psych.48.1.609]
PRENTICE, D. A. & Miller, D. T. (1993). Pluralistic ignorance and alcohol use on campus: Some consequences of misperceiving the social norm. Journal of Personality and Social Psychology, 64, 243–256. [doi:10.1037/0022-3514.64.2.243]
PUTNAM, R. (2000). Bowling Alone: the Collapse and Revival of American Community. New York: Simon and Schuster. [doi:10.1145/358916.361990]
SALZARULO, L. (2006). A continuous opinion dynamics model based on the principle of meta-contrast. Journal of Artificial Societies and Social Simulation, 9(1), 13 https://www.jasss.org/9/1/13.html.
SAMPSON, E. (1991). Social World, Personal Lives: An Introduction to Social Psychology. (6th Ed.) San Diego, CA: Harcourt Brace Jovanovich.
SEKIGUCHI, T. & Nakamaru, M. (2011). How inconsistency between attitude and behavior persists through cultural transmission. Journal of Theoretical Biology, 271(1), 124–135. [doi:10.1016/j.jtbi.2010.11.044]
SHERIF, M. (1935). A study of some social factors in perception. Archives of Psychology, 27(187). 17–22.
SHERIF, M. (1936). The Psychology of Social Norms. New York: Harper Collins.
STAUFFER, D., Sousa, A., & Schulze, C. (2004). Discretized opinion dynamics of the Deffuant model on scale-free networks. Journal of Artificial Societies and Social Simulation, 7(3), 7 https://www.jasss.org/7/3/7.html.
SUO, S. & Chen, Y. (2008). The dynamics of public opinion in complex networks. Journal of Artificial Societies and Social Simulation, 11(4), 2 https://www.jasss.org/11/4/2.html.
URBIG, D. (2003). Attitude dynamics with limited verbalisation capabilities. Journal of Artificial Societies and Social Simulation, 6(1), 2 https://www.jasss.org/6/1/2.html.
URBIG, D., Lorenz, J., & Herzberg, H. (2008) Opinion dynamics: the effect of the number of peers met at once. Journal of Artificial Societies and Social Simulation, 11(2), 4 https://www.jasss.org/11/2/4.html.
