 Abstract
Abstract
- An agent-based simulation was created to examine key parameters in mass shootings. The goal of the simulation was to examine the potential effectiveness of Senator Dianne Feinstein's (D-Calif.) assault weapons and high-capacity magazines bill. Based on the analysis, the proposed law would have a negligible effect on the number of people shot during mass shootings. The assault weapons portion of the proposed bill will have no effect on the number of people killed or wounded in a mass shooting. The assault weapons ban does not seek to decrease the rate of fire of any firearm. Of the parameters tested a weapon's rate of fire has the greatest effect on the number of people wounded or killed by that weapon. However, a ban on high-capacity magazines will result in a small number of lives saved during a mass shooting. This paper demonstrates simulation's ability to examine proposed policies and provide a framework for more meaningful discussions.
- Keywords:
- Mass Shootings, Public Policy, Criminology
 Introduction
Introduction
- 1.1
- The rise in frequency of mass shootings in the United States has recently resulted in the tragedy at Sandy Hook Elementary School in Newton, CT. The shooting left 27 victims dead, including 20 elementary students, and sparked a new round of debates on gun control. These debates focused on implementing background checks, gun registrations, and a high capacity magazines and assault weapons ban.
- 1.2
- Assault weapons and high-capacity magazines bans differ from gun registration and background checks in that they seek to limit the destructive power of a gunman. Additionally, these bans would place new restrictions on American freedoms by explicitly barring Americans from manufacturing, purchasing, and possessing these items. Senator Dianne Feinstein (D-Calif.) put forth a bill to ban both high-capacity magazines and assault weapons. This bill was a source of heated debate, with gun advocates and gun control proponents disagreeing on whether or not this bill would save lives.
- 1.3
- To further the national debate on gun control, an agent-based model is used to examine the number of people shot under different small arms configurations (i.e., magazine capacity, gun's accuracy, gun's range, etc.). An agent-based model is a simulation that focuses on individual agents, in this case people. Each agent is given a set of rules to follow. The agents are then allowed to interact with one another. The goal is to see how different parameters affect the number of people shot. With this information, two questions can be answered. First, how effective is the proposed assault weapons and high-capacity magazines ban? Second, what parameters are the most important in determining the number of people wounded or killed? Once these parameters are known, regulations can be designed to mitigate lives lost in mass shooting tragedies.
- 1.4
- It should be noted that this model is limited to interpreting the efficacy of the assault weapons and high-capacity magazine ban. Results of this model should not be extended to other policy decisions, such as deployment of security guards. The model was not designed to examine security guards and the disparate level of training security guards have.
- 1.5
- The next section will go into more detail about past mass shootings and the assault weapons ban. Afterward, previously-written agent-based models of small arms conflicts will be explored. A section on the methodology of the simulation will follow, including all relevant assumptions made. After this, the results of the paper are presented, followed by final thoughts and potential future work.
 Background
Background
-
Mass Shootings
- 2.1
- There are many definitions of mass shootings. Depending on the criteria used to define mass shootings, there have been at least 62 mass shootings in the United States since 1982 (Follman 2013). The criteria used to define mass shootings in this paper were the following:
- The shooter took the lives of at least four people
- The shooting occurred in a public place
- The shooting was not tied to gang violence
- 2.2
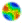
- In these shootings, a total of 143 firearms were recovered. Semiautomatic handguns made up 47% of the recovered firearms, while rifles made up 18%. Figure 1 below illustrates the proportion of weapons recovered at mass shootings (Follman et al. 2013).
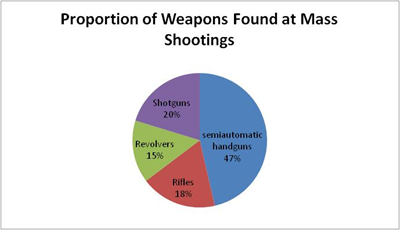
Figure 1. Proportion of Weapons Found at Mass Shootings - 2.3
- It is interesting to note that 48 of the 143 weapons would be banned under Senator Feinstein's assault weapons ban. A total of 42 weapons contained high-capacity magazines and 20 firearms were classified as assault weapons (Follman et al. 2013).
- 2.4
- From 1999 to 2012, there were approximately 28 mass shootings in the United States, with 10 occurring in 2012 alone. It should be noted that the Brady Campaign identified a larger number of mass shootings by using different criteria. However, the important thing to note is that mass shootings have become more commonplace in today's society (The Brady Campaign 2012; Telegraph 2012).
- 2.5
- Public mass shootings are generally carried out by males acting alone (Bjelopera 2013). Of the 28 mass shootings that have taken place since 1999, 71% have occurred indoors. This is an important statistic because being inside a facility limits the number of ways a person can escape. The most deadly shootings that resulted in the largest number of casualties was carried out indoors (58 shot in Aurora, CO 2012). Additionally, approximately 10% of mass shootings resulted in a gunfight between authorities and the perpetrator. This means that in the majority of shootings the gunman either committed suicide, surrendered to an armed response, or escaped before police arrived (The Brady Campaign 2012; Telegraph 2012; Bjelopera et al. 2013 ).
- 2.6
- Regardless of how mass shootings are classified, they are becoming more deadly and more frequent. In response to this increase in frequency and the tragedy at Newtown, Senator Feinstein introduced a bill to ban assault weapons and high-capacity magazines. The next section will go into more detail about the specific bill.
Assault Weapons Ban
- 2.7
- The Assault Weapons Ban of 2013 would make it illegal to purchase the assault weapons and high-capacity magazines identified in the ban. An assault weapon is defined specifically for rifles, shotguns and pistols. For a rifle to be considered an assault weapon it must be semiautomatic, meaning a repeating rifle that "utilizes a portion of the energy of a firing cartridge to extract the fired cartridge case and chamber the next round; and requires a separate pull of the trigger to fire each cartridge (Assault Weapon Ban 2013)". Additionally, in order to classify a rifle with a detachable magazine as an assault weapon it must contain at least one of the following:
- A pistol grip
- A forward grip
- A folding, telescoping or detachable stock
- A grenade launcher or rocket launcher
- A barrel shroud
- 2.8
- A rifle with a permanently attached magazine and a magazine capacity larger than 10 rounds are considered an assault weapon. A notable exception is for magazines that are of a tubular design and only capable of firing .22 caliber rim fire ammunition (Assault Weapons Ban of 2013). For a pistol with a detachable magazine to be classified as an assault weapon, it must also be semiautomatic and have the following characteristics:
- A threaded barrel
- A second pistol grip
- A barrel shroud
- The ability to accept a detachable magazine at some location outside of the pistol grip
- Be a semiautomatic version of an automatic design
- 2.9
- Pistols with permanently attached magazines that accept more than 10 rounds are classified as assault weapons. An assault weapon is any shotgun with a revolving cylinder or a semiautomatic shotgun with at least one of the following characteristics:
- A folding, telescoping, or detachable stock
- A pistol grip
- A permanently attached magazine with the capacity to accept more than 5 rounds
- 2.10
- The bill goes on to specifically outlaw several types of guns, such as all AR and Kalashnikov (AK) models, as well as several Bushmaster, Barrett, and Thompson guns (Assault Weapons Ban of 2013). Additionally, the bill bans high-capacity magazines, defined as magazines with the capability of accepting more than 10 cartridges. It is important to note that the ban does not limit the muzzle velocity, caliber, or rate of fire of any weapon that is not outlawed by this bill.
- 2.11
- The objective of this paper is to examine if these measures will limit the number of people shot in a mass shooting. Additionally, the goal is to identify key parameters that have the greatest impact on determining the number of people injured or killed. The use of agent-based models to illuminate effects of policy choices in combat situations is not novel. The next section will examine previous agent-based models that simulated small arms conflicts.
Agent-based Models on Small Arms Conflicts
- 2.12
- When modeling combat simulations, it has become common practice to use agent-based simulation. Erlenbruch (2002) designed an agent-based simulation of German peacekeeping operations. The simulation assessed different strategies against an armed mob. German peacekeeping troops, consisting of a platoon equipped with rifles, personnel carriers, and infantry fighting vehicles, were assigned to protect a high value target. The peacekeeping units were given a choice between a defensive and aggressive strategy. The effectiveness of each strategy was determined by the number of peacekeepers and civilians wounded or killed, as well as if the mob entered the high value target. It was found that an aggressive policy resulted in higher overall mission effectiveness.
- 2.13
- The aforementioned methodology was an extension of a simulated peacekeeping unit defending a location from an unarmed mob (Woodman 2000). A "tit-for-tat" strategy was compared to disproportionate response strategy, with the outcomes being measured by the number of peacekeepers and civilians injured or killed. The analysis found that responding aggressively against an unarmed mob resulted in less people wounded than a measured response. That is to say, people were scared off faster when the peacekeepers were more aggressive, resulting in an overall decrease in people injured or killed.
- 2.14
- It is important to note that lethality was measured deterministically, with agents given a certain amount of health points. Each weapon has a specific damage score. When an agent is hit by a weapon the damage score is subtracted for that agent's remaining health points. Agents' with health points of zero or less are considered dead (Woodman 2000).
- 2.15
- Agent-based modeling has also been used to simulate larger-scale conflicts. (Choo et al. 2007) simulate two forces engaging in armed combat. The agents are classified into red team and blue team. The blue team's objective is to capture a facility held by the red team. Red team is supplied with an evolutionary algorithm, which alters its strategy over different simulation runs. The goal is to test the robustness of the blue team's strategy to changes in behavior of the red team. It was found that red team can improve their survivability by 27% by becoming more aggressive and relying on ambushes. The model highlights the pros and cons of the blue team's strategy and thus provides the decision maker with more information. These studies demonstrate the acceptance of agent-based modeling by military leaders.
- 2.16
- Yuna Wong (2006) describes in his dissertation the need to model non-combatants in military operations. He separates non-combatant behavior into simple and complex. Simple behavior encompasses running away and hiding behind objects. In some circumstances it can be assumed that civilians will run away or hide once combat is initiated. However, in scenarios such as Somalia complex behaviors consisting of civilians rioting and acting as human shields occurred. The accurate modeling of non-combatants allows for realistic civilian casualty estimates. The agent-based simulation in this paper builds off the rich literature of combat agent-based models and expands the use of combat ABM into public policy modeling.
 Methodology
Methodology
- 3.1
- Agent-based modeling was developed to help understand interactions between individual organisms. An agent-based model (ABM) has a structure that includes a set of agents that interact with one other and their environment (Macal & North 2010). At each discrete time step, each agent is chosen in random order and allowed to make an action. As each agent makes an action it affects how other agents act and perceive their environment.
- 3.2
- The simulation is a zero-intelligence ABM, which means the gunman, security guards, and civilian population neither use complicated strategies to reach their objectives nor learn from past simulations. Previous combat agent-based simulations have found modeling civilians as zero-intelligent agents that run away from danger can be sufficient (Wong 2006). Additionally, most gunman in mass shootings are not well trained individuals, therefore they should not be expected to have tactical expertise.
Simulation Purpose and Agent Rules
- 3.3
- The purpose of this simulation is to determine how different parameters affect the number of people shot in mass shooting events. This model does not examine the lethality of the parameters. Instead, it is assumed that by lowering the number of people shot in mass shootings, the number of fatalities in these shootings will also decrease (Hayes et al. 2013a).
- 3.4
- There are several reasons that this study opted not to examine lethality. Firstly, previous agent-based models have demonstrated that accurately modeling lethality is not necessary to generate relevant and credible findings (Woodman 2000; Erlenbruch 2002). Furthermore, the authors do not have the necessary anatomy knowledge to accurately predict or measure the lethality of a bullets trajectory through a human body. Additionally, the bill proposed by senator Feinstein does not limit the caliber of bullets, which correlates to both how fast a projectile is fired and how heavy it is, ultimately determining the likelihood of a projectile killing or passing through the human body. Although, higher caliber rounds have a greater likelihood of killing or passing through the human body causing multiple casualties, it is assumed that bullets do not penetrate through walls or people in the simulation. However, because the bill does not address the caliber of bullets the authors made the aforementioned assumption.
- 3.5
- Two variations of the simulation were created; one is an outdoor scenario and the other is an indoor scenario. Once the parameters that most affect the number of people wounded or killed are identified, the potential effectiveness of Senator Feinstein's bill can be assessed. Additionally, recommendations can be made to mitigate the negative consequences of mass shootings.
- 3.6
- The two scenarios are similar to each other. The purpose of experimenting with both an indoor and an outdoor scenario is to see if any parameters become more or less important in determining the number of people shot. There are three types of agents in these simulations: civilians, armed security guards, and gunman. The rules that each agent class follows are described below. The gunman and security guards rules are held constant across scenarios.
Civilian Outdoor:
- Turn 180 degrees from gunman ± N(0,1)
- Move forward at assigned running speed
- If someone in the way, move to within 0.3 feet of them
- Considered safe if distance from gunman > gun's range + escape distance
- Turn in direction of closest door ± N(0,1)
- Move forward at assigned running speed
a. If someone in the way, move to within 0.3 feet of them
b. If wall/object in the way move to within 0.3 feet of wall/object - Considered safe if exit the room
- Are there bullets in the magazine? If not, reload for this turn and skip all remaining rules (reload takes assigned reload time)
- Aim at closest civilian ± N(0,σ)
- Fire X rounds
a. If less than X rounds left in the magazine, fire remaining rounds. - Move towards most recent agent fired at (move at assigned running speed)
- Are there bullets in magazine? If not, reload for this turn and skip all remaining rules (reload takes assigned reload time)
- If there is a civilian within 1.5 feet of a straight line between agent and the gunman, move to step 5 for this turn (won't shoot if a civilian is in the way)
- Aim at closest gunman ± N(0,σ)
- Fire X rounds at gunman
a. If less than X rounds left in the magazine, fire the remaining rounds. - Move toward the gunman at running speed
a. If gunman is within the distance, run this turn then tackle him
Parameter Description
- 3.7
- The simulation is considered complete when all civilians have either escaped or been shot and/or the gunman has been shot or tackled. The parameters (italicized above) that are used are defined below.
- Running speed – feet/second the agent can run
- X – the number of bullets fired a second
- σ – the standard deviation a gunman or security guard aims off center
- Capacity – number of rounds the magazine of the agent can hold
- Gun's Range – the range at which the bullet fired horizontally from 5feet 5inches will hit the ground
- Escape Distance – the distance past a gun's range that an agent needs to reach to be considered safe (assumed to be 200 feet in the simulation)
- 3.8
- The simulation environment consists of a two-dimensional Cartesian world. When it is either the gunman's or a security guard's turn to act, they aim directly for the center of their target. The bullet they fire is perturbed from this intended trajectory. This error represents both the gun's and the shooter's accuracy. A smaller perturbation is indicative of a more accurate gun and shooter. The perturbation is a normally distributed random variable. The baseline standard deviation (σ) of the random variable is calculated from the maximum effective distance of the gun. The maximum effective distance of a gun is considered the distance at which an average trained shooter can hit a human torso, assumed 1.4 feet in diameter, 50% of the time. Assuming a normal distribution, it becomes possible to determine the standard deviation or baseline measure of the accuracy for each weapon. Take for example the AR-15, which has an effective range of 1804.46 feet (Dockery 2007).
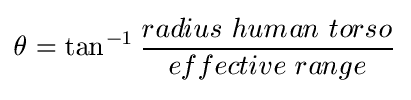
- 3.9
- Using the equation above, the AR-15's θ = 0.022 degrees. In other words, 50% of the time the AR-15 will fire a bullet within 0.022 degrees of the intended aiming line. The mean of the random normal distribution is assumed to be 0. To determine the standard deviation, the equation σ=θ/0.67 is used (Bertsekas & Tsisikil 2002).
- 3.10
- In the case of the AR-15, the standard deviation is 0.033. Any additional deviation is caused by the shooter; therefore to represent a less accurate shooter the standard deviation can be increased. We now have the information necessary to plot the trajectory of a bullet fired. The figure below illustrates the process. The shooter aims at the center of the target. For the gunman, this is the closest civilian and for the security guards this is the gunman. However, the bullet leaves at a trajectory that is altered by random normal distribution; for the AR-15 this is N(0,0.033 + human error). The bullet travels on this adjusted trajectory, and the first person that is less than 0.7 feet (assumed radius of the torso) off of the trajectory and within the range of the gun is considered shot. The bullet is assumed to travel instantaneously and does not penetrate through a person or wall.
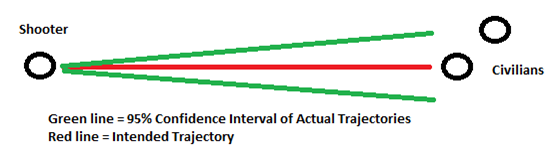
Figure 2. Bullet's Possible Trajectory - 3.11
- The range of the gun is calculated by assuming the gun is fired horizontally from a height of 5feet 5 inches. Throughout the bullet's flight, it is assumed to travel at the muzzle velocity. For the AR-15, this is 3250 feet/second. Using the equation below, this gives the AR-15 a range of 1100 feet (Dockery 2007). Where X represents distance, v represents velocity, a represents acceleration, and t represents time (Giancoli 2000). This means that in the outdoor simulation an agent must be a distance of 1300 feet from the gunman to be considered safe. The Beretta handgun on the other hand has a range of 400 feet, which means the escape distance from a gunman armed with a Beretta is 600 feet.
X = X0 + v0t +1/2at2 - 3.12
- The last two variables used to define a weapon were magazine capacity and rate of fire. For small arms there is a measure called the effective rate of fire. This is the rate of fire that maximizes both number of shots and accuracy. For the AR-15 this is 45 rounds/minute, and assuming a standard 30 round magazine, the AR-15 can be described in the graph below (Dockery 2007).

Figure 3. Graphical Description of Firearms - 3.13
- The aforementioned procedure was also used to describe the Beretta hand gun. Figure 3 illustrate the difference between the Beretta and the AR-15, range is represented in 1000s of feet and magazine capacity is represents in 100s of rounds. The AR-15 has a longer range, carries more rounds, and is more accurate than the Beretta. However, their rate of fire is the same. Using the four aforementioned parameters different combinations of gun configuration and gunman's skill can be tested.
Simulation Validation
- 3.14
- On July 20th, James Holmes committed a mass shooting in a midnight showing of The Dark Knight Rises. Mr. Holmes was armed with a 12-gague Remington 870 Express Tactical Shotgun, Smith & Wesson M&P 15 semi-automatic rifle, and a Glock 22 40-caliber handgun. It is important to note that all the aforementioned firearms violated Senator Dianne Feinstein assault weapon ban. After releasing tear gas into the theater, James Holmes fired approximately 110 rounds, striking 58 people (CBC News 2012; Fahrenthold 2012; Parker 2012). The Aurora Colorado shooting was used as a test case to validate the previously mentioned simulation assumptions.
- 3.15
- The movie theater layout was created using the minimum recommended dimensions for aisles and width of chairs (ABC 7 2012; Scribd). It is important to note that the movie theater is assumed to be flat. That is to say rear seats are not raised above seats in front of them. Civilians are assumed not to climb over chairs. However, approximately 10% of agents will hide in place. These civilians will not be harmed but other people crossing over them can only travel at 10% of their normal speed. If a civilian is shot they are assumed to fall to the ground and will slow other civilians crossing over them by 90%, to take into account the effect of darkness and tear gas. The average civilian running speed is slowed to approximately 3 feet/second.
- 3.16
- According to witness statements James Holmes remained close to the front theater exit. Therefore, the simulated gunman is assumed not to move. Additionally, the five shotgun rounds fired by Mr. Holmes were not simulated. Forty five rounds were fired from the M&P 15 and sixty rounds were fired from the Glock 22. Assuming a standard fifteen round magazine the Glock was reloaded three times. In the simulation this reload was assumed to take two seconds. The M&P15 was assumed to have a standard deviation of 2 degrees off center, while a Glock was assumed to have 3 degrees. The firing rate for both firearms was assumed to be 1 round a second. Range was not a factor, due to the size of the room. Figure 4 displays the simulated movie theater.
Figure 4. Simulated Movie Theater - 3.17
- The simulation was run 100 times and the number of people shot was recorded. The model is assumed to be accurate if the actual casualty number is close to the range of simulated casualties. The range of simulated casualties was [44, 58]. The actual number of people shot was 58, which is the maximum of the simulated range. This is to be expected because Mr. Holmes fired five additional shots from a shotgun, which was not simulated. Taking this into account the simulation is accurately predicting the number of people shot. Therefore, we assert that the previously mentioned assumptions do not significantly affect the outcome of the simulation. This simulation is stored at OpenABM.org (Hayes & Hayes 2013b). To ensure generalizable findings two experimental simulations were created to test the efficacy of Senator Dianne Feinstein's assault weapons and high-capacity magazines bill.
Experimental Procedure
- 3.18
- The purpose of the experiment is to determine key factors in the number of people shot during a mass shooting. The order of events is as follows:
- The gunman acts according to the previously defined rules
- Every civilian is chosen at random and then acts according to the previously defined rules
- Every security guard is chosen at random and then acts according to the previously defined rules
- Repeat steps 1–3 until aforementioned stopping condition is reached
- 3.19
- Every complete sequence of steps 1–4 is assumed to take one second. The parameters that are examined include the parameters of the gunman's weapon (i.e., rate of fire, accuracy, range, magazine capacity) and the number of armed security guards. Each parameter group is run thirty times to provide a large sample size. All security guards are initialized with the following set of values.
- Magazine capacity = 15
- Range = 500
- Standard Deviation of Trajectory (Accuracy- the smaller the number the better the accuracy) = 1
- Rate of Fire = 1 round/second
- Running Speed = 21.67 feet/second (80th percentile in 17 year old boy shuttle run)
- Reload Time = 2 seconds (was held constant for both gunman and security guard)
- 3.20
- The gunman is assumed to be in the 30th percentile in 17 year old boy shuttle run, giving him a running speed of 12.24 feet/second. Civilians are assumed to have a truncated normally distributed running speed, with a mean at 12.77 feet/second, a standard deviation of 8.9 feet/second, and a minimum running speed of 1 foot/second.
 Results
Results
- 4.1
- The outdoor scenario begins with a gunman starting in the center of a 200-person crowd, with the farthest person being no more than 420 feet away. As the scenario begins, the crowd disperses in all directions in an attempt to flee from the gunman. Each combination of the parameters depicted in Figure 5 is run 30 times. Figure 5 illustrates the average number of people shot over all simulations run, while that parameter equals the given value.
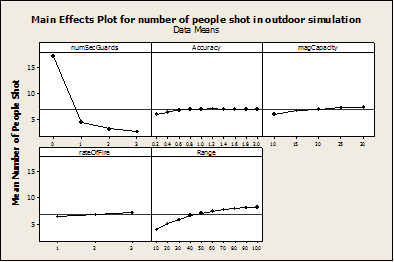
Figure 5. Main Effects Plot for Outdoor Simulation - 4.2
- The above picture illustrates that increasing the number of security guards greatly decreases the number of people shot. There is a large reduction in the number of people wounded or killed when the first security guard is added to the simulation, and smaller and smaller reductions as more are added. This illustrates a diminishing return; in other words, there is a smaller reduction in the number of people shot for every new security guard added. This is because the gunman acts first and is likely to shoot somebody on his first turn. Even if a guard is close by, the gunman has the element of surprise and is able to shoot somebody before the guard can react.
- 4.3
- The main effects plot also shows that the standard deviation of trajectory angles (accuracy) has very little effect on the number of people shot. As accuracy is decreased by increasing the standard deviation, the number of people shot goes up slightly. This is caused by multiple factors in the simulation. There are a large number of people in the crowd and bullets are not assumed to penetrate one person and hit another. Because the crowd begins in such a densely packed group, by shooting in a wider area the gunman is likely to hit multiple people in the first couple of seconds, thereby slightly increasing the number of people shot.
- 4.4
- To get a better understanding of the parameter values that most affect the number of people shot, an ordinary least squares model was fit. The equation below gives the best linear estimation of the number of people shot; the model gives a coefficient of determination of 53.34%. The equation below is used to demonstrate relative importance of the different parameters.
Number of people shot = -4.4 * Number security guards + 0.004 * range + 0.06 * magazine capacity + 0 .4 * rate of fire + .4* accuracy + 8.6 - 4.5
- The above equation provides a great deal of insight into what parameters affect the number of people wounded or killed during mass shootings. For every 1 additional armed security guard, an estimated 4 people will be saved. The reason this number seems small compared to the drop seen in Figure 5 is because it is fitted over all tested values of security guards. As stated earlier, there is a diminishing return in adding security guards. Therefore, this value must take into account this diminishing return and can be interpreted as the average number of lives saved for each additional security guard. The first security guard provides a large reduction in the number of people shot and the subsequent security guards provide smaller reductions thus diminishing the overall average reduction in number of people wounded or killed for each additional security guard.
- 4.6
- The rate of fire has the second largest effect on the number of people shot. For every additional bullet fired per second, an average of 0.4 additional people will be shot. Furthermore, for every 500 additional feet in range, an average of 2 additional people will be wounded or killed. The above equation provides better insight about which variables matter, but it does not tell the entire story.
- 4.7
- There are interactions effects (non-linear relationships) that exist between a subset of the variables. This can be seen in Figure 6 below. For readability purposes, only the largest interactions are illustrated on the graph below. If there are no armed security guards, range has a much larger effect on the number of people wounded than it does when there is a security guard present. The simulation illustrates that the shooter is capable of engaging targets farther away from him because he has not been confronted by armed resistance. However, once armed resistance is added into the simulation, the shooter does not have time to engage targets at a farther range. As the range of the firearm increases, the maximum capacity of the firearm becomes more important. The reload time is only two seconds, but it is evident that as magazine sizes are increased, the number of people shot on average will also increase.
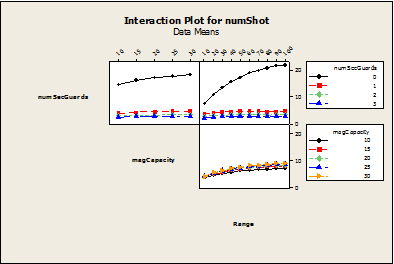
Figure 6. Outdoor Interaction plot - 4.8
- The same analysis was done for an indoor example. Two hundred people are in a 50 feet × 50 feet room. The exit door size is calculated using the 2000 NFPA Life Safety Code, which requires that a room with occupancy of 200 people have a door with an exit width of 40 inches or more (Illinois OFSM 2010). The simulation starts with the gunman (in red) in the southwest corner of the room and the exit door along the north wall, which is seen in the Figure 7 below. This simulation is stored at OpenABM.org (Hayes 2013a).

Figure 7. Initialization of Indoor Simulation - 4.9
- All the same parameters are tested, except the range of the weapon because the minimum range tested exceeds the maximum length of the room. The main effects plot is presented in Figure 8, along with the Least Square linear regression model. The linear model has a coefficient of determination of 65%.
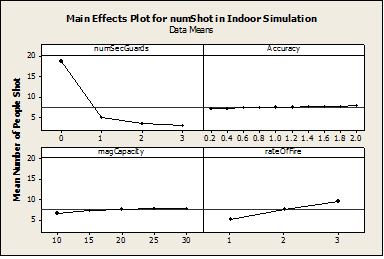
Figure 8. Main Effects Plot for Indoor Scenario - 4.10
- Figure 8 illustrates that magazine capacity and accuracy have very little effect in this scenario. The magazine capacity has a small effect because the scenario is limited to one room. Thus, the gunman may only reload once or twice before the entire simulation is concluded. If the simulation is expanded to larger complex, the magazine capacity would increase in importance. The main effects plot also illustrates that increasing the number of security guards again has the greatest effect on the limiting the number of people shot.
Number of people shot = -4.9 * Number security guards + 0.06 * magazine capacity + 2.1 * rate of fire + .4* accuracy + 9 - 4.11
- The results of the indoor simulation demonstrate that rate of fire is much more important in confined areas than in open areas. For every additional round of fire per second, on average 2 more people are wounded or killed in the simulation. This is caused by doors and to lesser degree hallways, which act as funnels (see Figure 9). As people approach a door, they are forced to assemble in a narrow space. This means the gunman is likely to hit somebody because the crowd of people becomes denser. The indoor simulation, even though it is limited to one room, has a larger number of people killed on average, which is exemplified by the intercept terms of both linear models. This is consistent with real-world events. By selecting a place with a limited number of possible egresses, a shooter can maximize the number of people shot.
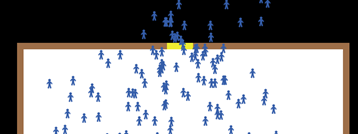
Figure 9. Example of Funneling - 4.12
- As before, the linear model does not tell the whole story; there are interactions effects between parameters. Figure 10 shows that rate of fire is more important when there are no armed security guards present. This is intuitive; in this scenario the gunman can sustain a longer rate of fire, thereby increasing the number of people shot.
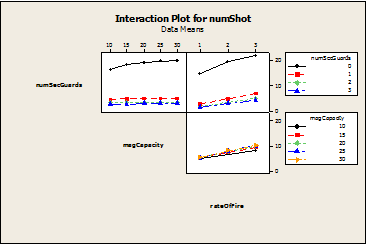
Figure 10. Interaction Effects of Indoor Simulation - 4.13
- Also, as the rate of fire increases so does the importance of the magazine. The larger the magazine capacity, the more rounds a gunman can fire within a finite amount of time. Thus, the more people he can shoot in this time period. The next section will provide final thoughts and ideas for future work.
 Conclusion and future work
Conclusion and future work
- 5.1
- Using the simulation we examined the assault weapons ban proposed by Senator Feinstein. In its current configuration the ban does not limit the rate of fire (Assault Weapons Ban 2013). The ban would allow for detachable magazines as well as semiautomatic pistols, shotguns, and rifles. In the best possible case, the assault weapons ban may make firearms slightly less accurate by disallowing forward grips and barrel shrouds. However, wearing a heat resistant glove would serve the same purpose as a barrel shroud. Additionally, the simulation illustrates that in crowded mass shooting events, lowering a weapon's accuracy may actually increase the number of people shot.
- 5.2
- As the crowd becomes denser, such as when people are going through a door, a gunman can widen his shooting area generating a deadlier impact. As the crowd assembles to get through a door, the crowd becomes significantly wider than it is deep. Thus, there are fewer people in front of a civilian then beside him, making the gunman more likely to hit somebody if he widens his target area. Therefore, we conclude that the assault weapons ban will not have any effect on the number of people shot during mass shootings.
- 5.3
- Excluding adding armed guards, of the parameters tested limiting a weapon's rate of fire, making it impractical to fire a weapon more than a defined number of times in a finite period, is the best way to decrease the number of people shot. The ban on high-capacity magazines seeks to accomplish this by forcing a shooter to reload more often. For example, if forcing a shooter to reload lowers the shooter's rate of fire by 0.2 bullets per second, this lowers the rate of fire by 12 bullets per minute. More extreme proposals could include banning semi-automatic weapons, which would lower the rate of fire because it would require the operator to perform an additional task when firing. Additionally, banning detachable magazines and requiring that magazines only allow for bullets to be individually loaded (i.e., revolver design) would lower the rate of fire because it would take longer to reload the weapon.
- 5.4
- The results of the model cannot be used to promote adding security guards. There are numerous factors that determine a security guard's effectiveness, from training to combat experience. Therefore, a prototypical "highly trained" guard was simulated to examine the nonlinear effects that arise as guards are added to the simulation. Although, the model determines adding security guards is the number one way of decreasing casualties, it does not take into account the varying skills that security guards will have. Therefore, this finding cannot be used to promote adding additional security guards.
- 5.5
- The simulation was designed with the purpose of gaining insight into the key parameters of mass shootings. A higher fidelity model can be created to examine these key parameters' effects on lethality, as opposed to simply the number of people shot. Additionally, allowing for bullets to pass through walls and people, as well as designing more realistic environments can also be used to increase the fidelity of the model. However, this model provides a framework for a more substantive debate on gun control by forcing regulators to ask the question, what is the regulation limiting and how would that affect a gunman's ability to perform a mass shooting?
- 5.6
- The next planned iteration of the simulation will examine and compare potential policies for mitigating mass shootings. One of the policies that will be examined is known as a lock down procedure. In this case civilians will enter enclosed rooms and barricade themselves in. The goal of this policy is to limit the number of potential targets. The addition of armed security will be another policy tested. As aforementioned guards of differing skill levels must be examined to determine the overall efficacy of armed security. Lastly, a policy of encouraging an armed public to engage active shooters will be examined. It has been argued that an armed citizenry will fare better than an unarmed citizenry in a mass shooting. However, this argument has several implicit assumptions. First, that the citizens can correctly identify the bad gunman from good citizens responding to the threat. Second, that the citizens can shoot the gunman without injuring a large number of people. The goal of the future study will be to provide a framework to test policies for different facilities.
 References
References
-
ABC 7 Denver (2012). Aurora Theater Reopening to the Public for First Time Since Shooting. http://www.thedenverchannel.com/news/aurora-theater-reopening-to-the-public-for-first-time-since-shooting. Archived at: <http://www.webcitation.org/6KccrnIZ5>
ASSAULT WEAPONS BAN of 2013, S.150, 113., 1.
BERTSEKAS, D. & Tsisikil, J. (2002). Introduction to Probability 1st ed. Massachusetts: Atlanta Scientific.
BJELOPERA, J., Bagalman E. Caldwell S. Finklea K. & McCallion G. (2013). Congressional Research Service. http://www.fas.org/sgp/crs/misc/R43004.pdf. Archived at: <http://www.webcitation.org/6KcdZgtTd>
THE BRADY CAMPAIGN. (2012). Major School Shootings in the United States Since 1997. Accessed Mar 25, 2013 https://www.dropbox.com/s/1bwx8hxm0w3wmk2/school-shootings.pdf
CBC NEWS. (July 20, 2012). Batman premiere gunman looked like 'assassin ready for war'. http://www.cbc.ca/news/world/story/2012/07/20/denver-shooting-movie-premiere.html. Archived at: <http://www.webcitation.org/6KcdxmyFT>
CHOO, C., Chua C. & Tay S. (2007). Automated Red Teaming: A Proposed Framework for Military Application. In Proceeding of 2007 Conference on Genetic and Evolutionary Computation (pp. 1936-1942). [doi:10.1145/1276958.1277345]
DOCKERY, K. (2007). Future Weapons. 1st ed. New York: Penguin Group, Inc.
ERLENBRUCH, T. (2002). Agent-Based Simulation of German Peacekeeping Operations for Units up to Platoon Level. Unpublished Master's Thesis: Naval Post Graduate School.
FAHRENTHOLD, D. (2012). The Washington Post. http://www.washingtonpost.com/national/explosives-removed-from-james-holmess-apartment-and-destroyed-officials-say/2012/07/22/gJQAL9XN2W_story.html. Access at: <http://www.webcitation.org/6Kcear2zV>
FOLLMAN, M., Aronsen G. & Pan D. (2013). Mother Jones. http://www.motherjones.com/politics/2012/07/mass-shootings-map. Access at: <http://www.webcitation.org/6KcekrXp9>
GIANCOLI, D. (2000). Physics for Scientists & Engineers 3rd ed. New Jersey: Prentice Hall.
HAYES, Roy Lee, & Hayes, Reginald Lee (2013a). "Mass Shooting Simulation" (Version 1). CoMSES Computational Model Library. Retrieved from: <http://www.openabm.org/model/3920/version/1>
HAYES, Roy L, & Hayes, Reginald L (2013b). "Auroa Shooting Model" (Version 1). CoMSES Computational Model Library. Retrieved from: <http://www.openabm.org/model/3993/version/1>
ILLINOIS OFSM Division of Technical Service. (2010). Safety Code. http://www.sfm.illinois.gov/documents/How_to_Calculate_Occupant_Load.pdf. Access at: <http://www.webcitation.org/6KcfF0FPM>
MACAL, C. & North M. (2010). Toward Teaching Agent-Based Simulation. In Proceeding of the 2010 Winter Simulation Conference. [doi:10.1109/WSC.2010.5679148]
PARKER, Ryan; Lee, Kurtis; Ingold, John; Steffen, Jordan; & Brown, Jennifer (July 20, 2012). "Family identifies 27-year-old victim of Aurora theater shooting". The Denver Post. Accessed Mar 25, 2013. http://www.denverpost.com/news/ci_21118201
Access at: <http://www.webcitation.org/6KcfT67Kf>
SCRIBD. Building Cinema. http://www.scribd.com/doc/7393680/Hints-for-building-a-perfect-Cinema-Complex. Access at: <http://www.webcitation.org/6KcfZbBfe>
THE TELEGRAPH. (2012). History of mass shootings in the US since Columbine. http://www.telegraph.co.uk/news/worldnews/northamerica/usa/9414540/A-history-of-mass-shootings-in-the-US-since-Columbine.html. Access at: <http://www.webcitation.org/6KcffZyN1>
WOODMAN, R. (2000). Agent-Based Simulation of Military Operations Other Than War Small Unit Combat. Unpublished Thesis: Naval Post Graduate School.
WONG, Y. (2006). Ignoring the Innocent. Non-combatants in Urban Operations and in Military models and Simulations. Unpublished Dissertation: Pardee Rand Graduate School.