Abstract
Abstract
- We present DIAL, a model of group dynamics and opinion dynamics. It features dialogues, in which agents gamble about reputation points. Intra-group radicalisation of opinions appears to be an emergent phenomenon. We position this model within the theoretical literature on opinion dynamics and social influence. Moreover, we investigate the effect of argumentation on group structure by simulation experiments. We compare runs of the model with varying influence of the outcome of debates on the reputation of the agents.
- Keywords:
- Dialogical Logic, Opinion Dynamics, Social Networks
 Introduction
Introduction
- 1.1
-
Social systems involve the interaction between large numbers of people, and many of these interactions relate to the shaping and changing of opinions. People acquire and adapt their opinions on the basis of the information they receive in communication with other people, mainly with the members of their own social network; moreover, this communication also shapes their network. We illustrate this with some examples.
- 1.2
-
Some people have radical opinions on how to deal with societal problems, for example, the climate and energy crisis or conflicts around the theme of immigration. "Radical" refers to strong or extreme convictions, and advocating reforms by direct and uncompromising methods. During a critical event, such as an accident in a nuclear reactor, a debate on the deportation of a young asylum seeker, or discussion on the solvency of an EU member state, opposing radical opinions are often broadcasted, which in recent years has been facilitated by social network sites, blogs and online posts. Opinions can have a strong impact, either being rejected or accepted by others, when they are transmitted through the social system.
- 1.3
-
If there are many interactions in a social system, unexpected cascades of interaction may emerge, facilitating for example the surprising revolutions in North Africa with the support of Facebook, and causing the near bankruptcy of Dexia after re-tweeted rumours on insolvency.1 This is because in such social systems, the adoption of a particular opinion or product by a small group of people can trigger certain other people to adopt the opinion, which may create a cascade effect. However, also rejections of certain opinions or products may be aired. For example, a negative remark of Jeremy Clarkson (Top Gear) on electrical cars might hamper a successful diffusion.2. The latter example also illustrates that some people have more power to convince and a higher reputation than others, which can be partly an emergent property of the number of followers they have. These subsequent adoptions and rejections give rise to the formation of sometimes rivalling networks of people that unite in rejecting the other party.
- 1.4
-
Of particular interest are situations where groups of people with opposing opinions and attitudes emerge. Due to these network effects, personal opinions, preferences and cognitions may display a tendency to become more radical due to selective interactions, which translates in societal polarisation and conflict. These processes can be relatively harmless, like the ongoing tension between groups of Apple and Microsoft users, but such polarisation processes may get more serious, like the current opinions on whether to abandon or to support the Euro and the controversy about global warming. These social processes may even get totally out of control, causing violent acts by large groups, such as in civil wars or by small groups, such as the so-called Döner killings 83 in Germany and the Hofstad Network 4 in the Netherlands, or by individuals, such as the recent massacre in Utøya, Norway.
- 1.5
-
In these and other examples, people shape their beliefs based on the information they receive from other (groups of) people, that is, by downward causation. They are more likely to listen to and agree with reputable people who have a basic position close to their own position, and to reject the opinion of people having deviant opinions. They are motivated to utter an opinion, or to participate in a public debate, as a reaction on their own changing beliefs, resulting in upward causation. As a result, in this complex communication process, groups may often wander off towards more extreme positions, especially when a reputable leader emerges in such a group.
To model the process of argumentation, and study how this contributes to our understanding of opinion and group dynamics, we developed the agent-based model DIAL (The name is derived from DIALogue). In this paper, we present the model DIAL for opinion dynamics, we report about experiments with DIAL, and we draw some conclusions. Our main conclusion will be that DIAL shows that radicalisation in clusters emerges through extremization of individual opinions of agents in normative conformity models, while it is prevented in informational conformity models. Here, normative conformity refers to agents conforming to positive expectancies of others, while informational conformity refers to agents accepting information from others as evidence about reality (Deutsch & Gerard 1955). - 1.6
-
DIAL is a multi-agent simulation system with intelligent and social cognitive agents that can reason about other agents' beliefs.
The main innovative features of DIAL are:
- Dialogue — agent communication is based on dialogues.
- Argumentation — opinions are expressed as arguments, that is, linguistic entities defined over a set of literals (rather than points on a line as in Social Judgement Theory (Sherif & Hovland 1961).
- Game structure — agents play an argumentation game in order to convince other agents of their opinions. The outcome of a game is decided by vote of the surrounding agents.
- Reputation status — winning the dialogue game results in winning reputation status points.
- Social embedding — who interacts with whom is restricted by the strength of the social ties between the individual agents.
- Alignment of opinions — agents adopt opinions from other agents in their social network/social circle.
- 1.7
-
An earlier version of DIAL has been presented in Dykstra et al. (2009). An implementation of DIAL in NetLogo is available.5
- 1.8
-
DIAL captures interaction processes in a simple yet realistic manner by introducing debates about opinions in a social context. We provide a straightforward translation of degrees of beliefs and degrees of importance of opinions to claims and obligations regarding those opinions in a debate. The dynamics of these opinions elucidate other relevant phenomena such as social polarisation, extremism and multiformity.
We shall show that DIAL features radicalisation as an emergent property under certain conditions, involving the role of whether opinions are updated according to normative redistribution or argumentative redistribution, spatial distribution, and reputation distribution.
- 1.9
-
The agents in DIAL reason about other agents' beliefs. This reasoning implies that a much more elaborate architecture for the agent's cognition is required than has been usual in agent-based models. Currently there is a growing interest in this type of intelligent agents (Wijermans et al. 2008; Zoethout & Jager 2009; Helmhout 2006), and considering the importance of dialogues for opinion change we expect that a more cognitive elaborated agent architecture will contribute to a deeper understanding of the processes guiding opinion and group dynamics.
- 1.10
-
Group formation is a social phenomenon observable everywhere. One of the earliest agent-based simulations, the Schelling model of segregation, shows how groups emerge from simple homophily preferences of agents (Schelling 1971). But groups are not only aggregations of agents according to some differentiating property. Groups have the important feature of possible radicalisation, a group-specific dynamic of opinions.
- 1.11
-
In DIAL, agents compete with each other in the collection of reputation points. We implement two ways of acquiring those points. The first way is by adapting to the environment; agents who are more similar to their environment collect more points than agents who are less similar. The second way is by winning debates about opinions.
The remainder of the paper is structured as follows. In Section 2 we discuss theoretical work to position DIAL within a wider research context of social influence and social knowledge construction. In Section 3 we present the framework of dialogical logic. In Section 4 we discuss the model implementation in NetLogo, which is followed by Section 5, in which we report experimental results about the influence of argumentation and the alignment of opinion on the social structure and the emergence of extreme opinions. Section 6 provides our interpretation of these results. In Section 7, we conclude and provide pointers for future research.
 Theoretical Background
Theoretical Background
- 2.1
-
Our theoretical inspiration lies in the Theory of Reasoned Action (Ajzen & Fishbein 1980) and Social Judgement Theory (Sherif & Hovland 1961).
The Theory of Reasoned Action defines an
attitude as a sum of weighted beliefs. The source of these beliefs is the social circle of the agent and the weighting represents that other agents are more or less significant for an agent. We interpret beliefs as opinions, which is intuitive given the evaluative nature of beliefs. In our model an agent's attitude is the sum of
opinions of members of its social group, each having a distinct importance.
- 2.2
-
Social Judgement Theory describes the conditions under which a change of attitudes takes place, with the intention to predict the direction and extent of that change.
Jager & Amblard (2004) demonstrate that the attitude structure of agents determines the occurrence of
assimilation and contrast effects, which in turn cause a group of agents to reach consensus, to bipolarise, or to
develop a number of subgroups. In this model, agents engage in social processes. However, the framework of Jager & Amblard (2004) does not include a logic for reasoning about the different agents and opinions.
- 2.3
-
Carley's social construction of knowledge proposes that knowledge is determined by communication dependent on an agent's social group, while the social group is itself determined by the agents' knowledge (Carley 1986; Carley et al. 2003). We follow Carley's idea of constructuralism:
''Constructuralism is the theory that the social world and the personal cognitive world of the individual continuously evolve in a reflexive fashion. The individual's cognitive structure (his knowledge base), his propensity to interact with other individuals, social structure, social meaning, social knowledge, and consensus are all being continuously constructed in a reflexive, recursive fashion as the individuals in the society interact in the process of moving through a series of tasks. [...] Central to the constructuralist theory are the assumptions that individuals process and communicate information during interactions, and that the accrual of new information produces cognitive development, changes in the individuals' cognitive structure.'' (Carley 1986, p.386)
- 2.4
-
In summary, agents' beliefs are constructed from the beliefs of the agents they interact
with. On the other hand, agents choose their social network on the basis
of the
similarity of beliefs. This captures the main principle of Festinger's Social
Comparison Theory (Festinger 1954), stating that people tend to
socially compare especially with people who are similar to them. This
phenomenon of ''similarity attracts" has been demonstrated to apply in
particular to the comparison of opinions and beliefs (Suls et al. 2002). Lazarsfeld & Merton (1954) use the term value homophily to
address this process, stating that people tend to associate themselves
with others sharing the same opinions and values. To capture this
''similarity attracts'' process in our model, we need to model the social
construction of knowledge bi-directionally. Hence, agents in the model prefer to
interact with agents having similar opinions.
- 2.5
-
The development of extremization of opinions has also been topic of investigation in social simulation. There are different approaches, see for example (Franks et al. 2008; Deffuant et al. 2002; Deffuant 2006).
Existing cognitive architectures offer an agent model with the capability of representing beliefs, but primarily knowledge is represented in the form of event-response pairs, each representing a perception of the external world and a behavioural reaction to it.
We are interested in beliefs in the form of opinions rather than in actions and in social opinion formation rather than event knowledge.
- 2.6
-
What matters for our purposes are the socio-cognitive processes leading to a situation in which a group of agents see where opinions radicalise and out-groups are excluded. To model the emergence of a group ideology, we need agents that communicate with each other and are capable of reasoning about their own opinions and the opinions they believe other agents to have. The buoyant field of opinion dynamics investigates these radicalisation dynamics. As in group formation we also have homophily preferences, usually expressed in the ''bounded confidence'' (Huet et al. 2008; Hegselmann & Krause 2002) of the agents. Bounded confidence means that influence between agents only occurs if either their opinions are not too far apart, or one is vastly more confident of its opinion than the other.
- 2.7
-
The distinction between informational and normative conformity was introduced by (Deutsch & Gerard 1955). They define a
normative social influence as an influence to
conform with the positive expectations of
another. By positive expectations, Deutsch and Gerard mean to refer to those
expectations whose fulfillment by another leads to or
reinforces positive rather than negative feelings, and
whose nonfulfillment leads to the opposite, namely to alienation
rather than solidarity. Conformity to negative expectations,
on the other hand, leads to or reinforces negative
rather than positive feelings. This influence is implemented in DIAL by increasing (or decreasing) each cycle the reputation of all agents proportional to their similarity with their environment (the patches they are on).
An informational social influence is defined by Deutsch and Gerard as an influence to accept information
obtained from another as evidence about reality. This is implemented by the adjustment of the reputation according to the outcome of debates about propositions.
- 2.8
-
Cialdini & Goldstein (2004) use this distinction between informational and normative conformity in their overview article on social influence. Motivated by (Kelman 2006; Kelman 1958), they add another process of social influence: compliance, referring to an agent's acquiescence to an implicit or explicit request. Cialdini and Goldstein refer to a set of goals of compliance:
- Accuracy. The goal of being accurate about vital facts.
- Affiliation. The goal to have meaningful relations.
- Maintaining a positive self-concept. One cannot adopt indefinitely all kinds of opinions. A consistent set of values has to remain intact for a positive self image.
- 2.9
-
For a more complex social reasoning architecture, see for example (Sun 2008; Breiger et al. 2003). The program ''Construct'' is a social simulation architecture based on Carley's work, see (Lawler & Carley 1996). There is also research concerning social knowledge directly. Helmhout et al. (2005) and Helmhout (2006), for example, call this kind of knowledge Social Constructs. Neither their agents, nor the agents in (Sun 2008; Breiger et al. 2003), have real reasoning capabilities, in particular they lack higher-order social knowledge (Verbrugge 2009; Verbrugge & Mol 2008).
- 2.10
-
Representing beliefs in the form of a logic of knowledge and belief seems well suited for the kind of higher-order reasoning we need to represent, see for example (Fagin & Halpern 1987). The most prevalent logic approaches for multi-agent reasoning are either game-theoretic, for example, (van Benthem 2001), or based on dialogical logic, for example, (Walton & Krabbe 1995; Broersen et al. 2005). Neither of these logic approaches is well suited for agent-based simulation due to the assumption of perfect rationality, which brings with it the necessity for unlimited computational power.
- 2.11
-
This ''perfect rationality and logical omniscience" problem was solved by the introduction of the concept of bounded rationality and the Belief-Desire-Intention (BDI) agent (Bratman 1987; Rao & Georgeff 1995; Rao & Georgeff 1991). The BDI agent has been used successfully in the computer sciences and artificial intelligence, in particular for tasks involving planning. See (Dunin-Keplicz, B. & Verbrugge 2010, Chapter 2)
for a discussion of such bounded awareness. Learning in a game-theoretical context has been studied by (Macy & Flache 2002). There are extensions to the basic BDI agent, such as BOID (Broersen et al. 2001a; Broersen et al. 2001b), integrating knowledge of obligations. There is also work on a socially embedded BDI agent, for example (Subagdja et al. 2009), and on agents that use dialogue to persuade and inform one another (Dignum et al. 2001).
- 2.12
-
In agent-based simulation, the agent model can be seen as a very simple version of a BDI agent (Helmhout et al. 2005; Helmhout 2006). Agents in those simulations make behavioural decisions on the basis of their preferences (desires) and in reaction to their environment (beliefs).
Their reasoning capacity is solely a weighing of options; there is no further reasoning. This is partly due to social simulations engaging with large-scale populations for which an implementation of a full BDI agent is too complex as well as possibly unhelpful. These BDI agents are potentially over-designed with too much direct awareness, for example with obligations and constraints built into the simulation to start with rather than making them emergent phenomena.The main problem with cognitively poor agents is that, although emergence of social phenomena from individual behaviour is possible, we cannot model the feedback effect these social phenomena have on individual behaviour without agents being able to reason about these social phenomena. This kind of feedback is exactly what group radicalisation involves in contrast to mere group formation.
- 2.13
-
In recent years in the social sciences, there has been a lot of interest in agents' reputation as a means to influence other agents' opinions, for example in the context of games (Brandt et al. 2003). McElreath (2003) notes that in such games, an agent's reputation serves to protect him from attacks in future conflicts. In the context of agent-based modelling, Sabater-Mir et al. (2006) have also investigated the importance of agents' reputations, noting that ''reputation incentives cooperation and norm abiding and discourages defection and free-riding, handing out to nice guys a weapon for punishing transgressors by cooperating at a meta-level, i.e. at the level of information exchange", see also (Conte & Paolucci 2003). This description couples norms with information exchange, in which, for example, agents may punish others who do not share their opinion. We will incorporate the concept of reputation as an important component of our model DIAL.
 The model DIAL
The model DIAL
- 3.1
-
In this section, we present the model DIAL. First we mention the main ingredients: agents, statements, reputation points, and the topic space. Then we elaborate on the dynamics of DIAL, treating the repertoire of actions of the agents and the environment, and the resulting dialogue games.
Ingredients of DIAL
- 3.2
-
DIAL is inhabited with social agents.
The goal of an agent is to maximize its reputation points. An agent can increase its number of reputation points by uttering statements and winning debates. They will attack utterances of other agents if they think they can win the debate, and they will make statements that they think they can defend succesfully.
- 3.3
-
Agents are located in a topic space where they may travel. Topic space is more than a (typically linear) ordering of opinions between (typically) two extreme opinions. On the one hand, it is a physical playground for the agents; on the other hand, its points carry opinions. The points in topic space 'learn' from the utterances of the agents in their neighbourhood in a similar way as agents learn from each other.
In DIAL, topic space is modeled as two-dimensional Euclidean space. It serves three functions:
- Agents move towards the most similar other agent(s) in its neighbourhood.
The distance between two agents can be considered as a measure for their social relation: this results in a model for social dynamics. Moving around in topic space results in changing social relations.
- The topic space is also a medium through which the utterances of the agents travel. The louder an utterance, the wider its spatial range. The local loudness of a utterance is determined by the product of the speaker's reputation, the square root of the distance to the speaker's position and a global parameter.
- Moreover, the points in the topic space carry the public opinions: they learn from the utterances of the agents in their neighbourhood in a similar way as agents learn from each other, using the acceptance function A defined in Appendix B. While agents decide to accept an utterance from another agent based on their relation with the speaker and its reputation, accept or ignore it, or remember it for a future personal attack on the speaker, the acceptance by the topic space is unconditionally, anonymous and without criticism. Opinions are gradually forgotten during each cycle. Evidence and importance of each proposition gradually converge to their neutral value (0.5, meaning no evident opinion).
- Agents move towards the most similar other agent(s) in its neighbourhood.
The distance between two agents can be considered as a measure for their social relation: this results in a model for social dynamics. Moving around in topic space results in changing social relations.
- 3.4
-
Topic space differs from physical space in the following respects.
- An agent can only be at one physical place at the same time, but it can hold completely different positions in two indepenent topic spaces. So for independent topics we can meaningfully have separate spaces, which enables complete independence of movement of opinion.
- For more complex topics we can have more than two dimensions, if we want our agents to have more mental freedom.
Dynamics of DIAL
- 3.5
-
A run of DIAL is a sequence of cycles.
During a cycle, each agent chooses and performs one of several actions. After the actions of the agents, the cycle ends with actions of the environment. The choice is determined by the agent's opinions and its (recollection of the) perception of its environment.
- 3.6
-
To model their social beliefs adequately, the agents need to be able to
- reason about their own and other agents' beliefs;
- communicate these beliefs to other agents;
- revise their belief base; and
- establish and break social ties.
- move to another place;
- announce a statement;
- attack a statement of another agent made in an earlier cycle;
- defend a statement against an attack made in an earlier cylcle;
- change its opinion based on learning;
- change its opinion in a random way.
- 3.7
-
The actions of announcing, attacking and defending a statement are called utterances. See Figure 1.
Figure 1: Flowchart of the main agent actions. The opinion change actions are left out of this flowchart for simplicity reasons. 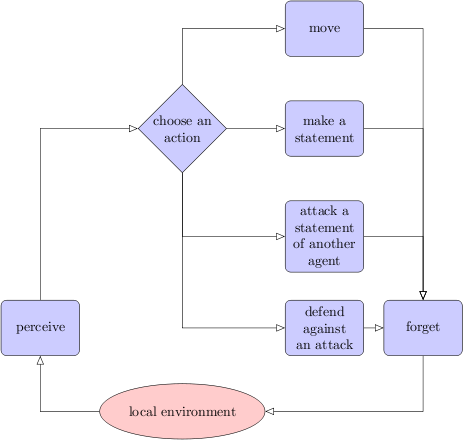
- 3.8
-
At the end of a cycle, all agents forget all announcements which are older than 10 cycles6. Moreover, the local public opinion in the topic space is updated at the end of a cycle in such a way that the topic space forgets its own opinion as time passes by and no opinions are uttered, by decreasing the distance between the opinion and the neutral value by a constant factor.
Dialogues
- 3.9
-
We begin with an example.
Example 1 Anya is part of a group where they have just discussed that schools are terribly underfunded and that language teaching for newly arrived refugees is particularly hard to organise. This leads to the following dialogue.
- Anya: If we do not have enough funding and refugees create additional costs, then they should leave this country.
[If nobody opposes, the statement becomes the new public opinion, but if Bob attacks, ...] - Bob: Why do you say that?
- Anya: Well, prove me wrong! If you can, I pay you 1 Reputation Point but if I am right you owe me a reward of 0.50 Reputation Points. [These odds mean that Anya is pretty sure about the truth of the first statement.] Everyone here says that schools are underfunded and that language teaching poses a burden!
- Bob: Ok, deal. I really disagree with your conclusion....
- Anya: Do you agree then that we do not have enough funding and that refugees create additional costs?
- Bob: Yes of course, that can hardly be denied.
- Anya: Right...– People, do you believe refugees should leave this country?
- Anya: If we do not have enough funding and refugees create additional costs, then they should leave this country.
- 3.10
-
The steps 1 and 2 form an informal introduction to the announcement of Anya in step 3, which expresses her opinion in a clear commitment. Every agent who hears this announcement has the opportunity to attack Anya's utterance. Apparently Bob believes that the odds of winning a dialogue about Anya's utterance is greater than one out of three, or simply he believes that he should make his own position clear to the surrounding agents. So Bob utters an attack on Anya's announcement in step 4. Since Anya uttered a conditional statement, consisting of a premise (antecedent) and a consequent, the dialogue game prescribes that a specific rule applies: either both participants agree on the premise and the winner of a (sub-) dialogue about the consequent is the winner of the debate, or the proponent defends the negation of the premise.
In this case Anya's first move of defence is: demanding agreement of Bob on the premise of her statement (step 5). Bob has to agree on the premise, otherwise he will lose the dialogue (step 6). Now all participants agree on the premise and the consequent is a logically simple statement, for which case the game rules prescribe a majority vote by the surrounding agents, Anya proposes to take a vote. (step 7).
- 3.11
-
The announcement of a statement can be followed by an attack, which in its turn can be followed by a defense. This sequence of actions forms a dialogue. The winner of the dialogue is determined by evaluation of the opinions of the agents in the neighbourhood. Depending on the outcome, the proponent (the agent who started the dialogue) and the opponent (the attacking agent) exchange reputation points.
Different rules are possible here:
- The proponent pays a certain amount, say 1RP
(reputation point) to the opponent, in case it loses the dialogue and gets nothing in case it wins. Only when an agent is absolutely sure about S
will it be prepared to enter into such an argument.
- The proponent offers 1RP
to the opponent if it loses the dialogue, but it receives 1RP
in case it wins the dialogue. This opens the opportunity to gamble. If the agent believes that the probability of S
being true is greater than 50 %, it may consider a dialogue about S
as a game with a profitable outcome in the long run.
- The proponent may specify any amount p it is prepared to pay in case of losing, and any amount r it wants to receive in case of winning the dialogue.
- The proponent pays a certain amount, say 1RP
(reputation point) to the opponent, in case it loses the dialogue and gets nothing in case it wins. Only when an agent is absolutely sure about S
will it be prepared to enter into such an argument.
- 3.12
-
The formal concept of dialogues has been introduced by Kamlah & Lorenzen (1973), in order to define a notion of logical validity that can be seen as an alternative to Tarski's standard definition of logical validity.
A proposition S
is logically true if a proponent of S
has a winning strategy (i.e. the proponent is always able to prevent an opponent from winning) for a formal dialogue about S
. A formal dialogue is one in which no assumption about the truth of any propositions is made.
In our dialogues, however, such assumptions about the truth of propositions are made: we do not model a formal but a material dialogue. In our dialogue game, the winner of a dialogue is decided by a vote on the position of the proponent. If the evidence value on the proponent's position is more similar to the proponent, it wins; otherwise the opponent wins8.
- 3.13
-
We now describe the dialogues in DIAL in somewhat more detail.
- An announcement consists of a statement S
and two numbers p, r
between 0 and 1.
When an agent announces (S, p, r)
, it says: 'I believe in S
and I want to argue about it: if I lose the debate I pay p
reputation points, if I win I receive r
reputation points'.
- The utterances of agents are heard by all agents within a certain range.
The topic space serves as a medium through which the utterances travel.
An agent can use an amount of energy called loudness for an utterance.
It determines the maximum distance of other agents to the uttering agent that are capable of hearing the utterance.
- An agent may respond to a statement uttered by another agent by attacking that statement.
The speaker of an attacked statement has the obligation to defend itself against the attack.
This results in a dialogue about that statement, giving the opponent the opportunity to win p
reputation points from the propopents reputation, or the proponent to win r
reputation points from its opponent.
The choice is made by an audience, consisting of the neighbouring agents of the debaters, by means of a majority vote.
- An announcement consists of a statement S
and two numbers p, r
between 0 and 1.
When an agent announces (S, p, r)
, it says: 'I believe in S
and I want to argue about it: if I lose the debate I pay p
reputation points, if I win I receive r
reputation points'.
- 3.14
-
For the acceptance of a particular statement S
, we use a acceptance function
A : [0, 1]2×[0, 1]2
 [0, 1]2
. However this function is not defined in terms of pay-reward parameters, but instead in terms of evidence-importance parameters, which system will be explained in the next subsection. So A
has two (e, i)
pairs as input (one from the announcer and one from the receiver) and combines them into a resulting (e, i)
pair. The evidence of the result only depends on the evidence of the inputs, while the importance of the result depends on the full inputs. The definition of A
and its properties are discussed in Appendix B. We will show that the evidence-importance parameter space is equivalent to the pay-reward space, but evidence-importance parameter space provides a more natural specification of an agent's opinion than the pay-reward space, which is especially adequate for dealing with the consequences of winning and losing dialogues in terms of reputation.
[0, 1]2
. However this function is not defined in terms of pay-reward parameters, but instead in terms of evidence-importance parameters, which system will be explained in the next subsection. So A
has two (e, i)
pairs as input (one from the announcer and one from the receiver) and combines them into a resulting (e, i)
pair. The evidence of the result only depends on the evidence of the inputs, while the importance of the result depends on the full inputs. The definition of A
and its properties are discussed in Appendix B. We will show that the evidence-importance parameter space is equivalent to the pay-reward space, but evidence-importance parameter space provides a more natural specification of an agent's opinion than the pay-reward space, which is especially adequate for dealing with the consequences of winning and losing dialogues in terms of reputation.
- 3.15
-
The acceptance function is used in DIAL in a weighted form: the more an agent has heard about a subject, the less influential announcements about that subject become on the cognitive state of the agent.
The belief of an agent: two represesentations
- 3.16
-
In the previous subsection, we have introduced an announcement of an agent as a triple (S, p, r)
where S
is a statement and (p, r)
is a position in the pay-reward space: p
and r
are the gambling odds the agent is willing to put on the statement winning in a specific environment. The pay-reward space is a two-dimensional collection of values that can be associated with a statement. It can be seen as a variant of the four-valued logic developed by Belnap and Anderson to combine truth and information: see Belnap (1977) and Appendix A. In this subsection, we give an example of the use of pay-reward values, and we introduce an alternative two-dimensional structure based on evidence and importance.
Example 2 Three agents A1, A2, A3 have different opinions with respect to some statement S : they are given in Figure 2. We assume that agent A1 has announced his position (S, 0.8, 0.2) , so it wants to defend statement S against any opponent who is prepared to pay r1 = 0.2 reputation points in case A1 wins the debate; A1 declares itself prepared to pay p1 = 0.8 points in case it loses the debate. A2 agrees with A1 (they are both in the N-W quadrant), but the two agents have different valuations. A2 believes that the reward should be bigger, r2 = 0.6 , on winning the debate, meaning A2 is less convinced of S than A1 . A3 disagrees completely with both A1 and A2 . A3 believes that the reward should be twice as high as the pay (p3 = 0.1 against r3 = 0.2 ). This means that A3 believes it is advantageous to attack A1 , because it expects to win 0.8 points in two out of three times, with the risk of having to pay 0.2 points in one out of three times. So the expected utility of A3 's attack on A1 is 0.8*2/3 - 0.2/3 = 0.4667 .
Figure 2: Belief values can be expressed either as an evidence–importance pair or as a pay–reward pair. The diagonal (left) represents evidence = 0.5, meaning doubt. The area left-above the diagonal represents positive beliefs with evidence > 0.5; the area right-under the the diagonal represents negative beliefs (evidence < 0.5). See Example 1 for more details about the beliefs of agents A1 , A2 and A3 . 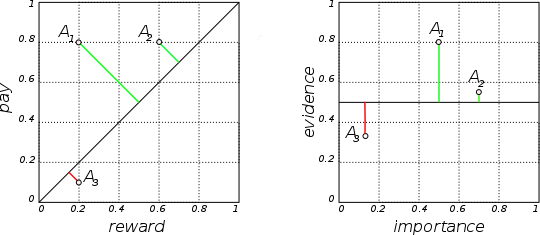
Agent Pay Reward Evidence Importance A1 0.8 0.2 0.8 0.5 A2 0.8 0.6 0.571 0.7 A3 0.1 0.2 0.333 0.15 - 3.17
-
Pay and reward are related to two more intrinsic epistemic concepts: the evidence (e
) an agent has in favour of a statement and the importance (i
) it attaches to that statement. We will use these parameters as dimensions of the evidence-importance space (to be distinguished from the pay-reward space).
The evidence e
is the ratio between an agent's positive and negative evidence for a statement S
. An evidence value of 1 means an agent is absolutely convinced of S
. An evidence value of 0 means an agent is absolutely convinced of the opposite of S
. No clue at all is represented by 0.5
. An importance value of 0 means a statement is unimportant and 1 means very important.
Importance is expressed by the sum of both odds. This means the more important an issue the higher the odds. In formula:
e =
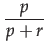 i =
i = 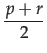
(In the unlikely case that p = r = 0 , we define e = 0.5 .) Conversely, we can compute the (p, r) -values from an (e, i) -pairp = 2 . e . i r = 2 . i . (1 - e)
This is illustrated with the computation of the (e, i )-values of the (p, r )-points A1, A2, A3 in the table in Figure 2. - 3.18
-
Since the reasoning capabilities of our agents are bounded, we need some form of generalisation. Verheij (2000) suggests that in a courtroom context, argumentation can be modelled by defeasible logic and empirical generalisation may be treated using default logic. Prakken et al. (2003) provide a review of argumentation schemes with generalisation.
We made communication efficient by providing agents with the capability to generalise by assuming a specific opinion to be representative of the agents in the neighbourhood. When an agent meets another previously unknown agent, it assumes that the other agent has beliefs similar to what is believed in its environment. This rule is justified by the homophily principle (Suls et al. 2002; Festinger 1954; Lazarsfeld & Merton 1954), which makes it more likely that group members have a similar opinion.
- 3.19
-
Much work has been done on the subject of trust starting with (Lehrer & Wagner 1981), which has been embedded in a Bayesian model in (Hartmann & Sprenger 2010). Parsons et al. (2011) present a model in an argumentational context. Our message-protocol frees us from the need to assume a trust-relation between the receiver and the sender of a message, because the sender guarantees its trustworthiness with the pay-value (p
).
We want the announcement of defensible opinions to be a profitable action.
So an agent should be rewarded (r
) when it successfully defends its announcements against attacks.
 The Implementation of DIAL
The Implementation of DIAL
- 4.1
-
As we mentioned in the Introduction, we have implemented DIAL in NetLogo.
In this section, we elaborate on some implementation issues.
- 4.2
-
The main loop of the NetLogo program performs a run, i.e. a sequence of cycles.
Agents are initialised with random opinions on a statement.
An opinion is an evidence/importance pair
(e, i)
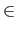 [0, 1]×[0, 1]
.
The probabilities of the actions of agents (announce a statement, attack and defend announcements, move in the topic space) are independent (also called: input, control, instrumental or exogeneous) parameters and can be changed by the user, even while a simulation is running (cf. Figure 3).
Global parameters for the loudness of speech and the visual horizon can be changed likewise.
At the end of a cycle, the reputation points are normalized so that their overall sum remains unchanged.
[0, 1]×[0, 1]
.
The probabilities of the actions of agents (announce a statement, attack and defend announcements, move in the topic space) are independent (also called: input, control, instrumental or exogeneous) parameters and can be changed by the user, even while a simulation is running (cf. Figure 3).
Global parameters for the loudness of speech and the visual horizon can be changed likewise.
At the end of a cycle, the reputation points are normalized so that their overall sum remains unchanged.
- 4.3
-
The number of reputation points RP
of an agent affects its loudness of speech.
There is a great variety in how to redistribute the reputation values during a run of the system. We distinguish two dimensions in this redistribution variety.
- Normative Redistribution rewards being in harmony with the environment. In each cycle, the reputation value of an agent is incremented/decremented by a value proportional to the gain/loss in similarity with its environment.
- Argumentative Redistribution rewards winning dialogues. Winning an attack or defence of a statement yields an increase of the permutation value of the agent in question, and losing an attack or defence leads to a decrease.
- 4.4
-
To illustrate differences in behaviour, we present the results of two runs of DIAL: one with only Normative Redistribution, another with only Argumentative Redistribution.
We adopt the parameter setting that is given in Figure 3. A complete description of all parameters can be found in Appendix C.
Figure 3: Independent parameters for the program runs of Figure 4. The behaviour related parameters (those parameters that start with chance) are normalized between 0 and 100. The ratio of the value of two behavioural parameters is equal to the ratio of the probabilities of the performance of the corresponding actions by the agents. 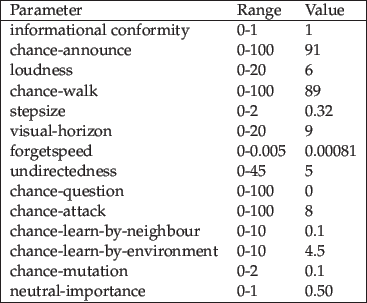
- 4.5
-
The outcome of a program run can be visualized in the interface of NetLogo.
Here we present the values of the importance and the evidence parameters.
When an agent utters a statement that is not attacked, or the agent wins the debate about a statement, the accordance between the agent and its environment increases.
If that statement was different from the ruling opinion in that area, it will be visualized as a bright or a dark cloud around the agent in the evidence pane of the user interface of NetLogo.
In the importance pane, a dark cloud will appear around an agent when it uttered a statement that is in agreement with the environment, indicating that this statement loses importance because the agents agree on it.
If, however, the uttered statement is in conflict with the ruling opinion, the colour of the surrounding cloud will become brighter, indicating a conflict area.
Those conflicts appear at the borders between dark and bright clusters.
A statement made will be slowly 'forgotten' and the cloud will fade away as time passes, unless a statement is repeated.
- 4.6
-
Most of the runs reach a stable configuration, where the parameters vary only slightly around a mean value.
It appears that most parameters mainly influence the number of cycles needed to reach a stable configuration, and only in a lesser degree the type of the configuration.
Figure 4 and Figure 5 illustrate two types of stable states: A segregated configuration and an authoritarian configuration. Agents are represented by circles.
- Segregated Configuration. In Figure 4, there are two clusters of agents: the blacks and the whites. Both are divided into smaller cliques of more similar agents. There is also a small cluster of 5-6 yellow agents in the center with a more loose connection than the former clusters. When the mutual distance is greater, the opinions differ more. Differences in RP are not very large. The number of different opinions is reduced; the extreme ones become dominant, but the importance, reflecting the need to argue about those opinions, drops within the black and white clusters. However, in the yellow cluster the average importance is high.
- Authoritarian Configuration. In Figure 5 only four agents have almost all the RP points and the other agents do not have enough status to make or to attack a statement. As a consequence, there are hardly any clusters, so there is no one to go to, except for the dictator or opinion leader in whose environment opinions are of minor importance. However, the distribution of opinions in the minds of the agents and their importance has hardly changed since the beginning of the runs. In this case the RP values become extreme.
Figure 4: Application of Normative Redistribution, leading after 481 cycles to a stable segregated state. Agents are represented by circles and the diameter of the agents shows their reputation status. In the left video (evidence), the agents' colour indicates their evidence, ranging from black (e=1) via yellow (e=0.5) to white (e=0). For clarity reasons the colour of the background is complementary to the colour of the agents: white for e=1, blue for e=0.5 and black for e=0. In the right video (importance) the importance of a proposition is depicted: white means i=1, black means i=0, and red means i=0.5 for the agents; the environment has the colours white (i=1), green (i=0.5), and black (i=0). The links between the agents of a cluster in the videos don't have any significance in the following experiments. (evidence) (importance) Figure 5: Application of Argumentative Redistribution, leading after 1233 cycles to a stable authoritarian state. Dimensioning and colouring as in Figure 4. The links between the agents of a cluster in the videos don't have any significance in the following experiments. (evidence) (importance) - 4.7
-
It turns out that the choice of reputation redistribution is the most important factor in the outcome of the simulation runs. If Normative Redistribution is applied, then a segregated configuration will be the result. If Argumentative Redistribution is applied, the result tends to be an authoritarian configuration.
We may paraphrase this as follows.
When argumentation is considered important in the agent society, an authoritarian society will emerge with strong leaders, a low group segregation and a variety in opinions. When normativity is the most rewarding component in reputation status, a segregated society emerges with equality in reputation, segregation, and extremization of opinions.
- 4.8
-
In the next section we discuss more experiments and their results, aimed at investigating the effects of the choice between normative and argumentative redistribution and of other parameters on the emergence of segregated- and authoritarian-type societies.
 Simulation experiments
Simulation experiments
- 5.1
-
In this section we investigate the results of several simulation experiments, focusing on possible causal relations between the parameters. First we explain how the dependent (output, response or endogeneous) parameters are computed. Then we take a look at how individual agents change their opinion, and we investigate what determines the belief components and their distribution by looking at the correlation between the simulation parameters. This information combined with a principal component analysis justifies the construction of a flowchart representing the causal relations.
- 5.2
-
In our experiments a run consists of 200-5000 consecutive cycles. If the independent parameters are not changed by the user, the situation becomes stable after 200-500 cycles.
We experimented with 25 -2000 agents in a run. It turns out that the number of agents is not relevant for the outcome of the experiments. We use 80 agents in the runs we performed for the pictures for reasons of esthetics and clarity.
- 5.3
-
We shall focus on six dependent parameters related to reputation, evidence and importance. We are not only interested in average values, but also in their distribution. We measure the degree of distribution by computing the Gini coefficient with the formula developed by Deaton:
Gini(X) =
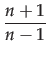 -
- 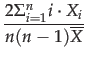
Here X = X1,..., Xn is a sequence of n values, sorted in reversed order, with mean value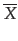 ; see (Deaton 1997). The Gini coefficient ranges between 0 and 1: the lower the coefficient, the more evenly the values are distributed.
; see (Deaton 1997). The Gini coefficient ranges between 0 and 1: the lower the coefficient, the more evenly the values are distributed.
- 5.4
-
The dependent parameters of the runs that we shall consider in the experiments are:
- Reputation Distribution the Gini-coefficient of the reputation of the agents;
- Spatial Distribution the Gini-coefficient of the evidence of the locations in the topic space;
- Average Belief the mean value of the evidence of the agents;
- Belief Distribution the Gini-coefficient of the evidence of the agents;
- Average Importance the mean value of the importance of the agents;
- Importance Distribution the Gini-coefficient of the importance of the agents.
- 5.5
-
The parameters 3-4 reflect the belief state of the agents and are for that reason referred to as belief parameters.
The values of the independent parameters which remain unchanged during the experiment are listed in Table 1. See Appendix C for an explanation of their meaning.
Some typical runs
- 5.6
-
We begin with some typical runs to illustrate the behaviour of the dependent parameters in the four extreme situations with respect to Normative Redistribution and Argumentative Redistribution.
- 5.7
-
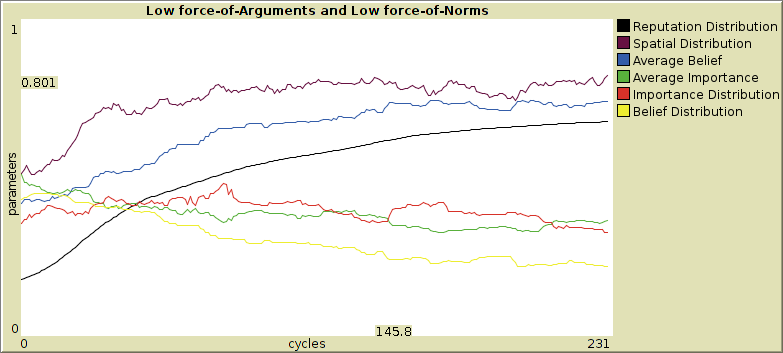
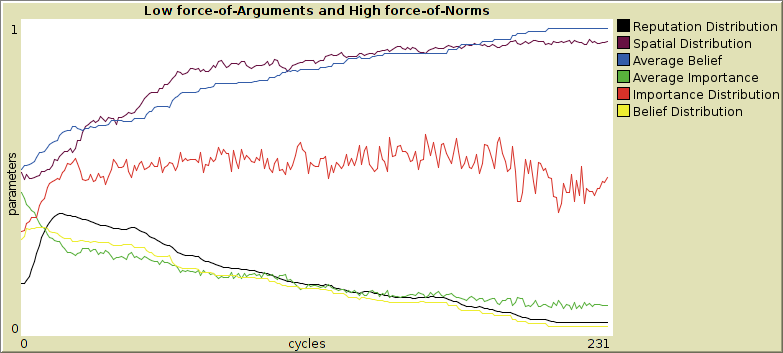
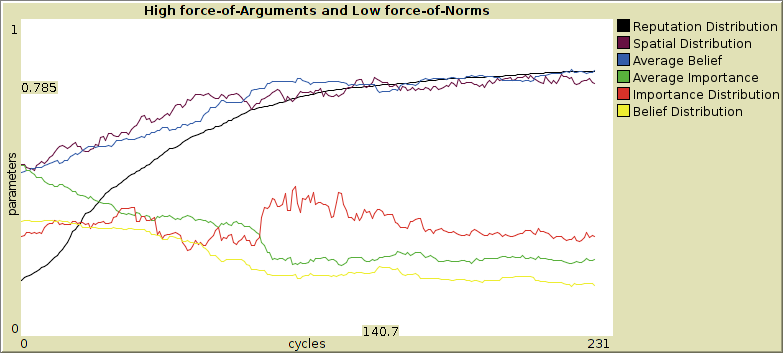
In Figure 6, 7, 8 and 9, we show the development of the dependent parameters for the extreme parameter values for normative and argumentative redistribution. In Figure 6 neither Normative Redistribution nor Argumentative Redistribution is active.
The attentive reader might expect a black horizontal line for Reputation Distribution, because none of the introduced factors that influence reputation are supposed to be active. However there is a nonzero parameter, lack-of-principle-penalty, which prescribes a reputation penalty for agent who change their opinion. These changes in reputation cause an increase in Reputation Distribution.
In Figure 7 and Figure 8 only Normative Redistribution respectively Argumentative Redistribution is active, and in Figure 9 both Normative Redistribution and Argumentative Redistribution are active.
- 5.8
-
We see that in all these extreme situations, Spatial Distribution and Average Belief tend to rise, while Belief Distribution and Average Importance tend to decrease. Moreover, Reputation Distribution rises in the beginning from a start value of about 0.2 to a value close to 0.5. This may be attributed to an initial process of strengthening of inequality: agents with high reputation gain, those with low reputation lose.
- 5.9
-
However, we see a clear distinction between the situations with high and with low Normative Redistribution. If Normative Redistribution is high, then Reputation Distribution decreases after the initial rise, while Importance Distribution fluctuates around an intermediate value and Spatial Distribution and Average Belief rise to values near 1. The relative instability of Importance Distribution may be related to the low level of Average Importance. These societies qualify as 'segregated', as explained in Section 4.
- 5.10
-
If Normative Redistribution is low, Reputation Distribution rises steadily, and Importance Distribution decreases slowly, while Spatial Distribution, Average Belief, Belief Distribution and Average Importance tend to less extreme values than in the high Normative Redistribution case. These are authoritarian-type societies.
Individual Changes of Opinion
- 5.11
-
So far, we have only seen plots of global parameters, but what happens to individual agents during a run? Do they frequently change their opinion or not? We present plots of the change in evidence during two runs, one with Normative Redistribution resulting in a segregated society, and one with Argumentative Redistribution resulting in an authoritarian society. There are 60 agents. Each agent is represented by a curve in the plots, which is coloured according to its initial opinion. The rainbow-colours range from red (evidence = 0) via orange, yellow, green, and blue to purple (evidence = 1).
Figure 10: History of the individual development of the evidence under Normative Redistribution (Segregated configuration). 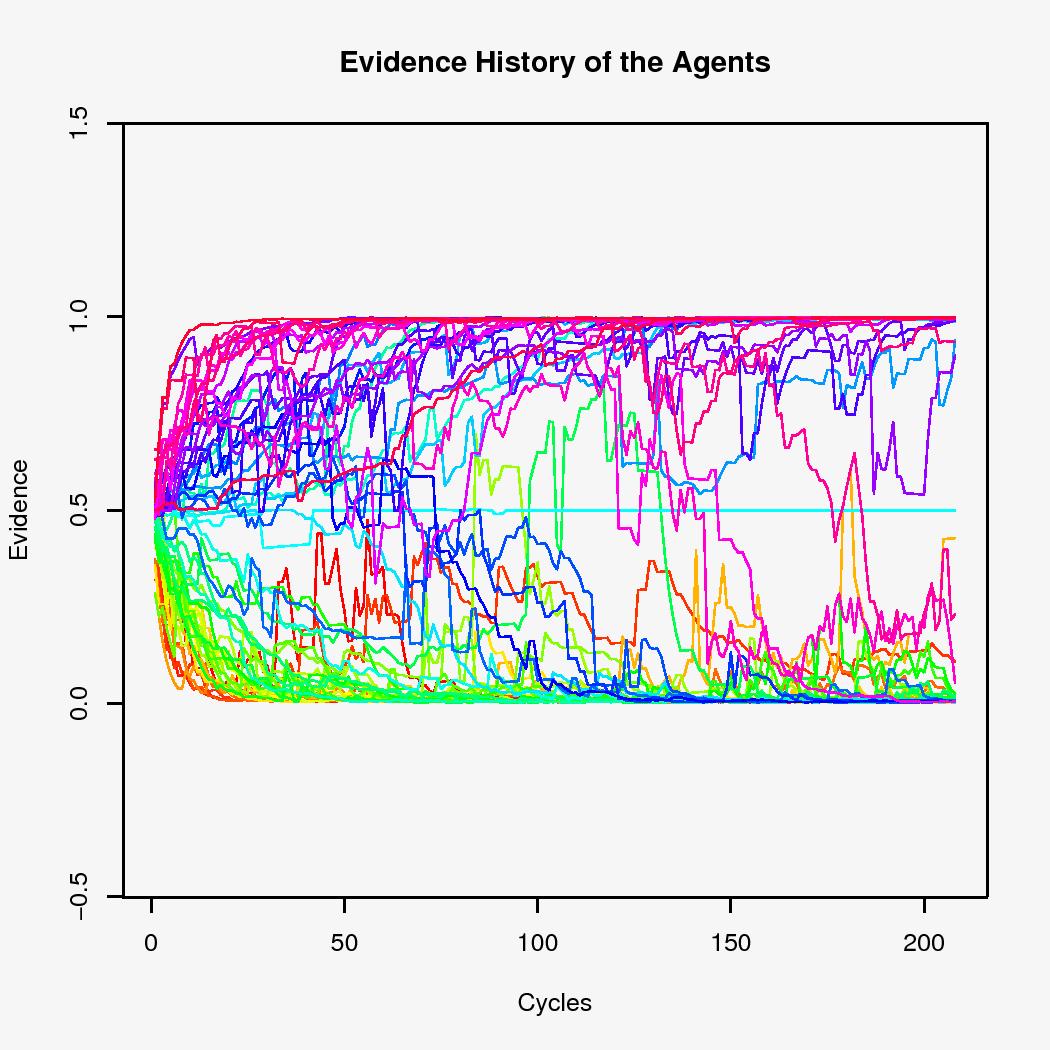
Figure 11: History of the individual development of the evidence under Argumentative Redistribution (Authoritarian configuration). 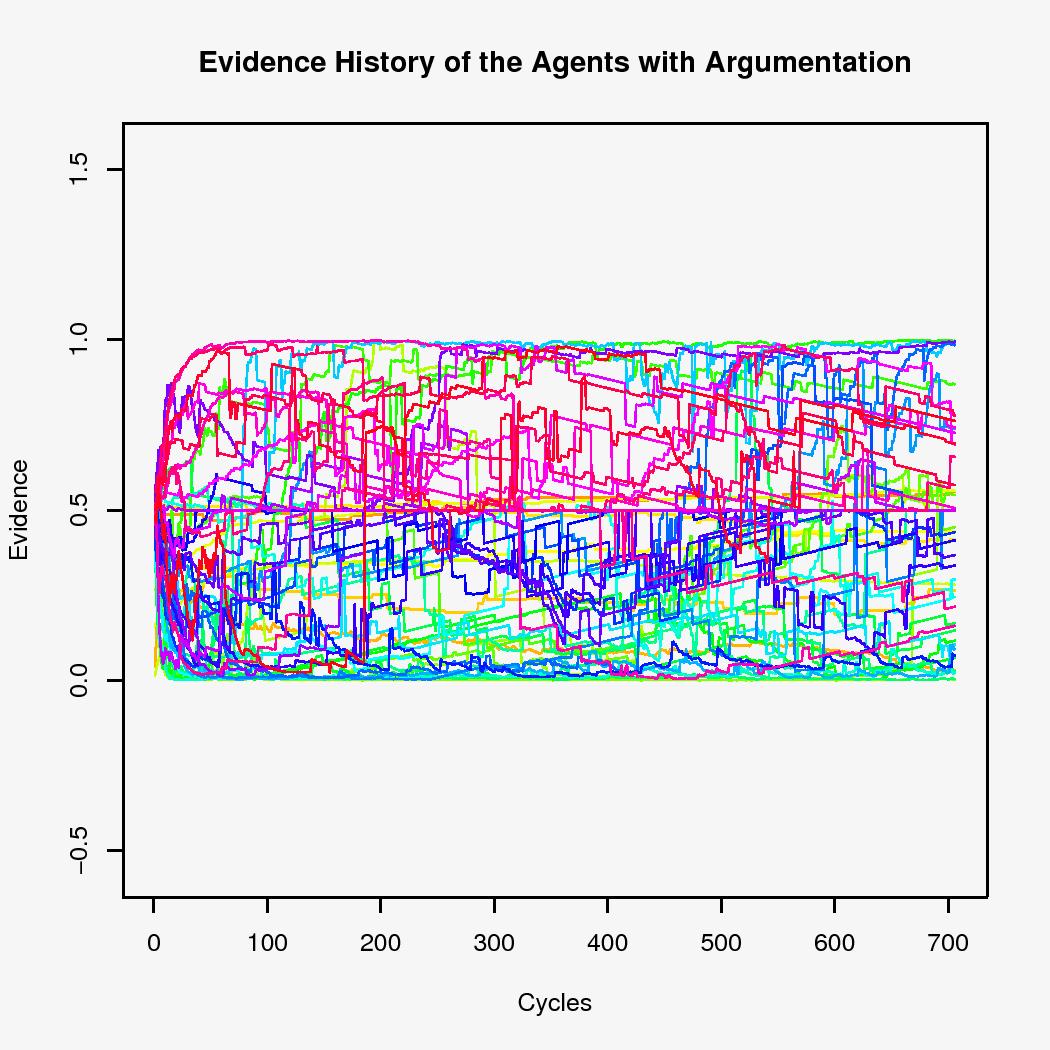
- 5.12
-
In a segregated configuration (Figure 10), the evidence of the agents tends to drift towards the values 0 and 1. The population becomes divided into two clusters with occasionally an agent migrating from one cluster to the other, i.e. changing its opinion in a number of steps.
- 5.13
-
In an authoritarian configuration (Figure 11), the driving forces towards the extremes of the evidence scale seem to be dissolved. Occasionally, agents change their opinion in rigid steps. But there is a force that pulls the evidence towards the centre with a constant speed. This is the result of a process of forgetting, which is more or less in balance with the process of extremization.
The agents are uniformly distributed over the complete spectrum of opinion values.
- 5.14
-
These pictures correspond to the consensus/polarization-diagrams in Hegselmann & Krause (2002). They describe segregation as caused by attraction and repulsion forces between agents with similar, respectively more distinct opinions. In our simulation model the segregation is similar; however, in contrast to Hegselmann & Krause (2002), the forces are not simply assumed, but instead they emerge in our model from the dynamics of the agents' communication.
Causal relations
- 5.15
-
We have seen that changing the independent parameters influences the dependent parameters, and we suggested some explanations for the observed facts. But are our suggestions correct? Is it the case that the independent parameters control Reputation Distribution and/or Spatial Distribution, which on their turn influence the belief parameters? Or could it be the other way around: are Reputation Distribution and Spatial Distribution influenced through the belief parameters Average Belief through Importance Distribution?
- 5.16
-
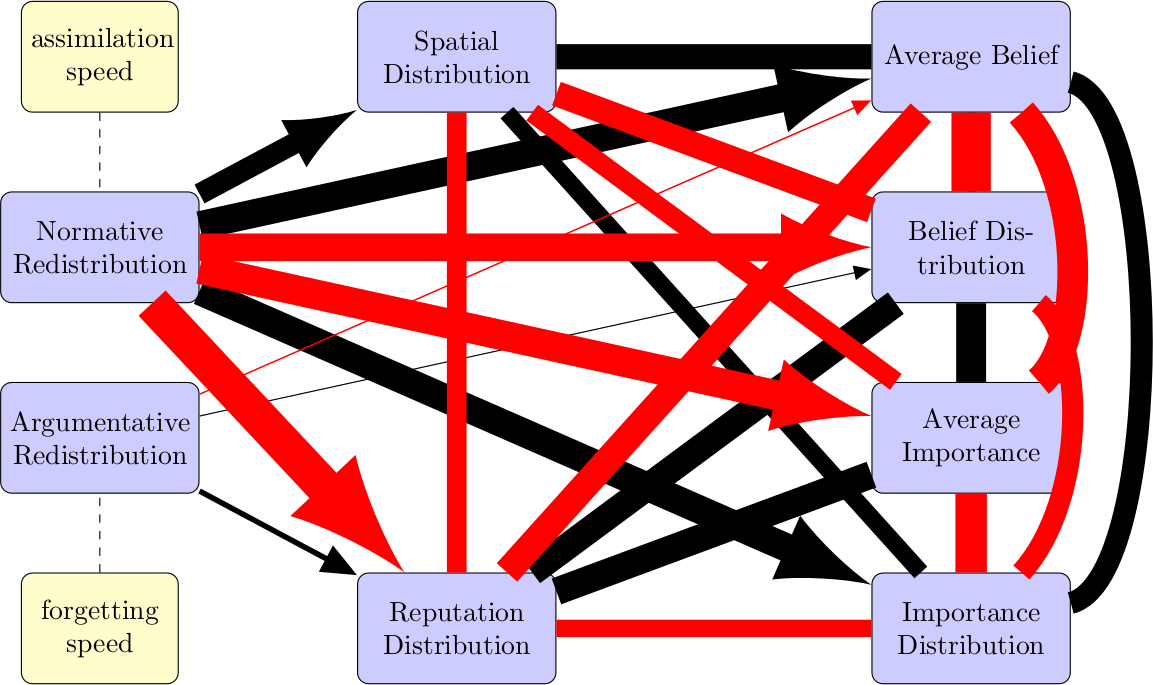
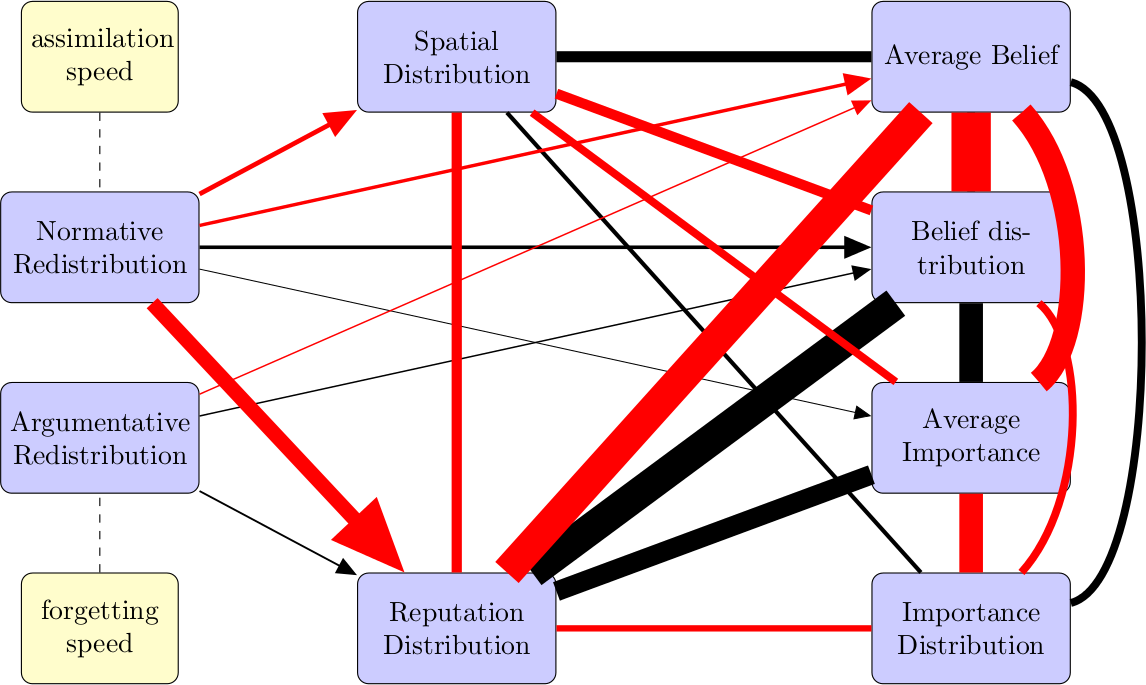
Our claim is that the causal relations are as shown in Figure 12.
We list some specific conjectures:
- Argumentative Redistribution influences Reputation Distribution positively and Spatial Distribution negatively.
- Reputation Distribution influences Average Belief negatively and Average Importance positively.
- Spatial Distribution influences Average Belief positively and Average Importance negatively.
Figure 12: The conjectured causality model. The relevant independent parameters are on the left hand side, the other parameters are the dependent parameters. Arrows that designate a positive influence have an white head. A black head refers to a negative force. 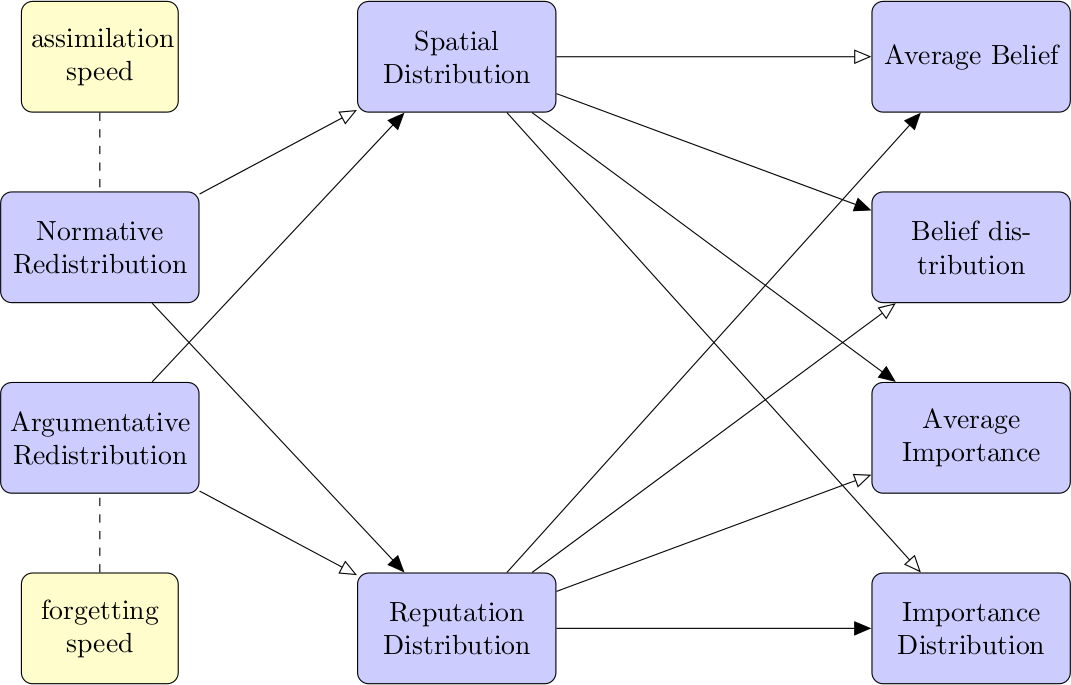
- 5.17
-
We will test these conjectures on the data from a larger experiment.
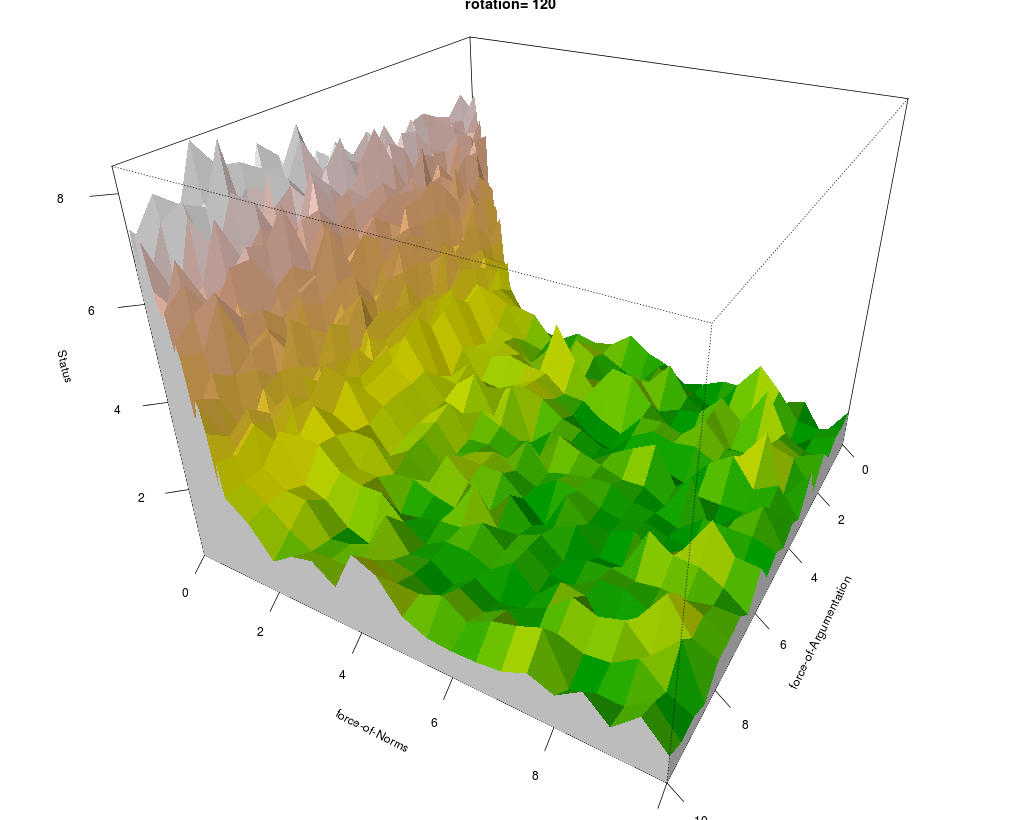
Initially, we performed runs of 200 cycles with 21 different values (viz. 0, 0.05, 0.1, ..., 0.95, 1) for each of the independent parameters force-of-Norms and force-of-Arguments, computing the six dependent parameters.
The outcomes suggested that most interesting phenomena occur in the interval [0, 0.1] of force-of-Norms.
We therefore decreased the stepsize in that interval to 0.005, so the force-of-Norms value set is (0, 0.005, 0.01, ..., 0,095, 0.10, 0.15, ..., 0.95, 1).
The evidence and importance values of the agents are randomly chosen at the start of a run, and so are the positions of the agents in the topic space.
All other parameters are fixed for all runs and are as in Table 1.
- 5.18
-
Since we have two independent parameters, each run can be associated with a point inside the square described by the points (0,0), (0,1), (1,1), (1,0).
This allows us to plot the values of the dependent parameters in 3d-plots.
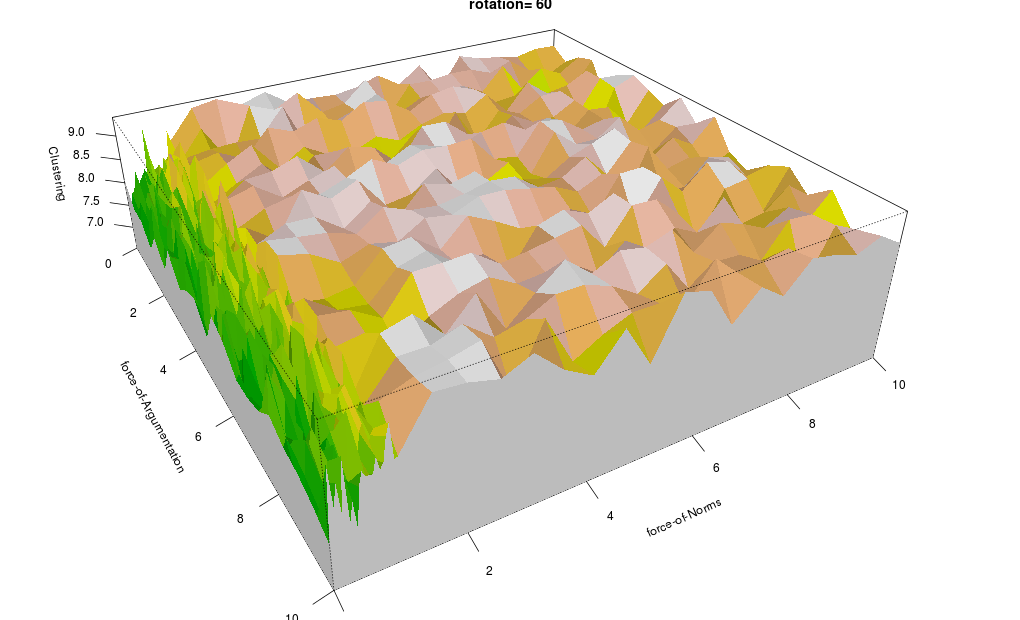
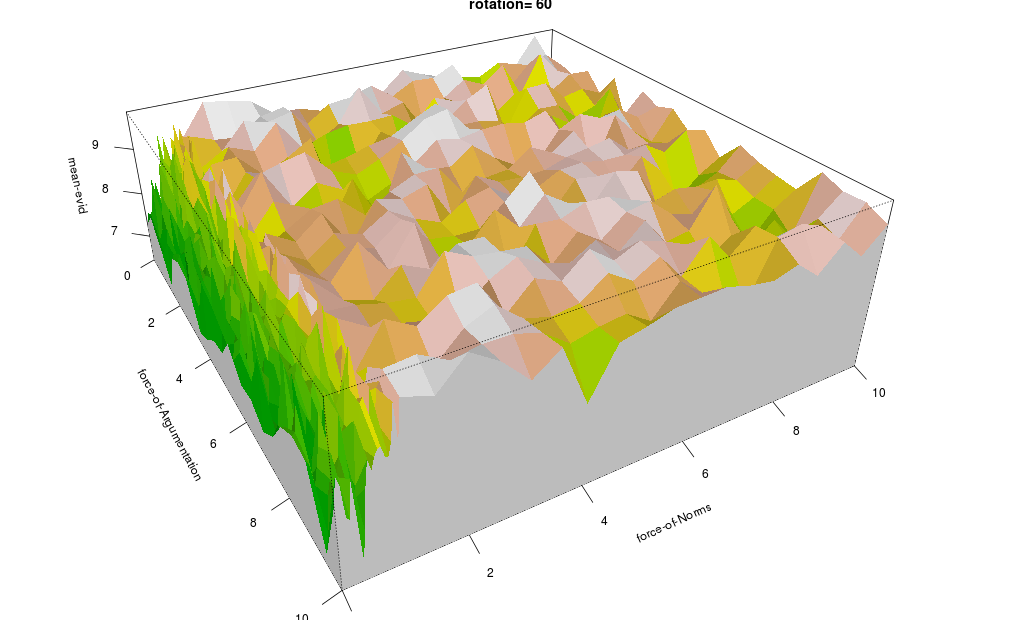
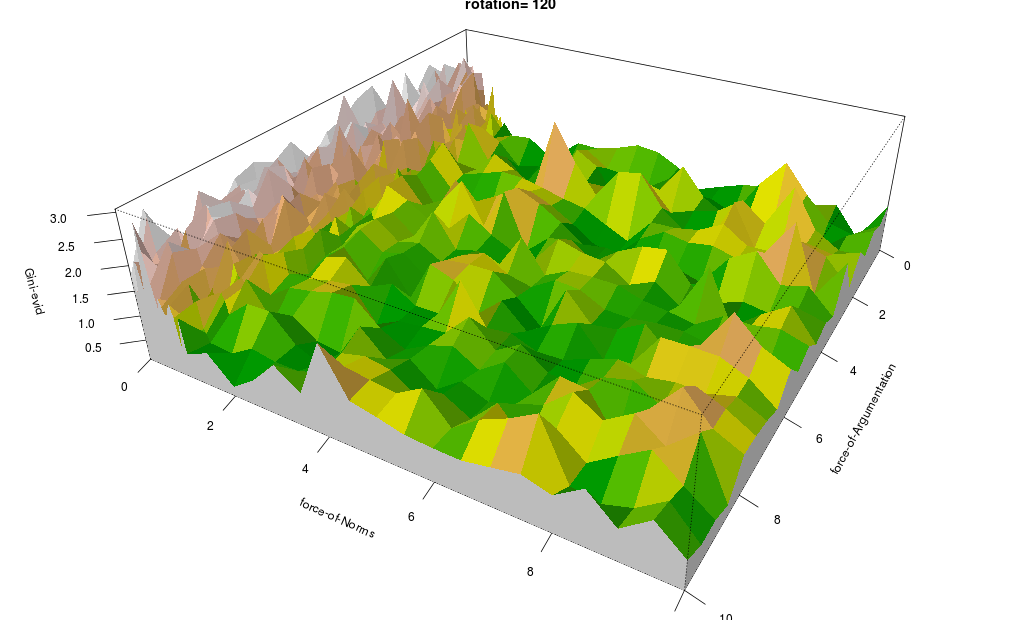
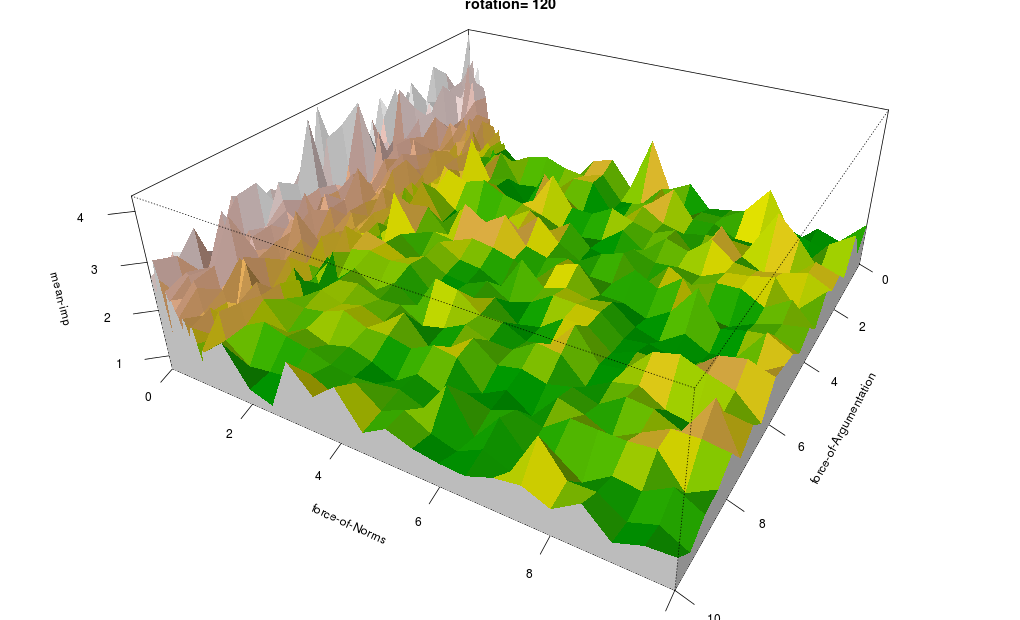
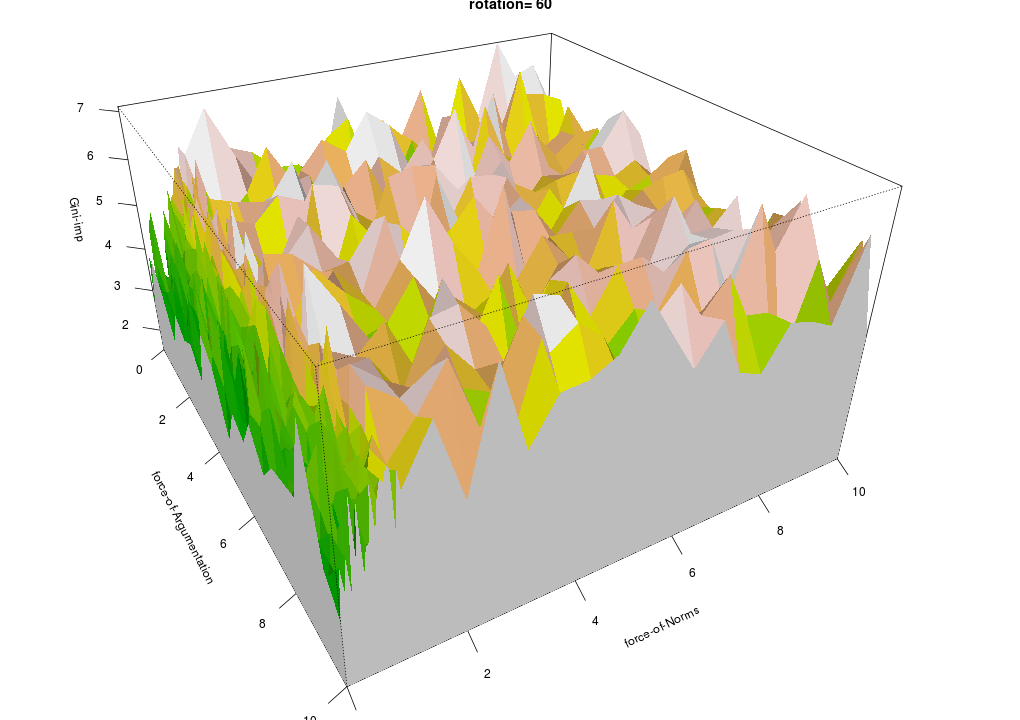
For each dependent parameter a plot is given, with the x-y-plane (ground plane) representing the independent parameters, and the vertical z-axis representing the value of the parameter in question.
The colouring ranges from green (low) via yellow (medium) to white (high); the other colours are shades.
- 5.19
-
In all Figures 13 to 18, a significant difference can be noticed between the area with low Normative Redistribution ( i.e. force-of-Norms values in the range [0, 0.1]) and the rest. These regions correspond with an authoritarian type and a segregated type, respectively.
Surprisingly, the level of Argumentative Redistribution does not seem to be of great influence.
- 5.20
-
Reputation Distribution is high (i.e. uneven distribution) when Normative Redistribution is low, and low when Normative Redistribution is high (Figure 13).
The same holds for Belief Distribution (Figure 16) and Average Importance (Figure 17), but to a lesser extent.
The reverse holds for Spatial Distribution, Average Belief and Importance Distribution (Figures 14, 15 and 18).
- 5.21
-
The bumpy area in Figure 18 reflects the same phenomenon as shown by the unstable Importance Distribution parameter in the Figures 7 and 9 and is a result of the low Average Importance.
- 5.22
-
To compare segregated type and authoritarian type runs, we distinguish two disjoint subsets: the subset with low Normative Redistribution (force-of-Norms in [0, 0.085], containing the authoritarian type runs) and the subset with high Normative Redistribution (force-of-Norms in [0.15, 1], containing the segregated type runs). Each subset contains
18×21 = 378
runs.
The boxplot of these subsets is given in Figure 19. It shows that both subsets differ in the value range of the dependent parameters.
For all dependent parameters we see that the central quartiles (i.e. the boxes) do not have any overlap.
A Welch Two Sample t-test on the Importance Distribution values of both subsets gives a p-value of 0.000007, which is smaller than 0.05. This means that the probability that both value subsets have the same mean and that deviaton between the average value of both subsets is based on coincidence is smaller than 0.05.
Therefore, both subsets should be considered different. For the other parameters the p-values are even smaller.
- 5.23
-
This confirms what we have already seen in the previous sample runs (Figures 7 to 8): Spatial Distribution is higher and Reputation Distribution lower in the segregated type runs.
Moreover, Average Belief, Belief Distribution and Average Importance are more extreme than in the low Normative Redistribution runs, which is coherent with the difference between segregated and authoritarian type runs.
Figure 19: Boxplot comparing low Normative Redistribution (authoritarian type, left hand side) and high Normative Redistribution (segregated type, right hand side). With the exception of Average Importance, all parameters have more extreme values in the high Normative Redistribution part. 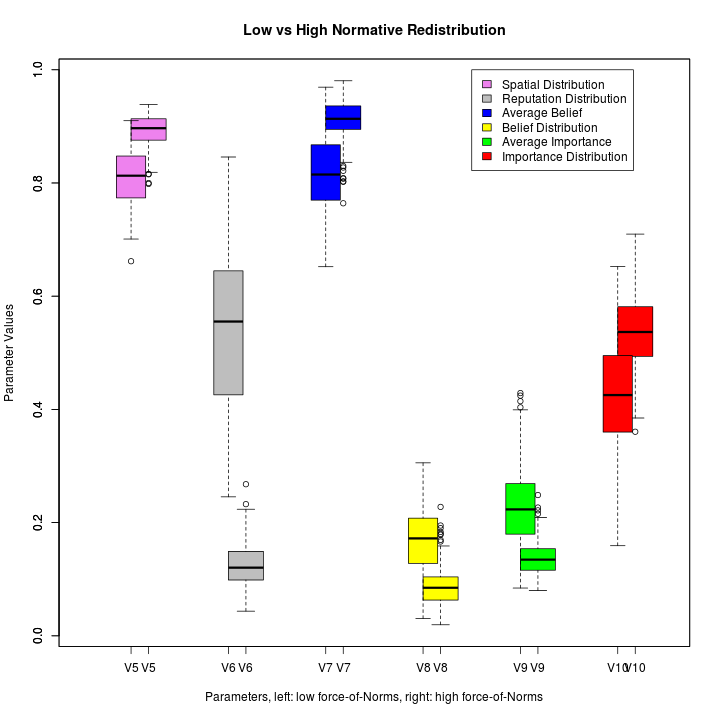
Correlations between the parameters
- 5.24
-
To give a better idea about the correlation between the independent and dependent parameters, we present pairwise plots of all the parameters.
Each tile (except those on the main diagonal) in the square of 64 tiles in the Figures 20 to 23 represents the correlation plot of two parameters.
One dot for each of the runs of the considered subset.
An idea about the value of the independent parameters of each dot is given by its colour.
The colours range from red, for low values, to blue, for high values.
- 5.25
-
Figures 20 and 21 represent the data of the low force-of-Norms (authoritarian type) subset, and Figures 22 and 23 represent the data of the high force-of-Norms (segregated type) subset.
Each tile in the square of 64 tiles in the Figures 20 to 23 represents the combination of two parameters, and contains one dot for each of the 378 runs of the considered subset.
The colour of a dot corresponds with the value of either force-of-Norms or force-of-Arguments, and ranges from red (low value) via orange, yellow, green, blue to purple (high value).
Figure 20: Low Normative Redistribution (force-of-Norms in [0,0.085]), colouring corresponds to Normative Redistribution. 
Figure 21: Low Normative Redistribution (force-of-Norms in [0,0.085]), colouring corresponds to Argumentative Redistribution. 
Figure 22: High Normative Redistribution (force-of-Norms in [0.15,1]), colouring corresponds to Normative Redistribution. 
Figure 23: High Normative Redistribution (force-of-Norms in [0.15,1]), colouring corresponds to Argumentative Redistribution. 
- 5.26
-
When the dots in a square form a line shape in the south-west to north-east direction, the plotted parameters have a positive correlation. The correlation is negative when the line shape runs from north-west to south-east. The narrower the line is, the higher the correlation. The absence of correlation is reflected in an amorphic distribution of dots over the square.
- 5.27
-
We see that the negative correlation between Average Belief and Belief Distribution is very high in both datasets, suggesting that both parameters express the same property. The consequence is that the fifth and sixth column (and the fifth and sixth row) mirror each other.
- 5.28
-
Figure 20 and Figure 21 show that Normative Redistribution (i.e. force-of-Norms) correlates with all dependent parameters.
For Argumentative Redistribution (force-of-Arguments) there are no such correlations.
This confirms our impression from Figures 13 to 18, that Argumentative Redistribution has very little influence on the state described by the six dependent parameters.
- 5.29
-
A difference between low and high Normative Redistribution is that the correlation between the dependent parameters is weaker when Normative Redistribution is high (with a few exceptions).
It is also remarkable that while combinations of high Reputation Distribution and high Average Belief are possible for low Normative Redistribution, it is not possible to have the opposite: low Reputation Distribution and low Average Belief. This asymmetry suggests that Reputation Distribution itself has a positive influence on Average Belief – which seems natural – for low Normative Redistribution.
- 5.30
-
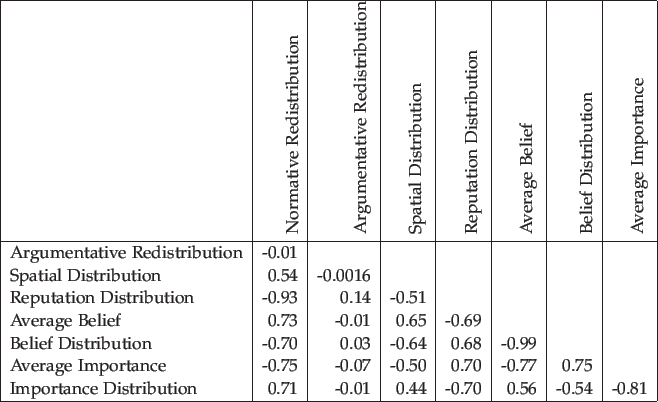
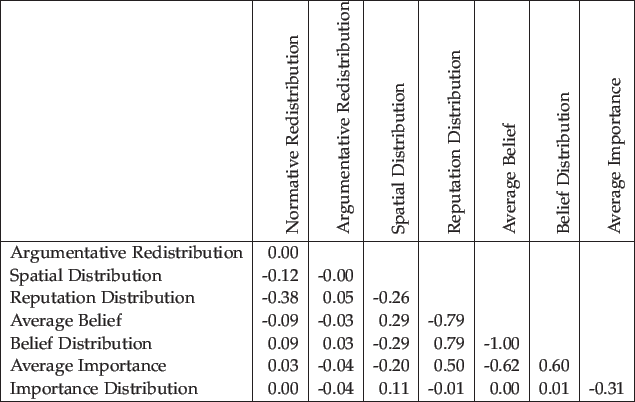
The matrices in Figure 24 and Figure 25 show the correlation between all parameters.
They confirm the conjectures that we formulated above, viz.
- Argumentative Redistribution influences Reputation Distribution positively and Spatial Distribution negatively.
- Reputation Distribution influences Average Belief negatively and Average Importance positively.
- Spatial Distribution influences Average Belief positively and Average Importance negatively.
- 5.31
-
The correlation matrices also show a strong negative correlation between Average Belief and Belief Distribution (0.99). Moreover, there is a negative correlation between Average Importance and Importance Distribution (-0.80) when Normative Redistribution is low. This supports our most important conclusion, namely that a strong Average Belief and low Average Importance imply a uneven distribution of these values among the agents. Exactly this is the cause of the emergence of extreme opinions in this model.
- 5.32
-
When we look at the relation between the belief and importance parameters, we see the strongest correlation (0.71
) between Average Belief and Importance Distribution, while the weakest correlation (-0.50
) is between Belief Distribution and Average Importance.
This bond between belief and importance is a result of the rule that the repetition of a statement increases its evidence, but decreases its importance.
Correlation Maps
- 5.33
-
In an attempt to visualize the causal relations between the parameters, we draw two correlation maps: Figure 26 and 27, based on the correlation matrices.
Now correlation between two variables may indicate causation, but the direction of causation is unknown.
Therefore we only draw arrows (indicating a possibly causal relation) from independent parameters: in all other cases, we draw only lines. Thickness of the lines is proportional to the correlation. Black lines indicate positive correlation; negative correlation is denoted by red lines.
- 5.34
-
It turns out that, when Normative Redistribution is low (Figure 26), all dependent variables depend on just one independent variable, viz. Normative Redistribution.
So we have in fact a one-dimensional system. Argumentative Redistribution has a minor positive influence on Reputation Distribution.
When Normative Redistribution is high (Figure 27), its influence is low, and the correlation of Normative Redistribution with all variables except Reputation Distribution has a changed sign in comparison with the low Normative Redistribution runs.
Not all correlations are weakened however: the correlation between Reputation Distribution on Average Belief and Belief Distribution is stronger than in the low Normative Redistribution case.
The correlation map suggests that the chain of causes starts with Normative Redistribution, which influences Reputation Distribution, which on its turn influences Average Belief and Belief Distribution; and they influence Average Importance, Importance Distribution and Spatial Distribution.
- 5.35
-
For the following observation we introduce the concept of a correlated triplet. This is a set of three parameters where all three pairs are correlated. It is expected that the number of negative correlations in a correlated triplet is either 0 or 2. To see this, imagine a correlated triplet
{A, B, C}
: when A
and B
are negatively correlated and also B
and C
, it seems plausible that A
and C
are positively correlated; so three negative correlations are very unlikely. Similarly, suppose A
and B
are positively correlated and also B
and C
: now it seems plausible that A
and C
are positively correlated; so exactly one negative correlation is unlikely, too. We observe that all correlation triplets in Figure 26 obey this restriction.
- 5.36
-
However, when Normative Redistribution is high (Figure 27) there are two correlation triplets where all correlations are negative, viz.
{ Normative Redistribution, Reputation Distribution, Spatial Distribution } , and
This is only possible if the correlations are very weak. This may explain why the influence of the force-of-Norms is surprisingly low when its value is high. All arrows leaving from force-of-Norms are much thinner than in Figure 26. The force-of-Norms value seems to have reached a kind of saturation level meaning that a stronger force-of-Norms does not have a stronger output.
{ Normative Redistribution, Reputation Distribution, Average Belief } - 5.37
-
We observe a very strong negative correlation between Average Belief and Belief Distribution. The correlation is so strong that it seems that both parameters are recorders of the same phenomenon, but this is not the case. It would be very well possible to have a simulation state with low Average Belief and low Belief Distribution, or a state with high levels for both parameters, but this never happens as can be seen in Figure 7 to 8. A similar negative correlation exists between Average Importance and Importance Distribution. This correlation is also non-trivial, and so is the positive corelation between Belief Distribution and Average Importance.
- 5.38
-
Since Belief Distribution is positively correlated to Average Importance, it follows that Average Belief and Importance Distribution are also positively correlated. And by a similar consequence, Average Belief and Average Importance are negatively correlated, and so are Belief Distribution and Importance Distribution. The correlation between Average Belief and Belief Distribution mirrors the correlation between Average Importance and Importance Distribution. In addition to that, we have the negative correlation between Spatial Distribution and Reputation Distribution. Spatial Distribution has a positive correlation with Average Belief and with Importance Distribution.
- 5.39
-
This correlation maps of Figures 26 and Figure 27 raise the following question:
Is there a hidden factor that makes Normative Redistribution lose and invert its influence?
Searching for a hidden factor
- 5.40
-
If there are hidden factors, the question is: how many? In an attempt to answer this question, we applied Principal Component Analysis (as embodied in the FactoMineR package of R: Lê et al. (2008)).
- 5.41
-
Figure 28 shows the percentage of the variance that can be explained by the different parameters, assuming the existence of 8 latent parameters (as is usual). The plots show that for low Normative Redistribution (left) only the first principal component is really important: it explains 64% of the total variance.
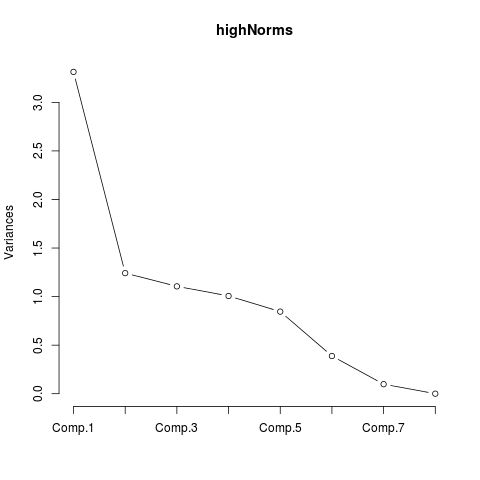
For high Normative Redistribution the importance of the main component decreases, and four auxilary components become more important as explaining factors.
- 5.42
-
Applying Principal Component Analysis, which is a form of Factor Analysis, is justified by a Bartlett test, a Kaiser-Meyer-Olkin test and the Root Mean Square errors (of the correlation residuals). The p-value of the hypothesis that two factors are sufficient for low Normative Redistribution (and 4 factors for high Normative Redistribution) is lower than 0.05. The Root Mean Square for both datasets are also below 0.05. The norm for the Kaiser-Meyer-Olkin test is that values have to be higher than 0.5, which is the case for both datasets. The results are given in Table 2.
Table 2: Justification tests for Principal Component Analysis. Test low Normative Redistribution high Normative Redistribution factors for Bartlett test 2 4 p-value Bartlett 3.27e-58 1.41e-112 KMO 0.79082 0.65695 RMS 0.045764 0.011741
Figure 28: Outcome of Pricipal Component Analysis applied to the correlation matrices for low and high Normative Redistribution. The degree of influence of 8 postulated independent parameters is plotted. Component eigenvalue percentage of variance cumulative percentage
of variancecomp 1 5.121246864 64.01558580 64.01559 comp 2 1.030778625 12.88473282 76.90032 comp 3 0.772543595 9.65679494 86.55711 comp 4 0.468223808 5.85279760 92.40991 comp 5 0.420790991 5.25988738 97.66980 comp 6 0.126523345 1.58154181 99.25134 comp 7 0.054744103 0.68430128 99.93564 comp 8 0.005148669 0.06435836 100.00000 Figure 29: Low Normative Redistribution. Only the first two components are significant because they have eigenvalues > 1. Component eigenvalue percentage of variance cumulative percentage
of variancecomp 1 3.3137638846 41.42204856 41.42205 comp 2 1.2416895774 15.52111972 56.94317 comp 3 1.1055887273 13.81985909 70.76303 comp 4 1.0063573718 12.57946715 83.34249 comp 5 0.8456376275 10.57047034 93.91296 comp 6 0.3882566455 4.85320807 98.76617 comp 7 0.0981938786 1.22742348 99.99360 comp 8 0.0005122872 0.00640359 100.00000 Figure 30: High Normative Redistribution. Components 1 - 4 have eigenvalues > 1 and are significant. 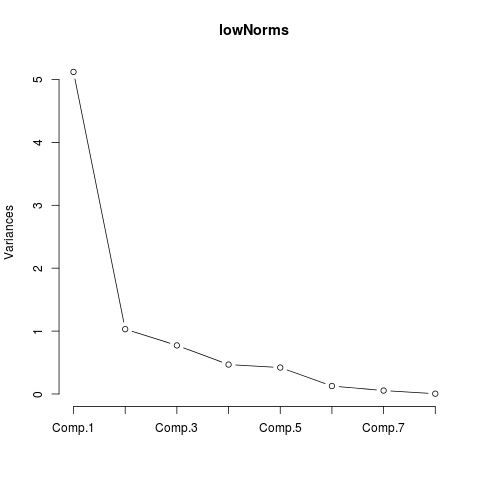
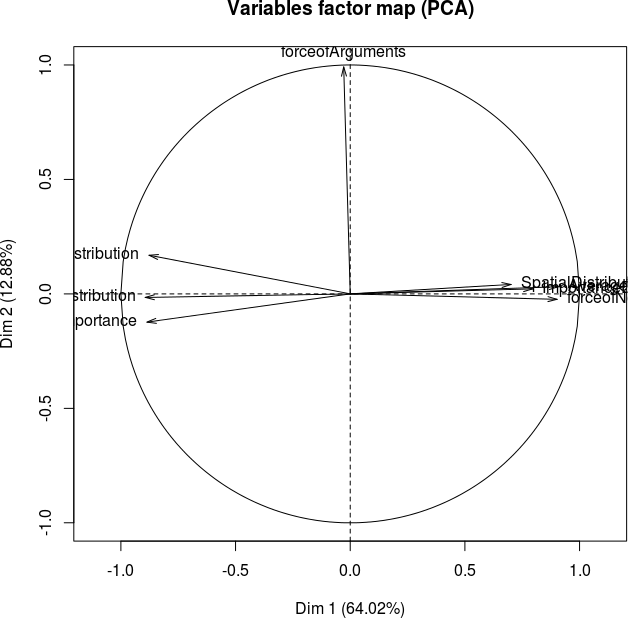
Now we want to know the identity of these components. For the low Normative Redistribution case we know that Normative Redistribution is the most important factor, and therefore it is likely that Normative Redistribution and the first principal component are actually the same. How the dependent parameters can be retreived from the calculated components is reveiled in te factor maps of Figure 31. The factor loadings for the Principal Component Analysis of both datasets are given in Table 4.
- 5.43
-
The left factormap of Figure 31 confirms this idea. Here the dependent variables are correlated with two latent components. High correlation with one component is expressed as an arrow in the direction of that component. If both components are equally important for the dependent parameter, the arrow has an angle of 45o
with both component axes.
We see that the first component positively influences Normative Redistribution, Spatial Distribution, Importance Distribution and Average Belief, while it influences Belief Distribution, Average Importance and Reputation Distribution negatively. We may conclude that the first component is in fact Normative Redistribution and the second component is Argumentative Redistribution, which has only a weak influence on Reputation Distribution and Average Importance.
- 5.44
-
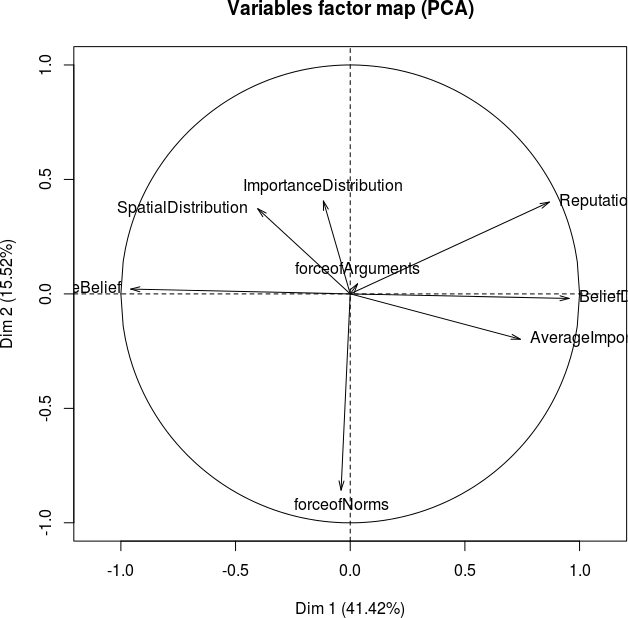
When Normative Redistribution is high, the right factormap of Figure 31 shows that Normative Redistribution is negatively correlated with the second principal component. The first component, which explains twice the amount of variance in comparison with the second component, is Belief Distribution (or negatively: Average Belief). So the first component is a true latent parameter, and it corresponds highly with Belief Distribution.
However it is not the same parameter, because Belief Distribution is a dependent parameter and the newly found latent parameter is an independent parameter (causing factor).
Therefore we will name this latent independent parameter Pluriformity. This expresses the degree of inequality in the beliefs of the agents in the population, which is precisely the meaning of Belief Distribution.
- 5.45
-
When we compare Pluriformity with the components in the (one-dimensional) low Normative Redistribution case, we see that it is not orthogonal but contrary to the Normative Redistribution parameter.
But how can a latent or independent parameter emerge in a simulation system?
This can be answered as follows.
When Normative Redistribution has reached its saturation level, the stochastic nature of agent actions in the simulation model still generates variety in the model states (the values of the dependent variables after 200 cycles) of the experiment. The dependencies that emerge in this situation, depend only on the pecularities of the underlying game. Principal component analysis reveals a possible explanatory component (causing force) for these dependencies in DIAL.
- 5.46
-
More components are relevant in the case of high Normative Redistribution; we also plotted the first component Pluriformity against two other components (Figure 32). It shows that the third component is to a degree synonymous with Importance Distribution and the fourth component is Argumentative Redistribution, which is highly independent of the other parameters. So the other principal components are the already known independent parameters.
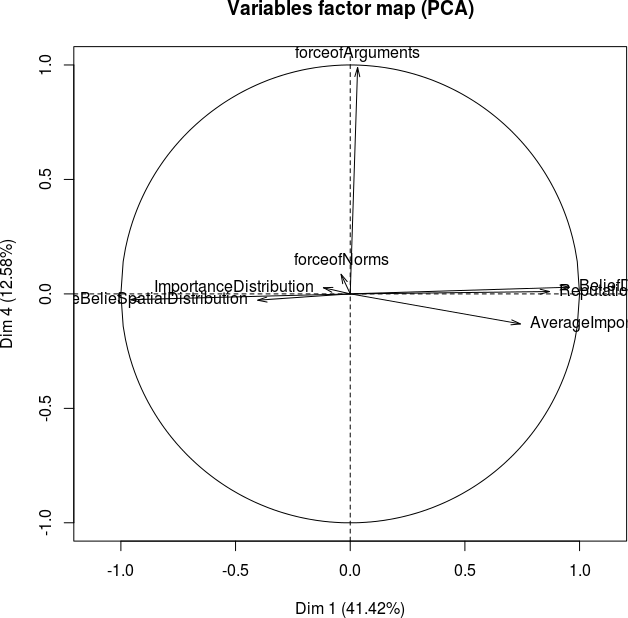
Figure 32: Factormap for (A) the first and third principal component and (B) the first and fourth principal component. 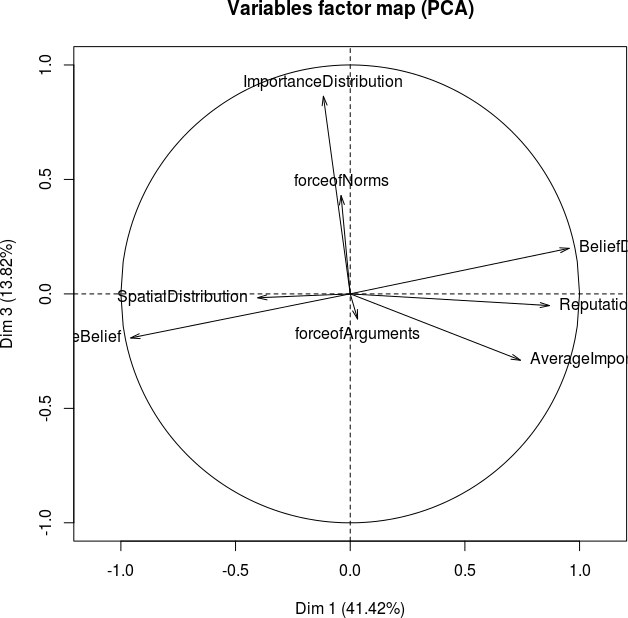
 (A) (B)
(A) (B)Table 3: Factor loadings low Normative Redistribution. Parameter comp1 comp 2 comp 3 comp 4 Normative Redistribution -0.043130 0.816307 0.135318 0.073938 Argumentative Redistribution 0.023861 -0.016411 0.016871 0.115345 Spatial Distribution -0.304245 -0.132709 0.045772 -0.256649 Reputation Distribution 0.885499 -0.441814 0.054505 0.146949 Average Belief -0.970050 -0.139624 -0.170281 0.044717 Belief Distribution 0.966860 0.139989 0.180188 -0.039016 Average Importance 0.689594 0.155347 -0.464526 -0.202780 Importance Distribution -0.084827 -0.100561 0.565485 -0.155203 Table 4: Factor loadings high Normative Redistribution. Parameter comp 1 comp 2 Normative Redistribution 0.896677 0.279955 Argumentative Redistribution -0.023683 -0.033705 Spatial Distribution 0.635191 -0.144248 Reputation Distribution -0.861629 -0.283399 Average Belief 0.928792 -0.387833 Belief Distribution -0.910489 0.398225 Average Importance -0.856628 -0.098496 Importance Distribution 0.755080 0.309945
 Discussion
Discussion
- 6.1
-
In our model we observe that, when dialogues do not play an important role in the agent society (high Normative Redistribution and low Argumentative Redistribution), clusters are formed on the basis of a common opinion. It turns out that the lack of communication between clusters enables the emergence of extreme opinions. On the other hand, when the outcomes of dialogues do play an important role (low Normative Redistribution and high Argumentative Redistribution), the formation of clusters based on a common opinion is suppressed and a variety of opinions remains present.
- 6.2
-
Principal Component Analysis has provided new information in addition to the established correlations:
- The direction of causation can be established. Normative Redistribution decreases Reputation Distribution, which has a negative influence on Average Belief and a positive influence on Belief Distribution. And a higher Average Belief (extremeness) leads to more Spatial Distribution.
- Pluriformity is a latent parameter which is the most important factor in the high Normative Redistribution runs. This is counterintuitive; we would expect that Normative Redistribution would be the most important factor.
- When Normative Redistribution is low, DIAL provides a one-dimensional model with strong dependencies between Normative Redistribution and all the dependent parameters.
- In the high Normative Redistribution runs the strong correlations between Normative Redistribution and the dependent parameters disappear and the working of a latent force is revealed, which correlates strongly with the strongly coupled Average Belief-Belief Distribution pair, which corresponds to the negative extremism scale. We called this force Pluriformity.
- Argumentative Redistribution is the second component (explaining 13 % of the variance) in the low Normative Redistribution range. It has more influence on Reputation Distribution and Average Importance in the high Normative Redistribution runs.
- Spatial Distribution seems to be directly influenced by Normative Redistribution in the low Normative Redistribution area, but this effect completely disappears in the high Normative Redistribution area. Then it is correlated to extremism in the pluralism scale.
- 6.3
-
Social Judgement Theory (Sherif & Hovland 1961) describes the conditions under which a change of attitudes takes place by assimilation and contrast effects. In DIAL assimilation to the environment is the source of changes in opinions. We reward well-adapted agents and/or agents who win debates with a higher reputation status. Together with homophily (Suls et al. 2002; Lazarsfeld & Merton 1954), which is implemented in the move behaviour, it results in clustering. Contrast effects emerge indirectly as a result of this form of segregation. In future work we will investigate an agent model with an acceptance-rejection strategy for utterances based on (Huet et al. 2008; Hegselmann & Krause 2002).
- 6.4
-
In DIAL the development of extremization of opinions Franks et al. (2008); Deffuant et al. (2002); Deffuant (2006) is caused by the way the acceptance function is defined. Once segregation (spatial distribution) has taken place and agents are not confronted anymore with utterances of different minded agents, the agent's opinion is bound to extremize with each utterance of a neighbouring agent. This explains the negative correlation between Spatial Distribution and Belief Distribution (pluraliformity) (see Figures 26 and 27). In our experiments we consider only one proposition. When we extend the simulation to more than one proposition, it will be more complicated for agents to avoid different-minded agents, which will hinder the extremization process (Dykstra et al. 2010) .
Reputation Distribution and its relation with norms was studied by Sabater-Mir et al. (2006) and Conte & Paolucci (2003). DIAL shows that Reputation Distribution is inhibited by the influence of norms in the low-force-of-Norms case. This negative influence even exists in the high force-of-Norms runs, although the inhibition by pluraliformity is more important (Figures 26 and 27). Reputation Distribution cannot be considered as an incentive to cooperation as in Sabater-Mir et al. (2006), because there is a negative correlation with Spatial Distribution. Brandt et al. (2003) and McElreath (2003) note that in games agent's reputation serves to protect him from attacks. Reputation Distribution has the same result in DIAL. The number of attacks drops in runs when Reputation Distributionstatus is high.
- 6.5
-
The interaction between opinion- and social network-dynamics, which is the basis of Carley (1986) and Festinger (1954), functions also in DIAL, but in circumstances with a low degree of Spatial Distribution a social structure is practically absent and social contacts are almost random.
 Concluding Remarks and Future Work
Concluding Remarks and Future Work
- 7.1
-
We have presented DIAL, a cognitive agent-based model of group communication. Agents are involved in a dialogue game in which they gamble reputation points on the truth of a statement. Dialogue conflicts are resolved by appeal to surrounding agents in such a way that the more supported statement wins the dialogue. Our model shows the radicalisation in clusters through extremization of individual opinions of agents in Normative Redistribution models and this phenomenon is prevented in Argumentative Redistribution models. This process is based on two simple ingredients: movement in topic space, and communication with others in dialogues.
The movement in topic space ensures that agents interact with others dynamically and that they are able to align themselves with others of similar opinions.
Extreme opinions are typical for isolated clusters.
To extrapolate the results from our model simulations to current society, we may tentatively conclude that, as far as social media like Twitter and Facebook are about creating an open society, they might be an effective weapon in fighting extremism.
- 7.2
-
An important question is:
Is DIAL realistic enough to reflect the social processes in human society?
In future research we plan to answer this question by testing more social, psychological and communicational aspects in DIAL. - 7.3
-
This paper is the first part of a trilogy. In the second part we will investigate the extension of DIAL with Fuzzy Logic to represent agent attitudes (Dykstra et al. 2010). We will introduce a set of a partial orderings on statements, which serves as the domain of the linguistic variables for the corresponding fuzzy sets.
With this extension, changes of opinions can be expressed according to Social Judgement Theory (Sherif & Hovland 1961).
- 7.4
- In a third part of our research program, we will investigate how aware agents need to be of their rôle in the social process, in order to explain phenomena such as the extremization of opinions in society. Does it really make a difference whether they possess the ability to reason about other agents' beliefs or not? After adding these new ingredients, we intend to investigate what would happen in a normative society, which has moved to an extreme position, when it is suddenly confronted with previously unused information flows like those provided by social media. For example, would this sudden open communication result in a strong force towards a pluriform society, or not? Rephrased in actual terms: could the North-African revolutions, which were facilitated by social media, result in a strong force towards a pluriform society or not?
 Appendix A
Appendix A
-
The 2-dimensional logic of Belnap & Anderson
A 2-dimensional Belnap & Anderson logic has been designed for a slightly simpler case (Belnap 3). Suppose an agent has no prior knowledge about a certain statement and asks two or more agents a yes - or - no question about the matter. What are information states the agent may achieve? Belnap and Anderson considered four outcomes that the agent could get:
- no answer at all ({})
, also denoted by
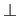 - the agent still has no clue,
- the agent still has no clue,
- some answers were yes and there weren't any no's ({true}) - the agent believes it's true,
- some answers were no and there weren't any yes's ({false}) - the agent believes it's false - and
- some answered yes and some answered no
({false, true})
, also denoted by
 - the information is contradictory.
- the information is contradictory.
When we represent the information states by pairs (p, k) with p, k
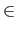 {0, 1}
, with p = 1
meaning ''there is a yes'' and p = 0
meaning ''there is no yes'' and similar for k
, then we have our 2-dimensional logic reduced to four values. Ginsberg, in (Restall 45), notice a relation between these values along two parameters similar to what we did above. He calls it the amount of belief in a value (t)
and the amount of information k
(for knowledge). t
corresponds with our notion of evidence, the degree of belief an agent has in the statement, and k
corresponds with i
- importance-, although it has a different interpretation. Both relations are partial orders, denoted by
{0, 1}
, with p = 1
meaning ''there is a yes'' and p = 0
meaning ''there is no yes'' and similar for k
, then we have our 2-dimensional logic reduced to four values. Ginsberg, in (Restall 45), notice a relation between these values along two parameters similar to what we did above. He calls it the amount of belief in a value (t)
and the amount of information k
(for knowledge). t
corresponds with our notion of evidence, the degree of belief an agent has in the statement, and k
corresponds with i
- importance-, although it has a different interpretation. Both relations are partial orders, denoted by 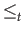 and
and 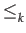 .
.
In Figure 33 (a) the area inside the square represents the possible belief values an agent may assign to a statement. The arrows have a special meaning: increasing belief and increasing importance as a simultaneous move on the R- and P-axis.
Figure 33: The square of possible belief assignments. Belnap's diamond (a) and our two dimensional belief space (b). k = (amount of) knowledge, t = truth P = Pay, R = Reward. 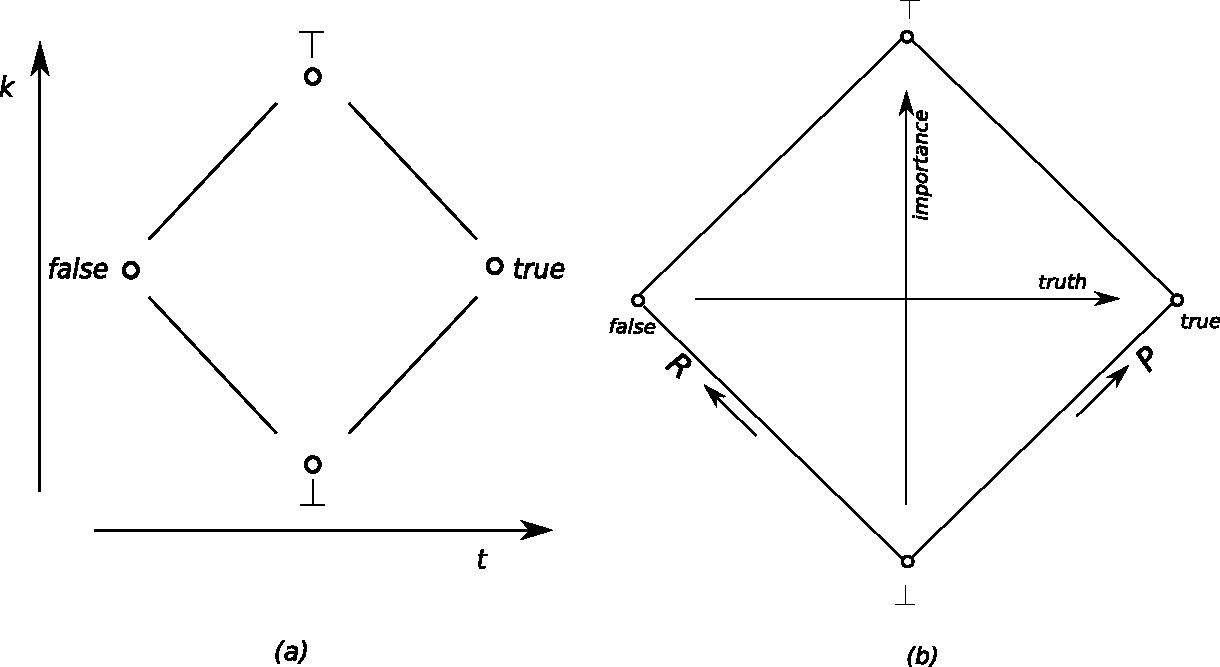
 Appendix B
Appendix B
Computing the acceptance function
We can distinguish two auxiliary functions AE : [0, 1]×[0, 1]
 [0, 1]
and
AI : [0, 1]2×[0, 1]2
[0, 1]
and
AI : [0, 1]2×[0, 1]2  [0, 1]
with
A((e1, i1),(e2, i2)) = (AE(e1, e2), AI((e1, i1),(e2, i2))).
[0, 1]
with
A((e1, i1),(e2, i2)) = (AE(e1, e2), AI((e1, i1),(e2, i2))).
Before we give the definition of AE and AI , we formulate some requirements:- A is continuous, i.e. small changes in its independent values lead to small changes in the result;
- AE is monotonic, i.e. when its independent values increase, the result increases;
- A is symmetric, i.e. A((e1, i1),(e2, i2)) = A((e2, i2),(e1, i1)) ;
- AE commutes with the negation function n(x) = 1 - x , i.e. AE(1 - e1, 1 - e2) = 1 - AE(e1, e2) ;
- AE
is confirmative: similar evidence is reinforced, contradicting evidence is weakened, i.e.
AE(e1, e2)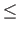 e1, e2
if
e1, e2
e1, e2
if
e1, e2  0.5
,
0.5
,
AE(e1, e2) e1, e2
if
e1, e2
e1, e2
if
e1, e2 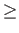 0.5
,
0.5
,
e1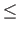 AE(e1, e2)
AE(e1, e2) 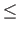 e2
if
e1
e2
if
e1 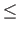 0.5
0.5 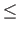 e2
;
e2
;
- AI
is controversial: similar evidence leads to weakening of importance, contradicting evidence leads to strengthening of importance, so
AI((e1, i1),(e2, i2))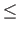 0.5(i1 + i2)
if
e1, e2
0.5(i1 + i2)
if
e1, e2 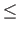 0.5
or
e1, e2
0.5
or
e1, e2 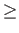 0.5
,
0.5
,
AI((e1, i1),(e2, i2))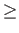 0.5(i1 + i2)
if
e1
0.5(i1 + i2)
if
e1 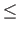 0.5
0.5 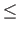 e2
.
e2
.
AE(e1, e2) = 2e1e2 if e1, e2 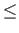 0.5
0.5= 2e1 +2e2 -2e1e2 - 1 if e1, e2  0.5
0.5= e1 + e2 - 0.5 otherwise
andAI((e1, i1),(e2, i2)) = 0.5(i1 + i2) + 0.125(2e1 -1)(2e2 -1)(2i1i2 - i1 - i2).
Checking the requirements for AE is straightforward, except for the second case in the confirmativity requirements. For this, we observe: if e1, e2 0.5
then
AE(e1, e2) = 2e1 +2e2 -2e1e2 -1 = e1 + (1 - e1)(2e2 -1)
0.5
then
AE(e1, e2) = 2e1 +2e2 -2e1e2 -1 = e1 + (1 - e1)(2e2 -1)  e1
, and similar for
AE(e1, e2)
e1
, and similar for
AE(e1, e2)  e2
.
e2
.
For a better understanding of the definition of AI , we observe that 0.25(2e1 -1)(2e2 - 1) plays the role of agreemement factor
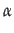 , ranging from -1 to 1: it is positive when
e1, e2 > 0.5
or
e1, e2 < 0.5
, negative when 0.5 is between e1
and e2
and zero when e1
or e2
equals 0.5.
We can define AI
also using
, ranging from -1 to 1: it is positive when
e1, e2 > 0.5
or
e1, e2 < 0.5
, negative when 0.5 is between e1
and e2
and zero when e1
or e2
equals 0.5.
We can define AI
also using 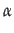 :
AI((e1, i1),(e2, i2)) =
:
AI((e1, i1),(e2, i2)) =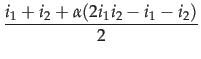
Depending on the value of this agreement factor, the value of AI((e1, i1),(e2, i2)) ranges from i1 + i2 - i1i2 when c = - 1 via 0.5(i1 + i2) when c = 0 to i1i2 when c = 1 .Moreover, we have the following limit properties of A . Suppose we have a sequence (e0, i0),(e1, i1),(e2, i2),... , abbreviated by ((en, in) | n
 N)
. We consider the result sequence
((rn, sn) | n
N)
. We consider the result sequence
((rn, sn) | n  N)
, obtained by repeatedly applying A
:
N)
, obtained by repeatedly applying A
:
(r0, s0) = (e0, i0) (rn+1, sn+1) = A((rn, sn),(en+1, in+1)) for alln  N
N
When does ((rn, sn) | n N)
converge to a limit? To formulate some properties, we use the following notion:
N)
converge to a limit? To formulate some properties, we use the following notion:
sequence (xn | n
and 'well above a ' is defined similarly. Now we have: N)
is well below a
if there is a b < a
and a m
N)
is well below a
if there is a b < a
and a m 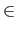 N
such that
xn
N
such that
xn 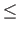 b
for all n
b
for all n 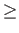 m
;
m
;
- if
(en | n
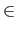 N)
is well below 0.5, then the result sequence of
((en, in) | n
N)
is well below 0.5, then the result sequence of
((en, in) | n  N)
converges to the limit (0,0);
N)
converges to the limit (0,0);
- if
(en | n
 N)
is well above 0.5, then the result sequence of
((en, in) | n
N)
is well above 0.5, then the result sequence of
((en, in) | n  N)
converges to the limit (1,0).
N)
converges to the limit (1,0).
 Appendix C
Appendix C
Description of the Model Parameters
A brief description of the independent and dependent parameters is given here. for the implementation details see the listing of the DIAL program.
Independent pararameters:
- number-of-agents. The number of the agents in a simulation.
- number-of-propositions. The number of the propositions the agents talk about in a simulation. In this case number-of-propositions = 1.
- Force-of-Arguments (informational-conformity). Determines the degree in which the agent's reputation is determined by winning and losing debates.
- Force-of-Norms (normative conformity). The degree in which the reputation is determined by the similarity with its environment.
Parameters influencing the choice of actions:
The folowing parameters determine the probability that an agent will chose the corresponding action:- chance-announce. Utter an announcement.
- chance-walk. Movement in the topic space.
- chance-attack. Attack a recently heard announcement. (The most different one from the own opinion with the highest probability)
- chance-question. Ask another agent about its opinion.
- chance-change-stategy. Probability of changing the walking direction (away from, or towards friends or perpendicular to the best friends' position).
- chance-learn-by-neighbour. Learn from the nearest neighbour.
- chance-learn-by-environment. Learn from the average opinion on the agents' location.
- chance-mutation. Change (e,i)–values of an opinion to a random value.
Parameters influencing behaviour:
- loudness. Determines the distance that a message can travel for anonymous communication. Anonymous communication affects the environment (patches) and indirectly its inhabitants through the learn-by-environment action.
- visual-horizon. Determines the maximum distance to other agents who's messages can be heard (including the sender, which is necessary for attacking.
- undirectedness. Randomness of the direction of movement.
- stepsize. Maximum distance traveled during a walk.
Parameters influencing reputation:
- inconspenalty. Penalty for having inconsistent opinions.
- lack-of-principle-penalty. Penalty for uttering statements that do not reflect the agent's true opinion.
Parameters influencing opinion:
- neutral-importance. The level of importance the environment returns to when no announcements are made and past announcements will be forgotten. (Typically 0.5)
- attraction. The largest distance in the evidence value of an uttered proposition and the evidence value of the same proposition of a receiving agent for which the receiver is inclined to adjust its opinion.
- rejection. The shortest distance in the evidence value of an uttered proposition and the evidence value of the same proposition of a receiving agent for which the receiver is inclined to attack the uttered proposition.
- winthreshold. The minimal difference between the evidence value of the proponent's - and the opponent's proposition that forces the loser of the debate to change its opinion immediately (instead of indirectly via learning by environment or learning by neighbour).
Parameters influencing memory:
- forgetspeed. The speed the evidence- and importance-values of the agents' opinion converges to neutral values (typically 0.5).
- neutral-importance. (May differ from 0.5.)
Dependent parameters:
- Reputation Distribution. The unequality (gini) of the distribution of reputation over the agent population(report-authority).
- Spatial Distribution. Degree of clustering of the agents (report-clustering).
- Average Belief. Mean deviation of the evidence from the neutral value (0.5) (report-eopop).
- Belief Distribution. Gini-evidence of the deviation of the evidence from the neutral value (0.5) (report-ginievid).
- Average Importance. Mean importance of the opinion (report-iopop).
- Importance Distribution. Gini-importance of the opinion (report-giniimp).
 Appendix D
Appendix D
extensions [array] turtles-own [ props ; a list of pairs: < evidence importance > ; the evidence of the p-th proposition is: first item p props ; the importance of the p-th proposition is: second item p props init-props ; a list of pairs: < evidence importance > the initial values announcements ; a list of 4-tuples: < key <evidence importance> ticks reputation> attacks ; a list of pairs: < attacking-agent prop > questions ; a list of pairs: < requesting-agent prop > profit-strategy ; list of learned profits for each strategy prior-size ; prior size for profit ; the reputation of an agent is represented by its size ] patches-own [pprops] globals [ delta ; a small value action-prob-pairs ; a list of odds-action pairs, ; one for each behavioral alternative current-prop ; the proposition which is pictured in the world number-of-props total-odds ; the sum of the odds of all behavioral alternatives change-reputation ; the change of the sum of the reputation of all agents ; during one cycle total-reputation ; the sum of the reputation of all agents filename agentsorderedatstart ; for reporting purposes strategy-shapes ; a list of shapes, one for each strategy ] ; Utility functions to-report second [l] report item 1 l end to-report zip [l m] ifelse empty? l [report l] [report fput (list (first l) (first m)) (zip (butfirst l) (butfirst m))] end to-report sign [x] ifelse x >= 0 [report 1] [report -1] end ; The Acceptance of Announcements to-report agreementfactor [e1 e2] report (2 * e1 - 1) * (2 * e2 - 1) end to-report accepte [e1 e2] ifelse e1 < 0.5 [ ifelse e2 < 0.5 [ report 2 * e1 * e2 ][ report e1 + e2 - 0.5 ] ][ifelse e2 < 0.5 [ report e1 + e2 - 0.5 ][ report 2 * e1 + 2 * e2 - 2 * e1 * e2 - 1 ] ] end to-report accepti [agree i1 i2] report (i1 + i2 + agree * (2 * i1 * i2 - i1 - i2)) / 2 end ; environment oriented procedures for accepting announcements and ; forgetting. the patches are used for anonymous communication. ; the information of announcements are accumulated in the patches ; according to the accept function. forgetting is a ; a gradual move towards neutral values ((e,i) = (0.5, 0.5)) to announce-patch [agnt loc evid imp]; patch procedure; input agent is a turtle ; update the patches with the information of the announcement ; this is proportional to the distance from the agent that made the announcement. let rsquared (distance agnt + 1) ^ 2 let pevid first item loc pprops let pimp second item loc pprops let agree (agreementfactor evid pevid) set pevid 0.5 + ((accepte evid pevid) - 0.5 + rsquared * (pevid - 0.5)) / (rsquared + 1) set pimp ((accepti agree imp pimp) + rsquared * pimp) / (rsquared + 1) set pprops replace-item loc pprops (list pevid pimp) end ; Forgetting means changing gradually the pevidence and pimportance ; to a neutral value (which is 0.5) to-report forget-pevidence [pevidence] report pevidence - sign (pevidence - 0.5) * forgetspeed end to-report forget-pimportance [pimportance] report pimportance - sign (pimportance - neutral-importance) * forgetspeed end ; Agent-agent communication, used in announcements, questions and ; replies on attacks. to update-announcement [w p ev i ] ; w = sender, p = proposition ; update memory let key number-of-agents * p + w let loc find-location key announcements ifelse loc != false [ set announcements replace-item loc announcements (list key (list ev i) ticks) ; do something with reputation ][ set announcements fput (list key (list ev i) ticks) announcements] ; now the SJT type attraction and rejection let evidence first item p props let importance second item p props let agree (agreementfactor evidence ev) if agree > 1 - attraction [ setopinion p (list (accepte evidence ev) (accepti agree importance i)) ] ; accept p if agree < rejection - 1 [ setopinion p (list (accepte evidence (1 - ev)) (accepti (agreementfactor evidence (1 - ev)) importance i)) ] ; attack agent w on p end to-report find-location [a b] report position a (map [first ?] b) end to forget-announcements ; all announcements older than 10 ticks are forgotten let yesterday ticks - 10 set announcements filter [ yesterday < item 2 ?] announcements end ; initialization and the main loop ;;to-report random-prop ; to create a proposition with random evidence ; and importance values, used in setup ;;report list (random-float 1) (random-float 1) ;;end to setup clear-all reset-ticks set delta 1e-5 set number-of-props number-of-propositions set current-prop min (list (position current-proposition ["a" "b" "c" "d" "e" "f" "g" "h" "i" "j"]) (number-of-props - 1)) ;; create turtles with random locations, evidence and importance values set strategy-shapes ["circle" "default" "face happy"] set-default-shape turtles "circle" ask patches [ set pcolor blue set pprops[] repeat number-of-props [ set pprops fput (list 0.5 neutral-importance) pprops] ] crt number-of-agents [ setxy random-xcor random-ycor set props generateopinions set init-props props set announcements [] set attacks [] set questions [] set color scale-color yellow first (item current-prop props) 1 0 set label who set label-color 66 set size (random-float 2) + 1 set profit-strategy [0 0 0] ] set total-reputation sum [size] of turtles setup-plot ;update-plotfile ;; !!!!!!! end to-report incr-total-odds [ee] set total-odds total-odds + ee report total-odds end to-report find-action [c l] while [c > first (first l) ] [set l but-first l] report first l end to go ; Determine the chances of all agent actions according to the values ; of the global parameters, chance-announce, chance-question, chance-attack, ; chance-walk, chance-learn-by-neighbour, chance-learn-by-environment, ; chance-mutation and chance-change-strategy set total-odds 0 set action-prob-pairs (map [list (incr-total-odds ?1) ?2] (list chance-announce chance-question chance-attack chance-walk chance-learn-by-neighbour chance-learn-by-environment chance-mutation chance-change-strategy) (list "announce" "question" "attack" "walk" "learn-by-neighbour" "learn-by-environment" "mutate" "change-strategy" )) set change-reputation 0 ask turtles [act] ; The forgetting of anonymous information ask patches [ ; to forget set pprops map [ list (forget-pevidence first ?) (forget-pimportance second ?)] pprops ] ; Rounding off: forget announcements, answer some questions which were put ; in this cycle and reply some attacks made by other agents in this cycle. ; These three actions are different from the previous ones by the fact that ; they are performed each cycle, so they are not subject to some choice ; constrained by global parameters. ask turtles [ forget-announcements answer-questions reply-attacks ] ; The change of reputation is normalized so that the sum of the reputations ; of all agents (total-reputation) remains constant over time. let f total-reputation / (total-reputation + change-reputation) ask turtles [set size max (list 0 (size * f))] show-world tick end to-report similar-attitude [a b] report sum (map [agreementfactor first ?1 first ?2] a b ) end to act set prior-size size run second (find-action (random-float total-odds) action-prob-pairs) let sim normative-conformity * similar-attitude props pprops / number-of-propositions - lack-of-princ-penalty * similar-attitude props init-props / number-of-propositions if size + sim > delta [ set size size + sim set change-reputation change-reputation + sim ] foreach [0 1 2] [ ifelse item ? strategy-shapes = shape [ set profit-strategy replace-item ? profit-strategy (size - prior-size) ][ set profit-strategy replace-item ? profit-strategy (item ? profit-strategy + delta) ] ] end ; The Agent's Actions to announce if size > announce-threshold [ ; select a proposition with likelihood proportional to importance let announce-odds sum map [second ?] props let choice random-float announce-odds let p 0 let choice-inc second first props while [choice > choice-inc] [ set p p + 1 set choice-inc choice-inc + second item p props ] let w who let evidence (first item p props + firmness-of-principle * first item p init-props) / (firmness-of-principle + 1) let importance (second item p props + firmness-of-principle * second item p init-props) / (firmness-of-principle + 1) let loud random-float loudness * size ask other turtles with [distance myself < loud] [ update-announcement w p evidence importance] ask patches with [distance myself < loud] [ announce-patch myself p evidence importance] ] end to question let imp map [second ?] props let max-imp-question position max imp imp ; my most important proposition let candidate one-of other turtles with [distance myself < visual-horizon] if candidate != nobody ; ask a passer-by [ask candidate [ set questions fput (list myself max-imp-question) questions]] end to answer-questions if not empty? questions [ let q one-of questions let ag first q let ag-dist distance ag let w who ; let pps props let evidence first (item (second q) props) let importance second (item (second q) props) ask other turtles with [distance myself <= ag-dist] [ update-announcement w (second q) evidence importance] ; ask patches with [distance ag < loud ] ; [ announce-patch ag (second q) evidence importance] set questions [] ] end to-report agrees [v] let i floor (first v / number-of-agents) let t (first v) mod number-of-agents ifelse [size] of turtle t < announce-threshold or distance turtle t < visual-horizon [report 1] [report agreementfactor (first item i props) first second v] end to attack ; attack an agent who made an announcement this agent disagrees with most if size > announce-threshold and not empty? announcements [ ; rank the announcements for attack let agree (map [agrees ?] announcements) let loc position (min agree) agree let key 0 if item loc agree < 0 [ set key first (item loc announcements) ask turtle (key mod number-of-agents) [ set attacks fput (list myself floor (key / number-of-agents)) attacks] show (word self " attacks " (key mod number-of-agents)) ] ] end to reply-attacks ; select one of the attacks for a reply if size > 1 [ let pr filter [[size] of first ? > 1] attacks ; only attacks one ofthe agents who have sufficient reputation if not empty? pr [ let a one-of pr ; win == s (Epro) = s (Eopenv + Eprenv) let p second a let epro first item p props let ipro second item p props let eop first item p [props] of first a let iop second item p [props] of first a let eprenv (first item p pprops + [first item p pprops] of first a) / 2 let win 0 ifelse agreementfactor epro eprenv > agreementfactor eop eprenv [ set win ipro * epro * informational-conformity][ set win (-( ipro * (1 - epro) * informational-conformity)) ] ifelse win > 0 [set win min (list win (delta + [size] of first a))] [set win max (list win (-(size + delta)))] set size size + win ask first a [set size size - win] ifelse win > 0 [ ask patches with [distance first a < loudness] [announce-patch first a p epro ipro] ][ ask patches with [distance myself < loudness] [announce-patch myself p eop iop] ] ; update the beliefs of the proponent and the opponent let agree (agreementfactor epro eop) ifelse win > 1 - winthreshold [ ; setopinion p (list (accepte epro epro) (accepti agree ipro ipro)) ask first a [setopinion p (list (accepte epro eop) (accepti agree ipro iop))] ][ if win < winthreshold - 1[ setopinion p (list (accepte eop epro) (accepti agree iop ipro)) ; ask first a [setopinion p (list (accepte epro eop) (accepti agree ipro iop))] ] ] show (word self "replies attack on " p " of " first a " and wins " win) ]] set attacks [] ; ask my-in-links [die] end to walk find-direction rt random undirectedness - random undirectedness fd random-float stepsize end to find-direction ; find a direction according to the selected strategy ; 1: (shape = circle) towards the area that corresponds best with the agent's ; opinion ; 2: (shape = default) perpendicular towards the most corresponding area ; 3: (shape = face happy) away from the most corresponding area let p props let b 0 ifelse (shape = "face happy") [set b min-one-of patches in-radius visual-horizon [similar-attitude p pprops]] [set b max-one-of patches in-radius visual-horizon [similar-attitude p pprops]] if b != nobody [face b] if shape = "default" [ifelse random 2 = 0 [right 90][left 90]] end to change-strategy ; select the first strategy with the highest profit for the its reputation let i position max profit-strategy profit-strategy set shape item i strategy-shapes end to learn-by-neighbour let nb one-of turtles-on neighbors if nb != nobody [ let i random number-of-props let evidence first item i props let importance second item i props let ev first (item i [props] of nb) let imp second (item i [props] of nb) let agree (agreementfactor evidence ev) setopinion i (list (accepte evidence ev) (accepti agree importance imp)) ] end to learn-by-environment ; adapt belief values of a proposition to the values of the environment ; with a chance proportional it the importance of the propositions let prop-odds sum map [second ?] props let choice random-float prop-odds let p 0 let choice-inc second first props while [choice > choice-inc] [ set p p + 1 set choice-inc choice-inc + second item p props ] setopinion p (item p pprops) end to mutate ; change the belief values of a random proposition to random values setopinion (random number-of-props) (list (random-float 1) (random-float 1)) end to setopinion [p evi] ; p = prop, evi = (evidence importance) set props replace-item p props evi end to-report generateopinions let evids [] repeat number-of-props [ set evids fput (random-float 1) evids] let imps [] repeat number-of-props [ set imps fput (random-float 1) imps] report zip evids imps end ; Computation of Dependent Parameters. ; Average Belief. to-report report-eopop report mean [abs (2 * first item preferredopinion props - 1)] of turtles end ; Average Importance. to-report report-iopop report mean [ second item preferredopinion props] of turtles end ; Belief Distribution. to-report report-ginievid report gini [abs (2 * first item preferredopinion props - 1)] of turtles end ; Importance Distribution. to-report report-giniimp report gini [ second item preferredopinion props] of turtles end ; Reputation Distribution. to-report report-authority report gini [size] of turtles end to-report gini [Lin] ;; expects a list of values. ; Orders by the lowest rank first (or highest value) let L sort-by [?1 > ?2] Lin let N length L if N <= 1 [report 0] let i 0 let numerator 0 while [i < N ] [ set numerator numerator + (i + 1) * (item i L) set i i + 1 ] let u mean L ifelse u = 0 [report 0] [ report (N + 1) / (N - 1) - 2 * numerator / (N * (N - 1) * u) ] end ; Spatial Distribution. to-report clustering ;; Spatial Distribution report 1 - mean [avg-dist] of turtles / visual-horizon end to-report avg-dist let m mean [distance myself] of turtles in-radius visual-horizon ifelse m = 0 [report 1][report m] end to-report ranks [n L] ; n = number of classes, L = data ; if L = [] [set L [1]] let al n-values n [0] let c 1 if max l != 0 [set c 0.999 * n / max L] let ar array:from-list al foreach L [ let v floor (c * ?) array:set ar v (array:item ar v) + 1] report array:to-list ar end to update-plot ;; Plot the parameter values for each cycle. ;; (For Figures 6 to 9) let tmp 0 set-current-plot "Distribution of Evidence" histogram [first item current-prop props] of turtles set-current-plot "Importance Distribution" histogram [second item current-prop props] of turtles set-current-plot plottitle set-current-plot-pen "Reputation Distribution";; black set tmp report-authority plot tmp set-current-plot-pen "Spatial Distribution" ;;"friend ratio" ;; green set tmp clustering plot tmp set-current-plot-pen "Average Belief" ;; blue set tmp report-eopop plot tmp set-current-plot-pen "Belief Distribution" ;; yellow set tmp report-ginievid plot tmp set-current-plot-pen "Average Importance" ;; green set tmp report-iopop plot tmp set-current-plot-pen "Importance Distribution" ;; yellow set tmp report-giniimp plot tmp end906 - no answer at all ({})
, also denoted by
 Notes
Notes
- 1
- Dexia refers to a Franco-Belgian financial institution, which was partially nationalized by the Belgian state in October 2011.
- 2
- In 2008, Jeremy Clarkson showed a track test of a Tesla Roadster car on the BBC program Top Gear, which included a battery that went flat after 55 miles, just over a quarter of Tesla's claimed range; the program led to a libel charge by the manufacturer in 2011.
- 3
- Over a number of years, in 2006-2011, a number of Turkish immigrants were killed in Germany, and the police thought that the perpetrators might form a mysterious Turkish criminal network. Finally it turned out in 2011 that the murderers actually were a small group of Neo-Nazis.
- 4
- The Hofstad Network (in Dutch: Hofstadgroep) is an Islamist group of mostly young Dutch Muslims, members of which were arrested and were tried for planning terrorist attacks.
- 5
- The model is available at openABM.
- 6
- In full-fledged computational cognitive models such as ACT-R, memory and forgetting are based on elaborate decay functions, related to frequency and recency of use of memory chunks (Anderson & Schooler 2).
- 7
- In the case r = 0 , an agent is prepared to pay when losing, but does not get a return in case of winning the dialogue. This makes sense only in case the agent believes that it stated an absolute (logical) truth.
- 8
- In recent years in algorithmic social choice theory, there has been a lot of attention for different voting methods, see for example (Saari 46).
 References
References
-
AJZEN, I. & FISHBEIN, M. (1980).
Understanding Attitudes and Predicting Social Behavior.
Englewood Cliffs, NJ: Prentice-Hall, 1st ed.
-
ANDERSON, J. R. & SCHOOLER, L. J. (1991).
Reflections of the environment in memory.
Psychological Science 2, 396-408.
[doi:10.1111/j.1467-9280.1991.tb00174.x] -
BELNAP, N. D. (1977).
A useful four-valued logic.
In: Modern Uses of Multiple-Valued Logic (DUNN, J. M.
& EPSTEIN, G., eds.). Dordrecht: D. Reidel Publishing Co., pp. 5-37.
[doi:10.1007/978-94-010-1161-7_2] -
BRANDT, H., HAUERT, C. & SIGMUND, K. (2003).
Reflections of the environment in memory.
Proc. R. Soc. Lond. B 270, 1099-1104.
[doi:10.1098/rspb.2003.2336] -
BRATMAN, M. E. (1987).
Intention, Plans, and Practical Reason.
Cambridge, MA: Harvard University Press.
-
BREIGER, R., CARLEY, K. M. & PATTISON, P. (2003).
Dynamic social network modelling and analysis: Workshop summary and
papers.
J. Artificial Societies and Social Simulation 6(4).
-
BROERSEN, J., DASTANI, M. & TORRE, L. V. D. (2001a).
Resolving conflicts between beliefs, obligations, intentions and
desires.
In: Symbolic and Quantitative Approaches to Reasoning with
Uncertainty, 6th European Conference, ECSQARU 2001, Toulouse, France,
September 19-21, 2001, Proceedings (BENFERHAT, S. & BESNARD, P.,
eds.), Lecture Notes in Computer Science. Berlin: Springer, pp. 428-447.
[doi:10.1007/3-540-44652-4_50] -
BROERSEN, J., DASTANI, M. & TORRE, L. V. D. (2005).
Beliefs, obligations, intentions and desires as components in an
agent architecture.
International Journal of Intelligent Systems 20(9),
893-920.
[doi:10.1002/int.20098] -
BROERSEN, J., DASTANI, M., HUANG Z., HULSTIJN, J. & TORRE, L. V. D.
(2001b).
The BOID architecture: Conflicts between beliefs, obligations,
intentions, and desires.
In: Proceedings of Fifth International Conference on Autonomous
Agents (AA'01) (ANDRé, F., SEN, S., FRASSON, C. & MüLLER, J.,
eds.). New York, NY: ACM Press, pp. 9 - 16.
-
CARLEY, K., REMINGA, J. & KAMNEVA, N. (2003).
Destabilizing terrorist networks.
In: NAACSOS Conference Proceedings (PENN, O. W.,
ed.). Pittsburgh, PA.
-
CARLEY, K. M. (1986).
Knowledge acquisition as a social phenomenon.
Instructional Science 14(4), 381-438.
[doi:10.1007/BF00051829] -
CIALDINI, R. B. & GOLDSTEIN, N. J. (2004).
Social influence: Compliance and conformity.
Annual Review of Psychology 55, 591-621.
[doi:10.1146/annurev.psych.55.090902.142015] -
CONTE, R. & PAOLUCCI, M. (2003).
Social cognitive factors of unfair ratings in reputation reporting
systems.
In: Proceedings of the 2003 IEEE/WIC International Conference
on Web Intelligence (WI'03). Washington, DC: IEEE Computer Society.
[doi:10.1109/WI.2003.1241210] -
DEATON, A. (1997).
Analysis of Household Surveys.
Baltimore MD: Johns Hopkins University Press.
[doi:10.1596/0-8018-5254-4] -
DEFFUANT, G. (2006).
Comparing extremism propagation patterns in continuous opinion
models.
Journal of Artificial Societies and Social Simulation
9(3).
-
DEFFUANT, G., NEAU, D., AMBLARD, F. & WEISBUCH, G. (2002).
How can extremism prevail? A study based on the relative agreement
interaction model.
Journal of Artificial Societies and Social Simulation
5(4).
-
DEUTSCH, M. & GERARD, H. B. (1955).
A study of normative and informative social influences upon
individual judgment.
Journal of Abnormal and Social Psychology 51(3),
629-636.
[doi:10.1037/h0046408] -
DIGNUM, F., DUNIN-KEPLICZ, B. & VERBRUGGE, R. (2001).
Agent theory for team formation by dialogue.
In: ATAL '00: Proceedings of the 7th International Workshop on
Intelligent Agents VII. Agent Theories Architectures and Languages
(CASTELFRANCHI, C. & LESPéRANCE, Y., eds.). Berlin:
Springer-Verlag.
[doi:10.1007/3-540-44631-1_11] -
DUNIN-KEPLICZ, B. & VERBRUGGE, R. (2010).
Teamwork in Multi-Agent Systems: A Formal Approach.
Chichester: Wiley.
[doi:10.1002/9780470665237] -
DYKSTRA, P., ELSENBROICH, C., JAGER, W., RENARDEL DE LAVALETTE, G. &
VERBRUGGE, R. (2009).
A dialogical logic-based simulation architecture for social agents
and the emergence of extremist behaviour.
In: The 6th Conference of the European Social Simulation
Association (EDMONDS, B. & GILBERT, N., eds.). Electronic
Proceedings 1844690172.
-
DYKSTRA, P., ELSENBROICH, C., JAGER, W., RENARDEL DE LAVALETTE, G. &
VERBRUGGE, R. (2010).
A logic-based architecture for opinion dynamics.
In: Proceeding of the 3rd World Conongress on Social Simulation
WCSS2010 (ERNST, A. & KUHN, S., eds.). (CD-ROM) Centre for
Environmental Systems Research, University of Kassel, Germany.
-
FAGIN, R. & HALPERN, J. Y. (1987).
Belief, awareness, and limited reasoning.
Artificial Intelligence 34(1), 39-76.
[doi:10.1016/0004-3702(87)90003-8] -
FESTINGER, L. (1954).
A theory of social comparison processes.
Human Relations 7(2), 117-140.
[doi:10.1177/001872675400700202] -
FRANKS, D. W., NOBLE, J., KAUFMANN, P. & STAGL, S. (2008).
Extremism propagation in social networks with hubs.
Adaptive Behavior - Animals, Animats, Software Agents, Robots,
Adaptive Systems Archive 16(4), 264-274.
[doi:10.1177/1059712308090536] -
GILES, R. (1978).
Formal languages and the foundation of physics.
In: Physical Theory as Logico-Operational Structure
(HOOKER, C. A., ed.). Dordrecht: Reidel Publishing Company.
-
HARTMANN, S. & SPRENGER, J. (2010).
The weight of competence under a realistic loss function.
Logic Journal of the IGPL 18(2), 346-352.
[doi:10.1093/jigpal/jzp061] -
HEGSELMANN, R. & KRAUSE, U. (2002).
Opinion dynamics and bounded confidence: Models, analysis and
simulation.
Journal of Artificial Societies and Social Simulation
5(3).
-
HELMHOUT, J. M. (2006).
The Social Cognitive Actor.
Ph.D. thesis, University of Groningen, Groningen.
-
HELMHOUT, J. M., GAZENDAM, H. W. M. & JORNA, R. J. (2005).
Emergence of social constructs and organizational behavior.
In: 21st EGOS Colloquium (GAZENDAM, H., CIJSOUW, R. &
JORNA, R., eds.). Berlin.
-
HUET, S., DEFFUANT, G. & JAGER, W. (2008).
A rejection mechanism in 2D bounded confidence provides more
conformity.
Advances in Complex Systems (ACS) 11(04), 529-549.
[doi:10.1142/S0219525908001799] -
JAGER, W. & AMBLARD, F. (2005).
Uniformity, bipolarization and pluriformity captured as generic
stylized behavior with an agent-based simulation model of attitude change.
Computational & Mathematical Organization Theory
10(4), 295-303(9).
[doi:10.1007/s10588-005-6282-2] -
KAMLAH, W. & LORENZEN, P. (1973).
Logische Propädeutik.
München, Wien, Zürich: B.I.-Wissenschaftsverlag.
-
KELMAN, H. (1958).
Compliance, identification, and internalization: Three processes of
attitude change.
Journal of Conflict Resolution 2(1), 51-60.
[doi:10.1177/002200275800200106] -
KELMAN, H. (2006).
Interests, relationships, identities: Three central issues for
individuals and groups in negotiating their social environment.
Annual Review of Psychology 57, 1-26.
[doi:10.1146/annurev.psych.57.102904.190156] -
LAWLER, R. W. & CARLEY, K. M. (1996).
Case Study and Computing : Advanced Qualitative Methods in the
Study of Human Behavior.
Norwood, NJ, Ablex.
-
LAZARSFELD, P. & MERTON, R. K. (1954).
Friendship as a social process: A substantive and methodological
analysis.
In: Freedom and Control in Modern Society (BERGER, M.,
ABEL, T. & PAGE, C., eds.). New York: Van Nostrand, pp. 18-66.
-
Lê, S., JOSSE, J. & HUSSON, F. (2008).
Factominer: An R package for multivariate analysis.
Journal of Statistical Software 25(1), 1-18.
[doi:10.18637/jss.v025.i01] -
LEHRER, K. & WAGNER, C. (1981).
Rational Consensus in Science and Society.
Dordrecht: D. Reidel Publishing Company.
[doi:10.1007/978-94-009-8520-9] -
MACY, M. & FLACHE, A. (2002).
Learning dynamics in social dilemmas.
Proceedings of the National Academy of Sciences U.S.A.
99(3), 7229-36.
[doi:10.1073/pnas.092080099] -
MCELREATH, R. (2003).
Reputation and the evolution of conflict.
Journal of Theoretical Biology 220(3), 345-357.
[doi:10.1006/jtbi.2003.3166] -
PARSONS, S., SKLAR, E. & MCBURNEY, P. (2011).
Using argumentation to reason with and about trust.
In: Argumentation in Multi-Agent Systems. Taipei, Taiwan, May
2011. In conjunction with AAMAS 2011. (MCBURNEY, P., PARSONS, S. &
RAHWAN, I., eds.).
-
PRAKKEN, H., REED, C. & WALTON, D. (2003).
Argumentation schemes and generalizations in reasoning about
evidence.
In: Proceedings of the 9th International Conference on
Artificial Intelligence and Law (ICAIL '03). New York, NY: ACM.
[doi:10.1145/1047788.1047794] -
RAO, A. S. & GEORGEFF, M. P. (1991).
Modeling rational agents within a BDI-architecture.
In: KR'91. San Mateo, CA: Morgan Kaufmann publishers Inc.
-
RAO, A. S. & GEORGEFF, M. P. (1995).
BDI agents: From theory to practice.
In: Proceedings of the First International Conference on
Mult-Agent Systems (ICMAS-95) (LESSER, V. & GASSER, L., eds.).
Cambridge, MA: MIT Press.
-
RESTALL, G. (2006).
Relevant and substructural logics.
In: Handbook of the History and Philosophy of Logic
(GABBAY, D. & WOODS, J., eds.), vol. 7. Amsterdam, Boston:
Elsevier, pp. 289-398.
[doi:10.1016/s1874-5857(06)80030-0] -
SAARI, D. G. (2001).
Decisions and Elections: Explaining the Unexpected.
Cambridge University Press.
[doi:10.1017/cbo9780511606076] -
SABATER-MIR, J., PAOLUCCI, M. & CONTE, R. (2006).
Repage: REPutation and imAGE among limited autonomous partners.
Journal of Artificial Societies and Social Simulation
9(2).
-
SCHELLING, T. C. (1971).
Dynamic models of segregation.
Journal of Mathematical Sociology 1(2), 143-186.
[doi:10.1080/0022250X.1971.9989794] -
SHERIF, M. & HOVLAND, C. (1961).
Social Judgment: Assimilation and Contrast Effects in
Communication and Attitude Change.
New Haven: Yale University Press.
-
SUBAGDJA, B., SONENBERG, L. & RAHWAN, L. (2009).
Intentional learning agent architecture.
Autonomous Agents and Multi-Agent Systems 18(3),
417-470.
[doi:10.1007/s10458-008-9066-5] -
SULS, J., MARTIN, R. & WHEELER, L. (2002).
Social comparison: Why, with whom and with what effect?
Current Directions in Psychological Science 11(5),
159-163.
[doi:10.1111/1467-8721.00191] -
SUN, R. (2008).
Prolegomena to integrating cognitive modeling and social simulation.
In: Cognition and Multi-Agent Interaction: From Cognitive
Modeling to Social Simulation (SUN, R., ed.). New York, NY:
Cambridge University Press, pp. 3-26.
-
SŹAŁAS, A. S. & SŹAŁAS, A. (2009).
Paraconsistent reasoning with words.
In: Aspects of Natural Language Processing (MARCINIAK,
M. & MYKOWIECKA, A., eds.), vol. 5070 of Lecture Notes in Computer
Science. Berlin: Springer.
-
VAN BENTHEM, J. (2001).
Games in dynamic-epistemic logic.
Bulletin of Economic Research 53(4), 219-48.
[doi:10.1111/1467-8586.00133] -
VERBRUGGE, R. (2009).
Logic and social cognition: The facts matter, and so do computational
models.
Journal of Philosophical Logic 38(6), 649-680.
[doi:10.1007/s10992-009-9115-9] -
VERBRUGGE, R. & MOL, L. (2008).
Learning to apply theory of mind.
Journal of Logic, Language and Information 17(4),
489-511.
[doi:10.1007/s10849-008-9067-4] -
VERHEIJ, B. (2000).
Dialectical argumentation as heuristic for courtroom decision-making.
In: Rationality, Information and Progress in Law and
Psychology. Liber Amoricum Hans F. Crombag (KOPPEN, P. J. V. &
ROOS, N. H. M., eds.). Maastricht: Metajuridica Publications.
-
WALTON, D. & KRABBE, E. (1995).
Commitment in Dialogue.
Albany, NY: State University of New York Press.
-
WIJERMANS, N., JAGER, W., JORNA, R. & VLIET, T. V. (2008).
Modelling the dynamics of goal-driven and situated behavior.
In: The Fifth Conference of the European Social Simulation
Association (ESSA 2008). Brescia, Italy.
-
ZOETHOUT, K. & JAGER, W. (2009).
A conceptual linkage between cognitive architectures and social
interaction.
Semiotica 175, 317-333.
[doi:10.1515/semi.2009.052]