Abstract
Abstract
- This paper discusses an extended version of the matching problem which includes the mate search problem; this version is a generalization of a traditional optimization problem. The matching problem is extended to a form of the asymmetric two-sided matching problem. An agent-based simulation model is built and simulation results are presented. Todd and Miller (1999) simulated the two-sided matching problem in a symmetric setting. In their model, there are the same number of agents in both parties (groups), each of whom has his/her own mate value. Each agent in a party tries to find his/her mate in the other party, based on his/her candidate's mate value and his/her own aspiration level for his/her partner's mate value. Each agent learns his/her own mate value and adjusts his/her aspiration level through the trial period (adolescence). Todd and Miller (1999) tried several search rules and learning mechanisms that are symmetric for both parties. In the present paper, Todd and Miller's (1999) model is extended to an asymmetric setting where the two parties have different numbers of agents, and the search rule and the learning mechanism for the two parties differ. Through the simulation, the search rules and the learning mechanisms which were identified to be appropriate in a symmetric setting are revealed to be inappropriate in the asymmetric setting and the reason why this is so is discussed. Furthermore, some general facts are derived using a mathematical theorem-proof approach. Some of these facts are used to direct a revision of the model, and a revised simulation model is presented. An implication is obtained for practical situations in asymmetric matching setting. For example, in the job hunting case, if job applicants want to finish their job hunting successfully, they should be modest at the beginning of the hunt.
- Keywords:
- Social Simulation, Agent-Based Models (ABM), Theorem-Proof Approach, Mate-Search Problem, Two-Sided Matching, Job Matching
 Introduction
Introduction
- 1.1
-
There is a well-known optimal stopping problem called the “Secretary Problem”.
A set of applicants for a secretary position is given to an employer who is searching for a secretary. Each applicant has a value that denotes how good the
applicant is for the employer. One can think of the value as an index that
indicates the capability of carrying out a secretary's job.
Therefore, the problem is how to find an employee with as high a value
as possible.
- 1.2
-
The employer cannot know the value of all applicants in advance, so
he/she has to examine each applicant's value by interviewing them one
by one.
In addition, the employer has to decide whether to hire each
applicant
at the time of the interview.
The employer is not allowed to change his/her mind afterward.
Therefore, once the employer
decides to refuse the
applicant, he/she can never hire that person.
- 1.3
-
There is only one job opportunity. Hence, once the employer decides
to hire the applicant, he/she has to stop interviewing, even though there
are applicants left who have not been interviewed.
So, the Secretary Problem is the challenge of finding the rule for deciding
whether to accept or refuse each interviewed applicant, and when to
stop the job
interviews in order to employ the applicant having the highest value with
as high probability as possible.
- 1.4
-
In the Secretary Problem, the optimal solution is called the “37%
rule” (Ferguson 1989).
The rule is as follows. First, conduct interviews one by one to examine the value of a
37%(= 1/e) sample of the entire set of applicants.
The applicants who are picked as the sample are interviewed, but
not employed. Call this stage the “sampling period”.
Secondly, enter the actual interview period when the interviews of
the sample applicants are finished, remembering the highest value observed in the
sampling period. In the actual interview period, once an applicant with a higher
value than the highest value in the sample is encountered, decide to accept that applicant as the secretary
and stop the interviews. (This part of the rule ensures that the probability of hiring
the applicant with the best value is as high as possible.) If
an applicant with a value higher than the best one in the sample is not encountered,
hire the last interviewee, no matter how small his/her value is.
(In this case, the employer has failed to hire the secretary with the highest value.)
- 1.5
-
There is a problem called the “Dowry Problem”, or the “Mate Search
Problem”, which is an interpretation of the Secretary Problem in
another context.
This problem is to determine how one finds a mate having the highest
value.
This interpretation is useful because it inspires us to extend the
problem to a two-sided search problem.
Generally speaking, a mate search is not one-sided, as in the Secretary
Problem case, where only the employer is trying to optimize the value of another person (the employee);
rather it is two-sided in that a matching that is desirable to both sides is
required.
Todd and Miller extended the Secretary Problem to a two-sided matching problem
and examined several search rules by computer
simulation (Todd 1997; Todd and Miller 1999). They
proposed several rules under assumptions that are appropriate for the usual
mate search situation and compared them to find a desirable
search rule in accordance with certain criteria, which will be described
below in detail.
- 1.6
-
Mate search activities involve building a one-to-one matching between two
parties, say, men and women. Therefore, the condition
for searching can be set symmetrically for both parties.
However, there are matching situations where this symmetry is not
appropriate. For example, job hunting is a problem in which
each agent in one party (firms) tries to find many member of the
other party (job applicants).
A special problem occurs in Japan, where
almost all colleges end their
academic year in March, and most graduates start their jobs in April.
Most college students in Japan start their job hunting about one year
ahead of their graduation.
Additionally, it is common for firms in Japan to employ new graduates
as almost all of their new employees.
This custom is called “simultaneous recruiting of new
graduates”.
Therefore, in Japan this matching takes place between a large number
of firms and students simultaneously.
This custom causes many social problems in
Japan (Economist 2012).
In recent years,
graduating students in Japan have ended their job hunting without
receiving any job offers from firms,
despite many firms not fulfilling their recruitment targets.
Once they fail in job hunting prior to graduation, it becomes very
difficult for
them to obtain job offers because most firms in Japan employ only new
graduates.
Examining why the mismatch between students and firms occurs can
help solve this problem.
- 1.7
-
We say a two-sided matching situation is asymmetric when properties of
the two parties (the number of agents and the number of acceptable mates
for each agent) and the decision rules of agents (how they decide their mates
and when to stop their search) in two parties differ.
In this paper, we try to extend Todd and Miller's (1999) simulation model to
an asymmetric situation and examine one of their
search rules under asymmetric conditions.
 Two-sided matching in the literature
Two-sided matching in the literature
- 2.1
-
Two-sided matching has been well analyzed using game theory.
In those discussions, the existence of stable matching solutions was
tackled and ways of finding them were sought.
Many theories have been developed within the game theoretical
framework (Roth and Sotomayor 1992).
Stable matching theory, pioneered, by Gale and Shapley (Gale and Shapley 1962),
was used to study the formation and dissolution of marriages by Mumcu and Saglam (2008) under the assumption of transferable utilities and by Saglam (2011) under the assumption of nontransferable utilities.
These assume two parties, such as men and women, colleges and
students, or firms and workers, and also assume that the preferences of each
agent for agents in the opposite party are given.
A stable matching solution refers to a matching at which no pair of agents
from the two parties who are not matched prefer each other.
It is known that stable matchings exist in many situations and an
algorithm called the “deferred acceptance” procedure can give one of
the stable matchings (Roth 1984a; Gale and Shapley 1962).
Using this procedure, Roth analyzed operations in the labor market, for example, the
situation in which intern medical students are allocated to internships in
hospitals in America (Niederle et. al 2008; Roth 1984b).
In these models, they assume that agents are able to hold the best
offer they have received, without accepting it
outright (Roth and Sotomayor 1992), and they focus on finding a procedure
(an algorithm) which gives stable matchings.
Additionally, in most cases they assume the existence of a centralized
clearinghouse which collects agents' preferences and runs the algorithm,
and try to answer the question, “how can we design the procedure
which the clearinghouse should follow?”.
- 2.2
-
However, in the job hunting situation in Japan, these assumptions do not hold.
Job allocation is carried out on an individual basis; therefore, we cannot
assume the existence of centralized clearinghouses.
Furthermore, potential workers most of whom are university students
have to decide whether to accept offers from firms within a short
time; therefore, they cannot hold the best offer to defer their answer
to firms.
The assumption that each agent can present his/her preferences to the
agents in the opposite party before the allocation procedure starts
does not apply, either.
The number of potential workers is very large and each of them is
unknown to firms before the job hunting starts.
The number of potential firms who would give offers to workers is also large
for each worker, and university students who apply to job vacancies do
not know the precise value of firms until they apply.
Therefore, we cannot rely on the game theoretical framework which
requires agents' preferences in advance.
- 2.3
-
As was mentioned in the previous section,
Todd and Miller (1999) carried out a simulation based on agents'
autonomous behavior
in the marriage mate search.
Their target was a symmetric two-sided matching situation, in which both the numbers
of agents in each party and also the mate search strategies of
the two parties are the same.
However, the job hunting situation is asymmetric in the sense that the
numbers of agents differ because the number of job seeking students
exceeds the number of firms, and the information held by individuals also differs between parties because
firms know their own values better than job applicants know their own
values.
Therefore, the search strategies in the two parties should be different.
As far as the author is aware, no agent-based simulation
of this type of asymmetric two-sided matching situation has been reported.
Hence, we will review Todd and Miller's (1999) symmetric model in
brief and then extend it to the asymmetric situation.
 Symmetric two-sided matching
Symmetric two-sided matching
- 3.1
-
In this section, we formalize Todd and Miller's (1999) model of the
symmetric two-sided
matching problem.
We will extend this model to an asymmetric setup in the next section.
Model
- 3.2
-
Let M and W be the sets of men and women, respectively. We assume
that the
number of people in each set is identical, say n. Hence,
|M| = |W| = n. We designate M and W as
M = {1, 2,…, n},W = {n + 1, n + 2,…, 2n},and call each element of these two sets an agent. Each agent i∈{1, 2,…, 2n} has two attributes. One is the mate value vi, which is the value of the agent as a mating partner. The other is the aspiration level ai for a mating partner. Agents' own mate values do not vary throughout mate search. On the other hand, ai changes, based on rules that will be described below, while agent i searches for his/her mate. Hereinafter, we assume that vi∈[0, 100]. These values are randomly assigned to agents in the simulations.
- 3.3
-
Agents search for mates in two sequential periods.
- Learning (adolescence) period
In this period, each agent in M and W exchanges information with some of the agents of the other party. In other words, the agents date each other. In this step, agents update their aspiration levels following a learning rule which is given in advance. They do not actually mate in this period. This period corresponds to the sampling period in the Secretary Problem. - Mating period
In this period, the actual mating takes place. If an agent finds a partner with a value greater than the aspiration level that he/she acquired in the learning period, then the agent proposes to the partner. If both of a pair propose to each other, they succeed in mating and stop their search. Agents who cannot mate with any candidate end up failing to find a mate. When all agents either succeed or fail, this period finishes.
- Learning (adolescence) period
- 3.4
-
Let c (%) denote the sampling ratio, the ratio of the number of people
whom each agent can date within the learning period to the number of
potential mating candidates n.
Therefore, all agents date with n*c/100 people in
their adolescence period. They cannot mate with candidates whom they
once dated. This is the same assumption as in the Secretary Problem.
- 3.5
-
Todd examined the following rules for learning the aspiration level
in the learning period. We describe how the aspiration level changes
through dating based on each learning rule when a man i∈M and
a woman j∈W date each other. We denote the aspiration level of
agent k(= i, j) before dating by ak, and that after dating by
a'k.
The learning rules are symmetric between men and women. Therefore, we
show the learning rules from the men's side only.
Take the Next Best (TNB) rule:
This is a generalization of the 37% rule in the Secretary Problem. This does not fix the sampling ratio to 37%. We can change it by altering c.a'i =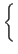
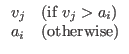
Hence, when an agent i dates an agent j with a higher mate value vj than his current aspiration level ai, he changes his aspiration level from the current value ai to the mate value vj of his date j. This means that he remembers the maximum mate value from among those he has previously dated. We assume that the initial value of ai is 0.
Mate Value-5 rule:
- This sets the aspiration level to
ai = vi - 5,and does not change it throughout the learning period. An agent with this rule is modest and does not have high aspirations. This rule assumes that he knows his own mate value beforehand. However, in general it is difficult for people to know accurately their mate value: few people know their own appeal to the opposite gender. The following rule assumes that agents cannot know accurately their mate value, and that they learn and approximate this value through dating and exchanging information with agents of the opposite gender.Adjust Relative/2 rule:
- This changes the aspiration level depending on whether the date proposes. “To propose” in the learning period is just to express that “You are my favorite”; here, agents do not actually mate. In addition, this rule adjusts the aspiration level depending on whether the proposing date's mate value is higher than the agent's own mate value, and vice versa when he is not proposed to. Actually, we are assuming that they cannot know accurately their own mate value, and therefore they use their aspiration level based on the assumption that their aspiration levels approximate their mate values well. The adjustment width varies depending on the difference between the date's value and the agent's own value (precisely speaking, their aspiration level), as follows:
a'i =where Δ = | vj - ai|/2. When proposed to (vi≥aj), and the date's value is greater than or equal to the approximation of his own mate value (vj≥ai), agent i adjusts his aspiration level upward. Δ is the adjustment width used in raising or lowering the aspiration level. Therefore, the adjustment is carried out to narrow the gap between his own aspiration level and the date's value. The initial value of ai when the learning period starts is set to 50, the middle of the mate value range.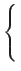
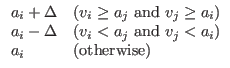 ,
,
- This sets the aspiration level to
- 3.6
-
Todd and Miller (1999)
presented several variations of the above adjustment
rule and concluded that the above rule
is the most sophisticated and the best one
among these variations.
We accept their conclusion and adopt this rule to model
agents' learning of their own values in the present paper.
Evaluation criteria of search rules
- 3.7
-
Todd and Miller (1999) claim that the desirable search rule
(or learning rule) should meet the following criteria (Todd and Miller 1999).
- It generates as many matings as possible. In other words, the
greater the total number of pairs generated by a successful mating,
the better the rule.
- The mate values of agents who end up successfully mating
are not biased as too high or too low. In other words, the
average mate value of those who successfully found their mates should
be near the middle of the mate value range, i.e., 50.
- The difference in mate values between the man and woman in the pair of a successful mating is not too large. In other words, the lower the average of the difference of mate values between the two agents in pairs generated by a successful mating, the better the rule.
- It generates as many matings as possible. In other words, the
greater the total number of pairs generated by a successful mating,
the better the rule.
- 3.8
-
The author replicated Todd and Miller's (1999) simulation model
written in C language and
NetLogo, and confirmed their conclusions as follows.
Readers can download the NetLogo version replicated by the author from the
OpenABM model archive (http://www.openabm.org/model/3575/version/2/).
The TNB rule generates markedly fewer successful matches.
And as was described above, the Mate Value-5 rule is based on the unrealistic
assumption that each agent knows accurately his/her own mate value.
The
result that the Adjust Relative/2 rule is the best comes from its
satisfying the three criteria described above.
In particular, with the Adjust Relative/2 rule the average value of successful agents
approaches 50 and the average of the value difference of successful matchings
decreases as the learning period lengthens.
Hence, we can conclude that the Adjust Relative/2 rule is the most
sophisticated rule in the situation
that agents do not know accurately their own values beforehand and have
to learn them in their learning period.
Confirming this result, we will extend Todd and Miller's (1999) model
to asymmetric situations.
 Asymmetric two-sided matching
Asymmetric two-sided matching
- 4.1
-
We extend Todd and Miller's (1999) model to apply it to the situation
of asymmetric
two-sided matching and then conduct computer simulations.
Model
- 4.2
-
Let A and F be the set of applicants and the set of firms,
respectively. Let the number of elements in A and F be m and
n, respectively. We assume that m > n.
As in the previous section, we call the elements of A and F agents.
And also, each agent
i∈{1, 2,…, m + n} has its own value
vi and aspiration level ai w.r.t. the value of matching
partners.
The firms' values indicate the degree of firms' desirability from
an applicant's perspective. On the other hand, applicants' values indicate the
applicants' capabilities of carrying out jobs in firms.
We sometimes refer to an applicant's values as a capability value.
Each firm agent has a recruitment number (number of applicants to be recruited) as an attribute.
For simplicity, we assume that all firm agents have the same
recruitment number, denoted by l.
Furthermore, we assume that
m = ln,that is to say, the total job vacancies being recruited for and the number of applicants seeking jobs are the same. We should note that this assumption is independent of the assumption of asymmetry. We are requiring this assumption to ensure that all applicants can find jobs and all job vacancies can be filled in principle. The actual job market in Japan can support this assumption because the recent ratio of job vacancies to job applicants has been around 1.2 (Recruit Works Institute 2013).
- 4.3
-
Firms interview each applicant applying to be recruited by them,
decide whether to accept or to refuse him/her, and tell the applicant
their decision. Once a firm gives a decision of refusal, it is not
allowed to recruit the refused applicant later, even if the firm still has an unfilled recruitment
position. Similarly, an applicant cannot reapply to
a firm that has already refused him/her.
- 4.4
-
In the symmetric two-sided matching case, agents in both parties learn their
aspiration level. In the asymmetric situation, we assume the following.
- Each firm i∈F has already learned
their value vi.
- Firms set their aspiration level ai lower than their value vi.
- Each firm i∈F has already learned
their value vi.
- 4.5
-
On the other hand, applicants do not necessarily know accurately their
values.
Therefore, they have to learn their values and adjust their aspiration
levels in their learning period.
As was confirmed by Todd and Miller (1999.)
in the symmetric agents model,
Adjust Relative/2 is the most sophisticated rule Todd and Miller (1999).
Hence, we assume that all applicants adopt the Adjust Relative/2
rule for learning their aspiration level.
Simulation
- 4.6
-
Based on the assumptions described above, we conduct computer
simulations with the Mate Value-5 rule for firms and the
Adjust Relative/2 rule for applicants under the following parameter
settings.
The author built two versions of the extended model written in C language and NetLogo.
Readers can download the NetLogo version built by the author from the
OpenABM model archive (http://www.openabm.org/model/3577/version/2/).
Number of firms: m = 100 Number of applicants: n = 1000 Recruitment number of each firm: l = 10 - 4.7
-
Each agent's value is randomly set to an integer taken uniformly from the interval
[0, 100].
We performed the simulations for a sampling ratio c% taken as the integers from
0 to 90.
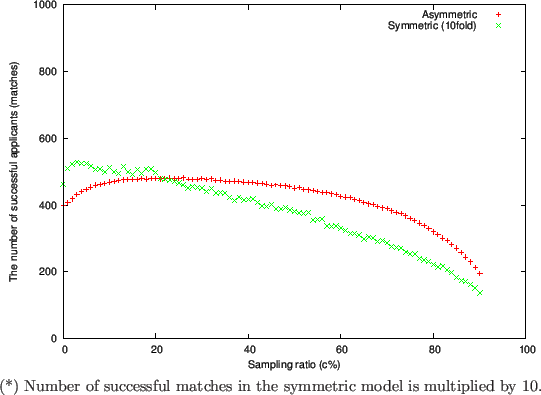
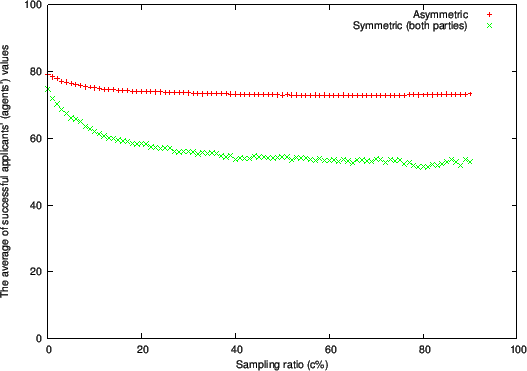
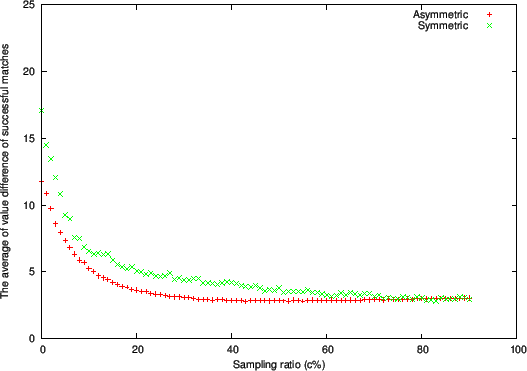
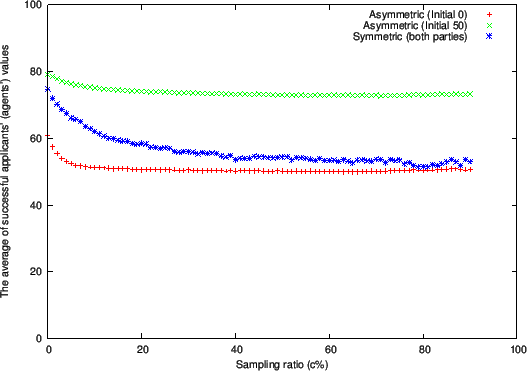
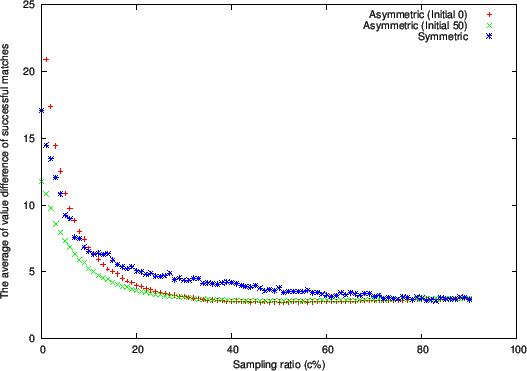
Figure 1 through 3 respectively show plots of the following quantities at the end of the matching process:
- Number of successful applicants (Figure 1)
- Average value of successful applicants (Figure 2)
- Average difference in value between an applicant and a firm in a successful matching (Figure 3)
- 4.8
-
Comparing with Adjust Relative/2 in Todd and Miller's (1999) symmetric
situation, we do
not observe a significant change in the number of successful agents
(Figure 1) or the average difference in value
(Figure 3).
However, the average agent value (Figure 2) does exhibit a
significant difference from Todd and Miller's symmetric situation.
In Todd and Miller's model, the average value of successful agents
with the Adjust Relative/2 rule
converges to about 50 as c increases,
giving agents more learning opportunity.
This means that both the agents with higher values and the ones with lower
values have similar levels of success at matching.
However, in the asymmetric situation with the Adjust Relative/2 rule, the
average only converges to about 70.
Therefore, in the asymmetric case, more applicants with low values end up failing in their job hunting
than those with high values.
- 4.9
-
Having observed these results, we take a theorem-proof approach in
order to find the reason why they occur.
 Theorem-proof approach and revised simulation model
Theorem-proof approach and revised simulation model
- 5.1
-
We next try to find the reason why the matching with the Adjust Relative/2
rule did not work well in asymmetric situations.
The agent-based simulation approach usually traces back through the simulation
process and discusses the reasons for the observed results, what is called “debriefing”.
In the present paper, we take another approach, the theorem-proof approach.
Some facts that hold in our model will be revealed in this section.
- 5.2
-
In the simulation, we
use the Mate Value-5 rule for firms. However, the numeral “5”, which denotes the degree
of modesty used, does not affect the following discussion. Therefore, we
generalize the rule as Mate Value-α for any
α > 0.
- 5.3
-
We also assume the following in this section.
- Firms adopt the Mate Value-α (
α > 0) rule. The parameter
α is common to all firms. Hence, aj < vj always holds for
any firm j∈F, and
vj - aj = α.
- Applicants adopt the Adjust Relative/2 rule.
Propositions
- Firms adopt the Mate Value-α (
α > 0) rule. The parameter
α is common to all firms. Hence, aj < vj always holds for
any firm j∈F, and
vj - aj = α.
- 5.4
-
Some terms should be defined in order to characterize the
behavior of applicants that affect their performance in job hunting.
Definition Idealistic/realistic agent
Let i∈A be any applicant. If he/she aspires to firms with higher values than his/her capability, i.e., ai > vi, we call him/her an idealist. Otherwise ( ai≤vi), we call him/her a realist.
- 5.5
-
In the following propositions, the difference in job hunting
behavior between idealistic agents and realistic ones will be shown.
In order to make this paper more readable, all of the proofs of the propositions
and theorems are placed in the appendix.
Proposition 1 If an applicant is an idealist, then he/she remains idealistic after an adjustment.
- 5.6
-
This proposition says that idealistic applicants do not become realists through the learning process with Mate Value-α firms.
- 5.7
-
The next two propositions refer to how the degree of idealism changes
because of an information exchange with a firm.
- 5.8
-
Therefore, an idealist with a large degree of idealism (i.e.,
| ai - vi| > α)
remains the same after each interaction, and so does one with a small
degree (i.e.,
| a'i - vi|≤α).
- 5.9
-
The next proposition refers to a realist's behavior.
Proposition 4 If any applicant i∈A is a realist, then he/she can become an idealist after an adjustment. A realist agent i becomes an idealist after an adjustment involving firm j∈F iff vi < (ai + vj)/2 holds. Whenever this condition is satisfied, | a'i - vi| < α/2 holds.
- 5.10
-
The above proposition says that a realist can become an idealist when a
condition on his/her value, his/her aspiration level, and the firm's value
is satisfied. However, the degree of idealism after
learning is small relative to α.
- 5.11
-
Combining the above four propositions, we can state the following theorem.
Theorem For any applicant agent i∈A, the following hold.
1) If vi < ai and | ai - vi| > α, then vi < a'i and | a'i - vi| > α.
2) If ai≤vi and vi < a'i, then | a'i - vi| < α/2.
- 5.12
-
We can restate the theorem in our target situation, job hunting, as
follows.
Corollary 1) Any idealistic applicant remains idealistic with a large degree of idealism throughout the learning period if he/she is an idealist with a large degree of idealism at the beginning of the learning period.
2) Any realistic applicant can become idealistic in the learning period. In this case, however, he/she remains idealistic with a small degree of idealism for the rest of his/her learning period.
- 5.13
-
It is obvious that it is harder for a idealistic applicant to find a
job than for a realistic one. We set the initial values of the
aspiration level for applicants as the middle value of the
range, 50. This implies that applicants with capability values under 50 remain
idealistic throughout their job hunting, and it is thus more likely that they
will fail in their job hunting. On the other hand, applicants with
capability values over 50 start their learning period as realists.
Some of them remain realists throughout the job hunting process, whereas other realists
become idealists.
These converted applicants
remain idealists with a small
degree of idealism throughout their job hunting.
These facts generate the observed bias in the average
capability values of successful applicants.
- 5.14
-
These considerations suggest that we can correct the observed bias by
using a new search rule which sets the initial aspiration level of
applicants lower than their capability values.
We name this rule “Adjust Relative/2 with Low Initial Aspiration”.
However, as was mentioned above, applicants do not know their own
capability values when they start their job hunting.
Therefore, we set the initial aspiration as zero.
Adjust Relative/2 with Initial 0 rule:
- This uses the same rule for adjustment as the one in the Adjust Relative/2 rule except for the initial value zero of aspiration ai for all i∈A.
- This uses the same rule for adjustment as the one in the Adjust Relative/2 rule except for the initial value zero of aspiration ai for all i∈A.
- 5.15
-
We refer to what was formerly called the “Adjust Relative/2” rule as the “Adjust Relative/2
with Initial 50” rule to distinguish it from the new rule.
In the next section, we revise the simulation settings and verify the
conjecture that the modified rule can correct the observed bias.
Revised simulations
- 5.16
-
Simulations were carried out with the same settings as in Section 4
except that the initial aspiration levels of applicants are all set to
zero. Therefore, all applicants start their learning as realists.
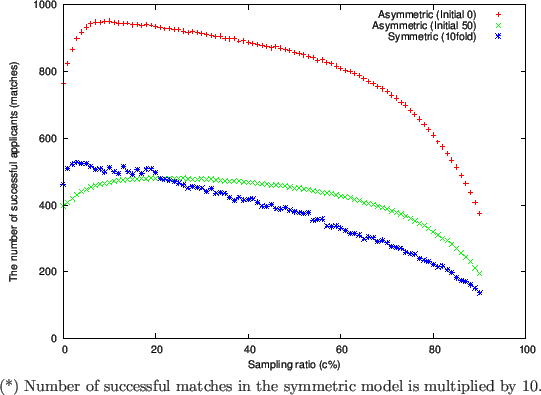
Figure 4 through 6 show the results for the asymmetric model with initial zero and
that with initial 50 aspiration levels.
They also show the results for the Todd and Miller's symmetric model
for comparison.
The plotted values for the symmetric matching in Figure 4 are multiplied by 10, as was done in the case of Figure 1 .
- 5.17
-
Figure 4 reveals that the number of successful applicants
increased dramatically relative to the Initial 50 case.
Figure 5 shows that
the average value of successful applicants converges to about 50.
Hence,
both high-valued and low-valued applicants succeeded in their job hunting.
There is little difference between the three setting for the average of
value difference of successful matching (Figure 6).
This implies that the difference between firms' values and applicants'
values remained small.
 Conclusion
Conclusion
- 6.1
-
We tried a hybrid method of combining agent-based simulations and
a mathematical theorem-proof approach for the asymmetric two-sided matching
problem. Todd and Miller's (1999) symmetric model was extended to an
asymmetric
situation, creating a framework that can be interpreted as a model of the job
hunting situation.
- 6.2
-
In the simulations, firms are assumed to know their own values
precisely and to set their aspiration levels lower than their values
(Mate Value-5 rule) in order to fulfill their recruitment targets.
Whether the Mate Value-5 rule (or the Mate Value-α rule in general) is the optimal
adjustment rule for the firms, given the search rule of the applicants
(Adjust Relative/2 rule),
in the described matching environment is the subject of future
research.
Under the assumptions we made, applicants with lower capability values tend to
fail relatively more in their job hunting.
We showed the reason for this simulation result by using a theorem-proof
approach. Applicants with lower capability values start their
job hunting as idealists.
Since idealists remain idealists throughout the job hunting process, more
such applicants fail to find their jobs than higher capability applicants.
On the other hand, some realists become idealists, but with a consistently low degree of
idealism.
This generates the biased result observed in our simulations.
- 6.3
-
These considerations have implications for college
students in Japan who are preparing for job hunting.
If they want to finish their job hunting successfully, they should follow
our proposed new rule, the relative adjustment with low initial aspiration.
That is, they should be modest at the beginning of their job hunting.
 Acknowledgements
Acknowledgements
-
The author is deeply grateful to Nigel Gilbert for his excellent comments and advice on this paper.
The author is also grateful to anonymous reviewers for valuable and constructive comments and suggestions to improve the quality of the paper.
This research is supported by an International Joint Research Grant from the College of Industrial Technology, Nihon University.
 Appendix
Appendix
-
Proof of Proposition 1
Proposition 1 If an applicant is an idealist, then he/she remains idealistic after an adjustment.Proof:Let i∈A and j∈F be any applicant and any firm, respectively. Assume that ai > vi. Let a'i denote the aspiration level of i after exchanging information with j. It suffices to show that a'i > vi. When adjustment of ai does not take place, we have a'i = ai and there is nothing to prove. Adjustment of the aspiration level ai of the applicant occurs only in the following two cases.- Upward adjustment (a'i ≥ ai) when vi≥aj and vj≥ai
- Downward adjustment (a'i < ai) when vi < aj and vj < ai
Q.E.D.Proof of Proposition 2
Proposition 2 For any idealistic agent i∈A, if | ai - vi | > α, then | a'i - vi | > α.Proof:In the proof of Proposition 1, case 1 guarantees that| a'i - vi | > | ai - vi | > α.For case 2, we havevi < aj < vj < a'i.Together with | vj - aj | = α from the firm behavior, it follows that | a'i - vi | > α.Q.E.D.Proof of Proposition 3
Proposition 3 For any idealistic agent i∈A, if | ai - vi | ≤ α, then | a'i - vi | ≤ α.Proof:Consider any idealistic agent i∈A. Then ai > vi. If a downward adjustment takes place, we have a'i < ai. Since vi < a'i holds from Proposition 1, it follows that| a'i - vi | < | ai - vi | ≤ α.Hence, it suffices to prove that | a'i - vi |≤ α when an upward adjustment takes place. This adjustment takes place when vi ≥ aj and vj ≥ ai holds. Since we have ai ≤ a'i ≤ vj from the Adjust Relative/2 rule, it follows that| a'i - vi | ≤ | a'i - aj | ≤ | vj - aj | = α.This completes the proof.Q.E.D.Proof of Proposition 4
Proposition 4 If any applicant i∈A is a realist, then he/she can become an idealist after an adjustment. A realist agent i becomes an idealist after an adjustment involving firm j∈F iff vi < (ai + vj)/2 holds. Whenever this condition is satisfied, | a'i - vi | < α/2 holds.Proof:Assume that ai≤vi. An adjustment occurs only in the following two cases.- Upward adjustment (a'i ≥ ai) when vi ≥ aj and vj ≥ ai
- Downward adjustment (a'i < ai) when vi < aj and vj < ai
vi < aj < vj < ai,which contradicts that ai ≤ vi.Assume that an upward adjustment occurs under the condition stated as case 1. Then we have
a'i = ai +Hence, we have a necessary and sufficient condition for a'i > vi,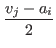 =
= 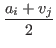 .
vi <
.
vi <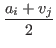 .
.
Finally, we assume that vi <
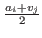 . We know that
vi < a'i. Hence, we only have to show that
a'i - vi < α/2 to prove that
| a'i - vi | < α/2.
We have two cases to prove.
. We know that
vi < a'i. Hence, we only have to show that
a'i - vi < α/2 to prove that
| a'i - vi | < α/2.
We have two cases to prove.
(Case I) Assume ai < aj.
a'i - vi ≤ a'i - aj (because aj≤vi) = 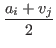 - aj
- aj= 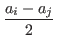 +
+ 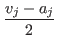
= 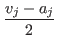 -
- 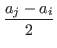
< 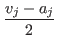 (because ai < aj)
(because ai < aj)= 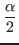
(Case II) Assume aj ≤ ai.
a'i - vi ≤ a'i - ai (because ai ≤ vi) = 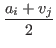 - ai
- ai= 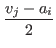
≤ 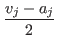 (because aj ≤ ai)
(because aj ≤ ai)= 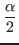
Therefore, we have that a'i - vi ≤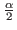 . But the
relation does not hold with equality because aj < vi implies that
vi = ai = aj does not occur and two equalities in the above derivation cannot
hold simultaneously.
Q.E.D.
. But the
relation does not hold with equality because aj < vi implies that
vi = ai = aj does not occur and two equalities in the above derivation cannot
hold simultaneously.
Q.E.D.Proof of Theorem
Theorem For any applicant agent i∈A, the following hold.
1) If vi < ai and | ai - vi | > α, then vi < a'i and | a'i - vi | > α.
2) If ai ≤ vi and vi < a'i, then | a'i - vi | < α/2.
Proof:1) Obvious from Proposition 1 and Proposition 2.2) Obvious from Proposition 3 and Proposition 4.
Q.E.D.
 References
References
-
ECONOMIST (2010). Hiring practices in Japan: A new ice age. The
Economist, http://www.economist.com/node/15720585?story_id=15720585.
Archived at http://www.webcitation.org/69HASTOV3.
FERGUSON, T.S. (1989). Who solved the secretary problem?. Statistical Science, 4(3), 282-296. [doi:10.1214/ss/1177012493]
GALE, D. and Shapley, L. (1962). College admissions and the stability of marriage. American Mathematical Monthly, 69, 9-15. [doi:10.2307/2312726]
MUMCU, A. and Saglam, I. (2008). Marriage formation/dissolution and marital distribution in a two-period economic model of matching with cooperative bargaining. Journal of Artificial Societies and Social Simulation, 11(4), 3 https://www.jasss.org/11/4/3.html.
NIEDERLE, M., Roth, A.E. and Sönmez, T. (2008). Matching and market design. In S.N. Durlauf and L.E. Blume (Eds.), The New Palgrave Dictionary of Economics, Second Edition. Palgrave Macmillan. [doi:10.1057/9780230226203.1058]
ROTH, A.E. (1984a). Stability and polarization of interests in job matching. Econometrica, 52, 47-57. [doi:10.2307/1911460]
ROTH, A.E. (1984b). The evolution of the labor market for medical interns and residents: A case study in game theory. Journal of Political Economy, 92, 991-1016. [doi:10.1086/261272]
ROTH, A.E. and Sotomayor, M. (1992). Two-sided matching. In R.J. Aumann and S. Hart (Eds.), Handbook of game theory with economic applications (pp.485-541). Amsterdam: Elsevier. [doi:10.1016/S1574-0005(05)80019-0]
SAGLAM, I. (2011). Divorce costs and marital dissolution in a one-to-one matching framework with nontransferable utilities. MPRA Paper 33841, Germany: University Library of Munich.
TODD, P.M. (1997). Searching for the next best mate. In R. Conte, R. Hegselmann and P. Terna (Eds.), Simulating Social Phenomena (pp.419-436). Berlin: Springer-Verlag. [doi:10.1007/978-3-662-03366-1_34]
TODD, P.M. and Miller, G.F. (1999). From pride and prejudice to persuasion, In G. Gigerenzer, P.M. Todd and the ABC Research Group (Eds.), Simple heuristics that makes us smart (pp.287-308). New York: Oxford University Press.
RECRUIT WORKS INSTITUTE (2013). Job vacancy ratio to university graduates in 2013 (in Japanese). Annual report, Tokyo: Recruit Holdings Co. Ltd.