Abstract
Abstract
- Computer-simulated synthetic populations are used by researchers and policy makers to help understand and predict the aggregate behaviour of large numbers of individuals. Research aims include explaining the structural and dynamic characteristics of populations, and the implications of these characteristics for dynamic processes such as the spread of disease, opinions and social norms. Policy makers planning for the future economic, healthcare or infrastructure needs of a population want to be able to evaluate the possible effects of their policies. In both cases, it is desirable that the structure and dynamic behaviour of synthetic populations be statistically congruent to that of real populations. Here, we present a parsimonious individual-based model for generating synthetic population dynamics that focuses on the effects that demographic change have on the structure and composition of households.
- Keywords:
- Demography, Synthetic Populations, Household Dynamics, Individual-Based Models
 Introduction
Introduction
- 1.1
- The structure and dynamics of a population are the outcome of many events occurring to its individual members. Understanding and predicting trends in population structure and dynamics is challenging, but has the potential to be of great utility to researchers, planners and policy makers. Synthetic populations can be used as a testbed for a variety of purposes, from simulating disease outbreaks and interventions (Ajelli & Merler 2009), to evaluating the impact of land-use and transport policies (Iacono et al. 2008; Spielauer 2010). To conduct corresponding experiments in real populations may be costly, unethical or otherwise infeasible.
- 1.2
- The key requirement for a useful synthetic population model is that it
generates populations whose structure and dynamics match those of real
populations (Gargiulo et al. 2010). It might seem that the method used to
synthesise a model population should be relatively independent of the purpose
to which that population is subsequently put. However, no model is a perfect
simulacrum of reality and a model's intended purpose will influence decisions
made in its design and construction. Pragmatics dictate that, for any
question, an appropriate model must focus on accurately representing those
aspects of a population most relevant to that question, while perhaps
tolerating some deviation in those aspects judged less
relevant (Taper et al. 2008).
As such, an essential step in model building is the specification of which
dimensions of a population are of greatest importance, and validation of model
behaviour against these dimensions.
- 1.3
- In this paper, we propose a parsimonious individual-based model of household
composition and dynamics, developed for the purpose of exploring interaction between demographic processes and patterns of infection and immunity. To
begin, we describe the specific questions that have motivated the development
of our model, and the requirements that these questions impose. We review how
these questions have been explored in a variety of different modelling
paradigms. We then describe our own model, together with three case studies
that demonstrate its ability to generate populations
under a range of demographic scenarios relevant to infectious disease. We conclude by discussing the strengths and
limitations of our model and its potential directions for its future development.
 Background
Background
-
Motivation
- 2.1
- This section outlines the questions motivating the development of our model,
and the requirements that these questions impose on the design of our model.
The primary goal of infectious disease modelling is to understand how diseases
spread and how they can be controlled, an endeavour in which modelling has long played an
important role (Anderson & May 1991). A key component
of infectious disease models is the representation of the population through
which a disease spreads. The age structure of a population can influence
patterns of susceptibility to disease (Anderson & May 1991). The social
structure of a population gives rise to contact networks that affect how
infection is transmitted through a population (Danon et al. 2011). Understanding
the demographic processes that underlie observed populations, and how they might
shape future populations, can help us explain current patterns of disease and
predict how these patterns will evolve over time, insights that will aid in the
design more effective strategies for disease control (John 1990).
- 2.2
- The assumptions and approximations made when designing a model constrain the
type of questions it can be used to address. One common assumption made by
infectious disease models is that the composition and structure of a population
is static over time. For disease outbreaks that occur over a period of weeks
or months, this assumption may be appropriate, as population structure
typically changes much more slowly than disease state. However, when modelling
endemic diseases that may persist in a population for years or decades, this
assumption becomes less appropriate, as demographic processes such as birth,
death and the formation and dissolution of households will have a significant
effect on population structure and composition. Households are an organisational unit of particular importance as they are a key locus of
disease transmission, particularly for young infants (Jardine et al. 2010). Households are also a target for
disease control strategies such as cocoon vaccination, which aims to provide a
protective environment for newborns by vaccinating their parents (Coudeville et al. 2008).
- 2.3
- In addition to the dynamics arising from individual life events, the underlying
structure of global populations has undergone dramatic changes over recent
centuries. The demographic transition model has been proposed to describe the
long term changes to population structure associated with industrialisation,
improvements in public health, education, and agriculture, and changing social
values (Kirk 1996; Murphy 2011). As an example, during the twentieth
century, increasing life expectancy and lower fertility rates in Australia have
increased the proportion of people aged over 65 from 4% to 14% of the
population, while the proportion of people aged under 15 decreased from 35% to
19%; the size of the average household has decreased from 4.5 to 2.6 people
over the same period (Hayes et al. 2010; Australian Bureau of Statistics 2006b). The effects of this type of
population change on patterns of disease are not yet well understood.
- 2.4
- The questions that we would like to use models to address concern the effect of demographic changes on observed patterns of infection and immunity. What
effect do shrinking household sizes have for the patterns of interaction
relevant to the spread of childhood diseases? How can we assess the long-term
effectiveness of vaccination strategies in a changing population? What are the
implications of the rapid demographic transitions currently occurring in
developing countries? A population model capable of addressing such questions must therefore capture:
- realistic patterns of household composition, in particular the household context of infants;
- the dynamic characteristics of households arising from patterns of birth, death, and household formation and dissolution;
- the differences in household dynamics across different demographic scenarios, corresponding to developed and developing countries; and
- the changes that occur to household dynamics over extended periods of time under changing demographic conditions.
- realistic patterns of household composition, in particular the household context of infants;
- 2.5
- This paper describes the design and validation of a synthetic population model aimed at satisfying these requirements. In the remainder of this section we briefly review how population structure, households and demography have been incorporated into existing infectious disease models.
Previous approaches
- 2.6
- Methods for generating synthetic populations based on empirical data have been
developed in parallel in the fields of demography, geography and social
science. Despite some recent convergence, there is no single general purpose
approach (Mannion et al. 2012; Birkin & Clarke 2011). There are several recent and comprehensive overviews of various methods for population projection and modelling (e.g., Stillwell & Clarke 2011; Wilson 2011; Spielauer 2010). Rather than attempting to replicate these efforts in this section, we focus specifically on approaches taken to representing populations in infectious disease models.
Mathematical models
- 2.7
- Mathematical models of infectious disease represent populations in terms of the prevalence of infection and immunity at a given point in time. A population is divided into 'compartments' corresponding to particular disease states (e.g., susceptible, infectious, recovered). The movement of individuals between these compartments is modelled by specifying transition rates between them. The entire system can then be represented as a set of ordinary differential equations and solved (analytically or numerically) to predict future patterns of disease (Hethcote 2000; Grassly & Fraser 2008).
- 2.8
- Demography can be included in mathematical models by further subdividing
compartments according to age or sex, and by introducing additional terms for
the birth and death of individuals (Anderson & May 1991). Mathematical models
that incorporate household structure have also been proposed, adopting
theoretical or empirical distributions for household
size (e.g., Ball et al. 1997; Ball & Neal 2002; Becker et al. 2005); however, these models
typically assume static populations. Glass et al. (2011) do propose a dynamic
household model, however the distribution of household sizes is held fixed and
the model does not include age structure. These trade-offs illustrate a
fundamental limitation of mathematical approaches to capturing complex
population structure. The explosion of terms that results from simultaneously
incorporating age, household properties, disease state, and other factors of
interest results in models that are analytically intractable.
Individual-based models
- 2.9
- To overcome the limitations of mathematical models, individual-based models
(IBMs)1 have also been applied to the problem of understanding the dynamics of
infectious disease. By explicitly modeling each individual, together with
their age, location, disease status and other relevant properties, IBMs
offer a great deal of flexibility in representing heterogeneous population
structures (Eubank et al. 2004; Elveback et al. 1976; Ferguson et al. 2005; Longini et al. 2005). Most of
these models have been aimed at capturing the dynamics of a single outbreak.
Hence, their primary focus has been on the dynamics of individual activity over
the course of a typical day, the resulting contact networks, and the patterns
of disease transmission that these networks support. The composition and
structure of the populations themselves are usually static. Compared to the
proliferation of static population models, fewer IBMs have considered the
relationship between the long term dynamics of population structure and the
spread of infectious disease.
- 2.10
- Those models that have considered longer time frames have adopted heuristic
approaches to capturing household structure. Ajelli & Merler (2009)
and Guzzetta et al. (2011) investigate long term patterns of hepatitis A and
tuberculosis respectively, using simulated populations that include birth,
death and household formation processes. They generate initial household
distributions from Italian census and survey data using a Monte Carlo sampling
method. Population demographics are updated annually, using empirical
mortality rates to determine individual deaths, and allocating births according
to household size and parental age. Silhol & Boëlle (2011) model the occurrence of
varicella using a population model that includes realistic age and household
structure and dynamics. Their approach to producing an appropriate
distribution of household sizes is to generate each household as a completed
unit including all children that will eventually be born there. This final
household is then 'rewound', resulting in the ages of younger children becoming
negative, and births occur over the course of a simulation when a child's age
becomes positive. An advantage of this approach is that household structure is
guaranteed to accurately reflect that of the real population; however, it does
not generalise in straightforward fashion beyond available data.
- 2.11
- While we have drawn upon aspects of these previous models in the design of the
model described in Section 3, we note that they do not fulfil our
requirement of capturing the changes in household dynamics arising from
demographic shifts.
Microsimulation models
- 2.12
- Microsimulation is an approach to experimenting with virtual societies by
modelling the actions of individuals in a population and (potentially) the
interactions between them that has its origins in
economics (Orcutt 1957). These models are used to explore the potential
impacts of policy decisions, where the choices made by individuals may depend
on policies in a nonlinear and context-dependent fashion. Dynamic
microsimulation models add in a temporal element, incorporating demographic
processes and individual life
courses (Mannion et al. 2012; Birkin & Clarke 2011; Spielauer 2010). Microsimulation models
and IBMs share many similarities. Their differences arise primarily from
having been developed and applied to different problems by different research
communities. Broadly speaking, microsimulation models have been more concerned
with empirical data and predictive accuracy, while IBMs tend to be more
theoretically oriented. While many microsimulation models are designed for the
purpose of forecasting future population trends and policy interactions, they
have also been applied to the challenge of elucidating historical demographic
patterns (e.g., Hammel 2005; Murphy 2011).
- 2.13
- Given the requirement of disease models for demographically plausible
populations, it seems at first surprising that, so far as we are aware, only
one infectious disease model (EpiSimS, Eubank et al. 2004) has explicitly made
use of a pre-existing microsimulation model (TRANSIMS, Barrett et al. 2000),
albeit one developed by the same research group. Possible reasons for this
include: availability of software—many microsimulation models are not
released publicly; tight coupling between model design and data requirements,
meaning that if the data required to initialise a population is not publicly
available, or not available in the correct form for the population of interest,
the model may not be suitable; limited extensibility, making it difficult to
extend an existing population model to include disease dynamics; and model
development effort—dynamic microsimulation models are notoriously
time-consuming and expensive to build (Harding 2007).
Summary
- 2.14
- A significant impediment to modelling the demographic dynamics of populations
is the limited availability of data with which to parameterise models.
Hypothetically, if sufficient data were available to estimate a probability for
each possible transition that an individual or household might undergo, using a
demographic microsimulation model to project a population forward would be a
trivial exercise. In practice, the number of possible transitions explodes
combinatorially with attributes of interest, and available data will always be
insufficient for this approach to be practicable.
- 2.15
- At the other extreme, an ideal individual-based model might simulate the
underlying cognitive and social behaviour of individuals in a population,
perhaps using some internal representation of individual utility together with
a forecasting model that predicts an individual's behaviour on the basis of its
history and current context. This approach has the potential to free demographic models from the reliance on the
massive quantities of data required by transition-based microsimulation models (Silverman et al. 2011). However, much rests upon the model used to represent individual
decision making. Successful individual-based models of demographic processes
have thus far typically been constrained to specific aspects of populations.
For example, Billari et al. (2007) use an IBM of marriage based on social
interaction to explore the emergence of observed trends in marriage age.
Extending such an approach to all facets of human behaviour remains an open
challenge.
- 2.16
- Recently, there has been a convergence of techniques from microsimulation and
individual-based modelling, as (some) IBMs encounter a need for more empirically
plausible populations, and microsimulation modules begin to include more
behavioural aspects (Wu & Birkin 2012). The resulting hybrid models use available
demographic data to calibrate distributions of individual attributes, and
stochastic behavioural models of individual decisions to generate particular
events.
 Our model
Our model
- 3.1
- The basic unit of description in our model2 is the individual.
Individuals are characterised by their age, sex and the household to which they
currently belong. A population consists of the set of currently alive
individuals, structured by a network of interpersonal ties that maps couple,
parent–child and household co-membership relations. The following sections
describe how a population is initialised, how it is updated over time, and how
it can be parameterised using available data on real populations.
Initialisation
- 3.2
- An initial 'bootstrap' population is created by randomly generating individuals
with ages drawn from a specified age distribution. These individuals are
assigned to households at random according to a specified household size
distribution.
Households of size one or two are assigned one or two adults respectively,
while households of size three or greater are assigned two adults and one or
more children. This initial population structure will diverge in several ways
from a real population; for example, constraints on birth interval and
inter-generational age difference will not be respected. If more detailed data
on household structure is available, more complex
methods (Gargiulo et al. 2010; Ajelli & Merler 2009) could be used to specify a more
realistic initial population structure. Alternatively, the approach we adopt
here is to update the state of the population until such time as all of these
bootstrap individuals and households have been replaced (i.e., for at least 100
years), at which stage internal constraints on population structure will be respected.
Updating
- 3.3
- The state of a population is updated in discrete time steps, where each step
corresponds to a specified number of days. All parameters controlling the
occurrence of demographic events are specified as annual probabilities and
rates, therefore these are scaled appropriately.
- 3.4
- Five types of demographic events can occur to an individual:
- Death: Age and sex specific mortality rates are used to determine
an individual's probability of death during each time unit (e.g., Figure 1(a)). If a death results
in a household containing only children then the household is dissolved. Any
adult children (i.e., aged 18 years or over) leave home and create new
single-person households, while any children under 18 years are randomly
relocated (fostered) to other households containing at least one child.
- Birth: Age (and optionally, parity3) specific fertility rates are
used to determine the probability that a birth occurs to a given
individual. As fertility is not an independent
process, rates are transformed into relative probabilities used to designate
the subset of the population from which the actual mother is then chosen (e.g., Figure 1(b)). Upon
giving birth, a mother is excluded from being a candidate for future births for
a number of days drawn from a truncated normal distribution, with a minimum duration of
270 days.
- Couple formation: An individual within a given age range who is
currently single has a fixed probability per time unit of forming a new couple.
The new partner is chosen from the pool of individuals who are currently
single, of the opposite sex, and whose age differs by a normally distributed
value. The newly coupled individuals move into a new household, together with
any dependents (e.g., children from previous couples).
- Couple dissolution: Any currently coupled individual within a given
age range has a fixed probability per time unit of dissolving the couple. Upon
dissolution, one member of the couple moves into a new single person household,
while the other remains in the original household together with any children.
- Leaving home: Individuals leave home automatically when they form a couple, otherwise any individual above a specified age leaves home with a fixed probability per time unit and forms a new single person household.
- Death: Age and sex specific mortality rates are used to determine
an individual's probability of death during each time unit (e.g., Figure 1(a)). If a death results
in a household containing only children then the household is dissolved. Any
adult children (i.e., aged 18 years or over) leave home and create new
single-person households, while any children under 18 years are randomly
relocated (fostered) to other households containing at least one child.
- 3.5
- The model can be used to simulate populations of fixed size (i.e., with
replacement level fertility), or populations that are increasing or decreasing
in size. Change in population size can result from an imbalance between the
number of births and deaths, or between the number of immigrants and
emigrants. In our model, growth due to excess births is implemented by
triggering additional birth events at each time step. Growth due to
immigration is implemented by introducing new individuals and households into
the population according to a specified distribution of age and household
structure. Specifying the age and family composition of migrants is a complex
issue, depending as it does on the circumstances of migration, country of
origin, and other factors. The default assumption made by the model is that
the migrant population is demographically similar to the target population.
Calibrating migration to reflect the demographic characteristics of specific
events would be relatively straightforward provided that suitable data were
available.
Parameterisation
- 3.6
- The input parameters that must be specified to initialise and update a
population are summarised in Table 1. A general principle
followed in designing the model was to parameterise the model in terms of
events occurring to individuals, and to allow the sizes and types of households
in a population to vary as a consequence of these individual-level events. For
example, individual births were allocated to parents using age- and
parity-specific fertility rates, but not to households of a specific size
or composition; thus, in contrast to existing
models (Silhol & Boëlle 2011; Ajelli & Merler 2009), household size distributions were not
controlled, but rather result from the interaction between patterns of household formation and dissolution arising from individual-level events. Further calibration against household-level data would of course be
possible, but reserving available household-level data for validation purposes
enables us to better evaluate the effectiveness of our simple event-based model.
Table 1: Model parameters Parameter Description General: Initial population size Number of individuals in population at start of simulation. Population growth rate Annual rate of change in population size due to natural increase. Immigration rate Annual rate of change in population size due to immigration. Death: Age- and sex-specific mortality probabilities Annual probabilities of death by sex and year of age. Birth: Age-specific relative fertility probabilities Relative probabilities, given the birth of a child, that the mother is of a specified age. Parity-specific relative fertility probabilities (optional) Relative probability, given the birth of a child, that it is to a woman with a specified number of previous children. Birth gap (mean and SD) Parameters governing the minimum inter-birth interval. Couple formation: Couple formation parameters Age range that a currently single individual is eligible to form a couple, and annual probability that this will occur. Partner age difference (mean and SD) Parameters governing the sex-dependent age difference between partners during couple formation. Couple dissolution: Couple dissolution parameters Age range that a currently coupled individual is eligible dissolve that couple, and annual probability that this will occur. Leaving home: Leaving home parameters Minimum age at which an individual currently living with a parent/guardian will form a new single-person household, and annual probability that this will occur. - 3.7
- Mortality data is often available in the form of life tables, a demographic
tool that shows, for each age, the probability of an individual of that age
dying in the next year. Fertility rates by age are also available for most
countries. These fertility rates can be used in two different ways. One
option is to use them to determine the probability that a woman of a particular
age will give birth in a given year. The number of births that occur in a year
will then emerge from the aggregate application of these probabilities across
the female population. The alternative (which we adopted here) is to specify
the number of births that occur in a year, and then use age-specific fertility
rates to determine the ages of the women to which those births occur.
Effectively, rather than asking “what is the probability of a woman of age x
giving birth this year?”, we ask “given that a birth occurred, what is the
probability that the mother was aged x?” An advantage of the latter
approach was that it enabled us to control the total size of a population. For
example, population size could be held constant by triggering sufficient births
each year to replace the individuals dying in that year, or constrained to grow
(or shrink) at a given rate.
- 3.8
- Couple formation and dissolution, and the departure of children from their
parents' household are all governed by simple models that assume a constant
probability of a particular event occurring per unit of time. Thus, these
probabilities are independent of age, duration of relationship, previous
marital status, and other potentially relevant factors. This approach is
considerably simpler than that taken by dynamic microsimulation models. These
more complex models rely heavily on the availability of appropriate statistical
data in order to parameterise the effects that diverse factors have on, for
example, marriage and divorce. Our primary motivation for adopting this
simpler approach was to be able to deal with the availability of data across a
variety of different countries and historic time periods.
- 3.9
- The specific parameter values, data sources, and estimation processes used to
specify the probability of individual events are detailed at the beginning of
each case study in the following section.
 Results
Results
- 4.1
- As described above, the primary motivation for the development of our model was to use it as a demographically plausible testbed in which to explore interactions between population dynamics and patterns of disease. In turn, this aim imposed requirements on model behaviour, as described in Section 2.1. In this section, we use three demographic scenarios to evaluate the extent to which our model meets these requirements. The first two scenarios consider populations corresponding to those of a developed and a developing country. The third scenario considers a population undergoing a demographic transition from high to low fertility.
- 4.2
- Quantitative comparison between model output and empirical data is an important
component of validation. However, suitable data for comparison is not always
available, and we also rely on comparison of more qualitative aspects of model
behaviour to build confidence in the validity of a
model (Korb et al. 2013; Grimm et al. 2005).
Case study 1: A developed country population
- 4.3
- Our first case study explored the ability of our model to capture patterns of household composition and dynamics comparable to those exhibited by Australian population at the beginning of the 21st century. Real populations are ever-changing: fertility rates that deviate from replacement and immigration act to increase or decrease the size of a population, while changes in longevity reshape its age structure. For this case study, we explore a simpler scenario in which population size, mortality and fertility rates and other event probabilities are fixed, and there is no migration. The resulting steady state population has a constant size and, over time, approaches a stable age structure. While such a scenario is obviously of only limited use for forecasting purposes, it does have the significant benefit of providing a stable background for theoretical investigation of interactions between the dynamics of demographic and epidemic processes (e.g., as described in Glass et al. 2011). In particular, it allows us to evaluate the model from the perspective of the first two requirements described in Section 2.1. A more realistic scenario with time-varying demographic parameters is explored in Case Study 3.
- 4.4
- The initial population was parameterised using recent Australian data on age
structure and households (de Vaus 2004; Australian Bureau of Statistics 2006b). Values for other
parameter were estimated on the basis of census data reported
in de Vaus (2004). Couple formation parameters were calibrated against
data on the percentage of individuals by age who had never married nor
cohabited. Couple dissolution parameters were calibrated against data on
percentage of marriages surviving by duration. Leaving home parameters were
calibrated against data on the number of individuals by age living at home,
accounting for those who had left to marry or cohabit. The population was
simulated for two hundred years, to ensure that a steady state had been
achieved, before composition and dynamics were analysed.
Table 1: Case Study 1: Model parameters Parameter Value / Data source Initial population size 20,000 Population growth rate 0% Immigration rate 0% Mortality probabilities Australia, 2006, by year of age (Australian Bureau of Statistics 2007) (see Figure 1(a)) Fertility probabilities Australia, 2006, by year of age (Australian Bureau of Statistics 2006a) (see Figure 1(b)) Birth gap mean: 365 days; SD: 90 days Couple formation parameters age range: 18–60 years; annual probability: 7.5% Partner age difference mean: 2 years; SD: 2 years) Couple dissolution parameters age range: 18–60; annual probability: 1.5% Leaving home parameters minimum age: 18; annual probability: 0.8% Figure 1: Australian census data used to parameterise the model in Case Study 1. (a) Mortality rates by age and sex; (b) Relative probability of a birth occurring to a woman by age. Data sources as in Table 2. 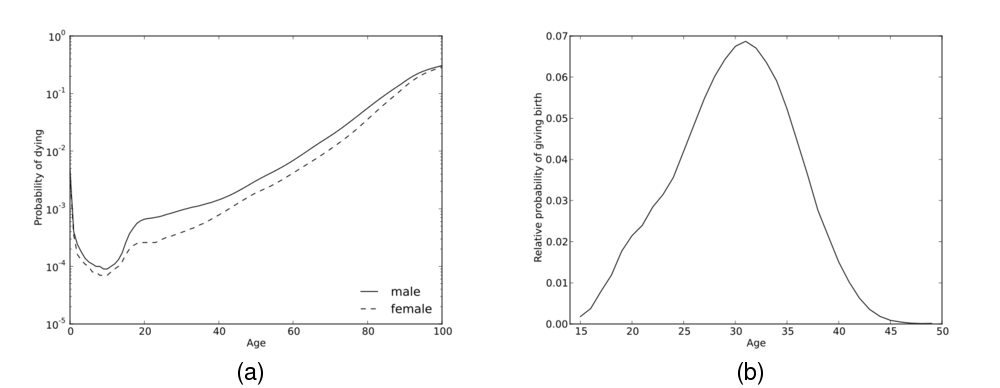
Age distribution
- 4.5
- Figure 2(a) shows the simulated age structure of the final
population for ten independent runs, together with the starting age
distribution (based on 2006 census data). In the absence of migration, the age
structure of a population is determined solely by births and deaths. When
age-specific rates of fertility and mortality remain constant over a long
period of time, and there is no migration, the resulting population is called
'stable'. Stable populations are characterised by constant age structure and
fixed growth rates. A stable population with a growth rate of zero is called
'stationary'. Stable and stationary population structures are largely
theoretical constructs that are rarely observed in real populations. Over the
last century, life expectancy in Australia has increased steadily, while
fertility and migration have fluctuated. One interpretation of the final age
structures shown in Figure 2(a) is that they represent what
Australia's population could look like after a century with replacement-level
fertility, no migration, and constant age-specific birth and death rates.
Figure 2: (a) The final age distributions of ten simulated populations (grey), compared to the empirical age distribution used to initialise the population (black). (b) The final household size distribution (white), averaged over the ten simulated populations (error bars indicate standard deviation), compared to empirical data (black). 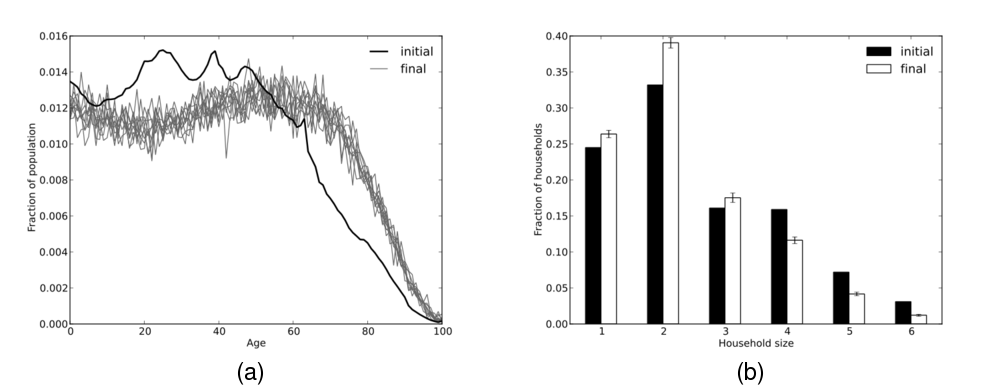
Household size distribution
- 4.6
- Household sizes and compositions were allowed to vary in response
to the individual level processes of leaving home, forming and dissolving
couples, birth and death. The final household size distribution after 200 years (mean and standard deviation across 10 independent runs) is shown in Figure 2(b). Some of the variation between simulated and empirical age structure can also be observed in the final household size distribution. Older individuals, who are over-represented in the simulated population, are more likely to live in households of size one and two, which are also over-represented in the simulated population.
- 4.7
- As individual households are formed and dissolved, the number of households of a particular size increases or decreases; however, because we are holding the demographic rates fixed, the shape of the household size distribution remains relatively constant, with some stochastic fluctuation (Figure 3(a)).
Figure 3: The evolution of (a) household size distribution and (b) family household type distribution over 100 years under fixed demographic conditions, for a single simulation run. 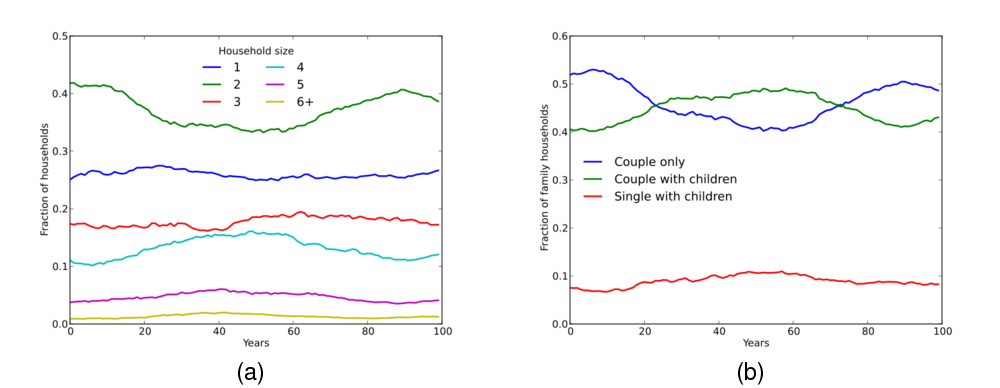
- 4.8
- To test how the final household size distribution depended upon the the household size distribution that was used to create the
initial bootstrap population (as described in Section 3.3) we also ran simulations in which the population was initialised
with uniformly distributed household sizes. By year 200 of these simulations,
the distribution of household sizes once again approximated the empirical
distribution. Thus, we are confident that the household size distribution is
an emergent property of the underlying individual-level demographic processes,
rather than a simple consequence of the initial conditions.
Household type distribution
- 4.9
- Beyond looking simply at household size, we also investigated the types of
household that individuals tended to belong to at different stages of their
lives. Figure 4 shows the proportion of individuals that
living in various types of household situation (couple with children, couple
without children, single parent, lone person, and living with parents), broken
down by age category (mean and standard deviation across 10 independent runs).
The simulation model produces a plausible representation of household type
prevalence observed in the Australian population. While there is some
variation, general trends across age groups are well captured; for example, the
proportion of individuals living in households without children initially
increases as individuals form couples, then decreases as these couples have
children, before finally increasing as these children leave the family
household.
Figure 4: Type of household by age group at the end of a simulation run (white; error bars indicate standard deviation), compared with empirical data (de Vaus 2004) (black). 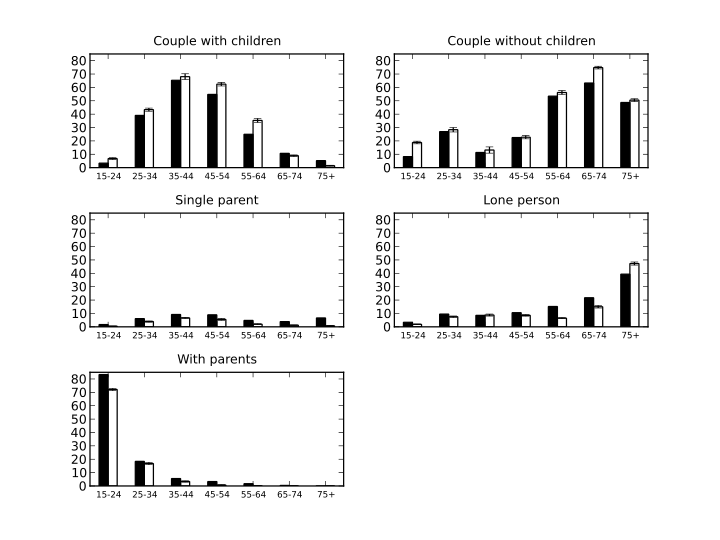
- 4.10
- Figure 3(b) indicates that, as with household size distributions, the proportion of family households fluctuates stochastically over the time period reported, but is generally stable.
Changes in household structure
- 4.11
- The distribution of household sizes (Section 4.1.2) and the
prevalence of household types (Section 4.1.3) both remain
stable over the course of a particular simulation run. However, this stability
hides the fact that the type of household that any one individual belongs to
changes multiple times over the course of their life
(see Section 4.1.5). An individual's household type can change
when they leave home, when they form or dissolve a couple, when their first
child is born or their last child leaves home, or when another member of their
household dies. While longitudinal data is not typically captured in a census, the Household, Income and Labour Dynamics in
Australia (HILDA) Survey (Wilkins et al. 2011) reports statistics on the proportion of individuals
who change household type over a five year period
(Table 3). Collating output from multiple simulation runs reveals a similar pattern of transitions between household types (Table 4).
Table 3: Changes in household structure, 2003 to 2008 (HILDA) (%) Couple only Couple with children Single with children Single person Couple only 75.3 14.0 0.8 8.4 Couple with children 10.1 76.8 6.0 4.9 Single with children 6.4 18.0 59.5 13.0 Single person 11.1 8.8 3.5 74.9 Table 4: Changes in household structure, mean and standard deviation over 10 runs (%) Couple only Couple with children Single with children Single person Couple only 78.2 (0.6) 11.3 (0.4) 0.6 (0.1) 9.8 (0.3) Couple with children 14.8 (1.3) 77.4 (1.8) 5.2 (0.8) 2.6 (0.2) Single with children 9.5 (0.6) 41.6 (3.0) 42.6 (2.4) 6.3 (0.9) Single person 8.8 (0.7) 11.6 (0.9) 1.2 (0.3) 78.3 (1.0) - 4.12
- Given that model behaviour was not explicitly calibrated against these
transition rates, there is a remarkable level of agreement between the dynamics
of real and simulated households. The primary point of disagreement is the
transition from 'single with children' to 'couple with children', which is
over-represented in simulated populations, suggesting a possible direction for
future refinement.
Family life cycle
- 4.13
- The family life cycle is a demographic pattern that captures the life
experience of a large proportion of the developed world's past, current, and
most probably future population:“most persons will grow up, establish
families, rear and launch their children, experience an empty nest period and
eventually reach the end of their life.” (Glick 1989, p. 123).
Figure 5 illustrates two different views of
the family life cycle from the perspective of an individual, showing the age
distribution at which various significant events occur. Exploring the
sequences of events that constitute a simulated individual's family life cycle
at both an individual and aggregate level provides a straightforward way to
verify that these life courses appear plausible.
Figure 5: The age distribution of (a) major life events (marriage, birth of first child and death) and (b) birth of first and subsequent children over the total sample population. 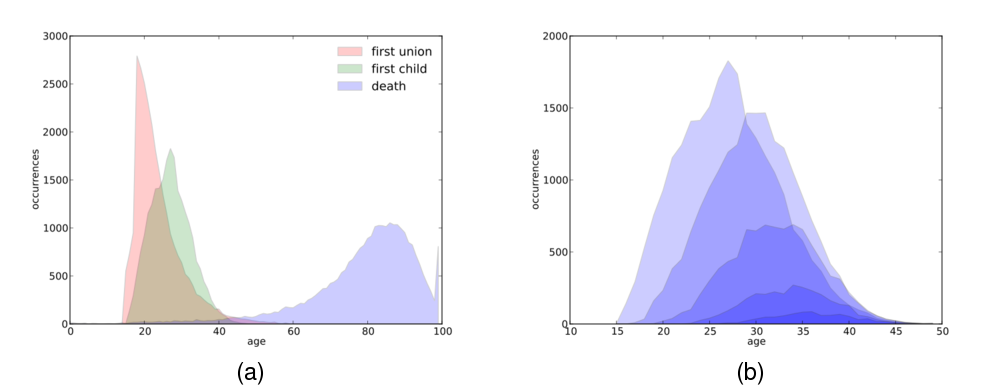
- 4.14
- The approach taken in Figure 5 to exploring the distribution of
significant events over an individual's life span can also be applied to
households. An issue that arises is how best to define a household's 'age'.
The approach taken here is to define the creation of a household as occurring
when either (a) an individual leaves her parents' household to form a new
single person household; (b) two individuals leave their parents' households to
form a new couple household; or (c) an individual leaves his spouse's household
after divorce and forms a new single person household. Other inter-household
movements do not result in the creation of a new household; for example, the
formation of a couple where at least one individual currently resides in a
single person household. In these cases, one household merges with another,
but no new household (i.e., of age zero) is created. A household is dissolved
when the last individual in that household dies or leaves; for example, if two
individuals, each living in a single person household, form a couple, then one
of these households will continue, and the other will be dissolved.
- 4.15
- Assigning households an age as described above then allows us to look at the
distribution of particular individual or household level events by household
age. Figure 6 represents the family life-cycle in terms of
household size: households typically begin their life with one or two
individuals (e.g., a new couple who have just left their own parents'
households). Household size increases steadily, peaking between twenty and
twenty-five years (when our example couple are in their forties and have had
all the children that they will have). Thereafter, household size declines
back to a mean of two by around forty-five years (with our example couple being
'empty nesters' in their sixties). The period of peak size represents the
stage when most or all of the children that will be born into that household
have been born, but none or few of them have yet left home.
Figure 6: Household size by age. Bold line indicates mean household size. Boxplots show median size (red bars), inter-quartile range (box), minimum/maximum within 1.5 of the inter-quartile range (whiskers) and outliers. The sample population of households used was the set of households that were both created and dissolved during the timeframe of the simulation run; that is, households created at the beginning and households still existing at the end of the run were excluded. 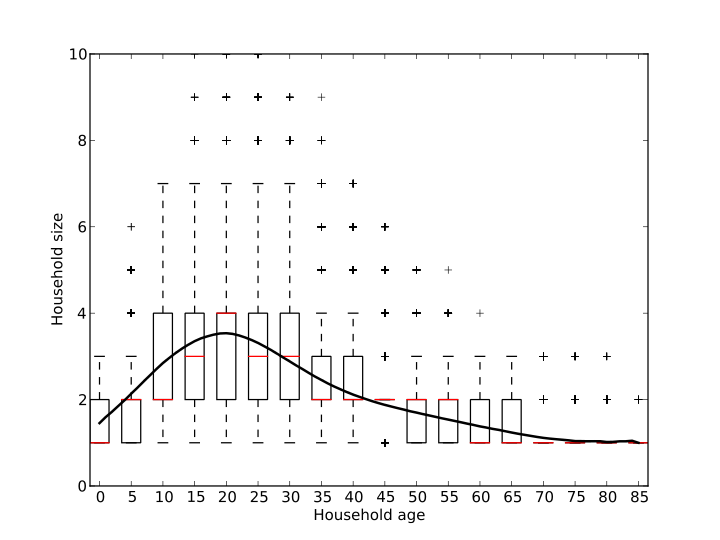
Household composition
- 4.16
- We simplify the issue of describing household composition by dividing
individuals into discrete age categories relevant for disease transmission:
infants under five years; school-children between five and seventeen years;
adults from eighteen to sixty-four years; and elderly individuals sixty-five
years and over. More or different categories could be chosen depending upon
the age groups that are of most interest in a particular application of the
model. Figures 7(a) and
7(b) show the distribution of individual ages
by household age and household size respectively in a single population at a
given point in time. These figures match observed trends of the household
locations of different types of individuals (de Vaus 2004). Elderly
individuals tend to be found primarily in smaller and older households.
Children are found primarily in households of intermediate age and
intermediate-to-large size.
Figure 7: Age distribution of individuals given (a) household age and (b) household size. Individuals are grouped according to age categories: < 5 years; 5-17 years; 18-64 years; 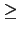 65 years.
65 years.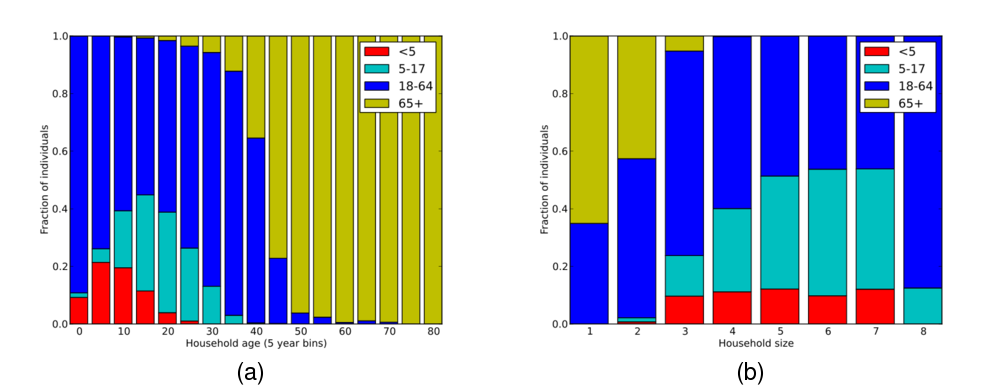
- 4.17
- Figure 7(b) depicts how individuals of
various ages are allocated across households of different sizes, but provides
no information on the co-occurrence of individuals from different age groups in
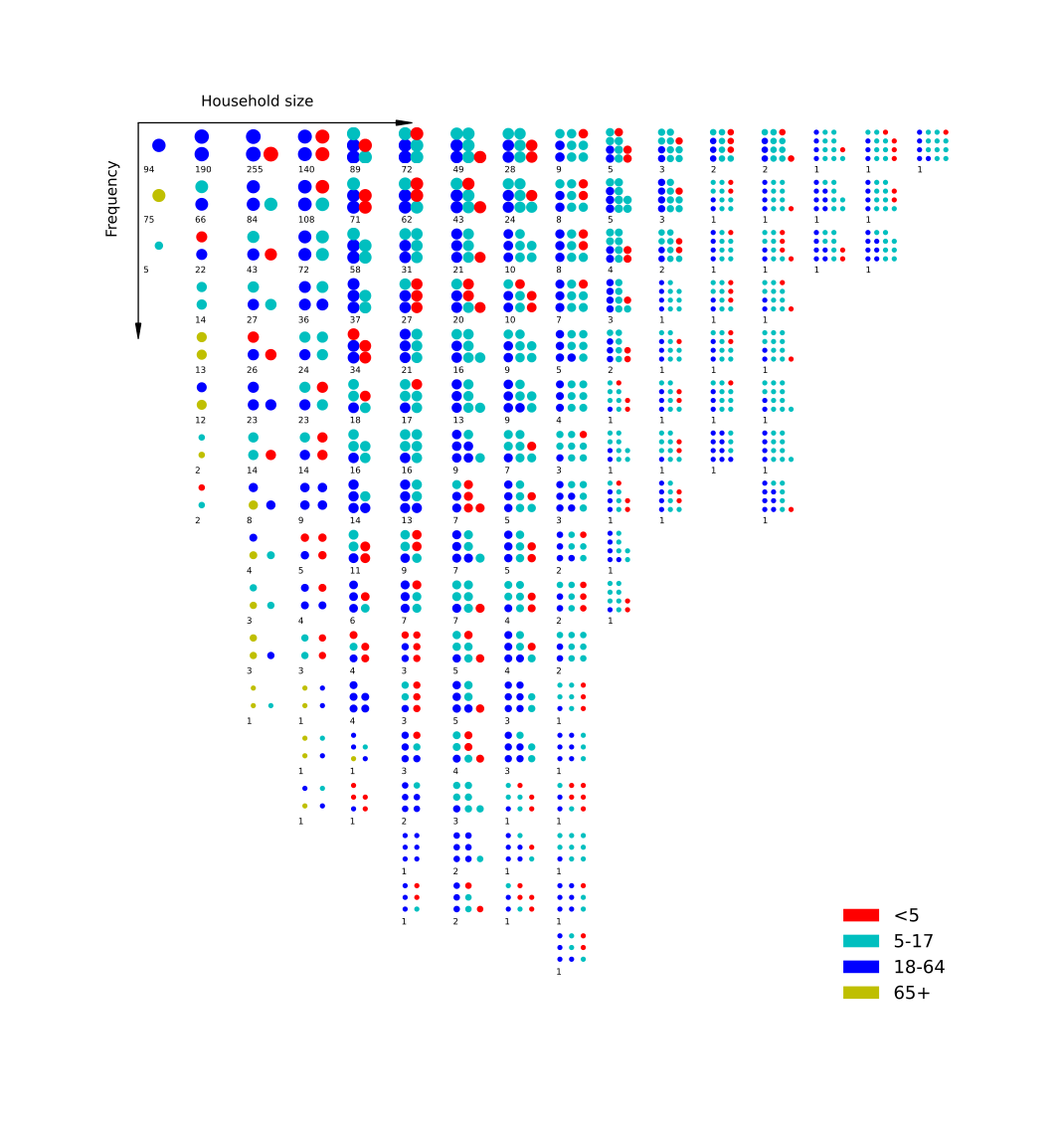
households. Figure 8 shows a novel approach to visualising the
types of households that appear in a population and their relative frequency.
As above, this figure represents a snapshot of a population at a given point in
time, rather than an aggregation across time. Each cluster of n circles
represents a unique type of household containing n individuals, with the
count of households of that type appended below. Each circle is coloured
according to the age category of the individual in that household type, and
circle size reflects household type frequency, with larger circles indicating
more common household types.4 Household types are further arranged by household
size (increasing left to right) and frequency (more frequent household types
appear at the top). The representation shown in Figure 8
provides a convenient overview of the diverse household structures that arise
in simulated populations. At the same time, it is straightforward to gain an
impression of which household types are most likely to contain infants and their frequency in the population.
Figure 8: A chart of household types appearing in a population at a given point in time. Each circle represents an individual (coloured by age category). Each cluster of circles represents a household type. The frequency with which a particular household type occurs in a population is written beneath, and represented visually by size (larger circles indicate more common household types). 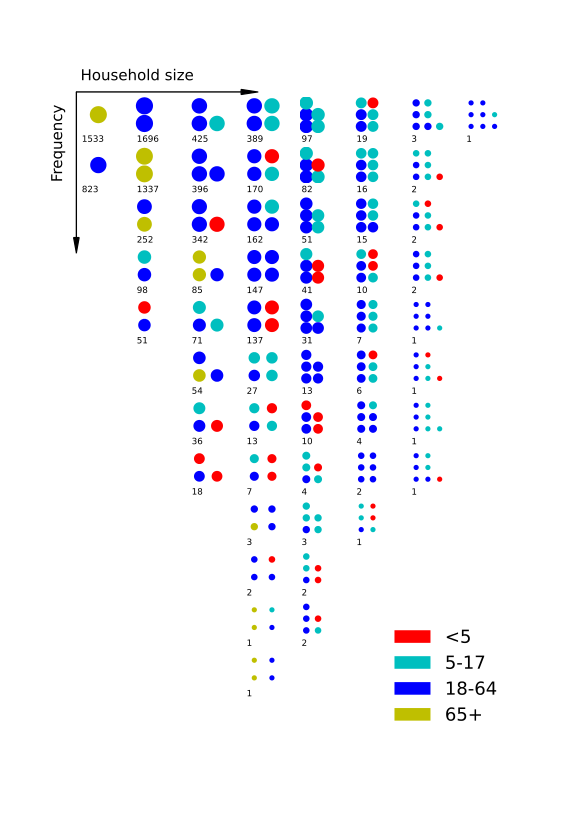
Case study 2: A developing country population
- 4.18
- The third requirement of our model was that it be able to produce plausible patterns of household dynamics across a variety of demographic scenarios. In particular, we are interested in exploring the dynamics of infection and immunity in a developing country setting. As discussed above, the demographic transition model describes a country's transition from a phase in which both fertility and mortality are high, through a phase where mortality falls, but fertility remains high, to a phase where both fertility and mortality have fallen. During the first and last phases, fertility and mortality are balanced, and population size is stable. By contrast, in the middle phase, fertility exceeds mortality, and population size increases. We chose Zambia as a country representative of this middle phase of demographic transition: both mortality and fertility rates are higher than Australia's, and population growth of approximately 2.5% per annum is almost entirely due to natural increase (rather than immigration). Compared to Australia, less data is available on the Zambian population, restricting the amount of validation possible. Here, we focus on age and household size distribution.
- 4.19
- We simulated an initial population of 500 individuals, growing at an annual
rate of 2.5% (giving a final population size of approximately 70,000 after 200
years). Age-specific mortality rates were obtained from (Lopez et al. 2000), and
age-specific fertility rates were obtained from the UNdata website
(data.un.org). Insufficient resources were available to estimate precise
values for couple formation and dissolution parameters. We therefore estimated
values based on comparison with values used in Case Study 1. Namely, we
specified an earlier age for couple eligibility, a lower rate of divorce and a
lower rate of leaving home as a single individual (Republic of Zambia Central Statistical Office 2000). As with the first case study, we model the hypothetical scenario in which demographic rates are constant over time.
Table 5: Case Study 2: Model parameters Parameter Value / Data source Initial population size 500 Population growth rate 2.5% Immigration rate 0% Mortality probabilities Zambia, 2000, 5-year age groups Lopez et al. (2000) Fertility probabilities Zambia, 2000, by year of age (data.un.org) Birth gap mean: 270 days, SD: 0 days (i.e., uniform) Couple formation parameters age range: 15–60 years; annual probability: 8% Partner age difference mean: 2 years; SD: 2 years Couple dissolution parameters age range: 18–60 years; annual probability: 0.1% Leaving home parameters minimum age: 18 years; 0.5% - 4.20
- As depicted in Figure 9(a), the age structure of the
Zambian population is captured with a high degree of accuracy. Household size distribution (Figure 9(b)) is
reproduced less accurately: small household sizes (1–4 people) are over-represented, while very large households (> 8) people are under-represented. One possible explanation is that our
parameter values were poorly chosen. However, we also note that Zambia has a
reasonably high level of multi-generational and multi-nucleus
households (Republic of Zambia Central Statistical Office 2000). Neither of these are currently represented in
our model, which may explain some of the discrepancy.
Comparing Figures 10 and 11 with the corresponding figures from the first case study (Figures 7 and 8)
demonstrates the considerable differences in patterns of household composition
that exist between countries with different demographic properties.
Figure 9: (a) The final age distributions of ten simulated populations (grey), compared to the empirical age distribution used to initialise the population (black). (b) The final household size distribution (white), averaged over the ten simulated populations (error bars indicate standard deviation), compared to empirical data (black). 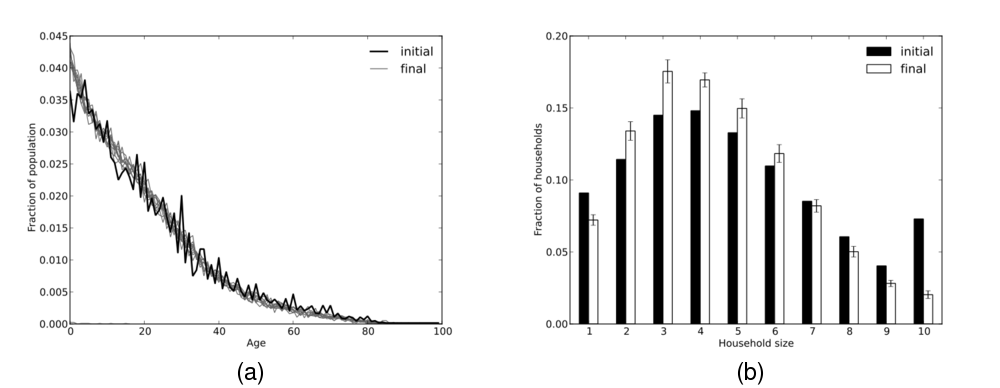
Figure 10: Age distribution of individuals given (a) household age and (b) household size. Individuals are grouped according to age categories: < 5 years; 5-17 years; 18-64 years; 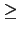 65 years.
65 years.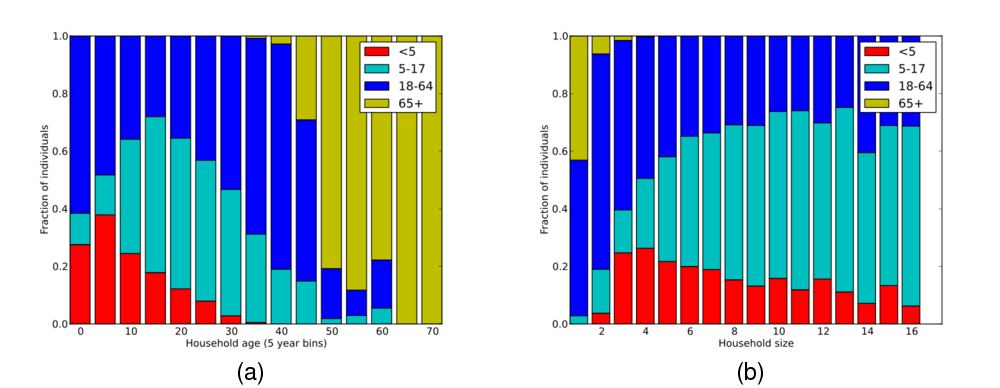
Case Study 3: A population undergoing demographic change
- 4.21
- The two previous case studies depict stable demographic scenarios: there is no
change to fertility and mortality rates over the simulated period. The final
requirement of our model was that it produce household dynamics of a population
across a period of demographic change. As discussed in
Section 2, patterns of infection and immunity emerge over
long time-frames, during which time population structure is neither static nor
changing in a uniform fashion. Rather, underlying demographic rates change as
life expectancy increases due to improvements in health and medicine, and
fertility patterns change in response to availability of birth control and
shifting social norms. As a test case, we parameterised our model with 100
years of Australian census data, covering the period from 1910-2010. During
this period, Australia's population increased from almost 4.5 million to over
22 million. While natural increase (i.e., resulting from birth rates being
higher than death rates) accounts for around two-thirds of this growth,
immigration has also played a significant role. At the conclusion of World War
II, Australia initiated a large immigration programme in an effort to boost
population numbers (Department of Immigration and Multicultural
Affairs 2001). To approximate this demographic history,
we used a starting population size of 500 individuals, growing at a rate of
2.5% per year during the initial 100 year initialisation period, and at a
decreasing rate during the following 100 years. We used an immigration rate of
0% prior to 1950 and 1% per year after 1950. The resulting final populations
contained approximately 30,000 people after 200 years of simulation. We
estimated time-varying couple formation and dissolution rates on the basis of
historical trends of increasing marriage age, and increasing divorce
rate (de Vaus 2004).
Table 6: Case Study 6: Model parameters Parameter Value / Data source Initial population size 500 Population growth rate 2.5% decreasing to 0.5% over 100 years Immigration rate 0% until 1950, 1% thereafter Mortality probabilities Australia, 1910-2008, varying frequency, by year of age (Australian Bureau of Statistics 2008) Fertility probabilities Australia, 1910-2008, varying frequency, 5 year age groups (Australian Bureau of Statistics 2008) Birth gap mean: 365 days; SD: 90 days Couple formation parameters age range: (15 increasing to 18 over 100 years)–60; annual probability: 7.5% Partner age difference mean: 2 years; SD: 2 years Couple dissolution parameters age range: 18–60; annual probability: 0.1% increasing to 1.5% over 100 years Leaving home parameters minimum age: 18; annual probability: 0.8% - 4.22
- The key demographic trends that were reproduced in the simulated populations
were the effects that time-varying demographic rates have on households.
Figure 12(a) shows how average household size decreases at a rate
comparable to that observed in the empirical data. Figure 12(b)
shows how the (rescaled) number of households changes over the same time
period, again compared to the empirical trend.
- 4.23
- Figure 13 shows two further perspectives on how households
evolve over the course of the simulation: the prevalence of households of size
one and two increases relative to larger households
(Figure 13(a)), and the prevalence of households containing
couples without children increases (Figure 13(b)). Only limited
data is available to validate these trends across the full time period;
however, rates of change across the most recent decades are in agreement with
census data. Empirical values for two time points (1981 and 2001) are overlaid
on the plot showing the evolution of household size distribution over time
(Figure 13(a)). Even after seventy years of simulated
population evolution, the model reproduces comparable rates of increase and
decrease in the occurrence of households of a given size. With respect to the
distribution of household types (Figure 13(b)), in our ten
simulated populations, the proportion of family households containing a couple
with children decreased by an average of 23% (SD 1.5%) over the penultimate
two decades, while the proportion containing only a couple increased by an
average 28% (SD 3.8%). The corresponding changes in the Australian
population between 1981 and 2001 were a 20% decrease and 28% increase
respectively (de Vaus 2004).
Figure 12: (a) Average household size over 100 years. (b) Number of households over 100 years (Number of households in 1910 = 100). Both figures show the output from 10 simulation runs compared with historical Australian census data (bold). 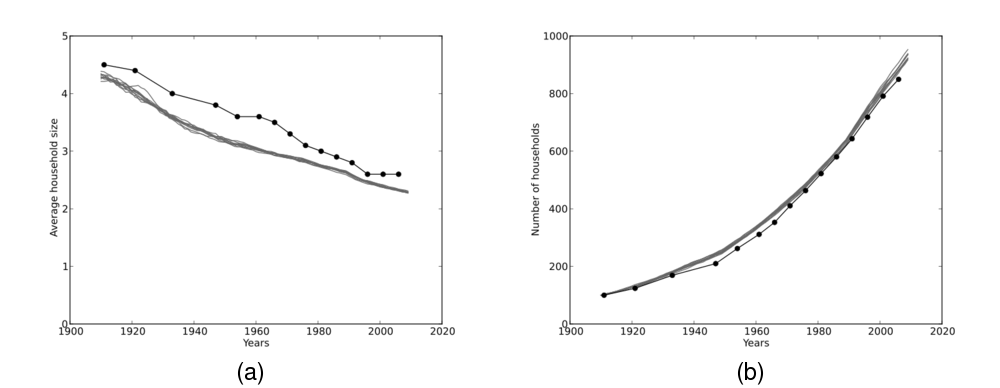
Figure 13: (a) Evolution of household size distribution over 100 years. (b) Evolution of family household type distribution over 100 years. Family households, in our model, include any household containing at least two people (i.e., single person households are excluded). Each figure shows the output from a single representative simulation run. 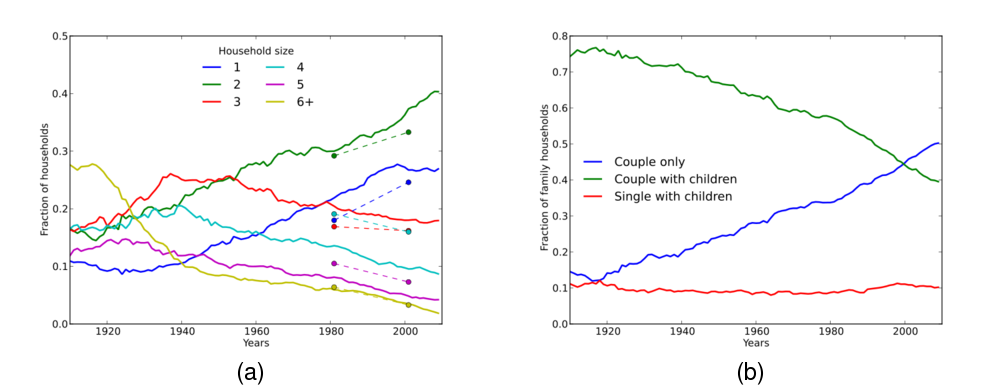
 Evaluation
Evaluation
- 5.1
- Many different forces act upon populations to produce their characteristic age and household structure. Over the last century, improvements to healthcare, government policies around migration and fertility, changing social norms, as well as unpredictable events such as wars and natural disasters have all played a role. Capturing all of these complex and interacting forces in a model is challenging, and we have favoured a general and flexible approach to mechanism design. That said, we believe that, for our research agenda, the model described in Section 3 represents a good balance between simplicity and plausibility. Currently, the data sources required to parameterise the model are relatively modest, hence it can be used to model populations for which only limited data are available (e.g., the international and historical populations considered in the second and third case studies) and hypothetical scenarios. Undoubtedly a closer fit to empirical data could be achieved, but this would inevitably come at the cost of introducing further data dependence into the model.
- 5.2
- In its current form, our model meets the four requirements set out in Section 2.1; namely, it can produce realistic patterns of household composition and household dynamics, while being flexible enough to capture a variety of demographic scenarios and transitions.
In endeavouring to design a parsimonious model, we have made several
simplifying approximations. We briefly discuss refinements to be considered in future model development: First the absence of extended family households, as noted above,
is an omission that must be addressed in order to more accurately
capture household composition in certain populations. The cultural and economic conditions under which extended family households arise vary by country and across time (Hammel & Laslett 1974). As with the model described by Murphy (2011), our model contains a great deal of information on kinship relationships between individuals that could be used to construct more complex household structures. From an epidemiological perspective, multi-generational may have implications for patterns of social contact and disease transmission (Mossong et al. 2008). Second, the model does not currently distinguish between marriage and
cohabitation. We judged that, from the perspective of household structures
relevant to infectious disease transmission, marriage and cohabitation are
effectively indistinguishable; however, households in which partners are
married as opposed to cohabiting do appear to have different characteristics
(such as duration of couple relationship) that may influence household
dynamics (de Vaus 2004).
Finally, a more realistic model of immigration is certainly possible. Specifically, immigrant populations are likely to have different demographic characteristics to the populations they join (Haug et al. 2002), and their arrival is therefore likely to influence age and household structure in non-trivial ways. Iannelli & Manfredi (2007) have shown how changes to the age structure of a population can have implications for disease dynamics.
- 5.3
- To conclude, mathematical and network models that work with stylised population structures will continue to provide important insights into the dynamics and control of infectious diseases. However, many open questions in infectious disease epidemiology concern the roles played by specific types of population heterogeneity. To answer these questions, more realistic population models, such as that described here, will prove invaluable.
As discussed at the beginning of this paper, synthetic population models find application in many domains, and there is no reason why the utility of our model could not extend beyond the domain of infectious diseases. For example, a similar approach is being used to explore issues around the provision of social care in ageing populations (Silverman et al. 2012), another issue for which changing patterns of household demography have important implications. However, the requirements guiding the development of our model were based on our particular research agenda, and it is critical to ensure that, for other applications, model behaviour is suited to the problem at hand.
 Appendix
Appendix
- Create initial population, according to initial age distribution and household size distribution.
- Scale all annual probabilities and rates to give rates per time step.
- At each time step, each individual has the possibility of experiencing a life event as follows (individual attributes that affect event probabilities are listed in parentheses):
- Test for death (age, sex). If death occurs, the following occurs:
- The dead individual is removed from the population. If this results in a household containing orphaned children, any children who are old enough (e.g., > 18 years) leave home, as per below, while any younger children are randomly allocated to another family household containing at least one child.
- The birth of a replacement individual is triggered, and a mother is chosen (age, sex, parity, time since last birth).
- Test for couple formation (age, sex). If couple formation is to occur, select a partner from the population with an appropriate age difference and update their households as follows:
- If both individuals live at home, they move into a newly created household.
- If either (or both) of the individuals have their own household, the other partner (together with any dependents) joins them in this household.
- Test for leaving home (age). If an individual leaves home, they form a single person household.
- Test for couple separation (age). If a couple separate, one individual remains in their former household, together with any dependents, while the other individual leaves to form a new single person household.
- Test for death (age, sex). If death occurs, the following occurs:
- Calculate the number of additional births due to natural increase. Mothers are chosen for each of these new individuals as above.
- Calculate the number of new arrivals due to immigration. Immigrants arrive as a household unit, with the size of the household and the age of its occupants drawn from the current population age and household size distributions.
- Repeat from Step 3.
 Notes
Notes
-
1
The terms 'agent-based models' and 'individual-based models' are frequently used interchangeably to describe models in which each unit in a population is explicitly represented. Where a distinction is made, the term agents is used to refer to entities whose behaviour is determined on the basis of cognitive functions, while the behaviour of individuals is governed by less complex behavioural rules (Parrott et al. 2011). We have chosen to use 'individual-based models' throughout.
2 A concise outline of the model is provided in the Appendix. The model is implemented in Python and source code is available from http://github.com/nlgn/sim-demog.
3 Parity refers to the number of children born to a particular woman. For example, a woman who has given birth to two previous children has a parity of two.
4 Representing household frequency by size helps to counteract the visual bias that otherwise results from the dominance of larger but less common household types.
 References
References
- AJELLI, M. & MERLER, S. (2009). An individual-based model of hepatitis A transmission. Journal of Theoretical Biology 259(3), 478-88. [doi:10.1016/j.jtbi.2009.03.038]
ANDERSON, R. M. & MAY, R. M. (eds.) (1991). Infectious Diseases of Humans: Dynamics and Control. Oxford, UK: Oxford University Press.
AUSTRALIAN BUREAU OF STATISTICS (2006a). Births, Australia, 2006, cat. no. 3301.0.
AUSTRALIAN BUREAU OF STATISTICS (2006b). Population by Age and Sex, Australian States and Territories, Jun 2006, Table 9. Estimated Resident Population By Single Year of Age, Australia.
AUSTRALIAN BUREAU OF STATISTICS (2007). Life Tables, Australia, 2005-2007, cat. no. 3302.0.55.001.
AUSTRALIAN BUREAU OF STATISTICS (2008). Australian Historical Population Statistics, 2008, cat. no. 3105.0.65.001.
BALL, F., MOLLISON, D. & SCALIA TOMBA, G. (1997). Epidemics with two levels of mixing. The Annals of Applied Probability 7(1), 46-89. [doi:10.1214/aoap/1034625252]
BALL, F. & NEAL, P. (2002). A general model for stochastic SIR epidemics with two levels of mixing. Mathematical Biosciences 180, 73-102. [doi:10.1016/S0025-5564(02)00125-6]
BARRETT, C. L., BECKMAN, R. J., BERKBIGLER, K. P., EUBANK, S. G., HENSON, K. M., ROMERO, P. R. & SMITH, J. P. (2000). TRANSIMS: Transportation analysis simulation. Tech. Rep. 00-1725, Los Alamos National Laboratory.
BECKER, N. G., GLASS, K., LI, Z. & ALDIS, G. K. (2005). Controlling emerging infectious diseases like SARS. Mathematical Biosciences 193(2), 205-21. [doi:10.1016/j.mbs.2004.07.006]
BILLARI, F., FENT, T., PRSKAWETZ, A. & APARICIO DIAZ, B. (2007). The ''wedding-ring'': an agent-based marriage model based on social interaction. Demographic Research 17, 59-82. [doi:10.4054/DemRes.2007.17.3]
BIRKIN, M. H. & CLARKE, M. (2011). Spatial microsimulation models : A review and a glimpse into the future. In: Population Dynamics and Projection Methods. Springer, pp. 193-208. [doi:10.1007/978-90-481-8930-4_9]
COUDEVILLE, L., VAN RIE, A. & ANDRE, P. (2008). Adult pertussis vaccination strategies and their impact on pertussis in the united states: evaluation of routine and targeted (cocoon) strategies. Epidemiology and infection 136(5), 604-20. [doi:10.1017/S0950268807009041]
DANON, L., FORD, A. P., HOUSE, T., JEWELL, C. P., KEELING, M. J., ROBERTS, G. O., ROSS, J. V. & VERNON, M. C. (2011). Networks and the epidemiology of infectious disease. Interdisciplinary Perspectives on Infectious Diseases 2011, 284909. [doi:10.1155/2011/284909]
DE VAUS, D. (2004). Diversity and change in Australian families: Statistical profiles. Melbourne, Australia: Australian Institute of Family Studies.
DEPARTMENT OF IMMIGRATION AND MULTICULTURAL AFFAIRS (2001). Immigration: Federation to century's end.
ELVEBACK, L. R., FOX, J. P., ACKERMAN, E., LANGWORTHY, A., BOYD, M. & GATEWOOD, L. (1976). An influenza simulation model for immunization studies. American Journal of Epidemiology 103(2), 152-65.
EUBANK, S., GUCLU, H., KUMAR, V. S. A., MARATHE, M. V., SRINIVASAN, A., TOROCZKAI, Z. & WANG, N. (2004). Modelling disease outbreaks in realistic urban social networks. Nature 429(6988), 180-4. [doi:10.1038/nature02541]
FERGUSON, N. M., CUMMINGS, D. A. T., CAUCHEMEZ, S., FRASER, C., RILEY, S., MEEYAI, A., IAMSIRITHAWORN, S. & BURKE, D. S. (2005). Strategies for containing an emerging influenza pandemic in Southeast Asia. Nature 437(7056), 209-14. [doi:10.1038/nature04017]
GARGIULO, F., TERNES, S., HUET, S. & DEFFUANT, G. (2010). An iterative approach for generating statistically realistic populations of households. PloS one 5(1), e8828. [doi:10.1371/journal.pone.0008828]
GLASS, K., MCCAW, J. & MCVERNON, J. (2011). Incorporating population dynamics into household models of infectious disease transmission. Epidemics 3, 152-158. [doi:10.1016/j.epidem.2011.05.001]
GLICK, P. C. (1989). The family life cycle and social change. Family Relations 38, 123-129. [doi:10.2307/583663]
GRASSLY, N. C. & FRASER, C. (2008). Mathematical models of infectious disease transmission. Nature Reviews Microbiology 6(6), 477-87. [doi:10.1038/nrmicro1845]
GRIMM, V., REVILLA, E., BERGER, U., JELTSCH, F., MOOIJ, W. M., RAILSBACK, S. F., THULKE, H., WEINER, J., WIEGAND, T. & DEANGELIS, D. L. (2005). Pattern-oriented modeling of agent-based complex systems: Lessons from ecology. Science 310, 987-991. [doi:10.1126/science.1116681]
GUZZETTA, G., AJELLI, M., YANG, Z., MERLER, S., FURLANELLO, C. & KIRSCHNER, D. (2011). Modeling socio-demography to capture tuberculosis transmission dynamics in a low burden setting. Journal of Theoretical Biology 289, 197-205. [doi:10.1016/j.jtbi.2011.08.032]
HAMMEL, E. A. (2005). Demographic dynamics and kinship in anthropological populations. Proceedings of the National Academy of Science, USA 102(6), 2248-2253. [doi:10.1073/pnas.0409762102]
HAMMEL, E. A. & LASLETT, P. (1974). Comparing household structure over time and between cultures. Comparative Studies in Society and History 16(1), 73-109. [doi:10.1017/S0010417500007362]
HARDING, A. (2007). Challenges and Opportunities of Dynamic Microsimulation Modelling, Plenary paper presented to the 1st General Conference of the International Microsimulation Association, Vienna, 21 August.
HAUG, W., COMPTON, P. & COURBAGE, Y. (eds.) (2002). The Demographic Characteristics of Immigrant Populations. No. 38 in Population Studies. Council of Europe Publishing.
HAYES, A., WESTON, R., QU, L. & GRAY, M. (2010). Families then and now: 1980-2010. Fact sheet, Australian Institute of Family Studies.
HETHCOTE, H. W. (2000). The mathematics of infectious diseases. SIAM Review 42(4), 599-653. [doi:10.1137/S0036144500371907]
IACONO, M., LEVINSON, D. & EL-GENEIDY, A. (2008). Models of transportation and land use change: a guide to the territory. Journal of Planning Literature 22(4), 323-340. [doi:10.1177/0885412207314010]
IANNELLI, M. & MANFREDI, P. (2007). Demographic change and immigration in age-structured epidemic models. Mathematical Population Studies 14(3), 161-191. [doi:10.1080/08898480701426241]
JARDINE, A., CONATY, S. J., LOWBRIDGE, C., STAFF, M. & VALLY, H. (2010). Who gives pertussis to infants? Source of infection for laboratory confirmed cases less than 12 months of age during an epidemic, Sydney, 2009. Communicable Diseases Intelligence 34(2), 116-121.
JOHN, A. M. (1990). Transmission and control of childhood infectious diseases: Does demography matter. Population Studies 44(2), 195-215. [doi:10.1080/0032472031000144556]
KIRK, D. (1996). Demographic transition theory. Population Studies: A Journal of Demography 50(3), 361-387. [doi:10.1080/0032472031000149536]
KORB, K. B., GEARD, N. & DORIN, A. (2013). A Bayesian approach to the validation of agent-based models. In: Ontology, Epistemology, and Teleology of Modeling and Simulation (TOLK, A., ed.). Germany: Springer-Verlag, pp. 255-269. [doi:10.1007/978-3-642-31140-6_14]
LONGINI, I. M., NIZAM, A., XU, S., UNGCHUSAK, K., HANSHAOWORAKUL, W., CUMMINGS, D. A. T. & HALLORAN, M. E. (2005). Containing pandemic influenza at the source. Science 309(5737), 1083-7. [doi:10.1126/science.1115717]
LOPEZ, A. D., SALOMON, J., AHMAD, O., MURRAY, C. J. L. & MAFAT, D. (2000). Life tables for 191 countries: data, methods and results. GPE Discussion Paper 9, World Health Organisation, Geneva.
MANNION, O., LAY-YEE, R., WRAPSON, W., DAVIS, P. & PEARSON, J. (2012). JAMSIM: a microsimulation modelling policy tool. Journal of Artificial Societies and Social Simulation 15(1), 8. https://www.jasss.org/15/1/8.html
MOSSONG, J., HENS, N., JIT, M., BEUTELS, P., AURANEN, K., MIKOLAJCZYK, R., MASSARI, M., SALMASO, S., TOMBA, G. S., WALLINGA, J., HEIJNE, J., SADKOWSKA-TODYS, M., ROSINSKA, M. & EDMUNDS, W. J. (2008). Social contacts and mixing patterns relevant to the spread of infectious diseases. PLoS Medicine 5(3), e74. [doi:10.1371/journal.pmed.0050074]
MURPHY, M. J. (2011). Long-term effects of the demographic transition on family and kinship networks in britain. Population and Development Review 37 (S1), 55-80. [doi:10.1111/j.1728-4457.2011.00378.x]
ORCUTT, G. H. (1957). A new type of socio-economic system. The Review of Economics and Statistics 39(2), 116-123. [doi:10.2307/1928528]
PARROTT, L., CHION, C., MARTINS, C. C. A., LAMONTAGNE, P., TURGEON, S., LANDRY, J. A., ZHENS, B., MARCEAU, D. J., MICHAUD, R., CANTIN, G., MéNARD, N. & DIONNE, S. (2011). A decision support system to assist the sustainable management of navigation activites in the st. lawrence river estuary, canada. Environmental Modelling & Software 26, 1403-1418. [doi:10.1016/j.envsoft.2011.08.009]
REPUBLIC OF ZAMBIA CENTRAL STATISTICAL OFFICE (2000). Housing and Household Characteristics: Analytical Report.
SILHOL, R. & BOëLLE, P.-Y. (2011). Modelling the effects of population structure on childhood disease: The case of varicella. PLoS Computational Biology 7(7), e1002105. [doi:10.1371/journal.pcbi.1002105]
SILVERMAN, E., BIJAK, J. & NOBLE, J. (2011). Feeding the beast: can computational demographic models free us from the tyranny of data? In: Advances in Artificial Life, ECAL 2011: Proceedings of the Eleventh European Conference on the Synthesis and Simulation of Living Systems. MIT Press.
SILVERMAN, E., BIJAK, J., NOBLE, J., CAO, V. & HILTON, J. (2012). Semi-artificial models of populations: connecting demography with agent-based modelling. In: 4th World Congress on Social Simulation.
SPIELAUER, M. (2010). What is social science microsimulation? Social Science Computer Review 29(1), 9-20. [doi:10.1177/0894439310370085]
STILLWELL, J. & CLARKE, M. (eds.) (2011). Population Dynamics and Projection Methods, vol. 4 of Understanding Population Trends and Processes. Springer. [doi:10.1007/978-90-481-8930-4]
TAPER, M. L., STAPLES, D. F. & SHEPARD, B. B. (2008). Model structure adequacy analysis: selecting models on the basis of their ability to answer scientific questions. Synthese 163, 357-370. [doi:10.1007/s11229-007-9299-x]
WILKINS, R., WARREN, D., HAHN, M. & HOUNG, B. (2011). Families, Incomes and Jobs, Volume 6: A Statistical Report on Waves 1 to 8 of the Household, Income and Labour Dynamics in Australia Survey. Melbourne, Australia: Melbourne Institute of Applied Economic and Social Research.
WILSON, T. (2011). A review of sub-regional population projection methods. Tech. rep., Queensland Centre for Population Research, School of Geography, Planning and Environmental Management, The University of Queensland.
WU, B. M. & BIRKIN, M. H. (2012). Agent-based extensions to a spatial microsimulation model of demographic change. In: Agent-Based Models of Geographic Systems (HEPPENSTALL, A. J., CROOKS, A. T., SEE, L. M. & BATTY, M., eds.). Springer, pp. 347-360. [doi:10.1007/978-90-481-8927-4_16]