 Abstract
Abstract
- A power law degree distribution is displayed in many complex networks. However, in most real social and economic networks, deviation from power-law behavior is observed. Such networks also have giant hubs far from the tail of the power law distribution. We propose a model based on information 'transparency' (i.e. how much information is visible to others), which can explain the power structure in societies with non-transparency in information delivery. The emergence of very high degree nodes is explained as a direct result of censorship. Based on these assumptions, we define four distinct transparency regions: perfectly non-transparent, low transparent, perfectly transparent regions and regions where information is exaggerated. We observe the emergence of some very high degree nodes in low transparency networks. We show that the low transparency networks are more vulnerable to attack and the controllability of low transparent networks is more difficult than for the others. Also, the low transparency networks have a smaller mean path length and higher clustering coefficients than the other regions.
- Keywords:
- Social and Economical Networks, Information Transparency, Super-Nodes and Monopolies
 Introduction
Introduction
- 1.1
- Several models for power law degree distribution of different kinds of complex networks have been proposed by many researchers in recent years (Barabasi and Albert 1999; Albert and Barabasi 2002; Newman 2003; Roohi et. al. 2010; Namaki et al. 2011). Barabasi-Albert model (BA model) was a basic attempt to describe this phenomenon. The main concern of this model was the preferential attachment. The model showed that preferential attachment in a growing network leads to a power law degree distribution, as well as a random attachment that leads to an exponential degree distribution. In recent years, there have been many different variations of this model (Barabasi and Albert 1999; Albert and Barabasi 2002). For describing the behavior of real systems, the main focus of these models is to reproduce the growth process in real networks. In essence, they describe the dynamic mechanisms that produce the network. The Dorogovtsev-Mendes-Samukian (DMS) model is a complete form of BA model that allows for the presence of the initial number of nodes (Dorogovtsev et al. 2000). Krapivsky et al. (2000) introduced a model with a nonlinear preferential attachment probability. Klemm-Eguiluz (KE) proposed a model known as structured scale-free model that describes the dynamic growth of the networks based on the memory of the nodes (Klemm and Eguiluz 2002).
- 1.2
- In addition to these models, there are other methods for describing the growth process of real networks (Vazquez et al. 2003; Holme and Kim 2002; Jin et al. 2001; Davidsen et al. 2002; Sole et al. 2002; Ferrer i Chancho and Sole 2003; Valverde et al. 2002). However, in some social structures, we observe that power (an interpretation of the effects on total network) consolidates in some nodes that break the scale free behavior. The deviation from scale free behavior can be explained by applying some modifications to the BA model (Bianconi and Barabasi 2001; Lambiotte and Ausloos 2007; Krapivsky and Redner 2005; Valverde and Sole 2005; Evans and Saramaki 2005). Such deviations were shown in Sornette's (2002, 2009) works on power law's distributions where the term "dragon kings" was introduced .
- 1.3
- In sociology, there is a phenomenon called the Matthew effect which describes the behavior of these Super-Nodes which are more powerful than the rest. In economy the Super-Nodes are called economical power while in the society they are called political power. The Matthew effect is the phenomenon where "the rich get richer and the poor get poorer" (Merton 1968, 1988; Gladwell 2008). In the networks, power can be realized by the nodes' degree, betweenness or closeness (Hanneman and Riddle 2005). In the BA model, everyone has full information about the other nodes, so information is available for them to attach to nodes with high degree. However, in social networks, this kind of information, diffuses through the network itself. The information diffusion, like all other diffusions, can be subjected to some restrictions. These restrictions will cause incomplete and non-accurate information. The rate of this diffusion can affect the structure of our network as the system grows. In the case of social networks, we found out that this rate has a crucial role that directly reflects in the structure of power in a society. Also, in economic networks, this diffusion rate has a close connection for describing the competitiveness of the economic environment.
- 1.4
- In this paper, we propose a definition of information transparency for nodes degree distribution. Then, we make the modified preferential attachments based upon this definition. The properties of these networks based on their different diffusion rates, are also studied.
 Modified Model
Modified Model
- 2.1
- The assumption of the preferential attachment in BA model is based on adding a new node which attaches to node i with a probability p that depends on the degree ki, so:
p(ki) = ki /·l kl (1) - 2.2
- The BA model assumes the availability of the information of nodes degrees for each new node introduced to the system. However, in the modified model, we consider that the new vertex first connects to node i randomly without any prior information about the degree of that node. Then, it finds out about other nodes degrees through the node i. The other degrees information known by node i has passed through several edges. Hence, it does not express the exact degrees of network's nodes. Actually, the degrees information would be decreased "r" proportion, each time passes an edge. This process is called the "information diffusion". Therefore, we introduce the term kji which is the degree of node j viewed by node i (the node j's degree has been diffused through the network before reaching the node i). kji is kj that has diffused d times:
kji = kj .(r ^dij) (2) which dij is the shortest path length between nodes i and j and the new node connects according to kji (Usually, most reliable information obtained from a node, is the information that comes from the shortest path). So the probability of connecting the new node to node j is:
p(kji) = kji / ·l kli (3) - 2.3
- Therefore, each new node makes m new edges to remain in the network. With the aid of this model, various deviations from scale free behavior can be explained by different values of diffusion rate. It is obvious that, r=0 will result in a randomly growing graph and r=1 represents the BA model. All above steps could be summarize as follows:
- Start with a small core network. (In our simulation we start with an m-clique where m is the edge number that connects the new node to the network.)
- Choose a random node i.
- Calculate the kji = kj .(r ^dij), which is the node j degree's viewed by node i.
- Connect a new node with m edges to the other nodes, with preferential attachment according to kji.
- Refresh ks and ds.
- Return to step (2).
- 2.4
- The following schematic example is presented to clarify this model. A new person in the town does not have accurate information about important (well-known) people of the city. He may come to a person randomly and ask him/her about the others. His judgment about the others is crucially dependent on how accurate was the information he gathered from the others. If we have a perfect transparency in information, i.e. r=1, then accurate information to make connections throughout the network is available. Then the network's growth follows BA model where the degree distribution posses a power-law behavior. However, with a perfect non-transparency in networks' information delivery, i.e. r=0, the new person would have no useful information about anyone and connects randomly to another node in the network, which means random growth and exponential behavior in nodes' degree distribution. Our results show that, between these two limits, there are some networks with very high degrees that are called "Super-Nodes". We consider edges between nodes to be homogenous which means they are all as of the same kind with the same diffusion rates.
 Results and discussion
Results and discussion
- 3.1
- The main purpose of this paper is to study the effect of information distortion in construction of networks. Based on the above model, we can construct different networks with respect to different diffusion rates "r" where r is the parameter that makes distortion in information delivery. If r changes from 1 to 0, it makes the nodes' degree to show lesser than the actual nodes degree. On the other hand, if r changes from 1 to higher values, it causes exaggeration and overestimation of the nodes degree.
- 3.2
- In Figure 1, we have developed networks based on this modified model for different diffusion rates. As expected for r=0 the network is a random graph and for r=1 it is the same as the BA model. As demonstrated when r=0.05 some powerful hubs emerge and when r=5 we observe random behavior again.
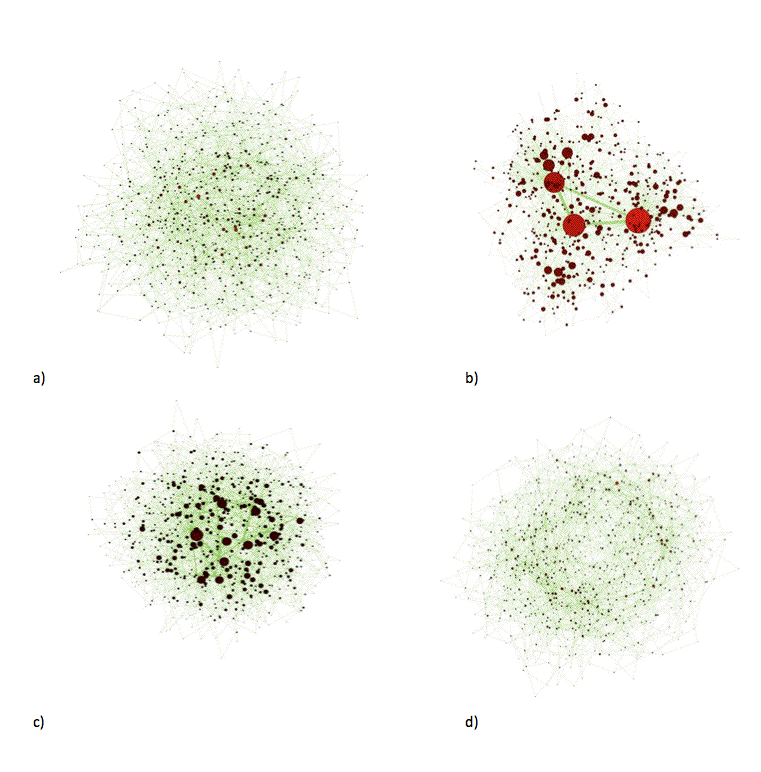
Figure 1. Network samples for different diffusion rates r a) 0, b) 0.05 c) 1, d) 5. The diameters of nodes show their degrees. Figures created by NWB Team (2006) - 3.3
- In Figure 2 we have depicted the degree distribution for different diffusion rates, based on the assumption of growing the network by adding nodes one by one with m=5 number of new edges, which are added for each new node. We have added nodes till N = 104 (Figure 2 a, d, b, e) and to demonstrate that the finite size effect is not an important matter in our growing process, we have shown results for N = 105 (Figure 2 c, f).
- 3.4
- The degree distribution moves from an exponential distribution to a power law distribution by increasing the diffusion rates from zero to one. Between these two points, there are some diffusion rates in which the networks with these rates have nodes with a high degree that cause deviation in the networks degree distributions from the power law behavior. r=0 is the state of no transparency in information delivery. This is equivalent to the state of random growing network with exponential degree distribution. r=1 is the state with a complete and accurate transfer of information throughout the network which reproduces the BA model with power law degree distribution.
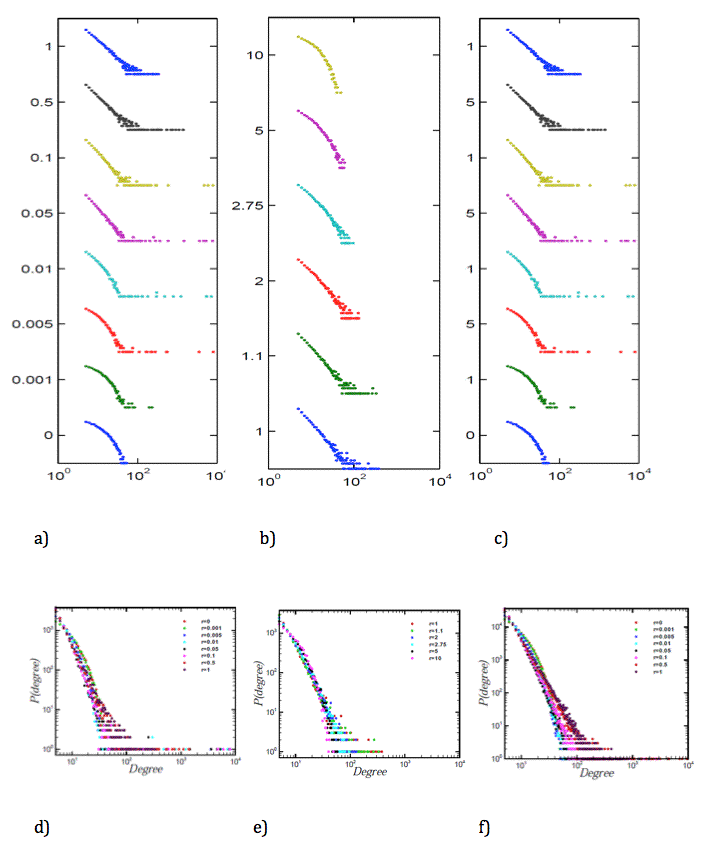
Figure 2. The degree distribution for different values of r = (0, 0.001, 0.005, 0.01, 0.05, 0.1, 0.5, 1) for the number of nodes equal to (a) 10000 and (c) 100000. (b) The degree distribution for different values of r = (1, 1.1, 2, 2.75, 5, 10). For more illustration of units and scales, the Figures 2 d, e, f show degree distributions in one plane. - 3.5
- In the low diffusion rates, lower than 0.01, we still observe exponential behavior for the majority of nodes with lower degree. Even though we have random behavior in the rest of the network with maximum degree about 102, the emergence of nodes with amazingly high degree about 104 is a noticeable fact, as the rate goes above 0.005. As the diffusion rate increases to 0.05, the network starts to show a power-law behavior while the nodes with ultra high degrees are still present. As demonstrated, there is a power law behavior in the beginning of some distributions (by eliminating the powerful nodes from the distribution), where the slope is 4.2±0.03 in r=0.05. By r increasing to 1.5, the slope decreases to 3. For r>1.5 the distributions do not have the power-law behavior.
- 3.6
- As the diffusion rate increases, the model gets closer and closer to the BA model. We then focused our attention on networks with r > 1. For diffusion rate increases above 1 as shown in Figure 2(b, e), disappearing of the powerful hub is observed as the rate goes up, and the whole system shifts towards an exponential behavior in a connectivity structure. In other words, the system shifts to the random growth as the diffusion rate increases above 1. In social interpretation, the network has experienced exaggeration of information, which results in a random behavior. This demonstrates equivalency of fake information and no information in the system. In essence, four distinct parts for the proposed model emerges: non-transparent, low transparent, perfect transparent and exaggerated regions.
- 3.7
- By considering different information diffusion rates, different social, economical and political situations involved in information delivery of societies can be explained. The emergence of Super-Nodes is interpreted as the emergence of powerful hubs (high power nodes which are dominant in size and importance) in social networks as a result of low-transparency in information delivery.
- 3.8
- Information is not only a tool for being dominant, but is the power itself. In some cases, information sources, adjust the diffusion rate on purpose in favor of a party. These are societies with the power, condensed in these monopoles as they try to maintain the power with the aid of censorship or supportive actions from government. Some famous examples of these structures are undemocratic governments, where power condensates in the hands of a powerful political elite group. Also, because of the low-transparent competitive environment, sometimes firms emerge as central nodes in economic networks. With total transparency in information delivery, which leads to societies without monopolies, it can be considered as an ideal model. This is the perfect case and most of the times; real phenomena are deviated from this ideal model.
- 3.9
- The new in town is in a situation of information overflow, which will lead the person to the same result of having no or less accurate information. This is observed when rate increases to values above one. In other words, having no information is the same as having a huge amount of information that is not accurate or is exaggerated. In real life scenario, societies at times are bombarded with propaganda that can totally restructure power systems to other random structures, this happens in some government structures. Some firms such as Medias, which control the amount of informal statements in societies, can restructure the power system to their desirable shape by controlling the amount or accuracy of the information.
- 3.10
- In order to have a better sense about the model, we have plotted Figure 3a which shows the maximum degree of developed networks by the model for different diffusion rates and the average of this maximum degree perceived by the other nodes. This perception reflects the opinion of the other nodes about the maximum degree in the network on average or their estimation of the size of the powerful hub. The Figure is in logarithmic scale, and the vertical error bars show the diversity of opinion about the size of this hub.
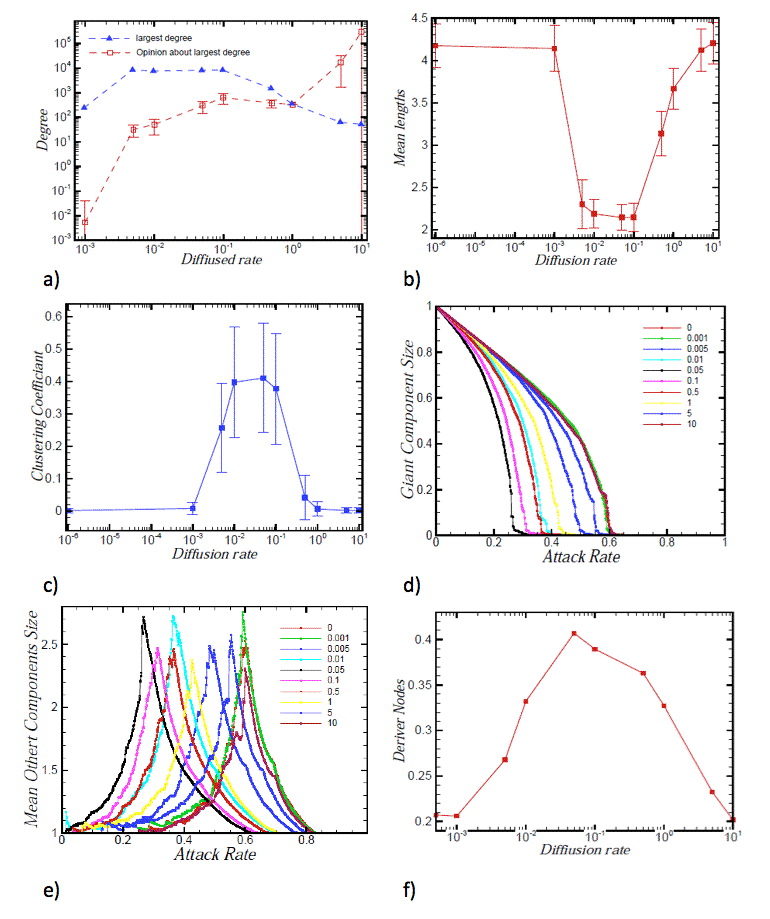
Figure 3. Figure 3: a) Largest node degree in different diffusion rates and the average of the other nodes' opinion about their degrees. b) The mean of the shortest paths in the networks with different diffusion rates. c) The mean clustering coefficients in the networks with different diffusion rates. d) The giant component size vs. removed nodes' percentage. Nodes are removed due to the rank of their degrees. Networks with low transparency show a more sensitivity to the attacks e) The mean of the other component sizes vs. the removed nodes' percentage. f) Driver nodes (nodes which should be controlled externally) in different diffusion rates. General network properties
- 3.11
- The emergence of nodes with high degree, will decrease the mean length, and increase the clustering coefficients of low degree nodes connected to them as shown in Figure 3b,c. The decrease in the mean length, as a result of emergence of ultra powerful hubs, is explained as a consequence of connection of most nodes to one or more nodes with ultra high degree which act like bridges in the network (Figure 3b). In economic and social networks, the mean length can show the speed of diffusion of crises among nodes of the system. When this item is very small, it shows that the crisis can diffuse very fast in the network. As seen in low transparent region, the mean length is much smaller than the other regions and we expect that the diffusion of any event among nodes has high speed. The increase in the average of the clustering coefficient of the nodes, even in nodes with low degree, is the result of the connectivity to powerful hubs as a dense core. The mean clustering coefficient of the economic and social networks shows the remaining probability of the crisis in different groups of clusters for a long time. In the low transparent region, it is obvious that the mean clustering coefficient is much larger than the other regions in Figure 3c.
Network robustness
- 3.12
- Here comes a peculiar question that whether a controlled censorship really works in keeping the powerful hubs from falling down. If these ultra powerful hubs encounter failure for any reason, will the network face a serious break down? To answer this question, we made attacks on the networks with different diffusion rates. Attack means removing nodes from the network due to some defined rules. There are several types of attacks (Albert et al. 2000). We attacked network nodes on their degree ranks. We eliminated nodes from the top degree to the bottom, and after each step, evaluate the giant component size and the mean size of the other components in the network (Albert et al. 2000). Results are depicted in Figures 3d and 3e for networks with different diffusion rates. As shown, the giant component size and the average size of the other components are more sensitive to the attacks in the low transparent networks. It is well known that a random network is more robust than a scale free one against targeted attacks (Albert et al. 2000). But, the main finding is that the low transparent networks (0 < r < 1), are more fragile, in comparison to both random and scale-free networks.
- 3.13
- The giant component size decreases rapidly in the low transparent networks, compared to other networks. In other words, in scale free models, the society is less dependent to a special person or node. But in low transparent systems, networks are highly dependent on the special nodes that are the center of connectivity.
- 3.14
- In economic networks, there are some powerful hubs that are considered to be "too big to fail" (Taleb and Tapiero 2010; Stern and Feldman 2004; Wessel 2009). In essence, emergence of these hubs is the result of low transparent competitive environments. These financial institutions are so large and so interconnected that their failure will be harmful to the economy. This concept results in the belief that these firms should become recipients of beneficiary financial policies from governments or central banks to keep them alive. It is thought that these firms have high-risk and are able to leverage these risks based on the supportive actions. This term has emerged as an important concept since 2007–2010 in global financial crisis, that bankruptcy of some giant companies has systemic effects on the total economy.
Controllability
- 3.15
- To control a system in real world, one method is to control the set of driver nodes that are driving them by an external signal that results in control the systems' dynamic. Liu et al. (2011) used a method, named maximum matching, for finding the minimum number of driver nodes to attain full control of a complex network with a dynamic behavior in its nodes. In this paper, we assume that our proposed networks are directed from the previous to the next nodes. Figure 3f shows that the number of the driver nodes that must be controlled in low transparent region is much more than the other regions, and in essence this makes controlling the network more costly.
- 3.16
- In low transparent networks, the social capital comes from the powerful hubs and the other nodes do not have common perceptions about each other. So, controlling these networks forces more cost to the powerful hubs. In low transparent societies, social cohesion sometimes has different structures based on relationships between powerful hubs and the other nodes in the social network. Most of the cohesion is because of the existence of the hubs. So in these networks, structural cohesion (the minimum number of members who, if removed from a group, would collapse the group (Moody and Douglas 2003)) is smaller than the other networks.
 Conclusion
Conclusion
- 4.1
- In this paper we have presented a new method for generating social networks. In this modified model, we have emphasized on the diffusion rates as a mean for measuring the information transparency in social and economical systems. The main interesting features of the model are symmetry breaking of nodes degree due to both exponential and power law distributions, despite of homogeneous primary conditions. This model shows the emergence of different groups of networks based on the different types of diffusion rates. This view can model the reality of the social and economical systems. In these systems, there are ultra powerful hubs (Super-Nodes) that lead to deviation from power law behavior and scale free concept. We have computed the mean length and the clustering coefficients of the networks based on different diffusion rates. It can be seen that there are indirect relations between the diffusion rates and the mean lengths, but there are direct relations between the clustering coefficients and the diffusion rates. Also, we investigated the behavior of the networks' structures with respect to the attack on the powerful hubs, and was seen that the networks with low diffusion rates are more sensitive to the attacks. We then investigated the controllability of the networks. Our results showed that the networks in low transparency region have more driver nodes and are harder to control than the other regions.
 Acknowledgements
Acknowledgements
- The authors would like to thank Shahin Rouhani for his very helpful comments and discussions, and Sara Zohoor, Soheil Vasheghani Farahani and Reza Shirazi for helping to edit the manuscript.
 References
References
-
ALBERT R., Barabasi A. (2002) Statistical mechanics of complex networks. Rev. Mod. Phys. 74: 47-97. [doi:10.1103/RevModPhys.74.47]
ALBERT R., Jeong H., Barabasi A.L. (2000) Error and attack tolerance of complex networks. Nature 406: 378-482. [doi:10.1038/35019019]
BARABASI A., Albert R. (1999) Emergence of scaling in random networks. Science 286: 509-512. [doi:10.1126/science.286.5439.509]
BIANCONI G. and Barabasi A.L. (2001) Bose-Einstein condensation in complex networks, Phys. Rev. Lett. 86, 5632 [doi:10.1103/PhysRevLett.86.5632]
DAVIDSEN, J., Ebel, H., Bornholdt, S. (2002) Emergence of a Small World from Local Interactions: Modeling Acquaintance Networks. Phys. Rev. Lett. 88: 128701. [doi:10.1103/PhysRevLett.88.128701]
DOROGOVTSEV, S.N., Mendes, J.F.F., Samukhin, A.N., (2000) Structure of growing networks with preferential linking. Phys. Rev. Lett. 5: 4633. [doi:10.1103/PhysRevLett.85.4633]
EVANS T.S. and Saramaki J.P. (2005) Scale Free Networks from Self-Organization, Phys. Rev.E 72, 026138. [doi:10.1103/PhysRevE.72.026138]
FERRER i Cancho, Sole R.V. (2003) Optimization in complex networks. Statistical Mechanics of Complex Networks. Lecture Notes in Physics, Springer (Berlin) 625: 114-125. [doi:10.1007/978-3-540-44943-0_7]
GLADWELL, M. (2008) Outliers: The Story of Success. Little, Brown and Company.
HANNEMAN, R. A. and M Riddle (2005) Introduction to social network methods, Chapter 10, online version. http://faculty.ucr.edu/~hanneman/nettext/Introduction_to_Social_Network_Methods.pdf
HOLME, P., Kim, B.J. (2002) Growing scale-free networks with tunable clustering. Phys. Rev. E 65: 26107. [doi:10.1103/PhysRevE.65.026107]
JIN, E.M., Girvan, M., Newman, M.E.J. (2001) Structure of growing social networks. Phys. Rev. E 64: 46132. [doi:10.1103/PhysRevE.64.046132]
KLEMM, K., Eguiluz, V.M. (2002) Highly clustered scale-free networks. Phys. Rev. E 65: 36123. [doi:10.1103/PhysRevE.65.036123]
KRAPIVSKY P.L. and Redner S. (2005) Network Growth by Copying, Phys. Rev. E 71, 036118. [doi:10.1103/PhysRevE.71.036118]
KRAPIVSKY P.L., Redner S, Leyvraz F (2000) Connectivity of growing random networks. Phys. Rev. Lett. 85: 4629. [doi:10.1103/PhysRevLett.85.4629]
LAMBIOTTE R. and Ausloos M. (2007) Growing network with j-redirection, Europhys. Lett., 77 58002. [doi:10.1209/0295-5075/77/58002]
LIU Y., Soltine J., Barabasi A. (2011) Controllability of complex networks. Nature 473: 167-173. [doi:10.1038/nature10011]
MERTON R. (1968) The Matthew effect in science. Science 159: 56-63. [doi:10.1126/science.159.3810.56]
MERTON R. (1988) The Matthew effect in science, II: Cumulative advantage and the symbolism of intellectual property Isis 79: 606-623. [doi:10.1086/354848]
MOODY J., Douglas R. (2003) Structural Cohesion and Embeddedness: A Hierarchical Concept of Social Groups. American Sociological Review 68(1): 103-127. [doi:10.2307/3088904]
NAMAKI, A. , Shirazi, A.H., Raei, R., Jafari, G. R. (2011) Network analysis of a financial market based on genuine correlation and threshold method, Physica A 390, 3835-3841. [doi:10.1016/j.physa.2011.06.033]
NEWMAN M.E.J. (2003) The structure and function of complex networks. SIAM Review 45: 167-256. [doi:10.1137/S003614450342480]
NWB Team. (2006). Network Workbench Tool. Indiana University, Northeastern University, and University of Michigan, http://nwb.slis.indiana.edu.
ROOHI A. A., Shirazi A. H.,Kargaran A.,Jafari G. R. (2010) Local Model of a Scientific Collaboration in Physics Network Compared with the Global Model, Physica A 389, 5439-5446. [doi:10.1016/j.physa.2010.08.007]
SOLE R.V., Pastor-Satorras R., Smith E., Kepler T.B. (2002) A model of large-scale proteome evolution. Advances in Complex Systems 5: 43-54. [doi:10.1142/S021952590200047X]
SORNETTE D. (2002) Predictability of catastrophic events: material rupture, earthquakes, turbulence, financial crashes and human birth. Proceedings of the National Academy of Sciences 99: 2522-2529. [doi:10.1073/pnas.022581999]
SORNETTE D. (2009) Dragon-Kings: Black Swans and the Prediction of Crises. International Journal of Terraspace Science and Engineering 2(1): 1-18. [doi:10.2139/ssrn.1596032]
STERN G. H., and Feldman R. J. (2004) Too big to fail. Washington, DC: Brookings Institution Press.
TALEB N., Tapiero C. (2010) Risk externalities and too big to fail. Physica A 389: 3503-3507. [doi:10.1016/j.physa.2010.03.014]
VALVERDE S. and Sole R.V. (2005) Logarithmic growth dynamics in software networks, Europhys. Lett. 72, 858-64. [doi:10.1209/epl/i2005-10314-9]
VALVERDE S., Cancho R.F., Sole R.V. (2002) Mixing patterns in networks. Europhys. Lett. 60: 512-517. [doi:10.1209/epl/i2002-00248-2]
VAZQUEZ A., Flammini A., Maritan A., Vespignani A. (2003) Modeling of Protein Interaction Networks. Complexus 1: 38-44 [doi:10.1159/000067642]
WESSEL D. (2009) Three Theories on Solving the 'Too Big To Fail' Problem. Wall Street Journal, October 28.