 Abstract
Abstract
- According to optimal distinctiveness theory (ODT), individuals prefer social groups that are relatively distinct compared to other groups in the individuals' social environment. Distinctive groups (i.e., groups of moderate relative size) are deemed "optimal" because they allow for feelings of inclusion and social connection while simultaneously providing a basis for differentiating the self from others. However, ODT is a theory about individual preferences and, as such, does not address the important question of what types of groups are actually formed as a function of these individual-level preferences for groups of a certain size. The goal of the current project was to address this gap and provide insight into how the nature of the social environment (e.g., the size of the social neighborhood) interacts with individual-level group size preferences to shape group formation. To do so, we developed an agent-based model in which agents adopted a social group based on an optimal group size preference (e.g., a group whose size represented 20% of the social neighborhood). We show that the assumptions of optimal distinctiveness theory do not lead to individually satisfactory outcomes when all individuals share the same social environment. We were able to produce results similar to those predicted by ODT when social neighborhoods were local and overlapping. These results suggest that the effectiveness of a social identity decision strategy is highly dependent on sociospatial structure.
- Keywords:
- Optimal Distinctiveness, ODT, Group Size, Social Cognition, Spatial Models
 Introduction
Introduction
- 1.1
- Within the field of psychology, researchers have had a long-standing interest in why individuals are attracted to certain social groups over others and what motivates them to self-categorize in terms of those group memberships (e.g., Tajfel & Turner 1986; Turner et al. 1994). This literature has demonstrated that under specifiable conditions, individuals exhibit preferences for groups that are higher in status, that are cohesive, and that are positively distinct—i.e., groups that differ from other social groups in a way that is positively valued by the group. In addition, research studies have documented a general preference for groups that are moderately-sized. All else being equal, individuals identify more strongly with groups that represent a numerical minority of the total observable population (Abrams 1994; Blanz et al. 1995; Brewer & Weber 1994; Ellemers & van Rijswijk 1997; Simon & Brown 1987; Simon & Hamilton 1994, Experiment 1).
- 1.2
- Optimal distinctiveness theory (ODT; Brewer 1991; Leonardelli, Pickett, & Brewer 2010) provides a basis for understanding this preference. In contrast to the idea that minority group membership constitutes a less valued and more vulnerable social identity than majority group membership, optimal distinctiveness theory suggests that minority status may be positively valued. Minority groups tend, on average, to provide sufficient inclusiveness within the group for individuals to feel a sense of inclusion and belonging and, at the same, time provide sufficient differentiation between the in-group and out-group to allow for feelings of distinctiveness to emerge. Thus, in comparison to majority groups that tend to be large and relatively undefined, minority groups are more likely to be considered by group members to be optimal. Preferences for modestly-sized groups may constitute a biologically or culturally evolved heuristic for simultaneously maximizing successful group cooperation, which is most effective in groups of small-to-moderate size (Olson 1971; Boyd & Richerson 1988), while maintaining group sizes large enough to reap the advantages of extended cooperation (Brewer 2004), such as defending group interests.
- 1.3
- Although optimal distinctiveness theory predicts individual-level group size preferences, what is unknown is how these preferences shape group formation. When individuals are able to freely choose a group membership based on their knowledge of the social environment—e.g., the group memberships of other individuals—does the aggregation of these individual choices lead to the formation of groups that are, in fact, optimal? This question has not been adequately addressed in the social psychological literature partly because social psychologists and other social scientists (e.g., political scientists and sociologists) typically study only one side of this problem, keeping the other constant. Social psychologists generally study individual identity processes, attempting to identify how people choose their group memberships and the processes that lead to identification with those groups (social identification). Although social psychological theories of social identification generally acknowledge the fluid nature of the social environment (e.g., Turner et al. 1994), the research itself tends to focus on the perceptual, cognitive, and behavioral processes of an individual in response to a social environment that does not change. At the opposite extreme, political scientists and sociologists focus on social environments, emphasizing organization and group decision making. They tend to assume stable demographics of individuals with fixed social identities. Models in these fields generally assume dynamic processes at the level of social organization but assume that individual social identities are static.
- 1.4
- To provide more explanatory breadth, a multilevel theory of social identity must include the interplay between individual- and group-level dynamics. By integrating individual-level dynamics into a theory of social identity, we will better understand group-level dynamics, such as the size, organization, and stability of social groups. By integrating the dynamics of social environments, we will better understand the forces shaping the cognitive processes involved in social cognition, as well as the adaptive functions of those processes.
- 1.5
- To begin to develop such a multi-level theory of social identity, we developed an agent-based model in which agents make social identity decisions (whether to select a particular group membership) based on the social identities of their neighbors. We assumed in the model that agents make these decisions in an attempt to satisfy their preference for groups that are optimally distinct. We then observed the resultant dynamics of group formation as a function of variations in group size preferences and the size of social neighborhoods. The results indicated that the ability of optimally-sized groups to form was highly dependent on particular characteristics of the social environment as well as group member preferences. This work highlights the fact that a complete understanding of how individuals are able achieve optimal distinctiveness requires knowledge of the broader social context and the interactions among individuals within that context.
ABM for social identity dynamics
- 1.6
- Connecting the dynamics of social cognition with the dynamics of social organization is difficult using the traditional methods of social psychologists. Empirical methods can illuminate individual behavior, but they tell us little about the social organization that emerges when individuals interact over time. After all, it may be difficult (not to mention unethical) to effect changes in individual social identities, and more difficult still to assess the effects of those changes on the people in that individual's social network. At the population level, theorists often use variable-based models (e.g., differential equations) to track frequencies of groups in populations, but these models have difficulty in accounting for either complex cognitive processes or structured sociospatial organization. Agent-based modeling (ABM) is an ideal framework for connecting theories of individual behavior with population-level phenomena (Epstein 2006; Miller & Page 2007; Railsback & Grimm 2012). ABMs that connect cognitive processes with social behavior are still relatively rare (but see French & Kus 2008; Hills & Todd 2008; Smith & Collins 2009; Sutcliffe & Wang 2012), but persuasive arguments have been made for the more widespread use of ABM in social psychology (Kenrick et al. 2003; Smith & Conrey 2007), and specifically in the realm of social identity processes (Pickett et al. 2011).
- 1.7
- Processes of social cognition are difficult to model. An often-heard statement among neuroscientists and cognitive scientists is that there is nothing in the universe more complex than the human brain. Social scientists can trump this, however—if one brain is complex, the interactions between many brains must be exponentially more so. Nevertheless, the types of decision rules used by individuals for a given domain may be relatively simple. For example, a common investment technique is to simply divide one's assets evenly among investments (Gigerenzer 2008), and this method been shown to outperform more complex "optimizing" techniques (DeMiguel et al. 2007). When each individual's decisions influence the decisions of others, even simple behavior rules can general complex and often unexpected population dynamics. The now-classic example is Schelling's simple model in which spatially-located individuals belonging to one of two categories (e.g., racial or politically-affiliated groups) stay put if enough of their neighbors belong to the same category as themselves and move to a random location otherwise. Severe segregation can emerge even when nobody minds being in a local minority (Schelling 1971). ODT, described in more detail below, could be viewed as a type of heuristic people use in making decisions about social identity. Our model will show that complex population dynamics can arise in a population of agents each using a simple decision rule to select a social identity.
Optimal distinctiveness theory
- 1.8
- In the current model, we focused on optimal distinctiveness as the major component in the choice of social identity. ODT outlines an opponent process model in which individuals' choice of social identity is influenced by the need for assimilation (i.e., the need for inclusion and belonging) and the need for differentiation (i.e., the need to differentiate oneself from others). These two needs operate in opposition to each other—e.g., groups that are relatively large satisfy individuals' need for assimilation but do a poor job of satisfying the need for differentiation. For this reason, people are, on average, likely to prefer and identify most strongly with groups that are of moderate size (Leonardelli & Brewer 2001). Optimal identities—e.g., minority groups—are those that maximize the satisfaction of both the need for assimilation and the need for differentiation simultaneously. The ABM that we developed was designed to capture this individual-level group size preference. However, we did so with the full knowledge that in real-world contexts multiple motivations may impinge on social identity choices—e.g., the need to enhance self-esteem (Tajfel & Turner 1986) or reduce subjective uncertainty (Hogg 2007). Although it would certainly be of interest to examine and model the interplay between different social identity motives, we limited this initial model to a single social identity motive—optimal distinctiveness—in order to derive relatively simple principles of how this single motive, in the context of other contextual variables, shapes group formation.
- 1.9
- ODT holds that social identification is strongest for social identities at the level of inclusiveness that resolves the conflict between needs for assimilation and differentiation. A logical conclusion from ODT is that individuals should adopt those optimally distinct social identities that result in a stable social context in which everyone is optimally distinct. Throughout the paper we will refer to agents "optimizing" their distinctiveness. This does not refer to an optimization process for efficiency in some process, such as those often used in computer simulation (e.g., simulated annealing, genetic algorithms), but rather to the agents choosing a social identity that is subjectively optimal in terms of the agents' preferences.
- 1.10
- In our model, individuals were initialized to one of several "social identities," and could choose a new identity if one was available that was more optimally distinct. In the first, non-spatial model, agents had full knowledge of the social identities of all other agents in the population (or, equivalently, full knowledge of the population frequencies of all extant social identities). We refer to this case as "well-mixed," because the population was unstructured. Next, we will introduce a spatial model in which individuals were located on a square lattice and based their decisions only on the social identities of close neighbors. We will show that in the case of the well-mixed model, individuals organize into too few identities, resulting in lower average distinctiveness than one would predict from ODT. We will then show that by embedding agents in space, so that agents respond only to local neighbors, stability of more social identities in the global population and the achievement of near-optimal levels of average distinctiveness emerge.
 Model Description
Model Description
- 2.1
- The model was briefly described elsewhere by the authors (Pickett et al. 2011) but neither a formal description nor an analysis has been previously presented. We assumed that an agent had only one social identity (SID), which was visible to its neighbors. Each agent changed its SID based the distinctiveness of each SID is in its local neighborhood. To model optimal distinctiveness, we had to decide how optimal distinctiveness would be calculated and how agents would use that information in their decisions. We started with a simple mechanism. If an agent did not have the most optimally distinct SID among the agents in its neighborhood, it switched to the SID that was closest to optimally distinct. We also assumed a finite number of SIDs and that individuals could only choose from these SIDs; new SIDs could not be created. Finally, we assumed that, except for location and SID, agents had no other individual differences. This assumption is justified in ODT because the theory proposes that the preference for optimal distinctiveness should have a direct influence on social identity choices all else being equal (Brewer 1991). Thus, to simplify the model, we assumed that all agents were in the same social domain and not influenced by other factors such as valenced evaluations of the SIDs.
- 2.2
- Agents made social identity decisions one at a time, and were scheduled in an order that was randomized at each time step. This is important for two reasons. First, so that each individual could respond to the changes in neighborhood characteristics effected by their neighbors' shifts in SID. Second, so that temporal and spatial dynamics have more meaning. Simultaneous updating is known to cause unrealistic artifacts in spatial models of social interaction (Huberman & Glance 1993). If everyone responded simultaneously, each agent would make the identical choice.
- 2.3
- Many models of population dynamics assume that populations are "well-mixed." This implies encounters are random and that each agent has an equal probability of encountering every other agent. This assumption is made for simplicity and mathematical tractability. Our baseline for our model incorporated this assumption for comparison with our spatial model. We might also describe this version of the model as "omniscient," because we assumed that each individual could simultaneously perceive everyone else in the population. Real populations have structure due to physical space and social networks. Spatial structure has long been recognized to influence the behavior of individuals and population phenomena such as market prices (Hotelling 1929), segregation (Schelling 1978), epidemiology (Epstein et al. 2008; Christakis & Fowler 2010); social learning (Rendell et al. 2009), cooperation (Nowak & May 1992; Koella 2000; Ohtsuki et al. 2006), and loneliness (Cacioppo et al. 2009). The spatial version of our model, in which agents react only to their local neighbors, allowed us to experiment with the influence of neighborhood size on the population dynamics.
- 2.4
- We begin by presenting the well-mixed model and the social identity dynamics that result. We then introduce the spatial model and present several example simulations of the model to provide an appreciation for the dynamics. We will then present data averaged across many simulations of the model for each condition to systematically analyze the behavior of a well-mixed population. Finally, we will test robustness of the model results to decision-making errors.
 The Well-Mixed Model
The Well-Mixed Model
- 3.1
- The model was written in Java, using the MASON simulation library (Luke et al. 2005), which randomized the order in which agents were "stepped" at each time step. Initially, N agents were each randomly assigned membership in one of k0 social identities. Each agent had an optimal distinctiveness, d*, which was the desired frequency of the agent's SID in the population. We assumed that d* was the same for all agents and did not change over time. At each time step, each agent i assessed the distinctiveness of each SID g in the population, dg, which was the frequency of agents who had that SID (i.e., dg = ng/N). The agent then switched to the SID with a frequency of membership closest to d*, as defined by the SID g with the minimum absolute difference |dg—d*|. If two or more SIDs were equally close to optimal, one was selected at random unless one was the agent's current SID in which case it retained its current social identity. For example, assume that there are three possible SIDs (g1, g2, g3) and that an individual is optimally distinct when his social identity is held by 33% of the population (d* = 0.33). If individual i's current SID, g1, is held by 15% of the population (d1 = 0.15), and he observes that d2 = 0.35 and d3 = 0.5, then he will switch his SID to g2.
- 3.2
- ODT predicts that individuals should change their SIDs until they are optimally distinct. Therefore, if no factors beyond optimal distinctiveness are used to make SID decisions, the intuition might be that the population should converge to
k* = round[1/(d*)] (1) where k* is the final number of active SIDs and the function round[x] returns the integer closest to x. For example, if d* = 0.2, the population should stabilize with five active SIDs.
Results
- 3.3
- We found that k* was always less than 1/d*. Thus, agents never achieved optimal distinctiveness. To illustrate why this occurred, let us consider an example with a population of N = 50 agents distributed uniformly among six SIDs, and let d* = 0.2 (Figure 1). Since agents always switch to the SID closest to d*, they should organize themselves into five SIDs, each with ten members. Because 50 is not divisible by six, some SIDs start with eight agents and some start with nine. Since an SID with nine is closer to optimally distinct than one with eight, agents from the smaller (more distinct) SIDs switch the larger (less distinct) SIDs. As this happens, the less distinct SIDs lose members, and become less and less optimal. Soon, even though some of the SIDs have too many members (and are therefore not distinct enough), they are still closer to optimally distinct than the SIDs with very few members, which are too distinct. This leads to extinction of some of the smaller SIDs and to an equilibrium with only three available SIDs, in which the average distinctiveness of each individual is 0.33, a level significantly higher than the optimal distinctiveness of 0.2.
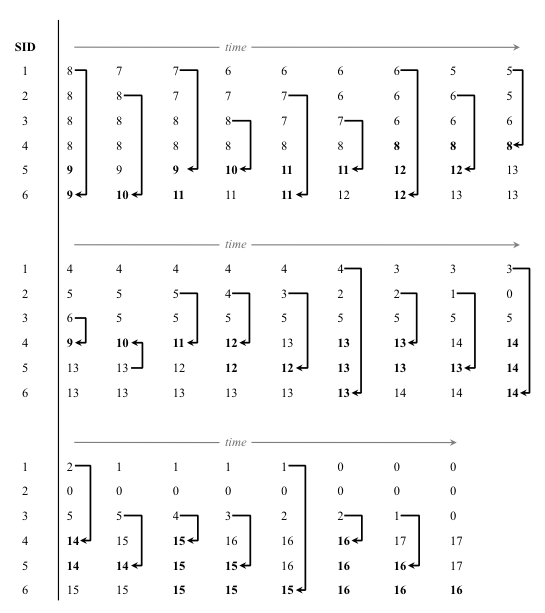
Figure 1. An example of the well-mixed model dynamics, initialized with N = 50 and k = 6. The numbers represent the number of agents with each SID. At the beginning, in the upper left, SIDs 1-4 each have eight agents, and SIDs 5 and 6 each have nine agents. At each step, a random agent switched to a more optimally distinct SID, indicated by the black arrows. The most optimally distinct SIDs are indicated in bold. The run ends with all individuals in one of three groups of approximately equal size. - 3.4
- A population that starts with all its members in optimally distinct SIDs will not change. If, however, a population is sufficiently large and the number of initial SIDs (k0) is greater than 1/d*, it turns out that there is a precise mathematical relationship between d* and the number SIDs at equilibrium. This is given by the equation
k*(d*) = floor[1/(2d*)] + 1 (2) where the function floor[x] yields the integer closest to but not exceeding x. Figure 2 illustrates the results of simulations with N = 3000 and k0 = 30, and demonstrates that the results exactly follow the relationship given by the above equation.
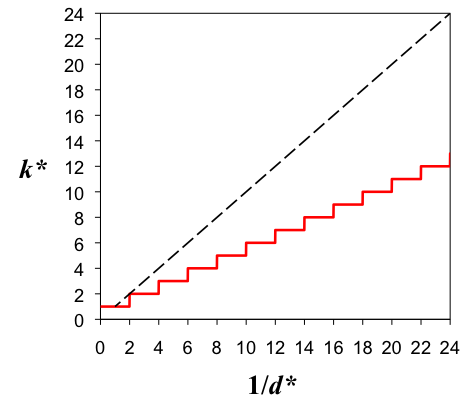
Figure 2. Number of SIDs with a nonzero number of members, k*, as a function of the inverse of the optimal distinctiveness, d*, at the end of runs for the well-mixed model (shown in red). The dotted line is the line k* = 1/d*.
 The Spatial Model
The Spatial Model
- 4.1
- A limitation of the well-mixed model is that it assumes that agents can determine the frequency of each SID in the entire population. This may be appropriate for small, isolated populations, but for large populations, people are limited by the number of people they can track. We assumed, therefore, that agents could only sample their local environments. This assumption can be interpreted in two equivalent ways: either (1) people are limited to information about their local neighborhoods to use as a representation of the whole population, or (2) they focus exclusively on the social identities of their local neighbors.
- 4.2
- In this extension, agents were situated on an L × L square lattice, with each site occupied by a single agent so that N = L2. Social identities were again randomly assigned to agents at initialization, as in the well-mixed model. At each time step, each agent (asynchronously) assessed the frequencies of all the SIDs among the agents located in its local neighborhood. This neighborhood was defined as a square of length 2r + 1, centered on the agent (e.g., r = 1 defines a 3 × 3 square that includes the agent and its eight nearest neighbors). The relevant neighborhood of an agent could therefore vary in size with the search radius r. The search radius allowed us to analyze the effects of different local neighborhood sizes. Because each agent had a different local neighborhood than its neighbors, the local distinctiveness of any given SID was unique for each agent i, and is given by
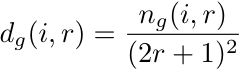
(3) where ng(i,r) is the number of agents in i's neighborhood with SID g. The agent then switched to the local SID that was closest to optimally distinct in the same way as in the well-mixed model, except for the restriction of local neighborhood. The source code for the spatial model is available from http://www.smaldino.com/Code.html.
 Spatial Results
Spatial Results
- 5.1
- Spatially restricted neighborhoods led to average distinctiveness levels that were much closer to optimal than those found by the well-mixed model, and also allowed for the emergence of interesting spatial patterns. We will first present a series of example runs with various values of d* and r in order to illustrate the dynamics of the model and to showcase some of these emergent patterns. Spatial organization dramatically changed the dynamics of social identities within the population. In addition to screen shots illustrating the spatiotemporal dynamics, we will also present time courses for the representation of each SID, the average distinctiveness in the population, and the frequency of agents that switch SID, which is a measure of population stability. After the examples, we will present the general results averaged from many runs of the model for different values of d* and r. For all spatial runs, we used L = 50 and k0 = 9.
Spatial run 1: spatial disorder (d* = .26, r = 1)
- 5.2
- The addition of spatial structure and local neighborhoods allowed populations to remain highly variable for far longer than in the well-mixed model. When r = 1, neighborhoods were very small, consisting of only nine agents. With d* = .26, agents preferred to have the same SID as exactly one other agent in their neighborhood (d = .222), but groups of this size were then desirable to others, who might join that SID and make it immediately less desirable (d = .333). This led the population to be in a state of indefinite flux, with agents constantly changing SID (Figure 3). In this run, close to half the population switched SID every time step, and all nine original SIDs persisted indefinitely.
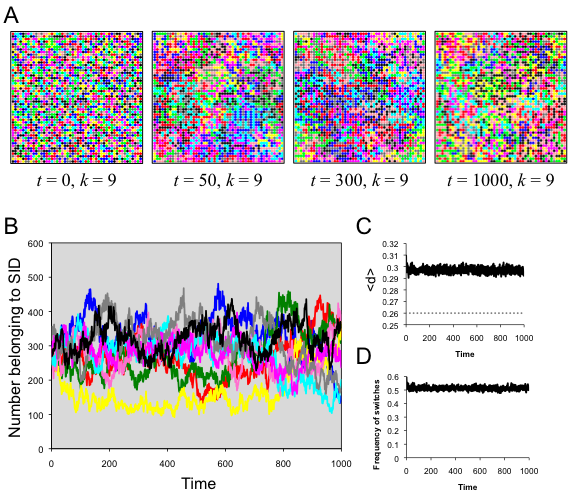
Figure 3. Results of spatial run 1. (A) Screenshots illustrate the spatiotemporal dynamics; each SID is indicated by a specific color. (B) The number of agents belong to each SID as a function of time, with colors corresponding to the SID in A. (C) The average distinctiveness in the population as a function of time. (D) The amount of flux in the population, indicated by the frequency of individuals switching SID at each time step. Spatial run 2: demographic zones (d* = .33, r = 1)
- 5.3
- Stability was achieved when agents preferred to shared an SID with exactly two of their eight neighbors, as when d* =.33. Figure 4 illustrates the dynamics involved in reaching that stability. As agents switched SIDs to optimize their distinctiveness, some of the original SIDs were lost. In the end, there were several stable zones, each of which supported alternating stripes of two SIDs, and which globally comprised five of the original nine SIDs (Figure 4). This configuration reached stability at t = 5212, with just a couple of individual agents switching back and forth. The average distinctiveness in the population at equilibrium was <d> = .3319, which was quite close to the population's optimal distinctiveness. In this case, spatial organization permitted the ODT decision rule to produce optimal distinctiveness in the population.
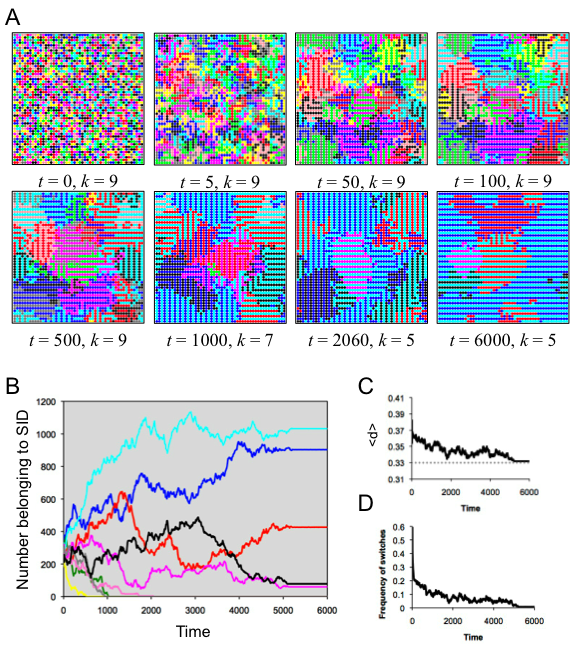
Figure 4. Results of spatial run 2. (A) Screenshots illustrate the spatiotemporal dynamics; each SID is indicated by a specific color. (B) The number of agents belong to each SID as a function of time, with colors corresponding to the SID in A. (C) The average distinctiveness in the population as a function of time. (D) The amount of flux in the population, indicated by the frequency of individuals switching SID at each time step. More spatial organization
Spatial run 3 (d* = .26, r = 3)
- 5.4
- Agents in this run also organized themselves into stripes of alternating SIDs. For a long time, a metastable condition held with four extant SIDs (Figure 5A, panels 5-7). As seen in figure 5, the ratio of magenta agents to navy blue agents fluctuated back and forth until eventually the magenta SID went extinct. Unlike in spatial run 2, the population never stabilized. At each time step, about 14% of agents switched SID (Figure 5D).
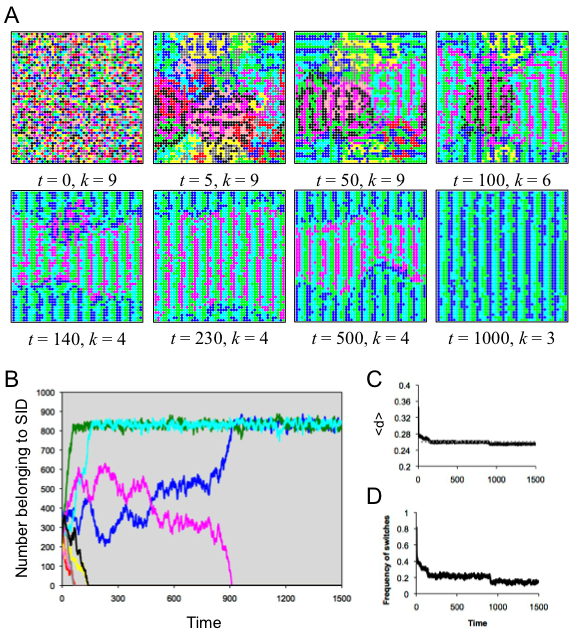
Figure 5. Results of spatial run 3. (A) Screenshots illustrate the spatiotemporal dynamics; each SID is indicated by a specific color. (B) The number of agents belong to each SID as a function of time, with colors corresponding to the SID in A. (C) The average distinctiveness in the population as a function of time. (D) The amount of flux in the population, indicated by the frequency of individuals switching SID at each time step. Spatial run 4 (d* = .45, r = 3)
- 5.5
- In this run, the optimal distinctiveness was set to d* = .45, which means that in a neighborhood of 49 (i.e., (2≈3 + 1)2) individuals, the most optimal SID was one held by 22 of the 49 agents therein. In the well-mixed model, the population immediately went to two identities. This spatial run, however, ended with seven stable SIDs (Figure 6). Spatial organization allowed the population to form interesting formations of geographically distinct groups in which agents no longer switched. Notice that at stability, one SID, black, was found between all other identities. This appears to have been a useful factor for stabilization. When this was not the case, as in the times prior to stability (see Figure 6B), instabilities were found in near group boundaries; this led to occasional chain reactions that altered the spatial patterns of identities. Certain spatial patterns held together for quite a long time before collapsing, such as the mixed subpopulation of magenta and blue individuals seen in the bottom right of figure 6A, panels 3 and 4.
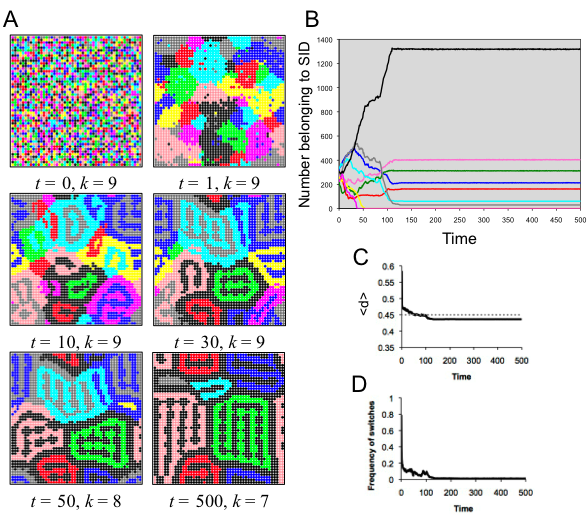
Figure 6. Results of spatial run 4. (A) Screenshots illustrate the spatiotemporal dynamics; each SID is indicated by a specific color. (B) The number of agents belong to each SID as a function of time, with colors corresponding to the SID in A. (C) The average distinctiveness in the population as a function of time. (D) The amount of flux in the population, indicated by the frequency of individuals switching SID at each time step. Spatial run 5 (d* = .19, r = 10)
- 5.6
- In the previously considered runs, individuals had relatively small local neighborhoods. Here we considered a larger search radius of 10, which translates to a 21 × 21 square neighborhood of 441 individuals. The population organized into a nice staggered pattern involving four identities in a hexagonal arrangement (Figure 7). The stability of this layout relied on the fact that the clusters of each color were significantly smaller than the local neighborhoods of the constituent agents, as shown for an example agent in the rightmost panel of Figure 7A. The current social identity for this individual is the closest to optimally distinct in his "visible" neighborhood, and this was the case for all agents at the end of this run (Figure 7C). This indicates that if neighborhood size is large enough and agents prefer to be in a minority group, they may self-organize into groups that are locally very homogeneous. A similar result has been obtained for agents with consistent group identities who change location to be in the minority (Muldoon et al. 2012); in that case, as here, individuals end up forming spatially uniform groups because each individual of a given type is subject to the same social forces.
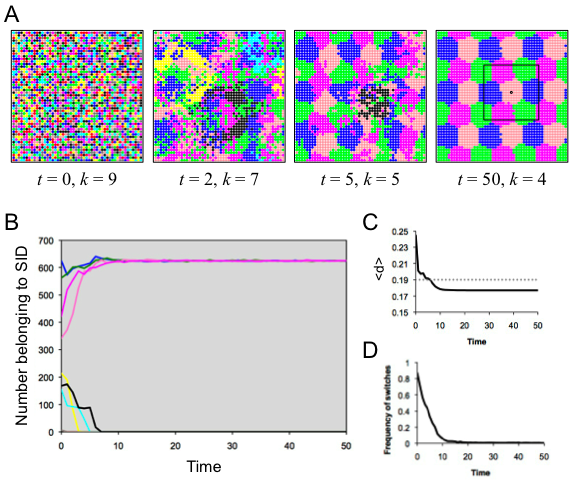
Figure 7. Results of spatial run 5. (A) Screenshots illustrate the spatiotemporal dynamics; each SID is indicated by a specific color. (B) The number of agents belong to each SID as a function of time, with colors corresponding to the SID in A. (C) The average distinctiveness in the population as a function of time. (D) The amount of flux in the population, indicated by the frequency of individuals switching SID at each time step. Runs when d* > 0.5
- 5.7
- In the well-mixed model, an optimal distinctiveness greater than 0.5 always led to a single identity, since everyone wanted to be in the most popular group. Spatial organization and local neighborhoods, however, allowed distinct geographical groups to form. Figure 8 gives shows some examples from runs in which d* = 0.7.
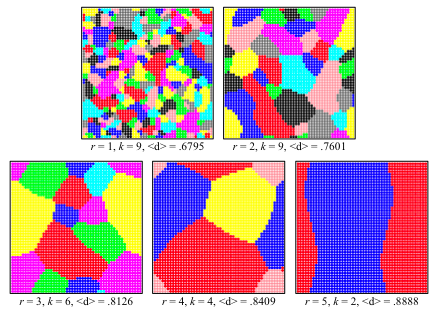
Figure 8. Snapshots of spatial stability for d* = 0.7. Each screenshot depicts a population at a stable equilibrium. Patterns of optimal distinctiveness and neighborhood size
- 5.8
- Paying close attention to example runs, as seen above, is an important way for gaining intuition into the model's emergent patterns. To characterize the model more precisely, we systematically varied d* and r. The values portrayed in Figure 9 are averaged from 30 simulation runs, assessed at time t = 5000. Most importantly, the average individual distinctiveness was very close to optimal for the spatial runs, particularly for d* < 0.3 (Figure 9A). For d* ≥ 0.3, average distinctiveness was still closer to optimal when compared to the well-mixed model, but was no longer strongly influenced by the specific value of d*. For 0.3 ≤ d* <0.5 and r ≥ 2, the average distinctiveness was approximately 0.42 regardless of d*. This is likely because, in each case, the number of active SIDs dwindled to k = 2, and thus the problem reduced to remaining in the minority group. When individuals preferred to be in majority groups, the precise value of d* was also unimportant, but the average distinctiveness and the number of active SIDs were more dependent on neighborhood size. For larger values of r, it more likely it was that one SID would eventually spread throughout the population.
- 5.9
- Smaller neighborhood sizes allowed for more social identities to be stable in the global population. When r = 1, all the initial social identities remained active for d* ≤ 0.22 because there was an insufficient flow of spatial information to effectively "tip" (Schelling 1971, 1978) the population into a stable configurations (see Figure 2 for a similar event when d* = 0.26). Stable patterns emerged when d* ≤ 1/9, fittingly with all nine of the original SIDs represented (Figure 9C), because the model landscape allowed for stable arrangements of nine SIDs in neighborhoods of nine agents. Stable patterns also emerged for d* > 0.5 for all runs, even though all of the initial SIDs remained active for r < 3 because individuals were able to organize into small groups where each agent was in a local majority (see Figure 8). The spike in switching frequency observed at d* = 0.5 (Figure 9C) is an artifact of the spatial layout: two neighboring groups would alternately gain and lose members along their borders as individual identity changes switched which group was more optimal.
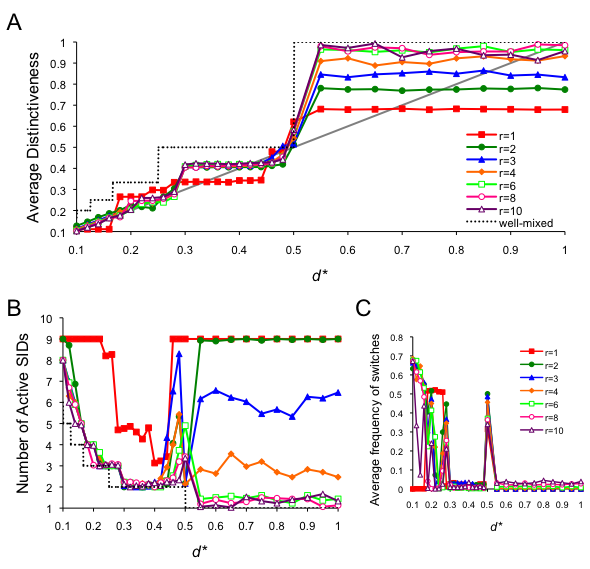
Figure 9. Full analysis of the spatial model. Data are averaged from 30 simulation runs for each condition, collected at t = 5000. (A) The average distinctiveness in the population, where the optimal distinctiveness is indicated by the grey diagonal line, (B) The number of active SIDs at equilibrium, and (C) the average frequency of individuals who switched SID at t = 5000. - 5.10
- Three important points may be gleaned from the data presented in Figure 9. First, spatial organization allows for more stable identities than predicted by the well-mixed model, and the number of stable identities increases as the neighborhood size shrinks. Second, when individuals want to be in the majority group, the well-mixed model predicts that they will all form one big group. However, if individuals only react to their local neighborhood, many more small groups of identities can be stable in the population, and this number again increases for smaller neighborhoods. Thus, as individuals adjusted their social identities to larger and larger radii of social influences, populations became more and more homogeneous. Finally, although the well-mixed model predicts that everyone will be dissatisfied in a less-than-optimally-distinct group, spatial organization, in which individuals react only to local neighborhoods (or social networks, as an alternative interpretation), allows individuals to organize in a way such that their distinctiveness is very close to optimal.
Error
- 5.11
- We checked to see whether our results were robust to errors in the decision processes. Each time step, an agent chose a random SID from the original nine (instead of the one that was most optimally distinct) with a probability of 0.01. Simulations were run with error for 4500 time steps, after which error was turned off, allowing the population to stabilize for another 500 time steps. In general, we found our results to be very robust to error, especially for d* < 0.5 (Figure 10). Some patterns of spatial organization were unstable, especially for d* > 0.5. In these cases, the population often went to a single, global SID. Additionally, some of the more intricate spatial patterns for d* less than, but approaching 0.5 were also unstable, such as the example shown above as spatial run 4 (Figure 6). All of the other example runs, including spatial run 5 with its hexagonal layout, were replicated even in the presence of error.
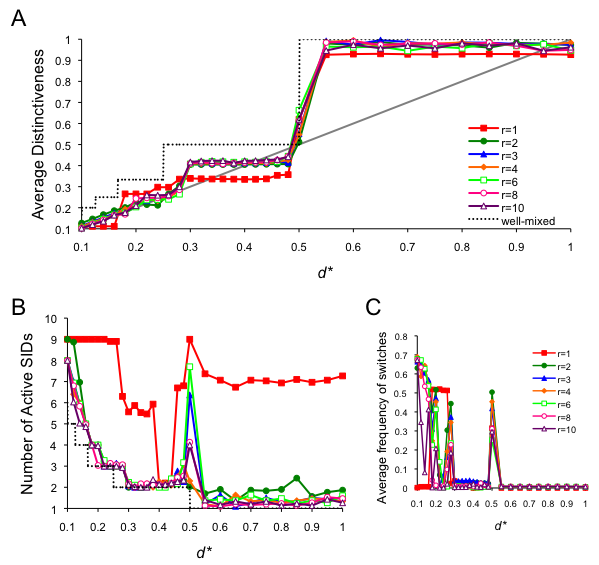
Figure 10. Full analysis of the spatial model with error. Data are averaged from 30 runs for each condition, collected at t = 5000. For the first 4500 time steps of each run, agents selected a random SID with probability .01. SID decisions were once again deterministic for the final 500 time steps. (A) The average distinctiveness in the population, where the optimal distinctiveness is indicated by the grey diagonal line, (B) The number of active SIDs at equilibrium, and (C) the average frequency of individuals who switched SID at t = 5000.
 Discussion
Discussion
- 6.1
- Optimal distinctiveness theory has generally assumed that individuals can achieve optimal distinctiveness by simply correcting their identity choices. "Individuals will resist being identified with social categorizations that are either too inclusive or too differentiating but will define themselves in terms of social identities that are optimally distinctive. Equilibrium is maintained by correcting for deviations from optimality." (Leonardelli et al. 2010, p. 68). However, ODT has not previously accounted for the influence of many individuals each simultaneously attempting to optimize their distinctiveness. Our model suggests that the individual-level decision strategy proposed by ODT is insufficient to generate an equilibrium in which all or even most individuals are optimally distinct if individuals have complete knowledge about the prevalence of all social identities in their populations. The model further suggests, however, that this decision strategy may be effective if knowledge about social identity prevalence is restricted to individuals' local social neighborhoods.
- 6.2
- Our model failed to yield optimally distinct individuals in a well-mixed population. If we like, we can consider agents as "happy" when their distinctiveness approaches their subjective optimal and "unhappy" when their distinctiveness differs from that optimal. Agents using ODT as a decision rule in a well-mixed population are doomed to be unhappy. When agents' decisions were based on restricted local neighborhoods, however, agents organized in such a way that their distinctiveness levels were very close to optimal, as long as they still preferred to identify with a minority group that constituted less than 30% of their local neighborhoods. In other words, basing their decisions only on the individuals in their local neighborhoods allowed agents to be happy. These results were robust to errors in social decision making.
- 6.3
- Spatial structure also allowed multiple social identities to stably co-exist even when all agents preferred to belong to a majority group. Additionally, more social identities could be maintained in the population—i.e., the population was more diverse, though it was organized into homogenous regions, or cliques. Because individuals responded locally, everyone could be in a local majority, but local neighborhoods could also differ from one another, leading to local segregation of social groups rather than global conformity. This result, however, was not very robust to error. The position of being in the majority for agents at the peripheries of group boundaries was precarious, and errors tended to disrupt group stability and lead to the emergence of a single, dominant SID. This did not always occur for very small r, however, as individual neighborhoods were too small and varied to spread effectively via a tipping phenomenon (Schelling 1971, 1978).
- 6.4
- Basing social identity decisions only on the social identities of close neighbors could be interpreted simply as a resource-management technique used by boundedly rational agents. Our results show that the heuristic of optimizing one's distinctiveness is actually a technique that has the best validity under conditions of limited, local information. This is an instance of ecological rationality (Gigerenzer & Brighton 2009), in which the performance of a simple heuristic is dependent on environmental constraints.
- 6.5
- Precise theories of social psychological phenomena are particularly difficult to formulate because individuals process social information that shapes their social behaviors, which in turn alters the social information received by others in the social environment. Here we have attempted to instantiate a simple act of social cognition in a multi-agent framework. Although it is a highly simplified view of the cognitive, behavioral, and environmental complexities of human interactions, our model is able to reveal key insights into the social identity dynamics implicit in optimal distinctiveness theory.
Limitations and future directions
- 6.6
- Our model was very simple in order to clearly establish links between a behavioral rule based on optimal distinctiveness and a dynamic population in which social identities shifted in response to one's neighbors. The model's simplicity naturally excludes many features of real human actors and their environments. Individuals may choose their social identities, but these choices are nonetheless constrained by culture, learning, social networks, and happenstance (Smaldino & Richerson 2012). Future models should include some of these additional complexities. For example, individuals could be heterogeneous in their distinctiveness preferences and have the ability to create novel social identities. Also, we assumed that social identities were orthogonal, and that decisions to change social identities were complete and instantaneous. Some social identities could be similar or antithetical, and changes to social identity could be modeled as more of a gradual process that might also be influenced by one's current social identity and the social identities of disliked members of one's social network (enemies) as well as friends. We also treated social identity as a single trait that was visible to everyone in an individual's social network. In reality, individuals have many social identities and domains of social identities, some of which may be nested in others. For example, a person may be an academic, a psychologist, and a social psychologist. These are nested identities, and the most salient level will depend on the setting for social comparison. Additionally, someone who is a psychologist may also be an athlete, a musician, a parent, a Jew, a Southerner, etc., and again the salience and importance of the social identity will depend on the setting. Multi-dimensional or nested trait profiles could be interesting additions to future models as long as their complexity does not obscure the model's inherent value, which lies in clarification through simplification.
- 6.7
- We modeled spatial structure as a simple 2-D lattice. Real social neighborhoods may have more complex structure. Social neighbors could take the form of specific network organizations observed in some social environments, such as small world networks (Watts & Strogatz 1998) or exponential random graphs (Wang et al. 2009). We also assumed that social networks were fixed. Strong social ties tend to persist (McPherson et al. 1992) within social networks, and the stability of social networks is often enforced by embeddedness in geographical location and institutional organization (Feld 1997). Nevertheless, individuals may move in social and/or physical space both to achieve specific social goals and also in the course normal events. The role of both goal-directed and random movement in social and physical space can have important influences on population dynamics for a range of phenomena (Schelling 1978; Beltran et al. 2006; Helbing & Yu 2009; Smaldino & Schank 2012a, 2012b). A possible future direction would be to investigate the co-evolution of social identities with network structure, similar to recent work on co-evolutionary games on graphs (Perc & Szolnoki 2009).
- 6.8
- Among those runs which reached complete stability (i.e., a state after which there were no more SID switches), there was considerable variation in the amount of time it took to reach stability, from several time steps to several thousand. Because the decision rules and the ability to instantly switch SIDs are dramatic simplifications, the specific time scale of the model cannot directly correspond to a real-world time scale. Nevertheless, models such as this one, when applied to realistic social network structures and/or spatial organizations, may allow researchers to predict qualitative difference in the spatiotemporal dynamics of social identity demographics. At the same time, experimenters should look at the temporal stability of social identities in different settings.
 Conclusion
Conclusion
- 7.1
- There is a growing need for multi-level models of social behavior that account for dynamic feedback between individual behavior and social organization. While social identity choices are often influenced by many factors, the extent to which they are based on the social identities of others typifies the class of social systems in which such multi-level models are appropriate. Theories of social identity dynamics will never be sufficiently explanatory if they only focus on solitary decision makers reacting to a static social environment. Because individual choices affect the stimulus landscapes for other decision makers, social identity decisions must be understood in terms of population dynamics as well as individual cognition.
- 7.2
- Our model demonstrates that the structure of social relationships and the inclusivity of social networks may play an important role in the organizational dynamics of social identity decisions, and provides a jumping-off point from which additional questions about group formation and social identity processes may now be investigated.
 Acknowledgements
Acknowledgements
- We thank Joshua Epstein, Elizabeth Matthews, and Jimmy Calanchini for valuable discussion in the development of ideas presented here.
 References
References
-
ABRAMS, D. (1994). Political distinctiveness: An identity optimising approach. European Journal of Social Psychology, 24, 357-365. [doi:10.1002/ejsp.2420240305]
BELTRAN, F. S., Salas, L., & Quera, V. (2006). Spatial behavior in groups: An agent-based approach. Journal of Artificial Societies and Social Simulation, 9(3), 5. https://www.jasss.org/9/3/5.html
BLANZ, M., Mummendey, A., & Otten, S. (1995). Positive-negative asymmetry in social discrimination: The impact of stimulus valence and size and status differentials on intergroup evaluations. British Journal of Social Psychology, 34, 409-420. [doi:10.1111/j.2044-8309.1995.tb01074.x]
BOYD, R., & Richerson, P. J. (1988). The evolution of reciprocity in sizable groups. Journal of Theoretical Biology, 132, 337-356. [doi:10.1016/S0022-5193(88)80219-4]
BREWER, M. B. (1991). The social self: On being the same and different at the same time. Personality and Social Psychology Bulletin, 17, 475-482. [doi:10.1177/0146167291175001]
BREWER, M. B. (2004). Taking the social origins of human nature seriously: Toward a more imperialist social psychology. Personality and Social Psychology Review, 8, 107-113. [doi:10.1207/s15327957pspr0802_3]
BREWER, M. B., & Weber, J. (1994). Self-evaluation effects of interpersonal versus intergroup social comparison. Journal of Personality and Social Psychology, 66, 268-275. [doi:10.1037/0022-3514.66.2.268]
CACIOPPO, J. T., Fowler, J. H., & Christakis, N. A. (2009). Alone in a crowd: The structure and spread of loneliness in a large social network. Journal of Personality and Social Psychology, 97, 977-991. [doi:10.1037/a0016076]
CHRISTAKIS, N. A., & Fowler, J. H. (2010). Social network sensors for early detection of contagious outbreaks. PLoS ONE, 5, e12948. [doi:10.1371/journal.pone.0012948]
DEMIGUEL, V., Garlappi, L., & Uppal, R. (2007). Optimal versus naive diversification: How inefficient is the 1/N portfolio strategy? Review of Financial Studies, 22, 1915-1953. [doi:10.1093/rfs/hhm075]
ELLEMERS, N., & van Rijswijk, W. (1997). Identity needs versus social opportunities: The use of group-level and individual-level management strategies. Social Psychology Quarterly, 60, 52-65. [doi:10.2307/2787011]
EPSTEIN, J. M. (2006). Generative Social Science. Princeton, NJ: Princeton University Press.
EPSTEIN, J. M., Parker, J., Cummings, D., & Hammond, R. A. (2008). Coupled contagion dynamics of fear and disease: Mathematical and computational explorations. PLoS ONE, 3, e3955. http://www.plosone.org/article/info%3Adoi%2F10.1371%2Fjournal.pone.0003955 [doi:10.1371/journal.pone.0003955]
FELD, S. L. (1997). Structural embeddedness and stability of interpersonal relations. Social Networks, 19, 91-95. [doi:10.1016/S0378-8733(96)00293-6]
FRENCH, R. M., & Kus, E. T. (2008). KAMA: A temperature-driven model of mate choice using dynamic partner preferences. Adaptive Behavior, 16, 71-95. [doi:10.1177/1059712307087598]
GIGERENZER, G. (2008). Rationality for Mortals: How People Cope with Uncertainty. Oxford, UK: Oxford University Press.
GIGERENZER, G., & Brighton, H. (2009). Homo heuristicus: Why biased minds make the best inferences. Topics in Cognitive Science, 1, 107-143. [doi:10.1111/j.1756-8765.2008.01006.x]
HELBING, D., & Yu, W. (2009). The outbreak of cooperation among success-driven individuals under noisy conditions. Proceedings of the National Academy of Sciences USA, 106, 3680-3685. [doi:10.1073/pnas.0811503106]
HILLS, T., & Todd, P. M. (2008). Population heterogeneity and individual differences in an assortative agent-based marriage and divorce model (MADAM) using search with relaxing expectations. Journal of Artificial Societies and Social Simulation, 11(4), 5. https://www.jasss.org/11/4/5.html
HOGG, M. A. (2007). Uncertainty-identity theory. In M. P. Zanna (Ed.), Advances in Experimental Social Psychology (vol. 39, pp. 69-126). San Diego, CA: Academic Press. [doi:10.1016/s0065-2601(06)39002-8]
HOTELLING, H. (1929). Stability in competition. The Economic Journal, 39, 41-57. [doi:10.2307/2224214]
HUBERMAN, B. A., & Glance, N. S. (1993). Evolutionary games and computer simulations. Proceedings of the National Academy of Sciences USA, 90, 7716-7718. [doi:10.1073/pnas.90.16.7716]
KENRICK, D. T., Li, N. P., & Butner, J. (2003). Dynamical evolutionary psychology: Individual decision rules and emergent social norms. Psychological Review, 110, 3-28. [doi:10.1037/0033-295X.110.1.3]
KOELLA, J. C. (2000). The spatial spread of altruism versus the evolutionary response of egoists. Proceedings of the Royal Society of London B, 267, 1979-1985. [doi:10.1098/rspb.2000.1239]
LEONARDELLI, G. J., & Brewer, M. B. (2001). Minority and majority discrimination: When and why. Journal of Experimental Social Psychology, 37, 468-485. [doi:10.1006/jesp.2001.1475]
LEONARDELLI, G. J., Pickett, C. L., & Brewer, M. B. (2010). Optimal distinctiveness theory: A framework for social identity, social cognition and intergroup relations. In M. Zanna & J. Olson (Eds.), Advances in Experimental Social Psychology (vol. 43, pp. 65-115). New York: Elsevier. [doi:10.1016/s0065-2601(10)43002-6]
LUKE, S., Cioffi-Revilla, C., Sullivan, K., & Balan, G. C. (2005). MASON: A multi-agent simulation environment. Simulation, 81, 517-527. [doi:10.1177/0037549705058073]
MCPHERSON, J. M., Popielarz, P. A., & Drobnic, S. (1992). Social networks and organizational dynamics. American Sociological Review, 57, 153-170. [doi:10.2307/2096202]
MILLER, J. H., & Page, S. E. (2007). Complex Adaptive Systems: An Introduction to Computational Models of Social Life. Princeton, NJ: Princeton University Press.
MULDOON, R., Smith, T., & Weisberg, M. (2012). Segregation that no one seeks. Philosophy of Science, 79, 38-62. [doi:10.1086/663236]
NOWAK, M. A., & May, R. M. (1992). Evolutionary games and spatial chaos. Nature, 359, 826-829. [doi:10.1038/359826a0]
OHTSUKI, H., Hauert, C., Lieberman, E., & Nowak, M. A. (2006). A simple rule for the evolution of cooperation on graphs and networks. Nature, 441, 502-505. [doi:10.1038/nature04605]
OLSON, M. (1971). The Logic of Collective Action (2nd ed.). Cambridge, MA: Harvard University Press.
PERC, M., & Szolnoki, A. (2010). Coevolutionary games: A mini review. BioSystems, 99, 109-125. [doi:10.1016/j.biosystems.2009.10.003]
PICKETT, C. L., Smaldino, P. E., Sherman, J. W., & Schank, J. C. (2011). Agent-based modeling as a tool for studying social identity processes: The case of optimal distinctiveness theory. In R. M. Kramer, G. J. Leonardelli, & R. W. Livingston (Eds.), Social Cognition, Social Identity, and Intergroup Relations: A Festschrift in Honor of Marilynn Brewer (pp. 127-143). New York: Psychology Press.
RAILSBACK, S. F., & Grimm, V. (2012). Agent-Based and Individual-Based Modeling: A Practical Introduction. Princeton, NJ: Princeton University Press.
RENDELL, L., Fogarty, L., & Laland, K. N. (2009). Rogers' paradox recast and resolved: Population structure and the evolution of social learning strategies. Evolution, 64, 534-548. [doi:10.1111/j.1558-5646.2009.00817.x]
SCHELLING, T. C. (1971). Dynamic models of segregation. Journal of Mathematical Sociology, 1, 143-186. [doi:10.1080/0022250X.1971.9989794]
SCHELLING, T. C. (1978). Micromotives and macrobehavior. New York: W. W. Norton.
SIMON, B., & Brown, R. (1987). Perceived intragroup homogeneity in minority-majority contexts. Journal of Personality and Social Psychology, 53, 703-711. [doi:10.1037/0022-3514.53.4.703]
SIMON, B., & Hamilton, D. L. (1994). Self-stereotyping and social context: The effects of relative in-group size and in-group status. Journal of Personality and Social Psychology, 66, 699-711. [doi:10.1037/0022-3514.66.4.699]
SMALDINO, P. E., & Richerson, P. J. (2012). The origins of options. Frontiers in Neuroscience, 6, 50. http://www.frontiersin.org/Decision_Neuroscience/10.3389/fnins.2012.00050/full [doi:10.3389/fnins.2012.00050]
SMALDINO, P. E., & Schank, J. C. (2012a). Human mate choice is a complex system. Complexity, 17(5), 11-22. [doi:10.1002/cplx.21382]
SMALDINO, P. E., & Schank, J. C. (2012b). Movement patterns, social dynamics, and the evolution of cooperation. Theoretical Population Biology, 82, 48-58. [doi:10.1016/j.tpb.2012.03.004]
SMITH, E. R., & Collins, E. C. (2009). Contextualizing person perceptions: Distributed social cognition. Psychological Review, 116, 343-364. [doi:10.1037/a0015072]
SMITH, E. R., & Conrey, F. R. (2007). Agent-based modeling: A new approach for theory building in social psychology. Personality and Social Psychology Review, 11, 87-104. [doi:10.1177/1088868306294789]
SUTCLIFFE, A., & Wang, D. (2012). Computational modelling of trust and social relationships. Journal of Artificial Societies and Social Simulation, 15(1), 3. https://www.jasss.org/15/1/3.html
TAJFEL, H., & Turner, J. (1986). An integrative theory of intergroup conflict. In S. Worchel & G. W. Austin (Eds.), The Social Psychology of Intergroup Relations (pp. 33-47). Monterey, CA: Brooks/Cole.
TURNER, J. C., Oakes, P. J., Haslam, S. A., & McGarty, C. (1994). Self and collective: Cognition and social context. Personality and Social Psychology Bulletin, 20, 454-454. [doi:10.1177/0146167294205002]
WANG, P., Sharpe, K., Robins, G. L., & Pattison, P. E. (2009). Exponential random graph (p*) models for affiliation networks. Social Networks, 31, 12-25. [doi:10.1016/j.socnet.2008.08.002]
WATTS, D. J., & Strogatz, S. H. (1998). Collective dynamics of 'small-world' networks. Nature, 393, 440-442. [doi:10.1038/30918]