 Abstract
Abstract
- In complex social systems such as those of many mammals, including humans, groups (and hence ego-centric social networks) are commonly structured in discrete layers. We describe a computational model for the development of social relationships based on agents' strategies for social interaction that favour more less-intense, or fewer more-intense partners. A trust-related process controls the formation and decay of relationships as a function of interaction frequency, the history of interaction, and the agents' strategies. A good fit of the observed layers of human social networks was found across a range of model parameter settings. Social interaction strategies which favour interacting with existing strong ties or a time-variant strategy produced more observation-conformant results than strategies favouring more weak relationships. Strong-tie strategies spread in populations under a range of fitness conditions favouring wellbeing, whereas weak-tie strategies spread when fitness favours foraging for food. The implications for modelling the emergence of social relationships in complex structured social networks are discussed.
- Keywords:
- Social Agents, Social Relationships, Trust, Evolution, Social Straegies
 Introduction
Introduction
- 1.1
- Socio-psychological theories of social relationships range from relationship formation based on exchange and expectations of reciprocity (Brown & Brown 2009) to explanations of human attitudes towards groups and the relationship between individual and group in terms of social identity (Reicher et al. 1995; Tajfel & Turner 1979), and from group socialisation (Moreland & Levine 1982) to wide-ranging frameworks encompassing success criteria for groups with models of their structure, and short-term evolution from formation to dissolution (Arrow et al. 2000; Tuckman 1965). In contrast, evolutionary theories of human social behaviour vary from cultural hypotheses which propose that social behaviour is a product of imitation, social learning and acquired norms of group behaviour (Boyd & Richerson 1988; Tooby & Cosimides 1989) to cognitive mechanisms grounded in plausible genetic origins (for example generalisation of kin recognition and altruistic behaviour predisposition from kin to intimate friendships: Akerman et al. 2007, Madsen et al. 2007).
- 1.2
- Hamilton's theory of inclusive fitness (1964) first demonstrated the generic basis for social cooperation among kin based on the survival payoff of related genes; however, why cooperation should evolve among unrelated individuals was intuitively less obvious. Subsequently, theoretical models of social behaviour among unrelated individuals have demonstrated the evolution of cooperative behaviour and altruism (Nowak & Sigmund 1998, 2005; Roberts & Renwick 2003), where reciprocal rewards accruing from social relationships outweigh the costs of social interaction, thereby providing the incentive to invest in cooperation. Cooperative behaviour spreads strongly when there is a payoff from repeated encounters with individuals within a population, as demonstrated in many models based on the repeated prisoner's dilemma (RPD) paradigm (Yamagashi et al. 1998). Cooperative strategies with strong reciprocity compete effectively with non-social defectors in social dilemma games across a wide range of models and frameworks (Rosasa 2010), so it appears that reciprocity, which is a key attribute of trust in human social relationships (Oswald et al. 2004), underpins cooperative behaviour. Cooperative behaviour spreads when memory of previous encounters with specific individuals is present, i.e. direct reciprocity is possible. Furthermore, cooperation also spreads when simpler reputation memory of an individual's previous cooperative acts is visible as that individual's 'image score' (Nowak & Sigmund 1998). The effect of trust in promoting the development of social relationships was demonstrated by Nowak and Sigmund's (1998, 2005) studies on reputation (the 'image scoring') in a coalitional version of the prisoner's dilemma game, showing that cooperation and altruism are likely to be widely adopted in populations where reputations are publicly visible. Hardy and Van Vugt (2006) also proposed that reputation systems are a necessary prerequisite of evolutionarily stable cooperation in large groups; furthermore, Roberts and Renwick (2003) demonstrated, in both experimental studies and computer simulations, that individual reputation based on histories of collaboration leads to the formation of social relationships. Hruschka and Henrich's (2006) model produced emergent social structures and preferential social relationships when agents possessed strategies favouring known collaborators, and social preference strategies ('cliquers') spread in populations across a range of cost/benefit ratios and defect rates. However, their model depended on a memory constraint, so only a limited number (10) of stronger relationships could be developed. Given that cooperation is reasonably well established as a foundation of social relationships in behavioural (Baumeister & Leary 1995; Brown & Brown 2009; Oswald et al. 2004) and evolutionary (Boyd & Richerson 1988) terms, the question arises about what patterns of social relationships might emerge from cooperative behaviour and how these might relate to the observed patterns of structure found in real-life social networks.
- 1.3
- Stratification of human social relationships into bands of best/close friends and less intimate casual friends is well established in the literature on friendship (Baumeister & Leary 1995; Brown & Brown 2009; Hays 1989) and in empirical studies on relationships in a variety of societies (Hill & Dunbar 2003; Wellman et al. 2001, 2006; Zhou et al. 2005). Nearly all studies of human friendship and social relationships report at least two bands of intensity (e.g. strong vs. weak ties: Granovetter 1973, 1985; close vs. casual relationships: Hays 1989, Wellman & Wortley 1990; core vs. peripheral ties: McPherson et al. 2006), so there appears to be a close agreement about intimacy layers being a key determinant of structure in human ego networks. It appears that people tend to 'favour the few' at the expense of the many in friendship. More importantly, a virtually identical layering of relationships with a similar scaling ratio to that found in humans has been reported for a range of other mammalian taxa that live in complex multi-level social systems (including elephants and many primates) (Hill et al. 2008). These social relationship patterns support the Social Brain Hypothesis (SBH), an evolutionary psychological theory which relates brain size evolution to social group size within primates (Dunbar 1998).
- 1.4
- Based on a general relationship for social group size and brain volume in primates, SBH predicts a typical group (or community) size for humans of ~150 individuals (Dunbar 1993, 1998). Different intimacy levels emerge from the fact that social time is inevitably limited (Lu et al. 2009), creating a selection pressure that might favour individuals focusing their social interactions on a few more intense relationships at the expense of many, more diffuse ones. In humans, the innermost two layers have been identified as the support clique (Dunbar & Spoors 1995; Stiller & Dunbar 2007) and the sympathy group (Buys & Larson 1979; Stiller & Dunbar 2007), followed by an affinity group of 50 and an active network of 150 individuals. If the tenets of SBH are true, evolution should have produced a predisposition towards structuring human relationships in layers of decreasing intimacy.
- 1.5
- Such social predispositions need to be explained in both behavioural and evolutionary terms. This paper explores the causal processes underlying the emergence of social structure by an agent-based computational model. We explore the behavioural predispositions which might have led to the evolution of the social relationship structures in humans, i.e. friendships organised in decreasing layers of intimacy. In our previous work (Sutcliffe & Wang 2012) we described a computer model of trust based on social interaction between agents and explored how different social predispositions such as favouring fewer strong, or more weak relationships effected the emergence of social structure and networks. This model was a 'behaviour-time' view of social interaction; in this paper we extend that model in evolutionary time to investigate how the genetic basis of social behaviour might emerge and compete under a range of selection pressures. The model investigates trade-offs between time spent foraging or socialising, with interactions between these fitness criteria and strategies that determine social interaction preferences. The paper addresses two research questions:
- Can social strategies that favour the few at the expense of the many lead to development of relationships in concentric layers of intimacy? This question tests the evolutionary influence of different social preferences in relationship formation.
- Which social preference strategies spread in populations to produce social network structures observed in human populations? Social preference strategies will be investigated over a range of fitness criteria for wellbeing benefits from social relationships and fitness derived from foraging and feeding as competing activities.
- 1.6
- In the following sections of this paper, first the modelling approach is described with a summary of the model of trust formation and relationship development which we reported in the previous paper (Sutcliffe & Wang 2012). Then the new evolutionary layer of the model is introduced to investigate competition between agents with different interaction strategies that reflect their social preferences. We next explore the evolution of different social strategies under a range of fitness criteria weightings. The paper concludes with a discussion of implications for the emergence of social network structures in evolutionary and behavioural time and the concordance between theoretical simulations and empirical observations.
 Trust and Social Relationship Modelling
Trust and Social Relationship Modelling
- 2.1
- We depart from the conventional RPD model of cooperative behaviour since we want to explicitly model the fact that all social species face competing demands on their time, such that they will eventually face a potential trade-off between time spent feeding (to maintain fitness) and time spent socialising (which yields increased survival of offspring and increased predator protection, and possibly increases the efficiency of finding food by exchange of information, or other benefits of social cooperation including alliances for hunting larger prey and inter-group competition: Tooby & Cosimides 1989). For simplicity, we restrict modelling to a simple trade-off between social and foraging/feeding time. The basis for our model is therefore strategies that offer the choice of spending more or less time feeding or socialising, reflected in the ratio of 'forage' vs. 'meet/socialise'.
- 2.2
- The trust model (Sutcliffe & Wang 2012) implemented a psychological mechanism for relationship development which is more sophisticated and concordant with the empirical literature than simple linear relationships between frequencies of cooperation/socialising and relationship strength. The key features of the model are as follows: through repeated interaction, trust changes from 'calculative mode' (in which an individual's trustworthiness is assessed on limited evidence) to relational trust based on social experience. In relational mode, deep trust is maintained by social emotions (e.g. belonging, pleasure in alters' company), hence less reinforcement is necessary to maintain the tie. In calculative mode, which precedes the development of emotional bonding, the frequency of interaction and strength of the tie have a linear relationship. In relational mode the relationship with interaction frequency becomes a logarithmic function as a 'law of diminishing returns'.
- 2.3
- The main components of the model are:
- Agents who interact and form trusting relationships. Frequency of interaction is equated with strength of relationships and trust, following empirical observations (Roberts & Dunbar 2011; Rose & Serafica 1986).
- Responding agents may choose to accept or reject an initiation, hence interactions may have positive or negative results.
- Trust accumulates for positive interactions, and is decreased by negative interactions.
- Agents have a memory of previous interactions with other agents.
- Agents have social preference strategies for initiating interaction according to the history of previous successful interaction. Four agent strategies are tested ranging from favour the few to favour many.
- Increase in trust is controlled by smoothing algorithms to implement the hypothesis that individuals in high-trust relationships exhibit different behaviour from those in low-trust relationships. This models the change from calculative to relational mode (Ostrom 2002; Rempel et al. 1985).
- Trust in relationships wanes over time at a slow rate. This models the empirical observation that relationship strength declines unless it is maintained by social interaction (Wellman et al. 2001, 2006).
- 2.4
- Trust accumulates between any two agents by one unit for each cooperative interaction. When A initiates interaction and B cooperates, A's trust in B increases (A→ B); but if B defects, the existing trust value (A→ B) is decreased by one unit. Initially trust increases linearly in proportion to the number of cooperative interactions with the responding agent. As trust in a relationship increases, a log ratio algorithm is applied; so the rate of increase progressively decreases as the value of trust rises. Since the log algorithm applies to negative as well as positive interaction, high-trust relationships are relatively immune to defections. This models the intuition that people forgive alters' indiscretions in high-trust relationships. Details of the formula for determining trust from interaction frequency are given in Sutcliffe and Wang (2012).
Agent Strategies
- 2.5
- A probabilistic search function determines how the focal agent chooses a target agent for interaction according to the history of previous cooperative interactions. Four strategies were implemented to model different preferences in relationship formation; three are static with a constant bias in alter selection, while the fourth, dynamic, strategy changes during the simulation run. The alter selection strategies are:
- Favour the few preference: the history-dependent search function favours cooperating with alters with whom the agent has had more previous successful interactions. This encourages development of high-trust relationships or strong ties; however, since the function is stochastic, there is a low probability of initiating interaction with low-trust alters and strangers without a previous interaction history.
- Medium ties: the search function is biased towards the mid-point in the relationship trust distribution.
- Favour the many: the search is biased towards the low-trust/interaction frequency part of the distribution.
- Staged: in this dynamic strategy, the search bias is changed over time so the ego agent initially favours the few but progressively favours initiating proportionately more interactions with strangers and low-trust (weak-tie) partners. This implements the behavioural predisposition manifest over an individual's lifetime, that strong ties are formed earlier in life, while weaker ties accumulate in later life and strong ties persist (Hays 1989).
Model Control Process
- 2.6
- The top-level algorithm for the model has two cycles. The first powers the simulation for the desired set of runs; in the simulations reported below this was set at 2000. The second cycle gives each focal agent a turn within a run and iterates according to the number of agents in the population.
Model-Control Initialise-model (N agents, strategies, run-cycles, parameters CR, W, D, FM) While Run-cycles Do For Agent (i) to N Do Select Focal Agent (i) {initially at random) If Forage-turn Then Increment Res by 1 {1} Else {Social-turn} Read Relationship History Search for Alter-agent {2} If Alter-response = Cooperate Then Increment Trust by (MaxCR-CI × Trust) {3} Else {Alter defects} Decrement Trust by (MaxCR-CI × Trust) Increment Defect by 1 End-If Decrement Trust by W {4} End-Do End-WhileNotes
- The forage : social turn is set by the FM ratio parameter.
- Search depends on the agent strategy as described previously, so initially when there is no relationship history the search algorithm for all strategies selects a stranger at random. As relationship histories accrue, the algorithm is chosen more selectively according to the agent's strategy.
- Trust compression is applied progressively as the relationship (i,j) increases. Initially there is no effect since there is no history.
- Waning is applied with a log function, so stronger relationships wane less than weaker ones.
- The parameters CR Compression Rate for Trust, W for the Waning rate and D for % Defection rate on response can be changed between experimental runs.
- More details of the algorithms and source code can be found at http://www.openabm.org/model/2934/version/1/view.
 Simulation Experiments
Simulation Experiments
- 3.1
- The experimental parameters (independent variables) in the computational model are:
- Defect rate = percentage of turns in which the respondent will not cooperate.
- Waning cost.
- Number of cycles in each model run.
- Proportion of agents by strategy in the population.
- 3.2
- The model outputs (dependent variables) are:
- Trust between agents for each strategy.
- Frequency of relationships for each ego ranked by trust relationship strength.
- Average number of relationships per ego, divided into strong, medium and weak ties.
- 3.3
- Since the distribution of trust values was continuous rather than discrete, strong ties were counted as relationships in the upper tercile (33.3%) of the distribution, weak ties in the lower tercile and medium ties as relationships falling between strong and weak. The history of trust development for individual relationships was inspected to see if these conformed to the appropriate pattern predicted by the theory, i.e. for strong ties the curve will rapidly approach maximal trust, weak ties exhibit a shallow gradient with perturbations, and medium ties intermediate curves with more marked perturbations.
- 3.4
- Strong and staged agents simulations produced a power law (or J curve) distribution of ties. The distributions were skewed towards a few stronger relationships, with a mid-range showing high variation in trust values, then a long tail of low-trust relationships with less variation. The layered distributions, with a small number of strong ties, a few more medium ties, followed by many weak ties after the gradient change in the curve, conformed approximately to SBH predictions with total ties N = 150 in agent populations of 200 and 300 with moderate waning (0.05) and defection rates (0.01).
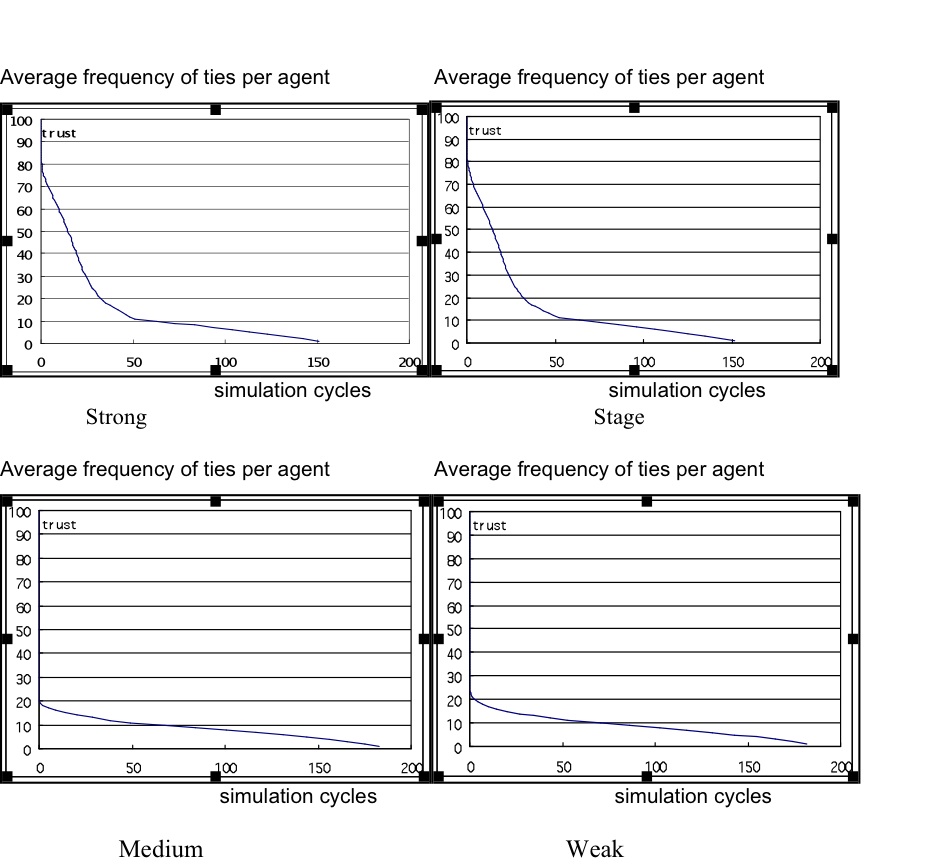
Figure 1. Sample simulation result for average (strong/medium/weak) ties per agent for each trust model version, showing the number of ties over 2000 simulation cycles - 3.5
- As expected, medium- and weak-tie strategy agents produced flatter distributions with little variation between relationships at their preferred strength (see Figure 1), while the strong and staged strategy agents contributed more strong- and medium-tie relationships. This suggests that strong and staged strategies are better explanations for social preferences to create the intimacy layers required by SBH.
- 3.6
- The trust-based model produced SBH distributions with an upper limit of circa 150 overall ties per ego within a range of population sizes from 200 to 500. The simulation shows that the number of overall relationships appears to be a function of agents' partner-preference strategy, and the trust increase/waning model.
 Natural Selection of Strategies
Natural Selection of Strategies
- 4.1
- To extend the previous behaviour-time simulations across generations into evolutionary timescales, we investigated how well each strategy would survive given fitness criteria of wellbeing, as a benefit of social interaction and relationships, and resource acquisition as the benefit accruing from foraging and finding food. Two hypotheses explored by the fitness criteria were:
- A few intimate social relationships will improve wellbeing more than many less intimate relationships.
- Many weaker relationships will improve food-finding capability by providing more information sources. This conjecture is based on Granovetter's (1973) view of the value of weak ties.
- 4.2
- Two fitness functions were defined:
Wellbeing
The fitness for wellbeing (WB) for the ith ego (i is the index of egos) is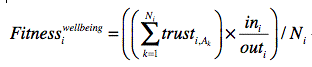
where Ni is the number of total ties for ego i, trustI,Ak is the trust from ego i to the jth tie (where j is the index of ties for the ith ego), ini is the total number of interactions from other agents to ego i, and outi is the total number of interactions from ego i to other agents.
Resource
The fitness for resource (R) for the ith ego is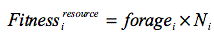
where Ni is the number of total ties for ego i and foragei is the total number of foraging turns for ego i. Food resource benefits from foraging turns were augmented by the number of ties per ego to model the benefit of weak ties providing information that could subsequently improve the ego's ability to find food. This function favours egos with more weak ties.
- 4.3
- Both functions were evaluated after a lifetime of 2000 interaction cycles. Fitness functions were ranked with selection operating on summed weighted ranks. Selection eliminated the weaker 20% of the population using summed ranks of both fitness criteria. Breeding replaced the agents by replicating individuals drawn at random from the top 20%. Mutation and crossover were included in later simulations (see Discussion section below); here we assessed fitness and competition. The initial population was set at N = 300 with equal numbers of the four strategies: strong, medium, weak ties and staged.
- 4.4
- Trust model parameters were taken from the optimal SBM fit simulation:
- Log increase/linear decrease
- MC ratio on increase = 10
- Waning rate = 0.08
- 4.5
- We took the SBH pattern of relationships as a goal and investigated the set of waning and defection parameters, fitness functions and social strategies that produced simulations matching the observed SBH structure. Two independent variables were tested:
- The forage:meeting (FM) ratio which changed the ratio of turns for each agent from 1:1 to favour either more time spent socialising or more time spent foraging.
- The fitness criteria pay-off for wellbeing and resources, set as a ratio to weight the fitness ranking algorithm.
- 4.6
- Over a range of FM ratios from 1:8 to 2:1 varying the resource:wellbeing ratio (R:WB) from 3:1 to 1:3, two patterns of results emerged with a R:WB tipping point around 1:1.5. Ratios favouring wellbeing all produced good-fit SBH layers, while ratios favouring resource created too many weak ties and too few strong and medium ties. The best fit SBH distribution occurred with R:WB = 1:3 and FM = 1:4, although strong and medium ties were slightly higher than the ideal SBH range (strong ties 6-7 vs SBH 5; medium ties 16-17 vs SBH 15). FM ratios 1:1 or more favourable to foraging all produced too many weak ties, and a range of R:WB settings from 10:1 to 1:1 favoured resource. The model requires frequent social interactions to enable trust and relationships to develop, and as long as turns are biased towards social interaction, relationship development persists over a range of fitness trade-offs, although a high bias towards resource fitness will overcome development of strong ties, as illustrated in Figure 2 for average ties per agent; and Figure 3, agents' survival by strategy.
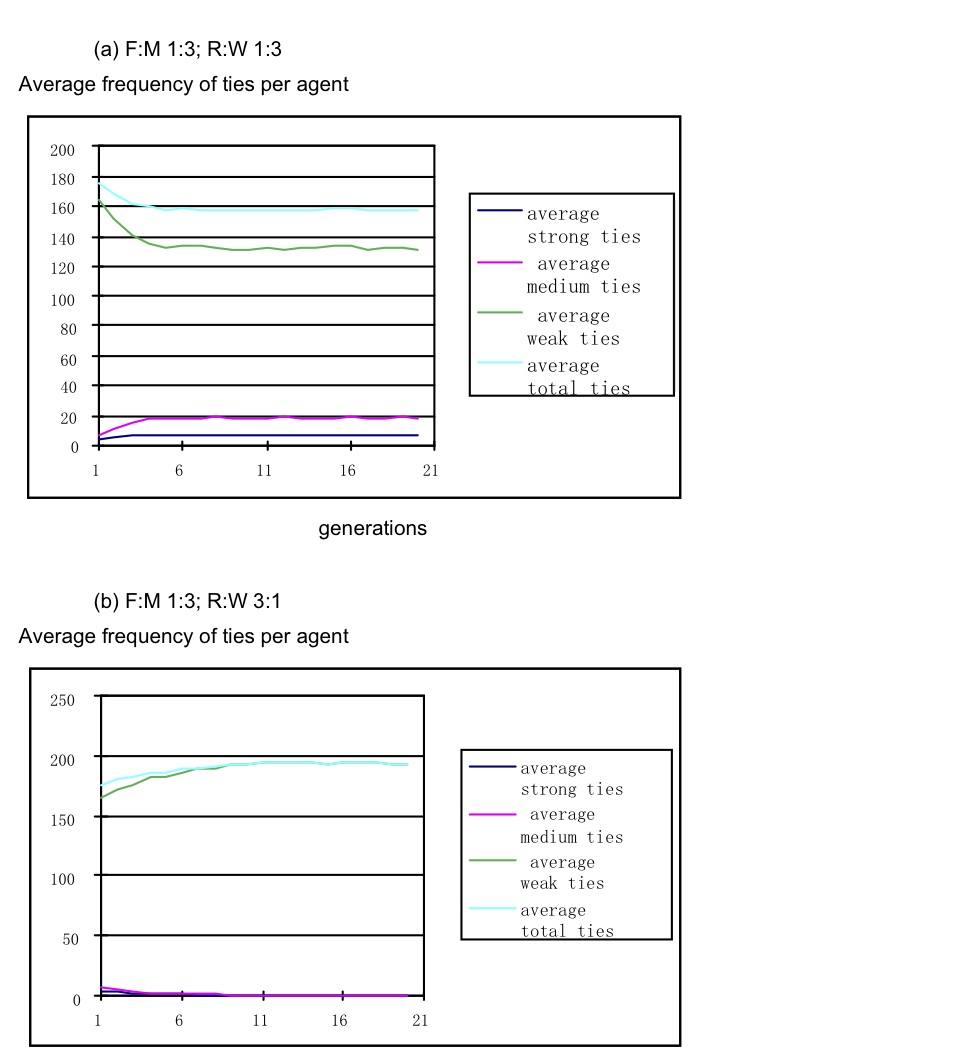
Figure 2. Average ties per ego in SBH layers with optimal objective function settings FM (1:3) and R:WB (1:3) 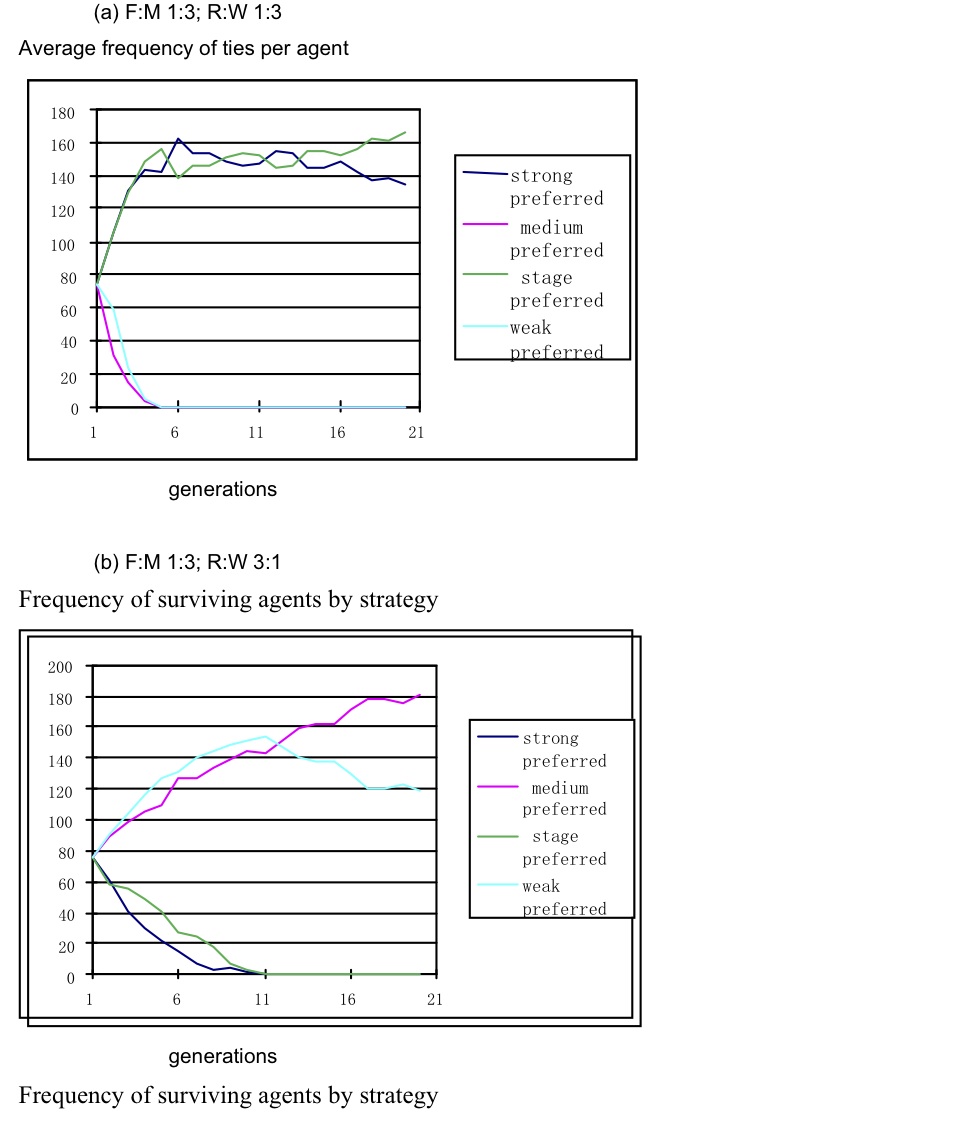
Figure 3. Survival of agents in a simulation. Average ties/ego and the agent strategies surviving over 20 generations with 10% defects, F:M 1:3 and RW 1:3 - 4.7
- When the FM ratio was 1:1 or more favourable, all simulations within the range of neutral to resource-favouring R:WB settings produced too few strong and medium ties and too many weak ties. Over the range of simulations, strong and staged were the more successful strategies, even in simulations that produced mainly weak ties (see Table 1).
- 4.8
- Weak and medium ties were only competitive when both the fitness criteria and the FM ratio were biased in favour of resources.
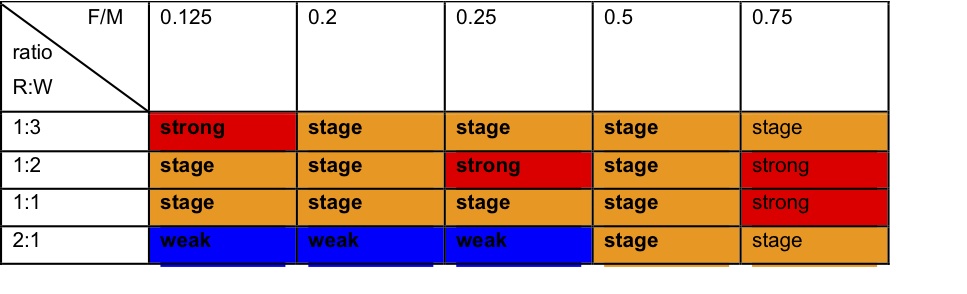
Table 1. Dominant strategies in the simulation runs, varying fitness criteria R (resource) WB (wellbeing) weights and agent behaviour by the F (forage) M (meet) ratio reflecting time spent foraging or socialising. - 4.9
- The simulations produced an approximation to the SBH predictions for the total number of social relationships over a range of parameters; however, the best fit to N = 150 total ties per ego was only observed when the FM ratio was 1:3 in favour of social interaction (see Table 2).
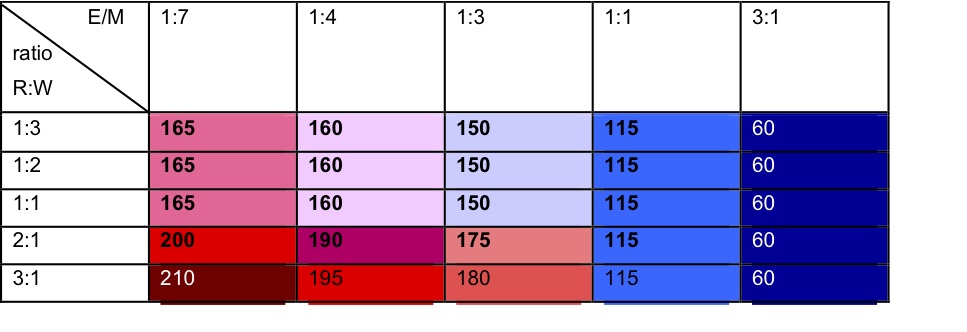
Table 2. Total ties observed in the simulations, with the same criteria and agent setting as in Table 1. - 4.10
- Lower FM ratios do not produce sufficient opportunity for relationships to develop, while high ratios favouring more social interaction produce excessive numbers of ties and a maximally networked population (i.e. circa 290+ relationship/ego in a population of 300).
- 4.11
- The same results were obtained with a larger population size, N=500, although the optimal MC and WR parameters for SBH were MC=20, WR =0.18, as trust in relationships developed more slowly in larger populations since interactions were distributed over more individuals.
Adding Kin to the Model
- 4.12
- In Dunbar's model, relationships may be either friends (non-kin) or related alters (kin). SBH does not predict how many kin will be present in each relationship layer; instead, it appears that kin and non-kin may substitute for each other at each level as if they compete for a set number of slots in the best friends (5-6), and close friends (15) layers (Dunbar & Spoors 1995; Roberts et al. 2009). To investigate this aspect of SBH, kin were introduced into the simulation as pre-set strong ties by assigning them high-trust values before the simulation began. Kin relationships were also carried forward to the next generation modelling parent-offspring as well as sibling kinship.
- 4.13
- Adding up to five kin did not affect the SBH distribution: the kin relationships just substituted for the emergence of strong ties. Even when kin ties were seeded at a lower level of trust equivalent to medium ties, the same result was observed. The strong kin ties were preserved by preferential treatment by the waning function irrespective of the focal agent's strategy. Their existence at the onset of the simulation biased the probability distribution of the staged and strong-ties strategies to favour reinforcing kin ties rather than forming new strong ties; hence the simulation model follows empirical evidence that kin appear to substitute for best friends within inner SBH layers. If more than 5 kin were introduced, the number of strong ties increased marginally to 6-7 and this was partially sensitive to the number of initial strong kin ties, but numbers did not increase much beyond 8-9 strong ties, indicating that the model self-limits too many strong relationships even if more kin are available.
Effect of Defections
- 4.14
- Defections decreased the number of strong and medium ties approximately in proportion to the defect rate. Low rates (≤5%) had a minor effect, reducing strong ties from 5-6 to an average 4-5 and medium ties from 16-17 to 14-15. As expected, a symmetrical impact, when both partners lose trust, was higher than asymmetric, when only the initiator/trustor loses (A loses when B defects). There was little difference between linear and log impact on trust, probably because defections were relatively infrequent. Higher defection rates reduced strong ties to an average 2-3, with medium ties averaging 11-12, although the strong and staged strategies remained competitive.
- 4.15
- The results showed 'tipping points' when FM and RWB settings changed from SBH concordant outputs to a preponderance of weak ties, following the same pattern as models without defections, suggesting that the SBH model and agent strategies tolerate moderate defection rates and show small deviations from the SBH pattern as defection rates increase.
 Competition between Strategies
Competition between Strategies
- 5.1
- To explore a more explicit evolutionary process, we used a simulation of a genotype with three genes each with four alleles:
- Social preference strategy: strong-, medium-, weak-tie preferences and staged as defined previously
- Social time predisposition: forage:meet/socialise ratio, 4 settings <8:1, 5:1, 4:1, 1:1>
- Social cooperativeness: defect ratio for the alter on social interaction, 4 settings <0.01, 0.025, 0.05, 0.075>
- 5.2
- Simulations were run with cross-over only and with cross-over and mutation. The cross-over rate was 0.9; one gene was selected at random per breeding cycle, and for the selected gene, pairing was random. Mutation was random on pseudo-continuous distributions for:
- FM range 0.125..0.5, (i.e. 8:1..1:1 ratios) divided into 1000 intervals
- Defect range 0.01..0.075, divided into 1000 intervals
- with a rate of 0.01 on all genes.
- 5.3
- R:WB ratios favouring resource (10:1, 5:1) produced stable populations after 50 generations with approximately 120 alters per ego, with very few strong or medium ties. Weak and medium tie strategies dominate, while the FM ratio rapidly stabilised at 0.5 and the defect rate at 0.02. An even R:WB weighting produced a similar outcome, although strong and staged strategies dominate and some strong (1) and medium ties (7) are produced, while defection approaches the minimum value 0.01. The SBH conformant result appears with R:WB ratio 1:5; see Figure 4. The number of ties/ego is slightly high for each SBH layer (total 160, with 20 medium and 7 strong), agents with the stage and strong strategies progressively spread in the population, while FM and defections are driven towards the lower extremes of their ranges: FM 0.15, defections 0.01.
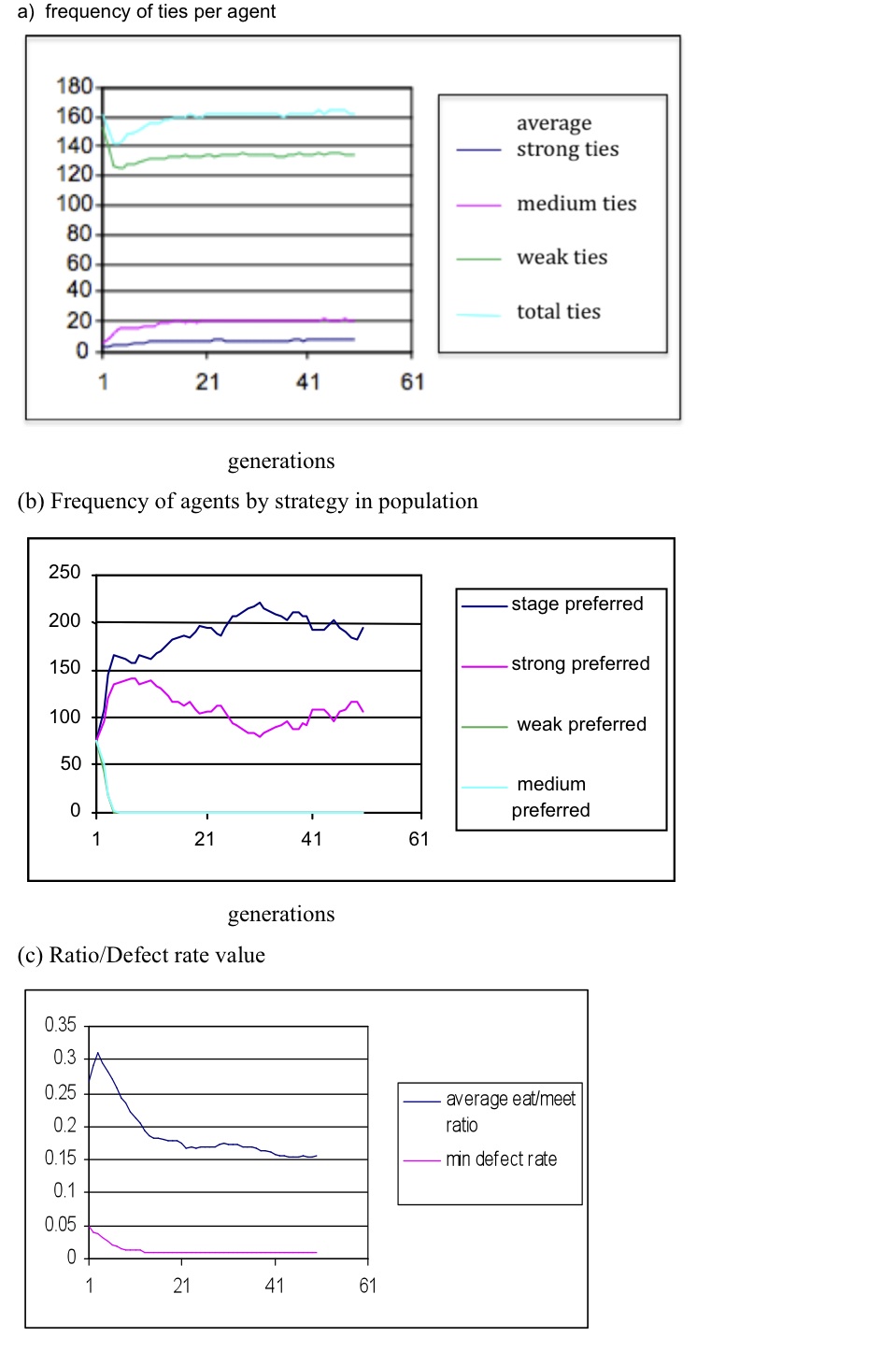
Figure 4. Survival of agents over 50 generations with equal seed populations and R:WB weightings 1:5 - 5.4
- When R:WB weightings are biased even more favourably in the social wellbeing direction, slightly more ties in each layer (e.g. ST 7-9, MT 20-22, Total ties 165) are produced with more marked selection pressure to reduce defections and increase social interactions at the expense of foraging. The tipping point between SBH-compliant and non-compliant simulations appears to be in the region of R:WB 1:5 to 1:6, although given the stochastic nature of selection a mix of non-compliant and compliant results appears from R:WB 1:3 to 1:9, with an increased frequency of compliant runs which dominate >50% within 50 runs where ratios were >1:5 in favour of WB.
- 5.5
- Since the strong and staged strategies were competitive over a wide range of fitness criteria, we tested their ability to spread in a population of weak-tie agents. When populations were seeded with 1% strong and 1% staged agents in a population of weak-tie agents with FM and defect gene settings assigned at random using a roulette algorithm, both strong and staged spread rapidly to dominate the population within 10-20 generations. The model outputs (see Figure 5) were the same as found in equal seed populations with SBH conforming patterns being produced when R:WB weightings were 1:5 or better and the weak tie dominant pattern in 1:1 or more resource-favourable ratios. As before, the FM ratio stabilised at 0.5 while the defect rate was driven down towards the minimal setting with an average 0.05. The same result was produced with 0.5 % seed populations of stage and strong agents, so it appears these strategies have a strong competitive advantage over a range of fitness criteria.
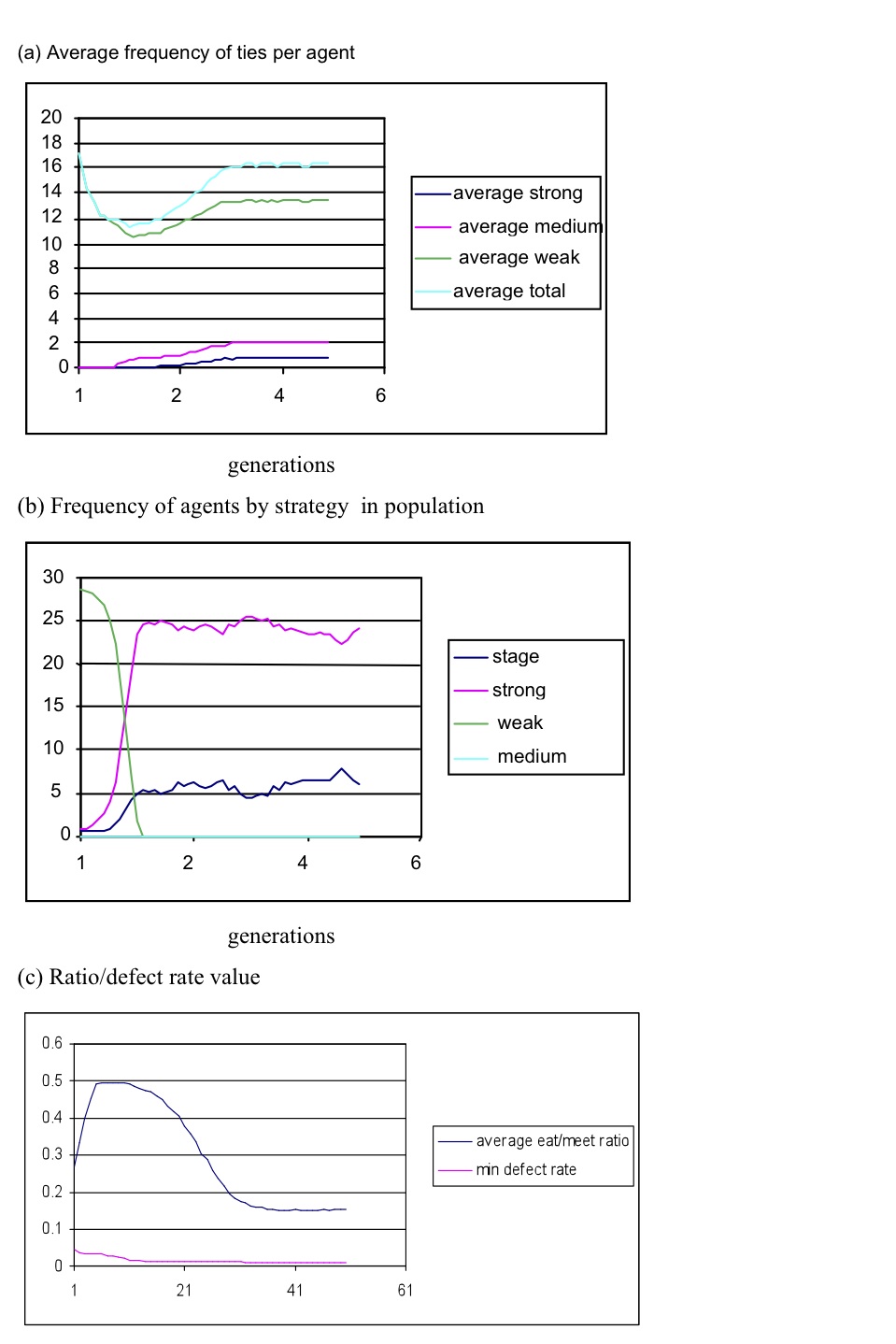
Figure 5. Survival of agents over 50 generations with 1% seed populations of strong and staged agents - 5.6
- Since the evolutionary simulations produced slightly different SBH patterns than the simulations with selection but no breeding, we examined a range of breeding manipulations. Crossover-only runs produced slightly better SBH conformant results, with similar FM and defect rate results. Mutation only with an initial homogeneous FM population set at 0.5 produced run-away increases in FM genes to favour foraging, with an average ratio of 0.7 on a mutation range 0 to 1.0; however, defection rates did not spread with similar initial settings and ranges.
- 5.7
- Multiple simulation runs (50) with tipping point R:WB 1:5 setting produced 22% non-SBH compliant results with weak-tie agents dominating and F:M ratios stabilising at 0.5 from an initial average 0.25. The other 78% were SBH-compliant with the staged strategy dominating with strong in 22 runs; strong dominating with staged in 12; and in five runs both strategies were approximately equal. In all these SBH-compliant runs, F:M ratios decreased from 0.25 to levels varying from 0.2 to 0.15, the latter being more frequent. As might be expected, multiple runs in the R:WB range of 1:1 to 1:10 produced a high proportion of SBH-compliant results as the ratio favoured wellbeing fitness with <5% non-compliant at 1:8 and zero at 1:10. These results suggest two evolutionary-stable scenarios: when fitness rewards foraging and feeding, populations become dominated by individuals that favour weak social ties and spending more time foraging; conversely, as wellbeing is favoured, populations are dominated by the social strategy favouring fewer stronger relationships, although weak ties also develop.
- 5.8
- Since our model was biased against defections, as there was little reward for increased defection, so a final manipulation explored increasing the opportunity cost reward of defection by giving defectors more foraging turns. Extra foraging turns (1,2,5,10) for each defection modelled the opportunity gained as additional feeding/foraging time by forgoing social interaction. The model was stable, producing a similar pattern as before, with SBH runs dominating when R:WB ratios were 1:5 or more favourable for WB. The distribution of ties per ego and the dominance of strong and stage strategies continued with higher defectors being eliminated until the defect reward was 5 additional foraging turns. At 5 or above, weak tie-high defector individuals were progressively more competitive even with R:WB ratios of 1:5 and above. Defector strategies therefore need a considerable reward to compete with social investment strategies.
 Discussion and Conclusions
Discussion and Conclusions
-
Properties of the Model
- 6.1
- The contribution of the model presented in this paper is to provide a software simulation tool for exploring the evolution of social strategies and social relationships. The tool provides a causal account for the development of complex social structures based on agent populations with different strategies governing how they manage trade-offs between social v. foraging time and social preferences to favour either the few or the many. Development of social structure could be investigated under a range of fitness conditions for a Wellbeing objective function which was rewarded by social interaction and Resource rewarded by foraging behaviour. The model was based on previous work which implemented a trust-modulated algorithm with logarithmic functions governing the relationship between interaction frequency and relationship strength (or trust) to model plausible behavioural assumptions for a law of diminishing returns for increasing interaction frequency on strengthening relationships, while also making stronger relationships more resilient to waning.
- 6.2
- The social:feeding contrast in the model could be satisfied by any pair of state variables that had the characteristics defined in the model. For example the variables don't have to be time budget components, just things that affect fitness in different ways that have costs to acquire or perform. Hence the model provides a mechanism for investigating a variety of contrasts between evolutionary pressures (or fitness functions) within a meeting - interaction - partner choice paradigm. While evolution of social structure and social relationship formation are the main foci of the model, it has the following more general properties which can be applied to modelling social phenomena:
- The probabilistic function for selection of alter agents can be parameterised towards different areas in the frequency distribution of prior interactions for the focal agent. This facilitates expression of different social preference strategies.
- The relationship between change in relationship strength and interaction frequency is parameterised to set the rate of change. This enables assumptions contained in the underlying trust model to be changed from log to linear increase/decrease.
- Fitness functions can be weighted to investigate a range of evolutionary selection pressures
- The initial population of agents, and their strategies, can be specified to explore survival of different population sizes and strategy mixes.
- Mutation rates, cross-over rules and frequency, and selection rates are all parameterised to facilitate sensitivity analysis of social structures under different reproductive and selection conditions.
- Cycles per generation and number of generations can be changed to explore different combinations of behavioural time (cycles) and evolution.
- Outputs are: (a) relationships per ego ranked by strength aggregated for the whole agent population; in tercile (strong, medium, weak) categories of the distribution for each cycle; (b) frequencies of agents by strategy surviving across generations; (c) totals of agents surviving after N generations aggregated across several model runs which varied fitness conditions; (d) social structures defined by distributions of strong/medium/weak ties aggregated across several model runs which varied fitness conditions, to enable cross-referencing to composition of surviving agents (see (c)).
Sociological Assumptions
- 6.3
- The model produced insight into plausible behavioural processes by which the distribution of relationships predicted by SBH might arise. The agent strategies implicit in SBH, favouring fewer stronger ties and the staged developmental strategy that favoured stronger ties earlier and more weaker ties later, produced results that best matched observed relationship distributions. These strategies are supported by empirical observations of human social relationships in which bands of best/close friends and less intimate casual friends (Baumeister & Leary 1995; Brown & Brown 2009; Hays 1989); and by empirical studies on relationships in a variety of societies (Hill & Dunbar 2003; Wellman et al. 2001, 2006; Zhou et al. 2005). Our model suggests that relationship layers based on a discrete distribution of emotional closeness can arise from social strategies favouring strong relationships within an envelope of parameter settings for waning and uncooperative responses.
- 6.4
- Social strategies (strong and staged) are highly competitive and invade populations from a low baseline; furthermore, they are robust and survive over a range of fitness criteria, even when defection is rewarded with a considerable opportunity/cost compensation. The model's tipping point of resource:wellbeing ratio 1:5 is of course arbitrary; however, these settings do have plausible justification insofar as ecological studies of social behaviour show that humans devote more time to social interaction, compared to other activities, than do other primates (Dunbar et al. 2008). Furthermore, the reward for wellbeing may be more important than feeding resource gain, since the social compensation of wellbeing fitness should be manifest not only in stress reduction, but also in increased survival of offspring as well as predator protection (Dunbar 2010; Shultz et al. 2004). The simulation indicates that the pattern of human relationships predicted by SBH and supported by the friendship literature may only arise in a small part of the parameter range which represents proportionately higher rewards for investing in social behaviour rather than foraging. This agrees with the observed ratio of social:foraging time, which is higher in humans than in other species, probably due to more efficient food gathering (Dunbar et al. 2009; Lehmann et al. 2007, 2008). Of course, these findings are constrained by the modelling assumptions, i.e relationships are simulated according to two forms of relationship sustaining dynamics, linear accumulation of strength from interaction frequency and a slow decaying function in which trust is implicit. Although our model does not directly distinguish between feeding time and resource gain as explored in optimal foraging models, the effect of the trade-off between social time and foraging will still be present.
- 6.5
- Kin and close friends play a similar role in our model, substituting for each other in competition for a limited number of 'slots' in the support and sympathy layers, which agrees with empirical observations. This suggests that inclusive fitness in the shared genetic kin sense (Hamilton 1964), may also apply to close friends where the benefits of reciprocity may have driven evolutionary predispositions to favour the few. However, whether such predispositions arise from social learning or longer-term genetic predisposition is a difficult issue to ultimately resolve, as demonstrated by debates in the evolutionary psychology literature (Tooby & Cosimides 1989). Our contribution is to illustrate how an evolutionary process could produce predispositions which underlie observed human social structures, with a plausible account of how the role of cognition in the form of trust might produce observed stratification of strong-, medium- and weak-ties relationships.
- 6.6
- Although we have demonstrated that SBH could evolve in social groups via simple social relationship strategies such as favour-the-few and a trust mechanism underpinning relationship formation, there are alternative explanations for the emergence of human social groups, although no rival theories explain the observed intimacy layers in human relationships. For example, a rival explanation for social cooperation is alliance formation for hunting, intergroup competition and predatory protection. Alternatively, 'favour-the-few' strategies might arise from social learning, if rewards from cooperation and reduced tension are apparent to reinforce learning, or imitation in social learning (Laland & Brown 2011; Tooby & Cosimides 1989; Whiten et al. 2011); however, social learning of such preferences should produce a concentration of strong ties to the exclusion of weaker ties, which is clearly not the case. Even if differential rewards are posited to argue for the strategies we propose arising from cognitive learning processes, variation in human social relationship structures across societies might be expected since the reward environment is unlikely to be uniform. Considerable evidence supports the SBH assertion that social relationship layers are remarkably similar across populations (Dunbar 2008, 2010; Dunbar & Schultz 2007; Dunbar & Spoors 1995). This argues for genetic predispositions. Nevertheless, we intend to explore the tension between socio-cultural and alternative genetic predispositions in our future research.
Related Research
- 6.7
- Simulation of the emergence of complex social networks in agent populations with strategies governed by exchange theory and social learning of relationship preferences (Pujol et al. 2005) is related to our simulation of social preferences; however, Pujol and colleagues modelled the emergence of social networks rather than the social structure of our model, which presents an aggregate view of social relationships within a population rather than a topology of relationships. The emergence of social predispositions within agent populations has been modelled for costly signalling theory, which originally explained trade-off between benefits accruing from signalling in mate selection set against the predation costs; this was adapted by Wildman and Sosis (2011) to investigate display trade-offs and group stability in human culture with different configurations of leaders' charisma and susceptibilities of other group members.
- 6.8
- Agent-based models of cooperation and social relationships have been motivated by a wide variety of contexts; for example, the balance between reward cooperation and punishment for anti-social behaviour in public goods games (Ye et al. 2011), collaboration in peer-to-peer networking systems with ranking schemes for agent selection (Yu et al. 2004), the development of trust in inter-organisation relationships (Kim 2009), and the extensive literature on the biological evolution of cooperation. Macy and Skorvetz (1998) showed that trust could evolve among strangers in local groups in simulations with reputation assessment strategies and options to cooperate, defect or refuse to participate. Others (Boyd & Richerson 1988, Nowak & Sigmund 2005) have demonstrated that reputation mechanisms (i.e. indirect reciprocity) can lead to formation of individual preferences underlying social relationships. However, most models were concerned with the tension between cooperation v. defection strategies rather than the evolution of complex social structures.
- 6.9
- Segmentation of social relationships into different intensities also emerges from simulations of interaction in social networks (Whitmeyer 2002). Whitmeyer assumed that time spent in social interaction influences relationship strength, and developed a social network model to predict the agents' social relationships showing that a few more intense relationships emerge at the expense of more diffuse ties, with optima similar to SBH (N=5). Whitmeyer adapted Heider's balance theory's constraint (Heider 1946) that too many connected friends increases the probability of conflict, and hence reduces trust. Risk of conflict may provide a constraint-based alternative explanation for the favour-the-few strategy; however, it does not explain the structure of medium and weak ties. Our investigations have extended previous models which demonstrate that social network structures emerge either when preferences for trustworthy individuals are present (i.e. 'cliquers': Whitmeyer 2002), or knowledge of altruistic and cooperative behaviour is spread in social networks as a collective memory (Mohtashemi & Mui 2003). However, in contrast to previous RPD models, we have demonstrated how a computational model of trust and social behaviour predispositions can lead to the emergence of social structures conforming to empirical studies of human friendship (Hays 1989; Oswald et al. 2004).
Limitations and Future Developments
- 6.10
- Our current model does not account for spatial effects, which have been modelled by Beltran et al. (2006) who demonstrated that groups can emerge from interactions within a lattice topology as a consequence of agents' preferences to maintain personal or social space.Defections are currently modelled as a global parameter, whereas in RPD social cooperation models, defection governs selection of social partners. Although we demonstrated that the SBH model was robust in the face of an increased reward for defecting, we did not use memory of previous defections as an influence in choosing social partners. Also our current model assumes an ego network view so the consequences for relationship development of interactions across a whole social network were not considered. Only two objective functions are currently considered - wellbeing and resources - which may be a limited view of the selection pressures on social relationships; for instance, more closer relationships increase stress and relationships expose individuals to risks when they have to reciprocate favours in alliances (Sutcliffe et al. 2012). In future we will extend the model with objective functions to explore the trade-off between negative (risk/stress) and positive (wellbeing) selection pressures.
 Acknowledgements
Acknowledgements
- This research was supported by ESRC/EPSRC Cognitive Foresight Programme project TESS, developing Theory for Evolving Socio-technical Systems. RD's research is also funded by the British Academy Centenary Research Project, the EU-FP7 SocialNets project and the EU-FP7 ICTe-Collective Project.
 References
References
-
AKERMAN, J.M., Kenrick, D.T. & Schaller, M. (2007). Is friendship akin to kinship? Evolution and Human Behaviour, 28, 365-374. [doi:10.1016/j.evolhumbehav.2007.04.004]
ARROW, H., McGrath, J.E. & Berdahl, J.L. (2000). Small groups as complex systems: Formation, coordination, development and adaptation. Thousand Oaks CA: Sage Publications.
BAUMEISTER R.F. & Leary, M.R. (1995) The need to belong: Desire for interpersonal attachments as a fundamental human motivation. Psychological Bulletin, 117(3), 497-529. [doi:10.1037/0033-2909.117.3.497]
BELTRAN, F.S., Salas, L. & Quera, V. (2006). Spatial behavior in groups: An agent-based approach. Journal of Artificial Societies and Social Simulation, 9(3),5 https://www.jasss.org/9/3/5.html
BOYD, R. & Richerson, P.J. (1988) The evolution of reciprocity in sizable groups. Journal of Theoretical Biology, 132, 337-356. [doi:10.1016/S0022-5193(88)80219-4]
BROWN, S.L. & Brown, R.M. (2009) Selective investment theory: Recasting the functional significance of close relationships. Psychological Inquiry, 17, 1-29. [doi:10.1207/s15327965pli1701_01]
BUYS, C.J. & Larson, K.L. (1979). Human sympathy groups. Psychology Reports, 45, 547-553. [doi:10.2466/pr0.1979.45.2.547]
DUNBAR, R.I.M. (1993) Coevolution of neocortex size, group size and language in humans. Behavioral Brain Sciences, 16, 681-735. [doi:10.1017/S0140525X00032325]
DUNBAR, R.I.M. (1998) The Social Brain Hypothesis. Evolutionary Anthropology, 6, 178-190. [doi:10.1002/(SICI)1520-6505(1998)6:5<178::AID-EVAN5>3.0.CO;2-8]
DUNBAR, R.I.M. (2008) Mind the gap: Or why humans aren't just great apes. Proceedings British Academy, 154, 403-423.
DUNBAR, R.I.M. (2010) Brain and behaviour in primate evolution. In P.H. Kappeler & J. Silk (Eds) Mind the gap: tracing the origins of human universals, 315-330. Berlin: Springer. [doi:10.1007/978-3-642-02725-3_15]
DUNBAR, R. & Shultz, S. (2007). Understanding primate brain evolution. Philosophical Transactions of the Royal Society London, 362B, 649-658. [doi:10.1098/rstb.2006.2001]
DUNBAR, R.I.M. & Spoors, M. (1995) Social networks, support cliques, and kinship. Human Nature, 6, 273-290. [doi:10.1007/BF02734142]
DUNBAR, R.I.M., Korstjens, A. & Lehmann, J. (2009) Time as an ecological constraint. Biological Reviews, 84, 413-429. [doi:10.1111/j.1469-185X.2009.00080.x]
GRANOVETTER, M. (1973) The strength of weak ties. American Journal of Sociology, 78, 1360-1380. [doi:10.1086/225469]
GRANOVETTER, M. (1985) Economic action and social structure: The problem of embeddedness. American Journal of Sociology, 91, 481-510. [doi:10.1086/228311]
HAMILTON, W.D. (1964) The genetical evolution of social behaviour, I and II. Journal of Theoretical Biology, 7, 1-16, 17-52. [doi:10.1016/0022-5193(64)90039-6]
HARDY, C.L. & Van Vugt, M. (2006) Nice guys finish first: The competitive altruism hypothesis. Personality and Social Psychology Bulletin, 32, 1402-1413. [doi:10.1177/0146167206291006]
HAYS, R.B. (1989) The day-to-day functioning of close versus casual friendships. Journal of Social and Personal Relationships, 6, 21-37. [doi:10.1177/026540758900600102]
HEIDER, F. (1946) Attitudes and cognitive organization. Journal of Psychology, 21, 107-112. [doi:10.1080/00223980.1946.9917275]
HILL, R.A. & Dunbar, R.I.M. (2003) Social network size in humans. Human Nature, 14, 53-72. [doi:10.1007/s12110-003-1016-y]
HILL, R.A., Bentley, A. & Dunbar, R.I.M. (2008) Network scaling reveals consistent fractal pattern in hierarchical mammalian societies. Biology Letters, 4, 748-751. [doi:10.1098/rsbl.2008.0393]
HRUSCHKA, D.J. & Henrich, J. (2006) Friendship, cliquishness, and the emergence of cooperation. Journal of Theoretical Biology, 239, 1-15. [doi:10.1016/j.jtbi.2005.07.006]
KIM, W.-S. (2009). Effects of trust on complex adaptive supply networks: An agent-based simulation study. Journal of Artificial Societies and Social Simulation, 13(3),4 https://www.jasss.org/12/3/4.html
LALAND, K.N. & Brown, G.R. (2011). Sense and nonsense: Evolutionary perspectives on human behaviour, 2nd ed. London: Oxford University Press.
LEHMANN, J., Korstjens, A.H. & Dunbar, R.I.M. (2007). Group size, grooming and social cohesion in primates. Animal Behaviour, 74, 1617-1629. [doi:10.1016/j.anbehav.2006.10.025]
LEHMANN, J., Korstjens, A.H., & Dunbar, R.I.M. (2008). Time management in great apes: Implications for gorilla biogeography. Evolutionary Ecology Research, 10, 515-536.
LU, Y.-E., Roberts, S., Lio, P., Dunbar, R. & Crowcroft, J. (2009). Size matters: Variation in personal network size, personality and effect on information transmission, CSE, International Conference on Computational Science and Engineering, 4, 188-193. doi: 10.1109/CSE.2009.179' , 2009. [doi:10.1109/CSE.2009.179]
MACY, M.W. & Skvoretz, J. (1998). The evolution of trust and cooperation between strangers: A computational model. American Sociological Review, 63(5), 638-660. [doi:10.2307/2657332]
MADSEN, E., Tunney, R., Fieldman, G., Plotkin, H., Dunbar, R.I.M., Richardson, J. & McFarland, D. (2007). Altruism and kinship: A cross-cultural experimental study. British Journal of Psychology, 98, 339-359. [doi:10.1348/000712606X129213]
MCPHERSON, M., Smith-Lovin, L., & Brashears, M.E. (2006) Social isolation in America: Changes in core discussion networks over two decades. American Sociological Review, 71, 353-375. [doi:10.1177/000312240607100301]
MOHTASHEMI, M. & Mui, L. (2003) Evolution of indirect reciprocity by social information: the role of trust and reputation in evolution of altruism. Journal of Theoretical Biology, 223(4), 523-531. [doi:10.1016/S0022-5193(03)00143-7]
MORELAND, R.L. & Levine, J.M. (1982). Socialization in small groups: temporal changes in individual-group relations. In L. Berkowitz (Ed.) Advances in experimental social psychology, 15. New York: Academic Press.
NOWAK, M. & Sigmund, K. (1998) Evolution of indirect reciprocity by image scoring. Nature, 383, 537-577. [doi:10.1038/31225]
NOWAK, M. & Sigmund, K. (2005) Evolution of indirect reciprocity, Nature, 437, 1291-1298. [doi:10.1038/nature04131]
OSTROM, E. (2002) Towards a behavioural theory linking trust, reciprocity and reputation. In E. Ostrom & J. Walker (Eds), Trust and reciprocity: Interdisciplinary lessons from experimental research, 19-79. New York: Russel Sage Foundation.
OSWALD, D.L, Clark, E.M. & Kelly, C.M. (2004) Friendship maintenance: An analysis of individual and dyad behaviours. Journal of Social and Clinical Psychology, 23(3), 413-441. [doi:10.1521/jscp.23.3.413.35460]
PUJOL, J.M., Flache, A., Delgado, J. & Sangüesa, R. (2005) How can social networks ever become complex? Modelling the emergence of complex networks from local social exchanges. Journal of Artificial Societies and Social Simulation, 8(4), 12 https://www.jasss.org/8/4/12.html
REICHER, S.D., Spears, R. & Postmes, T. (1995). A social identity model for deindividualisation phenomena. European Review of Social Psychology, 6, 161-198. [doi:10.1080/14792779443000049]
REMPEL, J.K., Holmes, J.G. & Zanna, M.P. (1985). Trust in close relationships. Journal of Personality and Social Psychology, 49(1), 95-112 [doi:10.1037/0022-3514.49.1.95]
ROBERTS, S.B.G. & Dunbar, R.I.M. (2011) Communication in social networks: Effects of kinship, network size and emotional closeness. Personal Relationships, 18(3), 439-452. [doi:10.1111/j.1475-6811.2010.01310.x]
ROBERTS, S.B.G. & Renwick, J.S. (2003) The development of cooperative relationships: An experiment. Proceedings of the Royal Society of London, 270, 2279-2283. [doi:10.1098/rspb.2003.2491]
ROBERTS, S.B.G., Dunbar, R., Pollet, T. & Kuppens, T. (2009) Exploring variations in active network size: Constraints and ego characteristics. Social Networks, 31, 138-146. [doi:10.1016/j.socnet.2008.12.002]
ROSASA, A. (2010) Evolutionary game theory meets social science: is there a unifying rule for human cooperation? Journal of Theoretical Biology, 264(2), 450-456. [doi:10.1016/j.jtbi.2010.02.015]
ROSE, S. & Serafica, F. (1986) Keeping and ending casual, close and best friendships. Journal of Social and Personal Relationships, 3(3), 275-288. [doi:10.1177/0265407586033002]
SHULTZ, S., Noe, R., McGraw, S. & Dunbar, R.I.M. (2004) A community-level evaluation of the impact of prey behavioural and ecological characteristics on predator diet composition. Proceedings of the Royal Society of London, 271B, 725-732. [doi:10.1098/rspb.2003.2626]
STILLER, J. & Dunbar, R. (2007). Perspective-taking and social network size in humans. Social Networks, 29, 93-104. [doi:10.1016/j.socnet.2006.04.001]
SUTCLIFFE, A.G. & Wang, D. (2012). Computational modelling of trust and social relationships, Journal of Artificial Societies and Social Simulation, 15(1), 3. https://www.jasss.org/15/1/3.html
SUTCLIFFE, A., Dunbar, R.I.M., Binder, J. & Arrow, H. (2012). Relationships and the social brain: integrating psychological and evolutionary perspectives. British Journal of Psychology (in press). [doi:10.1111/j.2044-8295.2011.02061.x]
TAJFEL, H. & Turner, J.C. (1979). An integrative theory of intergroup conflict. In W. Austin and S. Worchel (Eds), The social psychology of intergroup relations. Monterey CA: Brooks/Cole.
TOOBY, J. & Cosimides, L. (1989) Evolutionary psychology and the generation of culture, I: theoretical considerations. Ethology and Sociobiology, 10, 29-49. [doi:10.1016/0162-3095(89)90012-5]
TUCKMAN, B.W. (1965). Developmental sequence in small groups. Psychological Bulletin, 63, 384-399. [doi:10.1037/h0022100]
WELLMAN, B. & Wortley, S. (1990) Different strokes from different folks: Community ties and social support. American Journal of Sociology, 96, 558-588. [doi:10.1086/229572]
WELLMAN, B., Haase, A.Q., Witte, J. & Hampton, K. (2001) Does the internet increase, decrease, or supplement social capital? American Behavioural Scientist, 45, 436-455. [doi:10.1177/00027640121957286]
WELLMAN, B., Hogan, B., Berg, K., Boase, J., Carrasco, J.A., Côté, R., Kayahara, J., Kennedy, T. & Tran, P. (2006) Connected lives: the project. In P. Purcell (Ed.) Networked neighborhoods. Berlin: Springer. [doi:10.1007/1-84628-601-8_8]
WHITEN, A., Hinde, R., Laland, K.N. & Stringer, C. (2011) Culture evolves. Philosophical Transactions of the Royal Society B, 366, 938-948 [doi:10.1098/rstb.2010.0372]
WHITMEYER J.M. (2002) A deductive approach to friendship networks. Journal of Mathematical Sociology, 26(3), 147-165. [doi:10.1080/00222500212989]
WILDMAN, W.J. & Sosis, R. (2011) Stability of groups with costly beliefs and practices. Journal of Artificial Societies and Social Simulation, 14(3), 6. https://www.jasss.org/14/3/6.html
YAMAGASHI, T., Cook, K.S. & Watabe, M. (1998) Uncertainty, trust and commitment formation in the United States and Japan. American Journal of Sociology, 104(1), 165-194. [doi:10.1086/210005]
YE, H. Tan, F., Ding, M., Jia, Y. & Chen, Y. (2011) Sympathy and punishment: Evolution of cooperation in public goods game. Journal of Artificial Societies and Social Simulation, 14(4), 20. https://www.jasss.org/14/4/20.html
YU, B., Singh, M.P. & Sycara, K. (2004), Developing trust in large-scale peer-to-peer systems, IEEE First Symposium on Multi-Agent Security and Survivability, 30-31, 1-10, Los Alamitos: IEEE Computer Society Press.
ZHOU, W., Sornette, D., Hill, R.A. & Dunbar, R. (2005) Discrete hierarchical organization of social group sizes. Proceedings of the Royal Society of London, 272B, 439-444. [doi:10.1098/rspb.2004.2970]