 Abstract
Abstract
- In current research there is increasing evidence on why and how common-pool resources are successfully, i.e. sustainably, managed without the force of (often unsuccessful) top-level policy regulations. G. Hardin argued in 1968 in his Tragedy of the Commons (Hardin 1968) that commons must become depleted if users are free to choose extraction and resource use levels. In this study, we propose that socio-psychological factors can explain the success of resource use of a common without any top-level regulations. We exemplify this behavior by a spatio-temporally dynamic agent-based model of the Tragedy of the Commons using behavioral game theory and Nash equilibria calculation. By providing a spatio-temporal representation of Hardin's dilemma, the model could verify his argument in a temporal way if socio-psychological influence is disregarded, and indicated that under its influence the common can be sustained. We illustrated how dispositions such as cooperativeness, positive reciprocity, fairness towards others, and risk aversion broadly can support sustainable use, while negative reciprocity, fairness towards oneself, and conformity can inhibit it. Though, we also showed that it would be dangerous to generalize this kind of behavior, as changes in one of these dispositions can result in opposite system behavior, in dependence on the other dispositions. Due to this general capacity to account for such complex behavior that real common-pool system usually exhibit, and its ability to model intermediate equilibria, the proposed modelling approach, i.e. combining game-theory solution concepts with agent-based modelling, may be worth an assessment of its capacity to model empirical phenomena.
- Keywords:
- Agent-Based Model, Common-Pool Resources, Behavioral Game Theory, Nash Equilibria, Nash Extension NetLogo, Socio-Psychological Dispositions, Tragedy of the Commons
 Introduction
Introduction
- 1.1
- Since 1968, when G. Hardin published his article on the Tragedy of the Commons (Hardin 1968), there is a growing interest in understanding the failures and successes of the sustainability of shared resource use. In his example of a medieval pasture, Hardin argued, based on findings from game theory and insights of free-riding behaviour, that with insufficient policy regulations the pasture will become depleted, as the damage of overgrazing is shared among the players, while the benefits remain unshared. Following Hardin (1968), the benefit for a herdsman of increasing his cattle stock is a function of his cattle stock increment (e.g. net income), while the corresponding cost is a function of the additional overgrazing created by the increment. Despite wide acceptance of this image based on game theory and the problem of free-riding, numerous field-based studies showed that these conventional theories often failed to explain the many world-wide cases of sustainable and successful common-pool resource use (Ostrom et al. 1999). For the purpose of this study, we will call a system successful if system resources are used sustainably, and unsuccessful otherwise.
- 1.2
- To come closer to a realistic picture of those situations, Poteete, Janssen and Ostrom (2010) mention behavioural game theory - instead of conventional game theory - as one of the tools to better explain empirical cases of successfully managed common-pool resources. Among others, behavioural game theory attempts to integrate factors in conventional game theory that account for socio-psychological dispositions such as altruism, trust (e.g. Snijders 1996), inequity aversion (e.g. Fehr and Schmidt 1999) and reciprocity (e.g. Rabin 1993; Fehr and Gächter 2000). However, as a still young science, behavioural game theory tended to focus on specic dispositions instead of combining them. In this study, we therefore propose a model that integrates several dispositions frequently mentioned in research on common-pool resource use dilemmas, as summarized by Ebenhöh and Pahl-Wostl (2006), including fairness towards others and oneself, cooperativeness, conformity, positive and negative reciprocity and risk aversion. We integrated these dispositions in a strategic game equivalently to the way as Fehr and Schmidt (1999) did for feelings of fairness, and embedded the game in an agent-based model in NetLogo replicating the Tragedy of the Commons as closely as possible to Hardin's description.
- 1.3
- In our approach we use a solution concept (i.e. Nash equilibria calculation) within the agent-based model to solve the strategic game in each simulation time step. For this purpose, a NetLogo Nash calculation extension was written in Java, while the model is flexible to use other possibly more realistic solution concepts if corresponding extensions are created. The model then allows us not only to test the effect of different combinations of heterogeneous socio-psychological dispositions on resource extraction, but also the evolution of the (yet abstract) human-environment system over time. Model results show that the inclusion of socio-psychological dispositions in the Tragedy game can lead to non-linear emergent patterns of sustainable and unsustainable resource extraction, while without them, the common will be depleted, as prognosticated by Hardin.
- 1.4
- In Section 2 we will present a short overview on the background and rationale of our modelling purpose, while Section 3 will provide a detailed description of the model which allows its replication. Section 4 will deal with simulation results, and conclusions are given in Section 5.
 Background and Rationale
Background and Rationale
- 2.1
- In his powerful image of the Tragedy of the Commons, Hardin described a pasture open to all, in which it is to be expected that each herdsman will try to keep as many cattle as possible on the common. Hardin further assumed that, as a rational being, each herdsman seeks to maximize his gain. Therefore, each herdsman will always decide to add cattle to the pasture, as Hardin argues that the benefits of the herdsman's cattle increment, which remain individual, outweigh the costs induced by the additional overgrazing of the increment, which are shared due to the open-access nature of the pasture, ultimately leading to total depletion (Hardin 1968).
- 2.2
- However, increasing awareness of the prevalence of anomalies fostered the study of contradictory evidence by new research methods from a variety of disciplines. Among, them, the prominent initiative of the Common-Pool Resource (CPR) research program at Indiana University by Elinor Ostrom had the goal to develop better conceptual foundations for explaining success and failure of CPR systems, based on the screening of hundreds of related documents. However, in the end, the idea of identifying the specic rules that tended to generate success needed to be dropped (Poteete, Janssen and Ostrom 2010). One diagnosed that the complexity of common-pool resource systems impedes the identification of determinants for failure and success in jointly used resource environments (e.g. Schlager et al. 1994, Ruttan 2006 and 2008).
- 2.3
- Agent-based modelling (ABM) is a by now well-known approach to study complex phenomena. The main aim of such models is to identify the set of assumptions of micro-level mechanisms under which macro-level patterns evolve, such as cooperation in commons dilemmas (Poteete, Janssen and Ostrom 2010). However, agent-based models have usually been used in related research on cooperation as tools to determine to which equilibrium the modelled system converges over time while agents are learning (e.g. Krause et al. 2006; Bunn and Oliveira 2001), but not the other way round, i.e. to determine agents' actions via solution concepts. As the choice of decision-making algorithm is often a critical issue in ABM, we argue that such purely mathematical and universal decision-making concepts provide more unbiased representations of human decision making, being independent on the respective school of thought. Moreover, such a solution concept is robust enough to allow the integration of additional factors that explain cooperation, such as we propose in this article. We do so by following the approach of Fehr and Schmidt (1999) who integrate dispositions explaining psychological influences in the cooperation decision of the respective game, while we use the conventional Nash equilibrium to solve the game.
- 2.4
- We hypothesize i) that we can replicate the argument by Hardin (1968) by an ABM model in the setting he proposed, i.e. by assuming no psychological influences in the cooperation decision, ii) that psychological influences in the cooperation decision can explain cooperation, iii) and that the relation between a socio-psychological disposition and the cooperation decision can be non-linear and is dependent on the other disposition values, which would be in line with the findings by (Poteete, Janssen and Ostrom 2010) who found that the identification of specific rules explaining success/failure is hampered by the complex and non-linear behaviour of common-pool resource systems.
- 2.5
- The approach to solve games repeatedly by Nash equilibria calculation, which is still the most widely used solution concept for strategic games (Izquierdo and Gotts 2005), can be justified by the acceptable but simplified assumption that strategies of agents converge to a Nash equilibrium over each of the (annual) simulation time steps. Due to the lack of universally accepted equilibria refinement methods, whose choice can lead to contradictory results (Rasmusen 1989), and following our (arguable) view that the type of equilibrium is sensitive to unpredictable incidents or choice of learning mechanisms (e.g. in evolutionary game theory), we decided to test our model under the assumption that agent behaviour converges to a random but at least weakly Pareto-optimal equilibrium.
 Materials and Methods
Materials and Methods
-
A Multi-Agent System for the Tragedy Of the Commons (MASTOC)
- 3.1
- The Multi-Agent System of the Tragedy Of the Commons (MASTOC) was programmed in NetLogo 4.0.2 (Wilensky 1999) and is available online at www.openabm.org. It consists of a virtual landscape made up of a grid (33 × 33) of pixels/patches representing the pasture, non-mobile agents representing herdsmen, and mobile agents representing cattle owned by the herdsman agents, which are both initially randomly distributed on the landscape. In each time step, herdsmen agents modify their number of cattle agents on the pasture, cattle agents graze, and grass regrows, these processes forming a repeated time loop.
Variables
- 3.2
- Each agent i, i = 1, …, N, is endowed with two variables, ki ∈ ℕ, indicating the number of cattle owned and grazing in the current time step, and ai ∈ {-1, 0, 1}, the action the herdsman agent takes in each time step, corresponding to whether he removes a cattle agent from the pasture (-1), changes nothing (0), or adds a cattle agent (1). The cattle agents are endowed with an owner variable indicating the owning herdsman agent (owner ∈ {1, …, N}) and a feeding status (feedstat ∈ ℕ) indicating the number of patches browsed in the current time step. The patches are characterized by a variable (cover ∈ {"no grass", "grass"}) indicating whether the patch is covered by grass or not, whereby the cover of a browsed patch is turned from grass to no grass. Global (i.e. non-agent) variables include the price of a cattle agent (P ∈ ℝ), and the number of patches covered with grass (Veg ∈ {0, …, 1089}).
External parameters
- 3.3
- External parameters of MASTOC that can be set by the user comprise i) the number of patches each cattle agent needs to browse to survive in each time step (Requ ∈ ℕ \ {0}), ii) the net relative grass growth rate near zero vegetation (rate ∈ ℝ+ \ {0}), a constant for the used logistic growth function, iii) the total number of herdsman agents (N ∈ ℕ \ {0}), iv) the number of cattle agents for each agent i at time step zero (ki0 ∈ ℕ), v) the percentage of patches covered by grass at time step zero (Cov0 ∈ {0, 1, … ,100}), and vi) the overall values of the seven socio-psychological dispositions, comprising the tendency for cooperative behaviour (levelcoop), the tendency to prefer actions that reduce unfairness towards the playing agent (levelfairself), the tendency to prefer actions that reduce unfairness towards other agents (levelfairother), the tendency to execute negative reciprocal behaviour (levelnegrecip), the tendency to execute positive reciprocal behavior (levelposrecip), the tendency to conform with others (levelconf), and the tendency to avoid risky actions (levelrisk), all ∈ (0, 1), indicating to what degree these dispositions are existent in the herdsman agent population. For simplicity, here we assume uniform disposition values over the population, but they can be easily implemented heterogeneously for each agent.

Table 1. Explanations and domains of model parameters 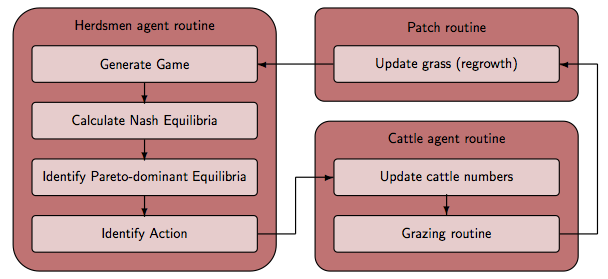
Figure 1. Annual simulation time loop of MASTOC Model setup
- 3.4
- After initialization, where the cover of Cov0 % of patches are set to grass and agents are generated, the model repeatedly runs through an annual time loop, represented by one simulation step (see Figure 1). The herdsman agent routine is the decision-making routine in which the ai are determined. To do so, the payoffs for the current game are calculated, and the game is solved via Nash equilibria calculation, being restricted to only weakly Pareto-optimal equilibria, among which a random equilibrium is chosen. Once such an equilibrium is chosen, the corresponding action ai for each agent i is calculated, the agent's number of cattle ki updated, and cattle agents start browsing grass patches in the cattle agent procedure. Grass regrows at the end of the time loop in the patch procedure, updating the cover variable. Complete details and equations are given below.
Herdsman agent routine
Generate game
- 3.5
- Strategic games are defined as games that have three components: a set of players, for each player a set of strategies, and additionally a payoff function indicating how desirable each game outcome is for the player. A strategic game is therefore fully described by the determination of payoffs for each agent for each possible combination of their actions (x1, … , xN), xj ∈ {-1, 0, 1}. Therefore, a payoff function Fi: (x1, … , xN) → pi , pi is payoff of agent i, needs to be determined. Following the approach by Fehr and Schmidt (1999), who apply a second function on a given payoff function in order to bias payoffs for fairness of payoff distribution, we develop first a basic payoff function without any biases by socio-psychological dispositions, and then apply the secondary bias functions, which we developed for MASTOC.
- 3.6
- We defined the basic payoff function to resemble Hardin's description, i.e. that the cost of a herdsman agent's action is a function of the additional overgrazing induced by his action, the function considering the divisive nature of overgrazing costs, while the benefit of the agent's action is a function of the agent's action itself. Given Hardin's vague definition of these functions, we defined the following payoff function, being dependent not only on the increment but also on the current cattle stock (equation 1).
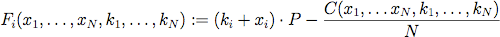
(1) where C (x1 , … , xN) is the cost function, representing the monetary loss/increase of grazing capacity in the next time step caused by increased/reduced grazing pressure in the current time step:
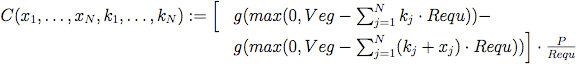
(2) with g the vegetation update function
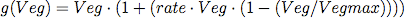
(3) with Vegmax = 1089 (total number of patches).
- 3.7
- We then define pibasic (x) := Fi (x1 , … , xN) as the basic payoff for agent i, x = (x1 , …, xN), upon which the secondary functions are applied representing the biases induced by the socio psychological dispositions. The dispositions that we selected correspond to those in Ebenhöh and Pahl-Wostl (2006), who propose seven socio-psychological dispositions that characterize people's individual inclination towards cooperation in social dilemmas. These include cooperativeness, negative and positive reciprocity, feelings of fairness towards the player himself and others, risk aversion, and conformity.
Cooperativeness
- 3.8
- Equivalent to the denition of cooperativeness in Ebenhöh and Pahl-Wostl (2006), cooperativeness defines the importance of group utility compared to individual utility. According to equation 4, maximum cooperativeness (levelcoop = 1) leads to the replacement of an agent's basic payoff by the sum of all agents' basic payoffs, while for levelcoop = 0 the agents' payoffs remain unchanged. pi coop (x) is the corresponding convex linear combination of these mappings, dependent on levelcoop (equation 4). Thus, intuitively, levelcoop is the tendency to favour actions that support group benefit instead of personal benefit.
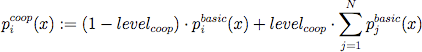
(4) pi coop (x) is used as a basis for the subsequent calculations. For each of the remaining dispositions, a value will be added to picoop (x), each having a maximum possible value of one time the basic payoff pibasic (x). This calibration ensures that we have an equitable weighing system for the remaining dispositions. The final payoff function pifinal that determines the final game is defined as:
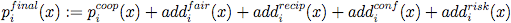
(5) where addifair (x), addirecip (x), addiconf (x) and addirisk (x) are the respective values representing the biases induced by feelings of fairness, reciprocity, conformity and risk aversion.
Fairness
- 3.9
- The calculation of addifair (x) was adopted from Fehr and Schmidt (1999) (equation 6) who propose that players experience inequity if they are worse off in material terms than the other players, and they also feel inequity if they are better off. The parameter levelfairself ∈ [0, 1] determines thus the tendency to refrain from actions that make the agent worse off than others, while levelfairother ∈ [0, 1] determines the tendency to refrain from actions that make the agent better off. For example, if all have equal basic payoffs, nothing is subtracted from the basic payoffs, regardless of the selected levels. If an agent has lower basic payoff than all others, his basic payoff is reduced, dependent on the payoff differences to others and the degree to how important these differences are (i.e. levelfairself).
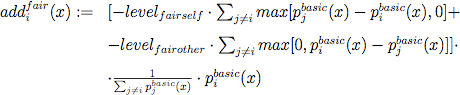
(6) Reciprocity
- 3.10
- The mapping addi recip (equation 7) is dependent on two parameters, levelnegrecip ∈ [0, 1], denoting the disposition to respond with negative actions to negative actions of others in the previous round, and levelposrecip ∈ [0, 1] the disposition to respond with positive actions to positive actions of others, respectively. Intuitively, the value of levelnegrecip can be interpreted as the tendency to choose actions that penalize others, e.g. if all other herdsman agents added a cattle agent in the previous round, and the tendency to taking revenge is maximum (i.e. levelnegrecip = 1), the basic payoff for adding a cattle agent in the current round is doubled. Similarly, the value of levelposrecip can be interpreted as the tendency to choose actions that reward others, e.g. if half of the other herdsman agents reduced their cattle stock in the previous round, and the tendency for rewarding is medium (i.e. levelposrecip = 0.5), the basic payoff for also reducing the cattle stock in the current round is increased by 25%.
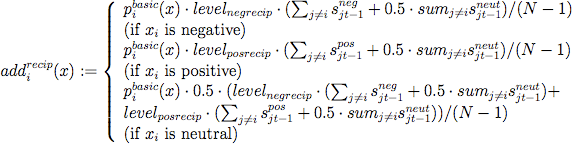
(7) where
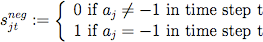
(8) 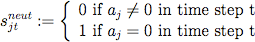
(9) 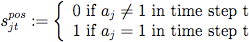
(10) Conformity
- 3.11
- Conformity describes behaviour that is in accordance with past behaviour of the herdsman agents as a group, with levelconf being the tendency to favour actions similar to past group behaviour. The mapping addi conf is calibrated in such a way that it has a maximum of pibasic(x) for a given x, as for the other dispositions. For example, if all herdsman agents increased their cattle stock in each time step in the past and levelconf = 1, the basic payoff for increasing the cattle stock in the current time step is doubled. If half of all past actions involved no change of cattle stock, a quarter an increase, and another quarter a decrease, while levelconf = 0.4, the basic payoff for no change in the current time step is increased by 20%, while the basic payoffs for the other two actions are increased by only 10%.
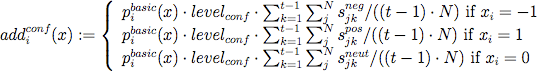
(11) Risk aversion
- 3.12
- We define risk aversion as the level to which losses are avoided, with levelrisk being the tendency to favor actions that minmize potential losses. For an action xi of agent i, we define the risk of selecting this action (riski (xi)) as the minimum basic payoff that agent i can get under the condition that he plays action xi (equation 12). We then based the calculation of addi risk (x) on this notion of risk (equations 13 and 14). Intuitively, if levelrisk is at maximum (=1), there is an increased tendency to choose the action that minimizes risk, i.e. that action that has the highest minimum payoff. This increased tendency is reflected by a doubling of the basic payoff for that specific action, while the basic payoff for the other actions remain unchanged. The lower levelrisk, both the less pronounced is the focus on the most riskless action, and the less is the change of the basic payoffs.
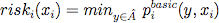
(12) where A = {-1, 0, 1}, y is defined as the vector (x1 , … , xi-1, xi+1 , … , xN), Y := AN-1, and pibasic(y,xi) := pi basic (x).
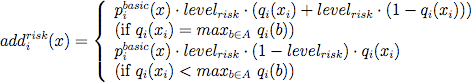
(13) where
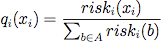
(14) Game solution and choice of action
- 3.13
- To determine the actual choice among alternatives of this game, we used Nash equilibria calculation. A Nash equilibrium is defined as a vector of strategies (s1* , … , sN*) for which no player can benefit by changing his or her strategy from si* unilaterally, that is
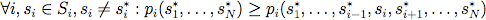
(15) where Si is the set of strategies and pi the payoff function for player i. Nash showed that all game matrices have at least one equilibrium strategy, but this strategy might be mixed (Nash 1951), a mixed strategy being a probability distribution that assigns to each available action a likelihood of being selected.
- 3.14
- As NetLogo, in which we implemented MASTOC, does not provide a tool for calculating Nash equilibria, we programmed a NetLogo extension in Java, using the gambit-enumpoly Nash calculation program of the open-source Gambit software, version 0.2007.01.30. Gambit is software for doing computation on finite, non-cooperative games developed by McKelvey, McLennan and Turocy (2004). From this open-source software, we extracted the executable UNIX file gambit-enumpoly, which reads a strategic game on standard input and computes Nash equilibria by solving systems of polynomial equations and inequalities. The NetLogo Java extension was programmed to convert the game file produced by MASTOC to a gambit-readable format, execute the Nash equilibrium calculation via gambit-enumpoly, and convert the output to a file format readable by NetLogo.
- 3.15
- Problematic is the fact that in many cases several Nash equilibria exist among which a choice must be made. Therefore, modellers must usually apply equilibrium refinement methods, e.g. restricting to strong equilibria or weakly Pareto-optimal equilibria, rule out strongly dominated strategies, or use iterated dominance (Rasmusen 1989). However, there is no single way for refinement, and it is up to modellers to make appropriate choices for their purposes. In MASTOC, we chose the restriction to weakly Pareto-optimal equilibria, an equilibrium a* being weakly Pareto-optimal if there is no equilibrium a' such that a' strongly Pareto dominates a*, i.e.:
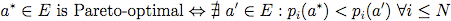
(16) where E is the set of equilibria. We then determined the action ai for each agent i corresponding to a random Pareto-dominant equilibrium.
Cattle agent routine
- 3.16
- According to the selected action ai of herdsman agent i, the number of cattle owned by agent i is updated, i.e. a random cattle agent is either removed (if ai = - 1), added (if ai = 1), or kept the same (if ai = 0). Next, each cattle agent moves and browses patches:
while (feedstat < Requ and any patches with cover = grass) [ move to nearest patch with cover = grass set cover no grass set feedstat (of cattle agent) feedstat + 1 ] if (feedstat < Requ) remove cattle agent
This removal process is independent of the herdsman agent decision-making process, but is an automatized reaction of the herdsman agent to remove cattle if after the browsing routine the cattle agents have not been fed adequately. We assume that insufficiently fed cattle can be sold in time, thus involving no cost for the herdsman agent, but simply reducing his cattle stock.Patch routine
- 3.17
- Noy-Meir (1978) suggests that for the type of simplified pasture like the one that we assume here (i.e. a pasture consisting of one plant species grazed by a herbivore population with a constant physiological status of intake), the growth rate of green biomass can be described by a function, dependent on green biomass, which increases at a low biomass level, and decreases at a high level. This way, the cost of degradation can be incorporated in the model. Noy-Meir (1978) proposes four growth functions that fulll these requirements, among them the logistic growth function that we used in MASTOC (see equation 3). However, different growth functions can theoretically be built into the model.
- 3.18
- The cover variable of patches is updated by:
- Update variable Veg
- Ask (g(Veg) - Veg) patches with cover = no grass: set cover grass
 Results
Results
- 4.1
- The purpose of this section is to test via simulations with MASTOC the hypotheses, i.e. i) that we can replicate the argument by Hardin (1968), ii) that psychological influences in the cooperation decision can explain cooperation, iii) and that the relation between a socio-psychological disposition and the cooperation decision can be non-linear and is dependent on the other disposition values. The first two hypotheses are tested by the scenarios Scen-P-0 (with absence of psychological influence), and Scen-P-1 (with those disposition values set to their maximum value that we suggest to have a positive influence on sustainable resource use) (Table 2) under varying values of the remaining parameters (Figures 2 and 3). Then we show via gradual shift of a mixed scenario Scen-M-1 (Table 2) that the dispositions behave in the intuitive manner proposed, and that intermediate equilibria of resource use are possible (Scen-M-0), which should reflect the model's realism. Finally, we test the third hypothesis, thereby giving an idea that cooperation is "a highly complex, variegated, and fragile phenomenon" (Macy and Flache 2002). For all scenarios, for simplicity and to increase computation speed we assumed a population of three herdsman agents, which can be justified by the fact that probes of simulations with up to eight agents showed comparable results. Each scenario was run 43 times in order to have a confidence interval of 95% and a maximum relative difference of 10% of the true success value, i.e. the true percentage of successes of the respective scenario. The estimated success value required to calculate the sample size was set to 0.1 respectively 0.9, which both lead to the same sample size. The sample size was sufficient to verify the hypotheses.
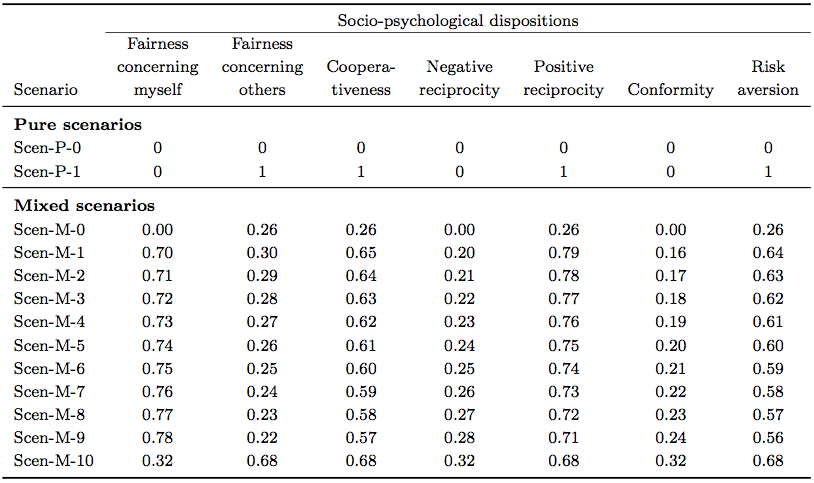
Table 2. Values of socio-psychological dispositions for simulated scenarios Simulation of extreme scenarios
- 4.2
- In order to account for the argument that the settings of the other external parameters might influence system behaviour, comprising initial grass cover (Veg) and number of cattle agents of each agent (ki), forage requirement (Requ), and grass growth rate near zero (rate) (see Table 1), we test both extreme scenarios Scen-P-0 and Scen-P-1 under combinations of different settings of these parameters. For this, we conducted simulations under all combinations of the following selected settings:
- Forage requirement: Requ = 1 and 2
- Initial grass cover: 100% and 50%
- Grass growth rate near zero: rate = 0.0010 and 0.0005
- Initial number of cattle agents for the three agents: (k1 , k2 , k3) = (1,1,1), (10,10,10), and (5,15,25)
- 4.3
- Simulations showed that under any of these combinations the common will be depleted in the extreme scenario Scen-P-0 (i.e. exclusion of dispositions) (Figure 2), which is in remarkable accordance with the prognostication by Hardin. The influence of the proposed initial conditions is confined to only the speed with which the common becomes depleted. We can therefore conclude that if only the monetary value of a payoff is considered, being unbiased by social and psychological phenomena, whose consideration we propose here, the sustainable use of the common will be predicted to fail, at least for the parameter settings that we tested in MASTOC.
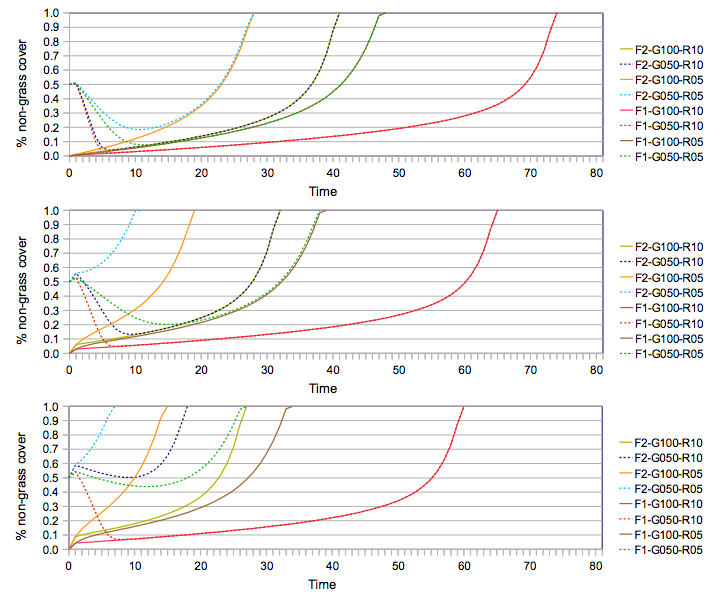
Figure 2. Simulated means of percentage of non-grass cover during time of Scen-P-0, for initial cattle stock settings (1,1,1) (top), (10,10,10) (middle), and (5,15,25) (bottom). F = forage requirement, G = initial percentage of grass cover, R = growth rate near zero vegetation - 4.4
- For the other extreme scenario Scen-P-1 we set the values of those dispositions to their maximum value, which we suggest to influence successful resource use in a positive way. These comprise i) fairness towards others, as a high value of this disposition may lead to the reduction of the agent's cattle stock if he is better off than others, ii) cooperativeness, which, if at maximum, leads to collectivized payoff thus reducing the incentive of free-riding, iii) positive reciprocity, which inherently leads to a tendency to reduce the cattle stock if others do so, and iv) risk aversion, which we assume to influence the risk aversion towards cost of degradation positively.
- 4.5
- Simulations of this scenario Scen-P-1 under all combinations of the other external factors as defined above showed that the common is sustainably used in a constant (i.e. no-cycled) equilibrium (Figure 3). In most of these equilibria, the cattle population remains stable at six to nine cattle agents, whereby a few of the more extreme cases even lead to a total removal of the cattle stock. However, the simulations showed that the integration of a disposition-based bias can lead to success of common-pool resource use, as hypothesized.
Simulation of mixed scenarios
- 4.6
- We illustrate via a scenario family that the dispositions generally behave in the inutitive manner outlined above, i.e. that fairness towards others, cooperativeness, positive reciprocity, and risk aversion are positively related to success of the common, while fairness towards oneself, negative reciprocity, and conformity are negatively related. For this purpose, we selected a plausible mixed scenario that leads to success (Scen-M-1), and created a scenario family (Scen-M-2 - Scen-M-9) by gradually shifting each disposition value towards its "unsuccessful" value, that is, to shift those dispositions that we consider to be positively related to success towards their minimum value, while shifting the other towards their maximum. The result shows a clear breakdown of the common during the shift (Figure 5). Furthermore, it is notable that the equilibria in the stable scenarios are characterized by cycles (Figure 4) whose amplitudes steadily increase in the scenario sequence from Scen-M-1 to Scen-M-5. A possible explanation for these cycles is that if the system has the tendency for degradation an upward movement is created, which may be stopped and reverted in time by the positive forces or dispositions before the common has reached a threshold where degradation is irreversible.
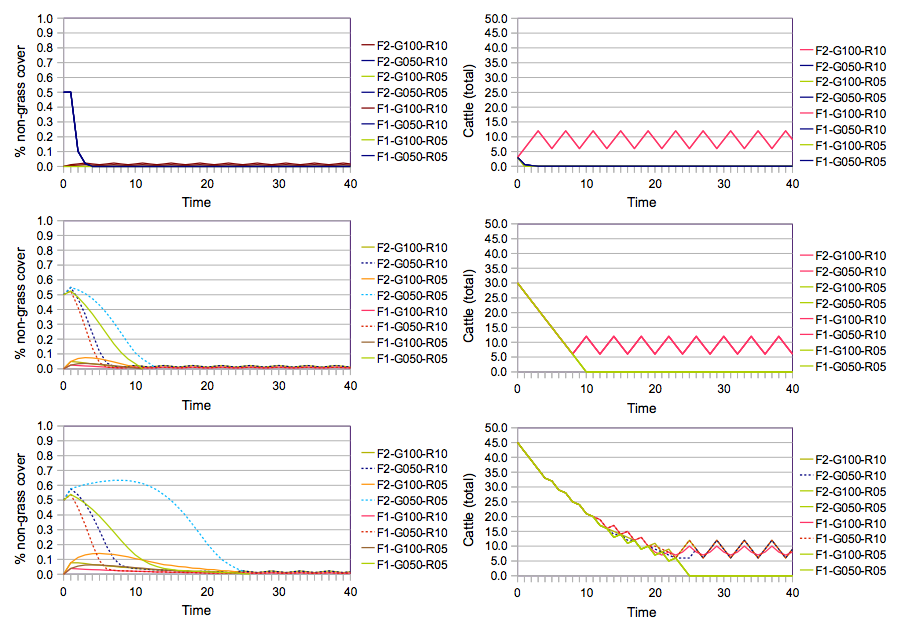
Figure 3. Simulated means of percentages of non-grass cover (left) and cattle stock (right) during time of Scen-P-1, for initial cattle stock settings (1,1,1) (top), (10,10,10) (middle), and (5,15,25) (bottom). F = forage requirement, G = initial percentage of grass cover, R = growth rate near zero vegetation - 4.7
- In general, the scenario family was chosen to provide a relatively plausible representation of a real human population, being characterized by higher fairness towards oneself than fairness towards others, which intuitively makes sense from an evolutionary perspective, relatively high cooperativeness and higher positive reciprocity than negative reciprocity, which both reflect a general good will of human, and low conformity but high risk aversion (Table 2). All scenarios in this family were simulated under 100% initial grass cover, a forage requirement of 2 patches/cattle agent per year, a grass growth rate near zero vegetation of 0.0010, and an unfair initial cattle stock distribution of 5, 15, and 25 cattle agents.
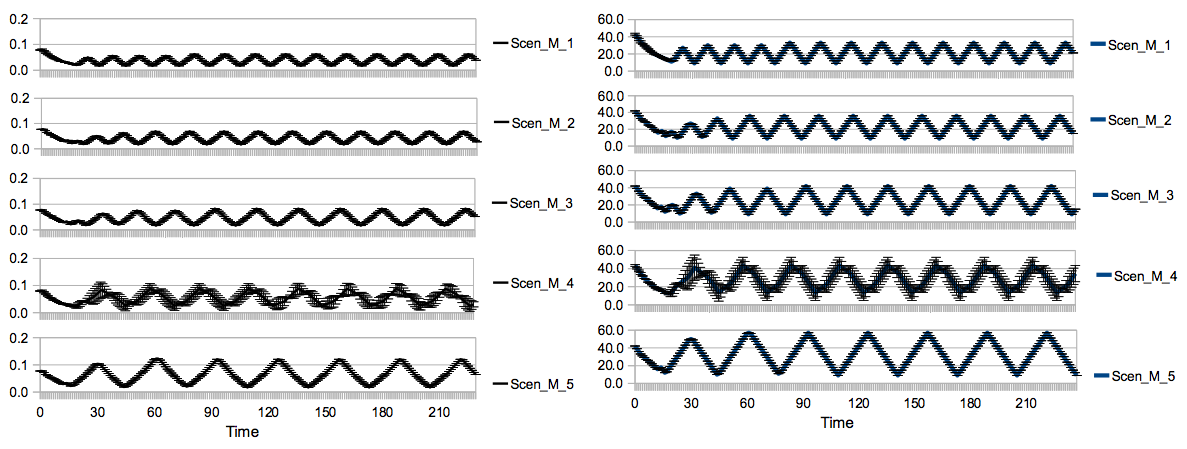
Figure 4. Simulated means and standard deviations of percentage of non-grass cover (left) and total cattle stock (right) during time of Scen-M-1 to Scen-M-5 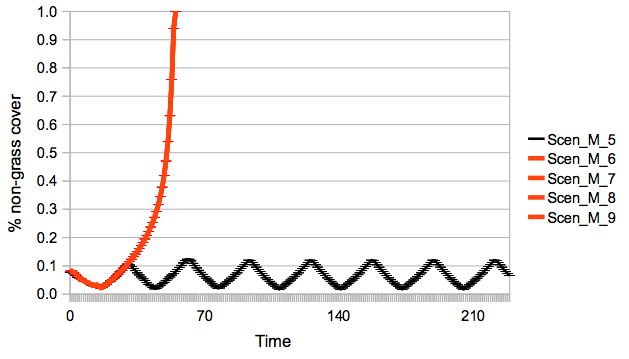
Figure 5. Simulated means and standard deviations of percentage of non-grass cover during time of Scen-M-5, and Scen-M-6 - Scen-M-9 - 4.8
- The successful of the above scenarios show a minimum of 9 - 12 cattle that is infinitely long held on the pasture, while the non-grass cover lies between 6.9% and 1.6%, which is very low, indicating that the pasture is in an equilibrium that keeps the pasture more or less ungrazed. In order to show that the model is in principle able to also simulate equilibria with a constantly grazed pasture we identified a scenario (Scen-M-0) (Table 2) where the other settings of the remaining parameters have been set to different values (i.e. 50% initial grass cover (Cov0 = 50), a forage requirement of 2 patches/cattle agent per year (Requ = 2), a grass growth rate near zero vegetation of 0.0004 (rate = 0.0004), and an initial cattle stock distribution of 1 cattle per herdsman agent (ki0 = 1, i = 1, 2, 3)). For an explanation of these values see Table 1. The scenario holds a minimum of non-grass cover of 14% and a minimum of 12 cattle (Figure 6).
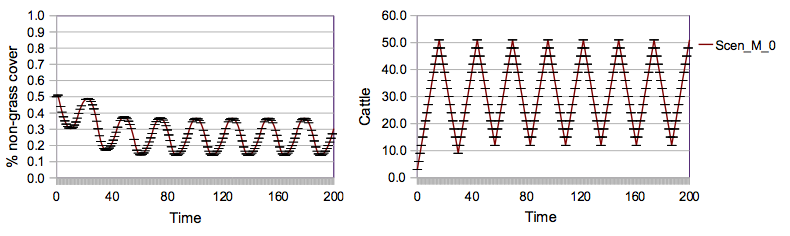
Figure 6. Simulated means and standard deviations of percentage of non-grass cover (left) and total cattle stock (right) during time of Scen-M-0 Sensitivity Analysis
- 4.9
- These results give the impression that we deal with dispositions that have a clear positive and dispositions that have a clear negative influence. There is truly a general tendency of some dispositions to influence the sustainability of the common one way or the other as shown in the section 4.1 and 4.2, but a closer look will reveal a much more complex picture. By sensitivity analysis of two case scenarios we give an idea of the unexpected behaviour of disposition values on the modelled system. We selected two scenarios that represent very unstable but yet successful systems. The first is Scen-M-5, which, as we saw in the section 6.2, fullls this requirement, and the second, Scen-M-10 has been identied with the same shifting method, but from the starting point Scen-P-1. For both scenarios, we conducted sensitivity analysis by shifting each disposition value from its minimum value (i.e. 0) to its maximum value (i.e. 1) in steps of 0.1 while letting the other dispositions constant at their default values.
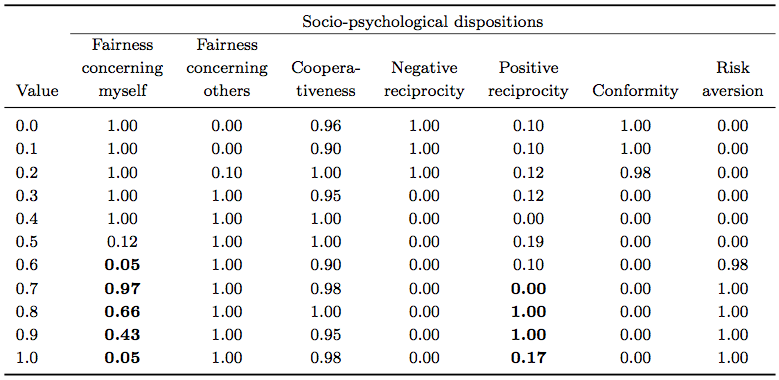
Table 3. Success values of simulated scenarios created by sensitivity analysis of Scen-M-5. Value = value of selected disposition while other dispositions remain at their default value 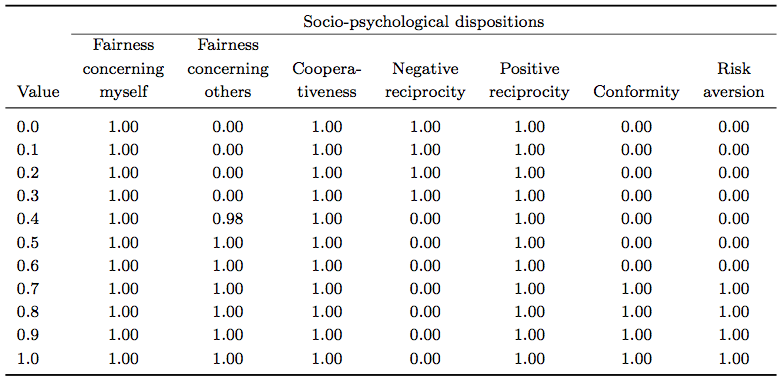
Table 4. Success values of simulated scenarios created by sensitivity analysis of Scen-M-10. Value = value of selected disposition while other dispositions remain at their default value - 4.10
- Results of the sensitivity analysis for Scen-M-5 show that the pattern of effects of dispositions is non-linear (Table 3: bold letters). The probability that this pattern has been created by chance is near zero. If the experiment would be repeated, the chance that the simulated success values deviate more than 10% from the ones simulated here, is less than 5%. This irregular pattern can be attributed to a curved border space between the successful and unsuccessful areas in the 7-dimensional space of the seven dispositions, thus giving the impression of an unpredictable pattern. The complexity of the interaction between the dispositions and the analytic intractability and non-linearity of the Nash equilibrium solution makes it almost impossible to provide explanations for this kind of system behaviour. Furthermore, if we compare the results of Scen-M-5 and Scen-M-10 (Tables 3 and 4), we note that the effect of changes in single dispositions must depend on the state of the other dispositions, as hypothesized, too.
 Conclusions
Conclusions
- 5.1
- The model that we developed can be viewed as an agent-based spatio-temporal implementation of the Tragedy of the Commons by Hardin, and more important, as an extension of the corresponding tragedy game, which allows the testing of payoffs biased by socio-psychological dispositions or feelings. Using MASTOC, we verified numerically the argument by Hardin if socio-psychological dispositions are disregarded, and showed that by consideration of selected dispositions successful and sustainable uses of the common can be explained. Very broadly, we indicated that the increase in values of cooperativeness, positive reciprocity, fairness towards others, and risk aversion support sustainable of use, while the increase of negative reciprocity, fairness towards the agent himself, and conformity support unsustainability. But we showed via sensitivity analysis that this general trend does not need to be necessarily true and can be irregular. Due to non-linearity of the relationship between sustainability and the single disposition and its dependence on other disposition values shifts in the dispositions can lead to counterintuitive and surprising behaviour. This finding is in line with the findings of meta-analyses such as by the Common-Pool Resource (CPR) research program, which identified that the CPR system's general complexity impedes the development of simple heuristics to determine its unsustainability.
- 5.2
- Due to the model's potential to account for such non-linearities - though still in theory - and its capacity to simulate intermediate equilibria of a stable but below maximum resource stock, the model framework if strengthened has the capacity to support the scientific understanding of the management of commons. It further may be worth an assessment of its capacity to model empirical phenomena. If extended and calibrated for case studies, stability and sustainability of the system could then be assessed via simulation, and if needed, sensitivity analysis could identify the critical factors or dispositions that may enhance the system's functioning. It may so possibly support the design of focused social policy interventions in a study area (e.g. education programs, group meetings) to trigger the enhancement of those social attitudes that may lead to successful and sustainable common resource use.
 References
References
-
BUNN D.W. and Oliveira F.S. 2001. Agent-based simulation - an application to the new electricity trading arrangements of England and Wales. IEEE Transactions on Evolutionary Computation 5(5): 493-503. [doi:10.1109/4235.956713]
EBENHÖH E. and Pahl-Wostl C. 2006. Agent-based modelling with boundedly rational agents. In J. P. Rennard, editor. Handbook of research on nature inspired computing for economy and management. Hershey-PA, USA.
FEHR E. and Schmidt K.M. 1999. A Theory Of Fairness, Competition, and Cooperation. The Quarterly Journal of Economics 114(3):817-868. [doi:10.1162/003355399556151]
FEHR E. and Gächter S. 2000. Cooperation and Punishment in Public Goods Experiments. American Economic Review 90 (4):980-994. [doi:10.1257/aer.90.4.980]
HARDIN G. 1968. The Tragedy of the Commons. Science 162:1243-1248. [doi:10.1126/science.162.3859.1243]
IZQUIERDO L. R. and Gotts N.M. 2005. The Implications of Case-Based Reasoning in Strategic Contexts. Lecture Notes in Economics and Mathematical Systems 564:163-174. [doi:10.1007/3-540-28547-4_14]
KRAUSE T., Beck E.V., Cherkaoui R., Germond A., Andersson G., Ernst D. 2006. A comparison of Nash equilibria analysis and agent-based modelling for power markets. International Journal of Electrical Power and Energy Systems 28 (9):599-607. [doi:10.1016/j.ijepes.2006.03.002]
MACY M. W., Flache, A. 2002. Proc. Natl. Acad. Sci. USA 99, Suppl. 3 , 7229-7236. [doi:10.1073/pnas.092080099]
MCKELVEY, R. D. and Palfrey T.R. 1998. Quantal Response Equilibrium for Extensive Form Games. Experimental Economics 1(1):9-41. [doi:10.1023/A:1009905800005]
McKelvey R., McLennan A., Turocy T. 2004. Gambit: Software tools for game theory, Version 0.2007.01.30. http://www.gambit-project.org.
NASH J. 1951. Non-cooperative games. The Annals of Mathematics 54(2):286-295. [doi:10.2307/1969529]
NOY-MEIR I. 1978. Stability in Simple Grazing Models: Effects of Explicit Functions. Journal of Theoretical Biology 71:347-380. [doi:10.1016/0022-5193(78)90165-0]
OSTROM E., Burger J., Field C.B., Norgaard R.B., Policansky D. 1999. Sustainability - Revisiting the commons: Local lessons, global challenges. Science 284: 278-282. [doi:10.1126/science.284.5412.278]
POTEETE A. R., Janssen M.A., Ostrom E. 2010. Multiple Methods in Practice: Working Together: Collective Action, the Commons, and Multiple Methods in Practice. Princeton University Press, Princeton, NJ.
RABIN M. 1993. Incorporating Fairness into Game Theory and Economics. The American Economic Review 83(5):1281-1302.
RASMUSEN E. 1989. Games and Information: An Introduction to Game Theory. Basil Blackwell, Oxford, Cambridge.
RUTTAN L. M. 2006. Sociocultural Heterogeneity and the Commons. Current Anthropology 47(5):843-853. [doi:10.1086/507185]
RUTTAN L. M. 2008. Economic Heterogeneity and the Commons: Effects on Collective Action and Collective Goods Provisioning. World Development 36(5):969-985. [doi:10.1016/j.worlddev.2007.05.005]
SCHLAGER E., Blomquist W., Tang S.Y. 1994. Mobile Flows, Storage and Self-Organized Institutions for Governing Common-Pool Resources. Land Economics 70(3):294-317. [doi:10.2307/3146531]
SNIJDERS C. 1996. Trust and Commitments. Thesis Publishers, Amsterdam.
WILENSKY U. 1999. NetLogo (and NetLogo User Manual). http://ccl.northwestern.edu/netlogo/.