 Abstract
Abstract
- An important way to maintain human cooperation is punishing defection. However, since punishment is costly, how can it arise and evolve given that individuals who contribute but do not punish fare better than the punishers? This leads to a violation of causality, since the evolution of punishment is prior to the one of cooperation behaviour in evolutionary dynamics. Our public goods game computer simulations based on generalized Moran Process, show that, if there exists a 'behaviour-based sympathy' that compensates those who punish at a personal cost, the way for the emergence and establishment of punishing behaviour is paved. In this way, the causality violation dissipates. Among humans sympathy can be expressed in many ways such as care, praise, solace, ethical support, admiration, and sometimes even adoration; in our computer simulations, we use a small amount of transfer payment to express 'behaviour-based sympathy'. Our conclusions indicate that, there exists co-evolution of sympathy, punishment and cooperation. According to classical philosophy literature, sympathy is a key factor in morality and justice is embodied by punishment; in modern societies, both the moral norms and the judicial system, the representations of sympathy and punishment, play an essential role in stable social cooperation.
- Keywords:
- Public Goods Game, Cooperation, Social Dilemma, Co-Evolution, Sympathy, Punishment
 Introduction
Introduction
- 1.1
- In a standard public goods game, free-riders (defectors) obtain more payoff than cooperators, so defection is clearly a dominant strategy. Thus, cooperators will ultimately be replaced by defectors in evolution, independently of their initial proportion in the population. In this way, highly efficient social cooperation is not possible. This is the so-called "social dilemma" (Dawes 1980; Messick and Brewer 1983). However, an impressive body of behavioural experiments shows that cooperation in fact exist in the social dilemma, although it is supposed to be impossible to emerge (Axelrod and Hamilton 1981; Güth et al. 1982; Forsythe et al. 1994; Berg et al. 1995; Andreoni 1988; Isaac et al. 1985). This poses a question to us: what induces people to give up their benefits of free-riding and turn to cooperation? It becomes a crucial problem in the research of the public goods game.
- 1.2
- One possible explanation to this question can be given by the reciprocity theories. Under the assumption of self-interestedness, reciprocity could induce significant cooperation. The reciprocity theories include direct and indirect reciprocity theories. The theories of direct reciprocity can explain cooperation in bilateral long-term interactions. However, direct reciprocity relies on repeated encounters between the same two individuals, and both individuals must be able to provide help. So the theories of direct reciprocity can not explain why cooperation is frequent in non-repeated interactions (Hamilton 1964; Trivers 1971; Axelrod and Hamilton 1981; Nowak 1995; Nowak 2006a). The theories of indirect reciprocity show how cooperation in larger groups can emerge when the cooperators can build a reputation. Yet these theories do not readily explain why cooperation is frequent when gains from reputation are small or absent. (Nowak and Sigmund 1998; Lotem 1999; Wedekind 2000; Fehr and Gächter 2002; Gintis 2003; Nowak 2006a) Additionally, the existence of reciprocity relies on the excludability of the income, which implies, that it cannot explain the existence of cooperation in non-excludable public goods games.
- 1.3
- In order to explain the existence of cooperation in public goods games, the theory of strong reciprocity was raised, which implies punishment or altruistic punishment (Gintis 2000; Bowles and Gintis 2004). Related studies have shown that the behaviour of punishment, a person's propensity to incur a cost in order to punish free-riders, can mitigate the social dilemma (Boyd and Richerson 1992; Boyd et al. 2003; Bowles and Gintis 2004). Results from behavioural experiments and neuroscience are consistent with this behaviour pattern: not only has this pattern been confirmed by observation (Ostrom et al. 1992; Fehr and Gächter 2000; Fehr and Gächter 2002; Henrich et al. 2006), but also has its neural basis been discovered by brain imaging (de Quervain et al. 2004). However, since punishment is costly, those who contribute but do not punish, i.e. so called second-order-free-riders, would fare better than the punishers. Thus, based on this model, such punishment is supposed to be undermined. This raises the "second-order social dilemma". To a large extent, the problem of explaining punishment has replaced that of explaining cooperation (Colman 2006).
- 1.4
- Various solutions to the second-order social dilemma have been proposed (Henrich and Boyd 2001; Milinski et al. 2002; Panchanathan and Boyd 2004; Henrich 2004). Recently, Hauert et al. (2007) and Sigmund et al. (2010) showed, that it can be solved if individuals have the option to abstain from the joint endeavor. In their research, this paves the way for the emergence and establishment of cooperative behavior based on the punishment of defectors. However, Boyd and Mathew (2007) pointed out, that it is a rare case that individuals can opt out of collective goods, because most of them are non-excludable, such as the security of a tribe, irrigation works, giant prey, etc.. Indeed, Hauert et al. provide a cogent mechanism that can explain the evolution of punishment, yet it reveals only a few cases being conform to this assumption. Therefore it is "a narrow road to cooperation" and "the challenge is now to understand how punishment can arise in the remaining cases".
- 1.5
- Lately, simulations conducted by Klaus Jaffe and Luis Zaballa (2010) show, that cooperative punishment, i.e. all the group members sharing the cost of the punishment, is an evolutionary stable strategy that performs better in evolutionary terms than non-cooperative punishment. In this way the second-order social dilemma is solved. Yet, cooperative punishment is a very strong constraint of the model. Firstly, cooperation is necessary for cooperative punishment to evolve. However, from an anthropological point of view, punishment behaviour is induced to explain the emergence of cooperation. Secondly, all individuals participate in punishment and share the cost. In this case, punishment is compulsory but not voluntary. This compulsory type of punishment suggests the existence of social authorities or social organizations, which need to be established.
- 1.6
- In our paper, we bring up a model with less rigorous constrains to solve the second-order social dilemma: if there exists a "behaviour-based sympathy" that compensates those who voluntarily punish at a personal cost, the punishing behaviour could emerge and dominate in the society. In this way, the "second-order social dilemma" dissipates. In reality, this sympathy can be expressed in many ways such as care, praise, solace, ethical support, admiration, and sometimes even adoration; in our computer simulations, we use a small amount of transfer payment to express "behaviour-based sympathy". No matter what the specific form of sympathy is, as long as it inspires punishment our simulations represent real world punishment.
- 1.7
- There are copious quantities of classical literature from psychology, anthropology and ethics indicating that sympathy is a part of humanity (Hume 1739; Smith 1759; Darwin 1871;Mencius 1970). Additionally, neuroscientists also discovered its neural basis by brain scan (Immordino-Yang et al. 2009; Singer et al. 2009). Economists such as Harsanyi (1955), Binmore (1998), Camerer (2003), Sally (2001), Bergstrom and Stark (1993), set sympathy as an emotional factor in the analysis of Game theory and decision-making process.
- 1.8
- Our computer simulations show that there exists co-evolution of sympathy, punishment and cooperation. Thus, we offer an alternative approach to solve the second-order social dilemma.
 Models and Methods
Models and Methods
- 2.1
- We assume, that there are three types of individuals in a population of constant size M. X: cooperators, who contribute to the public goods and sympathize punishers; Y: defectors, who refuse to contribute but exploit the contributions of the other two types of individuals; Z: punishers, who not only contribute to the public goods but also punish defectors. According to the method developed by Hauert et al. (2007), the groups engaging in a public goods game are given by multivariate hypergeometric sampling. Specifically, we randomly choose N individuals from the population to participate in a non-excludable public goods game. Among the N individuals, there are Nx cooperators, Ny defectors, and Nz punishers. Thus we have N= Nx+ Ny +Nz.
- 2.2
- We define:
c: contribution cost (c > 0); r: multiplier of return (r > 1); δ: strength of punishment (δ≥c); γ: punishment cost (γ < δ); s: strength of sympathy (s < γ);
Thus, the expected payoffs for the three types of individuals in each period of game are respectively:
(1) 
(2) 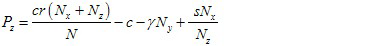
(3) - 2.3
- We assume that individuals will imitate each other, and that they are more prone to imitate those with higher payoff. This assumption implies, that individuals with higher payoff generally have higher fitness and are more evolutionarily advantageous. There are some alternative functions to generalize this assumption (Hauert et al. 2007; Traulsen et al. 2008). The most commonly adopted one, is the linear fitness function F=1-ω+ωP. Here, F denotes fitness, P payoff, and ω selection strength. This function is a linear combination of the "baseline fitness", which is normalized to 1 for all players, and the payoff from the public goods game (Hauert et al. 2007). However, when using a high selection strength, this approach cannot be used to analyze stochastic evolutionary dynamics in finite populations, since negative fitness values can occur. In order to obtain results with any selection strength (with 0 < ω < 1), we apply an exponential fitness-function with f=eωP to correlate payoff with fitness (Traulsen et al. 2008). Our results can be obtained in both approaches.
- 2.4
- We adopt a frequency-dependent Moran process to specify the stochastic dynamics of the finite population (Hauert et al. 2007). We tested three different generalized stochastic Moran processes: (i) "death-birth", (ii) "birth-death" and (iii) "genetic pool" ("offspring pool"). For the "death-birth", first a randomly selected individual is removed and afterwards another individual is selected for reproduction with a probability proportional to its fitness and produces a clonal offspring (Taylor et al. 2004; Nowak 2006b). For the "birth-death", first an individual is chosen for reproduction and then its clonal offspring replaces a randomly selected individual (Taylor et al. 2004; Nowak 2006b). For the "genetic pool" ("offspring pool"), first each individual in the population reproduces offspring proportional to its fitness comprising the "genetic pool". Then, one of these offspring is chosen randomly to replace an individual in the population (Fudenberg et al. 2004). Although, the three processes describe the dynamic differently, they all lead to the same results.
- 2.5
- Additionally, we assume that any individual of the population could randomly switch to another type with a small probability μ, which is referred to as mutation rate (Hauert et al. 2007).
- 2.6
- The five steps above are executed successively in the computer simulation (Figure 1).
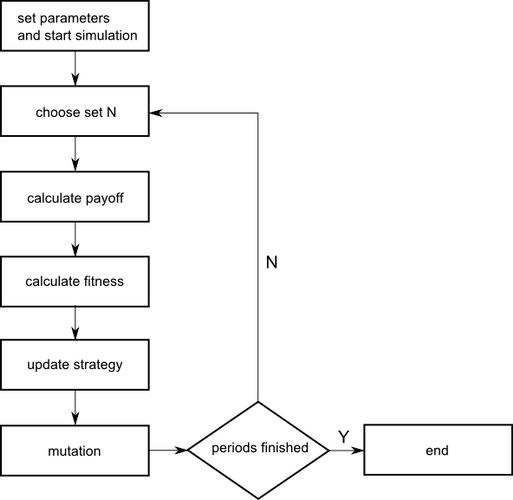
Figure 1. Computer Simulation Process - 2.7
- The sequence of the programmed actions is:
Read in parameters Initialize population Seed the random number generator While iteration smaller than Max_Iteration do Choose N individuals from population randomly Calculate payoff based on the set N If number of Punisher and Cooperator equals to zero in N Set all Payoffs to zero Else if number of any member type is zero in N Set this member type's payoff to zero End if If fitness_function is exponential Calculate fitness by F=e↑ωp Else Calculate fitness by F=1-ω+ωp End if If update type is genetic pool do For all types of members do Genetic pool members of this type = fitness of this member type * number of this type in population End do Choose one random member of the genetic pool to replace a random member of the population While one type has negative number of members do Choose again End do Else if update type is death-birth do Remove one member from the population randomly While one type has negative number of members do Choose again End do Choose one member type to reproduce one offspring with a probability proportional to fitness * number of members in population Else Choose one member type to reproduce one offspring with a probability proportional to fitness * number of members in population Remove one member from the population randomly While one type has negative number of members do Choose again End do End if For each member in population do If a random number is smaller than the mutation rate do Change member type to one of the other types (mutate) End if End do End iteration Produce output and statistics Print graphs and statistics to screen and to file
- 2.8
- We offer the simulation software on line. For more details, see PGG_sympathy v1.0.6.
 The Results of Simulations
The Results of Simulations
- 3.1
- Simulation results clearly show that, if there exists a behaviour-based sympathy, punishing behaviour will be advantageous. The evolution path shows that after an initial oscillation, punishers will dominate the population persistently and their regime cannot be invaded by other strategies. Thus the "second-order social dilemma" dissipates (Figure 2).
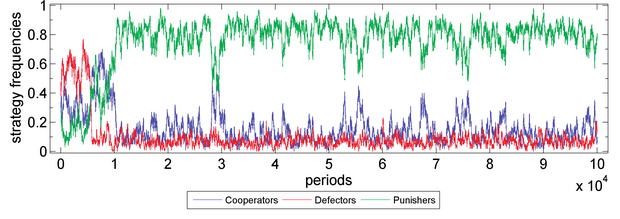
Figure 2. Public Goods Game with Sympathy Parameter values are X=30, Y=40, Z=30, M=100, N=5, c=1, r=3, s=0.15, δ=1, γ=0.3, ω=0.5, μ=0.001, periods=105. Fitness function: exponential function. Moran process: genetic pool.
- 3.2
- In public goods game without sympathy, punishing behaviour is not evolutionarily advantageous. The evolution path is governed by alternating short-term domination of each member type, showing a rock-paper-scissors-like style. Compared to the other two types of behaviour, defection is more advantageous. Without a stable cooperative order, the society falls into the "second-order social dilemma" (Figure 3).
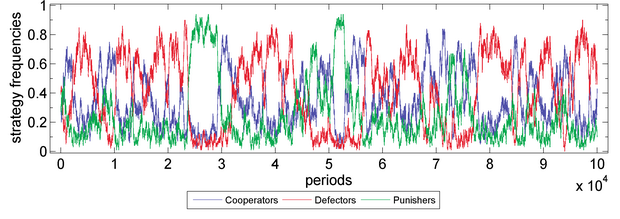
Figure 3. Public Goods Game without Sympathy Parameter values are X=30, Y=40, Z=30, M=100, N=5, c=1, r=3, s=0, δ=1, γ=0.3, ω=0.5, μ=0.001, periods=105. Fitness function: exponential function. Moran process: genetic pool.
- 3.3
- Our conclusions also withstand robust tests respectively on various parameters. Details are here. In 3.4, 3.5 and 3.6, we provide the robust test results of three important parameters: periods, initial state, and strength of sympathy.
- 3.4
- Robust tests on period. Our results withhold long period. See two examples on Figure 4 and 5.
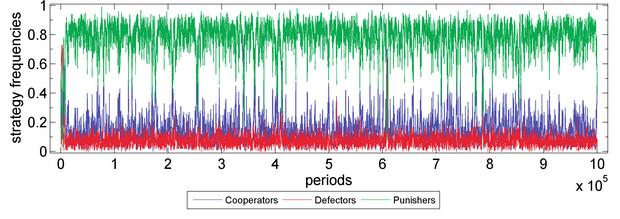
Figure 4a. Public Goods Game with Sympathy (with periods=106) Parameter values are X=30, Y=40, Z=30, M=100, N=5, c=1, r=3, s=0.15, δ=1, γ=0.3, ω=0.5, μ=0.001. Fitness function: exponential function. Moran process: genetic pool.
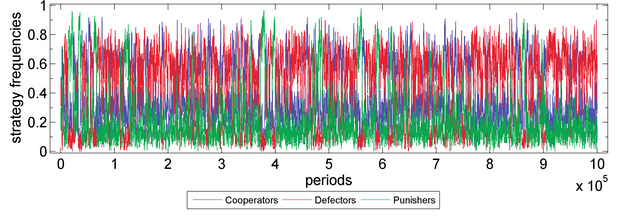
Figure 4b. Public Goods Game without Sympathy (with periods=106) Parameter values are X=30, Y=40, Z=30, M=100, N=5, c=1, r=3, s=0, δ=1, γ=0.3, ω=0.5, μ=0.001. Fitness function: exponential function. Moran process: genetic pool.
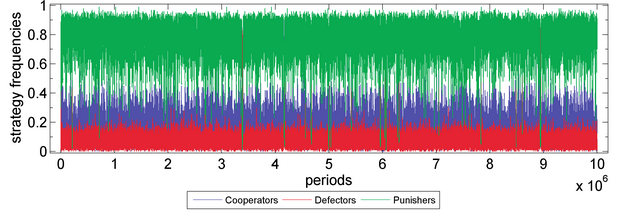
Figure 5a. Public Goods Game with Sympathy (with periods=107) Parameter values are X=30, Y=40, Z=30, M=100, N=5, c=1, r=3, s=0.15, δ=1, γ=0.3, ω=0.5, μ=0.001. Fitness function: exponential function. Moran process: genetic pool.
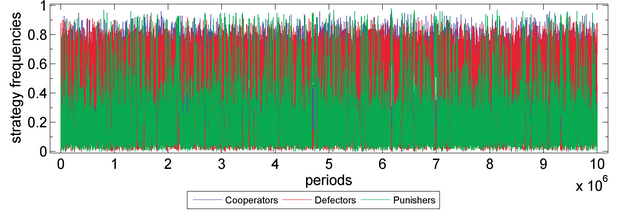
Figure 5b. Public Goods Game without Sympathy (with periods=107) Parameter values are X=30, Y=40, Z=30, M=100, N=5, c=1, r=3, s=0, δ=1, γ=0.3, ω=0.5, μ=0.001. Fitness function: exponential function. Moran process: genetic pool.
- 3.5
- Robust tests on initial state of different proportions for the three types of individuals in the population. Our results withhold different initial states. See two examples on Figure 6 and 7.
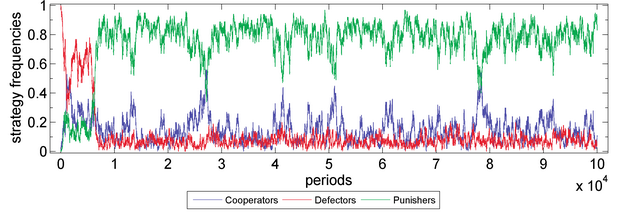
Figure 6a. Public Goods Game with Initially 100% Defectors (with Sympathy) Parameter values are X=0, Y=100, Z=0, M=100, N=5, c=1, r=3, s=0.15, δ=1, γ=0.3, ω=0.5, μ=0.001, periods=105. Fitness function: exponential function. Moran process: genetic pool.
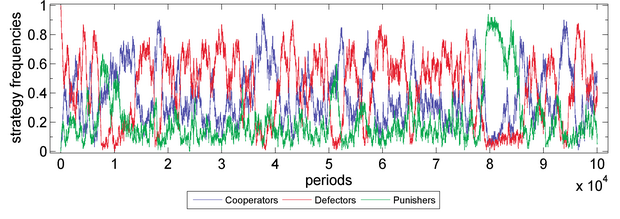
Figure 6b. Public Goods Game with Initially 100% Defectors (without Sympathy) Parameter values are X=0, Y=100, Z=0, M=100, N=5, c=1, r=3, s=0, δ=1, γ=0.3, ω=0.5, μ=0.001, periods=105. Fitness function: exponential function. Moran process: genetic pool.
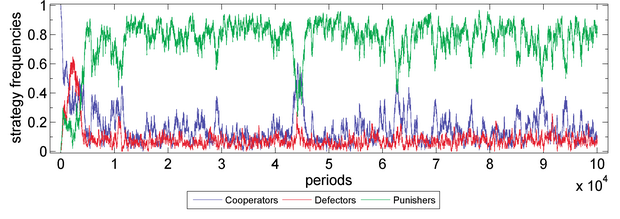
Figure 7a. Public Goods Game with Initially 100% Cooperators (with Sympathy) Parameter values are X=100, Y=0, Z=0, M=100, N=5, c=1, r=3, s=0.15, δ=1, γ=0.3, ω=0.5, μ=0.001, periods=105. Fitness function: exponential function. Moran process: genetic pool.
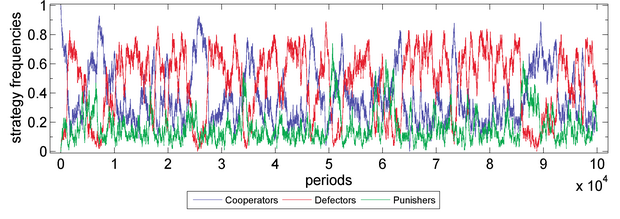
Figure 7b. Public Goods Game with Initially 100% Cooperators (without Sympathy) Parameter values are X=100, Y=0, Z=0, M=100, N=5, c=1, r=3, s=0, δ=1, γ=0.3, ω=0.5, μ=0.001, periods=105. Fitness function: exponential function. Moran process: genetic pool.
- 3.6
- Robust tests on strength of sympathy. We tested the evolutionary stability of the punishing behaviour respectively in cases of s=0_0.20 (with step length=0.05). Parameter values are X=30, Y=40, Z=30, M=100, N=5, c=1, r=3, δ=1, γ=0.3, ω=0.5, μ=0.001, periods=105. Fitness function: exponential function. Moran process: genetic pool. It shows that s is positive related to the evolutionary advantage of the punishing behaviour. See Figure 8.
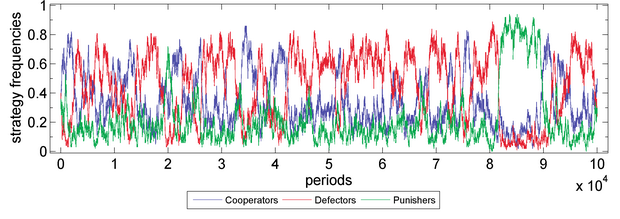
Figure 8a. Public Goods Game with s=0.00 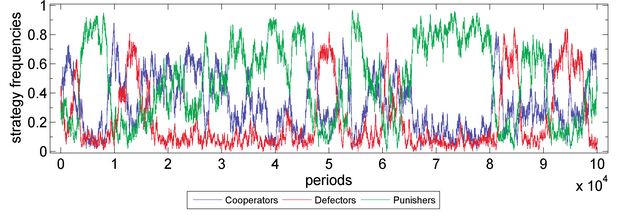
Figure 8b. Public Goods Game with s=0.05 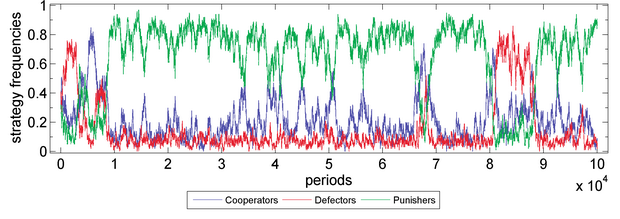
Figure 8c. Public Goods Game with s=0.10 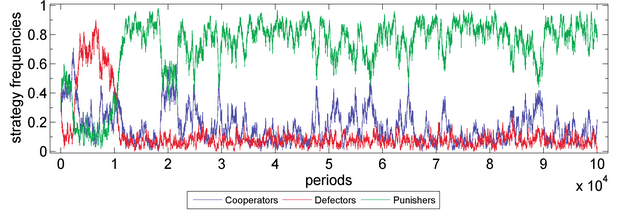
Figure 8d. Public Goods Game with s=0.15 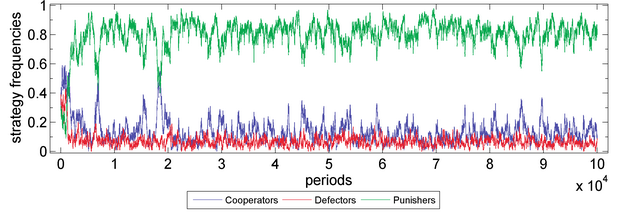
Figure 8e. Public Goods Game with s=0.20
 Analytic results
Analytic results
- 4.1
- We based our simulation model on the analysis in Imhof et al. (2005) and Hauert et al.(2007). The analysis of corresponding stochastic dynamics is greatly simplified in the limiting case μ→0. The population consists almost always of one or two types at most. This holds because the three monomorphic states are absorbing for μ=0. For sufficiently small μ, the transition among three types occurs when a mutant appears and spreads to fixation. This reduces to sampling from a hypergeometric distribution without replacement (Hauert et al. 2007; Imhof et al. 2005). Thus, in this limiting case we can obtain an approximate analytic expression corresponding to the evolution process.
- 4.2
- If μ→0, in a population of constant size M with mi individuals of type i and mj=M-mi of type j, the probability to select k individuals of type i and N-k of type j in N trials is:
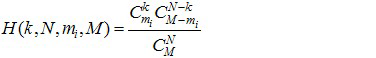
(4) - 4.3
- Thus, for a non-excludable public goods game the average payoff Pxy of cooperators against defectors and Pyx in a population of x (cooperator) and y=M-x (defector) are:
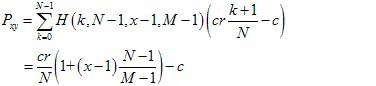
(5) 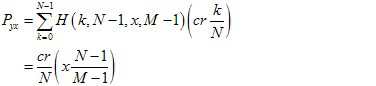
(6) Similarly, the average payoff between punishers and defectors are:
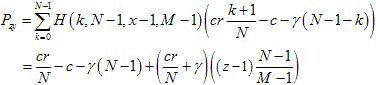
(7) 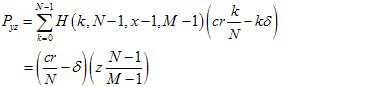
(8) And we assume that sympathy strength is s, and the expected payoffs of cooperators Pxz and punishers Pzx are
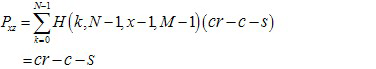
(9) 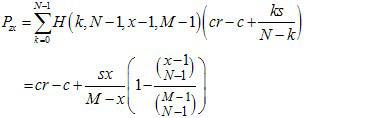
(10) - 4.4
- Just as we connect the payoff and the fitness by F=eωp, the fitness of an individual type i in a well-mixed population of i and j is the index function of its payoff, namely f ij(mi)=eωP ij( mi). The above payoffs together with the ω determine the probability to change the number of individual mi of type i by ±1, Tij±:
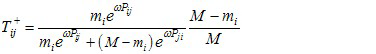
(11) 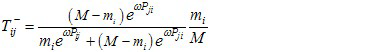
(12) - 4.5
- From these transition probabilities, a fixation probability _ij of a single mutant strategy of type i in a resident population of type j can be derived:
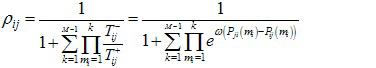
(13) - 4.6
- The fixation probabilities _ij define the transition probabilities of a Markov process between the three different homogeneous states of the population. The transition matrix A is given by:
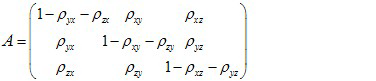
(14) - 4.7
- The normalized right eigenvector to the largest eigenvalue (which is 1 for the matrix A) determines the stationary distribution. It indicates the probability to find the system in one of the three homogeneous states. It is given by:
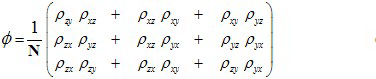
(15) Where the normalization factor N has to be chosen such that the elements of ø sum up to one.
- 4.8
- According to the presented model and algorithm, we plot the stationary distribution as a function of each variable as a supplement to the computer simulation. See Figure 9.
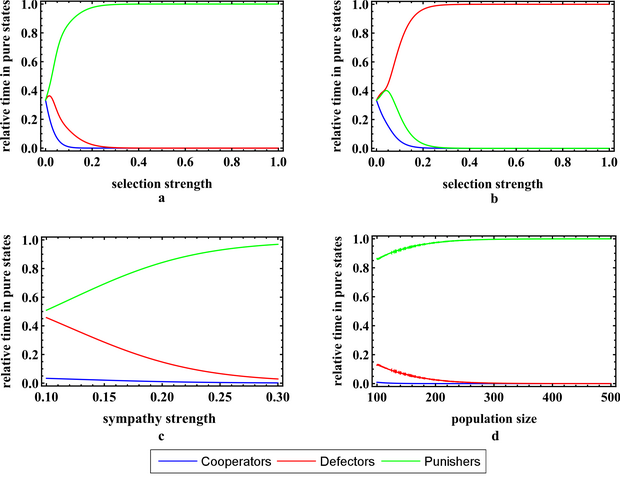
Figure 9. Stationary Distribution in the Limiting Case Parameter values are M=100 ( in a, b, c ), M=100~500 ( in d ), N=5, c=1, r=3, s=0.15 ( in a, d ), s=0 ( in b ), s=0.10~0.30 ( in c ), δ=1, γ=0.3, and ω=0~1 ( in a, b ), ω=0.5 ( in c, d ). a Punishers are obviously dominant in public goods game with sympathy. b Defectors are obviously dominant in public goods game without sympathy except for very weak selection cases. c Enhancing the sympathy strength obviously endows punishers with more evolutionary advantages and hence weakens defectors. d With the increase of the population size, the success of punishers is even more amplified in public goods game with sympathy.
 Conclusions
Conclusions
- 5.1
- Our research shows that the second-order social dilemma could be solved by inducing the behaviour-based sympathy. This is based on two reasons. On the one hand, punishment behaviour changes the relative payoff between cooperators and defectors, and enables the cooperators to be advantageous. On the other hand, the behaviour-based sympathy changes the relative payoff between punishers and cooperators, and enables the punishers to be more evolutionarily advantageous.
- 5.2
- Literature on biology, psychology, sociology and anthropology regard sympathy as part of humanity, or an emotional behaviour pattern (Darwin 1871; Eisenberg et al. 1989; Eisenberg et al. 1989; Candace 1987; Elizabeth 1995; Catherine and Geoffrey 1986). Observing ourselves and the people around us, we see that sympathy could be found on almost everyone. In our model, we research the effect this behaviour laid on the human society. Our simulation results show that: A possible way how cooperation appeared is the co-evolution of the sympathy, punishment and cooperation behaviour, since they could not evolve independently.
- 5.3
- On the philosophy aspect, sympathy is a key factor of morality (Smith 1759; Mencius 1970), and justice is embodied by punishment (Hume 1739; Plato 1976; Kant 1996); The computer simulation results also indicate that, the sense of morality (sympathy) and justice (punishment) with altruistic tendencies in human nature can co-evolve with the human cooperative behaviour, and this is consistent with the prospective of individual choice theory of modern biology (Wilson 1975). This corresponds with the key idea of Darwin's book "Descent of Man, and Selection in Relation to Sex" (Darwin 1871). In modern societies, not only the judicial system, but also the moral norms, the representation of sympathy and punishment, plays an essential role in sustaining the social norms.
 Acknowledgements
Acknowledgements
- This work is supported by Chinese Ministry of Education 211 Project Phase 3 fund, the Center for Research of Private Economy (one of the key research institutes of social sciences and humanities and national innovation bases of philosophy and social sciences, Chinese Ministry of Education) and Center for the Study of Language and Cognition (one of the national innovation bases of philosophy and social sciences, Chinese Ministry of Education), Zhejiang University. Thanks also go to our strategic partner, Zhejiang Hexin Flush Network Services Ltd., especially to Mr. Zhenqiu Cai for assisting us with the simulation software.
 References
References
-
ANDREONI, J (1988) Why Free Ride? Strategies and Learning in Public Goods Experiments. Journal of Public Economics, 37, pp. 291-304. [doi:10.1016/0047-2727(88)90043-6]
AXELROD, R and Hamilton, W D (1981) The Evolution of Cooperation. Science, 211, pp. 1390-1396. [doi:10.1126/science.7466396]
BERG, J, Dickhaut, J and McCabe, K (1995) Trust, Reciprocity and Social History. Games and Economic Behavior, 10, pp. 122-142. [doi:10.1006/game.1995.1027]
BERGSTROM, T and Stark, O (1993) How Altruism Can Prevail in an Evolutionary Environment, American Economic Review, 83(2), pp. 148-155.
BINMORE, K (1998) Game Theory and Social Contract, Vol. II: Just Playing. Cambridge, Mass: The MIT Press.
BOYD, R, Gintis, H, Bowles, S and Richerson, P J (2003) The Evolution of Altruistic Punishment. Proceedings of the National Academy of Science USA, 100, pp. 3531-3535. [doi:10.1073/pnas.0630443100]
BOWLES, S and Gintis, H (2004) The Evolution of Strong Reciprocity: Cooperation in Heterogeneous Populations. Theoretical Population Biology, 65, pp. 17-28. [doi:10.1016/j.tpb.2003.07.001]
BOYD, R and Mathew, S (2007) A Narrow Road to Cooperation. Science, 316, pp. 1858-1859. [doi:10.1126/science.1144339]
BOYD, R and Richerson, P J (1992) Punishment Allows the Evolution of Cooperation (or Anything Else) in Sizable Groups. Ethology and Sociobiology, 13, pp.171-195. [doi:10.1016/0162-3095(92)90032-Y]
CAMERER, C F (2003) Behavioural Game Theory. Experiments in Strategic Interaction. New York/Princeton: Russell Sage Foundation/Princeton University Press
CANDACE, C (1987) Sympathy Biography and Sympathy Margin. American Journal of Sociology, 93, pp. 290-321 [doi:10.1086/228746]
CATHERINE, L and Geoffrey M W (1986) The Anthropology of Emotions. Annual Review of Anthropology,15, pp. 405-436 [doi:10.1146/annurev.an.15.100186.002201]
COLMAN, A (2006) The Puzzle of Cooperation. Nature, 440, pp. 744-745. [doi:10.1038/440744b]
DARWIN, C (1871) The Descent of Man and Selection in Relation to Sex London: Murray.
DAWES, R M (1980) Social Dilemmas. Annual Review of Psychology, 31, pp. 169-193. [doi:10.1146/annurev.ps.31.020180.001125]
DE Quervain, D J et al. (2004) The Neural Basis of Altruistic Punishment. Science, 305, pp. 1254-1258. [doi:10.1126/science.1100735]
EISENBERG, N, Fabes, R A, Miller, P A, Fultz, J, Shell, R, Mathy, R M, Reno, R R (1989) Relation of sympathy and personal distress to prosocial behavior: A multimethod study. Journal of Personality and Social Psychology, 57(1), pp. 55-66 [doi:10.1037/0022-3514.57.1.55]
EISENBERG , N, Miller, P A, Schaller, M, Fabes, R A, Fultz, J, Shell, R, Shea, C L (1989) The Role of Sympathy and Altruistic Personality Traits in Helping: A Reexamination. Journal of Personality, 57, pp. 41-67 [doi:10.1111/j.1467-6494.1989.tb00760.x]
ELIZABETH, B C (1995) "The Sacred Rights of the Weak": Pain, Sympathy, and the Culture of Individual Rights in Antebellum America. Journal of American History, 82(2), pp. 463-493 [doi:10.2307/2082183]
FEHR, E and Gächter, S (2000) Cooperation and Punishment in Public Goods Experiments. American Economic Review, 90, pp. 980-994. [doi:10.1257/aer.90.4.980]
FEHR, E and Gächter, S (2002) Altruistic Punishment in Humans. Nature, 415, pp. 137-140. [doi:10.1038/415137a]
FORSYTHE, R, Horowitz, J L, Savin, N E and Sefton, M (1994) Fairness in Simple Bargaining Experiments. Games and Economic Behavior, 6, pp. 347-369. [doi:10.1006/game.1994.1021]
FUDENBERG, D, Imhof, L, Nowak, M A, Taylor,C (2004) Stochastic Evolution as a Generalized Moran Process, http://www.economics.harvard.edu/faculty/ fudenberg/files/moranprocess.pdf
GINTIS, H (2000) Strong Reciprocity and Human Sociality. Journal of Theoretical Biology, 206, pp. 169-179. [doi:10.1006/jtbi.2000.2111]
GINTIS, H (2003) Solving the Puzzle of Prosociality. Rationality and Society, 15, pp. 155- 187 [doi:10.1177/1043463103015002001]
GÜTH, W, Schmittberger, R, and Schwarze, B (1982) An Experimental Analysis of Ultimatum Bargaining. Journal of Economic Behavior & Organization, 3(4), pp. 367-388. [doi:10.1016/0167-2681(82)90011-7]
HAMILTON, W D (1964) The Genetical Evolution of Social Behavior. Journal of Theoretical Biology, 37, pp. 1-52. [doi:10.1016/0022-5193(64)90038-4]
HARSANYI, J (1955) Cardinal Welfare, Individualistic Ethics and Interpersonal Comparisons of Utility. Journal of Political Economy, 63, pp. 309-321. [doi:10.1086/257678]
HAUERT, C, Traulsen, A, Brandt, H, Nowak, M A and Sigmund, K (2007) Via Freedom to Coercion: the Emergence of Costly Punishment. Science, 316, pp. 1905-1907. [doi:10.1126/science.1141588]
HENRICH, J (2004) Cultural Group Selection, Coevolutionary Processes and Large-Scale Cooperation. Journal of Economic Behavior & Organization, 53, pp. 33-35. [doi:10.1016/s0167-2681(03)00094-5]
HENRICH, J et al. (2006) Costly Punishment Across Human Societies. Science, 312, pp. 1767-1770. [doi:10.1126/science.1127333]
HENRICH, J and Boyd, R (2001) Why People Punish Defectors-Weak Conformist Transmission Can Stabilize Costly Enforcement of Norms in Cooperative Dilemmas. Journal of Theoretical Biology, 208, pp. 79-89. [doi:10.1006/jtbi.2000.2202]
HUME, D (1739) A Treatise on Human Nature, L. A. Selby-Bigge, Ed. Oxford Univ. Press, 1964.
IMHOF, L A, Fudenberg, D, Nowak, M A (2005) Evolutionary cycles of cooperation and defection. Proceedings of the National Academy of Sciences, 102, pp. 10797 -10800 [doi:10.1073/pnas.0502589102]
IMMORDINO-YANG, M H, McColl, A, Damasio, H and Damasio, A (2009) Neural Correlates of Admiration and Compassion. Proceedings of the National Academy of Sciences, 106(19), pp. 8021-8026 [doi:10.1073/pnas.0810363106]
ISAAC, R M, McCue, K F and Plott, C R (1985) Public Goods Provision in an Experimental Environment. Journal of Public Economics, 26, pp. 51-74. [doi:10.1016/0047-2727(85)90038-6]
JAFFE, K and Zaballa, L (2010) Co-Operative Punishment Cements Social Cohesion. Journal of Artificial Societies and Social Simulation, 13(3)4, https://www.jasss.org/13/3/4.html
KANT, I (1996) The Metaphysical Elements of Justice, Cambridge Univ. Press.
LOTEM, A, Fishman, M A and Stone, L (1999) Evolution of Cooperation between Individuals. Nature, 400, pp. 226-227. [doi:10.1038/22247]
MENCIUS (1970). Mencius, tr. D. C. Lao. Harmondsworth: Penguin Books.
MESSICK, D M and Brewer, M B (1983) Solving Social Dilemmas: A Review. In L. Wheeler & P. Shaver (Eds.), Review of personality and social psychology (pp. 11-44). Beverly Hills, CA: Sage.
MILINSKI, M, Semmann, D and Krambeck, H-J (2002) Reputation Helps Solve the 'Tragedy of the Commons'. Nature, 415, pp. 424-426. [doi:10.1038/415424a]
NOWAK, M A (2006a) Five Rules for the Evolution of Cooperation. Science, 134, pp. 1560-1563. [doi:10.1126/science.1133755]
NOWAK, M A (2006b) Evolutionary Dynamics: Exploring the Equations of Life. Harvard University Press.
NOWAK, M A, May, R M and Sigmund K(1995) The Arithmetics of Mutual Help. Scientific American, 272, pp. 76-81. [doi:10.1038/scientificamerican0695-76]
NOWAK, M A and Sigmund, K (1998) Evolution of Indirect Reciprocity by Image Scoring. Nature, 393, pp. 573-577. [doi:10.1038/31225]
OSTROM, E J, Walker, J and Gardner, R (1992) Covenants With and Without a Sword: Self-Governance is Possible. American Political Science Review, 86, pp. 404-417. [doi:10.2307/1964229]
PANCHANATHAN, K and Boyd, R (2004) Indirect Reciprocity Can Stabilize Cooperation Without the Second-Order Free Rider Problem. Nature, 432, pp. 499-502 [doi:10.1038/nature02978]
PLATO (1976) Protagorus, Oxford: Clarendon Press.
SALLY, D (2001) On Sympathy and Games, Journal of Economic Behavior & Organization, 44(1), pp. 1-30. [doi:10.1016/S0167-2681(00)00153-0]
SIGMUND, K, De Silva, H, Traulsen, A, Hauert, C (2010) Social learning promotes institutions for governing the commons, Nature, 446, pp. 861-863. [doi:10.1038/nature09203]
SINGER, T, Critchley, H D and Preuschoff, K (2009) A common Role of Insula in Feelings, Empathy and Uncertainty. Trends in cognitive sciences, 13, pp. 334-340. [doi:10.1016/j.tics.2009.05.001]
SMITH, A (1759) The Theory of Moral Sentiments. In Liberty classics, edited by D. D. Raphael and A. L. Mactie. Indianapolis: Liberty Press, 1976. [doi:10.1093/oseo/instance.00042831]
TAYLOR, C, Fudenberg, D, Sasaki, A, Nowak, M (2004) Evolutionary Game Dynamics in Finite Populations. Bulletin of Mathematical Biology, 66, pp. 1621-1644. [doi:10.1016/j.bulm.2004.03.004]
TRAULSEN, A, Shoresh, N and Nowak, M A (2008) Analytical Results for Individual and Group Selection of Any Intensity. Bulletin of Mathematical Biology, 70, pp. 1410 -1424. [doi:10.1007/s11538-008-9305-6]
TRIVERS, R L (1971) The Evolution of Reciprocal Altruism. Quarterly Review of Biology, 46, pp. 35-57. [doi:10.1086/406755]
WEDEKIND, C and Milinski, M (2000) Cooperation through Image Scoring in Humans. Science, 288, pp. 850-852. [doi:10.1126/science.288.5467.850]
WILSON, E O (1975) Sociobiology: The New Synthesis, Harvard University Press, (Twenty-fifth Anniversary Edition, 2000)