 Abstract
Abstract
- Reputation systems have been used to support users in making decisions under uncertainty or risk that is due to the autonomous behavior of others. Research results support the conclusion that reputation systems can protect against exploitation by unfair users, and that they have an impact on the prices and income of users. This observation leads to another question: can reputation systems be used to assure or increase the fairness of resource distribution? This question has a high relevance in social situations where, due to the absence of established authorities or institutions, agents need to rely on mutual trust relations in order to increase fairness of distribution. This question can be formulated as a hypothesis: in reputation (or trust management) systems, fairness should be an emergent property. The notion of fairness can be precisely defined and investigated based on the theory of equity. In this paper, we investigate the Fairness Emergence hypothesis in reputation systems and prove that , under certain conditions, the hypothesis is valid for open and closed systems, even in unstable system states and in the presence of adversaries. Moreover, we investigate the sensitivity of Fairness Emergence and show that an improvement of the reputation system strengthens the emergence of fairness. Our results are confirmed using a trace-driven simulation from a large Internet auction site.
- Keywords:
- Trust, Simulation, Fairness, Equity, Emergence, Reputation System
 Introduction
Introduction
- 1.1
- In distributed, open systems (ODS), where the behavior of autonomous agents is uncertain and can affect other agents' welfare, fairness of resource or cost distribution is an important requirement. An example of such a situation are Peer-to-Peer systems that rely on the sharing of peers' resources. Unfair distribution of the provided resources can occur if some peers free-ride on others. While some systems (like Bittorrent) combat free-riders, they usually cannot achieve fair distributions of resources. In particular, peers who have provided many resources in the past may not receive a similar amount of resources when they need them. Another example are grid systems, where the scheduling of tasks should take into account the fair distribution of available computational resources.
- 1.2
- Assuring fairness of resource distributions in a system without centralized control is difficult. On the other hand, in such systems, trust management (TM) is widely used. Examples of practical use of trust management are (among others) reputation systems in online auctions and Peer-to-Peer file sharing systems. Trust management is aimed to provide procedural fairness: to ensure that peers who violate rules or norms of behavior are punished.
- 1.3
- The question considered in this paper is whether or not TM systems can also be used to assure or increase fairness of resource distribution. While this is different (and more difficult) from procedural fairness, the two concepts are related. Norms and rules of behavior are often defined with the fairness of resource or cost distribution in mind. As an example, consider the laws that oblige all citizens to pay taxes. Enforcing procedural fairness (abiding by the tax laws) has the goal of enabling efficient resource redistribution by the government (among its other duties). Such a resource redistribution should result in increased fairness of income distribution.
- 1.4
- The research problem described in this paper can be formulated as the following hypothesis: in successful reputation (or trust management) systems, fairness should be an emergent property[1]. We shall refer to this hypothesis as the Fairness Emergence (FE) hypothesis. In this paper, the FE hypothesis has been verified.
- 1.5
- We will use a simulation approach to verify the FE hypothesis. However, our goal is not just to see whether the hypothesis applies in an abstract model, but to verify the validity of the FE hypothesis in realistic conditions. In order to realize this goal, we need to study the behavior of a popular, well understood trust management system. The natural candidate for such a system is the reputation system used by Internet auctions. Previous studies have established that the use of reputation systems increases the total utility of agents (Pollock 1992; Resnick 2002), and investigated the sensitivity of reputation systems to selfish or malicious user behavior (Dellarocas 2000). This study investigates how the use of reputation impacts the fairness of the distribution of agents' utilities.
- 1.6
- The goal of verifying the FE hypothesis under realistic conditions can be fulfilled by a study of Internet auction systems under non-stationary conditions, and in the presence of selfish and malicious users. Reputation systems used in other applications, such as P2P networks, are vulnerable to the same effects (Wierzbicki, 2010). Therefore, our model of a reputation system is sufficiently general to apply to different applications, while at the same time we are able to draw on the well-known properties of reputation systems used in Internet auctions in order to increase the realism of our model. This is done at the risk of drawing conclusions that will apply mostly to Internet auctions. The realism of our study of reputation systems for Internet auctions is increased further by the use of trace-driven simulation (to our knowledge, this is the first such study described in the literature). We have obtained a large trace from a Polish Internet auction provider that is used in the second group of simulations to realistically model agent presence in the system. However, the results from our first group of simulations are sufficiently general to warrant drawing conclusions about the FE hypothesis in other applications domains. An example of such a domain is the division and scheduling of tasks in collaborative P2P applications.
- 1.7
- Also, the fairness of distributions of users' utilities in Internet auctions is an important goal in its own right. Buyers or sellers in Internet auctions expect that if they behave as fairly as their competitors, they should have a similarly high reputation. In other words, the users of a reputation system expect that the reputation system give a fair distribution of reputations. In the absence of other differentiating factors, this should also ensure a fair distribution of utilities. This expectation of users is a consequence of the general social norm: people expect fair treatment from many social and business institutions, like a stock exchange, or an Internet auction site.
- 1.8
- The questions considered in this work are therefore the following: is the FE hypothesis universally true? Does the FE hypothesis apply under realistic conditions? How sensitive is fairness emergence to the performance of a TM system? What are the conditions that can lead to a lack of fairness emergence due to the use of a TM system? Does fairness emergence occur if agents are infrequently unfair? Does fairness emergence occur if agents have a low sensitivity of to reputation? Does fairness emergence occur if agents employ discrimination? These and like questions can lead to a better understanding of the ability of trust management systems to increase fairness of distribution of costs or resources in an open, distributed system without central control.
- 1.9
- In order to evaluate distributional fairness, it becomes necessary to define it precisely. In this work, fairness is defined based on a strong theoretical foundation: the theory of equitable optimality (Kostreva 1999, 2004). The concept and criteria of fairness in trust management systems, based on the theory of equitable optimality, are discussed in the next section. Section 2 also discusses the chosen approach to test the FE hypothesis by laboratory evaluation of reputation systems. Section 3 describes the simulator used for verifying the FE hypothesis, along with the trace-driven simulation approach which is a major contribution of this work (to our knowledge, it is the first trace-driven simulation of a reputation system of an Internet auction site). Section 4 describes the results of a simpler experiment with a closed system, and the sensitivity of fairness emergence to various aspects of a reputation system. Section 5 describes the results of the trace-driven simulation that partially support the FE hypothesis. Section 6 concludes the paper.
 Related work
Related work
- 2.1
- Reputation systems have usually been studied and evaluated using the utilitarian paradigm that originates from research on the Prisoner's Dilemma. Following the work of Axelrod (1984), a large body of research has considered the emergence of cooperation. The introduction of reputation has been demonstrated as helpful to the emergence of cooperation[2]. In the Prisoner's Dilemma, the sum of payoffs of two agents is highest when both agents cooperate. This fact makes it possible to use the sum of payoffs as a measure of cooperation in the iterated Prisoner's Dilemma. This method is an utilitarian approach to the evaluation of reputation systems (Mui 2003; Dellarocas 2000; Wierzbicki 2006). In most research, a reputation system is therefore considered successful when the sum of utilities of all agents in the distributed system is highest. Note that the utilitarian paradigm is used even if the simulation uses a more complex model of agent interaction than the Prisoner's Dilemma.
- 2.2
- The use of Prisoner's Dilemma allows for an implicit consideration of agent fairness, while the sum of utilities is considered explicitly. Yet, in a more realistic setting, the assumptions of the Prisoner's Dilemma may not be satisfied, and it is possible to point out cases when the utilitarian approach fails to ensure fairness: in an online auction system, a minority of agents can be constantly cheated, while the sum of utilities remains high. A notable example of explicit consideration for fairness of reputation systems is the work of Dellarocas (2000). An attempt to demonstrate that explicit consideration of fairness leads to different results in the design and evaluation of reputation systems has been made in Wierzbicki (2007).
- 2.3
- This paper extends the preliminary results published in Wierzbicki (2009). The new contributions of this paper are the consideration of an open reputation system by the means of trace-driven simulation that controls the roles and activity of agents, which considerably improves the realism of conditions used to evaluate the FE hypothesis. Moreover, a better measure of inequality—the area below the Lorenz curve—is used in this paper (the previous work used the Gini coefficient which is less suitable for evaluation of fairness; see next section). The sensitivity of fairness emergence is studied in more detail because of the consideration of an improved reputation algorithm.
Distributional Fairness and the Theory of equitable optimality
- 2.4
- Much of the research on fairness has been done in the area of the social sciences, especially social psychology. The results of this research allow to understand what are the preference of people regarding fairness, and how people understand fair behavior. Interestingly, much of the research in that area has been influenced by the seminal work of Deutsch, who is also an author of one of the basic psychological theories of trust (Deutsch 1975, 1987). To begin our discussion of fairness, let us begin with three general kinds of fairness judgements identified by social psychology (Tyler 1998): distributive fairness, procedural fairness and retributive fairness. Distributive fairness is usually related to the question of distribution of some goods, resources or costs, be it kidneys for transplantation, parliament mandates, or the costs of water and electricity. The goal of distributive fairness is to find a distribution of goods that is perceived as fair by concerned agents. Procedural fairness focuses on the perceived fairness of procedures leading to outcomes, while retributive fairness is concerned with rule violation and the severity of sanctions for norm-breaking behavior. It is possible to think of distributive fairness as a special kind of procedural fairness. If a distribution problem can be solved fairly, then a fair procedure would require all agents to take a fair share of the distributed good or cost. Procedural fairness, however, is also applied in the case when a fair solution cannot be found beforehand or cannot be agreed upon. Both distributional fairness and procedural fairness aim to find fair solutions of distribution problems.
- 2.5
- The most abstract definition of fairness used in this paper is therefore as follows. Fairness means the satisfaction of justified expectations of agents that participate in the system, according to rules that apply in a specific context based on reason and precedent [3]. This general definition applies to distributive, procedural or retributive fairness. However, for the purpose of testing the Fairness Emergence hypothesis, we have decided to use the concept of distributive fairness, since people care most about the fairness of outcomes, not procedures (distributive fairness is a concept closely related to social justice (Rawls 1971) ). Although extensively studied (Young 1994), distributive fairness is a complex concept that depends much on cultural values, precedents, and the context of the problem. Therefore, a precise and computationally tractable definition is needed to use it in research.
- 2.6
- The understanding of the concept of distributional fairness in this paper is based on the theory of equitable optimality [4] as presented in Kostreva (1999, 2004). Before we introduce the theory formally, let us attempt to give a more intuitive understanding.
- 2.7
- In a fair distribution problem, all agents' outcomes must be taken into consideration. The problem of optimizing the outcomes of all agents can be formulated as a multicriteria problem. We shall refer to this as the efficient optimization problem. Efficient optimization of agent's outcomes need not have any concern for fairness. The outcomes can be the shares of goods or costs received by agents in an ODS. Let y=[y1,…,yn] be an outcome vector of the efficient optimization problem (assuming there are n agents that maximize their outcomes, and yi is the outcome of agent i)[5].
- 2.8
- Note that this formulation of the distribution problem does not use subjective agent utilities, but rather uses objective criteria that are the same for all agents (for example, if the problem is a distribution of goods, than an objective criterion could be the monetary value of the goods at a market price; although it is possible that agents would subjectively value some goods higher in spite of a lower or equal monetary value). However, the theory of equitable optimality can also be formulated using subjective utilities, under the assumption that these utilities are comparable (Lissowski 2008; Sen 1970). The following explanation of the theory of equitable optimality applies in both cases, but we have chosen to present it using objective criteria because of increased simplicity.
- 2.9
- Note that we assume that all agents are equally entitled or capable of achieving good outcomes. We shall call such agents similar agents. The theory of equitable optimality can be extended to take into account various priorities of agents, but this makes the definition considerably more complex (Ogryczak 2009). If the agents are not similar because they have different levels of expenditure or contribution and are therefore entitled to different outcomes, a common practice is to transform every agent's outcome by dividing them by the agent's contribution (Wierzbicki 2009). After such a transformation, it is possible to think of the agents as similar, because they are equally entitled to receive a unit of outcome per unit of contribution. If some agents are not similar for other reasons (in an Internet auction, the reason can be that various sellers have various quality of goods or services, and various marketing), then it is still possible to consider the fairness for a subset of agents that are similar according to these criteria. A system should be able to at least provide fairness to this subset of similar agents. This approach is equivalent to a ceteris paribus assumption from economics: when all other factors can be excluded and all agents are equally entitled, the theory of equitable optimality can be used for testing distributional fairness. In a laboratory setting, such conditions can be satisfied and we can design systems that realize the goal of fairness, even in the presence of adversaries that do not act in a procedurally fair manner.
The Lorenz Curve Two incomparable distributions Figure 1. Examples of Lorenz curves - 2.10
- Figure 1 shows one of the key concepts illustrating distributive fairness: the Generalized Lorenz curve. The Generalized Lorenz curve is obtained by taking the outcomes of all agents that participate in a distribution and ordering them from worst to best (the Generalized Lorenz curve is usually divided by the number of agents, n (Shorrocks 1983). In this paper, we use a rescaled version that is not divided by n). Let us denote this operation by a vector function θ(y) = [θ1 (y),…, θ n (y)] of the outcome vector y.
- 2.11
- Then, the cumulative sums of agents' utilities are calculated: starting from the utility of the worst agent (θ1), then the sum of utilities of the worst and the second worst (θ2), and so on, until the sum of all agents' utilities. This sum is denoted on the figure as θn. The second line on the figure, the equal distribution line, is simply a straight line connecting the points (1, θ1) and (n, θn). The area between the two curves, denoted by S, can be seen as a measure of inequality of the agent's utilities. The objective of distributive fairness is to reduce this inequality, bringing the Lorenz curve closer to the equal distribution line, while at the same time keeping in mind the total efficiency (sum of all agents' utilities), which is represented by the right end of the Lorenz curve at a value of θn. Note that these two objectives frequently form a trade-off (for example, if the distribution is constrained by a budget).
- 2.12
- The right part of the Figure 1 shows two Lorenz curves that correspond to different distributions among the same agents. The first distribution has a higher θn, but also a higher inequality, while the second distribution has a lower total of agents' utilities, but is more fair. In terms of equitable optimality, the two distributions on the right part of the Figure 1 are incomparable—the choice of one of them depends on the preferences of a decision maker[6]. However, the most desirable goal of the theory of equitable optimality is finding solutions that are equitably optimal. For any solution that is not equitably optimal, we can find another solution such that its Lorenz curve is at every point above the Lorenz curve of the equitably dominated solution.
- 2.13
- The area between the Lorenz curve and the equal distribution line can be simply calculated and used as a computable measure of inequality. The Gini coefficient (frequently used in economics) is the area S normalized by θn : Gini=S/2θn. Note that minimizing the Gini coefficient can lead to worse total outcomes (sums of all agent's utilities). This drawback can be overcome by taking into account the Gini coefficient and the sum of all utilities at the same time. When two distributions are compared, if one of them has a smaller Gini coefficient and a larger sum of all utilities, then it should be more equitable (although this is not a sufficient condition).
- 2.14
- It is also possible to use a different inequality measure: the area below the Lorenz curve (equal to BLC=(nθn/2)-S ). In this paper, we have chosen to use the BLC as an inequality measure. The reason for this choice is that an improvement in terms of the theory of equitable optimality (a new, equitably dominating solution) always causes an increase of the BLC. On the other hand, an equitably dominating solution can have a larger Gini than a dominated solution (consider for example a solution that just increases the outcome of the best-off agent. This solution may dominate another, but will have a larger Gini and a larger BLC). Therefore, the area below the Lorenz curve is the best criterion of inequality, according to the theory of equitable optimality. However, note that even if the area below the Lorenz curve increases, the distribution does not always become more equitable. An increase of the BLC and the total sum of outcomes gives a better assurance that the distribution is indeed more equitable, although it is still not a sufficient condition (only by considering all partial sums that form the generalized Lorenz curve are we able to verify equitable domination with certainty).
- 2.15
- It is necessary to use all fairness criteria with caution, since finding equitably optimal solutions is a multi-criteria problem that cannot be simply reduced to the comparison of single or two criteria. According to the theory of equitable optimality, an equitably optimal solution (or simply equitable solution) is any Pareto-optimal solution of the equitable optimization problem, which is obtained from the efficient optimization problem by the transformation θ of cumulative ordered sums. The criteria of the equitable optimization problem are simply the vector θy. The theory of equitable optimality allows not only to define fairness with precision, but also to search for equitable solutions by applying standard methods of multi-criteria optimization to the equitable optimization problem.
- 2.16
- The theory of equitable optimality also has an axiomatic expression (Kostreva 2004). The axioms of the theory of equitable optimality define a preference relation on the outcome vectors of the efficient optimization problem. An equitable preference relation is any symmetric and transitive relation satisfying the following axioms (Kostreva 2004):
- Impartiality - The ordering of the outcome values is ignored (e.g. a solution y=[4, 2, 0] is equally good as a solution y=[0, 2, 4]). First of all, fairness requires impartiality of evaluation, thus focusing on the distribution of outcome values while ignoring their ordering. That means, in the efficient optimization problem we are interested in a set of outcome values without taking into account which outcome is taking a specific value. Hence, we assume that the preference model is impartial (anonymous, symmetric). In terms of the preference relation it may be written as the following axiom
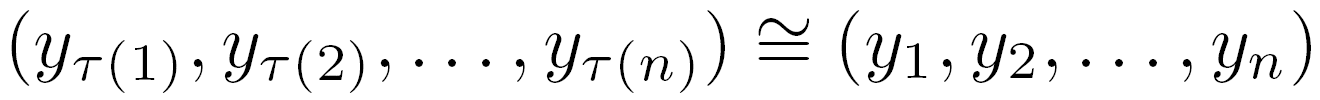
for any permutation τ of I (1) which means that any permuted outcome vector is indifferent in terms of the preference relation.
- Monotony - An outcome improving the value of one of the objectives is preferred, if the values of other objectives are not deteriorated (e.g. y=[4, 2, 0] is preferred to y=[3, 2, 0]). This axiom is actually a repetition of the requirement of efficiency. It guarantees that only efficient solutions will be chosen as equitable solutions. Another way of looking at it is that the monotony axiom prevents a phenomenon well-known in former Communist countries: that of "equating downwards", or making outcomes worse (and more equal, but not more equitable) for everyone. The same phenomenon could also occur if agents can cheat on effort, such as freeriders in P2P systems. The monotony axiom assures that a system that is dominated by freeriders will not be considered as good as a system where some peers provide content. The axiom can be expressed as follows:
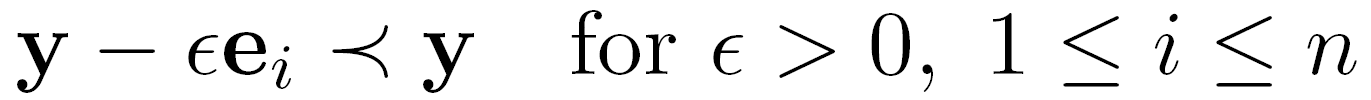
(2) Where ei is a unit vector that has coordinate i equal to 1 and all other coordinates equal to 0.
- Principle of transfers - A transfer of any small amount from an outcome to any other relatively worse-off outcome results in a more preferred outcome vector (e.g. y=[3, 2, 1] is preferred to y=[4, 2, 0]). Fairness requires equitability of outcomes which causes that the preference model should satisfy the (Pigou-Dalton) principle of transfers. The principle of transfers states that a transfer of any small amount from an outcome to any other relatively worse--off outcome results in a more preferred outcome vector. As a property of the preference relation it represents the following axiom
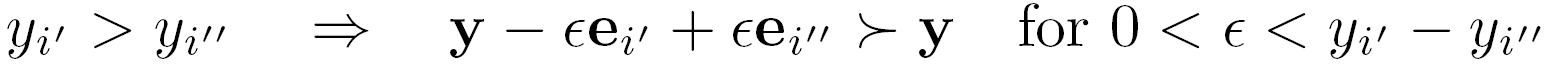
(3)
- Impartiality - The ordering of the outcome values is ignored (e.g. a solution y=[4, 2, 0] is equally good as a solution y=[0, 2, 4]). First of all, fairness requires impartiality of evaluation, thus focusing on the distribution of outcome values while ignoring their ordering. That means, in the efficient optimization problem we are interested in a set of outcome values without taking into account which outcome is taking a specific value. Hence, we assume that the preference model is impartial (anonymous, symmetric). In terms of the preference relation it may be written as the following axiom
- 2.17
- It can be shown that any equitably optimal solution (a Pareto-optimal solution of the problem max{θy}) is not dominated by any other solution in the equitable preference relation (Kostreva 2004). Thus, the concept of distributive fairness as expressed by the theory of equitable optimality is well understood by considering the three above axioms. These axioms show, among other things, that the theory of equitable optimality avoids the pitfall of preferring more equal, but less globally efficient solutions. According to the axiom of monotony, increasing any objective without worsening the others improves the overall solution in terms of the equitable preference relation.
- 2.18
- Using the theory of equitable optimality, the Fairness Emergence hypothesis can be reformulated as follows: if a good trust management system is used by agents, then distribution of similar agents' utilities should become more equitable. The inequality criteria described in this section, such as the Gini coefficient or the area below the Lorenz curve (BLC), can be used together with the total efficiency θn to check whether a distribution has become more equitable (in rare cases, these two criteria may not be sufficient to guarantee equitable domination, but that can be done only by checking all criteria of the equitable optimization problem). Taking into account the total efficiency alongside with BLC or Gini will allow us to check whether the reputation system is capable of finding equitable solutions that are also good in the utilitarian sense.
- 2.19
- Note that while the theory of equitable optimality has been expressed here for agents that have equal entitlements to shares of distributed goods or costs, this limitation may be removed. Agents can have various entitlements expressed by weights (for example, integer weights). The theory of equitable optimality is simply extended for such a case as follows: every weighed agent is cloned into a number of agents with weight 1. The number of cloned agents is equal to the weighed agent's integer weight. The outcome of the weighed agent is equal to the sum of outcomes of his clones. The theory of equitable optimality (and methods for finding equitable solutions) may be applied to the cloned agents that are equally entitled. For a more detailed introduction to the theory of equitable optimality, see (Wierzbicki, 2010).
 Design of Simulation Experiments
Design of Simulation Experiments
- 3.1
- To test the Fairness Emergence hypothesis, we have used simulation experiments. The FE hypothesis would hold if we could establish that the reputation system causes an increase of the equity of the distribution of utilities. In particular, we will be interested to study the impact of the quality of the reputation system on the equity of utility distributions.
- 3.2
- The simulator is based on the Repast 3.1 platform (Repast 2003) and resembles a reputation system of Internet auctions. In the design of the simulator, we had to make a decision about a sufficiently realistic, yet not too complex model of the auction system, of user behavior, and of the reputation system. We chose to simulate the reputation system and the behavior of its users as faithfully as possible (the only simplification is that we use only positive and negative feedbacks). The reputation system is always available and provides complete information based on available feedbacks (we do not take into account the incompleteness of results of searches for feedbacks, but this effect is similar to the lack of available feedback from the point of view of the agent). The provided information is processed by a reputation algorithm (in our simulations, we do not specify where this algorithm is executed—it could be done by the reputation system or by the agents themselves). In this paper, we consider two reputation algorithms: a simple ratio of positive feedbacks and an algorithm that takes into consideration implicit negative feedbacks.
- 3.3
- The auction system, on the other hand, has been simplified. We simulate the selection of users using random choice of a set of potential sellers. The choosing user (the buyer) selects one of the sellers that has the highest reputation in the set.
- 3.4
- After the buyer has selected a seller, a transaction between the two agents may occur. However, this is not always the case in our simulations, because the chosen seller may have a reputation that is too low for the buyer. If the chosen seller has a reputation below the buyer's acceptance threshold, no transaction will occur. Still, we count the number of such transaction attempts in our simulation. The number of transaction attempts is used as a measure of time in our simulation (since we assume that each transaction attempt would consume some time and effort on behalf of a buyer, the number of such transaction attempts is limited). Furthermore, the granularity of transaction attempts in our simulation is very high. To show meaningful results, we group several hundred subsequent transaction attempts into one turn. The turn is used as a measure of time for the demonstration of simulation results.
- 3.5
- In this paper, we describe two sets of simulation results. The first set was obtained from simulations of a closed system of agents—the set of agents was kept fixed for the duration of the simulation. This approach has been used initially to reduce the number of factors that could impact the results, and to study fairness emergence in a simpler setting. The second set of simulation results was obtained from a trace-driven simulation approach that was used to control the presence of sellers in the system. This allowed for a more realistic simulation of an open system of buyers and sellers, where the time a buyer or seller could spend in the system was controlled by the trace. The second set of simulation results takes into account more complex factors, but was used to verify the results from the first set.
Agent behavior
- 3.6
- In our simulator, a number of agents interact with each other. There are two types of agents in the system: fair and unfair agents. Unfair agents model adversaries. To test the FE hypothesis, we shall be interested in the fairness of utility distributions of fair agents. The total payoffs of fair and unfair agents will also be compared.
- 3.7
- In the closed system simulations, all agents are similar. In the trace-driven simulations that will be discussed in more detail below, agents can be buyers or sellers (this separation is a consequence of the separation of roles in real auction systems, where users mostly either buy or sell). This additional distinction makes the simulations more realistic.
- 3.8
- When an agent wants to carry out a transaction, it must make three decisions. The first decision concerns the choice of a transaction partner (seller) and whether or not to engage in the transaction. The agent chooses his partner from a randomly selected set of k other agents (in the simulations of the closed system, k has been equal to 3 or 1). From this set, the agent with the highest reputation is chosen. However, if the highest reputation is lower than a threshold pminchoice (in the closed system simulations, fair agents choose partners with reputation at least 0.45, and unfair agents: 0.3), then the choosing agent will not engage in any transaction. If the best agent's reputation is sufficiently high, the choosing agent will engage in the transaction with a certain probability p (in the simulations presented here, this probability was 1).
- 3.9
- The second decision concerns the agent's behavior in the transaction. This decision can be based on a game strategy that can take into consideration the agent's own reputation as well as the reputation of his partner, the transaction history and other information. We decided to use the famous Tit-for-tat strategy developed by Rapaport but extended with using a reputation threshold: if two agents meet for the first time and the second agents' reputation is below pmingame, the first agent defects. The strategy used in the simulations presented here has also been based on the threshold pmincheat. In the case when the partner's reputation is higher than pmincheat, the agent would act fairly; otherwise, it would cheat with a certain probability c. In the simulations presented here, fair agents never cheat, while unfair agents had a cheating probability of 0.2 and a reputation threshold of 0—meaning that unfair agents cheated randomly with a probability of 0.2. Both agents in a transaction can cheat (in an Internet auction, the seller can cheat the buyer by not sending goods, and the buyer can cheat by not paying the agreed amount after winning the auction).
- 3.10
- The third decision of the agent concerns the sending of reports. For positive and negative reports, an agent has separate probabilities of sending the report. In the simulations presented here, the probability of sending a positive report, prep+ was 1.0, while the probability of sending a negative report prep-varied from 0 to 1. This choice is based on the fact that in commonly used reputation systems (Wierzbicki 2006), the frequency of positive reports is usually much higher than of negative reports. In the simulation it is also possible to specify a number of agents that never send reports. This behavior is independent of the honesty or dishonesty of agents.
- 3.11
- The strategies of agents in our simulations do not evolve, but remain fixed for the duration of simulation. In this respect our work is different from the research on evolution of cooperation or indirect reciprocity (Wilson 1975, 1985). Our research is focused on verifying the effect of trust management on fairness, without considering how the strategy of using trust management or reputation has evolved—that is the concern of related and future work (Pollock 1992, Castelfranchi 1998).
- 3.12
- Note here that the presented model of agent behavior with respect to the reputation system matches many kinds of applications. The model has been described using Internet auctions as an example. Another kind of realistic application is a Peer-to-Peer system. A transaction in such a system is an exchange of data or services (resources). Unfair behavior in such a system is called free-riding: peers use resources of others, but do not reciprocate. A P2P application can use reputation to combat free-riding. The reputation system in a P2P application is distributed, in contrast to the reputation system used in Internet auctions. However, the discovery of proofs by the P2P reputation system is affected by the quality of the distributed search algorithms and by the presence of adversaries, who can attempt to drop negative proofs. A result is a smaller availability of negative reports, which has been modeled in the simulator by varying the probability prep- from 0 to 1. This type of adversary has been discussed frequently in the literature (Liu 2004; Lee 2003; Kamvar 2003). The first set of our simulations presents results that can apply also to P2P applications that use a reputation system.
Reputation system warm-up
- 3.13
- A real reputation system has a large initial history that can be used to evaluate infrequently present agents. In the simulation approach, this initial history had to be reproduced. In the closed system, for each simulation, the first 20 turns have been used to warm-up the reputation system by acquiring an initial history of agent behavior. This means that the payoffs have not been recorded, but an agents' reputation has been modified by positive and negative reports. This method has been used to model the behavior of a real reputation system, where the system has available a long history of transactions. Simulating the reputation system without a warm-up stage would therefore be unrealistic.
- 3.14
- In a closed system, it is possible to warm-up the reputation of all agents at the same time, at the beginning of the simulation. In the open, trace-driven approach, the trace represents a period of time taken from the operation of a real Internet auction site. Agents present in the trace could have been present in the system before the beginning of the trace. As this information is not available, it is also not realistic to simulate the system without a warm-up. However, this warm-up can be done separately for each seller. If a buyer would select a seller that was in the warm-up stage, the results of the transaction were not recorded in the utility of the buyer and the seller. The seller's reputation was updated. A fixed number of l transactions was used as a warm-up. This ensured that the reputation system had some initial information about each seller, before the buyers utilities were recorded. In the simulation results presented below, l=5. Reducing the length of the warm-up had a strong effect on emergence: emergence was not observed for l=0, for any other setting of simulation parameters.
Trace-driven simulation of an Internet auction system
- 3.15
- Trace-driven simulation allows to overcome two main drawbacks of simpler simulation approaches. The utilities of agents in the system will depend on the time that agents spend in the system. The simplest approach would be to simulate a closed system of agents; however, such an approach may not be sufficiently realistic, as agents in real ODS tend to join and leave the system frequently. This limitation may be removed by allowing agents to be in the system for a random number of rounds. This time of an agents' activity can chosen from a distribution that is similar to empirical data (for example, a Pareto distribution). Yet, this method of simulating an agent's activity is still not sufficiently realistic. For that reason, we have decided to use trace-driven simulations.
- 3.16
- We have obtained a trace from the largest Polish Internet auction site. The trace includes approximately 200 000 seller transactions from 6 months. In the trace, there were about 10000 sellers randomly selected from the auction house. The weekly number of seller transactions in the trace is shown on Figure 2. The trace was used to control the times spent by sellers in the simulated system. In other words, using trace-driven simulations allowed us to simulate an open system and to preserve the real processes of seller activity in the system. Figure 3 shows the distribution of the number of transactions made by a seller. It can be seen that this distribution resembles a heavy-tailed distribution.
- 3.17
- The behavior of sellers was not recorded in the trace, and it is therefore simulated as described in the previous section. Moreover, the buyers are not trace-driven. Buyers initiate transactions with sellers who are present in the system at a given time (in the trace-driven simulations, one turn is equivalent to one day of the trace. During this turn, only the sellers who offered auctions on that day are present in the system). Buyers choose sellers in the same way as in the simulations of the closed system, choosing a seller with the highest reputation from a random set of k sellers that are active in this turn. Buyers are also able to reject transactions if a chosen seller's reputation is below a threshold.
- 3.18
- The second drawback of simple simulation approaches is related to the lack of roles of agents. In the trace driven simulation, it was possible to divide agents into two sets of buyers and sellers, which allowed the simulations to resemble real Internet auctions. The proportions and activity distributions of buyers and sellers were preserved.
Figure 2. Daily number of seller transactions in the trace Figure 3. Distribution of number of transactions of a seller
 Fairness emergence in a closed system
Fairness emergence in a closed system
-
Experiment setup
- 4.1
- In simulations of the closed system, there was a total of 1500 agents, out of which 1050 where fair and 450 were unfair. While the proportion of unfair agents is high, they cheat randomly and at a low probability—so a unfair agent is really a "not totally fair agent". Also, considering that frauds in Internet auctions are among the most frequent digital crimes today, and considering that cheating in a transaction may be more frequent than outright fraud—it may be sending goods that are of worse quality than advertised—this proportion of unfair agents seems realistic.
- 4.2
- The simulator can compute reputations using all available feedbacks. The results of the simulation include: the reputations of individual agents and the total utilities (payoffs from all transactions) of every agent. In the simulations presented here, an agent's reputation is computed as the proportion of the number of positive reports about the agent to the number of all reports.
- 4.3
- All simulations were made using pseudo-random numbers, therefore the Monte Carlo method is used to validate statistical significance. For each setting of the simulation parameters, 50 repeated runs were made, and the presented results are the averages and 95% confidence intervals for every calculated criterion. The confidence intervals were calculated using the Student-t distribution.
- 4.4
- We decided to use transaction attempts instead of the number of successful transaction as a stop condition because we believe that an agent would consider each transaction attempt as an expense of time and effort. In most presented simulations for each turn, 500 transaction attempts have been made.
Closed System Simulation Results
- 4.5
- To verify the Fairness Emergence hypothesis, we have been interested to investigate the impact of a reputation system on the equity of the agents' utility distribution. Equity of utility distributions has been measured using fairness criteria based on the theory of equitable optimality; however, other criteria such as the sum of agent utilities are considered as well. The simulations revealed that the Fairness Emergence hypothesis holds in several cases, but not universally; therefore, we have investigated the sensitivity of fairness emergence to various factors that influence the quality of the reputation system.
Fairness Emergence in the Long Term
- 4.6
- The first studied effect has been the emergence of fairness in the long term. In the simulation experiment, we have measured the area under the Lorenz curve (BLC) and have run the simulation until the BLC stabilized. This experiment has been repeated using three scenarios: in the first one, the agents did not use any reputation system, but selected partners for transactions randomly. In the second experiment, the reputation system was used, but agents submitted negative reports with the probability of 0.2. In the third experiment, negative reports have always been submitted.
Figure 4. Fairness Emergence in the long term - 4.7
- The results of the three experiments are shown on Figure 4. The Figure plots the average BLC of fair agents from 50 simulation runs against the number of turns of the simulation. It can be seen that when agents do not use the reputation system, the BLC stabilizes for a value that is almost twice smaller than the value of BLC that is obtained when reputation is used. Furthermore, there is a clear effect of increasing the frequency of negative feedbacks: the BLC increases faster and stabilizes at a higher value when prep-=1 . The initial decrease of the BLC from 1 is due to the fact that at the beginning of the simulation, the distribution of fair agent utilities is equal (during the warm-up stage, utilities of agents are not recorded. All agents start with a zero utility after warm-up completes.)
- 4.8
- The result of this experiment seems to be a confirmation of the FE hypothesis. The distributions of fair agents' utilities have a higher BLC (and a higher total sum of utilities) when the reputation system is used. Yet, the problem here is that in realistic auction systems, most agents only have a small number of successful transactions, because they use the system infrequently. In our simulation, new agents did not join the system (although the number of agents was large). The average number of successful transactions of an agent has been about 270, which is much lower than the number of agents; this means that as in a real auction system, the chance of repeated encounters was low. However, this number is still large. The simulations were continued until a stable state was reached; in practical reputation systems, such a situation would not be likely to occur because of the influx of new agents and the inactivity of old ones. For that reason, we have decided to investigate the FE hypothesis in the short term, or in unstable system states.
Fairness Emergence in the Short Term
- 4.9
- The simulation experiments used to study short-term system behavior have been about 8 times shorter than the long-term experiments. For these experiments, the number of successful transactions of an average agent was about 60. Figure 5 shows the BLC of the distributions of fair agents' utilities. On the x axis, we show the number of turns. The figure shows two lines corresponding to different frequencies of sending negative reports by fair agents (unfair agents always sent negative reports). The results show that for low negative report frequencies fairness emerges more slowly. Increasing the available negative reports reduces the time needed for fairness emergence. This effect is apparent very quickly, even after 50 turns of simulation.
Figure 5. Fairness Emergence in the short term - 4.10
- From now on, fairness emergence in the short term is studied more closely to verify whether the improvement of reputation system quality will strengthen fairness emergence. In other words, until now we considered fairness emergence with time, and now we shall consider the sensitivity of fairness emergence to the reputation system's quality. All further experiments have been made in the short term, outside of the stable state of the system.
Effect of Better Usage of Reputation
- 4.11
- The usage of reputation by agents had a particularly strong influence on the emergence of fairness. In our simulations, during a transaction attempt, agents chose a seller with the highest reputation from a set of k candidates. The chosen candidate needed to have a reputation that was higher than the buyer's threshold. If k=1, then the transaction partner was chosen at random and only the threshold pmingame was used to consider reputation. If k=3, it was less likely that an agent with lower reputation would be chosen as a transaction partner. These two scenarios correspond to the real life situation of buyers who are able to select sellers from a larger set, based on their reputation; on the other hand, it could be possible that the choice is low, because only one seller has the required goods or services.
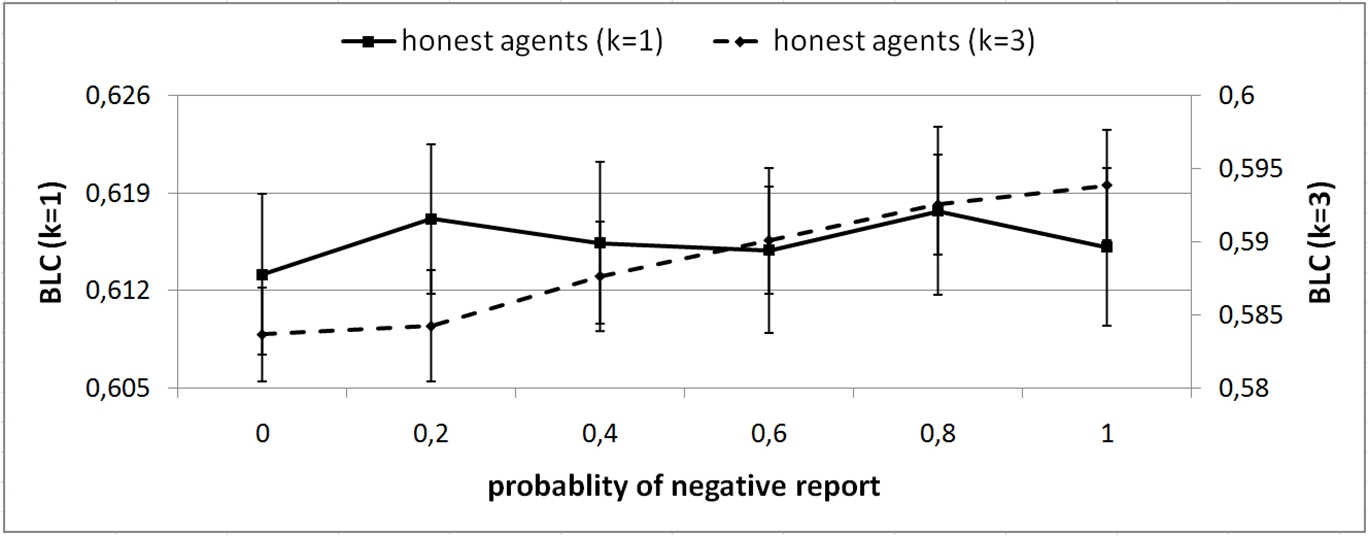
Figure 6. Effect of increased choice on BLC 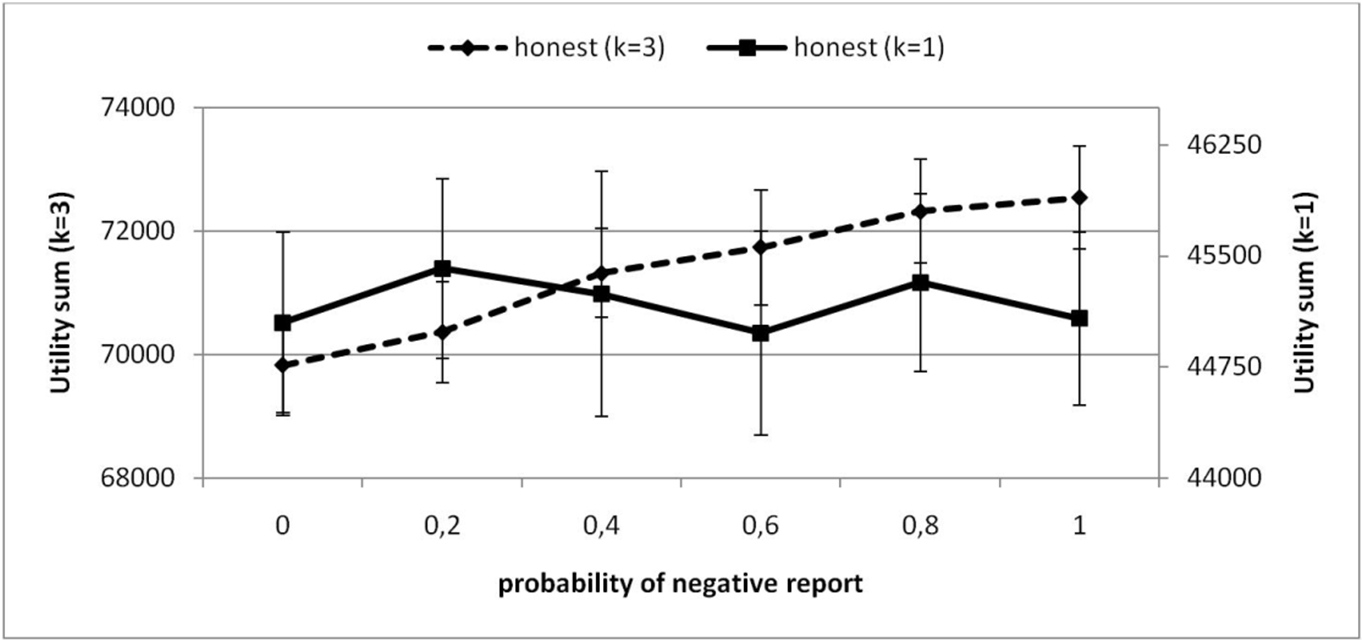
Figure 7. Effect of increased choice on sum of utilities - 4.12
- We have considered the two scenarios while investigating the impact of the frequency of feedbacks on the reputation system. It turns out that increasing the choice of agents is necessary for the emergence of fairness. Figure 6 shows the effect of increasing the frequency of negative feedback on the BLC of fair agents. The figure shows two lines that correspond to the scenarios of k=1 and k=3. It can be seen that if the choice of agents on the basis of reputation is possible (k=3), then the increase in the number of feedbacks leads to an increase of BLC. On the other hand, if the choice is limited (k=1), then the increase in the number of negative feedbacks does not have a statistically significant effect on the BLC. This effect is best explained by the fact that if choice is available, honest agents have a better chance at avoiding dishonest agents while at the same time they do not waste transaction attempts. If agents do not have choice, they can still avoid transactions with dishonest agents, but they will waste transaction attempts and have a lower utility.
- 4.13
- Figure 7 shows the effect of increased choice and varying negative feedback frequency on the sum of fair agents' utilities. It can be seen that once again, enabling the choice of partners based on reputation has a positive effect on the welfare of fair agents. For k=3, fair agents overall had a higher sum of utilities than for k=1, and this sum increased when the frequency of negative reports increased. This also explains why the BLC of fair agents for k=1 was higher than for k=3. Since the sum of utilities was lower for k=1, the BLC could also be lower, although this does not mean that the distribution of utilities for k=1 was more equitable than for k=3.
Effect of Better Feedback
- 4.14
- Better feedback is a prerequisite for increasing the quality of a reputation system. For that reason, we have chosen to investigate the effect of increased feedback on the emergence of fairness. As has been explained previously, the frequency of negative feedback has been varied from 0 to 1. We have also varied the frequency of positive feedbacks and negative feedbacks simultaneously; however, for the simple reputation algorithms considered in this paper, the only significant parameter is the proportion of negative to all feedbacks. For that reason, varying negative feedbacks' sending frequency is sufficient to evaluate the system's sensitivity to feedback availability. Another issue related to feedbacks is the possibility that agents send false feedbacks. Our studies indicate that a small amount of false feedbacks does not impact the results, but a significant amount of false feedbacks will confuse any reputation system. For this reason, in this analysis we disregard the possibility of sending false feedbacks by the agents.
Figure 8. Effect of increased feedback on sum of utilities of all agents - 4.15
- Figure 8 shows the effect of increasing the frequency of sending of correct negative feedback on the sum of utilities of all agents. If the frequency of sending negative feedback is 1, then the reputation system receives all information relevant to the computation of correct reputations. If the frequency is low, then the reputation system is missing important information that could decrease the reputations of unfair agents.
- 4.16
- It turns out that the total sum of all agents' utilities was not affected by the increase of negative feedback frequency. This seems to be a paradox, since we are using the iterated Prisoner's Dilemma as a model of our auction system. Increasing negative feedbacks from 0 to 1 should result in decreasing the ability of unfair agents to cheat, and should therefore increase the payoffs received by both agents in a transaction. However, the number of transactions may be affected, as well, and this can explain the apparent paradox.
Figure 9. Effect of increased feedback on fair and unfair agents' utilities - 4.17
- This experiment also shows that even assuming the use of a Prisoner's Dilemma as a model of a transaction, the use of the sum of all agents' utilities (the utilitarian paradigm) would lead to a wrong conclusion that the system behavior is not affected. From the utilitarian point of view, the reputation system works equally well when the frequency of negative reports is 0, as when it is equal to 1.
- 4.18
- Figure 9 shows that this is not the case. The sum of utilities of fair agents increases, as negative feedbacks are sent more frequently. On the other hand, the sum of utilities of unfair agents drops. The reason for this fact is that with higher frequencies of negative feedback, the reputations of unfair agents decrease, and therefore these agents have fewer successful transactions. On the other hand, fair agents manage to avoid unfair ones, and do not waste transaction attempts (therefore they have more successful transactions and higher payoffs in these transactions).
Figure 10. Effect of increased feedback on BLC - 4.19
- Figure 10 shows effect of increased negative feedback frequency on the BLC. Clearly, increased negative feedback frequency leads to an increased BLC of honest agents' utilities. Note that the effect is statistically significant for the variation of from 0 to 1 (also from 0.4 to 1). Note that these simulations have been made in the short term and that together with the results about the sum of utilities, they prove the FE hypothesis: increasing the quality of the reputation system does indeed lead to more equitable distribution of fair agents' utilities, as the hypothesis suggested.
Effect of Improved Reputation Algorithm
- 4.20
- Fairness emergence could be sensitive to a change in the algorithm that is used to calculate reputations. With better algorithms, perhaps it would be possible to improve fairness. That would be equivalent to fairness emergence with improved trust management system's operation.
Algorithm of implicit negative feedbacks
- 4.21
- The algorithm described in this section has been introduced in Wierzbicki (2006). Most online auction sites use a simple feedback-based reputation system (Resnick 2002). Typically, parties involved in a transaction mutually post feedbacks after the transaction is committed. Each transaction can be judged as 'positive', 'neutral', or 'negative'. The reputation of a user is simply the number of distinct partners providing positive feedbacks minus the number of distinct partners providing negative feedbacks (possibly normalized by the number of all distinct partners). As pointed out in (Malaga 2001), such a simple reputation system suffers from numerous deficiencies, including the subjective nature of feedbacks and the lack of transactional and social contexts. Yet another drawback of feedback-based reputation systems is that these systems do not account for psychological motivation of users. Many users refrain from posting a neutral or negative feedback in fear of retaliation, thus biasing the system into assigning overestimated reputation scores. This phenomenon is manifested by high asymmetry in feedbacks collected after auctions and, equally importantly, by high number of auctions with no feedback provided. Many of these missing feedbacks may convey implicit and unvoiced assessments of poor seller's performance which should be included in the computation of a seller's reputation.
Figure 11. Effect of improving reputation algorithm on BLC - 4.22
- As described in (Wierzbicki 2006), there can be many ways of identifying implicit feedbacks in a real-world reputation system, based on the observation of behavioral patterns. To evaluate the effectiveness of using implicit feedback, we have identified a simpler reputation algorithm that can be simulated and compared to the algorithm of most Internet auction houses.
- 4.23
- Consider a user u with a history of n auctions. Let us assume that only m ≤ n of these auctions have a feedback. Out of these m feedbacks m+ are positive or neutral feedbacks (in practice, neutral feedbacks in reputation systems have a meaning almost similar to negative feedbacks and are very rare), m- are negative feedbacks, while m* = n-m is the amount of missing feedbacks (transactions that had no feedback). Thus, m+ ≤ m ≤ n. The reputation ρu of the user u will be calculated as follows:
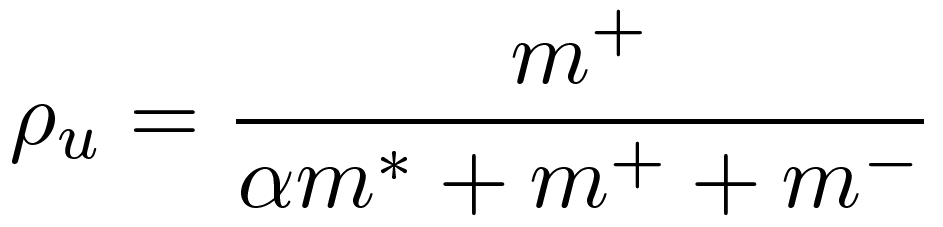
where 0 ≤ α ≤ 1.
- 4.24
- Thus, if α=0, the above reputation score becomes a simple ratio of the number of positive feedbacks received by the user u. In the case when the user has had no auctions, the above formula is undefined. In such case we set the reputation þu to an initial value, þ0. The coefficient α is used to control the importance of implicit negative feedbacks.
Figure 12. Effect of improving reputation algorithm on utility sum - 4.25
- To be precise, in our simulations we use a slightly more complex version of the above algorithm. Since agents in the simulator choose whom they want to interact with on the basis of reputation scores, it is necessary to avoid that the reputation would drop suddenly to a low level. This can happen in the initial phase of the simulation, when the reputation score has not yet stabilized (initially, a single negative feedback could decrease the initial reputation by a large degree). Therefore, we use a simple moving average to smooth reputation changes. The smoothed reputation
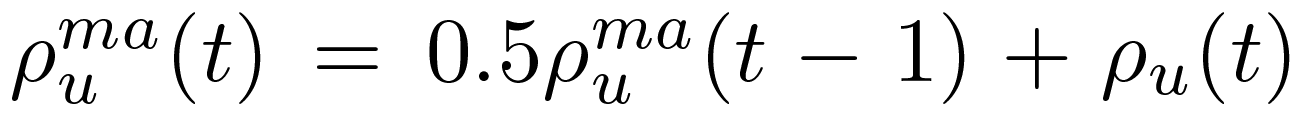
where t is time, and
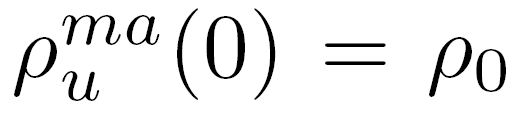
(the smoothed reputation is initialized by the initial reputation value). Note that over time, the impact of the initial reputation decreases exponentially.
- 4.26
- The results of increasing α from 0 to 0.2 on the BLC of honest agents' utility distribution and on the sum of honest agents' utilities are shown on Figure 11 and 12, respectively. The figures show several lines that correspond to various frequencies of negative reports. Increasing the role of implicit negative feedbacks clearly increases fairness, and the effect is strong and statistically significant. This behavior is a confirmation of the FE hypothesis in an unstable state, in the presence of adversaries, and when the probability of negative reports is low. The sum of honest agents' utilities also increases when α is increased.
- 4.27
- The observed effect can be explained similarly as the effect of increasing frequencies of sending negative feedback. Note that the effect of varying α from 0 to 0.2 is similar to the effect of increasing the probability of negative feedbacks. Larger values of α have been found to lead to a decrease of the Gini coefficient in our previous research (Wierzbicki 2007) but this effect has been obtained for a different, specific version of the simulations system and need to be studied further to allow generalization.
 Fairness emergence in the open system
Fairness emergence in the open system
- 5.1
- In the previously described simulations scenarios, all agents were treated equally (although we have referred to the agent who initiated a transaction attempt as a ''buyer'', all agents had an equal chance to become a ''buyer'' in the described simulations). Moreover, all agents had a similar level of activity in the system. Agents could not leave the system during the simulation and were chosen over and over again for transaction attempts. New agents could not join the system. This approach had an impact on the evaluation of the reputation system. In a realistic reputation system, the amount of information available about new agents would be considerably less than the amount of information available about agents that have been active for some time in the system. In the closed system, in the long term, the reputation system would have very good information about agents. Considering the operation of the reputation system in the short term partially reduces that problem, but does not fully solve it.
Figure 13. Fairness emergence in the open system - 5.2
- The reason for the use of the closed system is that without additional information or assumptions, it was not possible to specify how active the agents should be in the system. In this section, we are going to remove this limitation, based on the trace-driven approach described in section 3. On the other hand, the previously described results were more general and could apply to a variety of applications of reputation systems.
- 5.3
- To test the FE hypothesis in an open system, we have measured the utilities of two kinds of agents: the buyers and the fair sellers. By the FE hypothesis, the distribution of both kinds of utilities should become more equitable with an improvement of the reputation system. The results of the experiments partially support that hypothesis: the distributions of buyers become more equitable, but the BLC of the distributions of fair sellers does not vary significantly. We attribute this result to the chosen simulation scenario. Varying the probability of negative reports had an impact on a seller's reputation, but we have not simulated unfair buyers, so no effect on the utilities of fair sellers has been observed.
- 5.4
- Figure 13 shows the effect of increasing the probability of negative reports on the sum of utilities of all buyers and on the BLC of the distribution of buyers' utilities. Since both BLC and the utility sum increase, it can be concluded that the distribution of buyer's reputation indeed becomes more equitable. The effect becomes statistically significant for an increase of the probability of negative reports from 0 to 0.8. Thus, the FE hypothesis is partially confirmed in a realistic open system.
Figure 14. Utilities of unfair sellers in the open system - 5.5
- The reputation system effectively prevents unfair sellers from exploiting buyers. Figure 14 shows the sum of utilities of all unfair sellers that decreases with the increasing probability of negative reports. Once again, the effect becomes statistically significant for an increase of the probability of negative reports from 0 to 0.8.
Figure 15. Sensitivity of Fairness Emergence to unfair seller behavior - 5.6
- We have investigated the sensitivity of Fairness Emergence to the behavior of unfair sellers (adversaries). To observe this effect, the probability of cheating by a unfair seller was varied. The results are shown on Figure 15. As expected, the Fairness Emergence was strongest for the case when unfair sellers cheated with probability 1. This meant that the reputation system could easily spot adversaries. Decreasing the probability of cheating weakens Fairness Emergence, with the values of 0.5 as a threshold. For lower probabilities of cheating, Fairness Emergence was not observed. This result can be explained by the simple reputation algorithm used in our simulation scenario (recall that reputation is a simple ratio of the number of fair transactions to the number of all transactions).
Table 1: Comparison of simple and discriminating adversary strategies for a probability of negative reports of 0.8
BLC buyers Utility sum buyers Utility sum dishonest sellers Utility sum honest sellers Simple strategy 0.8461 27781 30674 31182 Discrimination strategy 0.778 28361 31358 30184 - 5.7
- Another, sophisticated adversary behavior is discrimination. An adversary seller that uses a discrimination strategy will cheat only a selected minority of buyers. His selection strategy could be based on the number of transactions that a buyer participated in: the discriminating seller would cheat only inexperienced buyers. In contrast, a simpler adversary would cheat all buyers with an equal probability. Discriminating sellers are harder to detect by the reputation system, because the information about them comes from a minority of buyers. Our simulations have shown that when discriminating strategies are used, fairness emergence is no longer statistically significant. Moreover, the differences in the total sum of utilities are also not statistically significant, while there is a strong increase in the Gini coefficient when a discriminating strategy is used instead of a simple adversary strategy. This result demonstrates the need of explicit consideration for fairness in the evaluation of reputation and TM systems. A comparison of results for discriminating and simple adversary strategies is shown on Table 1.
- 5.8
- More advanced types of reputation algorithms that attempt to recursively weigh received reports with the reputation of reporting agents would be even more vulnerable to discrimination strategies. These types of algorithms, proposed frequently in the literature (Kamvar 2003;Guha 2004), would erroneously overvalue the reputation of discriminating agents, if these act unfairly only towards a minority of discriminated agents.
 Conclusion
Conclusion
- 6.1
- The Fairness Emergence hypothesis may be viewed as a theoretical concept that is similar to the well-known "evolution of cooperation". The theoretical implications of the FE hypothesis are for example the possibility of emergence of distributive fairness in a society or social group that does not have trusted authorities or central institutions who can impose a fair solution to the distribution problem. Such societies could be primitive or extremely sophisticated (like groups of authors on Wikipedia). The central conclusion is that distributive fairness can emerge in such a society if there is a sufficient degree of mutual trust among the social agents. In the presented research, this condition has been assured by a successful reputation system that made the existence of such mutual trust possible.
- 6.2
- On the other hand, the presented research has an inherent practical value. First, if the FE hypothesis holds, then the problem of ensuring fairness in an open, distributed system without centralized control may have found a practical solution: it would suffice to use a good trust management system in order to provide fairness. Second, if the FE hypothesis would not be true in realistic conditions, then a reputation (or trust management) system would allow the existence of a degree of unfairness between similar agents. Such a situation would be highly undesirable from the point of view of users of trust management systems, leading to a disincentive of their usage.
- 6.3
- We have shown that the Fairness Emergence hypothesis applies in realistic conditions: in the presence of adversaries and in an unstable state of the system, and also in an open system where the presence of sellers was controlled by a trace from a real Internet auction site. Yet, this work also shows that the FE hypothesis does not apply universally. In particular, fairness emergence does not occur (or is very weak) if very few negative feedbacks are received by the reputation system. The FE hypothesis does not hold if the users of a reputation system are not sufficiently sensitive to reputation or do not have enough choice of transaction partners with a good enough reputation (this implies that if unfair agents would be a large fraction of the population, fairness could not emerge).
- 6.4
- Fairness Emergence among buyers was not observed in the open system if the system was not warmed up. The reason for this is that in the open system, some sellers are present only for a few transactions. If the reputation system does not have sufficient information about these sellers, the buyers cannot determine whether they are fair or unfair. It would be possible to initialize the reputations of sellers with a small value, but that would effectively exclude them from the system since it would make it impossible for a new seller to earn a higher reputation. There exists a practical way out of this difficulty: the transactions of new agents could be insured, until their reputation reaches a sufficiently high value. There also exists a practical threat that can lead to a lack of sufficient information about agents: if agents who have a low reputation can assume a new identity (an approach known as whitewashing), then fairness emergence would not occur. This behavior can only be prevented by using stronger authentication of agents.
- 6.5
- We have studied the sensitivity of fairness emergence to discrimination attacks. While fairness emergence can still be observed when sellers discriminate a minority of buyers, it is not statistically significant. In simulations when the discriminating agents formed a majority of the population, the FE hypothesis does not hold.
- 6.6
- From these results we can draw the following conclusions:
- trust management (reputation) systems can improve distributional fairness in ODS,
- trust management systems should explicitly consider fairness in their evaluation (also in the evaluation of their correctness),
 Appendix: Flow graph of the simulation
Appendix: Flow graph of the simulation
- The following flow graph is intended to give the reader an understanding of the sequence of agents behaviors and actions performed in the simulation.
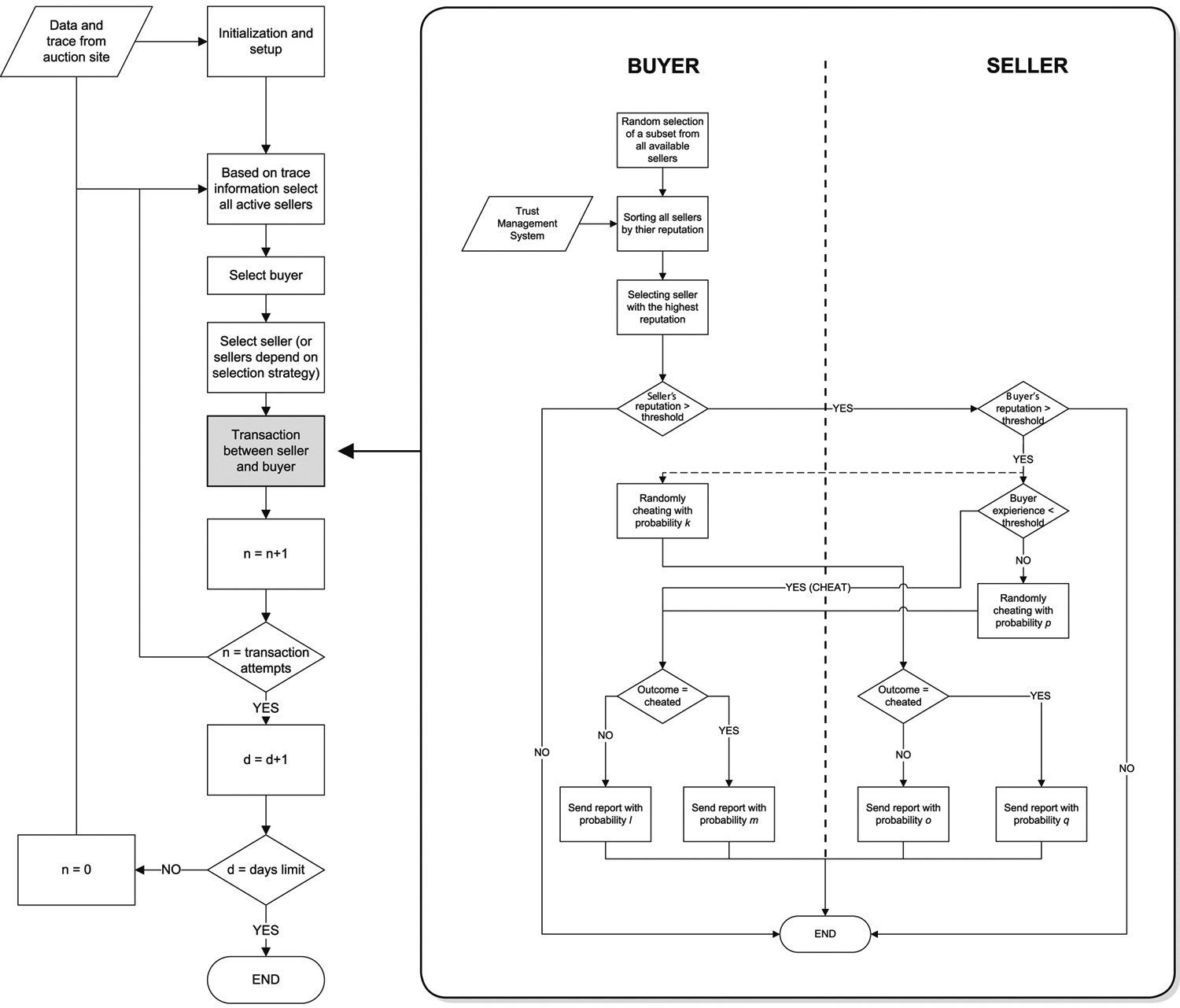
 Acknowledgements
Acknowledgements
- This research has been supported by the grants of the Polish Ministry of Science 69/NSINGAPUR/2007/0 (Adam Wierzbicki) and N N516 4307 33 (Radoslaw Nielek).
 Notes
Notes
-
Our ABM was written in Java and use Repast 3.1 framework. To access to the codes or for further detail, please visit http://nielek.pl/fairness/ or write to the authors.
1 By emergence we understand the arising of a complex property (fairness) out of simpler system behavior (the use of a reputation system by agents).
2 However, note that the existence of reputation information is a modification of the original Prisoner's Dilemma. Axelrod has explicitly ruled out the existence of reputation information in his definition of the game.
3 According to the Oxford English Dictionary, the word "fair" means: equitably, honestly, impartially, justly; according to rule.
4 The term theory of equitable optimality may be applied to various axiomatizations of equity described in the literature (Feurbaey 2008), as well as to work in ethics following the seminal work of Rawls. In this paper, we apply this term to a simple axiomatization that has a direct relation to the fairness criteria used in the Generalized Lorenz curve.
5 An optimal solution of this problem is any Pareto-optimal solution: a solution with the property that it is not possible to improve any of its outcome values without worsening another.
6 Incomparable distribution can also have identical total efficiencies θn.
 References
References
-
AXELROD, R. (1984) The Evolution of Cooperation, Basic Books, New York
CASTELFRANCHI, C., CONTE, R., PAOLUCCI, M. (1998) Normative Reputation and the Costs of Compliance, J. Artificial Societies and Social Simulations, 1(3)3 https://www.jasss.org/1/3/3.html
DELLAROCAS, C. (2000) Immunizing Online Reputation Reporting Systems Against Unfair Ratings and Discriminatory Behavior, In Proc. of the 2nd ACM Conference on Electronic Commerce, Minneapolis, MN, USA, pp. 150 - 157 [doi:10.1145/352871.352889]
DEUTSCH, M. (1975) Equity, equality, and need: What determines which value will be used as the basis of distributive justice?, Journal of Social Issues, pp. 137-149, vol. 31
DEUTSCH, M. (1987) Experimental studies of the effects of different systems of distributive justice, in: Social comparison, social justice, and relative deprivation, Lawrence Erlbaum, Hillsdale, NJ, pp. 151-164
ELGESEM, D. (2006) Normative Structures in Trust Management, Trust Management (iTrust 2006), Springer, LNCS 3986, pp. 48 - 61
FEURBAEY, M. (2008) Fairness, Responsibility and Welfare, Oxford University Press [doi:10.1093/acprof:osobl/9780199215911.001.0001]
GORDIJN, J., AKKERMANS, H. (2001) Designing and evaluating e-Business models, IEEE Intelligent Systems, vol. 16, pp. 11-17 [doi:10.1109/5254.941353]
GUHA, R., KUMAR, R., RAGHAVAN, P., TOMKINS, A. (2004) Propagation of trust and distrust, Proceedings of the 13th international conference on World Wide Web, pp. 403--412 [doi:10.1145/988672.988727]
KAMVAR, S. D., SCHLOSSER, M. T., GRACIA-MOLINA, H. (2003) The EigenTrust Algorithm for Reputation Management in P2P Networks, Proceedings of the Twelfth International World Wide Web Conference, pp. 640 - 651 [doi:10.1145/775152.775242]
KOSTREVA M., OGRYCZAK, W. (1999) Linear optimization with multiple equitable criteria, RAIRO Operations Research, 33:275-297 [doi:10.1051/ro:1999112]
KOSTREVA, M., OGRYCZAK, W., WIERZBICKI, A. (2004) Equitable aggregations and multiple criteria analysis, European Journal of Operational Research, 158:362-377 [doi:10.1016/j.ejor.2003.06.010]
LEE, S., SHERWOOD, R., BHATTACHARJEE, B. (2003) Cooperative peer groups in NICE, Proc. INFOCOM 2003, vol. 2, pp. 1272-1282 [doi:10.1109/infcom.2003.1208963]
LISSOWSKI, G. (2008) Zasady sprawiedliwego podziału dóbr (Principles of Fair Distribution of Goods), Wydawnictwo Naukowe Scholar, Warsaw
LIU, L., ZHANG, S., DONG RYU, K., DASGUPTA, P. (2004) R-Chain: A Self-Maintained Reputation Management System in P2P Networks., Proc. ISCA PDCS, pp. 131-136
MALAGA, R. A. (2001) Web-based reputation management systems: Problems and suggested solutions, Electronic Commerce Research, 4 vol. 1, pp. 403 - 417
MARKS M. B., SCHANSBERG E. D. (1996), Fairness and reputation effects in a provision point contributions process, Nonprofit Management and Leadership, 7 (3), pp. 235-251 [doi:10.1002/nml.4130070303]
MORZY, M., WIERZBICKI, A. (2006) The Sound of Silence: Mining Implicit Feedbacks to Compute Reputation, Proc. 2nd international Workshop on Internet & Network Economics (WINE'06), Springer, LNCS, pp. 365 - 376 [doi:10.1007/11944874_33]
MUI, L.(2003) Computational Models of Trust and Reputation: Agents, Evolutionary Games, and Social Networks, Ph.D. Dissertation, Massachusetts Institute of Technology
OGRYCZAK, W. (2009) On Principles of Fair Resource Allocation for Importance Weighted Agents, Proc. First International Conference on Social Informatics, Warsaw, pp. 57 - 62 [doi:10.1109/socinfo.2009.8]
PAOLUCCI M., CONTE R. (2009). Reputation: Social Transmission for Partner Selection. In Trajkovski G. P. & Collins S. G. (Eds.), Handbook of Research on Agent-Based Societies: Social and Cultural Interactions (pp. 243-260). Hershey: IGI Publishing. [doi:10.4018/978-1-60566-236-7.ch017]
POLLOCK, G. B., DUGATKIN. L. A. (1992) Reciprocity and the Evolution of Reputation, Journal of Theoretical Biology, pp. 25-37, vol. 159
RAWLS, J. (1971) The Theory of Justice., Harvard Univ. Press
REPAST Organization for Architecture and Development, http://repast.sourceforge.net; 2003
RESNICK, P., ZECKHAUSER, R. (2002) Trust among strangers in internet transactions: Empirical analysis of ebay's reputation system, Advances in Applied Microeconomics, 11, pp. 127 - 157 [doi:10.1016/S0278-0984(02)11030-3]
SABATER, J & SIERRA C (2005) Review on Computational Trust and Reputation Models, Artificial Intelligence Review, 24: 33-60 [doi:10.1007/s10462-004-0041-5]
SEN, A. (1970) Collective Choice and Social Welfare, San Francisco: Holden Day
SHORROCKS, A. (1983) Ranking Income Distributions, Economica, vol. 50, no. 197, pp. 3--17 [doi:10.2307/2554117]
TAN, Y., THOEN, W., GORDIJN, J. (2004) Modeling controls for dynamic value exchanges in virtual organizations, Trust Management: Second International Conference (iTrust), Oxford, UK, Springer, LNCS 2995, pp. 236-250
TYLER, T. R., SMITH, H. J. (1998) Social justice and social movements, in: The handbook of social psychology, McGraw-Hill, Boston, pp. 595-629
WIERZBICKI, A. (2006) Trust Enforcement in Peer-to-peer Massive Multi-player Online Games, Proc. Grid computing high-performance and Distributed Applications (GADA'06), Springer, LNCS, pp. 1163 - 1180 [doi:10.1007/11914952_7]
WIERZBICKI, A. (2007) The Case for Fairness of Trust Management; Proc. 3rd International Workshop on Security and Trust Management (STM 07), Elsevier, Electronic Notes in Theoretical Computer Science (ENTCS), Volume 197, Issue 2, pp. 73 - 89
WIERZBICKI, A., KASZUBA, T., NIELEK, R., DATTA, A. (2009) Trust and Fairness Management in P2P and Grid systems, in: Handbook of Research on P2p and Grid Systems for Service-oriented Computing: Models, Methodologies and Applications, Nick Antonopoulos, George Exarchakos, Maozhen Li, Antonio Liotta (Editors), IGI-Global, ISBN: 1-61520-686-8, pp. 748 - 773
WIERZBICKI, A. (2010) Trust and Fairness in Open, Distributed Systems, Springer Verlag, Studies in Computational Intelligence series, volume 298, Berlin Heidelberg
WILSON, E. O. (1975) Sociobiology, Harvard University Press, Cambridge, Massachusetts
WILSON, E. O. (1985) Social Evolution, Benjamin Cummings, Menlo Park,
YOUNG, H. P. (1994) Equity: In Theory and Practice, Princeton University Press