 Abstract
Abstract
- Opinion formation and innovation diffusion have gained lots of attention in the last decade due to its application in social and political science. Control of the diffusion process usually takes place using the most influential people in the society, called opinion leaders or key players. But the opinion leaders can hardly be accessed or hired for spreading the desired opinion or information. This is where informed agents can play a key role. Informed agents are common people, not distinguishable from the other members of the society that act in coordination. In this paper we show that informed agents are able to gradually shift the public opinion toward a desired goal through microscopic interactions. In order to do so they pretend to have an opinion similar to others, but while interacting with them, gradually and intentionally change their opinion toward the desired direction. In this paper a computational model for opinion formation by the informed agents based on the bounded confidence model is proposed. The effects of different parameter settings including population size of the informed agents, their characteristics, and network structure, are investigated. The results show that social and open-minded informed agents are more efficient than selfish or closed-minded agents in control of the public opinion.
- Keywords:
- Social Networks, Informed Agents, Innovation Diffusion, Bounded Confidence, Opinion Dynamics, Opinion Formation
 Introduction
Introduction
- 1.1
- One of the interesting topics in social and political science is opinion formation and diffusion. A significant amount of work in the literature of social networks has been assigned to modeling and analysis of these processes (Castellano et al. 2009; Sobkowicz 2009). These simplified models, although not able to precisely predict real world observations in some cases, help us understand important factors that govern these phenomena.
- 1.2
- In the existing models, society is described as a graph whose nodes represent the individuals and the edges represent their social relations. Each node has a property that represents its opinion. The opinion takes discrete (Alaali et al. 2008; Huang et al. 2008) or continuous (Galam 2008; Caruso & Castorina 2005) values.
- 1.3
- Opinions of individuals can affect each other based on different rules. In the voter model opinion of a randomly selected individual is updated to the opinion of one of its neighbors (Krapivsky & Redner 2003). Based on social impact theory in psychology a model is proposed in Latane (1981) which updates the opinion according to two factors: neighbors' strength of persuasiveness to change the opinion and supportiveness to keep the current opinion (Lewenstein et al. 1992). The evolution of continuous opinion based on neighbors whose opinions are close to the person is introduced in the bounded confidence model (Deffuant et al. 2001; Hegselmann & Krause 2002). In the Axelrod model culture of a person is represented by a vector of opinions. People who are similar will interact more and people become more similar when they interact (Axelrod 1997). In Viral marketing models, people based on their strength and neighbors' threshold can influence neighbors for changing their decision (Leskovec et al. 2006). In models based on game theory, two people would benefit only when they have same opinion or decision among available options (di Mare & Latora 2007).
- 1.4
- Although lots of research has been done on the mentioned models, in all of them except the bounded confidence model, opinion (or culture) is a binary variable (or vector) which is a good description for several situations. However, in cases such as opinion of an individual about political issues, the opinion can vary smoothly and describing that with only a binary value is oversimplified. Here a continuous opinion is more appropriate. Since opinion formation by informed agents, which is the focus of our study in this paper, is based on smooth and gradual changes in opinions, the bounded confidence model is adopted as the base model.
- 1.5
- Independent of opinion update rule, different approaches for opinion formation in a society can be used. Diffusion of opinion can accelerate where opinion leaders or key players are engaged (Valente & Davis 1999; Valente & Pumpuang 2006; Borgatti 2006). However, finding the opinion leaders needs global knowledge about the topology of the network. Moreover, convincing the leaders to accept and propagate our desired opinion might be costly, if not impossible.
- 1.6
- Another approach to opinion formation based on incorporating extremist agents has been investigated (Amblard & Deffuant 2004; Deffuant et al. 2004). It is shown for the bounded confidence model that, guiding the society toward a desired opinion is possible only when individuals of the society have great plasticity i.e. get influenced by the opinion of extremists even when it is very far from their belief. This assumption might not always hold.
- 1.7
- Instead of focusing on a subset of specific individuals, we would like to investigate whether common individuals are able to lead opinions in a society or not? And if so, how many of them are required? We think this could be possible when a small number of common individuals act in unison. These individuals should be aware of our desired opinion and act as our hidden advertisers; therefore they are called Informed Agents (Couzin 2009; Couzin et al. 2005).
- 1.8
- Couzin et al. (Couzin et al. 2005) showed that among a group of foraging or migrating animals only a small fraction of them have the proper information about the location of food source, or about the migration route. But these informed agents can guide the whole group through simple social interactions. The bigger the group is, the smaller the fraction of the required informed agents is. Halloy et al (Halloy et al. 2007) showed in real experiments that informed robots in a mixed-society of animals and robots can control the aggregation behavior of the mixed-society through microscopic interactions.
- 1.9
- Although informed agents internally have a different specific motivation, externally they could be chosen randomly or voluntarily. That is why we say informed agents are common people in the society different from special people or groups such as opinion leaders.
- 1.10
- Neither the informed agents nor regular agents are not aware of the type of other agents and no body monitor or control them; they are a swarm of dispersed individuals interacting with other people in the society. We assume agents are aware of opinion of their neighbors. The informed agents should pretend to have an opinion similar to their neighbors in the network, so their neighbors accept their words more easily. We think if informed agents, intentionally and gradually, change their own opinion toward the desired goal, these small changes would diffuse through the neighbors to the whole network. So a shift in the public opinion might arise
- 1.11
- In this paper we study the performance of informed agents and see how agents with different levels of plasticity influence the society. The proposed model, which we named Informed Agent (IA) model, is based on the bounded confidence model presented in (Deffuant et al. 2001; Hegselmann & Krause 2002; Lorenz 2007).
- 1.12
- The paper is organized as follows: First, the bounded confidence model is explained. Then our IA model and the proposed strategy for implicit coordination of informed agents are explained. Finally, the simulation process is described and the results are discussed.
 The bounded confidence model
The bounded confidence model
- 2.1
- In the bounded confidence model each individual has an opinion, x and an uncertainty level, u about its opinion. Neighbors whose opinion lie within [ x - u , x + u] can influence the individual. We refer to this region as the opinion interval of the individual.
- 2.2
- In (Deffuant et al. 2001) all individuals have the same uncertainties except for extremists whose opinions are set close to an extreme point and their uncertainties are assumed to be very small. If the difference between opinions of two neighbors is smaller than their uncertainty level, their opinion will be updated according to:
x = x + µ ( x' - x ) (1) x' = x' + µ ( x - x' ) (2) where x and x' are opinions of the individuals and µ is the convergence (or influence) factor taken between 0 and 0.5. The two agents will converge to the average of their opinions before the interaction for µ = 0.5. For any value of u and µ, the average opinion of the agents' pair is the same before and after interaction, so the average opinion of the population is invariant of dynamics (Castellano et al. 2009). Thus the bounded confidence model cannot model the public opinion shift in a society.
- 2.3
- Despite the initial uniform configuration of opinions, at each time step, two randomly chosen agents become closer to each other. So the initial distribution changes and the agents near the boundary of the opinion space are attracted to its center and gradually shape clusters of opinions. As time passes the clusters get closer. Once they got far enough from the other clusters, the difference of opinions for agents in different clusters exceeds the uncertainty. Thus only agents inside the same cluster can interact, and opinions of all agents in the cluster converge to the same value (Castellano et al. 2009). Monte Carlo simulations shows that the number of clusters at the end of simulation is approximated by1/(2u).(Fortunato 2004)
 Our proposed model
Our proposed model
- 3.1
- In our proposed model, opinion x(t) is represented by a real number in [ -1, +1 ]. Individuals are divided into two types: informed agent, and the majority. Informed agents are the individuals who intentionally and invisibly try to change the public opinion. They do this by pretending to have close opinion to their neighbors in order to strengthen their neighborhood and influence them meanwhile.
- 3.2
- This strategy has a social reason: if people think you sit on the other side they might ignore your opinion; whereas feeling you by their side, albeit disagreement in some cases might not seem an important matter to them (Burger 1999). It is assumed that neither the majority nor the informed agents are aware of the other informed agents. Each type of agent has its own opinion update rule.
- 3.3
- The opinion update rule for the majority is based on the bounded confidence model: Assume at time step t, a member of the majority is randomly selected with uniform distribution (say its opinion is xi (t) and its uncertainty level is ui). Then one of its neighbors is chosen randomly (say its opinion is xj (t)).
- 3.4
- Opinion of the majority is shaped from two force components: a social force, toward a neighbor, in order to accept influence from the neighbors and get close to them; and a self-force, toward its own opinion. If | xi (t) - xj (t) | < ui, the neighbor will influence the member of the majority by:
xi(t+1) = wiMN(t) xj(t) + wiMS(t) xi(t) (3) where wi MN and wi MS and are the weight of neighbor's and self opinion respectively. The weights are specified according to:
wiMN(t) = WMN * ( 1+ α * r1(t) )(4) wiMS(t) = WMS * ( 1+ α * r2(t) ) (5) where WMN and WMS are configuration constants and WMN +WMS=1. α ∈ [0,0.5] is also a configuration constant and r1 (t), r2 (t) ∈ [-1,+1] are uniform random numbers representing all sources that affect and change the amount of attention to neighbor's and self opinion in different people. Since (1+ α *r1 (t)) and (1+ α *r2 (t)) can become more than 1, depending on xj (t) and xi (t), the xi (t+1) may become larger than +1 or smaller than -1. Considering the definition of opinion in this model and the valid interval of [-1,+1], if xi (t+1) in Eq.3 becomes larger than +1 or smaller than -1, it will be cut to +1 and -1 respectively. It is assumed that Wi MS > Wi MN .
- 3.5
- The opinion update rule for the informed agents must satisfy three requirements: First, informed agents must be under influence of their neighbors in order to accompany to them. Second, the weight they give to themselves should be negligible in order to be in higher conformance with neighbors. Third, they should gradually move their opinion toward the desired goal wherever they can, except when social force dictates otherwise.
- 3.6
- Therefore, the opinion update rule for the informed agents has three force components: a social force and a self-force like the majority and a goal force, an attraction force toward the desired goal i.e. the opinion the informed agent would like the society to reach.
- 3.7
- To stay close to neighbors, informed agents should have a very wide uncertainty level. This way, neighbors can influence them and their opinion becomes near to the average opinion of the neighbors. Knowing that opinions belong to [-1, +1], it is enough to set the uncertainty level of the informed agents to 2.
- 3.8
- In summary, the opinion update rule for the informed agents can be described as:
xi(t+1) = wiIN(t) xj(t) + wiIS(t) xi(t) + wiID(t) xd (6) wiIN(t) = WIN * ( 1+ α * r3(t) ) (7) wiIS(t) = WIS * ( 1+ α * r4(t) ) (8) wiID(t) = WID * ( 1+ α * r5(t) ) (9) Where WIN, WIS, and WID are the weights of its neighbor's opinion, its own opinion and the desired goal respectively and WIN + WIS + WID =1. α ∈ [0,0.5] is also a configuration constant and r3 (t), r4 (t), r5 (t) ∈ [-1,+1] are uniform random numbers similar to r1 (t) and r2 (t). Like Eq.3, if xi (t+1) in Eq.6 become larger than +1 or smaller than -1, it will be set to +1 and -1 respectively.
 Simulations
Simulations
- 4.1
- At the beginning of a run a random network is built. Then some individuals are selected randomly and set as informed agents. At each time step a node and one of its neighbors are selected randomly. The opinion of the selected individual is updated according to Eq.3 or Eq.6 based on its type. The simulation goes on until the society reaches consensus or at most 100,000 steps are passed. Interpreting the opinion of each agent as his agreement (positive value) or disagreement (negative value) on a subject, the consensus can be supposed as a situation where most of the individual in the society agree or disagree on that subject. We say consensus is reached when more than 90% of the society either all have positive opinions (agree) or all have negative opinions (disagree).
- 4.2
- Informed agents try to move the consensus point to a positive value. So, +1 is defined as the desired goal of the informed agents. The parameter setting is shown in Table 1. In this table, average nodal degree means the average of number of neighbors of all individuals. In the next sections the parameters are same as this table except when it is mentioned explicitly. All simulations are averaged over 30 runs.
Table 1: Parameter settings for simulations Parameter Value Initial opinions Uniform(-1,+1) Average nodal degree (K) 30 Network type Random Maximum simulation steps 100,000 Total population size 1000 α 0.25 Majority Population 900 Uncertainty level (UM) 0.5 Weight of self-opinion (WMS) 0.7 Weight of neighbors' opinion (WMN) 0.3 Informed agents Population 100 Uncertainty level (UI) 2 Weight of self-opinion (WIS) 0.0 Weight of neighbors' opinion (WIN) 0.7 Weight of desired goal (WID) 0.3 Temporal evolution of opinions
- 4.3
- Fig.1 shows temporal evolution of opinion formation process. Fig.1a shows the number of individuals with positive opinion at different time steps. Fig.1b shows the averaged opinion of the informed agents, the majority and the whole society at each time step.
- 4.4
- As described before, at each time step a node and one of its neighbors are selected randomly and the opinion of the selected individual is updated according to Eq.3 or Eq.6 based on its type. On the other hand in all simulations population size is equal to 1000. So average number of interactions per agent during the simulations is t/1000, where t is the time step. (Both t and t/1000 are shown as labels of the related axis)
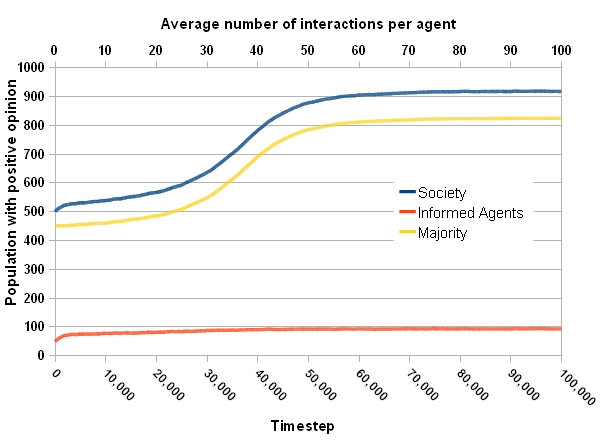
Figure 1a. Temporal evolution of the opinion formation process. (a) Number of individuals with positive opinion. 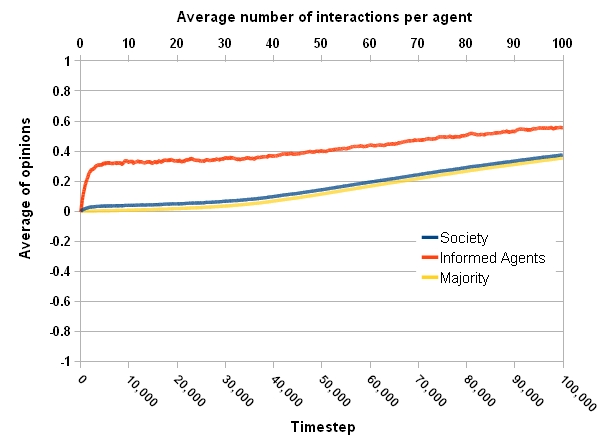
Figure 1b. Temporal evolution of the opinion formation process. (b) Averaged opinion of individuals. - 4.5
- From Fig.1a it is clear that at the beginning, 50% of the whole society, the majority, and the informed agents have positive opinions. Fig.1b shows the informed agents, who are distributed uniformly in the society, rapidly change their opinion and keep a fixed distance to the majority. Their opinion moves along with the majority and stay in their uncertainty interval. Meanwhile they move a little toward the desired goal, +1.
- 4.6
- After 30,000 time steps the gradual movement toward the desired goal is accelerated. After 70,000 time steps, more than 90% of the whole population has positive opinions. So a consensus is reached at this time step, however to see what happens afterward, the simulation is continued until 100,000 steps. Finally, informed agents could shift the public opinion close to 0.4.
- 4.7
- It was mentioned that in the bounded confidence model the individuals' opinion split into opinion clusters. However, it did not happen here. This is because the informed agents stay close to their neighbors and in their uncertainty interval. They try to influence their neighbors gradually, whenever it is possible. Little by little the society members change their opinion toward positive values. So nobody is left behind. However, as it is discussed in the next sections, depending on the characteristics of informed agents it is possible to split the society into two clusters of opinions.
Number of informed agents
- 4.8
- Fig.2a shows the fraction of whole population whose opinions are positive at the end (minimum of 100,000 time steps or reaching a consensus) of run versus the population size of the informed agents. The results show only 20 informed agents, i.e. 2% of the whole population, are required to shift the public opinion toward a point where almost 90% of opinions are positive. Even 5 informed agents can move 75% of the population towards +1. According to our definition of consensus, the fraction cannot go beyond 90% since the simulation is terminated at this point.
- 4.9
- Fig.2b shows that the consensus time decreases when population of informed agents increases. However when population reaches 30, consensus time does not decrease significantly.
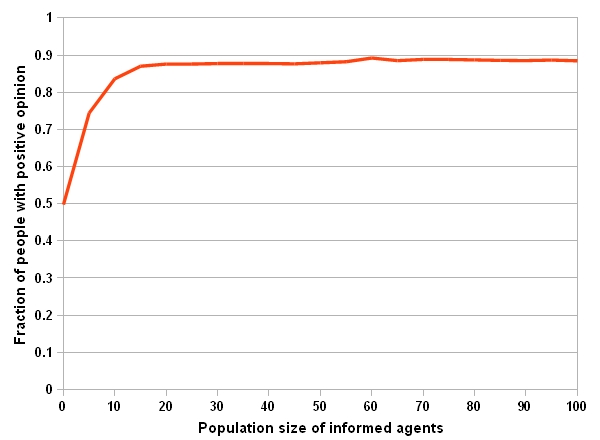
Figure 2a. Impact of the number of informed agents on consensus (a) Fraction of people with positive opinion 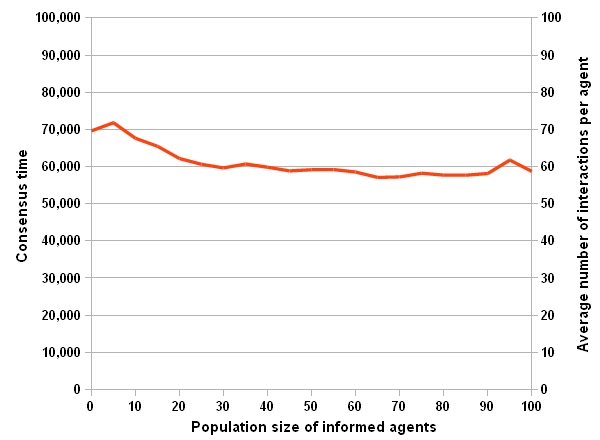
Figure 2b. Impact of the number of informed agents on consensus (b) Consensus time. Network Structure
- 4.10
- Three network structures are analyzed: random, scale-free, and small-world. The networks are built based on the methods described in (Boccaletti et al. 2006). The structural parameters are set according to Table 2.
Table 2: Structural network parameters Network Type Parameter Value Random Probability of link creation between two nodes 0.03 Scale-free Number of initial isolated nodes 25 Small-world Rewiring probability 0.02 Average nodal degree 30 - 4.11
- Fig.3 shows the fraction of whole population whose opinions are positive at the end of run versus the population size of the informed agents. The results show that performance of informed agents in random networks and scale-free networks are almost same. However, behavior of the small-world network is completely different; the informed agents seem to be unable to change the public opinion easily. Although their gain gets larger with the size of their population but the increase is very small comparing to the other network structures.
- 4.12
- In order to investigate this result we calculated the average distance and the clustering coefficient for the three types of graphs. Average distance is defined as the average length of the shortest path between pairs of nodes in a graph. Clustering coefficient for a node is defined as the number of available edges between neighbors of a node divided by the number of possible edges between them. Clustering coefficient for a graph is defined as the average clustering coefficient of its nodes. The average distance and clustering coefficient of a small-world network (Watts & Strogatz 1998) can be manipulated by changing the rewiring probability in the network creation process; the average distance and the clustering coefficient would decrease, if the rewiring probability increases.

Figure 3. Impact of network structure on consensus - 4.13
- In Fig.4 the average distance and the clustering coefficient are plotted along with the fraction of individuals with positive opinion for different type of graphs and different parameter settings. It is seen that as the average distance gets smaller, the fraction of individuals increases. By the time the distance gets close to 2.5, the fraction gets very close to 90% trend line. After that the fraction does not change a lot. This observation agrees with the claim made in (Borgatti 2006) about the importance of distance in solving Key Players Problem (positive version).
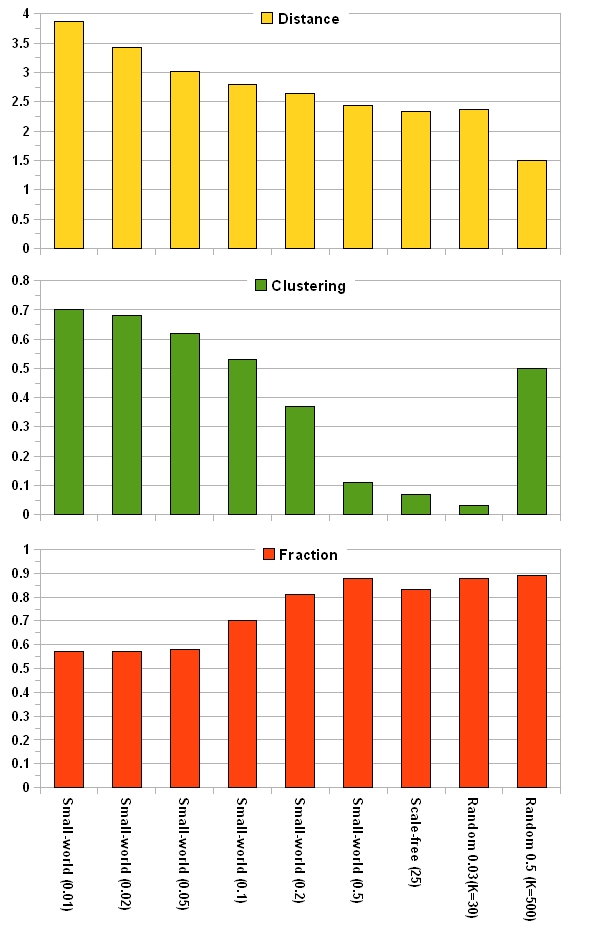
Figure 4. Network properties and their impacts on the fraction of individuals with positive opinion. The numbers that come with different types of graphs on the horizontal axis are: rewiring probability for small-world networks, number of initial nodes for scale free networks, and average nodal degree for random networks. - 4.14
- In the following, we explain what happens when the average distance decreases in different network types:
- 4.15
- In a small-world network with high clustering coefficient, members of communities are densely connected, while communities have relatively far distances. Therefore, these kinds of networks consist of communities with low within-community and high between-community distances. In these networks, opinion of informed agents passes a long distance and meanwhile gets attenuated. If the average distance is high, the opinion might get lost without reaching many individuals. Even if the influence of an informed agent extends sufficiently far through a network and reaches an individual, other members of its community can easily neutralize the efforts of the informed agent and reset the opinion of their neighbor. So, these communities have large inertia that makes them resist strongly against any change. As a result, the number of informed agents that is required to shift the public opinion in a small-world network increases with the clustering coefficient. This observation is in agreement with (Easley & Kleinberg 2010) on the relationship between clusters and cascades.
- 4.16
- In order to investigate this hypothesis about the impact of average distance and clustering coefficient, the performance of informed agents has to be studied on networks that had same average distance but different clustering coefficient and also in networks with same clustering coefficient and different average distance. So, the model of network with communities (Newman & Girvan 2003) was used. In this model, for a specific number of communities, it is possible to generate networks with different average distance and clustering coefficients through changing the within community probability and between communities probability.
- 4.17
- The results of simulations done with different networks can be summarized as:
- If the number of communities is high: informed agents succeed. √
- If the number of communities is low:
- If the average distance is low: informed agents succeed. √
- If the average distance is high:
- If the clustering coefficient is low: informed agents succeed. √
- If the clustering coefficient is high: informed agents fail. x
- 4.18
- When the number of communities is low, the results completely support the above hypothesis and show that the average distance is more important than the clustering coefficient.
- 4.19
- When the number of communities is high, the society is made up of a large number of small-sized comminutes. Since the informed agents are chosen randomly with uniform distribution among people in the society, in each of these small communities there probably exist an informed agent. Since the communities are small, the informed agents can easily influence other members and successfully shifts the average opinion of that community. So, in this situation independent of average distance and clustering, the informed agents succeed.
- 4.20
- The result for scale-free networks is similar to random networks with low average degrees and small-world networks with high-rewiring probabilities. All of them have relatively short average distances and low clustering coefficients. As a result, opinions of informed agents reach common individuals through relatively multiple short paths, without so much attenuation, and without the problem of neutralization by other members of the majority.
- 4.21
- A random network with high average degree has high clustering coefficient and relatively short average distance. These kinds of networks consist of entangled communities that have low within-community and low between-community distances (high density, high overlap). This time communities help, because opinions of informed agents reach common individuals through shorter paths without that much attenuation. As a result, the opinion remains longer in the society and can influence the members of the majority via multiple paths.
Nodal degree
- 4.22
- As defined before, average nodal degree means the average number of neighbors of all individuals. Fig.5 shows impact of the average nodal degree of individuals, K, on the opinion formation process in a random network. Simulations are done for four different values of K (5, 30, 500, and complete graph). Fig.5a shows the fraction of people with positive opinion at the end of runs and Fig.5b shows the required time for consensus to happen.
- 4.23
- It is clear in Fig.5a that higher nodal degrees do not affect the ultimate consensus point even in a complete graph. However, Fig.5b shows, higher nodal degrees lead to earlier consensus formation and in a complete graph the society reach a consensus before than the other networks. The reason is that all random networks have relatively short average distances (2.37, 1.5, 1 for K=30, 500, and complete graph respectively). The distance gets shorter by increasing the average nodal degree. The short average distance along with a high nodal degree leads to diffusion of opinion to more individuals in the society through short paths. So, spreading process is accelerated and thus consensus happens earlier.
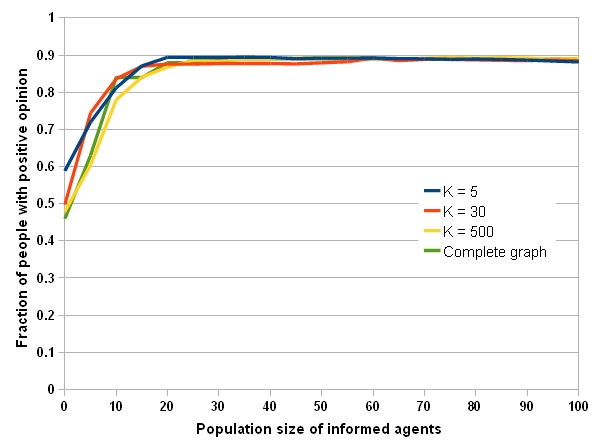
Figure 5a. Impact of average nodal degree on consensus (a) Fraction of people with positive opinion 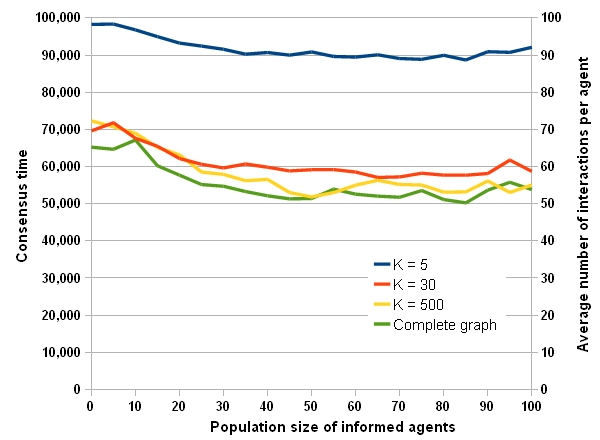
Figure 5b. Impact of average nodal degree on consensus (b) Consensus time. Characteristics of informed agents
- 4.24
- In the proposed model, WIS, WIN, and WID are the weight of attention to self-opinion, neighbor's opinion and, the desired goal, respectively. Also, UI is the uncertainty level of the informed agents. These parameters can be interpreted as characteristics of the informed agents. In this section impacts of these parameters are investigated.
- 4.25
- In the first experiments WID is fixed to 0.1 and WIS and WIN change so that WIS + WIN =0.9. An informed agent with high WIS and low WIN is like a selfish person whose opinion is not influenced by the others. An informed agent with low WIS and high WIN is like a social person who cares about the others more than himself. An informed agent with high uncertainty level is like an open-minded person who is open to be influenced by the opinion of different people.
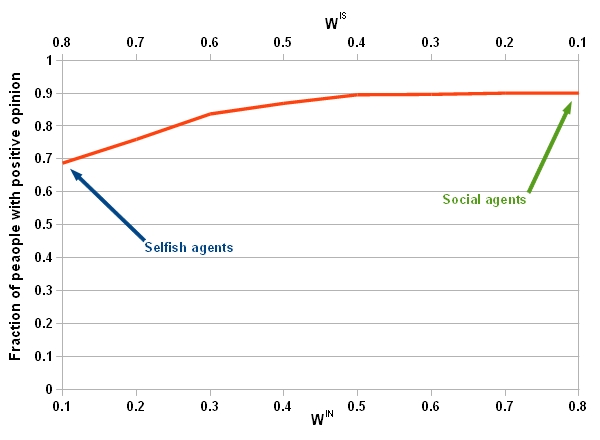
Figure 6. Impact of characteristics on the fraction of people with positive opinion: WID =0.1 and WIN =0.9 - WIS. - 4.26
- Fig.6 shows how the fraction of people with positive opinion at the end of run changes with WIS and WIN =0.9 - WIS. It is seen that by increasing WIS (consequently decreasing WIN) number of people with positive opinion decreases. In this situation the informed agents care less about their neighbors. So they move toward the desired goal very fast and leave their neighbors behind. Therefore, their opinion gets out of the uncertainty interval of their neighbors and loses the ability to exert influence over them.
- 4.27
- Fig.7 shows why this type of agent cannot efficiently influence the public opinion. Each pixel in the figure shows the number of people who have a specific opinion at a specific step of the simulation. The more the individuals that have the opinion the brighter the point is drawn.
- 4.28
- Fig.7a corresponds to selfish agents. Bifurcation into different localized opinion clusters which is similar to this situation has already been reported for the bounded confidence model (Deffuant et al. 2001). It is seen that the selfish agents move toward the desired goal very fast, so they leave some neighbors behind and the society is divided into two groups. However, social agents (Fig.7b), who try to stay close to their neighbors, are able to gradually shift almost the whole society toward the desired goal.
Figure 7a. Number of individuals with a specific opinion at different steps when the informed agents are (a) Selfish agents (agents that care about themselves more than the society). (Brighter colors indicate more individuals.) Figure 7b. Number of individuals with a specific opinion at different steps when the informed agents are (b) Social agents. (Brighter colors indicate more individuals.) - 4.29
- Fig.8 shows the temporal evolution of the opinion formation process for closed-minded agents ( UI =0.5). Comparing to Fig.1, it is evident that, closed-minded agents are unable to influence the society very well, neither on the average opinion nor the number of individuals with positive opinion. Fig.8a shows that closed-minded agents can increase the number of individuals with positive opinion only by 150 after 100,000 steps, while open-minded informed agents ( UI = 2) can change the opinion of more than 90% of society in less than 70,000 time steps (Fig.1a).
- 4.30
- Overally, we can say, when conflicting opinions can pose a serious obstacle against acceptance of an opinion, informed agents must comply with their neighbors in order to have their attention. The compliance can take place through both giving more value to neighbors' opinions and being more open to different opinions. Once they get the chance to influence on them (even very small) they bring the neighbor a bit closer to the goal. These small effects spread in the whole network and gradually bring the whole society to a closer distance of the ultimate goal.
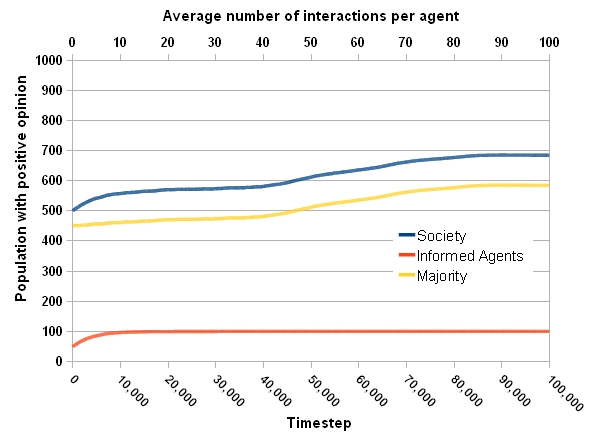
Figure 8a. Temporal evolution of the opinion formation process with closed-minded agents ( U I =0.5)). (a) Number of individuals with positive opinion. 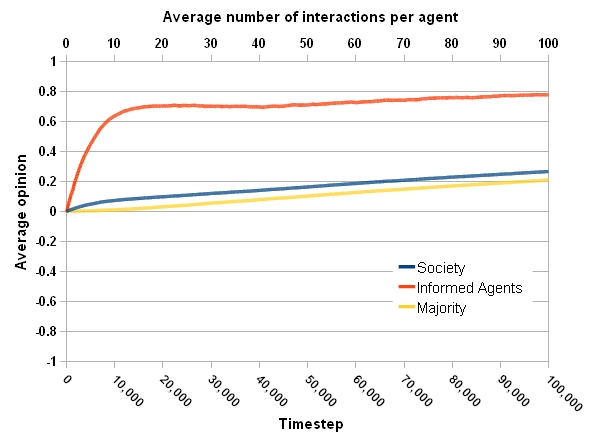
Figure 8b. Temporal evolution of the opinion formation process with closed-minded agents ( U I =0.5)). (b) Averaged opinion of individuals.
 Conclusion
Conclusion
- 5.1
- In this research a computational model for opinion formation by informed agents was proposed. Informed agents pretend to have similar opinion to other people in the society in order to get close to them and find the opportunity to influence them. Then, they move their opinion little by little and this way they are able to shift the public opinion toward a preplanned point.
- 5.2
- Simulations show that only a small number of informed agents, as a small minority, are required to successfully change the public opinion. Simulations also show that increasing the inter-connectivity of individuals, i.e. the average degree, can help the informed agents in decreasing the consensus time. However, creating communities with low within-community distances and high between-community distances (like small-world networks with high clustering coefficients) can easily disarm the informed agents. Finally, we showed that social and open-minded informed agents can affect the public opinion more rapidly and efficiently than selfish or closed-minded agents.
- 5.3
- For future we would like to study the effect of competing informed agents i.e. when two groups of informed agents with opposing opinion compete with each other.
- 5.4
- In our study we chose the informed agents randomly. Interesting topic would be to choose the informed agents among a specific subset of the nodes e.g. the hubs in a scale-free network.
- 5.5
- Another interesting work would be to study the effect of different opinions on each other. That is when opinion of a person is a vector that represents its opinion about multiple subjects. These subjects could either be independent or dependent.
 Acknowledgements
Acknowledgements
- This research was in part supported by a grant from IPM (No.CS1388-4-14). We would like to thank the anonymous reviewers for their valuable comments and through reviews.
 References
References
-
ALAALI, A., Purvis, M.A. & Savarimuthu, B.T.R., 2008. Vector Opinion Dynamics: An Extended Model for Consensus in Social Networks. In 2008 IEEE/WIC/ACM International Conference on Web Intelligence and Intelligent Agent Technology. Sydney, Australia, pp. 394-397. [doi:10.1109/WIIAT.2008.377]
AMBLARD, F. & Deffuant, G., 2004. The role of network topology on extremism propagation with the relative agreement opinion dynamics. Physica A, 343, 725-738. [doi:10.1016/j.physa.2004.06.102]
AXELROD, R., 1997. The Dissemination of Culture: A Model with Local Convergence and Global Polarization. Journal of Conflict Resolution, 41(2), 203-226. [doi:10.1177/0022002797041002001]
BOCCALETTI, S. et al., 2006. Complex networks: Structure and dynamics. Physics Reports, 424(4-5), 308, 175.
BORGATTI, S.P., 2006. Identifying sets of key players in a social network. Computational and Mathematical Organization Theory, 12(1), 21-34. [doi:10.1007/s10588-006-7084-x]
BURGER, J.M., 1999. The Foot-in-the-Door Compliance Procedure: A Multiple-Process Analysis and Review. Personality and Social Psychology Review, 3(4), 303 -325. [doi:10.1207/s15327957pspr0304_2]
CARUSO, F. & Castorina, P., 2005. Opinion dynamics and decision of vote in bipolar political systems. physics/0503199.
CASTELLANO, C., Fortunato, S. & Loreto, V., 2009. Statistical physics of social dynamics. Reviews of Modern Physics, 81, 591. [doi:10.1103/RevModPhys.81.591]
COUZIN, I., 2009. Collective cognition in animal groups. Trends in Cognitive Sciences, 13(1), 36-43. [doi:10.1016/j.tics.2008.10.002]
COUZIN, I.D. et al., 2005. Effective leadership and decision-making in animal groups on the move. Nature, 433(7025), 513-516. [doi:10.1038/nature03236]
DEFFUANT, G., Amblard, F. & Weisbuch, G., 2004. Modelling Group Opinion Shift to Extreme : the Smooth Bounded Confidence Model. cond-mat/0410199.
DEFFUANT, G. et al., 2001. Mixing beliefs among interacting agents. Advances in Complex Systems, 3, 98, 87.
EASLEY, D. & Kleinberg, J., 2010. Networks, Crowds, and Markets, Cambridge University Press. [doi:10.1017/CBO9780511761942]
FORTUNATO, S., 2004. Universality of the Threshold for Complete Consensus for the Opinion Dynamics of Deffuant et al. cond-mat/0406054.
GALAM, S., 2008. Sociophysics: A review of Galam models. arXiv:0803.1800v1 [physics.soc-ph].
HALLOY, J. et al., 2007. Social Integration of Robots into Groups of Cockroaches to Control Self-Organized Choices. Science, 318(5853), 1155-1158. [doi:10.1126/science.1144259]
HEGSELMANN, R. & Krause, U., 2002. Opinion dynamics and bounded confidence models, analysis, and simulation. Journal of Artifical Societies and Social Simulation (JASSS) vol, 5(3).
HUANG, G. et al., 2008. The strength of the minority. Physica A, 387(18), 4665-4672. [doi:10.1016/j.physa.2008.03.033]
KRAPIVSKY, P. & Redner, S., 2003. Dynamics of Majority Rule in Two-State Interacting Spin Systems. Physical Review Letters, 90(23). [doi:10.1103/PhysRevLett.90.238701]
LATANE, B., 1981. The psychology of social impact. American Psychologist, 36(4), 343-356. [doi:10.1037/0003-066X.36.4.343]
LESKOVEC, J., Adamic, L.A. & Huberman, B.A., 2006. The dynamics of viral marketing. In Proceedings of the 7th ACM conference on Electronic commerce. Ann Arbor, Michigan, USA: ACM, pp. 228-237. [doi:10.1145/1134707.1134732]
LEWENSTEIN, M., Nowak, A. & Latané, B., 1992. Statistical mechanics of social impact. Physical Review A, 45(2), 763-776. [doi:10.1103/PhysRevA.45.763]
LORENZ, J., 2007. Continuous Opinion Dynamics under Bounded Confidence: A Survey. International Journal of Modern Physics C, 18, 1819. [doi:10.1142/S0129183107011789]
DI Mare, A. & Latora, V., 2007. Opinion Formation Models Based on Game Theory. International Journal of Modern Physics C, 18, 1377-1395. [doi:10.1142/S012918310701139X]
NEWMAN, M.E.J. & Girvan, M., 2003. Finding and evaluating community structure in networks. cond-mat/0308217.
SOBKOWICZ, P., 2009. Modelling Opinion Formation with Physics Tools: Call for Closer Link with Reality. Journal of Artificial Societies and Social Simulation, 12(1), 11.
VALENTE, T.W. & Davis, R.L., 1999. Accelerating the Diffusion of Innovations using Opinion Leaders. The ANNALS of the American Academy of Political and Social Science, 566(1), 55-67. [doi:10.1177/0002716299566001005]
VALENTE, T.W. & Pumpuang, P., 2006. Identifying Opinion Leaders to Promote Behavior Change. Health Education & Behavior, 34(6), 881-896. [doi:10.1177/1090198106297855]
WATTS, D.J. & Strogatz, S.H., 1998. Collective dynamics of 'small-world' networks. Nature, 393(6684), 440-442. [doi:10.1038/30918]