 Abstract
Abstract
- Certain social preference models have been proposed to explain fairness behavior in experimental games. Existing bodies of research on evolutionary games, however, explain the evolution of fairness merely through the self-interest agents. This paper attempts to analyze the ultimatum game's evolution on complex networks when a number of agents display social preference. Agents' social preference is modeled in three forms: fairness consideration or maintaining a minimum acceptable money level, inequality aversion, and social welfare preference. Different from other spatial ultimatum game models, the model in this study assumes that agents have incomplete information on other agents' strategies, so the agents need to learn and develop their own strategies in this unknown environment. Genetic Algorithm Learning Classifier System algorithm is employed to address the agents' learning issue. Simulation results reveal that raising the minimum acceptable level or including fairness consideration in a game does not always promote fairness level in ultimatum games in a complex network. If the minimum acceptable money level is high and not all agents possess a social preference, the fairness level attained may be considerably lower. However, the inequality aversion social preference has negligible effect on the results of evolutionary ultimatum games in a complex network. Social welfare preference promotes the fairness level in the ultimatum game. This paper demonstrates that agents' social preference is an important factor in the spatial ultimatum game, and different social preferences create different effects on fairness emergence in the spatial ultimatum game.
- Keywords:
- Spatial Ultimatum Game, Complex Network, Social Preference, Agent Based Modeling
 Introduction
Introduction
- 1.1
- Classical game theory is not sufficient to explain the fairness or altruistic behavior commonly observed in social systems and experimental games. To resolve this issue, a number of researchers have deviated from the self-regarding rational choice paradigm in economics (Camerer 2003; Montet and Serra 2005) and have forwarded the social preference theory. In recent years, however, research on evolutionary games in network has likewise received significant attention. By adding the factor of spatial or network structure to the agents interaction model, researchers have discovered various interesting results (Lieberman et al. 2005; Szabóa and Fáth 2007). At present, it has been accepted that the structure of agent interaction indeed plays an important role in a significant number of spatial games. Further, it is worth mentioning that in the evolution of spatial games, social preference has received negligible attention.
- 1.2
- The evolutionary spatial game theory attempts to explain the emergence of fairness behavior. However, merely a handful of literature mention that agents may possess varying social preferences, a salient feature of human beings in society. When do agents display social preference in the game evolution process? Social preference is not merely the outcome of the evolution, but an important element in the fairness evolution process as well. It may have a substantial effect on evolution results. Since social preference has been proved useful in explaining fairness behavior in experimental games, it will be interesting to study whether social preference works in the spatial game situation as well.
- 1.3
- This paper focuses on the spatial ultimatum game. In the simple ultimatum game, two players are asked to divide a specific amount of money. One is chosen as the first player or proposer, while the other serves as the responder. The proposer suggests a way to split the money. If the suggestion is accepted by the responder, the money will be shared accordingly. If, however, the suggestion is rejected, both players will get nothing. According to the game theory (Rubinstein 1982), the Nash equilibrium of ultimatum game states that the proposer should extend the least possible amount of money to the responder. However, contrary to game theory predication, extensive experiments on the ultimatum game have revealed that the responder in most cases will reject the offer if he deems the suggestion unfair (Güth et al. 1982; Kahneman et al. 1986; Camerer 2003; Bolton and Zwick 1995; Cameron 1999; Croson 1996; Güth et al. 2007; List and Cherry 2000; Hoffman et al. 1996; Oosterbeek et al. 2004). Curiousity abounds as to why the game theory predication is different from social facts and experimental results. What happens if the agents are placed in a complex network and the ultimatum game is played again?
- 1.4
- Similar to the widely studied prisoner's dilemma game, the ultimatum game has received significant attention. One main research approach is the evolutionary spatial ultimatum game, which introduces the network structure among agents. Page, Nowak, and Sigmund (2000) first applied evolutionary game theory to analyze the spatial ultimatum game on a lattice grid. They demonstrated that natural selection chooses an unfair solution in a nonspatial setting. However, in a spatial setting, much fairer outcomes survive. Nowak, Page, and Sigmund (2000) developed another model which added the reputation factor. Their research results revealed that fairness would evolve if the proposer could obtain information on the responders' past behavior. As in other cooperative games and market competition games, the evolution of fairness is related to the agent's reputation. Killingback and Studer (2001) likewise demonstrated that considerably fair divisions are evolved in a spatial structured context, and the spatial structure provides a natural explanation for the collaborative behavior.
- 1.5
- Recently, Kuperman and Risau-Gusman (2008) focused on the topology's effect on the spatial ultimatum game. They studied the spatial non-homogeneous ultimatum game based on an agent model and analyzed the effect of the neighborhood and spatial structure's size. They observed that the increase in neighborhood size and disorder degree pushed agents to a more rational level.
- 1.6
- Other papers likewise tapped the agent-based simulation to study the evolutionary ultimatum game. A number treated the agent as an automaton playing the ultimatum game, and these research focused on agent behavior and evolution. However, none succeeded in placing agents in a complex network (Riechmann 2001, Hayashida 2007).
- 1.7
- Another research approach to the ultimatum game focuses on the agent's behavior, especially the social preference displayed by certain agents. Experimental economics and behavior science during the past decades have revealed that certain agents may exhibit social preference. Further, behavior economists have suggested some new utility functions to describe the agent's social preference (other-regarding). Although the social preference theory relaxes the selfish agent assumption, it still can be considered as a type of rational choice theory. Rabin (1993) developed a "fairness equilibrium" to include agent motivations in explaining experimental evidence. His main idea may be summarized as, "People like to help those who are helping them, and to hurt those who are hurting them." This reciprocal intention consideration has a significant effect on agent behavior. While Rabin's model assumes that an individual does not care about how the agent payoff distribution transpires, Bolton and Ockenfels (2000) proposed a model called "Equity, Reciprocity, and Competition"(ERC) where the agent is concerned about his relative payoff compared to others. The ERC model attempted to capture three features of behavior as reported from experiments: equity, reciprocity, and competition. The ERC model can explain the reciprocal pattern found in experiments on cooperation games. Fehr and Schmidt (1999) proposed an inequity aversion model similar to ERC. Their model assumed that there is a fraction of agents motivated by self-centered inequity aversion apart from the selfish agents. Andreoni and Miller (2002) proposed a social welfare preference model where agents care about social welfare as well as individual utility. Charness and Rabin (2002) integrated reciprocal preference and social welfare preference into their model. Aside from the above social preference models, a number of extensions and integrated models have been developed recently (Falk and Fischbacher 2006). Although social preference can explain agent behavior in experiments, the agent's social preference and its effect on complex network remain issues worth studying.
- 1.8
- The above models commonly assume that agents possess complete information on their neighboring agents' strategies. Under this circumstance, agents can imitate the strategy of the agent who achieves the biggest payoff in his neighborhood. What happens when this is no longer true? As game theory has demonstrated, information and players' moving sequence are critical in the games. Straub and Murnigh ( 1995) designed experiments to test the effect of information on the ultimatum game. Croson (1996) studied the role of information-money and relative fairness-in determining offer and response through experiments. Huck (1999) analyzed the responder behavior in ultimatum offer games with incomplete information. By endogenizing first moving advantage in the ultimatum game, Poulsen (2007) analyzed information's role in an evolutionary ultimatum game where responders possess acceptable thresholds and proposed offers are conditioned on any available information on the responders' thresholds. They demonstrated that the higher the probability of receiving correct information on the thresholds and the lower the price, the larger the share of the money obtained by the responders. Poulsen likewise pointed out that although information on responders' thresholds is desirable for an individual proposer, it will hurt proposers as a group in the long run.
- 1.9
- Based on the above mentioned studies, information can be considered to be an important factor in the ultimatum game. Therefore, it may be helpful to integrate this factor into the ultimatum game on networks as well. When the proposer's suggestion is rejected, the proposer will not obtain the exact information on his opponents' minimal acceptable money. The agent is unsure of other agents' strategies except for the offers he can receive. In this situation, agents cannot simply imitate the best strategy of their neighboring agents.
- 1.10
- The purpose of this paper is to study the ultimatum game while integrating social preference utility function with evolutionary game theory in a complex network through an agent-based approach. In this model, a few heterogeneous agents displaying social preference are allowed and their effects on the evolution of ultimatum game in a complex network are studied.
- 1.11
- Unlike the limited number of strategies such as cooperation or defection in the prisoner's dilemma game, the ultimatum game distinctly features a continuous strategy space. In various research, agents' strategies are assumed to be distributed over a unit interval [0, 1]. Through natural selection or imitation and agents' spatial interaction, the fittest survives. However, this assumption is not always realistic, and this approach fails to explain the emergence of fairness behavior as it merely addresses the question of which strategy will most likely survive in the evolution. Another feature of ultimatum game is that agents may only have incomplete information on other players. Even if the proposer's suggestion is rejected, he does not attain complete information on his opponents' minimal acceptable money. Agents are unsure of other agents' strategies, with the exception of the offer he can receive. Therefore, agents cannot merely imitate their neighbor's best strategy, which may be the case if they possessed complete information on other agents' strategies. Under such an environment, agents need to learn and probe in the strategy space, hoping to obtain the strategy which can raise the largest utility.
- 1.12
- This paper will explore social preference in fairness behavior emergence under the condition where each agent needs to determine the best strategy in a continuous strategy space because of limited information on other agents. Through agent-based simulation, the following questions will be investigated: Is social preference helpful in promoting fairness level in spatial ultimatum game? How do different social preferences affect the evolution of spatial ultimatum game? First, this study will address the case where agents possess fairness considerations, which prescribe the least money they wish to accept in the ultimatum game. Next, the case of inequity aversion preference in the network will be tested, where the agents care about other agents' payoffs. Finally, the case of social welfare preference, whose main feature is that an agent cares about social welfare other than his own payoff, will be tested as well.
 The Model
The Model
- 2.1
- The model consists of a set of N agents connected through a complex network. This network defines the neighborhood for each agent in the system. In each simulation step, every agent interacts with those in his own neighborhood. The network in question is a Watts-Strogatz (WS) small world network (Watts and Strogatz 1998).
- 2.2
- In the model's initial status, each agent is assigned a playing strategy s(oi ,ri), which is given by a pair of real numbers (oi,ri)∈[a,b]. Here, a≤b; oi is the offer of agent i when acting as a proposer, and ri is the reserve level or the least amount which agent i could accept when he is a responder. In a two-agent ultimatum game, the total sum allotted is equal to 1.
- 2.3
- In each step of the simulation, each agent must play separate ultimatum games with all his neighboring agents. In every game, the single ultimatum game between two directly linked players is played twice, while agents alternate between the roles of offerer and responder.
- 2.4
- If agent i with strategy s(oi ,ri) interacts with agent j with strategy s(oj ,rj), the payoff pij agent i will obtain is set as follows:
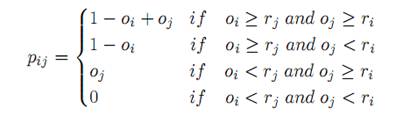
(1) The total payoff received by each agent is calculated after each has played with his entire neighborhood of agents. Each agent then decides to select a strategy for the current condition. In this model, both the oi and ri of agent i can be adjusted to maximize agents' payoff. However, as previously noted, agent i possesses no exact information on the least amount of money which other agents will accept. To model the adaptive learning behavior under this situation, Genetic Algorithm Learning Classifier System (GALCS) is employed, This is an evolutionary learning algorithm based on Holland's Learning Classifier System (Holland 1976).
- 2.5
- Based on the situations faced by the agent and the correspondent strategies' performance, GALCS will assign and update a probability vector in every state for the agents. This determines which strategy will most likely be utilized. The strategy is chosen according to the random number generated in the interval [0, 1]. GALCS may be considered as a type of reinforcement learning algorithm, though the rule is not based on a fixed (oj ,rj) value but on the situations in which the agent may be situated. Through the evolution process, the rules (strategy and current status) which have brought more payoffs will more likely survive and attain more opportunities for future use. Under the uncertain circumstance inherent in this study's model, GACLS is a reasonable learning mechanism. The more status included in the GALCS, the more efficient it will be for the strategies' evolution, even though its performance will be greatly lowered and convergence time will be longer. In the present spatial ultimatum game model, four factors are defined for identifying the situation determined by the four status agent i:
- Whether more than half of the neighboring agents accept the offer proposed by agent i
- Whether agent i's reserve level is greater than the average offer level of his neighboring agents
- Whether agent i's offer is greater than the average offer proposed by his neighboring agents
- Whether agent i's payoff is greater than his neighboring agents' average payoff
- 2.6
- These are the four most important factors in GALCS that can be observed by each agent. The probability vector assigned to agent i has nine elements corresponding to the nine strategies which may be employed (pi0 , pi1 , pi2, pi3, …, pi8), where
pi0 = probability that agent i will increase both oi and ri (by a certain exogenously specified adjustment step) when the agent enters the same status;
pi1 = probability that agent i will increase oi and decrease oi;
pi2 = probability that agent i will decrease both oi and ri;
pi3 = probability that agent i will decrease oi and increase ri;
pi4 = probability that agent i will increase oi and ri will remain unchanged;
pi5 = probability that agent i will decrease oi and ri will remain unchanged;
pi6 = probability that agent i will increase ri and oi will remain unchanged;
pi7 = probability that agent i will decrease ri and oi will remain unchanged; and
pi8 = probability that agent i's ri and oi will both remain unchanged. - 2.7
- Upon entering into a certain situation, agent i will choose a strategy from the corresponding probability vector based on the generated random number in the interval [0, 1]. Agent i plays with his neighboring agents using this strategy, and then adjusts the values of ri and oi accordingly based on this strategy's payoff. If the strategy under the current state provides agent i with more or less profit than the last simulation step, agent i will update the probability vector to reflect the profit difference. In other words, agent i will increase the probability for the just chosen strategy if it yields more payoff. If this strategy under the current state provides agent i with less profit than the last simulation step, agent i will decrease the probability just chosen in the probability vector. To ensure that the sum of the probability vector is equal to 1, other elements in the probability vector will likewise be modified at the same time; otherwise, agent i will not change his probability vector.
- 2.8
- To avoid cases where GALCS is overtrained, thus leaving space for all strategies, the probability of each strategy is limited to a certain upper limit value lower than one. Each element in the probability vector, therefore, will not be equal to zero.
- 2.9
- In this study's model, a number of agents exhibit the social preference feature, which assumes three forms. First, agents display a minimum acceptable level in the ultimatum game because of the fairness consideration. Numerous experiments on economics reveal that people will always refuse the proposal which appear to be exceedingly unfair. Second, certain agents display inequality aversion in the game. Following Fehr and Schmidt (1999) but using a localized approach to social preference, it is assumed that agent i's social preference utility of payoff allocation X={x1, x2, …, xn} for him and his n-1 neighboring agents is obtained through the following:
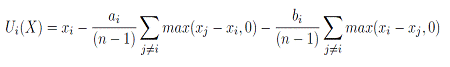
(2) Here, xi is the material payoff of agent i, and xj is the material payoff of agent j who is the neighbor of agent i. It is assumed that 0 ≤ ai < 1 and bi ≤ ai, where ai is the weight of agent i assigned to represent the degree of sufferance when his payoff is less than his neighboring agents' (envy), and bi is the weight of agent i assigned to represent the degree of sufferance when his payoff is higher than his neighboring agents' payoff (guilt).
- 2.10
- In the third kind of social preference, certain heterogeneous individuals are assumed to care about the welfare of other agents besides themselves. This consideration is limited within his neighborhood. It is assumed that agent i's social preference utility of payoff allocation X={x1, x2, …, xn} for himself and his n-1 neighboring agents is provided by the following formulae, where wi is the weight agent i places on the social welfare of his neighboring agents.
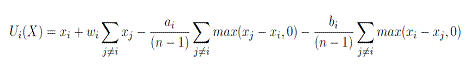
(3) Therefore, in the present ultimatum game model, the strategies of each agent will evolve accordingly and the agents will be driven by the pursuit of maximum profit through GALCS learning in a simulation process. The evolving process and agents' strategy distribution in this process can then be observed.
 Simulation Results
Simulation Results
- 3.1
- The simulation is carried out on a WS small world network with 2,000 agents. Although there is negligible differences between a WS small world network and a Newman-Watts (NW) small network model, simulation on the latter is likewise conducted. The WS small world is built using original WS small world algorithm (Watts and Strogatz 1998). During simulation, the effect of different social preference forms on the spatial ultimatum game is tested. At the same time, the parameters set of the model are varied. Each simulation is performed with 5,000 steps. The system's synchronous and asynchronous update mechanisms are compared, but the results reveal that these do not yield any significant difference. Thus, only simulation results from a synchronous updating mechanism are reported. The agent strategy updating step will likewise have a small effect on long-term fairness level, and its value is set to 0.1. The system may not evolve into a stable status because the agent will continuously update his strategy and formulate a decision according to probability during the simulation process. To achieve robust results, this study utilizes the values which are averaged over 30 individual simulations for each given set of model parameters.
Minimum acceptable level and the fairness level in ultimatum game
- 3.2
- The case begins when a few agents maintain a minimum or reserve acceptable level in the ultimatum game. When other agents' offers are lower than his reserve value, the agent will reject the offer directly, for his type has a strong requirement for fairness in the ultimatum game. It is a very simple form of social preference, but it does exist in many situations as shown in various experiments. It may appear obvious that if an agent anticipates that the other agents will reject his offer, which is lower than their reserve value, he will raise his offer level. Therefore, the overall offer levels will likewise be raised. However, the simulation results only support this assertion in part if agents are located in the complex network. The simulation results reveal that the fairness level is increased given the minimal reserve increases when the minimal reserve level is not extremely high. However, the fairness level will drop to a low level when the reserve level increases to a certain level. For example, when the minimum acceptable level is 0.5, the average offer level is even lower than the average reserve level, which is not observed in other situations.
- 3.3
- Figure 1 illustrates the dynamic processes of the average offer and the reserve money level, with certain agents' minimum acceptable level set between 0.2 and 0.5 (step is 0.1) in a WS small world network when random rewire probability is set to 0.05. The initial strategy distributions are all drawn from the interval [0, 0.5].
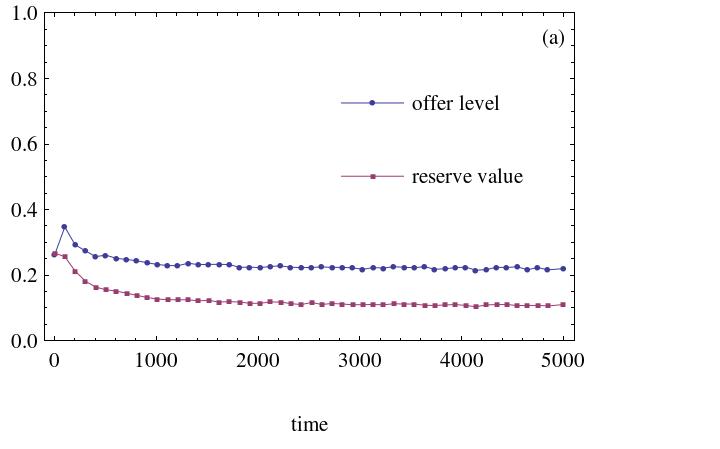
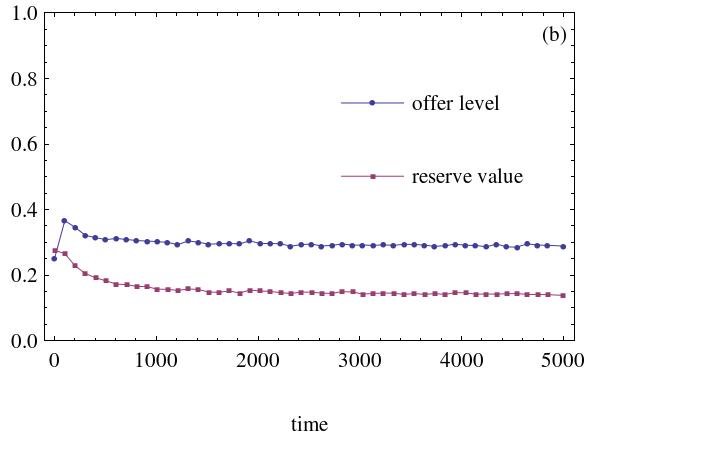
(a) Agents' minimum reserve level is 0.2 (b) Agents' minimum reserve level is 0.3 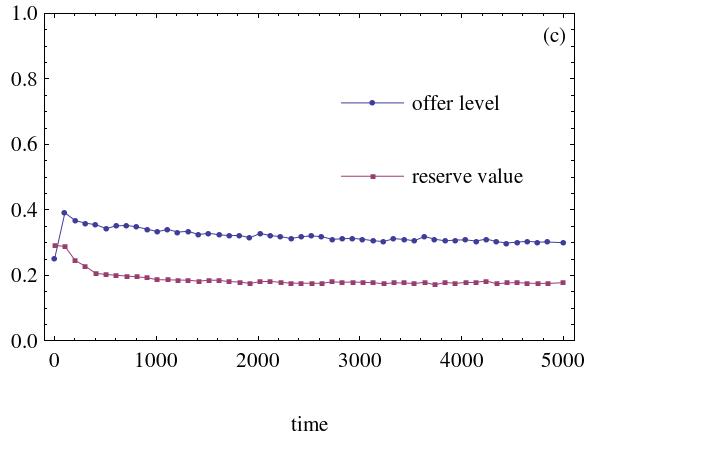
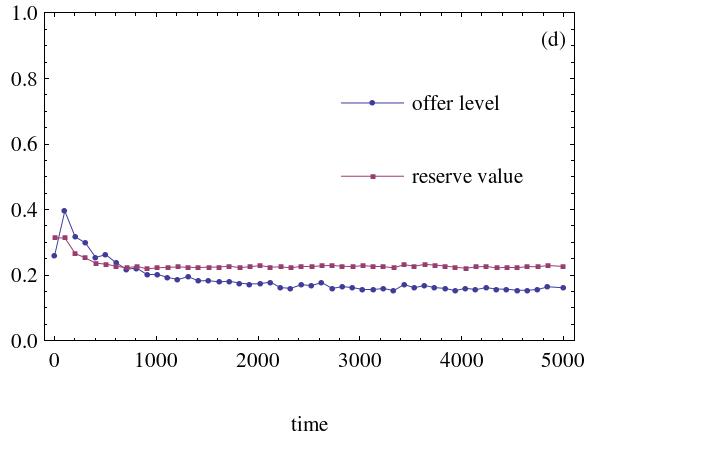
(c) Agents' minimum reserve level is 0.4 (d) Agents' minimum reserve level is 0.5 Figure 1. The effect of minimum reserve level. Heterogeneous social preference agents number is 500 - 3.4
- On the other hand, not all agents in the complex network adopt the same strategy because of their initial strategies and locations within the network. Final strategies distribution must thus be checked. The corresponding histograms are illustrated in Figure 2. From these graphs, majority of agents' final strategies distribution are discovered to depend on the minimum acceptable level.
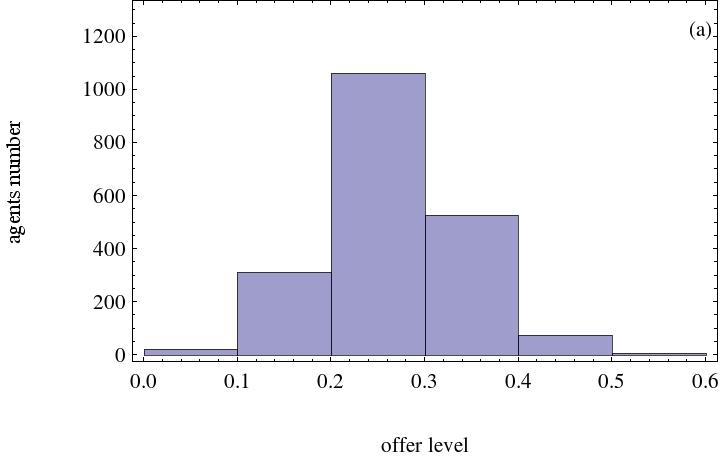
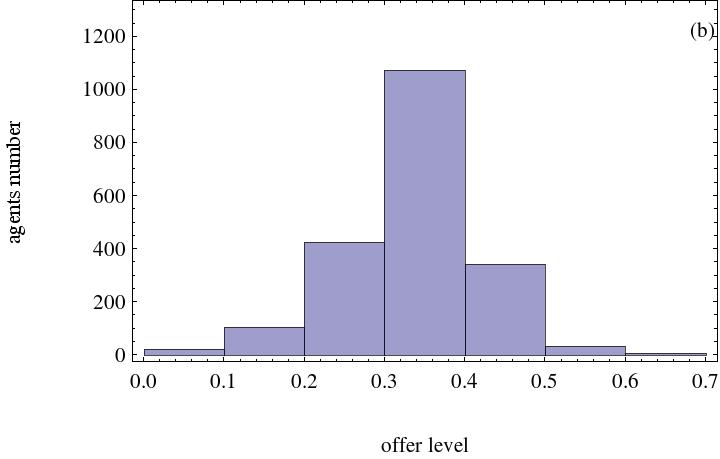
(a) Agents' minimum reserve level is 0.2 (b) Agents' minimum reserve level is 0.3 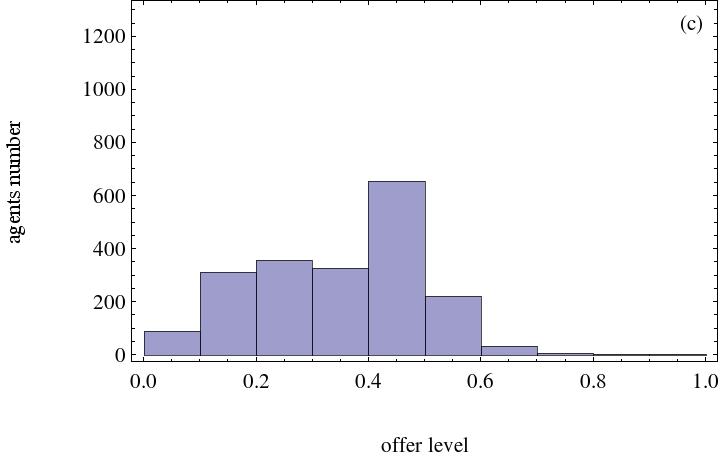
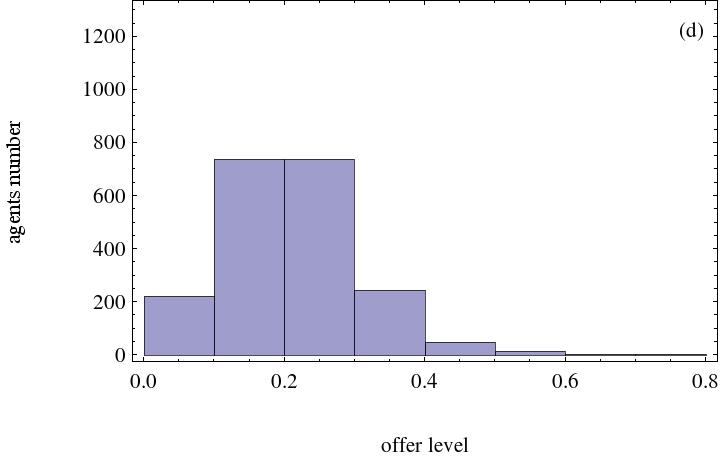
(c) Agents' minimum reserve level is 0.4 (d) Agents' minimum reserve level is 0.5 Figure 2. Histogram with the effect of minimum acceptable level. Heterogeneous social preference number is 500 - 3.5
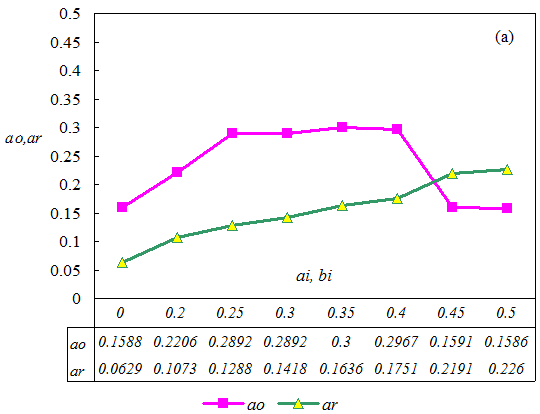
- The agents' strategies may always change along with those of other agents, thus a stable status may not be reached. To obtain robust results, the simulation is repeated 30 times, the results of which are summarized in Figure 3.
- 3.6
- The number of agents who display a social preference is 500. The minimum acceptable level is denoted by ma, the average offer level by ao, the average reserve level by ar, and the total payoff by tp. For comparison, the results when no social preference agents exist are likewise listed. Under this setting, when the minimum acceptable level is between 0.25 to 0.4, the attained fairness level is highest. When the minimum acceptable level increases continuously, the attained fairness level decreases. When the minimum acceptable level is 0.5, the attained fairness level is not extremely different from the case where no minimum acceptable level is set, though reserve level is a little higher. Although this result appears strange, it can be explained from two perspectives. First, agents are situated in the WS small world network and they play the ultimatum game with many neighboring agents, not merely the agent whose minimum acceptable level is high. Therefore, this agent will consider his strategy's effect on other agents when he modifies it. Second, even though the minimum acceptable levels of an agent's neighbors are high, this agent's learning algorithm may limit his offer continuously to meet the demand of the agents' highest minimum acceptable level. Therefore, in the complex network environment, merely raising the minimum acceptable level does not necessarily lead to a high fairness level in the ultimatum game in the WS small world network. Moreover, the overall payoff may be lowered when the minimum acceptable level is raised. This implies that though the minimum acceptable level may raise the fairness level to a certain extent, the system's total payoff is another issue.
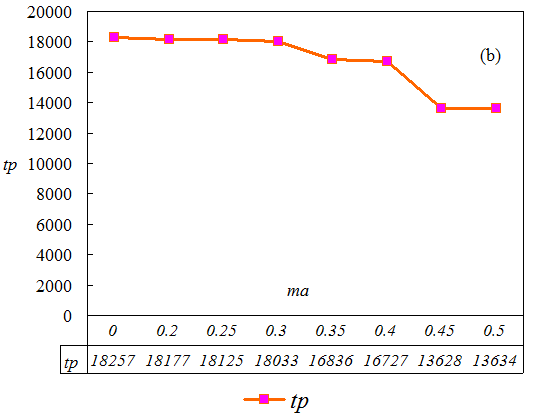
(a) Average offer and reserve level as the function of minimum acceptable level (b) Total payoff as the function of minimum acceptable level Figure 3. Statistical average results of the simulation when certain agents possess a minimum acceptable level in the ultimatum game The effect of agent inequality aversion social preference on spatial ultimatum game
- 3.7
- Fehr and Schmidt's (1999) model assumes that agents are heterogeneous. Although certain people are not interested in the allocation of wealth among the population, they are interested in their relative ranking in this wealth distribution. This social comparison depicts agents' social preference, and this is dubbed "self-centered in inequity-aversion". This model has successfully explained the observed behavior in many game experiments. However, what happens when agents are distributed in a network and they interact through the network connections? Can this inequality aversion preference help explain the fairness behavior in the spatial ultimatum game?
- 3.8
- Agent simulation enables this paper to explore this question. The number of inequality aversion agents is first set at 500, and then eventually at 1,500. The initial strategies distribution is drawn from the interval [0, 0.5]. The results are illustrated in Figure 4 (other cases yield similar results).
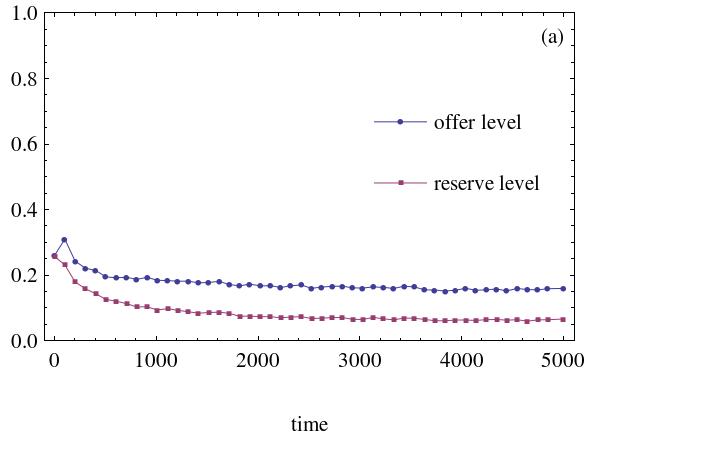
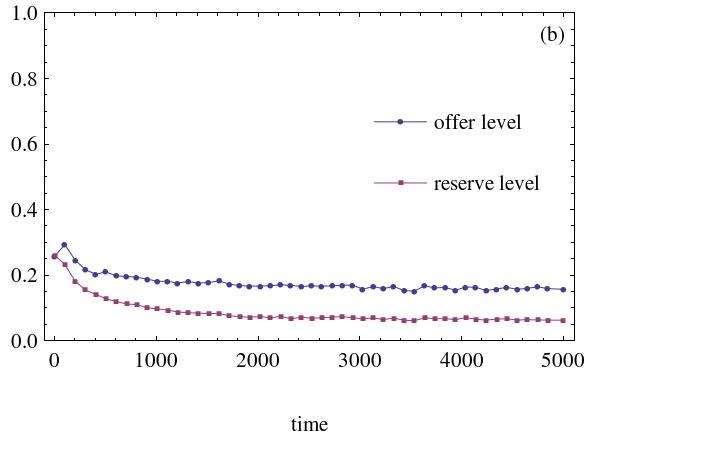
(a) Agents' inequality aversion weight is 0.2 and agents' initial strategies distribution is drawn from the interval [0,0.5] (b) Agents' inequality aversion weight is 0.5. Agents' initial strategies distribution is drawn from the interval [0,0.5] Figure 4. The dynamic processes of evolution with inequality aversion agents. The number of heterogeneous social preference agents is 500 The simulation results demonstrate that this kind of social inequality aversion has a small effect on the spatial ultimatum game's evolution process.
- 3.9
- The strategy distribution of all agents after running 5,000 steps is displayed in Figure 5. The results are not quite different from the case with no inequality aversion agents. Although there is a modest difference, simulation results reveal that inequality aversion agents do not play an important role in the spatial ultimatum game's evolution as a result of heterogeneous inequality aversion.
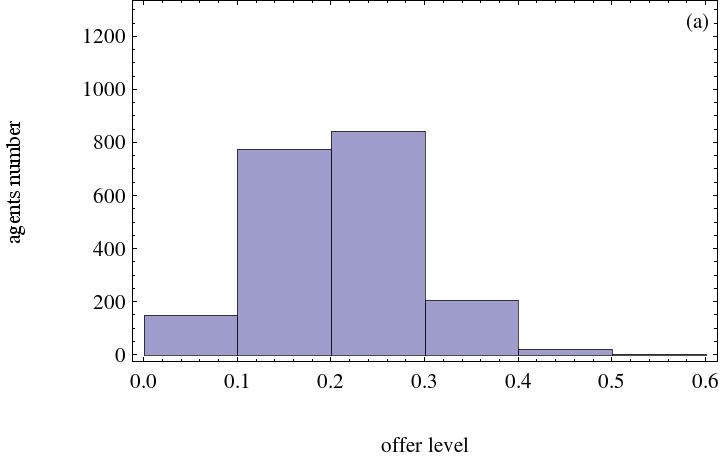
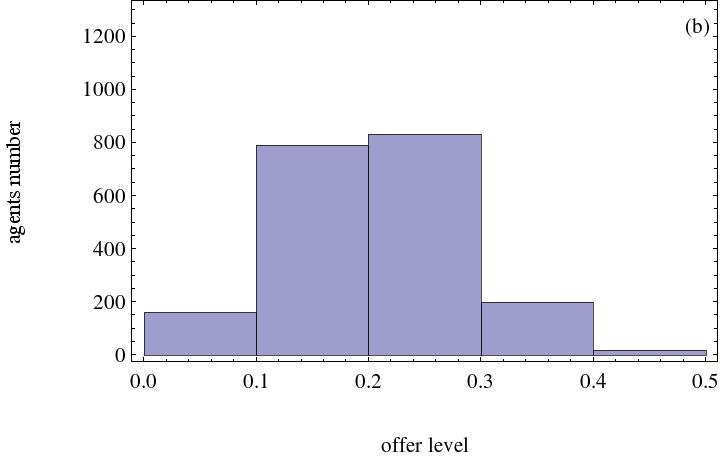
(a) Agents' inequality aversion weight is 0.2 and agents' initial strategy distribution is drawn from the interval [0,0.5] (b) Agents' inequality aversion weight is 0.5 and agents' initial strategies distribution is drawn from the interval [0,0.5] Figure 5. The effect of inequality aversion agents on final strategy distribution. Heterogeneous social preference number is 500 - 3.10
- The simulation is repeated 30 times, and the average results are summarized in Figure 6. The inequality aversion agent number is denoted by av. As previously stated, ai is the weight of agent i assigned to represent the degree of sufferance when his payoff is less than his neighbors', and bi is the weight of agent i assigned to represent the degree of sufferance when his payoff is higher than his neighbors'. The initial strategy distribution of agents is drawn from the interval [0, 0.5].
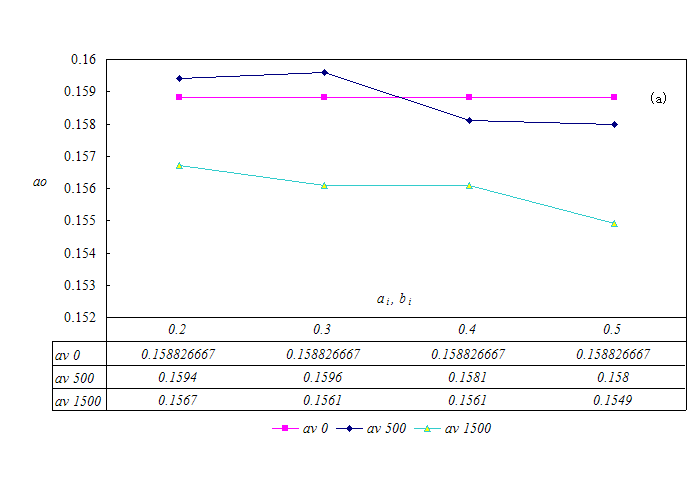
(a) Average offer level as the function of inequality aversion degree 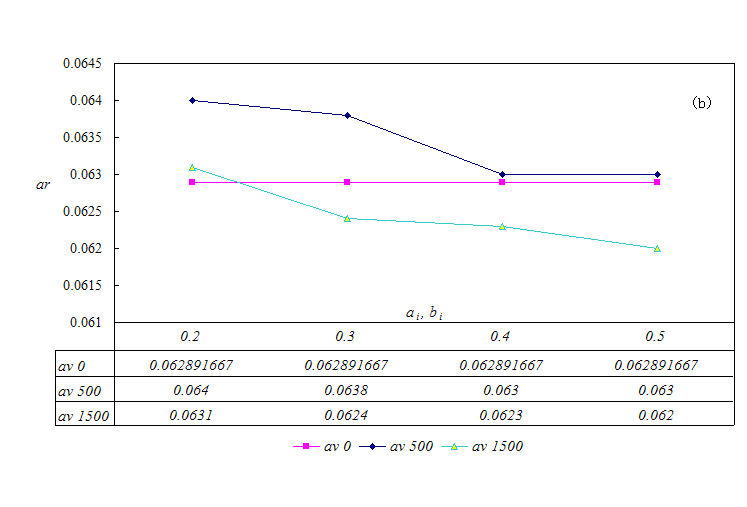
(b) Average reserve level as the function of inequality aversion degree 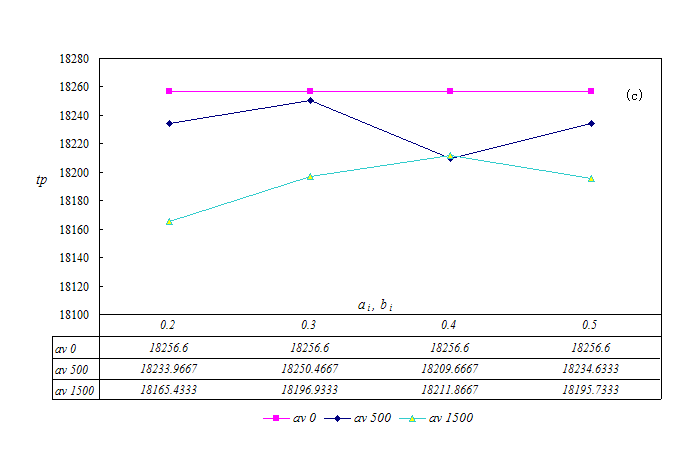
(c) Total payoff as the function of inequality aversion degree Figure 6. Statistical average results of the simulation when certain agents display inequality aversion in the ultimatum game - 3.11
- The results reveal that the achieved fairness level is smaller than the situation when no inequality aversion agents exist and the number of inequality aversion agents is large. In the case of total payoff in the system, inequality aversion agents will slightly lower the total payoff in the system. The reserve level, though, is slightly different. There is no simple relationship between reserve level and the number of inequality aversion agents. However, when inequality aversion agents exist, the reserve level is slightly higher than in other cases sometimes. Therefore, inequality aversion agents may lead to a smaller difference between offer level and reserve level. This is primarily a result of the fact that, under the complex network, agents interact with their neighboring agents and the inequality between agents is averaged. Further, the initial strategies are distributed among agents in the network. It is therefore reasonable to assume that inequality aversion does not have a significant effect on the spatial ultimatum game. If strategy distribution among agents is modified, the result may be different. This requires further research.
Social welfare preference and the ultimatum game
- 3.12
- Another social preference approach assumes that agents care about social welfare besides their own payoffs. This paper studies whether this kind of social preference will promote fairness level in the ultimatum game. It follows Kohler's model (2003), which integrates the concern of self-regarding, inequality aversion with social welfare. It is assumed that agents are merely concerned about their neighborhood's welfare. The simulation is conducted with three different numbers of social welfare preference agents in the network, and the weight agents assigned to the welfare of their neighboring agents are changed. The results reveal that concern over neighboring agents' welfare will promote fairness level in the spatial ultimatum, though the degree depends on the weight agents placed on the social welfare.
- 3.13
- The dynamic processes of the ultimatum game's evolution with social welfare preference agents are displayed in Figure 7. It is assumed that the initial strategies are randomly drawn from the interval [0, 0.5].
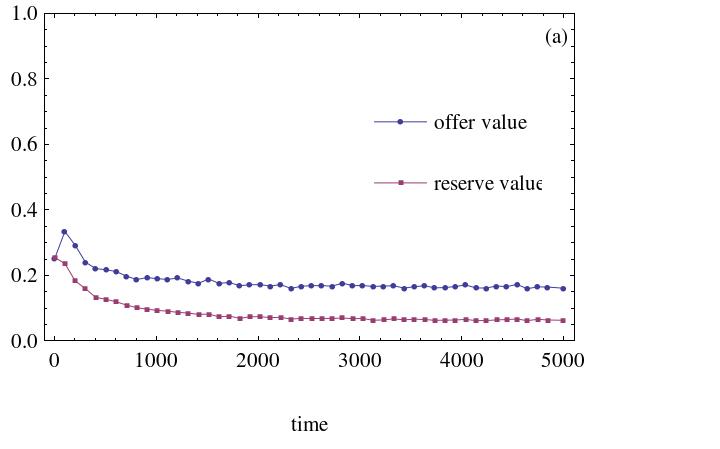
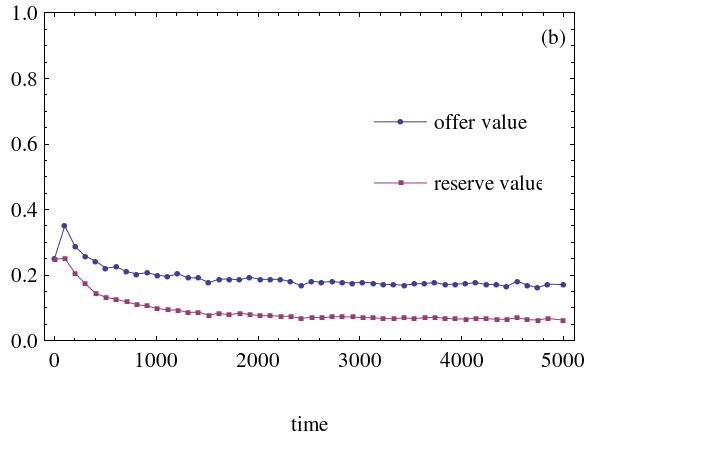
(a) The social welfare weight agents assigned is 0.3 (b) The social welfare weight agents assigned is 0.5 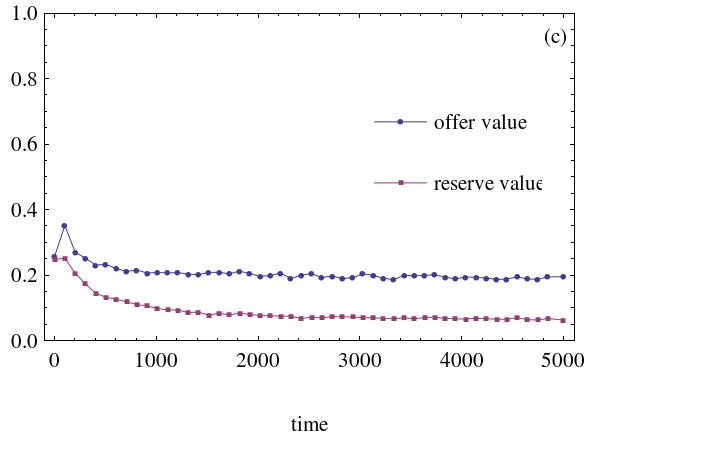
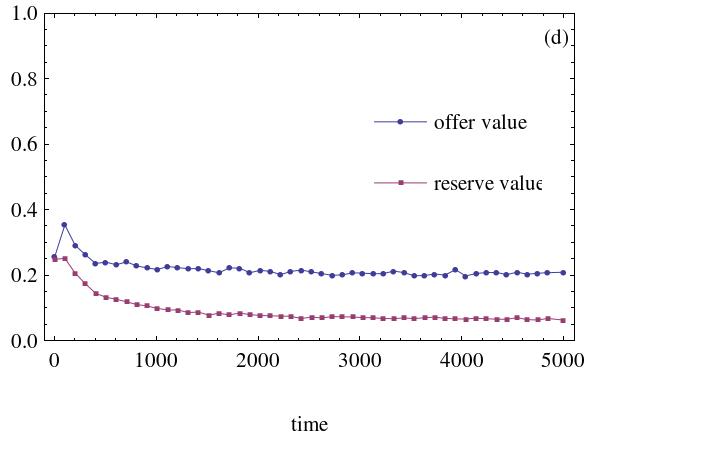
(c) The social welfare weight agents assigned is 0.7 (d) The social welfare weight agents assigned is 0.9 Figure 7. The dynamic process with social welfare preference agents. The number of heterogeneous social preference agents is 500 - 3.14
- The strategy distribution after running 5,000 steps is displayed in Figure 8.
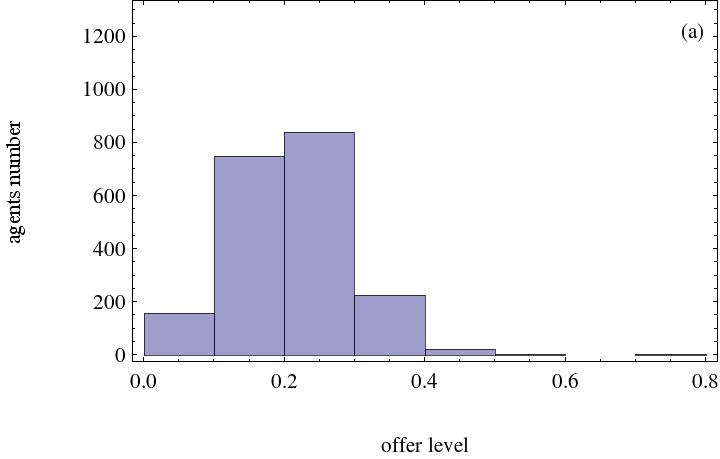
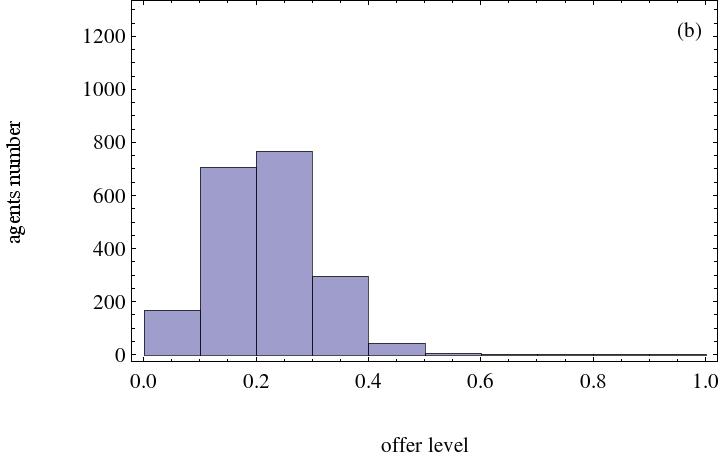
(a) The social welfare weight agents assigned is 0.3 (b) The social welfare weight agents assigned is 0.5 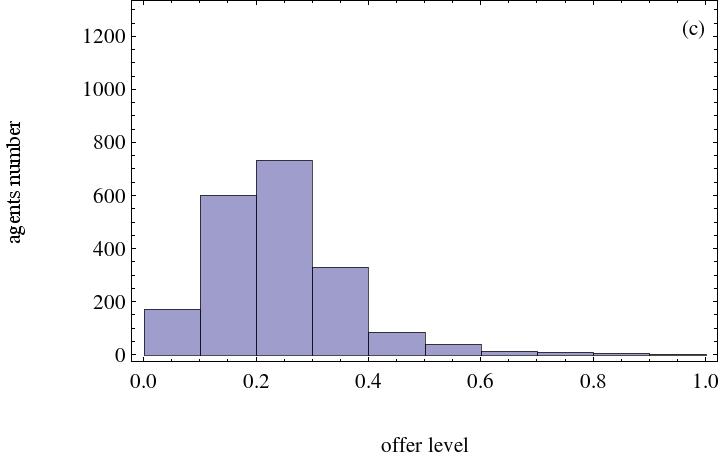
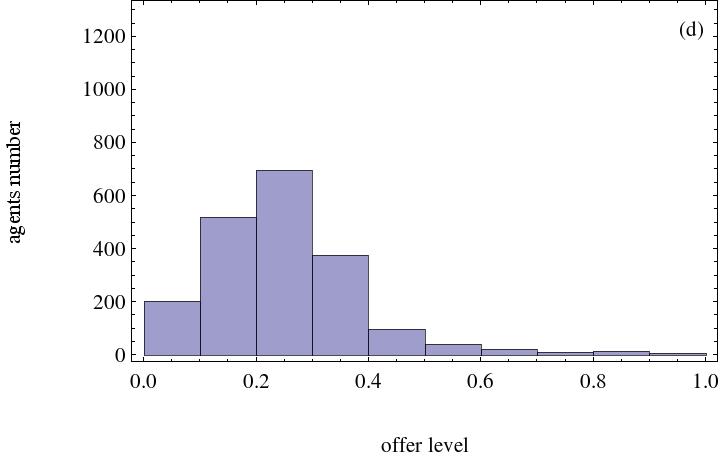
(c) The social welfare weight agents assigned is 0.7 (d) The social welfare weight agents assigned is 0.9 Figure 8. Histogram with social welfare preference agents. The number of heterogeneous social preference agents is 500 - 3.15
- The simulation is repeated 30 times under different sets of parameters, the average results of which are summarized in Figure 9. The social welfare preference agents' number is denoted by av, and wi is the weight which agent i places on the social welfare of his neighbors. ai and bi are set to 0.2.
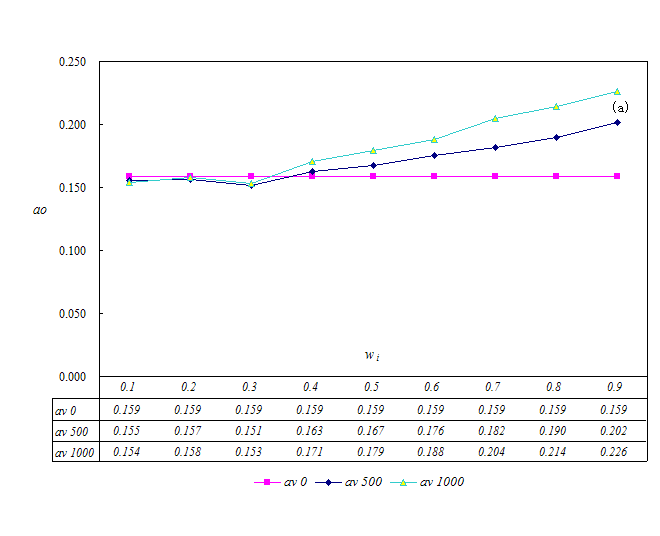
(a) Average offer level as the function of social preference degree 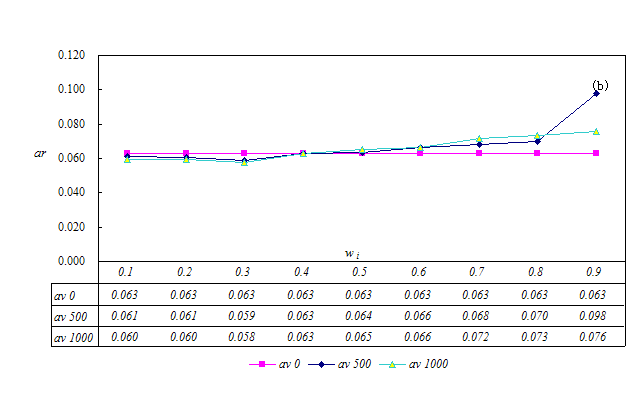
(b) Average reserve level as the function of social preference degree 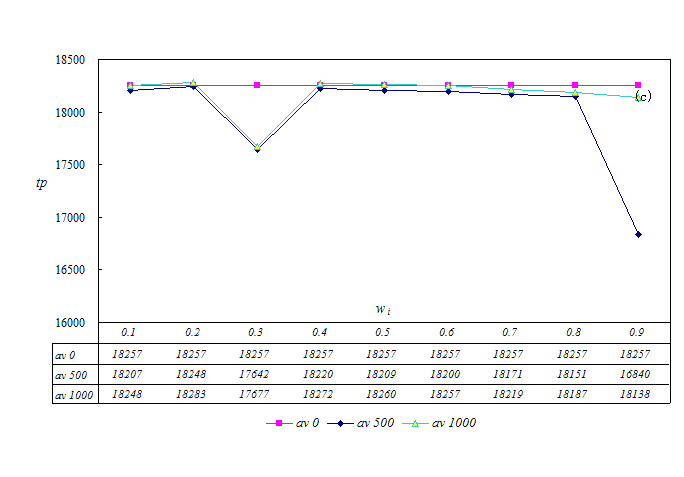
(c) Total payoff as the function of social preference degree Figure 9. Statistical average results of simulations when certain agents possess social welfare preference in the ultimatum game - 3.16
- It is evident from the above simulation results that the more the social welfare preference agents and the more weight the agent places on social welfare, the higher the fairness level. This signifies that social welfare preference agents favor the emergence of fairness among agents in the network. Otherwise, the difference in achieved fairness level in the ultimatum game is small. Simulation results demonstrate that more agents will raise their offer levels if more social welfare preference agents exist. Owing to the existence of social welfare preference agents, an individual will care about others and will be more likely to assume a strategy that is beneficial to the welfare of neighboring agents.
 Conclusion
Conclusion
- 4.1
- An agent-based model has been designed to study the effects of various forms of social preference on fairness evolution in spatial ultimatum games. Although many social preference models can explain the agent behavior in the experiment, a number are not as effective when the ultimatum game is extended to a network version.
- 4.2
- Three kinds of social preference theories have been tested: fairness requirement, inequality aversion, and social welfare preference. The simulations imply that fairness requirement can promote fairness level in society only in certain parameter intervals. However, when the minimum acceptable level is high and not all agents in the system display social preference, the attained fairness level will be lower. Simulation results likewise reveal that inequality aversion among agents has a slight effect on the spatial ultimatum game's evolution. In the spatial ultimatum game, the existence of inequality aversion agents does not create a significant difference on the average offer and acceptable level.
- 4.3
- The case of social welfare preference is quite different. Its effects depend on the number of social welfare preference agents and the weight placed on it. The more the number of social preference agents and the more weight placed on the social welfare utility, the higher the fairness level that will be achieved by society. The factor of social welfare changes the strategy distribution among the population as well.
- 4.4
- By adding social preference and incomplete information to the agent model of spatial ultimatum game, the fairness behavior in the ultimatum game can be explained in a more realistic way. As it depicted in the behavior game theory, many social factors will affect the fairness level which emerges in the ultimatum game. Incomplete information leads to a fairness level that is lower than in the case when agents have complete information on other agents, as demonstrated by Page, Nowak, and Sigmund (2000), Kuperman and Risau-Gusman (2008), and other empirical results (Camerer 2003). At the same time, this study likewise confirms the idea that information is an important factor in the ultimatum game, as pointed out by Poulsen (2007). This is applied in a spatial version of ultimatum. However, this study has proved that with adequate social preference, the fairness level will be enhanced.
- 4.5
- Further, this study has demonstrated that social preference models have various implications on the complex network, which is different from cases where agents have no network connections between them. Although inequality aversion preference has explained fairness behavior in a simple ultimatum game, it fails to do so in a spatial ultimatum game. This implies that agents' interaction cannot remove the effect of social preference. This is likewise a feature of a complex system that is composed of the interactions between agents. Therefore, it cannot be reduced to the behavior of a single agent. However, social preference is considered a feature for agents living in a society, and certain social preferences indeed promote fairness level in the spatial ultimatum game. This study demonstrates that the relationship among evolution, social preference, and fairness behavior is rather complex. Further study must be conducted in this field, with special focus on the effect of agents' psychology and mutual reciprocity on fairness emergence and the spatial games' evolution process. Nevertheless, social preference can play an important role in the evolution of the spatial ultimatum game.
 Appendix: Pseudo-code of the model and algorithm of GALCS
Appendix: Pseudo-code of the model and algorithm of GALCS
- A.1
- The model presented in this work was implemented using Repast Simphony.
Model class
- Generate 2000 agents. Initialize the agents. Set the agents' offer and reserve level randomly from the given interval.
- Build the WS small world network; Agents are located on the vertices of the network.
- Randomly select given number of agents to be the agents possessing social preference;
- Build the simulation schedules as follows:
// Because in the simulation process, each agent needs to get some neighboring agents' information, // thus it is needed to make sure that each agent's change of status will not affect other agents' //computation during the same step or tick in simulation
// t signifies time step or tick If t=0{ //Prepare to begin the model, first compute the payoff and social preference payoff // in the model. Step 1 begins with the strategy choice after which each agent can // adjust the strategy vector according to the results in this step.
for each agent on the network
{ // Compute the payoff each agent has received, here no social preference involved. computePayoff(); //Compute the social preference payoff if this agent displays social preference. computeSocialPreference(); } for each agent on the network { // Update the status of this agent when the other works in this step are done. postUpdate(); > } } //t[stop] is the time step or tick when simulation stops. for t = 1 to t[stop] { for each agent on the network { //Choose one strategy according to the probability vector. chooseStrategy(); //Adjust the offer and reserve level values. adjustStrategy(); } for each agent on the network { computePayoff(); // Compute the payoff when this agent has modified his offer and reserve level values. computeSocialPreference(); //Compute the social preference payoff if this agent displays social preference. } for each agent on the network { // Update the strategy vector according to the payoff current strategy achieved. The strategy // which has achieved more utility will increase its probability to be used in future under the // current condition. updateStrategyProbability (); } for each agent on the network) { // update the status of this agent after the other works in one step are done. postUpdate(); } } If t=t[stop]{ Perform data recording work, write needed data to output file. End the model; }
Agent class
The following methods are defined. They are the methods deployed by the agents during their interactions in the spatial ultimatum game.- GameAgent() initializes agents, especially sets strategy vector, all strategies will be set with the same value at first. The strategy vector is a five dimension array, the first four signify the condition agent faces, each has three elements, the last represents the strategy which has nine elements, and it is denoted by the integers from 0 to 8.
- play(agent1, agent2) computes the payoff of single play between this agent with one of his neighboring agents.
- computePayoff() computes total payoffs when an agent plays ultimatum game with neighboring agents.
- computeSocialPreference() computes the social preference according to social preference utility function if this agent is set to display social preference.
- chooseStrategy () chooses the strategy in t.
chooseStrategy() { Compute the average payoff and average offer level of the neighboring agents; Compute current offer accepted number and check whether current reserve level is larger than average offer level of neighboring agents; Identify the status agent faces, including four factors now: // conditionO represents how many agents accept the offer in this agents' neighborhood if (more than half of the neighboring agents accept this agent's offer) conditionO=0; else conditionO=1; //conditionR represents whether the reserve level is larger than //the average offer level of neighboring agents if (reserve level < average offer level of neighboring agents) conditionr=0; else conditionR=1; if(offer level>=average neighboring agents' offer) conditionN=0; else conditionN=1; if(current payoff>=average neighboring agents' payoff) conditionT=0; else conditionT=1; //choose the strategy according to the above parameters; choose(conditionO,conditionR,conditionT,conditionN,conditionA); } - adjustStrategy() adjusts the values of offer and reserve level according to the choosen strategy.
switch(choosen strategy){ case 0: increase offer and reserve level; case 1: increase offer, decrease reserve level; case 2: decrease offer, increase reserve level; case 3: decrease offer and reserve level; case 4: only decrease offer level, reserve value unchanged; case 5: only increase offer level, reserve value unchanged; case 6: only increase reserve level, offer value unchanged; case 7: only decrease reserve level, offer value unchanged; case 8: nothing changed; } - updateStrategyProbability () updates the strategy vector i;
updateStrategyProbability() { Identify the condition this agent faces; if (current social preference utility > previous social preference utility) { if (current social preference utility + adjustment step < upper value of the probability) { Raise the probability of this strategy by a given step under the current condition; Adjust other elements in the vector to keep the sum of all elements equal to 1 under this condition; } } else if (current social preference utility + adjustment step < upper value of the probability){ Decrease the probability of this strategy by a given step under the current condition; Adjust other elements in the vector to keep the sum of all elements equal to 1 under this condition; } else return; //nothing changed; }
 Acknowledgements
Acknowledgements
- The author thanks the NSFC (Grant No.70673118). The author thanks the anonymous referees for their valuable suggestions.
 References
References
-
ANDREONI, J and Miller, J (2002). Giving according to garp: An experimental test of the consistency of preferences for altruism. Econometrica, 70(2), pp. 737-753. [doi:10.1111/1468-0262.00302]
BOLTON, G E and Ockenfels, A (2000). ERC: A theory of equity, reciprocity, and competition. American Economic Review, 90(1), pp. 166-193. [doi:10.1257/aer.90.1.166]
BOLTON, G E and Zwick, R (1995). Anonymity versus punishment in ultimatum bargaining. Games and Economic Behavior, 10(1), pp. 95-121. [doi:10.1006/game.1995.1026]
CAMERER, C F (2003). Behavioral Game Theory. University Press, Princeton.
CAMERON, L A (1999). Raising the stakes in the ultimatum game: Experimental evidence from Indonesia.Economic Inquiry, 37(1), pp. 47-59. [doi:10.1111/j.1465-7295.1999.tb01415.x]
CHARNESS, G and Rabin, M (2002). Understanding social preferences with simple tests. Quarterly Journal of Economics, 117, pp. 817-869. [doi:10.1162/003355302760193904]
CROSON, R T A (1996). Information in ultimatum games: An experimental study. Journal of Economic Behavior& Organization, 30(2), pp. 197-12. [doi:10.1016/S0167-2681(96)00857-8]
FALK, A and Fischbacher, U (2006). A theory of reciprocity. Games and Economic Behavior, 54(2):293-15. [doi:10.1016/j.geb.2005.03.001]
FEHR, E and Schmidt, K M (1999). A theory of fairness, competition, and cooperation. The Quarterly Journal of Economics, 114(3), pp. 817-868. [doi:10.1162/003355399556151]
GÜTH, W, Schmidt, C, and Sutter, M (2007). Bargaining outside the lab - a newspaper experiment of a three-person ultimatum game. Economic Journal, 117(518), pp. 449-69. [doi:10.1111/j.1468-0297.2007.02025.x]
GÜTH, W, Schmittberger, R, and Schwarze, B (1982). An experimental analysis of ultimatum bargaining. Journal of Economic Behavior & Organization, 3(4), pp. 367-8. [doi:10.1016/0167-2681(82)90011-7]
HAYASHIDA,T, NISHIZAKI I and KATAGIRI H (2007). Agent-based simulation analysis for an ultimatum game. The 51st Annual Conference of the Institute of Systems, Control and Information Engineers, SCI'07, edited by The Institute of Systems, Control and Information Engineer, Kyoto, Japan.
HOFFMAN, E, McCabe, K A, and Smith, V L (1996). On expectations and the monetary stakes in ultimatum games. International Journal of Game Theory, 25(3), pp. 289{301. [doi:10.1007/BF02425259]
HOLLAND, J H (1976). Adaptation in Natural and Artificial Systems. University of Michigan Press, Ann Arbor.
HUCK,S (1999). Responder behavior in ultimatum offer games with incomplete information. Journal of Economic Psychology, 20, pp. 183-206. [doi:10.1016/S0167-4870(99)00004-5]
KAHNEMAN, D, Knetsch, J L, and Thaler, R (1986). Fairness as a constraint on profit seeking: Entitlements in the market. The American Economic Review, 76(4), pp. 728-41.
KILLINGBACK, T and Studer, E (2001). Spatial ultimatum games, collaborations and the evolution of fairness. Proc Biol Sci, 268(1478), pp. 1797-801. [doi:10.1098/rspb.2001.1697]
KOHLER, S (2003). Difference Aversion and Surplus Concern. An Integrated Approach, Mimeo. European University Institute, Florence.
KUPERMAN, M N and Gusman, S R (2008). The effect of the topology on the spatial ultimatum game. The European Physical Journal B, 62(2), pp. 233-38. [doi:10.1140/epjb/e2008-00133-x]
LIEBERMAN, E, Hauert, C, and Nowak, M A (2005). Evolutionary dynamics on graphs. Nature, 433(7023), pp. 312-316. [doi:10.1038/nature03204]
LIST, J and Cherry, T (2000). Learning to accept in ultimatum games: Evidence from an experimental design that generates low offers. Experimental Economics, 3(1), pp. 11-29. [doi:10.1023/A:1009989907258]
MONTET, C and Serra, D (2005). Game theory and economics. Palgrave.
NOWAK, M A, Page, K M, and Sigmund, K (2000). Evolutionary games on graphs. Science, 289(5485), pp. 1773-1775. [doi:10.1126/science.289.5485.1773]
OOSTERBEEK, H, Sloof, R, and van de Kuilen, G (2004). Cultural differences in ultimatum game experiments: Evidence from a meta-analysis. Experimental Economics, 7(2), pp. 171-188. [doi:10.1023/B:EXEC.0000026978.14316.74]
PAGE, K M, Nowak, M A, and Sigmund, K (2000). The spatial ultimatum game. Proc Biol Sci, 267(1458), pp.2177-2182. [doi:10.1098/rspb.2000.1266]
POULSEN, A U (2007). Information and endogenous first mover advantages in the ultimatum game: An evolutionary approach. Journal of Economic Behavior & Organization, 64(1), pp. 129-143 [doi:10.1016/j.jebo.2005.05.013]
RABIN, M (1993). Incorporating fairness into game theory and economics. The American Economic Review, 86(5), pp. 1281-1302.
RIECHMANN, T (2001). Another Paper on Ultimatum Games.This Time: Agent Based Simulations. Center for Nonlinear Dynamics in Economics and Finance in its series CeNDEF Workshop Papers, January 2001 with number 2B.1.
RUBINSTEIN, A (1982). Perfect equilibrium in a bargaining model. Econometrica, 50(1), pp. 97-110. [doi:10.2307/1912531]
STRAUB, P G and Murnigh, J K (1995). An experimental investigation of ultimatum games: information, fairness, expectations, and lowest acceptable offers. Journal of Economic Behavior & Organization, 27(3), pp. 345-364. [doi:10.1016/0167-2681(94)00072-M]
SZABA, G and Fáth, G (2007). Evolutionary games on graphs. Physics Reports, 446, pp. 97-216. [doi:10.1016/j.physrep.2007.04.004]
WATTS, D and Strogatz, S (1998). Collective dynamics of 'small-world' networks. Nature, 393, pp. 440-442. [10.1038/30918]