Guillaume Deffuant (2006)
Comparing Extremism Propagation Patterns in Continuous Opinion Models
Journal of Artificial Societies and Social Simulation
vol. 9, no. 3
<https://www.jasss.org/9/3/8.html>
For information about citing this article, click here
Received: 04-Jan-2006 Accepted: 10-Apr-2006 Published: 30-Jun-2006
 Abstract
Abstract|
|
(1) |
|
|
(2) |
In the next paragraph, we list the variants of the models corresponding to different choices for ku.
|
|
(3) |
|
|
(4) |
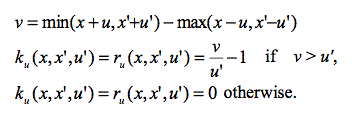
|
(5*) |
| * The author is grateful to Sascha Holzhauer for having noticed an error in formula (5), which has been corrected in May 2012. |
The value of this function is 1 when the segment [x'-u',x'+u'] is totally included in the segment [x-u, x+u]. Otherwise, it is lower than 1.
|
|
(5) |
With this kernel, if u is much smaller than u', then the change is necessarily small, because then gu(u',0) is small.
|
|
| Figure 1. The 3 convergence types. N = 50, 2 extremists at +1 and -1, ue = 0.01 (represented in red), μ = 0.3. Top: U = 0.3, RA model. Moderate convergence (X=0.62, n =3.8). Middle: U = 0.9, RA model. Double extreme convergence (X=0.99, n=1.77). Bottom : U = 1.3, GBCU model. Single extreme convergence (X=0.97, n=1.08). See paragraph 3.2 for definitions of X and n |
|
|
(7) |
In practice, we chose ε = 0.01.
epsilon := 0.01; toDo := indices of initially moderate agents; clusters := List.new; while (toDo.size > 0): currentCluster := List.with(toDo[1]); newAdded := List.with(toDo[1]); while(newAdded.size > 0): newAdded := List.new; for (j := 1, toDo.size) if (distance(currentCluster, toDo[j]) < epsilon) newAdded.add(toDo[j]); toDo.removeAll(newAdded); currentCluster.addAll(newAdded); end while clusters.add(currentCluster); end while return(clusters)
|
|
(8) |
the generalised number of clusters, noted n, which is a smooth number of clusters obtained following the method defined in Derrida and Flyvbjerg (1986). Considering a final state of the population involving k clusters of opinion xi, including a proportion pi of the initially moderate, the generalised number of clusters is defined by:
|
|
(9) |
steps := 500; Xchange := 0.2; Xlast := computeX(); X := Xlast; XchangeThreshold := 0.01; XMax := 0.9; while ((Xchange > XchangeThreshold) | (X < XMax)): repeatNbTimes(steps * population.size): agent1 := population[random(1, N)]; neighbs := agent1.neighbours; agent2 := population[neighbs[random(1, neighbs.size)]]; k12 := kernel(agent1.unc, agent1.op, agent2.op, agent2.unc); k21 := kernel(agent2.unc, agent1.op, agent2.op, agent1.unc); agent1.setOp(agent1.op + (mu * k12 * (agent2.op - agent1.op))); agent1.setUn(agent1.unc + (mu * k12 * (agent2.unc - agent1.unc))); agent2.setOp(agent2.op + (mu * k21 * (agent1.op - agent2.op))); agent2.set(agent2.unc + (mu * k21 * (agent1.unc - agent2.unc))); end repeat; X := computeX(); Xchange := abs(X - Xlast); Xlast := X; end while;
|
|
| Figure 2. BC and GBC models in total connection. Each dot represents one simulation, and the colour codes for the convergence type: • single extreme, • double extreme, • between single and double extreme, • moderate. Number of individuals: N = 400, intensity of interactions: μ = 0.3, uncertainty of extremists: ue = 0.01 |
|
|
| Figure 3. BC and GBC models on random networks with 4 neighbours on average. Each dot represents one simulation, and the colour codes for the convergence type: • single extreme, • double extreme, • between single and double extreme, • moderate. Number of individuals: N = 400, intensity of interactions: μ = 0.3, uncertainty of extremists: ue = 0.01. |
|
|
| Figure 4. BC and GBC models on a lattice. Each dot represents one simulation, and the colour codes for the convergence type: • single extreme, • double extreme, • between single and double extreme, • moderate. Number of individuals: N = 400, intensity of interactions: μ = 0.3, uncertainty of extremists: ue = 0.01 |
|
|
| Figure 5. RA and GBCU models in total connection. Each dot represents one simulation, and the colour codes for the convergence type: • single extreme, • double extreme, • between single and double extreme, • moderate. Number of individuals: N = 400, intensity of interactions: μ = 0.3, uncertainty of extremists: ue = 0.01 |
|
|
| Figure 6. RA and GBCU models on a random network with 4 neighbours on average. Each dot represents one simulation, and the colour codes for the convergence type: • single extreme, • double extreme, • between single and double extreme, • moderate. Number of individuals: N = 400, intensity of interactions: μ = 0.3, uncertainty of extremists: ue = 0.01 |
|
|
| Figure 7. RA and GBU on a lattice. Each dot represents one simulation, and the colour codes for the convergence type: • single extreme, • double extreme, • between single and double extreme, • moderate. Number of individuals: N = 400, intensity of interactions: μ = 0.3, uncertainty of extremists: ue = 0.01 |
|
|
| Figure 8. BC and GBC for total connection. Same colour codes as in the previous figures. Number of individuals: N = 400, intensity of interactions: μ = 0.7, uncertainty of extremists: ue = 0.01 |
|
|
| Figure 9. Example of double extreme convergence for the RA model in total connection, with intensity of interactions: μ = 0.7. N = 100, uncertainty of extremists: ue = 0.01, pe = 0.15, U = 1.2. The colours indicate the value of uncertainties (see the legend). In one interaction, an extremist modifies dramatically the opinion and the uncertainty of a moderate |
|
|
| Figure 10. RA and GBCU for total connection. Same colour codes as in the previous figures. Number of individuals: N = 400, intensity of interactions: μ = 0.02, uncertainty of extremists: ue = 0.01 |
|
|
| Figure 11. Example of double extreme convergence for the RA model in total connection, with intensity of interactions: μ = 0.02. N = 100, uncertainty of extremists: ue = 0.01, pe = 0.15, U = 1.2. The colours indicate the value of uncertainties (see the legend). The split occurs when the average uncertainty is below 1 |
|
|
| Figure 12. Convergence patterns with a population of size 2500 for RA and BC models in total connection (μ = 0.3). In both cases, the frequency of single extreme convergence is smaller than with a population of size 400 |
|
|
| Figure 13. Convergence patterns with a population of size 2500 for RA and GBC on a lattice network (μ= 0.3). The RA model does not show significant difference with the case of a population of size 400, whereas the GBC model shows much less single extreme convergence |
|
|
| Figure 14. RA and GBCU for a random network with 4 neighbours on average. Same colour codes as in the previous figures. Number of individuals: N = 400, intensity of interactions: μ = 0.02, uncertainty of extremists: ue = 0.01 |
|
|
| Figure 15. RA and GBCU for a random network with 4 neighbours on average. Same colour codes as in the previous figures. Number of individuals: N = 400, intensity of interactions: μ = 0.02, uncertainty of extremists: ue = 0.01 |
|
|
| Figure 16. Strong local diffusion. Example of simulation for the RA model on a lattice with only one extremist at the beginning. μ = 0.1, ue = 0.01, N = 400, U = 1.5. The colours represent the opinion level (between -1 and +1), and the grey levels the uncertainty. Each individual is connected to four neighbours. Rapidly the extremist propagates its extreme opinion and certainty to its neighbours, which do the same. The final mean absolute value of the opinion is X = 0.95 |
|
|
| Figure 17. Weak local diffusion. Example of simulation for the BC model on a lattice with only one extremist at the beginning. μ = 0.1, ue = 0.01, N = 400, U = 1.5. The colours represent the opinion level (between -1 and +1) of the individuals located on a lattice. Each individual is connected to four neighbours. Rapidly the neighbours of the extremist have an opinion which is close to the extreme, and they influence the extremist, increasing its uncertainty. The extremist then becomes unstable, and is attracted by the moderates. The final mean absolute value of the opinion is X = 0.27 |
|
|
| Figure 18. Global diffusion. Example of simulation for the GBC model on a lattice with only one extremist at the beginning. μ = 0.1, ue = 0.01, N = 400, U = 1.5. The colours represent the opinion level (between -1 and +1) of the individuals located on a lattice. Each individual is connected to four neighbours. The moderates tend to keep a similar opinion, which is globally and very slowly influenced by the extremist. The final mean absolute value of the opinion is X = 0.91. The role of μ is crucial here, because for μ = 0.3 we get a weak local diffusion |
|
|
| Figure 19. BC model with single initial extremist, random network 4 neighbours, N = 400, μ = 0.1, ue = 0.01, U = 1.5. The evolution is of the global diffusion type, whereas it is a weak local diffusion on a lattice for the same parameters |
|
|
| Figure 20. Shortest path distribution. Population size N = 400. Average result for 400 trials in the case of the random network |
|
|
| Figure 21. Convergence patterns for RA and GBCU models on scale-free networks with 4 links per node on average (network parameter equals 2). Population size N = 400, μ = 0.1 |
BARABASI A.L. and Reka A., 1999. Emergence of Scaling in Random Network. Science, vol. 286, October, 15th, 1999, pp. 509-512.
DEFFUANT, G., Neau, D., Amblard, F., Weisbuch, G. - 2001. Mixing beliefs among interacting agents, Advances in Complex Systems, 3, pp87-98, 2001.
DEFFUANT, G., Amblard, F., Weisbuch, G. and Faure, T. 2002. How can extremism prevail? A study based on the relative agreement interaction model, Journal of Artificial Societies and Social Simulation, vol.5, 4. https://www.jasss.org/5/4/1.html
DEFFUANT, G., Amblard, F., Weisbuch, G. 2004. "Modelling group opinion shift to extreme: the smooth bounded confidence model", Proceedings of the European Social Simulation Association Conference, Valladolid, September 2004.
DERRIDA, B. and H. Flyvbjerg, 1986. Multivalley structure in Kauffman's model: analogy with spin glasses J. Phys. A19, L1003-L1008.EDMONDS, B., 2006, Assessing the Safety of (Numerical) Representation in Social Simulation. pp. 195-214 in: Agent-based computational modelling, edited by F.C. Billari, T. Fent, A. Prskawetz and J. Schefflarn, Physica Verlag, Heidelberg 2006.
GALAM, S. and Moscovici, S., 1991, Towards a theory of collective phenomena: consensus and attitude changes in groups. European Journal of Social Psychology. 21 49-74.
HEGSELMANN, R. and Krause, U. 2002. Opinion Dynamics and Bounded Confidence Models, Analysis and Simulation. Journal of Artificial Societies and Social Simulation, vol.5, 3. https://www.jasss.org/5/3/2.html
HEGSELMANN, R. and Krause, U. 2005. Opinion Dynamics Driven by Various Ways of Averaging. Computational Economics. Vol 25, Issue 4 , Pages 381-405.
STAUFFER D., Sousa, A. Schulze C., 2004. Discretized Opinion Dynamics of The Deffuant Model on Scale-Free Networks. Journal of Artificial Societies and Social Simulation, vol 7, 3. https://www.jasss.org/7/3/7.html
URBIG D. Attitude Dynamics With Limited Verbalisation Capabilities. Journal of Artificial Societies and Social Simulation. vol. 6 no. 1, 2003. https://www.jasss.org/6/1/2.html
URBIG D. and Lorenz J., 2004. Communication regimes in opinion dynamics: Changing the number of communicating agents; Proceedings of the Second Conference of the European Social Simulation Association (ESSA), Valladolid, Spain, September 16-19.
WEISBUCH, G. Deffuant G., Amblard, F., Nadal J.P. 2002. Meet, Discuss and segregate!. Complexity, vol 7, issue 3, 55-63.
WEISBUCH, G. Deffuant G., Amblard. 2005. Persuasion dynamics. Physica A, vol 353 pp 555-575.
YOUNG, P., 1998. Individual Strategy and social structure. Princeton University Press.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]