Michael Makowsky (2006)
An Agent-Based Model of Mortality Shocks, Intergenerational Effects, and Urban Crime
Journal of Artificial Societies and Social Simulation
vol. 9, no. 2
<https://www.jasss.org/9/2/7.html>
For information about citing this article, click here
Received: 05-Oct-2005 Accepted: 03-Feb-2006 Published: 31-Mar-2006
 Abstract
AbstractQuaint old town of toil and traffic, quaint old town of art and song, Memories haunt thy pointed gables, like the rooks that round them Throng
from "Nuremburg," by Henry Wadsworth Longfellow
If I knew I was going to live this long, I'd have taken better care of myself.
Mickey Mantle
Major consistent differences in subjective life expectancy…were found between successful and unsuccessful employees…Employees who failed to stay on the job were found to have shorter lifespan predictions.In short, those with longer SLE's were more interested in building human capital in the form of occupational experience and tenure. The notion of an agent's time horizon as related to his propensity, or potential, to commit crime was explored by Banfield (1970), casting the criminal as being more "present oriented" - essentially agents with higher discount rates of time are more likely to weigh the benefits of crime higher than the costs. Discounting and temporal factors are explored in much greater detail by Wilson and Herrnstein (1985), noting that crime, versus non-crime, is differentiated by benefits preceding costs. Wilson presents this differentiation as a set of benefit and cost curves based on the laboratory studies of Farrington and Knight (1979). It is with these results in mind that the model is initially parameterized.
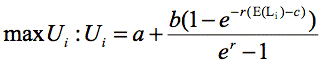 |
(1) |
where a is the lump sum payment received for choosing the occupation, b is the income received each turn in the simulation, and c is the turns spent pre-employment.[9] Agents discount future utility at a uniform interest rate, r, of 3%.
The heuristic for SLE, Expected Lifespan, E(Li) [Formula 2] is a function of the average lifespan,![]() , of each patch, j, in the agents neighborhood of ni total patches.
, of each patch, j, in the agents neighborhood of ni total patches.
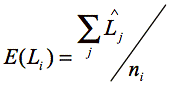 |
(2) |
The lump sum a is positive for the criminal (pecuniary and non-pecuniary benefits inclusive), zero for the laborer, and negative for the professional (education costs). These parameters are in alignment with the experimental findings of Farrington and subsequent analysis of Wilson. Income is an adjustable parameter for each occupation, but for simulations pursued here it is assumed that laborers earn a yearly income greater than criminals, and professionals in turn earn an income greater than laborers. In such a model what matters is not absolute lifespan, but rather lifespan relative to the lump sum benefits of crime, the costs of education, and the lifetime earnings potential of skilled and unskilled occupations. In such a world crime can persist in the face of a growing economy, so long as the a's keep pace with the b's.

|
| Figure 1. Runs #1, 2, 3, and 4 of 100. Each compares all four regions. Region #1 experience a morbidity shock in from time 40 until time 49. Regions 2 - 4 were not shocked, but 2% of the adult population moves each turn |
|
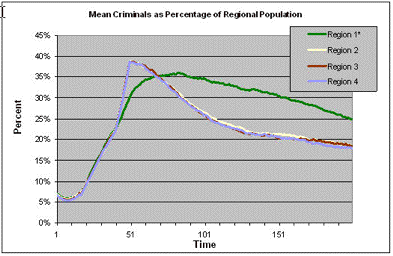
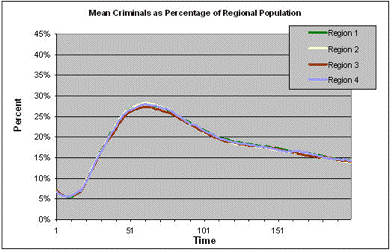
| Figure 2a. The mean percentage of each region with a criminal career, across 100 runs, each consisting of 200 turns, with a 10 turn mortality shock in region 1 at turn 40 |
|
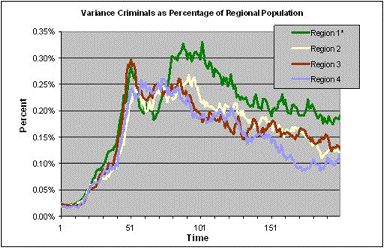
| Figure 2b. Control Experiment; The mean percentage of each region with a criminal career, across 100 runs, each consisting of 200 turns, without the mortality shock. Note that the peak (~ 28%) is considerably lower than in 2a, as is the final rate (~ 14%) The rate of crime rises early while information is limited, but drops naturally as the history develops and agent information sets come to reflect the underlying probabilities governing the model |
|
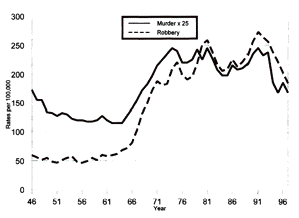
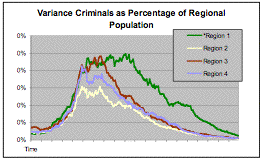
| Figure 3. The variance of the percentage of each region with a criminal career, across 100 runs, each consisting of 200 turns, with a 10 turn mortality strike at turn 40 |
|
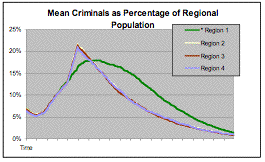
| Figure 4. from Lafree (1999), Murder and Robbery Rates, 1946 -1997, data supplied by the U.S. Federal Bureau of Investigation, "Crime in the United States," Uniform Crime Reports annual, 1946 to 1997 (Washington D.C., Government Printing Office) |
| Table 1: Rationality Control Experiment | |||||
| Turns Completed | 50 | 100 | 150 | 200 | 250 |
| Mean Differential (SLE - Mean Lifespan ) | -1.73 | 3.61 | 3.83 | 3.08 | 2.59 |
| Percent Differential (Differential / Mean Lifespan) | -3.64% | 7.24% | 7.52% | 5.95% | 4.96% |
2 CAMSIM is designed within the NetLogo application (Wilensky 1999)
3 Simon refers to this as "'intendedly' rational"
4 In making an explicit effort to bound the rationality of agents there remains the valid critique that CAMSIM may be leaving behind agents of perfect omniscience only to employ agents of staggering myopia. This paper contends that 1) The other end of the spectrum must be visited before the truth can be found in the middle, 2) A rational agent of relative myopia bears a closer resemblance to reality than homo economicus and 3) The limitations placed upon agents in forming subjective determinations of life expectancy have been validated by empirical work to be discussed later in the paper.
5 Heterogeneity of agent discount rates could result in "genetic" drift leading directly to regional differences in crime rate, as well as various evolutionary selection possibilities. Uniform discount rates control for this.
6 This is sometimes synonymously referred to as "verification," but programmers will also use verification to refer to confirming that the program code is executing as intended.
7 Succinctly put, calibration requires the correct objective/utility function, whereas validation only requires that the form of the function is appropriate and relevant.
8 If an agent reaches age 89 he will automatically perish upon the subsequent turn.
9 This will be familiar to many as the formula for the present value of an annuity. Utility is calculated subtracting years already lived, sixteen, from the expected total. An additional 2 years are subtracted from laborers to account for finishing secondary school and, and an additional 6 years are subtracted from professionals to account for finishing high school and a college degree.
10 Less shocking, but no less important is the assumption that agent choices regarding career are irreversible. The model becomes unwieldy if agents are allowed to re-optimize later in their life.
11 One row and one column of patches were used as regional "border" patches
12 This is a generic shock; it can be interpreted as representative of a number of potential "shocks" to an urban area, such as drug-related violence, war and accompanying conscription, or an environmental health crisis.
13 Observing representative runs in conjunction with variance and spread can be useful. The real world is always "one run" as alternate realities are not typically readily available for analysis. The data must be confirmed as non-anomalous in general structure, but means and medians can "smooth away" useful information regarding how the artificial history plays out.
14 This is unlikely in this case, as the shocked region has considerably reduced population density.
15 It has always been very difficult for proponents of genetic and aptitude theories of criminal propensity to explain significant booms or busts as gene pools are not so easily shifted.
|
|
(3) |
Here the weighted utility, Uweighted, is a function of Utility and the reference group weighting. When an agent chooses a career (professional, laborer, or criminal) she weights the expected utility of each career: α if the none of the agents in her neighborhood have that career, 1 if at least one neighborhood agent has it, and λ if it is the most popular career in the neighborhood. When the experiments from this paper were duplicated using the reference group weightings, with α = 0.98 and λ = 1.02, the results were similar in character to the previous results, though the magnitudes of all of the criminal percentages were reduced proportionately.
|
| Figure A1 and A2. The mean (A1) and variance (A2) of the criminal percentage of the population over 200 turns, with a shock at turn 50, using the reference group weightings, α = 0.98 and λ = 1.02 |
(1) Main loop
While time < 201
For each patch [p] p.calculateAverageLifespan
Random (0.02 * total population) agents move to a new location
For each agent [a] {
If 16 < age < 45 and (random number from 1 to 1000) < birthrate) [add new agent ]
Agents-grow-up
}
Stats-collector
If 39 < time < 50 [random 15 of region-one agents die]
End-while
(2) Agents-grow-up procedure
For each agent[a]
If a = child [
Age++
If (random number from 1 to 1000) < childDeathRate [agent dies]
If age = 16 [
ExpectedLife = mean [AverageLifespan from patches in Moore Neighborhood]
Calculate-Expected-Utilities
choose career with maximum Expected Utility
if local patch open [move to local patch]
else [if random patch open [move to random patch]]
]
If a = adult [
Age++
If age < 50
[If (random number from 1 to 1000) < a.career.adultDeathRate [a.dies]]
If 50 <= age < 90
[If (random number from 1 to 1000) < a.career.adultDeathRate + 20 [a.dies]
If age >=90 [a.dies]
]
(3) Calculate-Expected-Utilities [note: the jail function has been turned off in CAMSIM for this experiment, so the expected jail time is zero)
a.ExpUtilityProfessional = ((-4 * EducationCost) + ((ProIncome * (1 - exp(- rate * (ExpectedLife - 22 )))) / (exp(rate) - 1)))
a.ExpUtilityLabor = ((LaborIncome * (1 - exp(- rate * (ExpectedLife - 18 )))) / (exp(rate) - 1))
a.ExpUtilityCriminal = (CrimeLumpSum + ((CrimeIncome * (1 - exp(- rate * (ExpectedLife - 16 - ExpectedJail )))) / (exp(rate) - 1)))
BECKER, G. S. (1964). Human capital; a theoretical and empirical analysis, with special reference to education. New York, National Bureau of Economic Research; distributed by Columbia University Press.
BECKER, G. S. (1968). "Crime and Punishment: An Economic Approach." The Journal of Political Economy 76(2): 169-217.
BEHRMAN, J., L. Kletzer, et al. (1998). "Microeconomics of College Choice, Careers, and Wages." The Annals of the American Academy of Political and Social Science 559(The Changing Educational Quality of the Workforce): 12-23.
BOTTOMS, A. E. (1997). Environmental Criminology. The Oxford Handbook of Criminology. R. M. Mike Maguire, and Robert Reiner. Oxford, Clarendon Press: 585-656.
BRANTINGHAM, P. J., P. Brantingham, et al. (1986). Perceived and Actual Crime Risks. Metropolitan Crime Patterns. R. M. e. a. Figlio. NY, Criminal Justice Press: 139-160.
BRANTINGHAM, P. J. and P. L. Brantingham (1981). Environmental criminology. Beverly Hills Calif., Sage Publications.
COLEMAN, J. S. (1990). Foundations of Social Theory. Cambridge, The Belknap Press of Harvard University Press.
COOK, K. S. and M. Levi (1990). The Limits of rationality. Chicago, University of Chicago Press.
CORMAN, H. and H. N. Mocan (2000). "A Time-Series Analysis of Crime, Deterrence, and Drug Abuse in New York City." American Economic Review 90(3): 584-604.
DAVIS, M. L. (1988). "Time and Punishment: An Intertemporal Model of Crime." The Journal of Political Economy 96(2): 383-390.
DENES-RAJ, V. and H. Ehrlichman (1991). "Effects of Premature Parental Death on Subjective Life Expectancy, Death Anxiety, and Health Behavior." Omega 23(4): 309-321.
DONOHUE III, J. J. and S. D. Levitt (2000). "The Impact of Legalized Abortion on Crime." Quarterly Journal of Economics.
DURLAUF, S. N., H. P. Young, et al. (2001). Social dynamics. Cambridge, Mass.: MIT Press; Brookings Institution Press.
EHRLICH, I. (1996). "Crime, Punishment, and the Market for Offenses." The Journal of Economic Perspectives 10(1): 43-67.
EPSTEIN, J. M., R. Axtell, et al. (1996). Growing artificial societies social science from the bottom up. Washington, D.C., Brookings Institution Press.
FARRINGTON, D. P. and B. J. Knight (1979). "Two non-reactive field experiments on stealing from a "lost" letter." British Journal of Social and Criminal Psychology 18: 277-284.
FERRI, E. (1898). Criminal sociology. New York, D. Appleton and company.
FISHER, J. D., P. A. Bell, et al. (1984). Environmental psychology. New York, Holt Rinehart and Winston.
GLADWELL, M. (2000). The tipping point: how little things can make a big difference. Boston; London, Little Brown.
GLAESER, E. L. and B. Sacerdote (1999). "Why Is There More Crime in Cities?" Journal of Political Economy 107(6, Part 2: Symposium on the Economic Analysis of Social Behavior in Honor of Gary S. Becker): S225-S258.
GLAESER, E. L., B. Sacerdote, et al. (1996). "Crime and Social Interactions." Quarterly Journal of Economics 111(2): 507-48.
HAMERMESH, D. S. (1985). "Expectations, Life Expectancy, and Economic Behavior." The Quarterly Journal of Economics 100(2): 389-408.
HARRIES, K. D. (1973). The geography of crime and justice. New York, McGraw-Hill.
HARRIES, K. D. (1980). Crime and the environment. Springfield, Ill., Thomas.
HARRIES, K. D. (1988). "Regional Variations in Homicide, Capital Punishment, and Perceived Crime Severity in the United States." Geografiska Annaler. Series B. Human Geography 70(3): 325-334.
HERBERT, D. T. (1982). The geography of urban crime. London; New York, Longman.
HYMAN, H. H. (1942). The psychology of status. New York: 95.
HYMAN, H. H. and E. Singer (1968). Readings in reference group theory and research. New York, Free Press.
KEANE, M. P. and K. I. Wolpin (1997). "The Career Decisions of Young Men." Journal of Political Economy 105(3): 473-522.
KELLING, G. L. and National Institute of Justice (U.S.) (1999). "Broken windows" and police discretion. Washington, DC, U.S. Dept. of Justice Office of Justice Programs National Institute of Justice.
KRIVO, L. J. and R. D. Peterson (1996). "Extremely Disadvantaged Neighborhoods and Urban Crime." Social Forces 75(2): 619-648.
LAFREE, G. (1999). "Declining Violent Crime Rates in the 1990s: Predicting Crime Booms and Busts." Annual Review of Sociology 25: 145-168.
LEUNG, S. F. (1995). "Dynamic Deterrence Theory." Economica 62(245): 65-87.
MACDONALD, W. L. (1998). Secularization in the United States: Scientific versus Religious Authority. American Sociological Association Meeting.
MANSKI, C. F. (1993). "Identification of Endogenous Social Effects: The Reflection Problem." The Review of Economic Studies 60(3): 531-542.
MATHUR, V. K. (1978). "Economics of Crime: An Investigation of the Deterrent Hypothesis for Urban Areas." The Review of Economic Statistics 60(3): 459-466.
MCCLOSKEY, D. N. (1996). The vices of economists, the virtues of the bourgeoisie. Amsterdam, Amsterdam University Press.
MCCLOSKEY, D. N. (1998). The rhetoric of economics. Madison, Wis., University of Wisconsin Press.
MOTCHENKOVA, E. and P. M. Kort (2006 (forthcoming)). "Analysis of the Properties of Current Penalty Schemes for Violations and Antitrust Law." Journal of Optimization Theory and Applications 128.
NAM, C. B. and T. M. Harrington (1986). Factors Shaping the Morbidity-Mortality Expectations of Youth: A Socialization Model. Fertility and mortality: theory, methodology, and empirical issues. K. Mahadevan, P. J. Reddy and D. A. Naidu. New Delhi; Beverly Hills, Sage Publications: 351.
NELSON, L. d. and J. A. Honnold (1980). "Socialization and Demographic Determinants of Mortality Expectations." Population and Environment 3(1): 10-22.
PARSONS, T. (1949). The structure of social action; a study in social theory with special reference to a group of recent European writers. Glencoe, Ill., Free Press.
PHILIPSON, T. J. and R. A. Posner (1996). "The Economic Epidemiology of Crime." Journal of Law and Economics 39(2): 405-433.
POTTS, J. (2000). The new evolutionary microeconomics: complexity, competence, and adaptive behaviour. Cheltenham, UK; Northampton, MA, E. Elgar Pub.
SCHELLING, T. C. (1978). Micromotives and Macrobehavior. New York, W. W. Norton Company.
SHAW, C. R. and H. D. McKay (1942). Juvenile delinquency and urban areas, a study of rates of delinquents in relation to differential characteristics of local communities in American cities. Chicago, Ill., The University of Chicago Press.
SIMON, H. A. (1955). "A Behavioral Model of Rational Choice." The Quarterly Journal of Economics 69(1): 99-118.
SIMON, H. A. (1956). "Rational Choice and the Structure of the Environment." Psychological Review 63(2): 129-138.
SIMON, H. A. (1959). "Theories of Decision-Making in Economics and Behavioral Science." The American Economic Review 49(3): 253-283.
SIMON, H. A. (1982). Models of bounded rationality. Cambridge, Mass., MIT Press.
SIMON, H. A. (1986). "Rationality in Psychology and Economics." Journal of Business 59(4, Part 2: The Behavioral Foundations of Economic Theory): S209-S224.
SMITH, A. (1981 [1776]). An inquiry into the nature and causes of the wealth of nations. Indianapolis, Liberty Classics.
SWEDBERG, R. (1990). Economics and Sociology. Redifining their Boundaries: Conversations with Economists and Sociologists. Princeton, Princeton University Press.
TAYLOR, R. B. (2001). Breaking away from broken windows: Baltimore neighborhoods and the nationwide fight against crime, grime, fear, and decline. Boulder, Colo., Westview Press.
TEAHAN, J. and R. Kastenbaum (1970). "Subjective Life Expectancy and Future Time Perspective as Predictors of Job Success in the "Hard-Core" Unemployed." Omega 1: 189-200.
TRUMBULL, W. N. (1989). "Estimations of the Economic Model of Crime Using Aggregate and Individual Level Data." Southern Economic Journal 56(2): 423-439.
TVERSKY, A. and D. Kahneman (1974). "Judgment Under Uncertainty: Heuristics and Biases." Science 185: 1124-1131.
WILENSKY, U. (1999). NetLogo, Center for Connected Learning and Computer-Based Modeling, Northwestern University, Evanston, IL.
WILSON, J. Q. and R. J. Herrnstein (1985). Crime and human nature. New York, Simon and Schuster.
WILSON, J. Q. and G. Kelling (1982). "Broken Windows: The Police and Neighborhood Safety." Atlantic Monthly: 29-38.
WILSON, W. J. (1987). The truly disadvantaged: the inner city, the underclass, and public policy. Chicago, University of Chicago Press.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]