David Chavalarias (2006)
Metamimetic Games: Modeling Metadynamics in Social Cognition
Journal of Artificial Societies and Social Simulation
vol. 9, no. 2
<https://www.jasss.org/9/2/5.html>
For information about citing this article, click here
Received: 29-Jul-2005 Accepted: 06-Mar-2006 Published: 31-Mar-2006
 Abstract
Abstract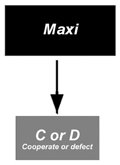
|

|

|
|
|
| a.: Nowak and May (1992) | b.: Kaniovski et al. (2000) | c.: Orléan (1998) | d: Henrich and Boyd (1998) | e: Schematic representation of models |
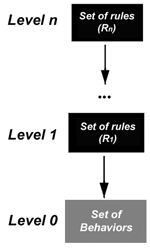
| Table 1. Modellers in the social sciences generally represent agents as a hierarchy of rules, where rules at each level evolve under the dynamics defined by their meta-rules | ||||
In order to develop a science of man, we must compare human imitation with animal mimetism and separate the modalities of mimetic behaviours specific to humans, if they exist.
Definition: Imitation rule
Given an agent A and its neighbourhood ΓA, an imitation rule is a process that:
- Assigns a value ν(B, ΓA) belonging to an ordered set (the set of real numbers for example) to each agent B in ΓA. ν will be called a valuation function.
- Selects some traits to be copied from the best agents (according to the values given in 1) and defines the copying process.
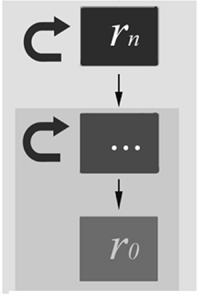
|
| Figure 1. Schematic representation of a metamimetic chain |
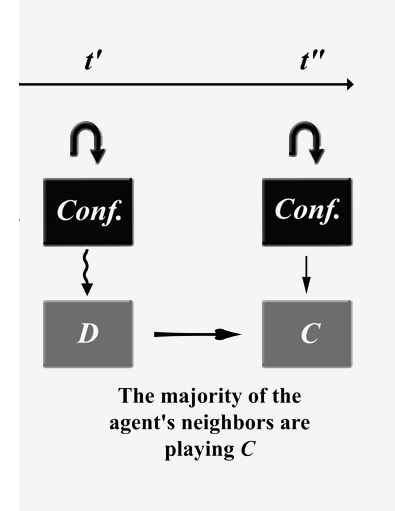
|
| Figure 2. Update of an intermediary modifiable trait. A conformist agent A observes that the majority of agents is playing C, and decides to update its behaviour to C (modifiable trait of level 0). |
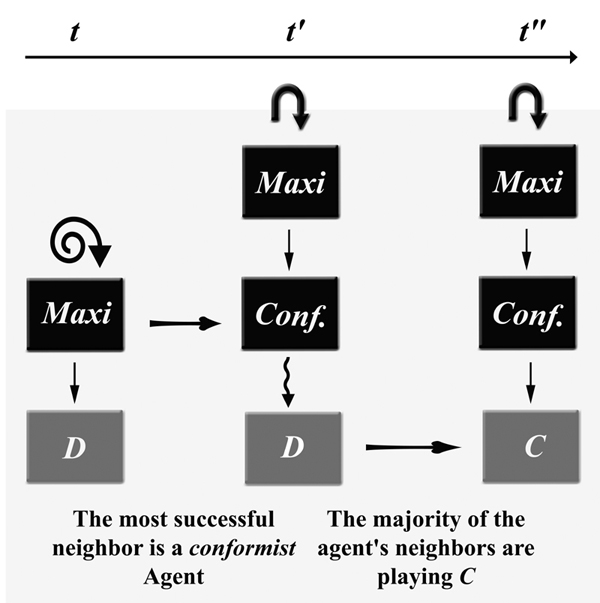
|
| Figure 3. Endogenous variation in the length of metamimetic chains. At time t, a Maxi agent A has a conformist neighbour that is more successful than all agents in ΓA. A will then adopt the conformist rule at its first meta-level, keeping in mind that it is only a means for maximizing its payoffs (second meta-level). Thereafter, it might be that according to this conformist rule, the current behaviour is not the best one and has to be changed. |
In that case, the complexity of B's strategy and the cognitive bound of A enable A to keep in mind its initial rule r1. B's strategy is a temporary means for achieving the goals defined by r1. This kind of transition enables the agent to change endogenously the length of its metamimetic chain. We do this kind of mental operation every day every time we decide that the realization of a goal G' is the best way to achieve a goal G.
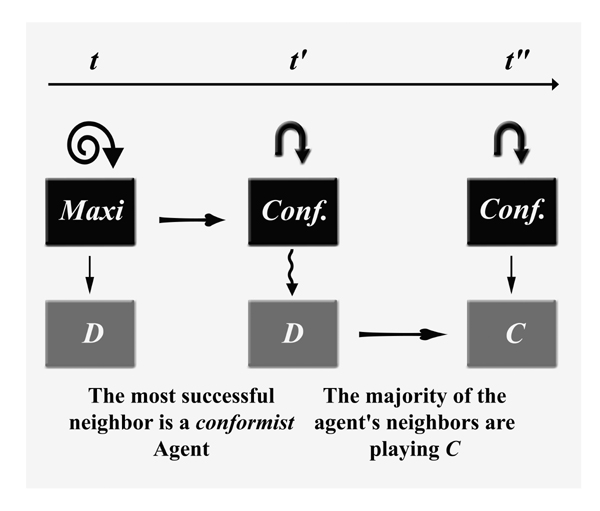
|
| Figure 4. Reflexive update at the limit of the cognitive bound. At time t, a Maxi agent A has a conformist neighbour that is strictly more successful than all other neighbours. Consequently, A adopts the conformist rule. Thereafter, it might be that according to this rule, the current behaviour is not the best one, and has to be changed. |
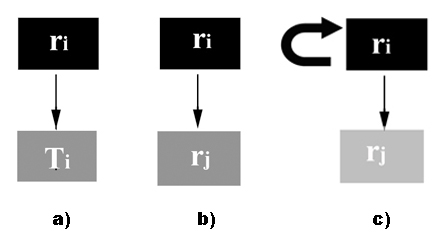 |
| Figure 5. An imitation rule can act upon a modifiable trait Ti (a), When imitation rules are modifiable traits, they can be modified by other rules (b) and can be modifiable traits for themselves (c). |
Moreover, the three following conditions should be satisfied:
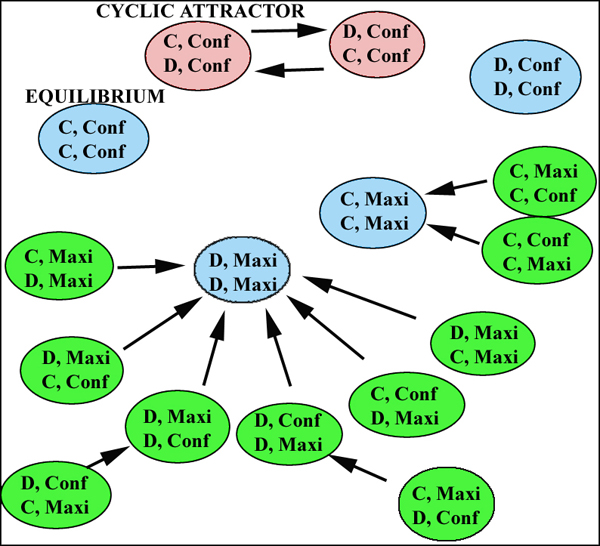
|
| Figure 6. The dynamics in a minimal metamimetic game. Each arrow represents the mimetic transition that the current state requires (here with probability 1 everywhere) |
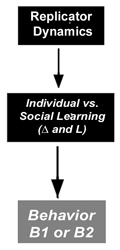
Proposition: Every metamimetic game G={N,Γ,R,B,CB} can be associated with a unique matrix P0 that determines the Markov process representing the internal dynamics of the game. P0 defines the metadynamics of the social cognition process.
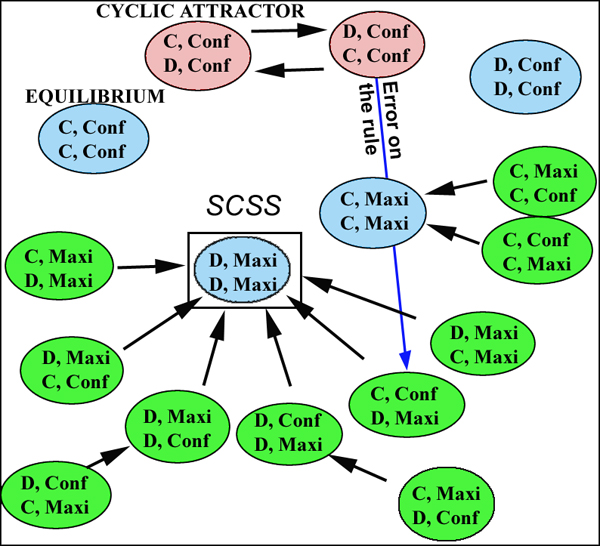
|
| Figure 7. Minimal example of a noisy metamimetic game. An error of one of the agents can lead the system toward a new metamimetic attractor. When the system is constantly disturbed, the only state in the SCSS is the state where all agents are (D,maxi) |
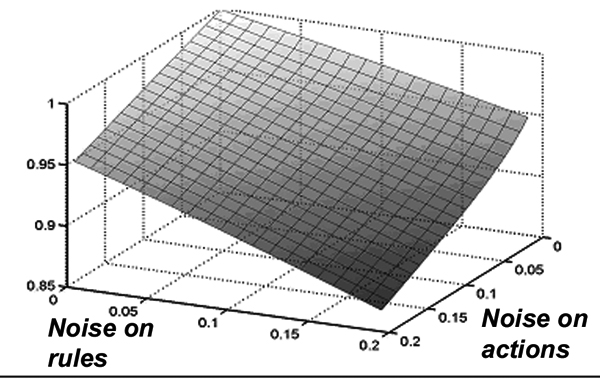
|
| Figure 8. Frequency of the SCSS at the attractor. In our minimal example, the proportion of the SCSS in the limit distribution when (εr, εa) tends to zero quickly converges to 1. Here the proportions have been plotted for 0,01<εi<0,2. (It should be noticed that since all states are taken with an equal probability in case of mistake, here half then errors are corrected. The real level of noise is then εi/2) |
|
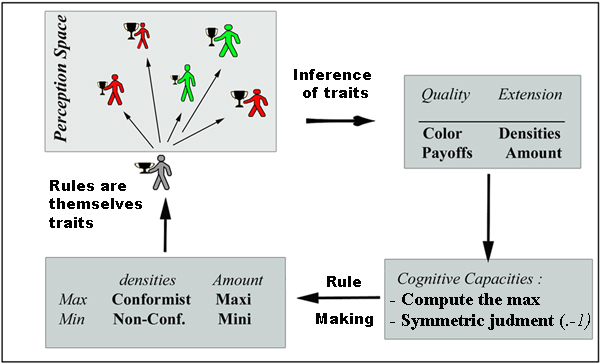
| Figure 9. Our approach suggests defining the set of imitation rules in a generative way. Agents are embedded in their environment from which they infer some traits like colours and payoffs. Then, they do some computations on the inferred distributions of these traits: computation of the densities, computation of the maximum of payoffs, computation of the minimum, etc. These computations are used as a basis for building imitation rules that are themselves traits agents can try to infer. |
| Δxct=xct+1 - xct =Σc' xc't. ptc'c - xctΣc' ptcc' | (1) |
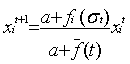
|
with
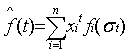
|
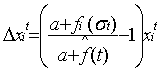
|
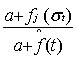 . Since each neighbourhood contains the whole population (the graph is complete), we then have:
. Since each neighbourhood contains the whole population (the graph is complete), we then have:
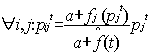
|
| Δxit=Σj xjt. ptji - xitΣj ptij |
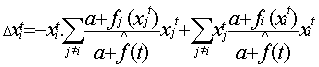
|
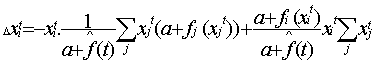
|
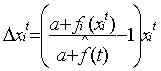 |
The discrete replicator dynamics translated in terms of metamimetic dynamics is thus equivalent to the particular case of a metamimetic game with a single meta-rule that can be formulated by "imitate neighbours at random with a probability proportional to their fitness".
| ptc'c | (C,conf) | (D,conf) | (C,maxi) | (D,maxi) |
(C,conf) or (D,conf) | Equals 1 if conf. agents are in majority and C is the most common behaviour, 0 otherwise. | Equals 1 if conf. agents are in majority and D is the most common behaviour, 0 otherwise. | Equals 1 if maxi agents are in majority and C is the most successful behaviour, 0 otherwise | Equals 1 if maxi agents are in majority and D is the most successful behaviour, 0 otherwise |
(C, maxi) or (D, maxi) | Equals 1 if conf. agents are the richest and C is the most common behaviour, 0 otherwise. | Equals 1 if conf. agents are the richest and D is the most common behaviour, 0 otherwise. | Equals 1 if maxi agents are the richest and C is the most successful behaviour, 0 otherwise. | Equals 1 if maxi agents are the richest and D is the most successful behaviour, 0 otherwise. |
3 "Pour élaborer une science de l'homme, il faut comparer l'imitation humaine avec le mimétisme animal, préciser les modalités proprement humaines des comportements mimétiques si elles existent" (Girard 1978).
4Also it could be interesting to consider different sets of rules depending on the agents — as in Selten & Ostmann 2001 — and the cognitive level, but this would be superfluous given the present purpose.
5The term coherent should be understood before all from the modeller's perspective. Agents themselves are not looking for coherence but are simply applying their rules. A rule is self-coherent if its application does not tend to change the rule itself.
ALVARD M. S. (2003) The Adaptive Nature of Culture, Evolutionary Anthropology, 136-149.
ARBIB M.A., Billard A., Lacoboni M., Oztop M. (2000) Synthetic brain imaging: grasping, mirror neurons and imitation, Neural Networks 13 975-997.
ARTHUR B. W. (1994) Inductive reasoning and bounded rationality, Am. Econ. Assoc. Papers and Proc 84, 406-411.
AXELROD R. (1997) The Dissemination of Culture: A Model with Local Convergence and Global Polarization, Journal of Conflict Resolution, 41, 203-26.
BALDWIN J. M. (1897), Mental Development in the Child and the Race.
BOURGINE P. (2004) What is Cognitive Economics, in Cognitive Economics, Bourgine P, Nadal J-P (ed.),Springer, pp1-12.
BOWLES S., Gintis H. (2003) The Origins of Human Cooperation, Peter Hammerstein (ed.) The Genetic and Cultural Origins of Cooperation, Cambridge: MIT Press. pp429-443.
BOYD R., Richerson P.J. (1985) Culture and the Evolutionary process, Chicago, IL: University of Chicago Press.
BREAZEAL C., Buchsbaum D., Gray J., Gatenby D. & Blumberg B., (2005) Learning From and About Others: Towards Using Imitation to Bootstrap the Social Understanding of Others by Robots, Artificial Life 11(1-2):5 -11.
BYRNE R.W., Russon A.E. (1998), Learning by Imitation: a Hierarchical Approach, Behavioural and Brain Sciences 21(5):667-84.
CAMERER C. F. (2003) Behavioural Game Theory. Experiments in Strategic Interaction, Princeton University Press.
CHAMINADE T., Meltzoff A. N. & Decety J. (2002) Does the End Justify the Means? A PET Exploration of the Mechanisms Involved in Human Imitation, NeuroImage 15, 318-328.
CONTE R., Paolucci M. (2001) Intelligent Social Learning, Journal of Artificial Societies and Social Simulation vol. 4, no. 1, https://www.jasss.org/4/1/3.html.
DAMASIO R. A. (1999) The Feeling of What Happens: Body and Emotion in the Making of Consciousness, New York: Harcourt Brace.
DAY R. and Huang W. (1990) Bulls, bears and market sheep, Journal of Economic Behaviour and Organization, 14, 299-329.
DONALD M. (1991) Origins of the Modern Mind, Cambridge, MA: Harward University Press.
DUPUY J.-P. (2004) Economics as symptom, In Lewis, PA, ed. Transforming Economics: Perspectives on the Critical Realist Project. London and New York: Routledge, p. 227-251.
EDMONDS B. (1999) Capturing Social Embeddedness: a constructivist approach, Adaptive Behaviour, 7:323-348.
FEHR E., Fischbacher U. (2003) The nature of human altruism, Nature, Vol 425, pp785-791.
FELDMAN M. W., Laland K. N. (1996) Gene-culture coevolutionary theory, TREE Vol 11 (11) Elsevier pp454-457.
FOSTER D., Young P. (1990) Stochastic Evolutionary Game Theory, Theoretical Population Biology 38, 219-232.
FRANK J., (2003) Natural selection, rational economic behaviour, and alternative outcomes of the evolutionary process, Journal of Socio-Economics, Vol. 32 - 6 (12), p 601-622.
GALAM S. (1998) Sous les chemises de la symétrie, Pour la Science, Hors série ``Symétries", juillet pp16-19.
GANS E. (1995) Mimetic Paradox and the Event of Human Origin, Anthropoetics - The Electronic Journal of Generative Anthropology Volume I, number 2.
GERGELY G., Bekkering H. & Király I. (2002), Rational imitation in preverbal infants, Nature, Vol 415, p755.
GINTIS H. (2003) Game Theory Evolving, Princeton Univ. Press.
GIRARD R. (1961) Mensonge romantique et Vérité romanesque, Girard R., Grasset.
GIRARD R.(1978) Des choses cachés depuis la fondation du monde, Girard R., Ed. Grasset.
GOULD S. J. (1987) An urchin in the storm, London Penguin.
HENRICH J., Boyd R. (1998) The Evolution of Conformist Transmission and the Emergence of Between-Group Differences, Evolution and Human Behaviour 19: 215-241.
HENRICH J. and Gil-White F. J. (2001) The Evolution of Prestige, Evolution and Human Behaviour 22:165-196.
HOFBAUER J., Sigmund K. (1988) The Theory of Evolution and Dynamical Systems, London Mathematical Society, Cambridge University Press.
HÜCK S., Normann H.-T. and Oechssler J. (1999) Learning in Cournot oligopoly — An experiment. Economic Journal, 109, C80-85.
JACOB P. (1998) Memory, learning and metacognition, Comptes rendus de l'Académie des sciences, 321, 2-3, 235-59.
JANSEN B., De Vylder B., de Boer B., and Belpaeme T. (2003) Emerging shared action categories in robotic agents through imitation, In Dautenhahn, K. & Nehaniv, C. L. (eds.) Proceedings of the AISB Second International Symposium on Imitation in Animals and Artifacts, Aberystwyth: University of Wales, pp. 145-152.
JANSSEN M., Jager W., (1999) An integrated approach to simulating behavioural processes:A case study of the lock-in of consumption patterns, Journal of Artificial Societies and Social Simulation vol. 2, no. 2, https://www.jasss.org/2/2/2.html.
KAHNEMANN, D. (2002), Maps of Bounded Rationality: A Perspective on Intuitive Judgment and Choice, Prize Lecture.
KANIOVSKI Y. M., Kryazhimskii A. V. and Young H. P. (2000) Adaptive Dynamics in Games Played by Heterogeneous Populations, Games and Economic Behaviour 31, 50-96.
KIRMAN A. (1991) Epidemics of opinion and speculative bubbles in financial markets, in M. Taylor (ed) Money and financial markets. Blackwell, Oxford, 354-368.
LIEBERMAN M. D., Gilbert D. T., Gaunt R. and Trope Y. (2002), Reflection and Reflexion: A Social Cognitive Neuroscience Approach to Attributional Inference. In : Advances in Experimental Social Psychology, 34, 199-249.
MELTZOFF A. N. & Gopnik, A. (1993) The role of imitation in understanding persons an developing theories of mind. In: Baron-Cohen S., Tager-Flusberg H. & Cohen D. (Eds.), Understanding other minds: perspectives from autism (pp. 335-366). Oxford Univ. Press.
MELTZOFF A. N. and Prinz W. ed. (2002) The Imitative Mind: Development, Evolution, and Brain Bases, Cambridge University Press.
MOUNOUD P. (1995) From direct to reflexive self-knowledge: A recursive model. About (self-produced) actions considered as transformations., P. Rochat (Ed.) The Self in Early Infancy. Theory and Research Amsterdam: North Holland. Elsevier Science Publishers pp141-160.
NOWAK M. A., May, R.M. (1992) Evolutionary Games and Spatial Chaos, Nowak M. A., May, R.M., Nature, 359: (6398) 826-829.
NOWAK M. A., Bonhoeffer, S. & R. M. May (1994) More Spatial Games, Int. J. of Bifurcation and Chaos, Vol.4, n°1, 35-56.
ORLÉAN A. (1985), Monnaie et spéculation mimétique In: Paul Dumouchel (ed) Violence et Vérité, Autour de René Girard, Colloque Cerisy, Grasset, pp147-158.
ORLÉAN A. (1998) The evolution of imitation, In Patrick Cohendet, Patrick Llerena, Hubert Stahn et Gisèle Umbhauer (eds.), The Economics of Networks, Berlin, Heidelberg et New-York, Springer-Verlag, Chap 15, 325-339.
PACHERIE E. (1998) Représentations motrices, imitation et théorie de l'esprit. In H. Grivois & J. Proust (eds.) Subjectivité et Conscience d'Agir: Approches Cognitives et Cliniques de la Psychose, PUF, 1998, pp. 207-248.
RENDELL L., Whitehead H. (2001) Culture in whales and dolphins, Behavioural and Brain Sciences 24 (2): 309-382.
ROGERS, A. R. (1988) Does biology constrain culture? American Anthropologist, 90: 819-831.
SELTEN, R., Ostmann, A. (2001) Imitation Equilibrium, Homo oeconomicus, 43, 111-149.
SMITH J.D., Shields, W. E. & Washburn D. A (2003) The Comparative Psychology of Uncertainty Monitoring and Metacognition, Behavioural and Brain Sciences, Volume 26, Issue 3, 261-283.
SPERBER D. (2000) Metarepresentaitons in an evolutionry perspective, Metarepresentations: A Multidisciplinary Perspective. Oxford UniversityPress, pp.117-137.
STANOVICH, K. E., and West, R. F. (2000). Individual differences in reasoning: Implications for the rationality debate. Behavioural and Brain Sciences, 23, 645-665.
TARDE G. (1890) Les Lois de l'Imitation; English Translation (1962): The Laws of Imitation, translated by E.C. Parsons with introduction by F.Giddings, reprint, Gloucester, MA, Peter Smith.
TOMASELLO M. (1999) The Cultural Origins of Human Cognition., Harvard University Press.
VARELA F. (1979), Principles of biological autonomy, North Holland, New York.
VARELA F. (1983). L'auto-organisation: de l'apparence au mécanisme, In: L'auto organisation, de la physique au politique, J-P Dupuy & P. Dumouchel, Seuil, Paris, pp147-165.
VRIEND N. J. (2002) Was Hayek an Ace?, Soutthern Economic Journal, 68(4), 810-840.
WEIBULL J. W. (1995) Evolutionary Game Theory, MIT press.
WILSON E.O. (1975) Sociobiology: the new synthesis., Harward University Press, Cambridge.
YOUNG H. P. (1993) The Evolution of Conventions, Econometrica, Vol. 61, Issue 1, 57-84.
YOUNG H. P. (2001), Individual Strategy and Social Structure: An Evolutionary Theory of Institutions, Princeton Univ. Press.
ZELAZO P. D., Frye D. and Rapus T., (1996) Age Related Dissociation Between Knowing Rules and Using Them, Cognitive Development, 11, 37-63.
ZELAZO P.D., Lourenco S.F. (2003), Imitation and the dialectic of representation, Developmental Review 23: 55-78.
ZLATEV J. (2000) The Mimetic Origins of Self-Consciousness in Phylo-, Onto- and Robotogenesis In Proceedings of the 26th Annual Conference of the IEEE Industrial Electronics Society, October 2000, Nagoya.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]