Jan Lorenz (2006)
Consensus Strikes Back in the Hegselmann-Krause Model of Continuous Opinion Dynamics Under Bounded Confidence
Journal of Artificial Societies and Social Simulation
vol. 9, no. 1
<https://www.jasss.org/9/1/8.html>
For information about citing this article, click here
Received: 06-Jun-2005 Accepted: 28-Sep-2005 Published: 31-Jan-2006
 Abstract
Abstract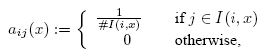
Given an initial opinion profile x(0) we define the HK process of opinion dynamics as a sequence of opinion profiles (x(t))t recursively defined through x(t+1) = A(x(t)) x(t).
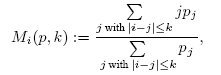
With abbreviation Mi = Mi(p,k) we define the HK transition matrix B(p,k) as
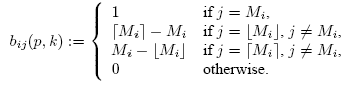
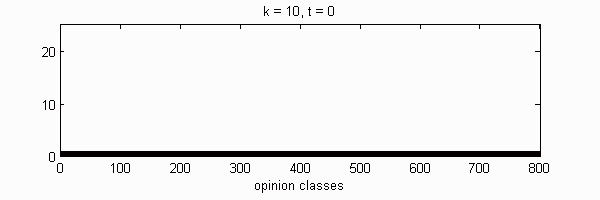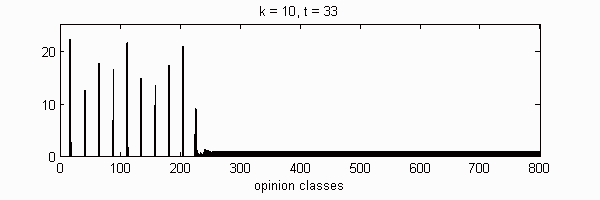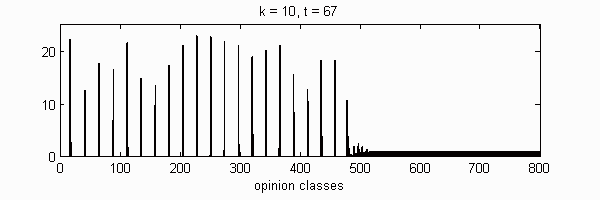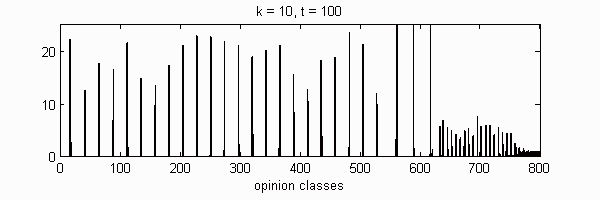
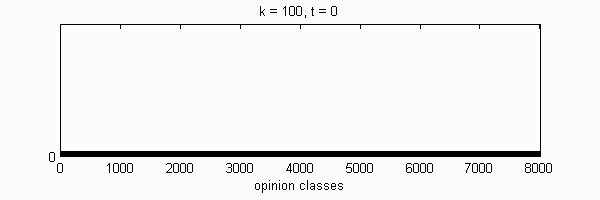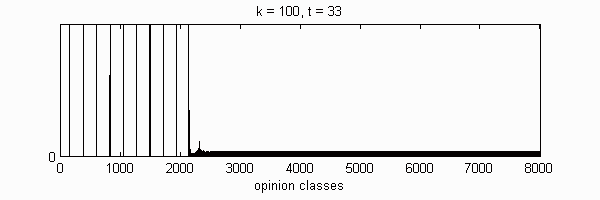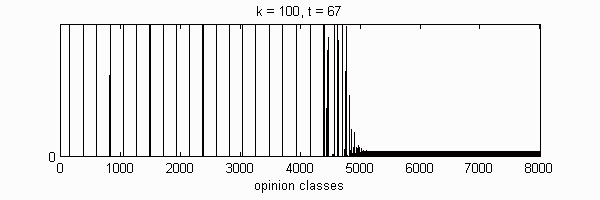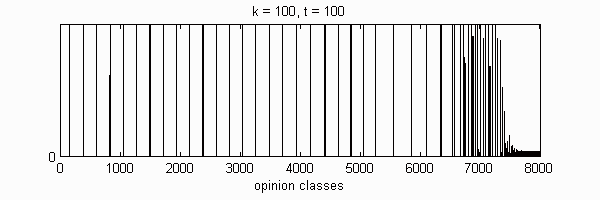
| Cluster | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| t | k = 10 | 8 | 11 | 15 | 18 | 21 | 24 | 27 | 31 | 34 | 37 |
| k = 100 | 8 | 12 | 15 | 18 | 21 | 25 | 28 | 31 | 34 | 37 | |
| Δ | k = 10 | - | 24.41 | 23.74 | 23.45 | 23.38 | 23.29 | 23.21 | 23.16 | 23.16 | 23.08 |
| k = 100 | - | 228.86 | 225.33 | 222.56 | 221.73 | 220.65 | 221.95 | 220.35 | 219.64 | 219.70 | |
| # | k = 10 | 24.93 | 24.11 | 23.64 | 23.40 | 23.35 | 23.31 | 23.18 | 23.10 | 23.22 | 23.08 |
| k = 100 | 238.84 | 227.48 | 224.91 | 222.57 | 220.90 | 220.50 | 223.13 | 220.75 | 216.69 | 220.87 | |
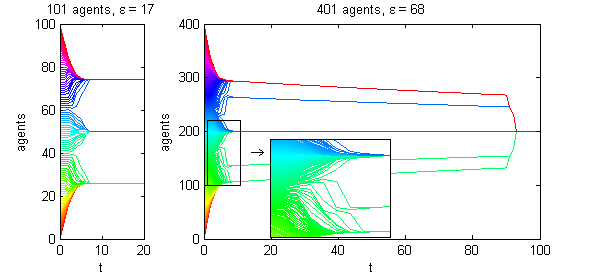
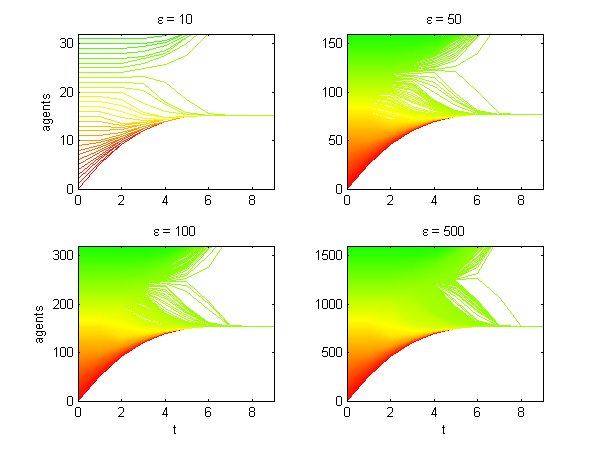
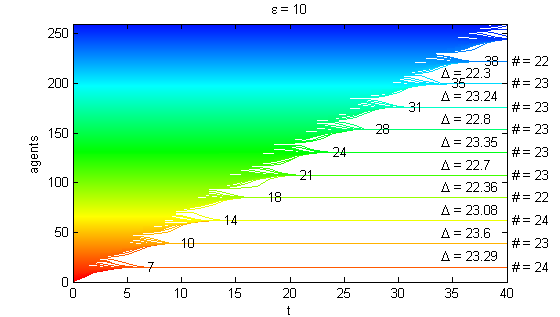
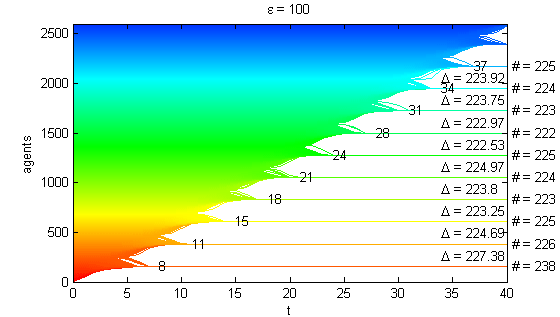
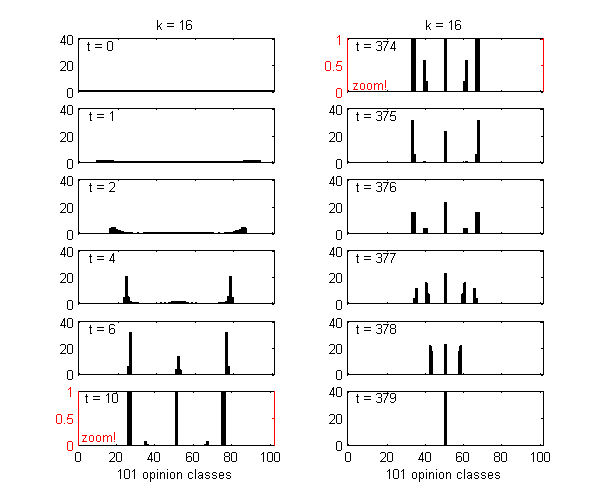
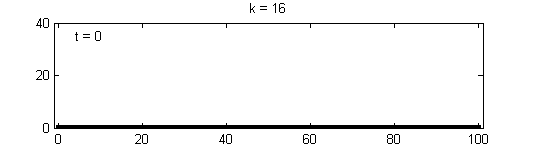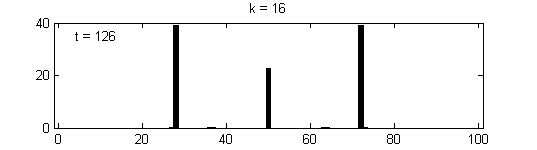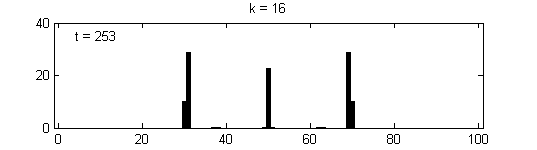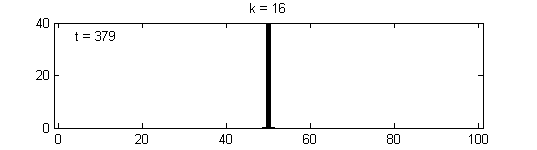
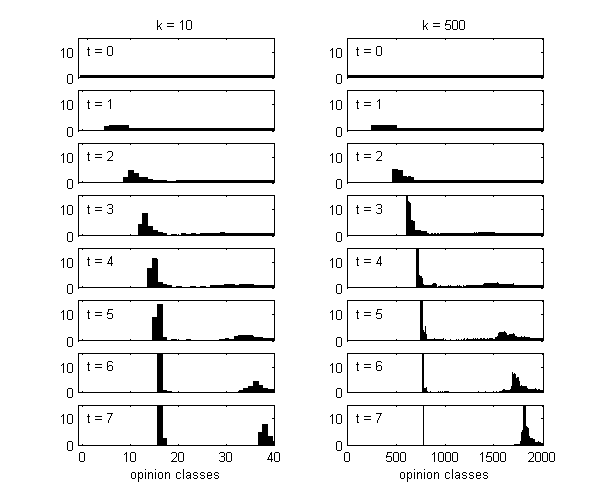
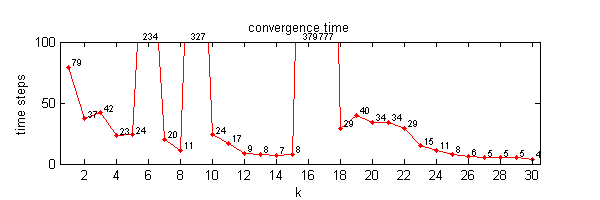
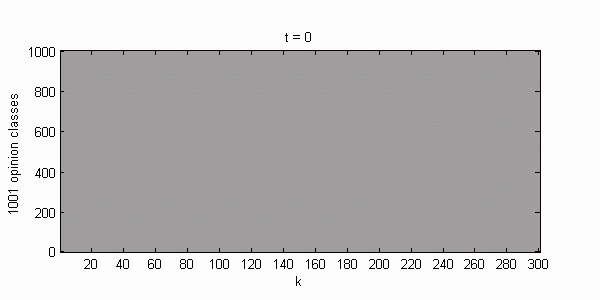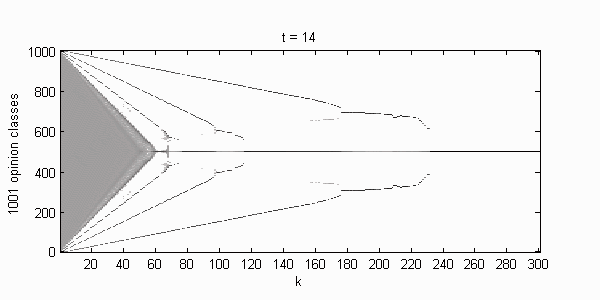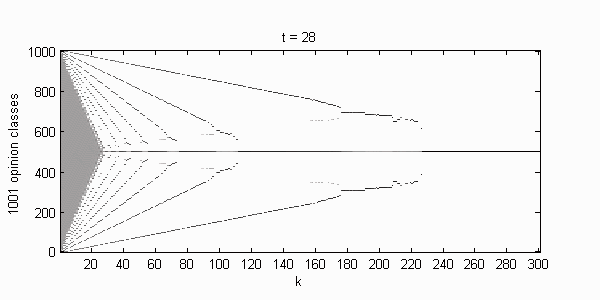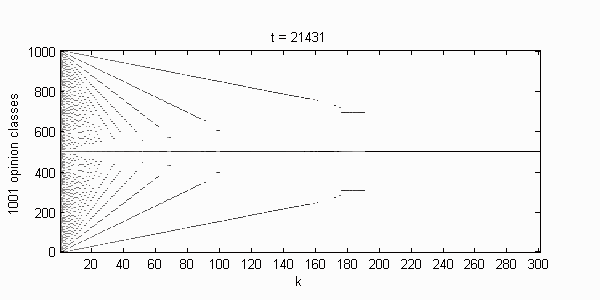
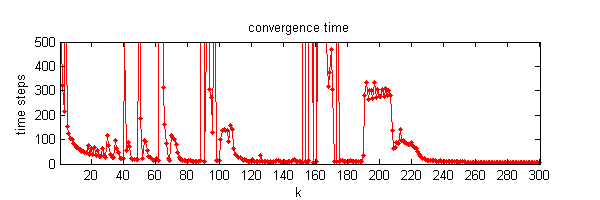
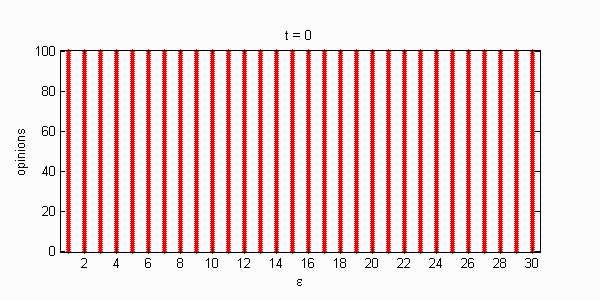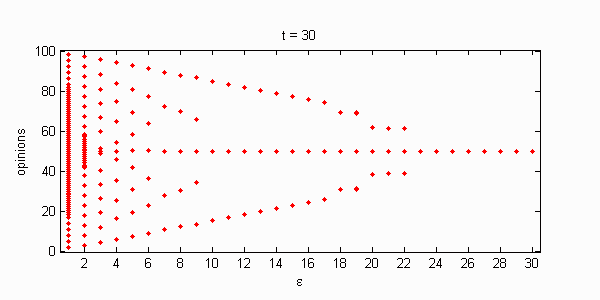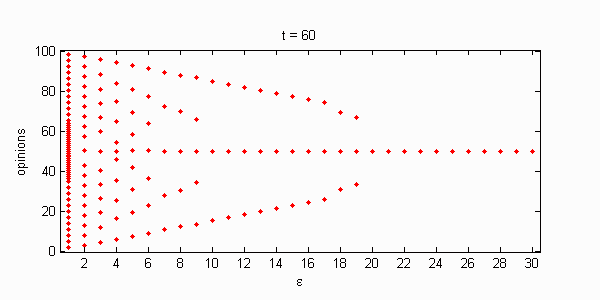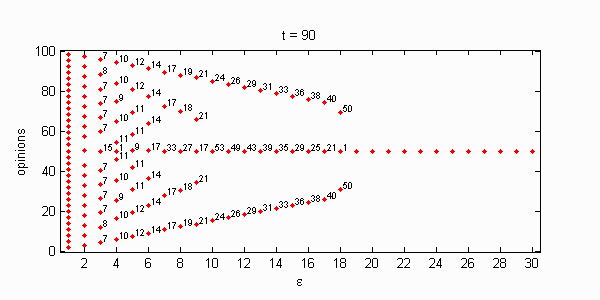
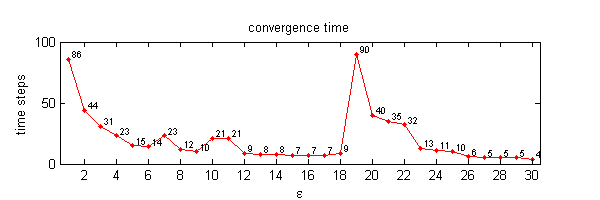
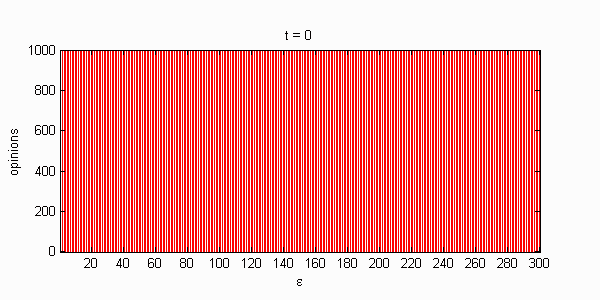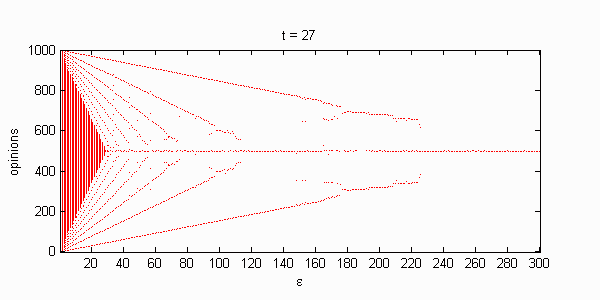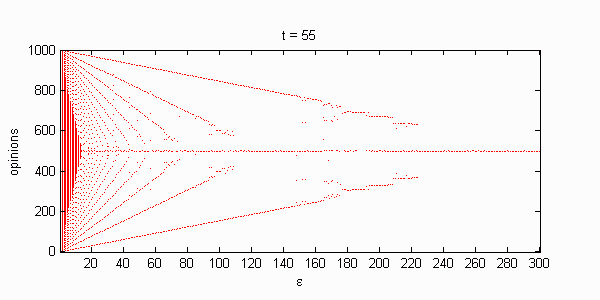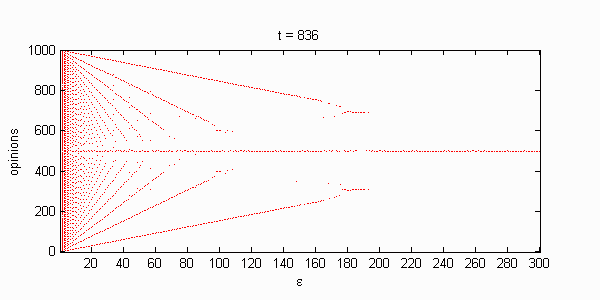
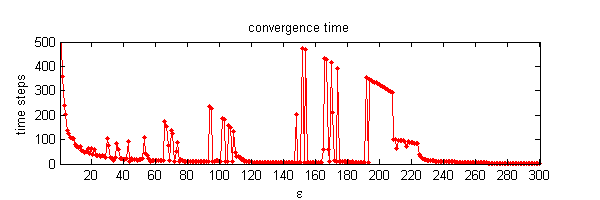
We calculate the interactive Markov chains until stabilisation for the uniform initial distribution and all interesting discrete bounds of confidence. Figure 10 shows the results for n = 100 and k = 1, ..., 30 in an animation stabilising in a kind of bifurcation diagram.
AMBLARD, F. and DEFFUANT, G. (2004), The role of network topology on extremism propagation with the relative agreement opinion dynamics, Physica A, vol. 343, 725-738
BEN-NAIM, E., KRAPIVSKY, P.L. and REDNER S. (2003), Bifurcation and Patterns in Compromise Processes, Physica D, vol. 183, 190-204
CONLISK, J. (1976), Interactive Markov Chains, Journal of Mathematical Sociology, vol. 4, 157-185
DEFFUANT, G., NEAU, D., AMBLARD, F. and WEISBUCH, G. (2002), How can extremism prevail? A study based on the relative agreement interaction model, Journal of Artificial Societies and Social Simulation, vol. 5, no. 4, https://www.jasss.org/5/4/1.html
DITTMER, Jan Christian (2001), Consensus Formation under bounded Confidence, Nonlinear Analysis, vol. 47, 4615-4621
HEGSELMANN, R. (2004). Opinion Dynamics ñ Insights by Radically Simplifying Models,.In: Gillies D. (Ed), Laws and Models in Science, London, 1-29.
HEGSELMANN, R. and KRAUSE, U. (2002) Opinion Dynamics and Bounded Condence Models, Analysis and Simulation, Journal of Artificial Societies and Social Simulations, vol. 5, no. 3, https://www.jasss.org/JASSS/5/3/2.html
HERMANNS, H. (2002), Interactive Markov chains: and the quest for quantified quality, Springer
HORST, U. (2001), Convergence of locally and globally interacting Markov chains, Stochastic Processes and their Application, vol. 96, 99-121
JAGER, W. and AMBLARD, F. (2005), Uniformity, bipolarisation and pluriformity captured as generic stylized behaviour with an agent-based simulation model of attitude change, Computational and Mathematical Organization Theory, vol. 10, 295-303
LORENZ, J. (2005), A Stabilization Theorem for Dynamics of Continuous Opinions, Physica A, Vol. 355 (1), 217-223
LORENZ, J. (2005), Continuous Opinion Dynamics: Insights through Interactive Markov Chains; In Proceedings of IASTED Conference "Modelling, Simulation and Optimization ~MSO 2005~", August 29-31, 2005, Oranjestad, Aruba available at http://www.janlo.de
NEAU (2000), D. Révisions des croyances dans un systéme díagents en interaction, rapport díoption de líécole polytechnique, available at http://www.lps.ens.fr/~weisbuch/rapneau.ps
POLHILL, G. and IZQUIERDO, L. (2005), three papers in JASSS
URBIG, D. (2003), Attitude Dynamics with Limited Verbalisation Capabilities, Journal of Artificial Societies and Social Simulation, vol. 6, no. 1, https://www.jasss.org/6/1/2.html
URBIG, D. and LORENZ, J. (2004), Communication regimes in opinion dynamics: Changing the number of communicating agents; Proceedings of the Second Conference of the European Social Simulation Association (ESSA), Valladolid, Spain, September 16-19, 2004, available at http://www.janlo.de
WEISBUCH, G., DEFFUANT, G., AMBLARD, F. and NADAL, J. (2002), Meet, Discuss and Segregate!, Complexity, vol. 7 no. 3, 55-63
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2006]