Jill Bigley Dunham (2005)
An Agent-Based Spatially Explicit Epidemiological Model in MASON
Journal of Artificial Societies and Social Simulation
vol. 9, no. 1
<https://www.jasss.org/9/1/3.html>
For information about citing this article, click here
Received: 02-Feb-2005 Accepted: 15-Dec-2005 Published: 31-Jan-2005
 Abstract
Abstract
|
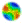
| Figure 1. A flowchart of possible states in an epidemic model |
|
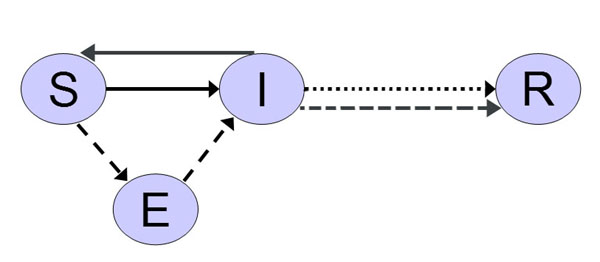
| Figure 2. Two-layered network (Bian 2004) |
|
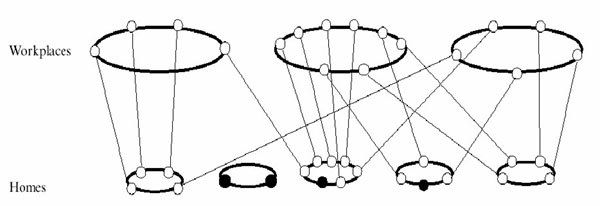
| Figure 3. Simulation display window. Susceptible agents are shown in green, exposed in blue, infected in red, and removed in black |
| Table 1: Basic simulation parameters | ||
| Parameter | Default Value | Description |
| XMIN | 0 | Controls display size and shape |
| XMAX | 800 | Controls display size and shape |
| YMIN | 0 | Controls display size and shape |
| YMAX | 600 | Controls display size and shape |
| DIAMETER | 8 | Physical size of agents |
| NUM_HUMANS | 40 | Total humans in simulation |
| NUM_INFECTED | 5 | Number of humans initially infected |
| NUM_REMOVED | 0 | Number of humans initially removed |
| NUM_EXPOSED | 0 | Number of humans initially exposed |
| DAY_LENGTH | 500 | Number of time steps per simulation day |
| Table 2: Disease-specific simulation parameters | ||
| Parameter | Default Value | Description |
| SIR_MODEL | True | Flag to indicate inclusion of removed state. |
| SEIR_MODEL | False | Flag to indicate inclusion of exposed/latent state. |
| INFECTION_DISTANCE | 20 | Radius of infectiousness |
| MEAN_INFECTED_TIME_DAYS | 1.0 | |
| MAX_INFECTED_TIME_DAYS | 1.0 | |
| MIN_INFECTED_TIME_DAYS | 1.0 | |
| MEAN_EXPOSED_TIME_DAYS | 1.0 | |
| MAX_EXPOSED_TIME_DAYS | 1.0 | |
| MIN_EXPOSED_TIME_DAYS | 1.0 | |
| INFECTIVITY_RATE_EXPOSED_DAYS | 0.75 | |
| INFECTIVITY_RATE_DAYS | 0.5 | |
| Table 3: Societal and personal simulation parameters | ||
| Parameter | Default Value | Description |
| health_factor | Between 0 and 1 | Index of a human''s general health |
| ACCEPTANCE | 0.5 | Likelihood of taking a sick day when ill |
| HOME_MEAN | 2.59 | Mean home size |
| HOME_SD | 1.42 | Standard deviation of home size |
| WORK_MEAN | 10 | Mean workplace size |
| WORK_SD | 3.5 | Standard deviation of workplace size |
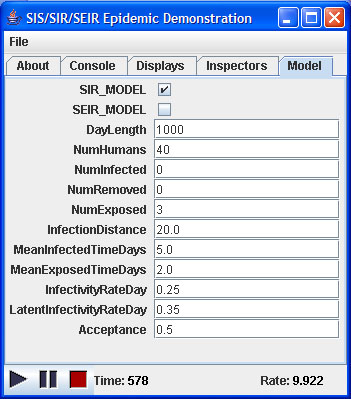
|
| Figure 4. The simulation console |
Alternatively, simulation parameters can be specified using an input file. Using the input file allows control over the full set of parameters, including setting maximum and minimum exposed and infection lengths to allow variable lengths for these phases. Home and workplace size distributions can also be varied using input files.
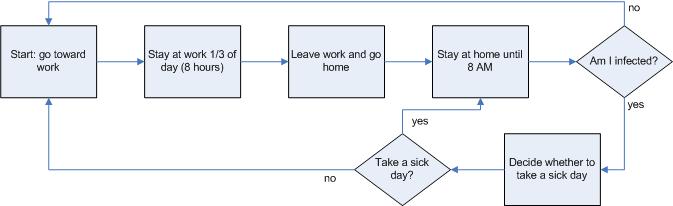
|
| Figure 5. Human behavior rules |
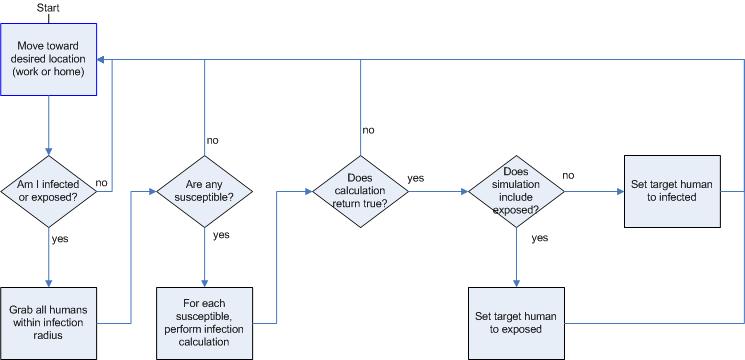
|
| Figure 6. Infection behaviors |
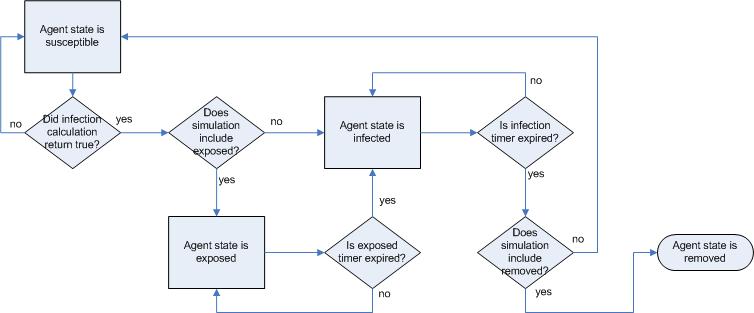
|
| Figure 7. Movement through the infection phases |
| Table 4: Some parameters used for influenza-like epidemic demonstration |
|
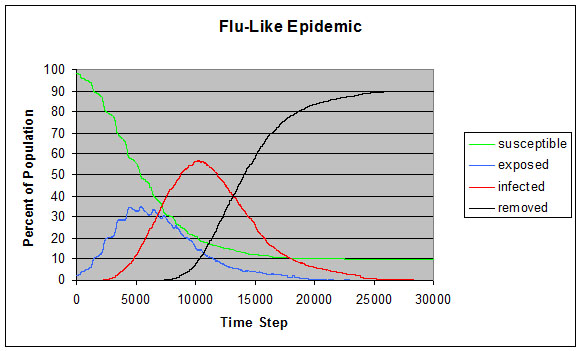
INFECTION_DISTANCE =20 DAY_LENGTH =1000 MEAN_INFECTED_TIME_DAYS=5.0 MAX_INFECTED_TIME_DAYS=6.0 MIN_INFECTED_TIME_DAYS=4.0 INFECTIVITY_RATE_DAYS=0.2f MEAN_TIME_EXPOSED_DAYS=2.0 MAX_TIME_EXPOSED_DAYS=5.0 MIN_TIME_EXPOSED_DAYS=1.0 INFECTIVITY_RATE_EXPOSED_DAYS=0.3f NUM_HUMANS =100 NUM_INFECTED =0 NUM_REMOVED =0 NUM_EXPOSED =2 ACCEPTANCE =0.5f SIR_MODEL =1 SEIR_MODEL =1 |
|
| Figure 8. Flu-like epidemic |
| Table 5: Some parameters used for RSV-like epidemic demonstration |
|
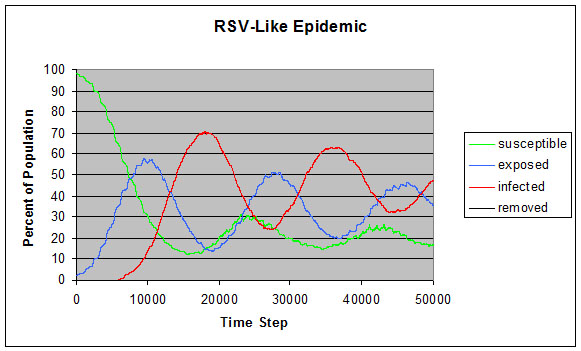
INFECTION_DISTANCE =20 DAY_LENGTH =1000 MEAN_INFECTED_TIME_DAYS=8.0 MAX_INFECTED_TIME_DAYS=10.0 MIN_INFECTED_TIME_DAYS=6.0 INFECTIVITY_RATE_DAYS=0.25f MEAN_TIME_EXPOSED_DAYS=5.0 MAX_TIME_EXPOSED_DAYS=8.0 MIN_TIME_EXPOSED_DAYS=2.0 INFECTIVITY_RATE_EXPOSED_DAYS=0.25f NUM_HUMANS =100 NUM_INFECTED =0 NUM_REMOVED =0 NUM_EXPOSED =2 ACCEPTANCE =0.7f SIR_MODEL =0 SEIR_MODEL =1 |
|
| Figure 9. RSV-like epidemic |
| Table 6: Some parameters used for Lassa-like epidemic demonstration |
|
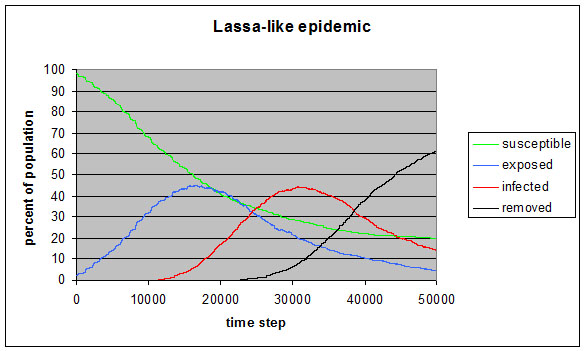
INFECTION_DISTANCE =10 DAY_LENGTH =1000 MEAN_INFECTED_TIME_DAYS=10.0 MAX_INFECTED_TIME_DAYS=20.0 MIN_INFECTED_TIME_DAYS=5.0 INFECTIVITY_RATE_DAYS=0.15f MEAN_TIME_EXPOSED_DAYS=10 MAX_TIME_EXPOSED_DAYS=21.0 MIN_TIME_EXPOSED_DAYS=6.0 INFECTIVITY_RATE_EXPOSED_DAYS=0.35f NUM_HUMANS =100 NUM_INFECTED =0 NUM_REMOVED =0 NUM_EXPOSED =2 ACCEPTANCE =1.0f SIR_MODEL =1 SEIR_MODEL =1 |
|
| Figure 10. Lassa-like epidemic demonstration |
|
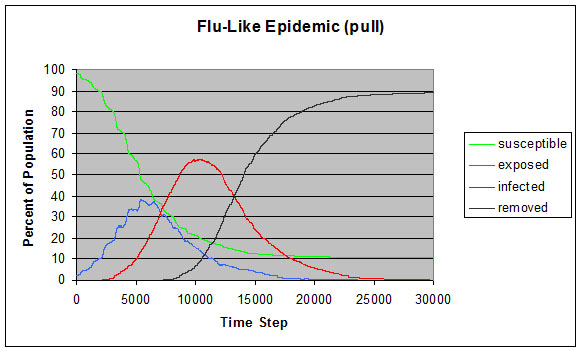
| Figure 11. Flu-like epidemic using infection pull instead of push |
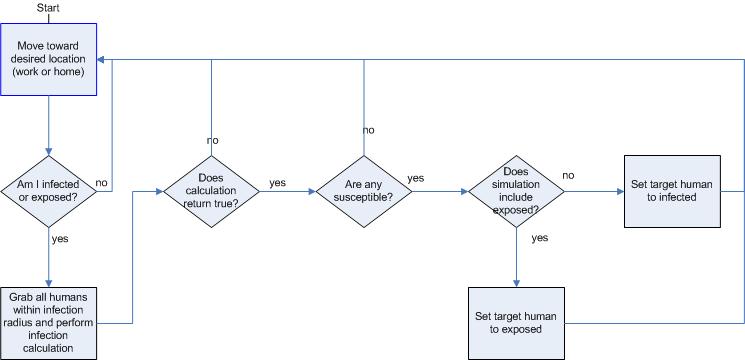
|
| Figure 12. Revised infection flowchart |
BIAN, L. (2004). "A Conceptual Framework for an Individual-Based Spatially Explicit Epidemiological Model." Environment and Planning B: Planning and Design 31: 381-395.
US CENSUS BUREAU (2000). American Fact Finder.
DEIEKMANN, O. and J. A. P. Heesterbeek (2000). Mathematical Epidemiology of Infectious Disease: Model Building, Analysis, and Interpretation. New York, John Wiley & Sons, Inc.
DIBBLE, C. (2004). GeoGraph Models for Controlling Epidemics. School of Computational Sciences Research Colloquium. George Mason University.
DIBBLE, C. and P. G. Feldman (2004). "The GeoGraph 3D Computational Laboratory: Network and Terrain Landscapes for RePast." Journal of Artificial Societies and Social Simulation 7(1).
DIMACS (2004). Center for Discrete Mathematics and Theoretical Computer Science, Rutgers University.
DWORKIN, A. (2004). Mathematical supermodels refine epidemic predictions. The Oregonian. Portland, Oregon.
EPSTEIN, J., D. A. T. Cummings, et al. (2002). "Toward a Containment Strategy for Smallpox Bioterror: An Individual-Based Computational Approach." Brookings Institute Center on Social and Economic Dynamics Working Paper #31.
HAWKER, J., N. Begg, et al. (2001). Communicable Disease Control Handbook. Oxford, Blackwell Science Ltd.
LIPSITCH, Marc, Ted Cohen, et al. (2003). "Transmission Dynamics and Control of Severe Acute Respiratory Syndrome." Science 300:5627:1966-1970.
LUKE, S., C. Cioffi-Revilla, et al. (2004). MASON: A New Multi-Agent Simulation Toolkit. 2004 SwarmFest Workshop.
VENKATACHALAM, Sangeeta, Armin Mikler, A. R. (2005). Towards Computational Epidemiology : Using Stochastic Cellular Automata in modeling spread of diseases. Proceedings of the 4th Annual International Conference on Statistics, Mathematics and Related Fields, Honolulu, HI.
WASSERMAN, S. and K. Faust (1994). Social Network Analysis: Methods and Applications, Cambridge University Press.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]