Victor Palmer (2006)

Deception and Convergence of Opinions Part 2: the Effects of Reproducibility

Journal of Artificial Societies and Social Simulation vol. 9, no. 1
<https://www.jasss.org/9/1/14.html>

For information about citing this article, click here

Received: 31-Jul-2005    Accepted: 07-Oct-2005    Published: 31-Jan-2006

Abstract

Recently Martins (Martins 2005) published an article in this journal analyzing the opinion dynamics of a neutral observer deciding between two competing scientific theories (Theory A and Theory B). The observer could not perform any experiments to verify either theory, but instead had to form its opinion solely by reading published articles reporting the experimental results of others. The observer was assumed to be rational (modeled with simple Bayesian rules) and the article examined how the observer's confidence in the correctness of the two theories changed as a function of number of articles read in support of each theory, and how much, if any, deception was believed to be present in the published articles. A key (and somewhat disturbing) result of this work was that for even relatively small amounts of perceived deception in the source articles, the observer could never be reasonably sure of which theory (A or B) was correct, even in the limit of the observer reading an infinite number of such articles. In this work we make a small extension to the Martins article by examining what happens when the observer only considers experimental results which have been reproduced by multiple parties. We find that even if the observer only requires that the articles he or she reads be verified by one additional party, its confidence in one of the two theories can converge to unity, regardless of the amount of amount of deception believed to be present in the source articles.

Keywords:

Opinion Dynamics, Epistemology, Rational Agents, Deception, Confirmation Theory

Introduction

Overview

1.1

The study of opinion dynamics examines how an individual forms opinions through interactions with external influences. This type of analysis is useful in many domains such as analyzing the dynamics of a group which must come to a consensus decision, for example Hegselmann and Krause (2002) and Edwards (2002), or looking at how consumers form opinions about products based on the opinions of others, such as Lane (1997).

1.2

In this vein, an article was recently published by Martins (2005) in this journal which examined how a neutral 'observer' agent-scientist might go about forming an opinion on which of two competing theories (Theory A and Theory B) was correct ... solely by reading published articles about experiments performed by others. These articles/experiments would support or cast doubt on each of the two theories, and by assuming that the observer agent was rational (in a Bayesian sense), Martins was able to simulate what the observer's opinion on each of the two theories should be after reading a given number of such articles.

1.3

The techniques used to attack opinion-dynamics problems such as this tend to be widely varied, and, depending on the domain, everything from physically-inspired models such as Sznajd-Weron and Sznajd (2000) to simple Bayesian statistics have been used. The Martins work falls in the latter category, since he models the observer as a rational agent which updates its beliefs according to Bayesian rules. This approach is advantageous since it allows us to specify the observer's pre-article-exposure beliefs as priors in the Bayesian framework, and track how those beliefs evolve with time. Through this mechanism, Martins was able to simulate what happens when the agent observer initially believes that some of the articles that it reads are not accurate, but are in fact deceptions. Depending on the amount of deception the observer agent believes to exist in the articles it reads, it was shown that the observer's confidence in which theory (A or B) is correct can never exceed a given threshold, no matter how many such reports/articles are read. This effect was pronounced — even for a relatively small amount of suspected deception (say 20%), it was found that the observer's confidence in either theory could never exceed about 90%, with more limiting thresholds resulting from higher levels of perceived deception.

1.4

Obviously this study is (or should be) interesting to the scientific community since to a large extent, it models how the majority of scientists go about forming their opinions about many important, field-defining issues. That is, for any given topic in a scientific discipline, it is unlikely that every interested party will be able to experimentally verify, for him/herself, every result which may be found to be interesting or useful. As such, the scientific community as a whole has generally adopted the very reasonable practice of accepting the published accounts of other scientists' experimental results as fact — or at least as nearly as good as the results of a self-performed experiments. Additionally, it seems reasonable that some level of deception must exist in such published scientific articles. For whatever reason, whether it be malicious deception or accidental carelessness, it hardly seems plausible that 100% of the articles circulating in any body of literature are completely accurate.

1.5

As such, the Martins article is disturbing on at least two fronts. First, it makes one reflect on how confident scientists can actually be about their beliefs given that a certain level of deception exists in published works. Second, the article brings into sharp relief an idea put forth in Jaynes (2003) which says that a scientist would never be convinced of a phenomenon (such as ESP, etc.), no matter how much evidence was brought to bear for the affirmative, as long as the scientist was convinced that a given level of deception existed in the evidence. Thus, no matter how objective an observer scientist might like to be about an issue, the pre-conceived beliefs of the scientist would seem to play a significant role in determining how he or she views, interprets, and interacts with scientific literature. Perhaps what is most disturbing about this line of thought is that even a small amount of deception can significantly and generally harm all scientists' ability to confidently come to conclusions about important issues. Even if the majority of a scientific community is honest, a small deceptive minority can 'ruin' the entire community's ability to operate confidently.

1.6

In this present work we make a small addition to the work done by Martins and allow the scientific community to fight back against deceptive articles by independent replication and verification of experimental results. Practically, this means that the observer agent can now read not only reports of experiments performed by other scientists, but can also read about studies attempting to replicate those reports. We look at the number of such replications needed to counteract a given level of suspected deception and find that for all the cases considered in the Martins work, only a single replication is necessary to allow the agent scientist to overcome any effects of perceived deception and rationally come to a confident conclusion about the correctness of the two theories.

Reading Articles

Review of the Non-Deception and Deception Case

2.1

The setup for the problem domain in the Martins article goes something like this: An observer (we will, as Martins, model the observer as a rational agent, and thus it may be referred to as the observer agent, etc.) attempts to take an educated stance on some controversial issue to which two competing theories have been proposed (creatively titled Theory A and Theory B). Perhaps because of the nature of the issue, the observer agent is itself unable to perform experiments to determine which theory is correct, but instead, must rely on published accounts of experiments performed by other scientists. Each published article must entirely endorse one of the two theories and as such, each article can be classified as a Theory A-supporting article (denoted R_a) or a Theory B-supporting article (R_b), depending on which side of the issue it supports.

2.2

Further, we will allow that because of the nature of the issue, experiments are not always reliable. Specifically, we will say that even if Theory A is correct, there is a probability a that any specific experiment will actually come out in favor of Theory A and a probability (1-a) that the experiment will come out in favor of Theory B. The same logic holds if Theory B is true: b percent of honest experiments will support Theory B, and (1-b) will support Theory A. We take a and b to be known a priori.

2.3

Note that this does not mean that the experiments are not reproducible ... if Experiment X supports Theory A, then Experiment X will always come out in favor of Theory A. Thus, for example, the probability b means that if Theory B is actually correct, out of all experiments that could be done to test the validity of Theory B, only b fraction of them will actually turn up in favor of Theory B ... just because of the nature of the problem.

2.4

With the setup we have so far, a rational agent would view the situation as follows: If there is a probability p that Theory A is true, we would expect the probability q of encountering an article in support of Theory A to be:

q = f(Ra | p, a, b) = pa + (1-p)(1-b)

(1)

2.5

Since a and b are already known, we can estimate p (how certain the agent is that Theory A is true) by simulating the reading of articles and obtaining an estimate on q.

2.6

However, if we consider the possibility that some of the published articles read by our agent may in fact be deceptions, we must modify the expression for q. Here, by deception, it is meant that an article has nothing to do with reality at all — the authoring scientist simply fabricated the result. If there is a probability e that any given article is a deception, and there is a probability d that a deceptive article favors Theory A (with, of course, a 1-d probability that a deceptive article favors Theory B), our expression for q becomes:

q = f(Ra | p,e,d,a,b) = ed + (1-e)[pa + (1-p)(1-b)]

(2)

2.7

We can no longer obtain an estimate for p simply by sampling q since we have added two unknowns e and d. Martins's solution (and the approach we will use here) is to create priors for these two unknowns (eventually a uniform prior for d and a Beta distribution for e) representing the agent scientist's a priori beliefs about the integrity of the articles it reads.

Replication of Previous Results

3.1

To begin with, we reproduced Martins's results by implementing a MATLAB version of their FORTAN simulator. The simulator is available for download here (the file mainloop.m contains the executable interface to the simulator). Specifically, we replicated two sets of results — one simulating the limit in which our observer agent reads an infinite number of articles, and the other simulating the beliefs of our agent when it reads a more 'reasonable' (finite) number of articles.

The Infinite Article Limit

3.2

We performed the simulation reported in Martins, which consisted of assuming a uniform prior for the variables p and d and a Beta distribution for e. In each run of the simulation, the agent's beliefs were seeded to favor neither theory (p=0.5) and at each iteration the agent was exposed to one article and its beliefs were updated according to Bayes rule depending on whether the article supported Theory A or Theory B. The prior Beta distribution for e was constructed by choosing an average and standard deviation value for e and then calculating the corresponding alpha and beta values. In all cases, as in Martins, the average value and standard deviation of e were the same — representing how as the average amount of suspected deception increases, our agent would probably be less likely to know the exact amount of deception as well. The purpose of the simulation was to see how the views of the agent end up after being exposed to a very large number of articles. In Martins, the agent was exposed to 10000 articles for this 'infinite-article' limit, however, we found little induced change in p after the 1000 article mark, so we simply doubled that number and used 2000 articles for our 'infinite article' limit. The results of this simulation are displayed in Figure 1.

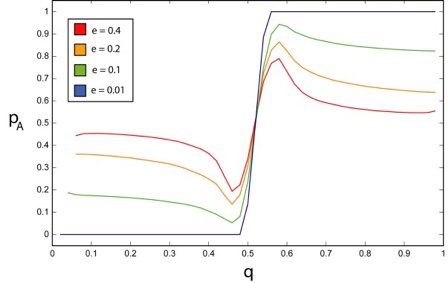
Figure 1. This figure shows our replication of the Martins results for the infinite article limit. Notice that for small deception (small e and small e variation), the p versus q graph is almost a step function whereas for even for small amounts of deception unity p is never reached. This trend continues monotonically, with less and less step-like behavior observed for increasing e. In all cases a = b = 0.55.

The Sparse Article Limit

3.3

Another way of demonstrating the effect of deception on the opinion dynamics of our observer agent is to see how many articles the agent must read before it can become 99% sure that Theory A is correct (as we will see, in this series of simulations we take q > 0.5, so Theory A is always correct). We exposed our agent to as many articles as it took until its confidence (p) became 0.99 or higher. If p < 0.99 by the time the agent had been exposed to 10000 articles, we considered the simulation unable to converge. The results of this simulation for two values of a are plotted in Figure 2, in all cases the natural log was used. As Martins pointed out, and as we observe here, the number of articles that our observer must read before it can reach the 99% certainty level scales super-exponentially with the amount of suspected deception.

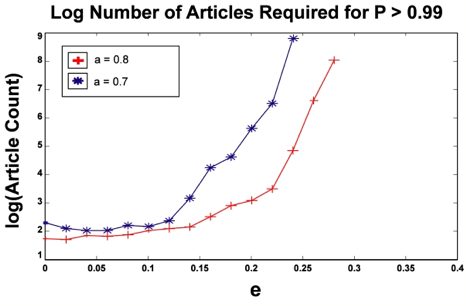
Figure 2. For two values of a, we plot the number of articles our agent observer must read to be 99% sure that Theory A is correct. For this series of simulations we set q = a since that is always the point of maximum p in the "p versus q" graph. Our simulation did not converge for e > 0.24 for the a = 0.7 case and for e > 0.28 for the a = 0.8 case.

What Replication Buys Us

The Deception Case with Replication

4.1

As we saw in the last section, if our agent believes that there is a certain amount of deception present in the articles it is sampling, then for reasonable values for a and b, even moderate amounts of perceived deception can significantly limit the maximum level of confidence that the agent can have in the truth of either theory. The effect of deception was generally heightened by taking a and b close to 0.5 (which would represent a case where even honest experiments were fairly noisy indicators of which theory was correct), and so, in all the simulations that follow, we took a = b = 0.55.

4.2

If our agent was a real scientist, actually trying to decide between these two theories in the possible presence of deception, one useful technique would be to utilize the scientific community's ability to replicate experimental results. In the real-world, although it almost certain that some deception must exist, subjectively there seems to be a measure of confidence bestowed by the fact that scientists can independently replicate each other's work and, by doing so, keep each other honest and relatively error-free. Barring massive conspiracies or extremely bad luck, it seems that by reading enough accounts of supposedly unaffiliated scientists replicating a given experimental result, one should be able to overcome any doubt introduced by the possibility of deception. The only question is how much replication is necessary to overcome a given level of assumed deception?

4.3

Going back to our observer agent, we can model the effects of replication on its beliefs by the following: Instead of reading each article it encounters, our agent will only read articles which report results that have been replicated by an independent source. We will assume that replications of articles adopt the same statistics as articles themselves. If so, the probability that our agent encounters such an article/replication pair where both the article and its replication support Theory A is the following:

q = f( {Ra ,Ra} | p,e,d,a,b) = (ed)2 + 2(ed)(1-e)[pa + (1-p)(1-b)] + (1-e) 2 [pa + (1-p)(1-b)]

(3)

Where each term is justified below:

(ed)2	The probability that both the article and its replication are deceptions and that both support Theory A
2(ed)(1-e)[a + (1-p)(1-b)]	The probability that the article is a deception and supports Theory A, but its replication is NOT a deception and also happens to support Theory A. The factor of 2 is to account for an identical term (since ordering is not important) that occurs when the article is honest and its replication is a deception in support of Theory A.
(1-e)2[pa + (1-p)(1-b)]	Both the article and its replication are honest and both support Theory A. Notice that the factor [pa + (1-p)(1-b)] is not squared in the expression — as we said earlier, this factor determines the likelihood of a randomly selected experiment coming up in favor of Theory A — once the experiment is selected (by the initial article), its replication will always come out in favor of the same theory.

4.4

We could extend this analysis to the case of only allowing our agent to read articles that had been replicated N times, but as we will see shortly, even a single replication almost completely eliminates any effects of the suspected presence of deception.

Replication Results

Infinite Article Case

5.1

We ran the MATLAB version of the Martins simulation code with the updated, replication-conscious expression for q. Starting first with the infinite-article limit, the same suite of tests were performed as in Section 3 and the results are shown in Figure 3.

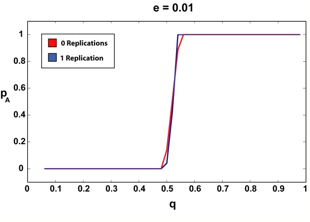
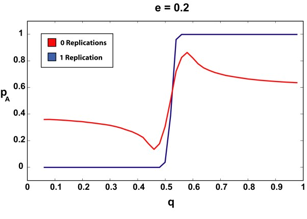
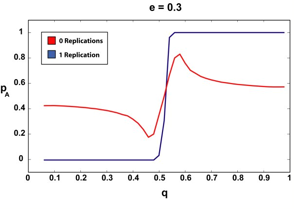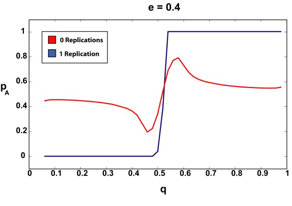
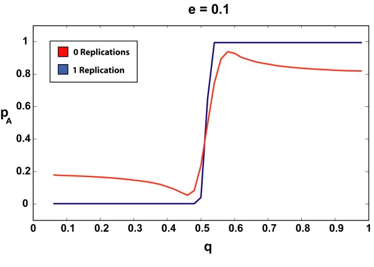
Figure 3. The infinite article (2000) limit for 0 and 1 replications and various e. The sharper, step-like curves correspond to the 1-replication case. Notice how the 1-replication p curve is relatively unchanged as we increase the amount of a priori suspected deception (e).

We can see that if our agent requires that the articles it reads have been replicated, even once, the "p versus q" curve remains more or less a step function, regardless of the amount of assumed deception. There are no doubt pathological cases (perhaps an a very, very close to 0.5, for example) where requiring a second replication could offer our agent additional advantages, but since in all the cases we tested, step-function type behavior was observed for the single-replication case, we were not able to test this.

Sparse Article Limit

5.2

Next we performed a series of experiments to test out the effect of replication in the finite-article limit. As in Section 2, the goal was to see how many articles our observer agent needed to read before it could be 99% percent sure that Theory A was correct (p >= 0.99). As before q = a in all these simulations, since this is the point of maximum p. We ran simulations for the a=0.7 and a=0.8 cases as before.

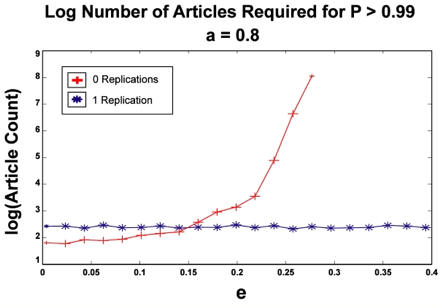
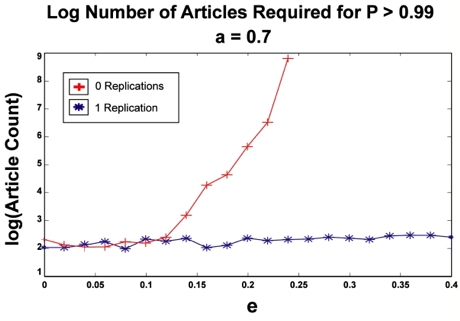
Figure 4. The sparse article limit simulation for 0 and 1 replications. For the no replication case (strongly increasing curve), as we increase e, the number of articles that our observer agent must read to be 99% sure that Theory A is correct grows super-exponentially. However, for even a single replication, the number of required articles remains more or less constant with increasing e. Notice that once again, our 0-replication simulation never converged for several values of e.

In the cases we tested, the presence of deception had no visible effect on the number of articles required by our agent to reach certainty — while the 0-replication case diverged super-exponentially with deception as before, the single-replication case remained relatively constant. However, it seems unreasonable that we should observe a true shift from super-exponential scaling to no scaling just by requiring a single replication — instead, we hypothesize that the scaling of our results was still super-exponential in nature, only with a drastically smaller scaling constant. In other words, we guess that the number of required articles still grows super-exponentially under replication, but just very, very slowly. Again, there are probably some pathological conditions where two or more replications would yield additional scaling benefits, but since we never saw a situation where the single-replication case scaled at all, this was not testable.

Conclusion

6.1

We have simulated a rational observer agent that forms an opinion about the truth of two competing theories solely by reading the published experimental accounts of others. We found that while the presence of suspected deception in the source accounts can significantly limit the ability of the agent observer to ever become well-convinced of the truth of either theory, replication of the experimental accounts can mitigate the effects of this deception. Specifically, we found that if our observer only reads articles that have been replicated even once, that the effect of any presumed deception is almost entirely negated.

6.2

The inclusion of replication in our simulation model had a profound effect on the beliefs of our observer agent. We saw that even for small amounts of replication (one replication), the beliefs of our agent behaved almost as though there was no suspected deception. Intuitively this makes sense — one would imagine that if enough independent parties told you X, that you should accept X with a fair degree of confidence. However, the effect of replication turns out to be extremely powerful (in this simulation setup at least), so powerful in fact that we were unable to test out the effects of multiple replications simply because additional replications offered no visible advantage.

6.3

It should be somewhat reassuring that even in the face of significant deception, scientific order can prevail by utilizing the presence of a large and generally honest scientific community. Such results highlight the importance of processes such as peer-review in journals, and generally of a community-wide interest in replicating the results of others. Since a single replication is hardly difficult to achieve — probably this condition is satisfied for almost every result most people in the modern scientific community care about — it seems that as long we there exists a strong, contributing community, our beliefs as scientists are well-protected.

Acknowledgements

This work was supported by a Fannie and John Hertz Foundation fellowship.

References

EDWARDS M., Huet S., Goreaud F., and Deffuant G. (2002) Comparing an Individual-Based Model of Behaviour Diffusion with Its Mean Field Aggregate Approximation, Journal of Artificial Societies and Social Simulations, vol. 6, no. 4.

HEGSELMANN, R. and Krause, U. (2002) Opinion Dynamics and Bounded Condence Models, Analysis and Simulation, Journal of Artificial Societies and Social Simulations, vol. 5, no. 3.

JAYNES, E.T. (2003) Probability Theory: The Logic of Science.Cambridge: Cambridge University Press.

LANE, D. (1997) Is What Is Good For Each Best For All? Learning From Others In The Information Contagion Model, in The Economy as an Evolving Complex System I (ed. by Arthur, W.B., Durlauf, S.N. and Lane, D.), pp. 105-127. Santa Fe: Perseus Books.

MARTINS, A. (2005) Deception and Convergence of Opinions, Journal of Artificial Societies and Social Simulations, vol. 8, no. 2.

SZNAJD-WERON, K. and Sznajd, J. (2000) Opinion Evolution in Closed Communities, Int. J. Mod. Phys. C 11, 1157.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2006]