AMBLARD, F. and Deffuant, G. (2004),
The role of network topology
on extremism propagation with the relative agreement opinion dynamics, Physica
A, vol. 343, pp. 725-738.
BRAUER, M., Judd, C. (1996), Group
polarization and repeated attitude expressions: A new take on an old
topic, in W. Stroebe and M. Hewstone (Eds.), European
Review of Social Psychology, vol. 7, John Wiley & Sons,
chapter 6, pp. 173-207.
DAVID, B. and Turner, J. C. (1996),
Studies in self-categorization and minority conversion: Is being a
member of the out-group and advantage?, British Journal of Social
Psychology, Vol. 35, pp. 179-199.
DAVID, B. and Turner, J. C. (1999),
Studies in self-categorization and minority conversion: The in-group
minority in intragroup and intergroup contexts, British Journal of
Social Psychology, Vol. 38, pp. 115-134.
DEFFUANT, G., Amblard, F., Weisbuch, G.
and Faure, T. (2002), How can extremism prevail? A study based on
the relative agreement interaction model, Journal of Artificial
Societies and Social Simulation, Vol. 5, No. 4, <https://www.jasss.org/5/4/1.html>.
DEFFUANT, G., Neau, D., Amblard, F. and
Weisbuch, G. (2000), Mixing beliefs among interacting agents, Advances
in Complex Systems, Vol. 3, pp. 87-98.
DITTMER, J. (2001), Consensus formation
under bounded confidence, Nonlinear Analysis, Vol. 47,
pp. 4615-4621.
HASLAM, S. A. and Turner,
J. C. (1995), Context-dependent variation in social
stereotyping 3 : Extremism as a self-categorical basis for polarized
judgement, European Journal of Social Psychology,
Vol. 25, pp. 341-371.
HEGSELMANN, R. and Krause, U. (2002),
Opinion dynamics and bounded confidence models, analysis, and
simulation, Journal of Artificial Societies and Social Simulation,
Vol. 5, No. 3, <https://www.jasss.org/5/3/2.html>
.
ISENBERG, D. (1986), Group polarization:
A critical review and meta-analysis, Journal of Personality and
Social Psychology, Vol. 50, No. 6, pp. 1141-1151.
JAGER, W. and Amblard, F. (2005),
Uniformity, bipolarisation and pluriformity captured as generic
stylized behaviour with an agent-based simulation model of attitude
change, Computational and Mathematical Organization Theory,
Vol. 10, pp. 295-303.
KRAUSE, U. (2000), A discrete nonlinear
and non-autonomous model of consensus formation, in S. Elaydi,
G. Ladas, J. Popenda and J. Rakowski (Eds.), Communications
in Difference Equations, Gordon and Breach Science Publishers,
Amsterdam, pp. 227-236.
MACKIE, D. (1987), Systematic and
nonsystematic processing of majority and minority persuasive
communications, Journal of Personality and Social Psychology,
Vol. 53, No. 1, pp. 41-52.
MCGARTY, C., Turner, J., Hogg, A., David,
B. and Wetherell, M. (1992), Group polarization as conformity to
the prototypical group member, British Journal of Social Psychology,
Vol. 31, pp. 1-20.
OAKES, P. J., Haslam, S. A. and
Turner, J. C. (1994), Stereotyping and social reality,
Blackwell, Oxford, Cambridge.
OAKES, P. J., Turner, J. C. and
Haslam, S. A. (1991), Perceiving people as group members : The
role of fit in the salience of social categorizations, British
Journal of Social Psychology, Vol. 30, pp. 125-144.
SALZARULO, L. (2004), Formalizing
self-categorization theory to simulate the formation of social groups,
presented at the 2nd European Social Simulation Association
Conference, Valladolid, Spain, 16th-19th September 2004.
TINDALE, R., Davis, J., Vollrath, D.,
Nagao, D. and Hinsz, V. (1990), Asymmetrical social influence in
freely interacting groups: A test of three models, Journal of
Personality and Social Psychology, Vol. 58, No. 3,
pp. 438-449.
TURNER, J. C., Hogg, M. A.,
Oakes, P. J., Reicher, S. D. and Wetherell, M. S. (Eds.)
(1987), Rediscovering the social group : A self-categorization
theory, Blackwell, Oxford.
WATTS, D. and Strogatz, S. (1998),
Collective dynamics of «small-world» networks, Nature,
Vol. 393, pp. 440-442.
WEISBUCH, G., Deffuant, G. and Amblard,
F. (2005), Persuasion dynamics, Physica A, Vol. 353,
pp. 555-575.
 Abstract
Abstract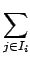 xj .
xj .![\includegraphics[width=0.6\linewidth]{P_2agents_pol}](13/img21.png)
![\includegraphics[width=0.6\linewidth]{P_2agents_cons}](13/img22.png)
![\includegraphics[width=\textwidth]{stetson_hat.eps}](13/img23.png)
![\includegraphics[width=\linewidth]{phase_random_update_rinf.eps}](13/img24.png)
![\includegraphics[width=\linewidth]{phase_theo_random_update_rinf.eps}](13/img25.png)
![\includegraphics[width=0.6\linewidth]{phase_transition_w0.6.eps}](13/img26.png)
![\includegraphics[width=0.5\linewidth]{indiv_traj_a0.05_w0.8.eps}](13/img29.png)
![\includegraphics[width=0.5\linewidth]{indiv_traj_a0.15_w0.4.eps}](13/img30.png)
![\includegraphics[width=0.5\linewidth]{indiv_traj_a0.15_w0.2.eps}](13/img31.png)
![\includegraphics[width=0.5\linewidth]{indiv_traj_a0.05_w0.05.eps}](13/img32.png)
![\includegraphics[width=0.5\linewidth]{indiv_traj_a0_w0.4_1.eps}](13/img33.png)
![\includegraphics[width=0.5\linewidth]{indiv_traj_a0_w0.4.eps}](13/img34.png)
![\includegraphics[width=0.5\linewidth]{phase_random_update_r1_sw0_50x50.eps}](13/img35.png)
![\includegraphics[width=0.5\linewidth]{phase_random_update_r1_sw0.1_50x50.eps}](13/img36.png)
![\includegraphics[width=0.5\linewidth]{phase_random_update_r1_sw1_50x50.eps}](13/img37.png)
![\includegraphics[width=0.5\linewidth]{snapshot_a0.000_w0.400_r1_p0.000_i250000.eps}](13/img39.png)
![\includegraphics[width=0.5\linewidth]{snapshot_a0.180_w1.000_r1_p0.000_i250000.eps}](13/img40.png)
![\includegraphics[width=0.5\linewidth]{indiv_traj_a0.0_w0.41_swn1_cons.eps}](13/img41.png)
![\includegraphics[width=0.5\linewidth]{indiv_traj_a0.0_w0.41_swn1_bipol.eps}](13/img42.png)
![\includegraphics[width=0.5\linewidth]{indiv_traj_a0.0_w0.41_swn1_single.eps}](13/img43.png)
![\includegraphics[width=0.5\linewidth]{phase_single_update_10x10.eps}](13/img44.png)
![\includegraphics[width=0.5\linewidth]{coupe_w0.6_phase_single_update_10x10.eps}](13/img45.png)
![\includegraphics[width=0.5\linewidth]{nb_op_single_it_w0.2.eps}](13/img46.png)
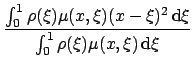
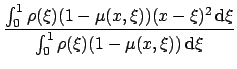 .
.![$\displaystyle {\frac{{w\left[ (x-1)\exp\left(-\left(\frac{x-1}{w}\right)^2\righ...
...t)^2\right)\right]}}{{\sqrt{\pi}\gerf \left(\frac{x-1}{w},\frac{x}{w}\right)}}}$](13/img53.png)
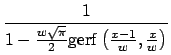
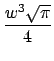 gerf
gerfReturn to Contents of this issue