Scott Wheeler (2005)
It Pays to Be Popular: a Study of Civilian Assistance and Guerilla Warfare
Journal of Artificial Societies and Social Simulation
vol. 8, no. 4
<https://www.jasss.org/8/4/9.html>
For information about citing this article, click here
Received: 15-Feb-2005 Accepted: 09-Jul-2005 Published: 31-Oct-2005
 Abstract
Abstract

|
| Figure 1. Example board |
|
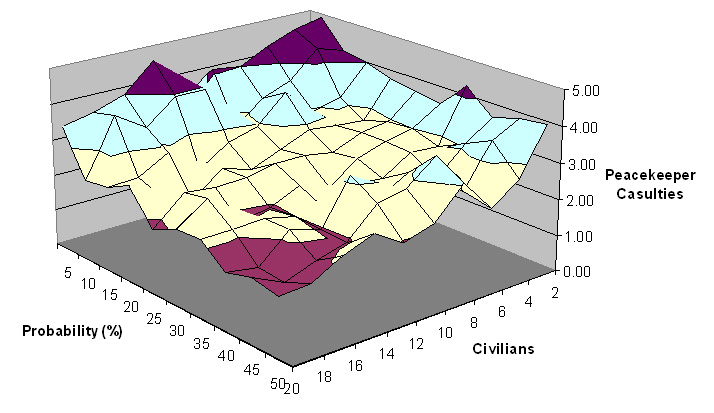
| Figure 2. UN peacekeeper casualties with nc and pscan varying |
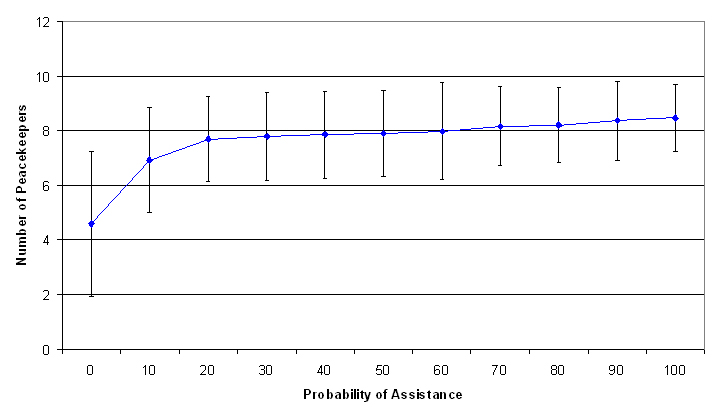
| Table 1: Simulation results | ||
| pscan | Savg | StDev(Savg) |
| 0 | 4.585 | 2.673 |
| 10 | 6.935 | 1.931 |
| 20 | 7.700 | 1.566 |
| 30 | 7.790 | 1.615 |
| 40 | 7.851 | 1.606 |
| 50 | 7.917 | 1.573 |
| 60 | 7.985 | 1.769 |
| 70 | 8.155 | 1.453 |
| 80 | 8.215 | 1.363 |
| 90 | 8.365 | 1.432 |
| 100 | 8.465 | 1.231 |
|
| Figure 3. Plot of Savg against pscan |
As indicated in Figure 3, the number of UN peacekeepers surviving the peacekeeping operation exhibits a non-linear relationship to pscan. Hence, we propose to explain how survival rates for UN peacekeepers relate to pscan by testing for significant differences between the values of interest for pscan of 0, 10, 20, 60 and 100. The differences between the two values for pscan of 10x and 10x+10, x = 2,...,9, for example between 40 and 50 or 50 and 60, are not significant at the 90% confidence level.
|
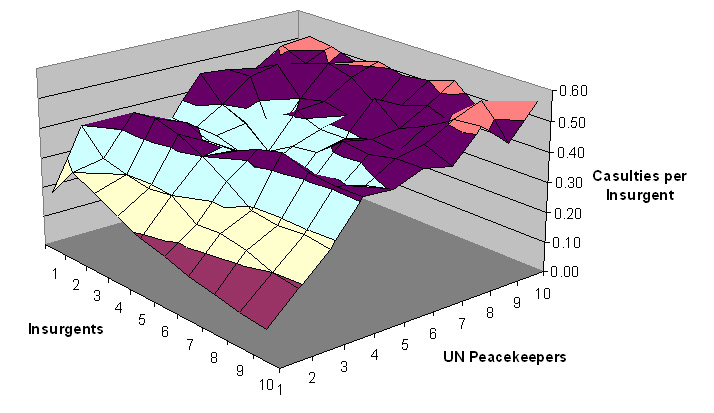
| Figure 4. UN peacekeeper casualties per insurgent with np and ni varying |

|
| Figure 5. Example danger levels on a 500 by 500 unit board |
CHAPMAN T, Mills V, Kardos M, Stothard C and Williams D (2002) The Use of the Janus Wargame Simulation to Investigate Naturalistic Decision-Making: A Preliminary Examination. DSTO-TR-1372. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.
COMMONWEALTH OF AUSTRALIA (2002) Bringing Rigour to Army Experiment in Getting It Right. Australian Defence Science, 10 (1). p. 12.
COMMONWEALTH OF AUSTRALIA (2004) Complex Warfighting. Puckapunyal, Australia: Future Land Warfare, Land Warfare Development Centre.
CORDESMAN A H (2003) Lessons of the Iraq War: Main Report. Washington D C: Center for Strategic and International Studies. 11th working draft dated July 21.
DEXTER P (2004a) Historical Analysis of Population Reactions to Stimuli - A Case Study of Aceh. DSTO-TR-1592. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.
DEXTER P, Hobbs W S R and Grieger D (2005) Preliminary Modelling of Asymmetric Warfare and the Contemporary Conflict Environment. DSTO-TR-1621. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.
DEXTER R M (2004b) The Close Action Environment (CAEn) V9.2 Training Manual, Part One: Graphical User Interface Overview. DSTO-GD-0404. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.
EPSTEIN J, Steinbruner J and Parker M (2001) Modelling Civil Violence: An Agent-Based Computational Approach. Working paper. Washington D C: Center on Social and Economic Dynamics, Brookings Institution.
GRIEGER D (2002) Using Agent Based Distillations to Support Land Warfare Studies. Unpublished publicly released General Document. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.
HOBBS W S R, Dexter P, Egudo M and Grieger D (2005) An Analytical Framework for the Study of Asymmetric Warfare. DSTO-TR-1670. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.
MILLIKAN J A, Castles T D and Brennan M J (2003) Close Action Environment Modelling of a Combined Arms Sub-Unit in an Urban Environment. DSTO-TN-0485. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.
RECORD J and Terrill W A (2004) Iraq and Vietnam: Differences, Similarities, and Insights. Pennsylvania: United States Army War College, Strategic Studies Institute.
REYNOLDS C W (1987) "Flocks, Herds, and Schools: A Distributed Behavioural Model". In Stone M C (Eds.), Computer Graphics, Proceedings of the ACM SIGGRAPH '87 Conference, Anaheim, California, July 1987, 21 (4). pp. 25-34.
RYAN A and Grisogono A-M (2004) "Hybrid Complex Adaptive Engineered Systems: A Case Study in Defence". In Proceedings of the International Conference on Complex Systems, Boston.
STEPHENS A K W, Connell R B and Davies P J (2004) Urban Intelligence Preparation of the Battlespace: Methods for Determining Spatial Vulnerability in Urban Environments. DSTO-TR-1541. Edinburgh, Australia: Land Operations Division, Defence Science and Technology Organisation.
TAYLOR J G (1983) Lanchester Models of Warfare. Arlington: Operations Research Society of America.
WILNESKY U (1999) NetLogo User Manual, Version 2.1. Evanston, IL: Center for Connected Learning and Computer-Based Modeling, Northwestern University.
YIU S Y, Gill A W and Shi P (2003) Using Agent Based Distillations to Model Civil Violence Management. Journal of Battlefield Technology, 6 (1). pp. 1-6.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]