Chung-Yuan Huang, Chuen-Tsai Sun and Hsun-Cheng Lin (2005)
Influence of Local Information on Social Simulations in Small-World Network Models
Journal of Artificial Societies and Social Simulation
vol. 8, no. 4
<https://www.jasss.org/8/4/8.html>
For information about citing this article, click here
Received: 29-Aug-2004 Accepted: 31-Jul-2005 Published: 31-Oct-2005
 Abstract
Abstract
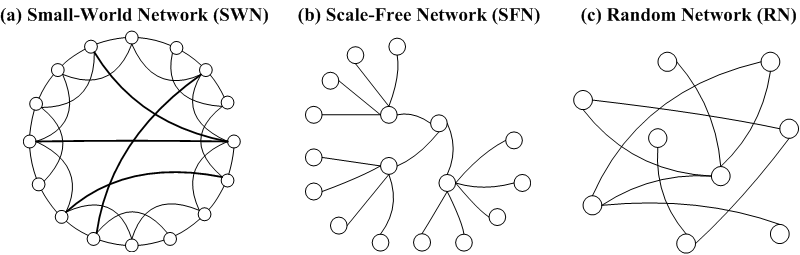
|
| Figure 1. Complex networks: (a) small-world (SWN), (b) scale-free (SFN), (c) random (RN). |
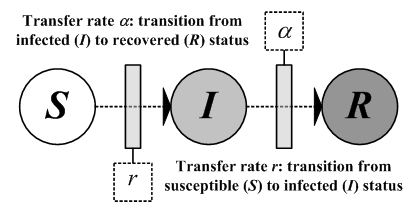
|
| Figure 2. General SIR state transfer diagram: S, susceptible; I, infectious; R, removed |
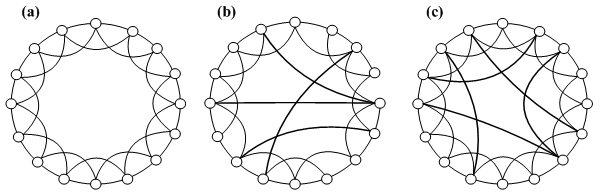
|
| Figure 3. (a) A one-dimensional regular graph with each node connected to its four adjacent nodes. (b) Watts and Strogatz's (1998) original SWN model, with four rewired edges. (c) Newman and Watts' (1999a) improved SWN model with five additional shortcuts. |
|
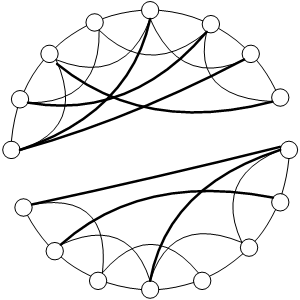
| Figure 4. An example of a broken graph in Watts and Strogatz's (1998) SWN model |
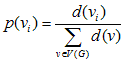
|
(1) |
|
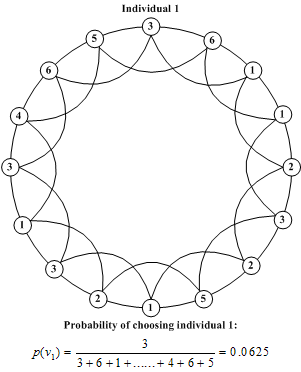
| Figure 5. An example of calculating the probability of a node being selected |
|
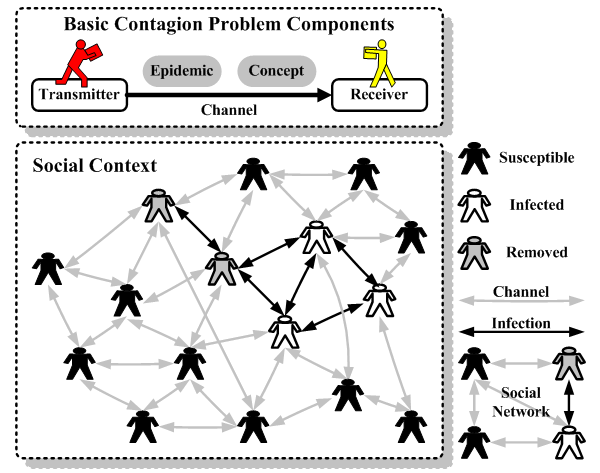
| Figure 6. Contagion problem model |
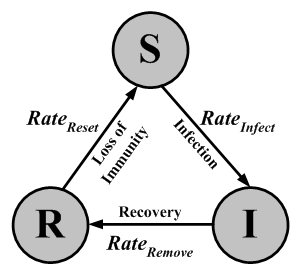
|
| Figure 7. A SIR state transfer diagram showing a repetitive cycle |
|
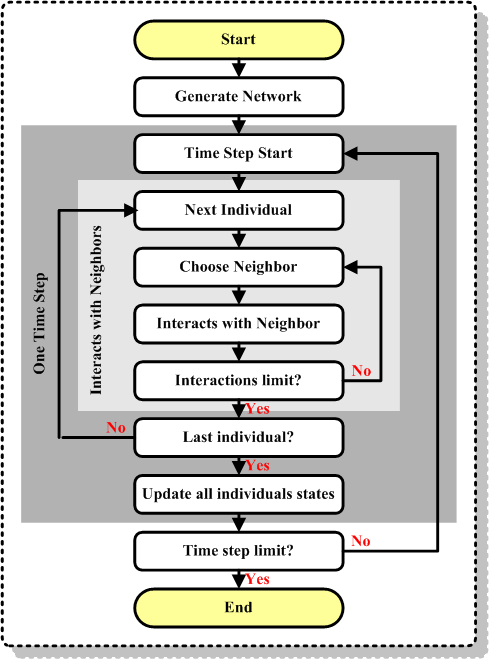
| Figure 8. Simulation flowchart for a contagion problem model |
for 1 to Time Step Limit do loop
for all Individual Ii in Population do loop
if Interaction Mode = All then
Interaction Limit ← All degree numbers of Individual Ii
else
Interaction Limit ← 3
end if
for 1 to Interaction Limit do loop
if Interaction Mode = All then
Individual Itarget ← Choose a neighbor of Ii by order
else
Individual Itarget ← Choose a neighbor of Ii by random
end if
SIR(Ii, Itarget)
next
next
for all Individual Ii in Population do loop
if Ii.NowState = I then
if random value r < RateRemove then
Ii.NextState ← R
end if
end if
if Ii.NowState = R then
if random value r < RateReset then
Ii.NextState ← S
end if
end if
next
comment from time t to time (t + 1)
for all Individual Ii in Population do loop
Ii.NowState ← Ii.NextState
next
next
procedure SIR (Individual Ia, Individual Ib) is
if Ia.NowState = I and Ib.NowState = S then
if random value r < RateInfect ◊ Ib.Resist then
Ib.NextState ← I
end if
end if
if Ia.NowState = S and Ib.NowState = I then
if random value r < RateInfect ◊ Ia.Resist then
Ia.NextState ← I
end if
end if
return
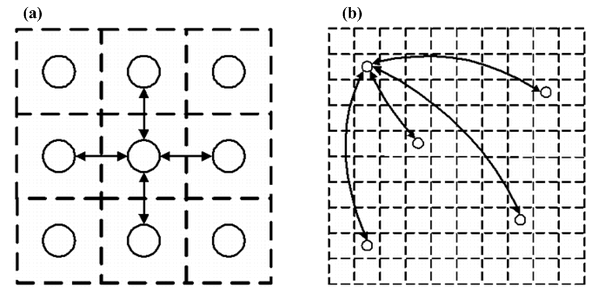
|
| Figure 9. (a) Each individual in a cellular automata has four neighbors. (b) Each individual can have 0 to n connecting shortcuts to other randomly selected individuals |
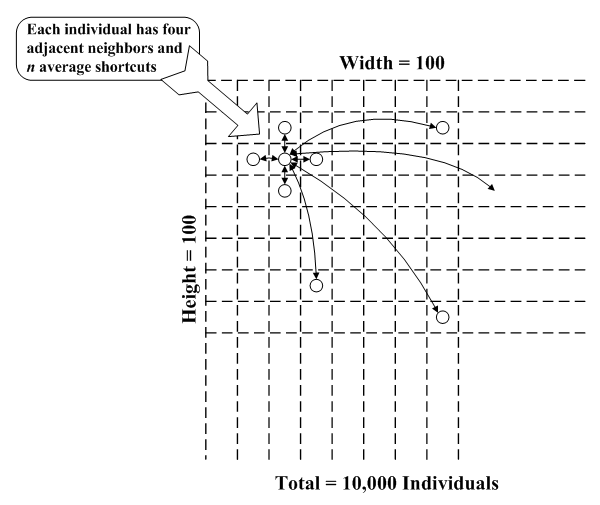
|
| Figure 10. Simulation model schematic diagram |
| Table 1: The six simulation models | |||||||
| Simulation Model | SWN#1* | SWN#2 | SWN#3 | SWN#4 | SWN#5 | SWN#6 | |
| Average number of shortcuts per individual | 17 | 1 (20) | 2 (21) | 4 (22) | 8 (23) | 16 (24) | |
| Average degree of separation | 2.45 | 6.57 | 5.35 | 4.45 | 3.59 | 3.02 | |
| Infection rate | 0.05 ~ 0.33 (based on number of interactions) | ||||||
| Removal rate | 0.9 | ||||||
| Reset rate | 0.1 | ||||||
| 2-D cellular automata | Height | 100 | |||||
| Width | 100 | ||||||
| Population size | 10,000 | ||||||
| Neighborhood structure | von Neumann, with periodic boundary conditions | ||||||
| Table 2: Simulation model parameters | |||||
| Scope | Class | Attribute | Type | Range | Description |
| Global | Simulation model | Time Step Limit | Integer | (0, +∞) | Total number of time steps during each simulation (default value = 90). |
| Interaction Limit | Integer | (0, +∞) | Number of interactions between an individual and its neighbors during each time step (default value based on interaction mode value). | ||
| Interaction Mode | Symbol | Interaction mode: either 3 or the number of all connected individuals (default value defined according to experiment needs). | |||
| SIR model | RateInfect | Real | (0, 1) | Infection rate | |
| RateRemove | Real | (0, 1) | Removal rate (default value = 0.9). | ||
| RateReset | Real | (0, 1) | Reset rate (default value = 0.1). | ||
| 2-D cellular automata with shortcuts | Width | Integer | (0, +∞) | Width of the 2-D cellular automata (default value = 100). | |
| Height | Integer | (0, +∞) | Height of the 2-D cellular automata (default value = 100). | ||
| Population Size | Integer | (0, +∞) | Total numbers of individuals in the simulated society (default population size = 10,000). | ||
| Neighborhood | Symbol | von Neumann, with periodic boundary conditions | |||
| Average number of shortcuts | Integer | (0, +∞) | Average numbers of shortcuts per individual | ||
| Experiment | Radius r | Real | [0, 1] | Distribution radius of weak individuals (default value = 1.0). | |
| Local | Individual | Resist | Real | (0, +∞) | Resistance to epidemic disease, trend, or idea (default value = 1.0). |
| Weighted Vertex Degree | Real | (0, +∞) | Weighted vertex degree when choosing shortcuts (default value = 1.0). | ||
| NowState | Symbol | Current epidemiological state | |||
| NextState | Symbol | Epidemiological state in the next time step | |||
| Table 3: Experimental results using different vertex degree data with the six simulation models | ||||||||
| Simulation Model | SWN#1 | SWN#2 | SWN#3 | SWN#4 | SWN#5 | SWN#6 | ||
| Average accumulated number and standard deviation of infectious individuals produced by simulation model (Mean±Std) | Interactions with 3 connected individuals | Infection Rate | 0.3 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 |
| Constant Mode | 23979 ±451 | 11854 ±588 | 18074 ±494 | 21751 ±582 | 25158 ±466 | 26854 ±403 | ||
| Uniform Distribution | 23571 ±507 | 12008 ±459 | 17823 ±530 | 21974 ±514 | 24961 ±405 | 26997 ±418 | ||
| Normal Distribution | 23685 ±402 | 11896 ±527 | 17986 ±494 | 21917 ±559 | 25199 ±529 | 27079 ±487 | ||
| Experiment Results | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | ||
| Interactions with all connected individuals | Infection Rate | 0.05 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | |
| Constant Mode | 33887 ±351 | 15913 ±416 | 30244 ±342 | 45147 ±241 | 58287 ±233 | 68492 ±197 | ||
| Uniform Distribution | 34274 ±317 | 16286 ±478 | 30514 ±370 | 45220 ±407 | 58060 ±367 | 68340 ±206 | ||
| Normal Distribution | 34155 ±266 | 16038 ±388 | 30270 ±463 | 45303 ±243 | 58249 ±343 | 68394 ±212 | ||
| Experiment Results | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | ||
| Conclusion: | As long as small-world phenomena exist and the average degree of separation does not change, variation (e.g., constant mode, uniform distribution, and normal distribution) in the detailed topological structure exerts only a slight influence on the contagion problem transmission dynamics of SWN models. | |||||||
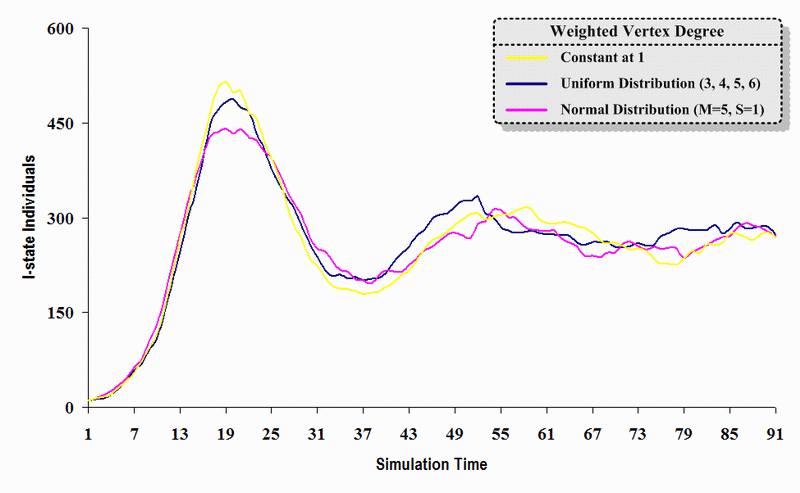
|
| Figure 11. A comparison of three sets of experimental results from the first simulation model (SWN#1) using different vertex degree data in a simulation where one individual interacts with three randomly chosen individuals per time step. Each time grid shows the resulting number of I (infectious) individuals produced by the proposed simulation model per time step. |
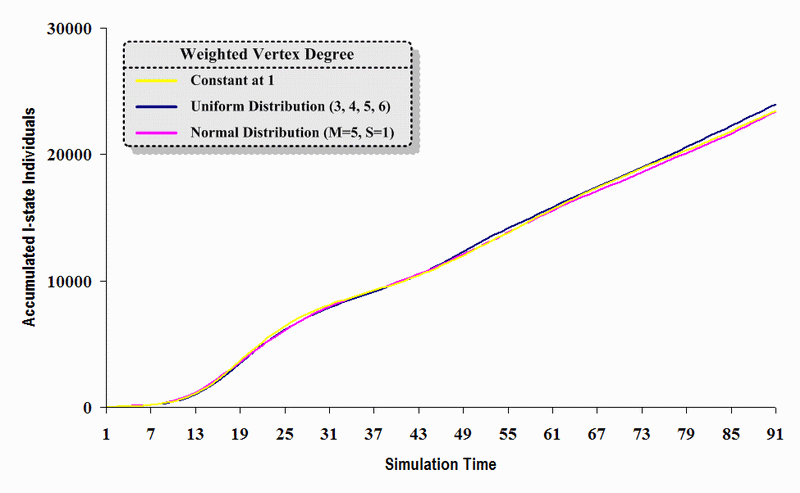
|
| Figure 12. A comparison of three sets of experimental results from the first simulation model (SWN#1) using different vertex degree data in a simulation where one individual interacts with three randomly chosen individuals per time step. Each time grid shows the accumulated number of I (infectious) individuals produced by the proposed simulation model. |
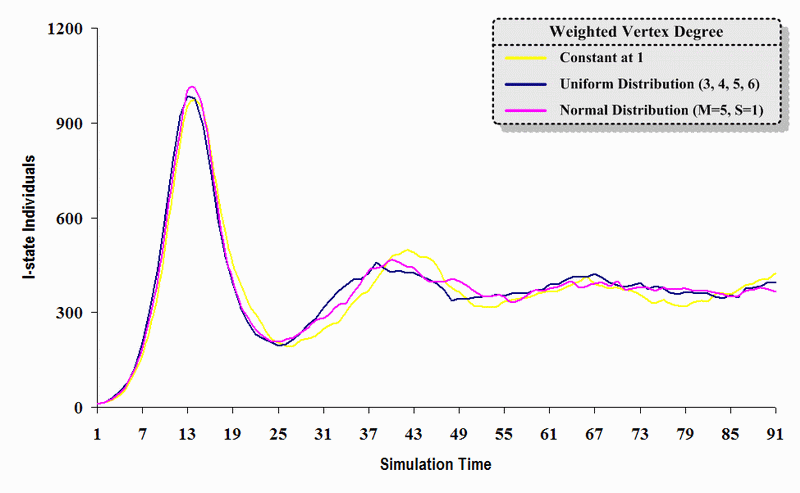
|
| Figure 13. A comparison of three sets of experimental results from the first simulation model (SWN#1) using different vertex degree data in a simulation where one individual interacts with all of its connected individuals per time step. Each time grid shows the resulting number of I (infectious) individuals produced by the proposed simulation model per time step |
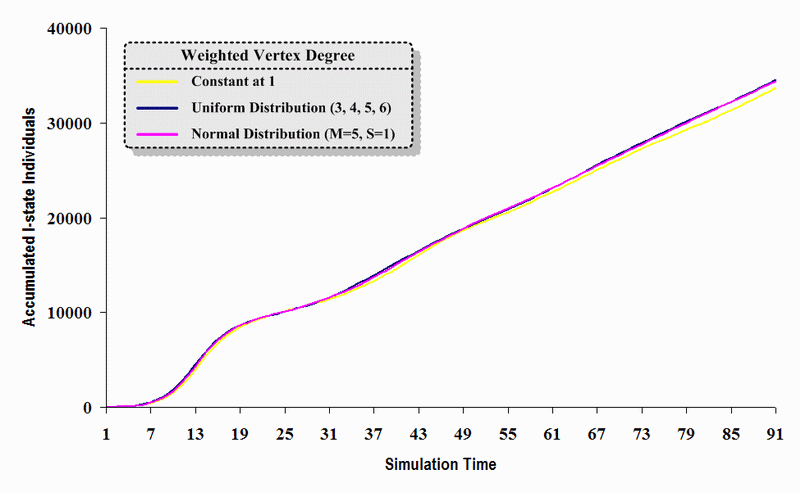
|
| Figure 14. A comparison of three sets of experimental results from the first simulation model (SWN#1) using different vertex degree data in a simulation where one individual interacts with all of its connected individuals per time step. Each time grid shows the accumulated number of I (infectious) individuals produced by the proposed simulation model |
| Table 4: Experimental results using different proportions of weak individuals with the six simulation models | ||||||||
| Simulation Model | SWN#1 | SWN#2 | SWN#3 | SWN#4 | SWN#5 | SWN#6 | ||
| Average accumulated number and standard deviation of infectious individuals produced by simulation model (Mean±Std) | Interactions with 3 connected individuals | Infection Rate | 0.3 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 |
| 0% Weak Individuals | 23288 ±451 | 12250 ±346 | 17727 ±427 | 22221 ±428 | 25135 ±344 | 26707 ±409 | ||
| 1% Weak Individuals | 24032 ±327 | 12953 ±457 | 18329 ±370 | 22770 ±394 | 25546 ±447 | 27175 ±436 | ||
| 5% Weak Individuals | 26892 ±517 | 15373 ±594 | 21326 ±423 | 24450 ±505 | 27744 ±523 | 29489 ±484 | ||
| 10% Weak Individuals | 29794 ±487 | 18951 ±426 | 24015 ±436 | 26849 ±383 | 30055 ±419 | 31894 ±370 | ||
| 30% Weak Individuals | 33814 ±318 | 27704 ±532 | 31126 ±374 | 34281 ±454 | 36879 ±457 | 38084 ±506 | ||
| 50% Weak Individuals | 37124 ±418 | 32638 ±544 | 36517 ±380 | 40172 ±353 | 41165 ±308 | 42088 ±358 | ||
| Experiment Results | Sensitive Parameter | Sensitive Parameter | Sensitive Parameter | Sensitive Parameter | Sensitive Parameter | Sensitive Parameter | ||
| Interactions with all connected individuals | Infection Rate | 0.05 | 0.2 | 0.2 | 0.2 | 0.1 | 0.1 | |
| 0% Weak Individuals | 33858 ±418 | 15576 ±425 | 30299 ±328 | 45073 ±305 | 35645 ±379 | 54764 ±252 | ||
| 1% Weak Individuals | 34211 ±376 | 16358 ±391 | 31010 ±489 | 45518 ±215 | 36069 ±375 | 55030 ±168 | ||
| 5% Weak Individuals | 36478 ±250 | 18965 ±388 | 32787 ±436 | 46620 ±293 | 37761 ±391 | 55831 ±172 | ||
| 10% Weak Individuals | 41574 ±328 | 21585 ±368 | 34795 ±327 | 48108 ±431 | 39056 ±487 | 56895 ±248 | ||
| 30% Weak Individuals | 46971 ±314 | 29448 ±349 | 40295 ±419 | 51986 ±282 | 44214 ±337 | 59804 ±338 | ||
| 50% Weak Individuals | 48971 ±212 | 34018 ±354 | 43874 ±227 | 54768 ±224 | 47766 ±231 | 61765 ±234 | ||
| Experiment Results | Sensitive Parameter | Sensitive Parameter | Sensitive Parameter | Sensitive Parameter | Sensitive Parameter | Sensitive Parameter | ||
| Conclusion: | The percentage of weak individuals exerted a significant influence on the contagion problem transmission dynamics of SWN models when small-world phenomena exist and the average degree of separation does not change. | |||||||
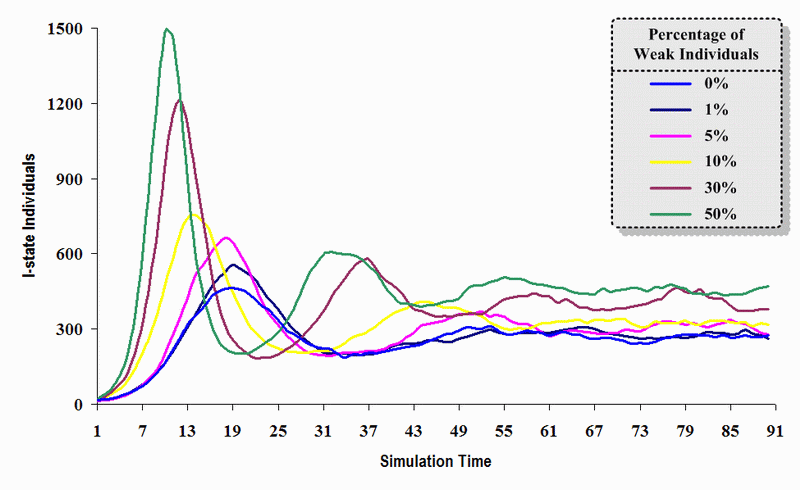
|
| Figure 15. A comparison of six sets of experimental results from the first simulation model (SWN#1) using different proportions of weak individuals in a simulation where one individual interacts with three randomly chosen individuals per time step. Each time grid shows the resulting number of I (infectious) individuals in the proposed simulation model per time step |
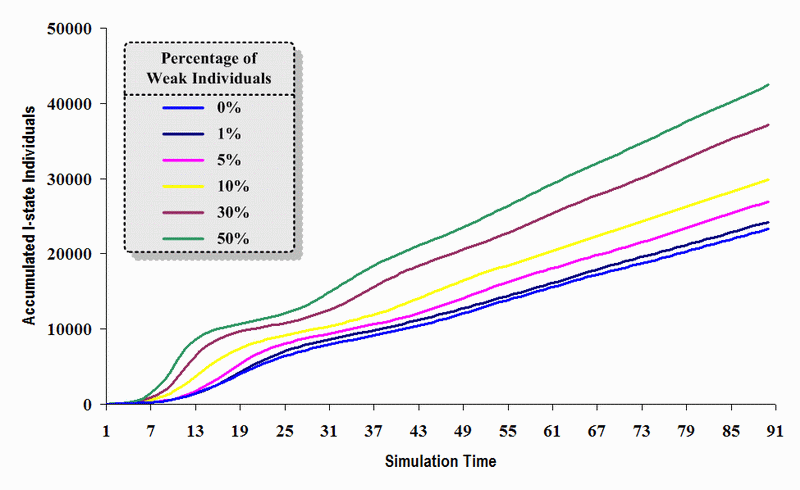
|
| Figure 16. A comparison of six sets of experimental results from the first simulation model (SWN#1) using different proportions of weak individuals in a simulation where one individual interacts with three randomly chosen individuals per time step. Each time grid shows the accumulated number of I (infectious) individuals in the proposed simulation model |
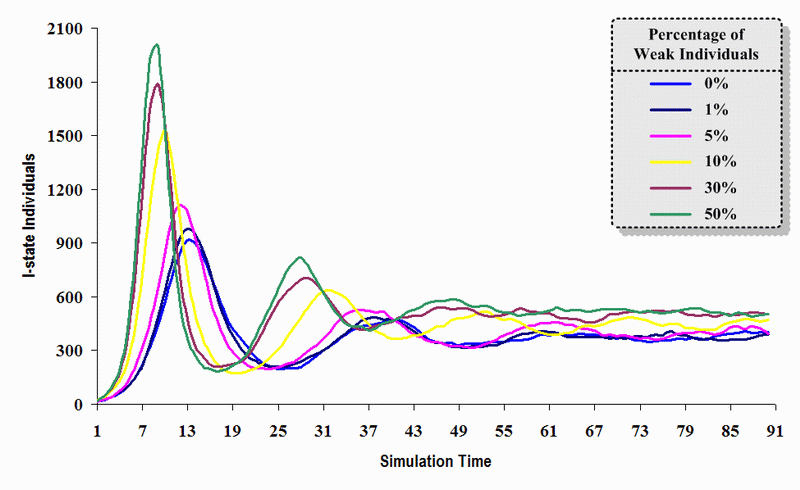
|
| Figure 17. A comparison of six sets of experimental results from the first simulation model (SWN#1) using different proportions of weak individuals in a simulation where one individual interacts with all of its connected individuals per time step. Each time grid shows the resulting number of I (infectious) individuals in the proposed simulation model per time step |
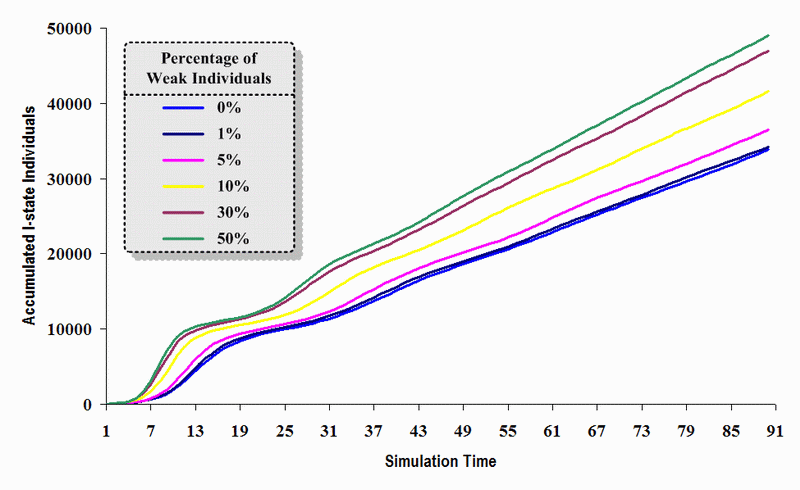
|
| Figure 18. A comparison of six sets of experimental results from the first simulation model (SWN#1) using different proportions of weak individuals in a simulation where one individual interacts with all of its connected individuals per time step. Each time grid shows the accumulated number of I (infectious) individuals in the proposed simulation model |
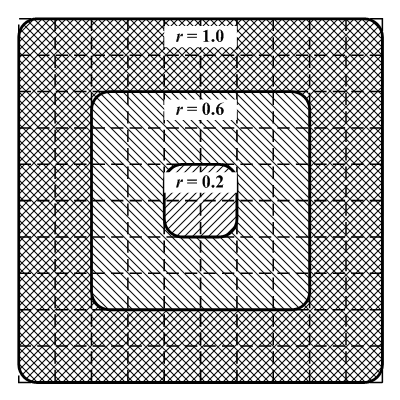
|
| Figure 19. Schematic diagram of regions covered by different radius parameters (r). |
| Table 5: Experimental results using different scattered radii of weak individuals with the six simulation models | ||||||||
| Simulation Model | SWN#1 | SWN#2 | SWN#3 | SWN#4 | SWN#5 | SWN#6 | ||
| Average accumulated number and standard deviation of infectious individuals produced by simulation model (Mean±Std) | Interactions with 3 connected individuals | Infection Rate | 0.3 | 0.33 | 0.33 | 0.33 | 0.33 | 0.33 |
| Distribution Radius 0.0 | 24109 ±482 | 12748 ±513 | 18220 ±509 | 22621 ±435 | 25745 ±382 | 27339 ±218 | ||
| Distribution Radius 0.2 | 24097 ±344 | 12854 ±415 | 18032 ±408 | 22813 ±603 | 25568 ±327 | 27084 ±346 | ||
| Distribution Radius 0.4 | 24346 ±591 | 12954 ±535 | 18264 ±510 | 22749 ±294 | 25451 ±499 | 27372 ±241 | ||
| Distribution Radius 0.6 | 23975 ±227 | 12706 ±364 | 18229 ±310 | 22555 ±356 | 25584 ±505 | 27490 ±279 | ||
| Distribution Radius 0.8 | 23849 ±405 | 12796 ±518 | 18641 ±311 | 22639 ±583 | 25301 ±452 | 27349 ±364 | ||
| Distribution Radius 1.0 | 24278 ±419 | 12993 ±329 | 18185 ±367 | 22948 ±459 | 25306 ±506 | 27274 ±414 | ||
| Experiment Results | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | ||
| Interactions with all connected individuals | Infection Rate | 0.05 | 0.2 | 0.2 | 0.2 | 0.1 | 0.1 | |
| Distribution Radius 0.0 | 34299 ±271 | 16359 ±375 | 30833 ±480 | 45426 ±296 | 35914 ±373 | 55003 ±233 | ||
| Distribution Radius 0.2 | 33817 ±307 | 16334 ±395 | 30790 ±450 | 45468 ±248 | 35791 ±327 | 54814 ±251 | ||
| Distribution Radius 0.4 | 34240 ±255 | 16321 ±498 | 31149 ±296 | 45683 ±335 | 35846 ±338 | 54982 ±310 | ||
| Distribution Radius 0.6 | 34065 ±391 | 16221 ±398 | 30964 ±223 | 45532 ±275 | 35690 ±441 | 54946 ±201 | ||
| Distribution Radius 0.8 | 34085 ±249 | 16408 ±360 | 31241 ±417 | 45432 ±330 | 35794 ±355 | 54948 ±297 | ||
| Distribution Radius 1.0 | 34525 ±299 | 16254 ±338 | 30888 ±375 | 45402 ±337 | 35910 ±210 | 54990 ±168 | ||
| Experiment Results | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | Insensitive Parameter | ||
| Conclusion: | As long as small-world phenomena exist and the average degree of separation does not change, the distribution patterns of weak individuals do not exert any influence on the contagion problem transmission dynamics of SWN models. | |||||||

|
| Figure 20. A comparison of six sets of experimental results from the first simulation model (SWN#1) using different scattered radii of weak individuals in a simulation where one individual interacts with three randomly chosen individuals per time step. Each time grid shows the resulting number of I (infectious) individuals produced by the proposed simulation model per time step |
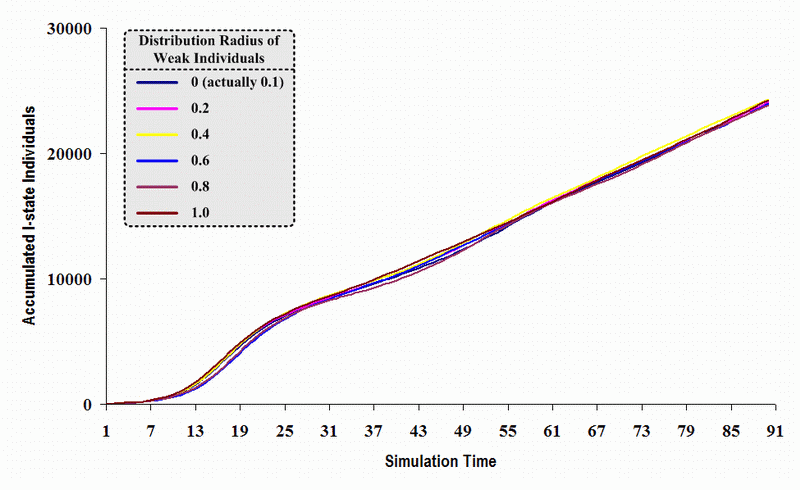
|
| Figure 21. A comparison of six sets of experimental results from the first simulation model (SWN#1) using different scattered radii of weak individuals in a simulation where one individual interacts with three randomly chosen individuals per time step. Each time grid shows the accumulated number of I (infectious) individuals produced by the proposed simulation model |
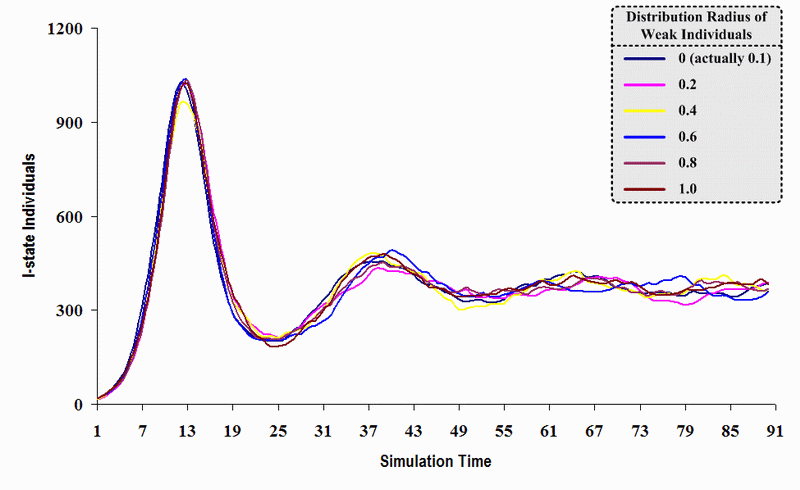
|
| Figure 22. A comparison of six sets of experimental results from the first simulation model (SWN#1) using different scattered radii of weak individuals in a simulation where one individual interacts with all of its connected individuals per time step. Each time grid shows the resulting number of I (infectious) individuals produced by the proposed simulation model per time step |
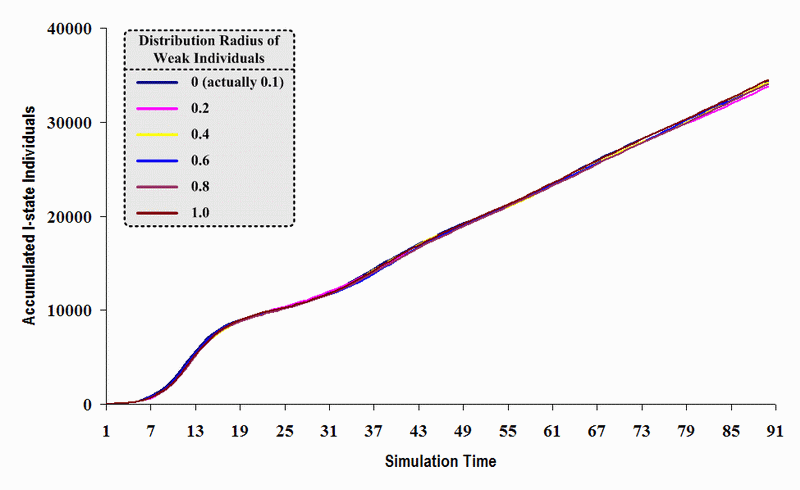
|
| Figure 23. A comparison of six sets of experimental results from the first simulation model (SWN#1) using different scattered radii of weak individuals in a simulation where one individual interacts with all of its connected individuals per time step. Each time grid shows the accumulated number of I (infectious) individuals produced by the proposed simulation model |
ALBERT R, Jeong H, and Barabási A-L (1999) Diameter of the World Wide Web. Nature, 401, pp. 130-131.
BARABÁSI A-L, Albert R, and Jeong H (1999) Mean-field Theory for Scale-Free Random Networks. Physica A, 272, pp. 173-187.
BARABÁSI A-L and Albert R (1999) Emergence of Scaling in Random Networks. Science, 286(5439), pp. 509-512.
BLACKMORE S (1999) The Meme Machine. Oxford: Oxford University press.
BOOTS M and Sasaki A (1999) "Small Worlds" and the Evolution of Virulence: Infection Occurs Locally and at a Distance. Proceedings of the Royal Society of London, Series B, 266(1432), pp. 1933-1938.
BRODIE R (1996) Virus of the Mind: The New Science of the Meme. Seattle, WA: Integral Press.
CHWE M S Y (2001) Rational Ritual: Culture, Coordination, and Common Knowledge. Princeton NJ: Princeton University Press.
COMELLAS F, Ozon J, and Peters J G (2000) Deterministic Small-World Communication Networks. Information Processing Letters, 76(1-2), pp. 83-90.
DEZSÖ Z and Barabási A-L (2002) Halting Viruses in Scale-Free Networks. Physical Review E, 65(5 Pt 2). 055103.
EDELETEIN-KESHET L (1988) Mathematical Models in Biology. Random House, New York.
ERDÖS P and Renyi A (1959) On the Evolution of Random Graphs. Publication of the Mathematical Institute of the Hungarian Academy of Science, 5, pp. 17-60.
FALOUTSOS M, Faloutsos P, and Faloutsos C (1999) On Power-law Relationships of the Internet Topology. Computer Communications Review, 29, pp. 251-263.
HUANG C Y, Sun C T, Hsieh J L, and Lin H (2004) Simulating SARS: Small-World Epidemiological Modeling and Public Health Policy Assessments. Journal of Artificial Societies and Social Simulation, 7(4), https://www.jasss.org/7/4/2.html.
KEELING M J (1999) The Effects of Local Spatial Structure on Epidemiological Invasions. Proceedings of the Royal Society of London, 266, pp. 859-867.
KERMACK W O and McKendrick A G (1927) Contributions to the Mathematical Theory of Epidemics. Proceedings of the Royal Society of London, Series A, 115, pp. 700-721.
KUPERMAN M and Abramson G (2001) Small World Effect in an Epidemiological Model. Physical Review Letters, 86(13), pp. 2909-2912.
LILJEROS F, Edling C R, Amaral L A N, Stanley H E, and Aberg Y (2001) The Web of Human Sexual Contacts, Nature, 411, pp. 907-908.
LYNCH A (1996) Thought Contagion: How Belief Spreads Through Society: The New Science of Memes. New York, NY: Basic Books.
MARSDEN P (1998) Memetics and Social Contagion: Two Sides of the Same Coin? Journal of Memetics - Evolutionary Models of Information Transmission, 2(2), pp. 171-185.
MEDINA A, Matta I, and Byers J (2000) On the Origin of Power-laws in Internet Topologies. ACM Computer Communications Review, 30(2), pp. 18-28.
MILGRAM S (1967) The Small World Problem. Psychology Today, 2, pp. 60-67.
MOORE C and Newman M E J (2000a) Epidemics and Percolation in Small-world Networks. Physical Review E, 61(5 Pt B), pp. 5678-5682.
MOORE C and Newman M E J (2000b) Exact Solution of Site and Bond Percolation on Small World Networks. Physical Review E, 62, pp. 7059-7064.
MORENO Y, Pastor-Satorras R, and Vespignani A (2002) Epidemic outbreaks in complex heterogeneous networks. European Physical Journal B, 26(4), pp. 521-529.
NEWMAN M E J and Watts D J (1999a) Renormalization Group Analysis of the Small-world Network Model. Physics Letters A, 263, pp. 341-346.
NEWMAN M E J and Watts D J (1999b) Scaling and Percolation in the Small-World Network Model. Physical Review E, 60(6 Pt B), pp. 7332-7342.
NEWMAN M E J (2000) Models of the Small World: A Review. Journal of Statistical Physics, 101, pp. 819-841.
NEWMAN M E J (2002) Spread of epidemic disease on networks. Physical Review E, 66 (1 Pt 2). 016128.
PASTOR-SATORRAS R and Vespignani A (2001) Epdiemic Spreading in Scale-Free Networks. Physical Review Letter, 86, pp. 3200-3203.
PASTOR-SATORRAS R and Vespignani A (2002) Epidemics and Immunization in Scale-Free Networks. In Bornholdt S and Schuster H G (eds.), Handbook of Graphs and Networks: From the Genome to the Internet, Wiley-VCH, Berlin.
SHANNON CE and Weaver W (1949) The Mathematical Theory of Communication. Urbana, IL: University of Illinois Press.
TSIMRING L S and Huerta R (2003) Modeling of Contact Tracing in Social Networks. Physica A, 325, pp. 33-39.
WANG X F and Chen G (2003) Complex Networks: Small-World, Scale-Free and Beyond. IEEE Circuits and Systems Magazine, First Quarter, pp. 6-20.
WATTS D J (1999) Small Worlds: The Dynamics of Networks between Order and Randomness. Princeton NJ: Princeton University Press.
WATTS D J and Strogatz S H (1998) Collective Dynamics of 'Small-world' Networks. Nature, 393(6684), pp. 440-442.
ZANETTE D H (2003) Models of Social Processes on Small-World Networks. AIP Conference Proceeding, 658, pp. 187-203.
ZEKRI N and Clerc J P (2001) Statistical and Dynamical Study of Disease Propagation in a Small World Network. Physical Review E, 64(5), 056115.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]