Günter Küppers and Johannes Lenhard (2005)
Validation of Simulation: Patterns in the Social and Natural Sciences
Journal of Artificial Societies and Social Simulation
vol. 8, no. 4
<https://www.jasss.org/8/4/3.html>
For information about citing this article, click here
Received: 02-Oct-2005 Accepted: 02-Oct-2005 Published: 31-Oct-2005
 Abstract
AbstractThe validation problem is an explicit recognition that simulation models are like miniature scientific theories.
(Kleindorfer and Ganeshan 1993, 50)
Validation of simulation models is thus the same as (or least analogous to) validation of theories. (Troitzsch 2004)
Assessment of transformational accuracy (verification), assessment of behavioral or representational accuracy (validation), and independently assuring sufficient credibility (certification) of complex models and simulations pose significant technical and managerial challenges. (Balci 2003)
three general circulation models (…) were used for parallel integrations of several weeks to determine the growth of small initial errors. Only Arakawa's model had the aperiodic behaviour typical of the real atmosphere in extratropical latitudes, and his results were therefore used as a guide to predictability of the real atmosphere. This aperiodic behaviour was possible because Arakawa's numerical system did not require the significant smoothing required by the other models, and it realistically represented the nonlinear transport of kinetic energy and vorticity in wave number space. (Phillips 2000, xxix)
"It is my goal to take the best models and compute the last hundred thousand years. And if they succeed to simulate the rapid changes, ice-ages, that occurred in the past, yes, then I have hundred percent confidence" (transcript from interview).
|
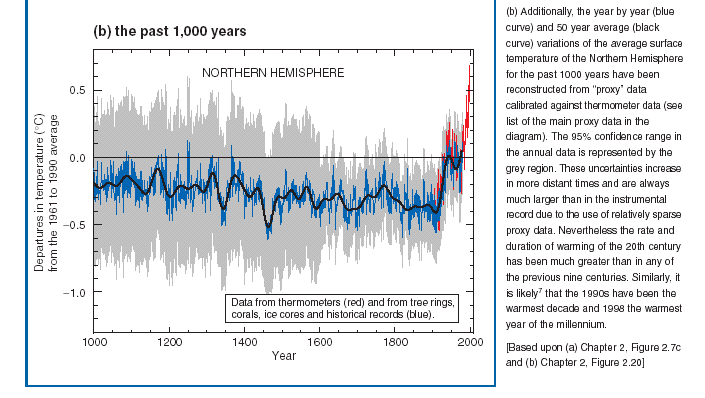
| Figure 1. Mean global temperature, observed and estimated, from IPCC Assessment Report |
The shaft shows a good fit between observed and retrospectively predicted data. This fit is taken to validate the prediction — the substantial rise of the mean temperature.
There has never in the history of Economics and Management Science been a correct forecast of macroeconomic or financial market turning points or turning points in retail market sales. I know less about sociology, but my reading of the journals in that field suggests that no sociological theory offers systematically well validated predictions, either. (Moss 2003)
|
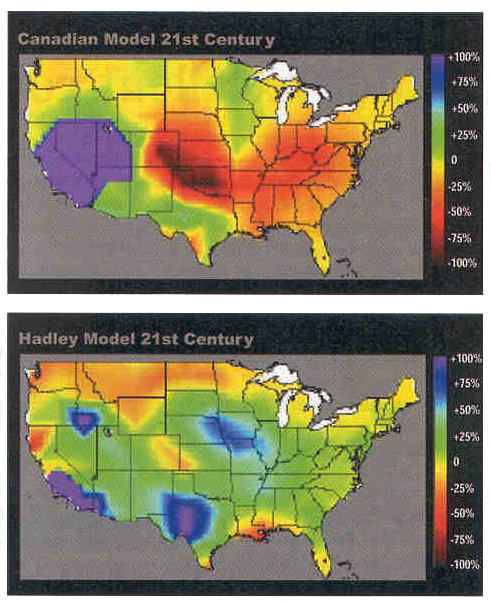
| Figure 2. Predicted precipitation in US according to Canadian (upper part) and UK (lower part) simulation model |
ALLEN, M. R., P. A. Stott, et al. (2000). "Quantifying the uncertainty in forecasts of anthropogenic climate change." Nature 407: 617-620.
ARAKAWA, A. (1966). "Computational Design for Long-Term Numerical Integration of the Equations of Fluid Motion: Two-Dimensional Incompressible Flow. Part I." J. Comp. Phys. 1: 119-143.
ARAKAWA, A. (2000). A Personal Perspective on the Early Years of General Circulation Modeling at UCLA. General Circulation Model Development. D. A. Randall. San Diego, Academic Press: 1-66.
AXELROD, R. (1997). Advancing the Art of Simulation in the Social Sciences. Simulating Social Phenomena. R. Conte and R. Hegselmann. Berlin, Springer: 21-40.
BALCI, O. (2003). Verification, Validation, and Certification of Modeling and Simulation Applications. Proceedings of the 2003 Winter Simulation Conference. Piscataway, NJ, IEEE: 150-158.
CONTE, R., B. Edmonds, et al. (2001). "Sociology and Social Theory in Agent Based Social Simulation: A Symposium." Computational and Mathematical Organization Theory 7(3): 183-205.
EPSTEIN, J. M. and R. Axtell (1996). Growing Artificial Societies. Cambridge, MIT Press.
FRIEDMAN, M. (1953). Essays in Positive Economics. Chicago, University of Chicago Press.
FULLER, S. (1995). "Symposium on social psychological simulations of science. On Rosenwein's and Gorman's simulation of social epistemology." Social Epistemology 9(1): 81-85.
GALISON, P. (1996). Computer Simulations and the Trading Zone. The Disunity of Science: Boundaries, Contexts, and Power. P. Galison and D. J. Stump. Stanford, Calif., Stanford Univ. Press: 118-157.
GILBERT, G. N. and K. G. Troitzsch (1999). Simulation for the Social Scientist. Buckingham, Open University Press.
HALES, D., J. Rouchier, et al. (2003). "Model-to-Model Analysis." Journal of Artificial Societies and Social Simulation 6(4).
HALPIN, B. (1999). "Simulation in Sociology." American Behavioral Scientist 42(10): 1488-1508.
HEGSELMANN, R., Ed. (1996). Modelling and Simulation in the Social Sciences from the Philosophy of Science Point of View. Dordrecht, Kluwer.
HUMPHREYS, P. (1991). Computer Simulations. PSA 1990. Fine, Forbes and Wessels. East Lansing, Philosophy of Science Association. 2: 497-506.
KERR, R. A. (2000). "Dueling Models: Future U.S. Climate Uncertain." Science 288: 2113.
KLEINDORFER, G. B. and R. Ganeshan (1993). The Philosophy of Science and Validation in Simulation. Proceedings of the 1993 Winter Simulation Conference. G. W. Evans, M. Mollaghasemi, E. C. Russell and W. E. Biles: 50-57.
KÜPPERS, G. and J. Lenhard (2005). "Computersimulationen: Modellierungen zweiter Ordnung." Journal for General Philosophy of Science, to appear.
LEHMAN, R. S. (1977). Computer Simulation and Modeling : an Introduction. Hillsdale, NJ, Erlbaum.
LEWIS, J. M. (1998). "Clarifying the Dynamics of the General Circulation: Phillips's 1956 Experiment." Bull. Am. Met. Soc. 79(1): 39-60.
LORENZ, E. (1967). The Nature of the Theory of the General circulation of the Atmosphere. Geneva, World Meteorological Organization WMO, Technical Paper No. 218, 115-161.
MACY, M. W. and R. Willer (2002). "From Factors to Actors: Computational Sociology and Agent-Based Modeling." Annual Review of Sociology 28: 143-166.
MORRISON, M. and Morgan, M. S. (1999). Models as autonomous agents. Models As Mediators. Perspectives on Natural and Social Science. M. S. Morgan and M. Morrison. Cambridge, Cambridge University Press: 38-65.
MOSS, S. (2003). "Simulation and Theory, Simulation and Explanation. Contribution to the SIMSOC mailing list." www.jiscmail.ac.uk/archives/simsoc.html 14 November 2003.
NAYLOR, T. H. and J. M. Finger (1967). "Verification of Computer Simulation Models." Management Science 14: B92-B101.
PHILLIPS, N. (1956). "The General circulation of the Atmosphere: a Numerical Experiment." Quat. J. R. Met. Soc. 82(352): 123-164.
PHILLIPS, N. (2000). Foreword. General Circulation Model Development. D. A. Randall. San Diego: xxvii-xxix.
ROHRLICH, F. (1991). Computer Simulation in the Physical Sciences. PSA 1990. F. Forbes, Wessels. East Lansing, Philosophy of Science Association. 2: 507-518.
ROSENWEIN, R. and M. Gorman (1995). "Symposium on social psychological simulations of science. Heuristics, hypotheses, and social influence: a new approach to the experimental simulation of social epistemology." Social Epistemology 9(1): 57-69.
SARGENT, R. G. (1992). Validation and Verification of Simulation Models. Proceedings of the 1992 Winter Simulation Conference. J. J. Swain, D. Goldsman, R. C. Crain and J. R. Wilson. Arlington, Virginia: 104-114.
TROITZSCH, K. G. (2004). Validating Simulation Models. Networked Simulations and Simulated Networks. G. Horton. Erlangen and San Diego, SCS Publishing House: 265-270.
WEART, S. (2001). Arakawa's Computation Trick, American Institute of Physics. 2001, http://www.aip.org/history/climate/arakawa.htm.
WINSBERG, E. (2003). "Simulated Experiments: Methodology for a Virtual World." Philosophy of Science 70: 105-125.
ZEIGLER, B. P. (1976). Theory of Modelling and Simulation. Malabar, Krieger.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]