Stephen Younger (2005)

Reciprocity, Sanctions, and the Development of Mutual Obligation in Egalitarian Societies

Journal of Artificial Societies and Social Simulation vol. 8, no. 2
<https://www.jasss.org/8/2/9.html>

To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary

Received: 26-Oct-2004    Accepted: 17-Dec-2004    Published: 31-Mar-2005

Abstract

Discrete agent simulation was used to study several models of reciprocity and sanctions in a model egalitarian society. We found that mutual obligation between agents was maximized for indiscriminant sharing, the same condition that has been observed in several traditional cultures. Alternate sharing strategies, including ones based on kinship or sharing with those who share in return, reduced mutual obligation. When theft and sanctions were introduced into the simulations, we found that mutual obligation was maximized when individual norms were strong, i.e. when there was little tolerance to theft. Collective sanctions, represented by the ostracism of non-normative agents, produced levels of mutual obligation comparable to the case of strong individual norms, but with significant risk of population collapse. The probability of long term survival was highest when tolerance to transgressions was either very low or very high and we propose that this may be one reason for the similarity of normative systems across diverse egalitarian cultures.

Keywords:

Reciprocity, Sanctions, Egalitarian Societies

Introduction

1.1

Gift giving was a ubiquitous feature in egalitarian societies around the world. (Gurven 2003) At the individual level, generosity was a means of establishing and maintaining personal reputation; in aggregate, it created a network of mutual obligation among the members of a population, an essential ingredient in social cohesion. Societies living in resource rich environments, in which sharing was not essential for survival, offer a particularly vivid illustration of the role of gift giving in maintaining the social fabric. For example, on many islands of the South Pacific it was possible for an individual or family to secure the basic needs of life with only a few hours of foraging and fishing per day, yet sharing was an important part of such cultures. Bliege Bird and Bird (1997) found that unmarried males on Mer Island shared hard-to-obtain turtle meat with little or no consideration given to kinship, social groups, or the past generosity of the recipient. Indiscriminant generosity enhanced the individual prestige of the giver, useful in securing a mate and in resolving future land disputes. Kent (1993), in her observations of the Kutse, noted that "sharing is a mechanism that structures, maintains and perpetuates social relationships … highly egalitarian societies use sharing to create social solidarity." Even beyond the biological imperative to mate, human beings desire companionship and wish to believe that others will assist them in times of need. The issue is how to optimize the experience of living in a group, of balancing cost versus benefit. An extensive discussion of the role of gift exchange is given by Mauss (1990 [1950]).

1.2

Not all behavior in gift-giving cultures was altruistic. Peterson (1993) proposed the concept of "demand sharing" wherein an individual was induced to part with objects that he or she would otherwise have preferred to keep. Blurton Jones (1984) went further with his notion of "tolerated theft" wherein an individual would not expend the effort to resist the theft of an object or recover it if the cost of confronting the thief was greater than the value of the object. However, there is usually a limit to tolerance and past a certain point sanctions are applied against those who refuse to share, persist in theft, or commit other transgressions. The remarkable uniformity in sanctions applied by egalitarian peoples around the world (Boehm 1999) suggests that there might be an underlying reason related to the structure and dynamics of simple societies.

1.3

There are several challenges in evaluating such theories. First, the two quantities under discussion are qualitatively different in nature. One can measure food distribution by caloric value, but it is much harder to put quantitative values on social cohesion. How does one determine whether the "social cost" of recovering an item is greater than its economic value? Second, while there is much anecdotal information on sanctions, there has been no systematic study of the consequences of not abiding by behavioral rules in gift-giving societies. If social cohesion does indeed depend on a network of reciprocity, what level of non-normative behavior can be tolerated before the breakdown of such cohesion? What is the advantage, if any, of tolerance schemes such as demand sharing and tolerated theft over strict individual enforcement of accepted norms? Finally, what is the relative efficacy of individual vs. group sanctions in controlling damage done by non-normative behavior within a population?

1.4

We investigate these questions by means of a discrete agent simulation of a simple artificial society designed to mimic some of the essential features of hunter-gatherer cultures. We compare results from several alternative models for sharing with the observations of Bliege Bird and Bird (1997), Kaplan and Hill (1985), and others. Following Kent's (1993) hypothesis that sharing creates a network of mutual obligation within the society, we study how this mutual obligation varies with the tolerance level for theft and with the imposition of group sanctions. By running the simulation over many generations of agents, we show that populations imposing strong individual sanctions on non-normative agents can obtain high levels of gift-generated social cohesion. In the absence of strong individual sanctions, group sanctions can improve a bad situation, but at some risk for the survival of the population.

1.5

Simulations offer a useful tool for the evaluation of social theories in that their parameters are entirely under the control of the investigator. Sometimes the members of a traditional society lack the analytical or communications skills required to explain the reasons for their behavior. What if the norms were different? How would that affect key aspects of social performance? While simulations certainly do not replace detailed field studies, they provide a means for examining the effect of variations from observed patterns of behavior. We use this approach to evaluate several different models of reciprocity in a simple model society.

1.6

Simulation has been applied to a number of topics related to reciprocity in simple societies. Jaffe (2002) studied the benefits of altruistic sharing. Younger (2003) added theft in studies of reciprocity in several simple social structures. Castelfranchi et al (1998) and Younger (2004) simulated the effect of communicating normative reputation on social performance. In this paper we extend these studies to include the effect of individual and collective sanctions in a model society of agents practicing positive and negative reciprocity.

1.7

The next section lays out the basic methodology used in our simulation or reciprocity and social cohesion. We then present the results of simulations of various models of reciprocity and compare them to the observations of Bliege Bird and Bird (1997) and Kaplan and Hill (1985). Sanctions are considered in the following section. A discussion of the principal conclusions of the work, along with suggestions for future studies, ends the paper.

Methodology Used for the Simulation of Positive and Negative Reciprocity

2.1

We modeled an isolated population by placing 100 agents on a 20 × 20 square grid containing five fixed sources of food. The initial population was divided equally between male and female agents and between agents who shared food and those who stole food. Agents had a finite lifetime and could reproduce, as discussed below. Unless otherwise noted, normative character was permanent, so that sharing agents did not steal and stealing agents did not share, regardless of their experiences with one another.

2.2

Each of the five food sources had an initial allocation of 100 points and was replenished at a rate of 20 points per timestep. Since each agent required one food point per timestep, this meant that an average population of 100 agents could be sustained. Agents had the ability to sense food sources from a distance of five squares in each direction. This finite sensing range prevented them from seeing the entire landscape in a single view and required them to move about to search for a food source that was in supply. When an agent sensed a food source it recorded in its personal memory the location and the amount of food present.

2.3

An agent's need for food was increased by one unit per timestep and was decreased by the number of food units consumed. An agent died and was removed from the population if its need for food exceeded 200 units. Agents lived a maximum of 4000 timesteps, at which point they died of old age. To avoid having a large number of agents simultaneously die of old age, the age of the agents in the initial population was uniformly distributed over the range 0 - 2000. At the beginning of the simulation the agents were randomly scattered across the landscape. Simulations were run for 40,000 timesteps or ten agent lifetimes.

2.4

Agents were divided into two social groups. Being in a social group had the advantage that an agent received a preference in sharing from other members of the group. Other features of social groups will be discussed below.

2.5

The sequence of agent decisions was as follows: If the need for food was greater than 100 points, 50% of the maximum, then the agent tried to find and consume food. If the need for food was less than 100 points, then the agents explored the landscape and noted which food sources had food for future use. When they encountered another agent, they had the options of mating, sharing or stealing food, and communicating information on the normative reputation of other agents.

2.6

In the eating routine an agent first checked to see if it was carrying food. If so, it consumed that food. If the agent was collocated with a food source, then it consumed food from that center and, if there was any left over, it collected up to a maximum of 100 units to take along on its travels. If the agent was not carrying any food and it was not at a food source, it searched its memory for the nearest food source at which it remembered that food was present. It then moved one square in the direction of that food source. If the agent did not know the location of any food source that was in supply, it set out in a random direction in hopes of finding one. The boundaries of the landscape were reflective, so that when an agent reached an edge it chose another random direction of movement that would keep it on the grid.

2.7

When two agents occupied the same location, and when one of them was carrying food, there was the opportunity for sharing or theft to occur. If the carrying agent was a sharing agent, it shared its food equally among the other agents occupying that square. Agents in the same group as the sharing agent received a full share. (A "share" is here defined as the total amount carried divided by the number of collocated agents.) Agents not in the same group as the sharing group received a half-share. This difference gave an advantage to membership in the group with the largest number of sharing agents. If a stealing agent occupied the same square as an agent carrying food then the stealing agent stole all of that food. Note that there was no explicit cooperation involved in the acquisition of food — individual agents collected it and, if they had a sharing character, they distributed it to others.

2.8

An interaction matrix, imx, tallied the history of interactions between the agents. When agent j shared with agent k, the amount of food shared was added to matrix element imx(k,j); when agent m stole from agent n, the amount stolen was subtracted from imx(n,m). The non-symmetric interaction matrix represented a form of normative reputation for the agents: positive interactions (sharing) enhanced the reputation of an agent whereas negative interactions (stealing) decreased its reputation. Victims did not associate their assailant with a group — there was no labeling in the simulation. Also, there was no sense of personal pride or guilt in the simulation — diagonal elements in the interaction matrix element, corresponding to self-opinion, were set to zero.

2.9

Normative reputation was communicated between collocated agents by averaging their interaction matrix elements for all of the other agents. For example, agents j and k, upon meeting, would each derive a new reputation for agent n via the average imx (j,n)_new = imx (k,n)_new = ¹/₂ (imx (j,n)_orig + imx (k,n)_orig). In this manner agents would obtain information on the normative character of other agents without having personal experience of those other agents. The rationale for averaging is that agents who had no experience with an agent would have no opinion and would not be affected as much by sharing or theft as the agent who directly experienced that behavior. Conversely, the agent who did have personal experience might temper its opinion based on the lack of a view held by its communicant. Note that sharing agents always had zero or positive reputations and stealing agents always had zero or negative reputations. The net reputation of an agent within the total population, obtained by summing all of the other agents' opinions of that agent, was simply the total amount shared or stolen by that agent. The communication of normative reputation constituted a type of praise of sharing agents and ridicule of stealing agents and simulated gossip, an important factor in the functioning of traditional societies. No memory of who told what to whom was maintained, nor was there any possibility that an agent could keep an action secret from the other agents since at minimum the victim of theft or the recipient of generosity would know of the interaction.

2.10

Female agents chose a mate upon reaching the minimum reproductive age of 1000 time units. They selected the unmarried male with whom they had the highest interaction matrix element i.e. the male with the best reputation. A female could refuse to mate with a male, or a male could refuse the offer of mating, if the interaction matrix element linking them to the best potential mate was less than a tolerance parameter called toltheft. Since sharing added to interaction matrix elements and theft reduced them, a negative toltheft allowed agents who had stolen to secure a mate. Thus toltheft was related to the amount of theft that was tolerated before sanctions, in this case a refusal to mate, were applied. It could also be interpreted as the maximum amount of "forgiveness" that would be afforded a non-normative agent. A positive toltheft required an agent to have shared at least that amount in order to be accepted as a mate. Mating was monogamous and the female was required to collocate with her husband for the remainder of his life. If either mate died, the survivor was free to choose another mate.

2.11

Mates aged between 1000 and 3000 timesteps could produce offspring. The probability of conception was 0.004 per timestep, chosen to allow a population to survive but not overpopulate the landscape given the limited food resources and the finite lifetime of the agents. Offspring appeared immediately, with no gestation period, and were assigned the normative character (sharing or stealing) and group identification of their mother. (Other models for the assignment of normative character were considered and will be discussed below.)

2.12

Consistent with the role of sharing in developing and maintaining social cohesion within traditional societies, we defined the mutual obligation factor as the sum of interaction matrix elements linking agents in a defined subpopulation. In a population of mainly sharing agents, the mutual obligation factor was positive. If there were a large number of stealing agents, the obligation factor was negative.

2.13

The code used in this paper consisted of about 7000 lines of Visual Basic and is a simplification of the one described in Younger (2003) and Younger (2004). A typical run took between one and two hours on a 3 GHz desktop computer. We have performed extensive studies to examine the sensitivity of the results to the specific parameters used here and find that, over a very wide range, the qualitative results are robust against the number of agents, the size of the landscape, agent lifetime, etc.

Simulation of Models of Reciprocity and Comparison to the Foraging Culture on Mer Island

3.1

We first investigate how different types of sharing compare to observations made by Bliege Bird and Bird (1997) for the Murray Islanders. The Murray Islands are a trio of small islands located in the Torres Strait off the northern coast of Queensland, Australia. Well into the 20^th century, these islanders practiced a subsistence culture based on gathering, gardening, and fishing. Sharing was esteemed as a high social value even though food was plentiful and there was often no imperative to share outside of the family. Beckett (1987) describes the culture of the Torres Strait islanders and provides references to earlier ethnological studies.

3.2

Bliege Bird and Bird (1997) compared the predictions of four sharing models against their observations of the inhabitants of Mer Island, the principal residence location within the Murrays:

• Kin selection in which sharing was focused on the family of the giver
• Tolerated theft in which the cost of retaining food against a request is greater than the value of the food to the owner
• Risk-reduction reciprocity in which sharing was focused on those who shared in return
• Trade in which hunters controlled the distribution of prey for their own benefit.

They focused on the sharing of hard-to-obtain turtle meat as a quantity that was readily measurable but not required for essential nutrition. The results of their study indicated a pattern of indiscriminant sharing that took little or no account of kinship or social hierarchy. In fact, they found that the frequency of sharing was inversely proportional to the distance separating giver and receiver — whoever happened to be nearby received a share of the meat.

3.3

One explanation for indiscriminant sharing is that it was done to build a sense of prestige for the individual and to develop social cohesion within the group. Via gossip, personal generosity became known throughout the small population, partially obviating the need to focus it on the families of prospective mates or on others who might provide some future advantage. By repeated gift-giving of turtle meat and other items, individuals became bound to one another in a complex web of mutual obligation, cementing the society and maintaining a strong egalitarian ethic.

3.4

We hypothesize that the pattern of sharing observed on Mer maximizes the mutual obligation within the population. To test this hypothesis we constructed four variants of our model in which agents either shared or did not share but did not steal. (Non-sharers represented "free riders" who benefited from the generosity of others at no cost to themselves. The effect of theft will be considered in the next section.) The variants studied were:

• Indiscriminant sharing in which all agents shared with all other agents
• Family sharing in which all agents shared but only with members of their immediate family (mate, mother, father, sibling, or offspring)
• Household sharing in which all agents shared but only with the head of a household
• Reciprocal sharing in which agents only shared with other sharing agents.

In the last case, the initial population was evenly divided between agents who shared and those who did not share. All other parameters of the modified simulation were the same as described in the above section on general methodology. Twenty runs were performed for each case.

Table 1: Effect of different models of sharing on the total mutual obligation within the artificial society
Model for Sharing	Mutual Obligation	Standard Deviation
Indiscriminant Sharing	330	58
Share Only with Head of Household	160	21
Share Only Within Family	190	21
Share Only With Other Sharing Agents*	210	20
* Only six of the twenty runs in this case had a population that survived until the end of the run. All other models, had a non-zero population at the end of every run.

3.5

The results of the simulations are given in Table 1 and are compared with three of the observations of Bliege Bird and Bird (1997) in Table 2. We found that mutual obligation for the total population was maximized for indiscriminant sharing, just as was observed on Mer Island. Specifically, mutual obligation was higher in the case of indiscriminate sharing (330) than it was for preferential sharing within the family of the giver (190), when the unit of division was the household rather than the individual (160), or when agents only shared with other sharing agents (210). Sharing was not required on this resource rich island and if the motivation for the giver was a near-term return on investment then one would expect his generosity to be focused on those who would be most likely to provide a future benefit. Indiscriminant generosity, by contrast, optimized a network of mutual obligation which could be drawn upon should some need arise in the future.

Table 2: Comparison of the simulation results with the observations of the Mer Islanders. The first three columns are taken from Bliege Bird and Bird (1997)
	Observations of the Mer Islanders			Simulation
Model	Prediction	Result		Rule	Result
Kinship	Households with no patrilineal kin nearby should send shares to kin living farther away rather than share with nonkin neighbors	Not supported		Share only within family	Mutual obligation lower than for indiscriminant sharing
Tolerated Theft	Larger households should receive larger portions of turtle meat from the distributing household at each butchery event	Supported		Share with head of household only independent of size of family	Mutual obligation lower than for sharing with each individual
Risk-reduction Reciprocity	Households that never hunt should never receive shares	Not supported		Do not share with non-sharing agents	Mutual obligation lower than for indiscriminant sharing

3.6

Kaplan and Hill (1985) observed similar sharing patterns among the Ache of Paraguay. Among their findings were that food sharing did not follow an inverse relationship with kinship distance, as would be expected for sharing among kin, and that those who shared did not receive more in return. However, they found that hunters consumed less of their own kills than they shared with others, consistent with indiscriminant sharing but conflicting with a prediction based on tolerated theft. On the other hand, they write that "an additional impetus to sharing might be that others would attempt to take the food forcibly if it were not shared," which is consistent with an interpretation of tolerated theft or demand sharing.

3.7

Hence, where comparisons between simulations and field observations are possible, both the Mer Islanders and the Ache display sharing behavior consistent with the maximization of mutual obligation. While this was suspected, it was not obvious before the simulations were run since it was possible that preferential sharing within a family unit could have resulted in enhanced survival of family members, more opportunities for procreation, and a higher mutual obligation. This phenomenon was observed in our earlier work (Younger 2003) where we found that clustering in family units enhanced the opportunity to share and increased the probability that an agent would survive into old age.

3.8

In human society it is likely that several or all of the competing theories of sharing are simultaneously active, their relative importance depending on details of the culture and the environment. Hence, in a locale where protein input is heavily dependent on large-game, one would expect that risk reduction reciprocity might play a greater role than in a case where protein was reliably acquired by individuals. It would be interesting to study sharing vs. the size of the package to be shared; asynchrony of hunting success could play a role in the motivation for sharing and the subsequent development of mutual obligation within the society.

Results for the Simulation of Sanctions and Comparison to Hunter-Gatherer Societies

4.1

In the previous section we examined the role of sharing in a society in which all agents shared or one in which some agents shared and some agents did not share. In this section we examine the role of sanctions in a population where some agents shared and some agents stole. Stealing was a specific act, rather than the absence of an act and, in conjunction with sharing, served to highlight contrasting normative character in the agent population, an important element in deciding the imposition of sanctions. Stealing food provided a short term benefit to non-normative agents at the expense of a long term disadvantage in finding a mate and, ultimately, rejection or ostracism from social groups. Sharing reduced the food available to the sharer, a near term disadvantage, but provided a long term advantage in securing a mate and in insuring group membership, which in turn enabled it to receive larger shares from other members of the group. We study the effect of several types of sanctions on social performance, emphasizing the role of those sanctions on the maintenance of mutual obligation within the society.

4.2

Sanctions are applied when an individual crosses a threshold in the violation of accepted norms of behavior. Not every offense is punished, and the degree of punishment is usually adjusted to fit the magnitude of the transgression. For example, theft of easily replaced food would not be punished, if it were punished at all, with the same vigor as would murder. Put in terms of tolerated theft, the social cost for punishment of minor transgressions would be greater than the value of the object stolen. However, a persistent thief could accumulate a sufficient negative opinion within the group that sanctions of some form might be applied. It is both the magnitude and the frequency of transgression that determines the imposition of sanctions.

4.3

The most commonly applied sanction in traditional egalitarian societies was ridicule. Verbal criticism could be vicious and could extend over very long periods. As a next stage in individual sanctions, a person might refuse to share with someone for whom they held a negative opinion. In extreme cases, members of a band or tribe could agree on stronger measures, including ostracism or even execution. In harsh climates, such as prevail in the artic, ostracism from the group was tantamount to a death sentence. In more benign climates, ostracism had the effect of social isolation. On an island where the population numbered in the few hundreds and where escape was difficult, ostracism from all social groups was a heavy penalty. Crimes for which ostracism might be applied include wife-stealing, murder and, as in our simulations, persistent theft and/or refusal to share.

4.4

Sanctions were not the only means of dealing with bad actors in traditional societies. A positive response for a victim of abuse was to simply move to another group, away from past bad actors. This was common in many societies in which several bands lived in close proximity to one another and in which bonds of kinship extended across band boundaries. Even the smallest islands usually had several distinct social groups.

4.5

We studied the effect of sanctions within a gift-giving society via four scenarios referred to as Baseline, Transfer, Rejection, and Ostracism. In the Baseline scenario, no change of group affiliation was permitted nor was ostracism an option. Agents were born into a group and remained associated with that group for their entire lives. (Recall that in our simulations there are only two groups to which an agent might belong.) In the Transfer scenario, an agent changed affiliation from its existing group to the other group when the sum of interaction matrix elements connecting it to the members of the other group exceeded twice the sum for its present group. The twofold threshold was intended to prevent changes based on small differences in affection and so represented a degree of conservatism regarding group affiliation. (We investigated other thresholds for group change ranging from none to ten times. The results were qualitatively similar to those reported here, though at very high thresholds fewer transfers were observed.) In the Rejection scenario, the receiving group had the option of rejecting the applicant if the sum of the group members' interaction matrix elements for the applicant was below the variable tolerance level toltheft. In the Ostracism scenario, an agent was ostracized from its current group if the sum of interaction matrix elements connecting it to that group fell below toltheft. Once an agent became ostracized from one group it could apply to the other group for membership. If it was rejected from that group, it became an ostracized agent. An ostracized agent could not mate with members of a group and members of groups did not share with it. Since interaction matrix elements were reduced only by theft, only non-normative agents faced ostracism. These effects were cumulative so that the Rejection scenario included the ability to transfer group affiliation and the Ostracism scenario included the ability to transfer group affiliation and the opportunity for groups to reject applicants.

4.6

Since toltheft represented the threshold at which the social cost of responding to non-normative behavior fell below the value of the goods stolen, toltheft = 0 implied that there was no tolerance to theft — a single stealing event permanently labeled the offender as subject to sanctions. The more negative the value of toltheft, the more theft was tolerated before the transgressor faced individual or group sanctions.

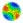
Figure 1. Percentage of runs where one, both, or neither subpopulation of normative and non-normative agents survive until the end of the run. Note that for toltheft = -1000000, no sanctions were ever applied to non-normative agents, so we present only the results of the Baseline and Transfer scenarios

4.7

Figure 1 shows the survival probability of normative and non-normative subpopulations for three values of toltheft: 0, -20, and - 10⁶. Fifty runs were done for each case. For toltheft = - 10⁶, the tolerance to theft was so great that no agent could accumulate enough points to cross the threshold beyond which it would suffer rejection or ostracism. Whereas normative agents had to find their own food at food sources or be the beneficiaries of sharing from others, stealing agents found their own food, could accept sharing, and could forcibly take the quantity held back by the sharer. With no inhibition to mating with demonstrated non-normative agents, the short-term advantage of theft was retained in the long term. Matrilineal inheritance of normative character then produced a mainly non-normative population.

4.8

The reverse situation held when toltheft was set to zero. In this case, individual agents had no tolerance for theft so that once an agent displayed its non-normative character by stealing it was excluded from the pool of potential mates. The result was that the non-normative population disappeared within two or three generations of the start of the simulation. Sharing agents paid the short term cost of shared food for the long term benefit of acquiring a mate, a form of delayed reciprocity. Indiscriminant sharing makes sense since at the time of sharing the sharer did not know its ultimate mate and thus could not focus generosity on that agent or its family. When individuals had little tolerance for transgressions then collective sanctions were unnecessary.

4.9

The value toltheft = -20 represented an interesting middle ground. In some of the runs the small tolerance to theft in mate selection resulted in the rapid disappearance of non-normative agents. In other cases, the short-term benefits of theft resulted in the disappearance of the normative population, however the resulting non-normative population never survived for more than a few generations since persistent theft reduced interaction matrix elements and prevented mating. About half of the runs with toltheft = -20 resulted in total population collapse by the end of the run. An entirely normative population could survive with toltheft = -20, as could a mixed population of normative and non-normative agents, but not one consisting entirely of non-normative agents.

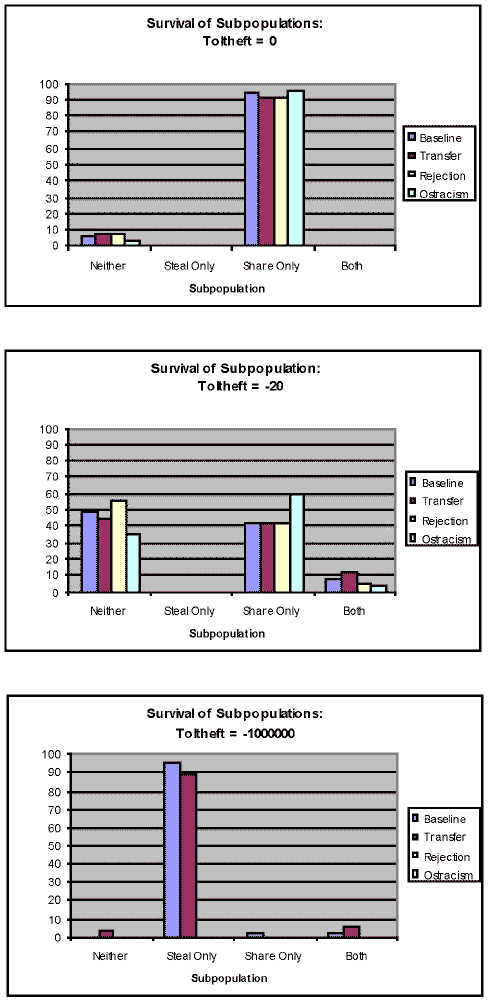
Figure 2. Left: Probability of survival for normative and non-normative subpopulations as a function of toltheft, the tolerance to theft. Right: Percent probability of collapse for the total population. Here toltheft = 0 implies zero tolerance to theft and toltheft = -120 implies a large tolerance to theft. All curves were computed for the Baseline scenario

4.10

We further explored this effect by running the Baseline scenarios for several values of toltheft from 0 to -120. The results are shown in Figure 2. Near toltheft = 0, only normative populations survived until the end of the run. For the Baseline scenario, the probability of total population collapse increased as toltheft decreased until, at about toltheft = -60, the tolerance level became sufficient to enable a completely non-normative population to be sustained. Thereafter the probability of collapse decreased until, at very large tolerance levels, an entirely non-normative population survived over 90% of the time. This is an intriguing result, suggesting that there is a band of tolerance toward non-normative behavior that is inconsistent with the long term survival of a population. The population survived if it was either very intolerant of transgressions or very tolerant, but not in between. Of course, our matrilineal model for the inheritance of normative character is much simpler than what happens in real society, but one might posit that other schemes for the establishment of normative character, such as learned normative behavior, might produce similar results. (We will discuss variations on the matrilineal model below.) If this is true, then it would point to a set of necessary normative conditions for the survival of an egalitarian population and might help explain why disparate egalitarian societies practice similar modes of sanctioning.

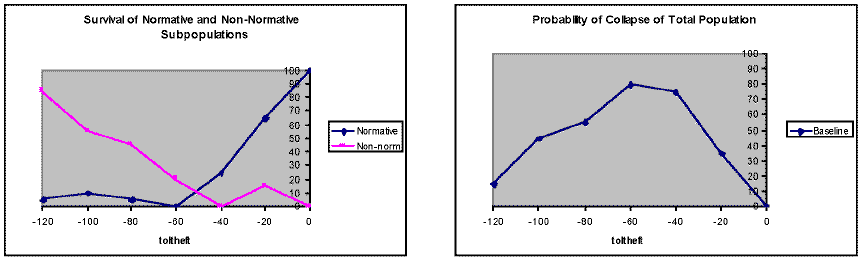
Figure 3. Mutual obligation factors for the total population and for agents in groups. Mutual obligation was defined as the sum of the interaction matrix elements connecting agents in the population. Sharing contributed to, and stealing detracted from, the interaction matrix elements

4.11

Figure 3 shows the mutual obligation — the sum the interaction matrix elements linking agents — for the total population and for agents in groups. (The mutual obligation for agents in groups differs from the total mutual obligation since the latter includes interactions between agents in different groups.) Each point on the plots represents a single run. Mutual obligation is plotted vs. the fraction of normative agents in the population, a parameter that was found to be important in previous studies (Younger 2003 and 2004) of reciprocity in artificial societies.

Table 3: Averages and standard deviations for key parameters taken over all runs that had a non-zero population at the end of the run
	Tolerance = 0				Tolerance = -20				Tolerance = -1,000,000
	Baseline	Transfer	Rejection	Ostracism		Baseline	Transfer	Rejection	Ostracism		Baseline	Transfer
Fraction Normative	0.96	0.96	0.95	0.95		0.76	0.74	0.78	0.88		0.16	0.16
Standard Deviation	0.0038	0.0031	0.0044	0.028		0.18	0.18	0.14	0.054		0.13	0.13
Mutual Obligation
Normative Agents	350	400	410	400		370	400	400	400		130	120
Standard Deviation	50	61	51	47		73	73	76	65		57	66
Non-Normative Agents	-140	-140	-140	-130		-810	-910	-820	-260		-3400	-3400
Standard Deviation	16	22	18	17		400	490	360	84		920	1000
Total Population	330	370	390	370		37	-5.7	96	310		-2900	-2900
Standard Deviation	48	58	48	48		380	440	360	84		990	1120
Agents in Groups	300	400	430	400		79	110	220	380		-2400	-2500
Standard Deviation	85	75	74	62		350	410	300	98		1200	1200
Sharing Rate per Agent	0.045	0.051	0.050	0.050		0.038	0.039	0.040	0.049		0.0087	0.0091
Standard Deviation	0.0053	0.0030	0.0038	0.0061		0.010	0.0089	0.0066	0.0039		0.0055	0.0075
Stealing Rate per Agent	0.039	0.039	0.039	0.037		0.020	0.023	0.019	0.011		0.044	0.045
Standard Deviation	0.00040	0.00042	0.00043	0.00045		0.012	0.015	0.012	0.0059		0.0061	0.0043
Percent Runs that Survive	94	92	92	96		50	54	44	64		100	96

4.12

Table 3 gives key parameters averaged over all runs where the population survived until the end of the run. These aggregate values allow a comparison of the relative efficiency of various sanctions given the stochastic nature of the individual runs. For toltheft = 0, the surviving population was entirely normative and the total mutual obligation was about 360. For toltheft = -10⁶, in which the surviving population was entirely non-normative, the total mutual obligation was about -2900. The fact that the points for toltheft = 0 are tightly clustered around a population of 95% normative agents indicates that the non-normative population was quickly extinguished. For toltheft = -10⁶, the normative population persisted until later in the run, producing a wider distribution of points vs. the fraction of normative agents.

4.13

The total mutual obligation amongst normative agents was about the same for toltheft = 0 and -20, indicating that they formed an island of normative behavior in a mixed population. The mutual obligation amongst non-normative agents decreased with toltheft, consistent with a larger number of non-normative agents in the population who could commit thefts. It was the larger fraction of non-normative agents that caused the total and group mutual obligation to be smaller in the case of toltheft = -20.

4.14

For toltheft = -20, the ability of an agent to choose its own group (Transfer scenario) and the ability of the group to reject the application of known non-normative agents (Rejection scenario) were not sufficient to insure high mutual obligation. Only for the Ostracism scenario was mutual obligation about the same as for the scenarios with toltheft = 0, leading to the conclusion that collective norms can indeed enhance social cohesion, as measured by the mutual obligation factor, to values comparable to what obtains when individual norms are strong. However, in the Ostracism scenario the population survived in only 64% of the runs, compared to 96% for the Baseline scenario. There is a price to be paid for weak individual norms.

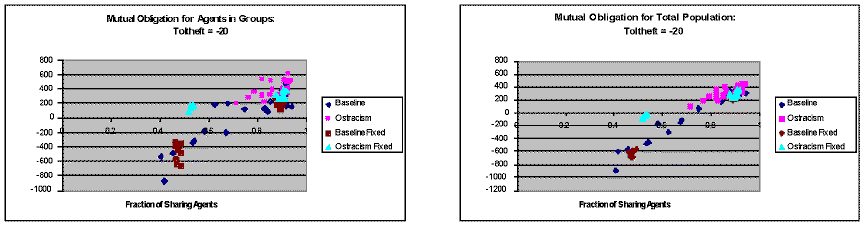
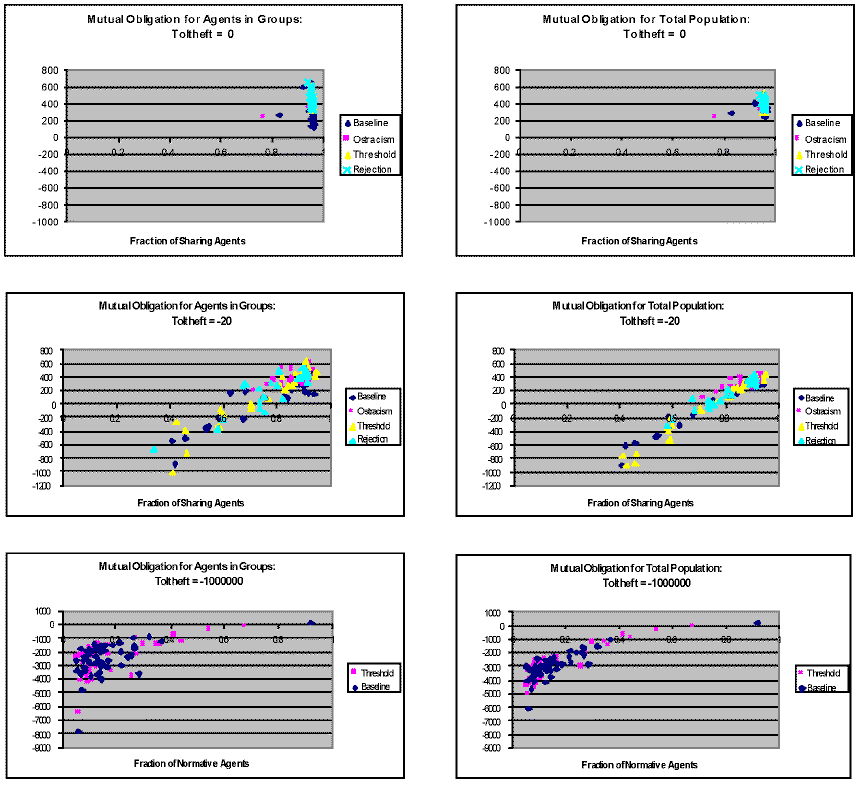
Figure 4. Comparison of the mutual obligation for the total population and for agents in groups for the case of matrilineal inheritance of normative character and for a fixed distribution of 50% and 90% sharing agents. Mutual obligation was defined as the sum of the interaction matrix elements connecting agents in the population. Sharing contributed to, and stealing detracted from, the interaction matrix elements

4.15

We used a matrilineal inheritance model for determining the normative character of newborn agents. Other models could be employed and some have been tried in test studies. For example, a fixed distribution of normative and non-normative agents, the results for which are given in Figure 4, was found to produce values of mutual obligation comparable to those found from the matrilineal inheritance model for the Baseline Scenario. (No population survived with an equal mix of sharing and stealing agents for the matrilineal inheritance model in the Ostracism Scenario, so a direct comparison was not possible for this point.) We also tried a "genetic" scheme wherein the tendency to share or steal was treated as a variable in the range 0-1 and where offspring were assigned the average of their parents' character. An agent was considered "sharing" if its variable character was > 0.5 and "stealing" if it was < 0.5. In this model we allowed experience (nurture) to affect character: being the recipient of sharing added 0.1 to variable character and being the victim of theft subtracted 0.1, so the behavioral character of an agent could change during the course of the simulation from sharing to stealing or vice versa. Again, we found results qualitatively similar to the matrilineal inheritance model. It was the distribution of agents with normative vs. non-normative character that was important in determining mutual obligation and not the means by which that distribution was achieved.

4.16

Our sharing model required a sharing agent to share when it was carrying food and when there were other agents present at the same location. We have investigated other models where sharing was dependent on the hunger of the sharing agent and where the ratio of the agent's hunger to the maximum hunger before death was compared to an "altruism parameter" that was set randomly between 0 - 1 at the beginning of the agent's life. While the results of these variations differ in detail from those reported in this paper, the qualitative conclusions are not affected. A more extended discussion of alternate models of sharing will be presented in a future report.

4.17

Unfortunately, there has been no systematic study of sanctions or how they were decided and applied within traditional cultures; a good summary of existing data can be found in Boehm (1999). One thing that does appear clear is that individual sanctions were much more commonly employed than collective ones. Such individual sanctions included ridicule and a refusal to share with the offender. However, we know from anecdotal accounts (e.g. Woodburn 1982) that ostracism was occasionally imposed after a prolonged refusal to cooperate in reciprocity or as a result of transgressions considered sufficiently serious to warrant removal of the offender from social intercourse. As an example of the former, some Pacific societies had a subclass of individuals referred to as "rubbish men," those who lived at the periphery of society, sometimes actually subsisting on the refuse of a village. Group members did not share with such people and they were considered undesirable as mates. Examples of more serious crimes include wife-stealing and murder. In some Eskimo cultures, groups of ostracized people would form their own community, enabling them to survive in a climate in which an individual would almost certainly perish. We observed a similar phenomenon in our simulations where an ostracized community would attain a size that it could propagate itself over several generations. While ostracized agents were not permitted to mate with group members, they could mate with one another. On some occasions the ostracized population was the only one to survive, representing a collapse of cooperative group activity. Note, however, that the ostracized agents did not form a "group" per say, but only represented the population that was excluded from the formally defined groups. The simulation was not complex enough to enable them to identify one another as a common cohort — they merely had the opportunity to mate with and steal from one another.

4.18

An alternate approach to understanding the role of toleration in the imposition of sanctions is to examine what levels of tolerance are required for fixed rates of non-normative behavior. If every transgression resulted in permanent ill will toward the offender, then there would be a real danger of population collapse as mating privileges were withheld from almost any likely spouse. We have shown in a separate report (Younger 2004b) that this tolerance level increases with the number of non-normative agents within a population. Using the same parameters as this paper, we found that for a population with a constant fraction of 10% stealing agents, a tolerance level of 4 could sustain population roughly 50% of the time. This positive value of toltheft corresponded to a requirement to share. For 50% stealing agents a tolerance level of -16 was required to sustain the population about 50% of the time and for a population of 90% stealing agents a tolerance level of about -80 was required. More non-normative behavior implied that more tolerance was needed to sustain the population given our assumption that reputation was a factor in mate selection. In a real society one would expect that biological necessity might overcome reputation, but one would still be left with much lower levels of mutual obligation in societies with large numbers of non-normative agents.

Discussion

5.1

Three principal points can be derived from our simulations. First, we found that mutual obligation was optimized for the same the type of indiscriminant sharing as prevails in many hunter-gatherer cultures. Indiscriminate sharing, combined with the communication of normative reputation, creates a web of interconnections within the society that contributes to social cohesion. Second, when individual norms were strong, i.e. when the tolerance for theft was small or zero, the imposition of collective sanctions had very little effect. When individual norms were weak, i.e. when the tolerance level for theft was high, then ostracism was effective at maintaining a high degree of mutual obligation within the group, but with increased risk of total population collapse. Third, the probability of survival of the population was highest at the extremes of tolerance, suggesting that some normative systems may be better than others at maintaining a viable culture.

5.2

Indiscriminant sharing enhanced personal reputation and maximized the total mutual obligation within the model society. We found that any attempt to restrict generosity to those most likely to provide near-term advantage (e.g. family members or other agents who shared) actually reduced the total mutual obligation. Viewed in economic terms, sharing was an exchange of material goods for the non-material reward of reputation and the comfort that a future return could be expected should a need arise. Indiscriminant sharing had the added advantage of eliminating the need for strict accounting of transactions; there is less need to track the value of individual transactions when they are small and frequent. (Limited mathematical skills in traditional cultures also encouraged this approach.)

5.3

One problem in evaluating theories of sharing in simple societies is that the expected return might occur far in the future, the near term cost representing a type of insurance payment on an eventuality that might never occur. (Gurven et al 2000) In our model, sharing represented a type of costly signaling, in which food is given away in order to build a reputation useful for securing a mate. Generosity signaled the advantages of a prospective mate since it was better to have a generous mate in close proximity than one who would steal. This behavior is observed in many egalitarian societies where the most efficient and generous providers of food enjoy improved mating opportunities. However, it is quite possible that even after persistent sharing an individual might be unable to find a mate; the achievement of the goal is made more probable by sharing, but there is no certainty.

5.4

The fact that the population was most likely to survive for either low or high values of tolerance to theft is suggestive that not all normative systems are equally effective at maintaining a viable culture. Our results suggest that mutual obligation is optimized when individual norms are strong, i.e. when there is a low tolerance to theft. In this case collective sanctions, which put greater stress on the population, are seldom required. Strong individual sanctions seem to be ubiquitous in egalitarian societies. An intriguing hypothesis is that the implicit or explicit recognition of the superiority of individual sanctions may partly explain the relative rarity of observations of collective sanctions in egalitarian societies. Boehm (1999) remarks that he "had to examine scores of forager ethnographies to find a few dozen usable reports of egalitarian sanctioning, and I believe that the sensitivity of most hunter-gatherers to subtle social cues is a factor in this relatively modest level of reported political conflict. With respect to deviance, bands tend to be highly conformist societies — in spite of the heavy emphasis on personal autonomy." Hill (2004) believes that the Ache may be among the most forgiving of all such cultures yet "they still insist on reciprocity in order to continue interacting" even if the return is delayed into the indefinite future. Furthermore, all documented examples of egalitarian societies demonstrate a low tolerance to transgressions on the part of individuals — I was able to find no example of a human society that tolerates large amounts of non-normative behavior, the other extreme that optimizes the survival probability of a population. Identification of such a situation in other primates or animal groups is complicated by hierarchal structures in some species, but the question may be worth further research.

5.5

The simulations reported here focused on the role of positive and negative reciprocity in the construction of mutual obligation with a gift-giving society. However, other factors contributed to individual reputation and social cohesion in real-world societies. Kinship constituted a strong bond between individuals. Friendship, personal charisma, athletic ability, dancing skills, and help with work projects added to an individual's reputation. Negative behavior such as the perception of dishonesty and the desire to dominate other people detracted from social reputation. Also, we did not consider avoidance of sanctions as a motivation in agent behavior. Such effects should be included in more sophisticated models of individual cultures.

5.6

Communication of normative reputation, here represented by the averaging of interaction matrix elements for third parties, was vital in making indiscriminant sharing effective at increasing personal reputation. In a real society, gossip played an important role in the social life of the tribe. It was the confidence that one's generosity would be communicated throughout the population that permitted one to ignore otherwise important reasons for focusing sharing on those who might provide a return benefit. Communication was also important in determining and applying group sanctions in societies lacking central leadership.

5.7

An interesting point that might be explored in future work is the role of self-depreciation and ridicule as social leveling mechanisms. Boehm (1999) argues that members of egalitarian societies actively work to suppress any significant differentiation with the group. Hence a successful provider of food might disparage his own ability or others might comment that his success was merely a matter of luck. Future simulations might explore what happens when frequent sharing has an adverse effect on the agent's reputation, or where there are multiple types of reputation that can be affected by sharing.

5.8

In most egalitarian societies there was little personal property and the accumulation of wealth was socially unacceptable. We focused on theft in our simulations not because it played an important economic role in simple societies but because it was a type of negative behavior that could be easily monitored in terms of the quantity of food involved. One might perform similar studies of the role of information transfer, truthful and untruthful, on social reputation.

5.9

In our simulations, ostracism was applied as a result of non-normative behavior. In real societies, ostracism also occurs through no fault of the individual, as in the case of racial, ethnic, or economic discrimination. Hales (2002) studied some aspects of group labeling but more needs to be done to elucidate the effects of discrimination on social performance. It would be interesting to study the interaction of groups with different sanctions and/or different tolerance levels, such as occurred during colonization of traditional societies or during military invasions.

5.10

Traditional societies, especially those living in relative isolation, offer an interesting laboratory for the comparison of social theories. They typically have populations numbering in the few hundred and, in the case of egalitarian societies, lack complex leadership structures. These cultures either imported or developed a normative system that enabled them to survive for many generations. By examining what worked for them, and using simulation as a tool for exploring the effect of significant excursions, one might better understand why certain forms of behavior evolved in the manner in which we find them.

Acknowledgements

This report was prepared as an account of work sponsored in part by an agency of the United States Government. Neither the Regents of the University of California, the United States Government nor any agency thereof, nor any of their employees make any warranty, express or implied, or assume any legal liability or responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represent that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by trade name, trademark, manufacturer, or otherwise does not necessarily constitute or imply its endorsement, recommendation, or favoring by the Regents of the University of California, the United States Government, or any agency thereof. The views and opinions of authors expressed herein do not necessarily state or reflect those of the Regents of the University of California, the United States Government, or any agency thereof.

References

BECKETT J (1987) Torres Strait Islanders: Custom and Colonialism (Cambridge University Press, Cambridge)

BLIEGE BIRD RL and Bird, DW (1997) "Delayed Reciprocity and Tolerated Theft: The Behavioral Ecology of Food-Sharing Strategies", Current Anthropology 38, 49-78.

BLURTON JONES, NG (1984) "A Selfish Origin for Human Food Sharing: Tolerated Theft", Ethology and Sociobology 5, 1-3.

BOEHM C (1999) Hierarchy in the Forest: The Evolution of Egalitarian Behavior (Harvard University Press, Cambridge).

CASTELFRANCHI C, Conte R, and Paolucci M (1998) "Normative Reputation and the Costs of Compliance", Journal of Artificial Societies and Social Simulation 1 (3).

HALES D (2002) "Group Reputation Supports Beneficent Norms", Journal of Artificial Societies and Social Simulation 5 (4).

GURVEN M, Allen-Arave W, Hill K, and Hurtado M, (2000) "It's a Wonderful Life: Signaling Generosity Among the Ache of Paraguay", Evolution and Human Behavior 21, 263-282.

GURVEN M (2003) "To Give or Give Not: The Behavioral Ecology of Human Food Transfers", Behavioral and Brain Sciences

HILL K (2004) Private Communication.

JAFFE K (2002) "An Economic Analysis of Altruism: Who Benefits from Altruistic Acts?" Journal of Artificial Societies and Social Simulation 5 (3).

KAPLAN H and HILL K (1985) "Food Sharing Among Ache Foragers: Tests of Explanatory Hypotheses", Current Anthropology 26, 223-246.

KENT S (1993) "Sharing in an Egalitarian Community", Man, 28, 479-514.

MAUSS M (1990[1950]) The Gift: The Form and Reason for Exchange in Archaic Societies (Norton, New York).

PETERSON N (1993) "Demand Sharing: Reciprocity and the Pressure for Generosity among Foragers", American Anthropologist, New Series 95, 860-874.

WOODBURN J (1982) "Egalitarian Societies", Man 17, 431-451.

YOUNGER S M (2003) "Discrete Agent Simulations of the Effect of Simple Social Structures on the Benefits of Resource Sharing", Journal of Artificial Societies and Social Simulation 6 (3).

YOUNGER SM (2004) "Reciprocity, Normative Reputation, and the Development of Mutual Obligation in Gift-Giving Societies", Journal of Artificial Societies and Social Simulation, 7(1).

YOUNGER SM (2004b) "Reciprocity, Tolerated Theft, and Reproduction Strategies in Foraging Societies", Los Alamos National Laboratory Report LA-UR-04-7119.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2005]