Loet Leydesdorff (2005)
Anticipatory Systems and the Processing of Meaning:
a Simulation Study Inspired by Luhmann's Theory of Social Systems
Journal of Artificial Societies and Social Simulation
vol. 8, no. 2
<https://www.jasss.org/8/2/7.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 29-Sep-2004 Accepted: 30-Jan-2005 Published: 31-Mar-2005
 Abstract
Abstract
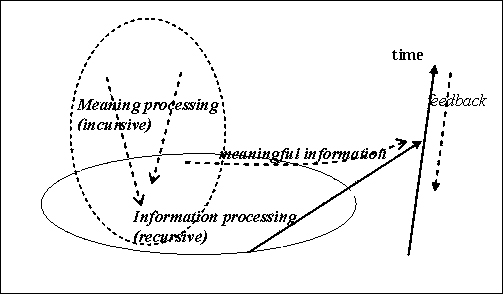 |
| Figure 1. The incursive processing of meaning interacts with the recursive processing of information as a feedback mechanism. The result of the interaction can be considered as the production of meaningful information. |
| x(t + Δ t) = x(t) + Δ t f(x(t)) | (1a) |
or equivalently backward as:
| x(t - Δ t) = x(t) - Δ t f(x(t)) | (1b) |
It follows that:
| x(t) = x(t - Δ t) + Δ t f(x(t)) | (1c) |
The latter function allows for the following rewrite after one time-step Δ t:
| x(t + Δ t) = x(t) + Δ t f(x(t + Δ t)) | (1d) |
Equation (1d) is different from Equation (1a) in terms of the time suffixes so that different classes of solutions can be expected. In Equation (1d) the state of a system at time (t + Δ t) depends on the state at the present time t, but also at the next moment in time (t + Δ t). The prediction 'includes' (or 'implies') its own next state. Dubois (1998) proposed that this evaluation be labeled incursion.
| x(t) = a x(t-1) {1 - x(t-1)} | (2) |
This equation can be used for modeling the growth of a population. The feedback term {1 - x(t)} inhibits further growth of the system represented by x(t) as the value of x(t) increases over time. This so-called 'saturation factor' generates the bending of the sigmoid growth curves of systems for relatively small values of the parameter (1 < a < 3). For larger values of a, the model bifurcates (at a ≥ 3.0) or increasingly generates chaos (3.57 < a < 4).
| x(t) = a x(t-1) {1 - x(t)} | (3) |
In this model the selection pressure prevailing in the present is analytically independent of the previous state of the system that produced the variation. The recursion on x(t-1) can be considered as the historical subdynamic. As noted, technological systems which develop historically within an economy experience interaction with the market at each moment of time. In other words, the horizontal diffusion in the market stands in orthogonal relation to the historical development of the technology over time. The results of the interactions are continuously input to a next cycle that builds both recursively on the previous state and incursively experiences another feedback of the market at a next moment. However, the incursive subdynamics can be expected to have properties different from those of the recursive one (from which it was derived). For example, the anticipatory model based on the logistic equation does not exhibit bifurcation or chaos for larger values of the parameter a.
| x(t) = a x(t-1) {1 - x(t)} | (3) |
| x(t) = a x(t-1) - a x(t-1). x(t) | |
| x(t) + a x(t-1). x(t) = a x(t-1) | |
| x(t){1 + a x(t-1)} = a x(t-1) | |
| x(t) = a x(t-1) / {1 + a x(t-1)} | (4) |
Equation 4 specifies x(t) as a function of x(t-1), but it remains equivalent to a model for incursion embedded in historical recursions as specified in Equation 3. In the case of pure incursion (that is, only environmental determination in the present as represented by the second term of Equation 3), one would no longer be able to produce a simulation because one would loose the historical axis of the system in the model. In other words, the anticipatory model containing both recursive and incursive factors imports the global or system's perspective into systems which are developing historically. The incursive term enriches the historically developing system with an orientation towards the future.
| (x, y)t = a (x, y)t-1 {1 - (x, y)t-1} | (2a) |
This equation is used, for example, in line 130 of the computer program exhibited in Table 1.
10 SCREEN 7: WINDOW (0, 0)-(320, 200): CLS 20 RANDOMIZE TIMER: a = 2.1 30 ' $DYNAMIC 40 DIM scrn(321, 201) AS SINGLE 50 FOR x = 0 TO 320 ' array and screen are filled in 60 FOR y = 0 TO 200 70 scrn(x, y) = .1: PSET (x, y), (10 * scrn(x, y)) 80 NEXT y 90 NEXT x 100 DO 110 x = INT(RND * 320) ' an array element is randomly 120 y = INT(RND * 200) ' selected 130 scrn(x, y) = a * scrn(x, y) * (1 - scrn(x, y)) 140 PSET (x, y), (10 * scrn(x, y)) 150 LOOP WHILE INKEY$ = '' 160 END |
| Table 1. Model for the logistic curve in BASIC (a = 2.1) |
| This code may be downloaded from here and run under Windows |
Both the array and the screen are initially filled with a constant value in line 70; the screen is painted monochromatically. In the next loop (lines 100-150), a pixel is accessed randomly (lines 110-120), evaluated (line 130), and repainted accordingly (line 140). This transformation is performed continuously.
|
|
| Figure 2. Resulting screen of Table 1 with bifurcation for a = 3.1 |
For the value of a = 2.1 (line 20), for example, the colour of the screen changes gradually because the distributed system exhibited on the screen goes through a transition.[4] For a = 3.1, however, bifurcation is expected. This leads to a screen distributed randomly in two colours (Figure 2): when an agent is activated (lines 110-120), the colour on the screen changes into the alternative one at this place. Thus, the bifurcation leads to an oscillation between the two colours on the screen. For higher values of the parameter a, the system exhibits increasingly chaotic patterns of change.
1 CLS : LOCATE 10, 10: INPUT 'Parameter value'; a 2 IF a > 4 THEN a = 4 ' prevention of overflow 10 SCREEN 7: WINDOW (0, 0)-(320, 200): CLS 20 RANDOMIZE TIMER 30 ' $DYNAMIC 40 DIM scrn(321, 201) AS SINGLE 50 FOR x = 0 TO 320 60 FOR y = 0 TO 200 70 scrn(x, y) = .1: PSET (x, y), (10 * scrn(x, y)) 80 NEXT y 90 NEXT x 100 DO 110 x = INT(RND * 320) 120 y = INT(RND * 200) 130 IF y > 100 GOTO 140 ELSE GOTO 150 ' split of screens 140 scrn(x, y) = a * scrn(x, y) / (1 + a * scrn(x, y)): GOTO 160 150 scrn(x, y) = a * scrn(x, y) * (1 - scrn(x, y)) 160 PSET (x, y), (10 * scrn(x, y)) 170 LOOP WHILE INKEY$ = '' 180 END |
| Table 2. Incursion and recursion in the case of the logistic curve |
| This code may be downloaded from here and run under Windows |
|
|
| Figure 3. Upper half of the screen incursive, lower half recursive; a = 3.1 |
Figure 3 shows that the incursive simulation leads to a transition, while the representation of the recursive system in the lower half of the screen exhibits the same bifurcation as in Figure 2. The incursive model converges to a stable state (in this case, exhibited as white) because the incursive version of the logistic model {(ax / (1+ax)} grows towards unity with increasing values of x. In a mathematical formulation: Limx→∞ {ax/(1+ax)} = 1. A fixed point is reached independently of the starting value.
[...] 100 DO 110 x = INT(RND * 320) 120 y = INT(RND * 200) 130 IF RND > .5 GOTO 140 ELSE GOTO 150 140 scrn(x, y) = a * scrn(x, y) / (1 + a* scrn(x, y)) : GOTO 160 150 scrn(x, y) = a * scrn(x, y) * (1 - scrn(x, y)) 160 PSET (x, y), (10 * scrn(x, y)) 170 LOOP WHILE INKEY$ = '' 180 END |
| Table 3. Incursion and recursion alternating randomly, but using the same data set |
| This code may be downloaded from here and run under Windows |
When the incursive model operates within a recursive system of which it is also a part, the incursive routine reduces the uncertainty produced by the recursive one. The recursive formulation can produce probabilistic entropy, but incursion drives steadily towards a transition in the long run.
1 a = 3.3
10 SCREEN 7: WINDOW (0, 0)-(320, 200): CLS
11 LINE (1, 100)-(320, 100)
20 RANDOMIZE TIMER
30 ' $DYNAMIC
40 DIM scrn(321, 201) AS INTEGER
41 FOR x = 0 TO 320
42 FOR y = 0 TO 200
43 scrn(x, y) = INT(RND * 16) ' change to 16 colours
44 PSET (x, y), scrn(x, y) ' (see note 4)
45 NEXT y
46 NEXT x
50 DO
60 y = INT(RND * 200)
70 x = INT(RND * 320)
80 IF (x = 0 OR y = 0) GOTO 160 ' prevention of network errors
85 IF y > 100 GOTO 90 ELSE GOTO 100
90 scrn(x, y) = a * scrn(x, y-100) / (1 + a* (scrn(x, y-100) / 16))
95 GOTO 140 ' paint upper screen
100 scrn(x, y) = a * (scrn(x, y) * (1 - (scrn(x, y)) / 16))
' spread new value in the Von Neumann environment
110 scrn(x + 1, y) = scrn(x, y): scrn(x - 1, y) = scrn(x, y)
120 scrn(x, y + 1) = scrn(x, y): scrn(x, y - 1) = scrn(x, y)
140 PSET (x, y), ABS(scrn(x, y))
160 LOOP WHILE INKEY$ = ''
170 END
|
| Table 4. The generation of an observer by using incursion |
| This code may be downloaded from here and run under Windows |
In order to generate an observable structure at each moment in time (because one cannot recognize patterns in the random observation of randomness), a small network effect was first added to the observed system (in lines 110-120 of Table 4). This network effect spreads the update in the lower-level screen in the local (Von Neumann) neighbourhood of the randomly affected cell. (The Von Neumann environment is defined as the cells above, below, to the right, and to the left of the effect.) Note that the network effect structures the system at each moment of time and locally, whereas incursion and recursion are defined over the time axis of the system.
scrn(x, y-100). The result of this evaluation is attributed to the upper half of the screen and to the corresponding array value of scrn(x, y). The effect is that an observer is generated as exhibited in Figure 4.
|
|
| Figure 4. Incursion generates an observer in the top-level screen (a = 3.3) |
|
|
| Figure 5. Incursion and recursion with different parameter values produce observers with potentially different positions and corresponding blind spots (a = 3.2 and b = 1.6). |
1 CLS
2 LOCATE 10, 10: INPUT 'Parameter value for recursion (a) '; a
3 LOCATE 11, 10: INPUT 'Parameter value for incursion (b) '; b
4 IF a > 4 THEN a = 4
10 SCREEN 7: WINDOW (0, 0)-(320, 200): CLS
20 RANDOMIZE TIMER
30 ' $dynamic
40 DIM virtual scrn(321, 201) AS INTEGER
41 FOR x = 0 TO 320
FOR y = 0 TO 200
scrn(x, y) = INT(RND * 16)
PSET (x, y), scrn(x, y)
NEXT y
NEXT x
50 DO
60 y = INT(RND * 201)
70 x = INT(RND * 321)
80 IF (x = 0 OR y = 0) GOTO 160 ' prevention of errors by
81 IF (x = 320 or y = 200) GOTO 160 ' effects at the margins
85 IF y > 100 GOTO 90 ELSE GOTO 100
90 scrn(x, y) = b*scrn(x,(y-100))/(1 + b*(scrn(x,(y-100))/16))
95 GOTO 140 100 scrn(x, y) = a * scrn(x, y) * ((1 - (scrn(x, y)) / 16))
110 scrn(x + 1, y) = scrn(x, y): scrn(x - 1, y) = scrn(x, y)
120 scrn(x, y + 1) = scrn(x, y): scrn(x, y - 1) = scrn(x, y)
140 PSET (x, y), ABS(scrn(x, y))
160 LOOP WHILE INKEY$ = ''
170 END
|
| Table 5. Incursion and recursion with different parameters |
| This code may be downloaded from here and run under Windows |
By playing with the parameters, one can see that an observer perceives more detail when the parameter for the incursive routine is lower than for the recursive one. High values for the incursion parameter (b) drive the observing system into a more homogeneous state (because of the above noted limit transition in the formula), while higher values of the recursive parameter (a) drive the historically developing system towards more chaotic bifurcations.
1 a = 3.2: b = 1.6: c = 1.9
10 SCREEN 7: WINDOW (0, 0)-(320, 200): CLS
20 RANDOMIZE TIMER
30 ' $DYNAMIC
40 DIM scrn(321, 201) AS INTEGER
41 FOR x = 0 TO 320
FOR y = 0 TO 200
scrn(x, y) = INT(RND * 16)
PSET (x, y), scrn(x, y)
NEXT y
NEXT x
50 DO
60 y = INT(RND * 201)
70 x = INT(RND * 321)
80 IF (x = 0 OR y = 0) GOTO 160 ' prevention of errors at the margins
81 IF (x = 320 OR y = 200) GOTO 160
IF x < 160 AND y >= 100 THEN N = 1
IF x >= 160 AND y >= 100 THEN N = 2
IF x < 160 AND y < 100 THEN N = 3
IF x >= 160 AND y < 100 THEN N = 4
SELECT CASE N
CASE IS = 1 ' upper left screen
scrn(x, y) = b * scrn(x, (y-100)) / (1 + b*(scrn(x, (y-100)) / 16))
PSET (x, y), ABS(scrn(x, y))
CASE IS = 2 ' upper right screen
scrn(x, y) = c *scrn((x-160),(y-100))/(1 + c*(scrn((x-160),(y-100))/ 16))
PSET (x, y), ABS(scrn(x, y))
CASE IS = 3 ' lower left screen
100 IF RND > .5 GOTO 101 ELSE GOTO 110
101 scrn(x, y) = b * scrn(x, y) / (1 + b * (scrn(x, y)) / 16): GOTO 140
110 scrn(x, y) = a * scrn(x, y) * ((1 - (scrn(x, y)) / 16))
scrn(x + 1, y) = scrn(x, y): scrn(x - 1, y) = scrn(x, y)
scrn(x, y + 1) = scrn(x, y): scrn(x, y - 1) = scrn(x, y)
140 PSET (x, y), ABS(scrn(x, y))
CASE IS = 4 ' lower right screen
scrn(x, y) = c * scrn((x-160),(y+100))/(1 +c*(scrn((x-160),(y+100))/ 16))
150 scrn(x,y) = (scrn(x,y)/2)
+ (b * scrn(x,(y+100)) / (1 + b*(scrn(x,(y+100))/16))) / 2
PSET (x, y), ABS(scrn(x, y))
END SELECT
160 LOOP WHILE INKEY$ = ''
170 END
|
| Table 6. Two observers (incursion with b = 1.6 and c = 1.9) observe the same screen (recursion with a = 3.2) and each other. The left-side observer is additionally embedded (line 101). |
| This code may be downloaded from here and run under Windows |
 |
| Figure 6. Two observers observing a single screen and each other (lower right screen). (Colours optimized in black and white by using the negative of the picture for the visualization.) |
|
|
| Figure 7. Part of Figure 6 ten times enlarged |
[...]
CASE IS = 4 ' lower right screen
scrn(x, y) = c * scrn((x-160),(y+100))/(1 +c*(scrn((x-160),(y+100))/ 16))
150 scrn(x, y) = (scrn(x, y))
* (b * scrn(x,(y+100)) / (1 + b*(scrn(x,(y+100))/16)))
151 scrn(x, y) = d * scrn(x, y) ' interaction parameter d
PSET (x, y), ABS(scrn(x, y))
END SELECT
160 LOOP WHILE INKEY$ = ''
170 END
|
| Table 7. The effect of interaction among the two observations |
| This code may be downloaded from here and run under Windows |
In order to see the pure effect of interaction — that is, without aggregation — I changed the plus sign in line 150 of Table 6 into a multiplication sign in Table 7. By adding a parameter d for the interaction (in line 151), one can then produce representations that are as rich in colours as the originally observed system (d = 0.2 exhibited in Figure 8) or as poor as an observer who only observes in black and white (d = 1.0).
|
|
| Figure 8. Interaction effects among the two observations with interaction parameter d = 0.2 |
 |
| Figure 9. Interaction and aggregation of observations combined |
| The code may be downloaded from here and run under Windows |
The resulting picture (in the lower right quadrant) shows the two effects described above: (a) the aggregation makes the observations uncertain in terms of the boundaries, and (b) the interaction shows the dynamics of the system under observation as pixels that temporarily light up on the screen. Because the two observers operate at random frequencies and with different parameters for the incursion, they are out of pace and entertain different representations. The latter effect provides a static uncertainty and the former a dynamic one.
2The extension to more than two dimensions is straightforward (Leydesdorff 2001).
3I used Microsoft's QBasic, but the programs can easily be adapted for higher or commercial versions of Basic, and for other languages. In Visual Basic the programs formulated in this paper can be imported as subroutines.
4In the compiled simulations, the values of the colours were augmented with five in order to use the brighter colours in the palette of QBasic.
5In order to prevent overflow while running this model, values of the parameter a larger than 4 are reset to a = 4 (in line 2).
6The subsystem entertaining the model of the system in the present state can be considered as an endogenous observer of the system's history. Endogenous means here that this observer remains a result of the network in which the observer effect is generated (Maturana 1978). One can consider this observer as an incursive subroutine of the complex system. Note that the metaphor is biological because this observer is not positioned refexively in a (next-order) communication among observers. The observer remains completely embedded and follows the development in the observed system reflexively.
7In the program in Table 5, the two parameters (a for the recursion and b for incursion, respectively) can be chosen by the user in the lines 2 and 3 of the routine. In Visual Basic the more sophisticated user interface would require the programming of an additional subroutine.
8The emergence of such a new dimension can, for example, be modeled as the effect of an unintended 'lock-in' (Arthur 1989 and 1994). I intend to elaborate on this further development of the social system in a next study.
9From a perspective along the time axis, these stabilizations can be considered as condensations of the expectations because of potential resonances among them (Smolensky 1986; Leydesdorff 1995).
ARTHUR W B (1994) Increasing Returns and Path Dependence in the Economy. Ann Arbor: University of Michigan Press.
AXELROD R (1997) The Complexity of Cooperation: agent-based models of competition and collaboration. Princeton: Princeton University Press.
COVENEY P and Highfield R (1990) The Arrow of Time. London: Allen.
DEVANEY R (2003) An Introduction to Chaotic Dynamical Systems, 2nd edition, Boulder, CO: Westview. pp. 33 ff.
DITTRICH P, Kron T and Banzhaf W (2003) On the Formation of Social Order: Modeling the Problem of Multi and Double Contingency following Luhmann. Journal of Artificial Societies and Social Simulation, 6 (1) https://www.jasss.org/6/1/3.html [21 September 2004].
DUBOIS D M (1998) "Computing Anticipatory Systems with Incursion and Hyperincursion." In Dubois D M (Ed.), Computing Anticipatory Systems: CASYS'97, AIP Proceedings 437. pp. 3-29.
DUBOIS D M (2000) "Review of Incursive, Hyperincursive and Anticipatory Systems — Foundation of Anticipation in Electromagnetism." In Dubois D M (Ed.), Computing Anticipatory Systems CASYS'99, AIP Proceedings 517. pp. 3-30.
DUBOIS D M (2002) "Theory of Incursive Synchronization of Delayed Systems and Anticipatory Computing of Chaos." In Trappl R (Ed.), Cybernetics and Systems, 1. Vienna: Austrian Society for Cybernetic Studies. pp. 17-22.
DUBOIS D M and Sabatier P (1998) "Morphogenesis by Diffuse Chaos in Epidemiological Systems." In Dubois D M (Ed.), Computing Anticipatory Systems: CASYS'97, AIP Proceedings 437. pp. 295-308.
EPSTEIN J M and Axtell R (1996) Growing Artificial Societies: Social Science from the Bottom Up. Cambridge, MA: MIT Press.
GIDDENS A (1979) Central Problems in Social Theory. London, etc.: Macmillan.
GIDDENS A (1984) The Constitution of Society. Cambridge: Polity Press.
HUSSERL E (1929) Cartesianische Meditationen und Pariser Vorträge. [Cartesian meditations and the Paris lectures.] Edited by S. Strasser. The Hague: Martinus Nijhoff, 1973.
KAUFFMAN S A (2000) Investigations. Oxford, etc.: Oxford University Press.
LAZARSFELD P F and Henry N W (1968) Latent structure analysis. New York: Houghton Mifflin.
LEYDESDORFF L (1995) The Operation of the Social System in a Model based on Cellular Automata. Social Science Information, 34(3). pp. 413-441.
LEYDESDORFF L (2001) Technology and Culture: The Dissemination and the Potential 'Lock-in' of New Technologies. Journal of Artificial Societies and Social Simulation, 4(3) https://www.jasss.org/4/3/5.html [Retrieved at 21 September 2004].
LEYDESDORFF L (2003) The Construction and Globalization of the Knowledge Base in Inter-Human Communication Systems. Canadian Journal of Communication, 28(3). pp. 267-289.
LEYDESDORFF L (2005) "Meaning, Anticipation, and Codification in Functionally Differentiated Social Systems." In Kron T, Schimank U, Winter L (Eds.), Luhmann simulated - Computer Simulations to the Theory of Social Systems, Münster, etc: Lit Verlag.
LEYDESDORFF L and Dubois D M (2004) Anticipation in Social Systems, Internation Journal of Computing Anticipatory Systems, 14. pp. 203-216.
LUHMANN N (1982) Liebe als Passion. Frankfurt a.M.: Suhrkamp.
LUHMANN N (1984) Soziale Systeme. Grundriß einer allgemeinen Theorie. Frankfurt a. M.: Suhrkamp.
LUHMANN N (1986) "The autopoiesis of social systems." In Geyer F, Van der Zouwen J (Eds.), Sociocybernetic Paradoxes, London: Sage. pp. 172-192.
LUHMANN N (1997) Die Gesellschaft der Gesellschaft. Frankfurt a.M.: Surhkamp.
LUHMANN N. (1999) "The Paradox of Form." In Baecker D (Ed.), Problems of Form, Stanford: Stanford University Press, pp. 15-26.
LUHMANN N (2002) "The Modern Sciences and Phenomenology." In Rasch W (Ed.), Theories of Distinction: Redescribing the descriptions of modernity. Stanford, CA: Stanford University Press. pp. 33-60.
MACKENZIE A (2001) The Technicity of Time. Time & Society, 10(2/3). pp. 235-257.
MATURANA H R (1978) "Biology of Language: the Epistemology of Reality." In Miller GA, Lenneberg E (Eds.), Psychology and Biology of Language and Thought. Essays in Honor of Eric Lenneberg. New York: Academic Press. pp. 27-63.
MATURANA H R and Varela, F (1980) Autopoiesis and Cognition: The Realization of the Living. Boston: Reidel.
NELSON R R and Winter S G (1982) An Evolutionary Theory of Economic Change. Cambridge, MA: Belknap Press of Harvard University Press.
PARSONS T (1963a) On the Concept of Political Power, Proceedings of the American Philosophical Society 107 (3). pp. 232-262.
PARSONS T (1963b) On the Concept of Influence. Public Opinion Quarterly 27 (1). pp. 37-62.
PEARL R (1924) Studies in Human Biology. Baltimore: William and Wilkins.
ROSEN R (1985) Anticipatory Systems. Oxford, etc.: Pergamon Press.
SHANNON C E (1948) A Mathematical Theory of Communication. Bell System Technical Journal, 27. pp. 379-423 and 623-356.
SIMON H A (1969) The Sciences of the Artificial. Cambridge, MA/London: MIT Press.
SMOLENSKY P (1986) "Information Processing in Dynamical Systems: Foundation of Harmony Theory." In Rumelhart D E, McClelland J L, and the PDP Research Group (Eds). Parallel Distributed Processing. Cambridge, MA/ London: MIT Press, Vol. I. pp. 194-281.
VERHULST P-F (1847) Deuxième mémoire sur la loi d'accroissement de la population, Mém. de l'Academie Royale des Sci., des Lettres et des Beaux-Arts de Belgique, 20. pp. 1-32.
WHITLEY R D (1984) The Intellectual and Social Organization of the Sciences. Oxford: Oxford University Press.
WOLFRAM S (2002) A New Kind of Science. Champaign, IL: Wolfram Media.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]