Rob Koper (2005)
Increasing Learner Retention in a Simulated Learning Network Using Indirect Social Interaction
Journal of Artificial Societies and Social Simulation
vol. 8, no. 2
<https://www.jasss.org/8/2/5.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 31-Oct-2004 Accepted: 21-Feb-2005 Published: 31-Mar-2005
 Abstract
AbstractThe idea is that indirect social interaction will advise learners to select a path that has been shown to be effective. This is particularly significant when learners must choose between different alternative paths in the network, all leading to the same targets, but having different chances of success. Through indirect social interaction, the path that the learners ultimately follow is expected to converge with the path that offers them the greatest chance of success.
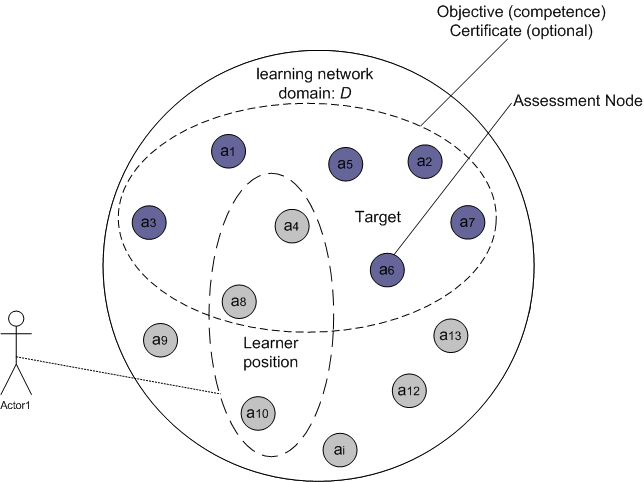
|
| Figure 1. Position and Target in an LN |
number of learners = number attained + number studying + number searching + number dropping out
The only known factor in most systems is the number of learners who have attained their targets (when there are official completion activities, like exams). Whether a learner is 'still studying a UOL', 'searching for a new UOL' or is a 'drop-out' is hard to determine. As a consequence, for this study we will concentrate on the proportion of learners who have attained their target by completing the necessary UOLs.

|
| Figure 2. Summary of the model |
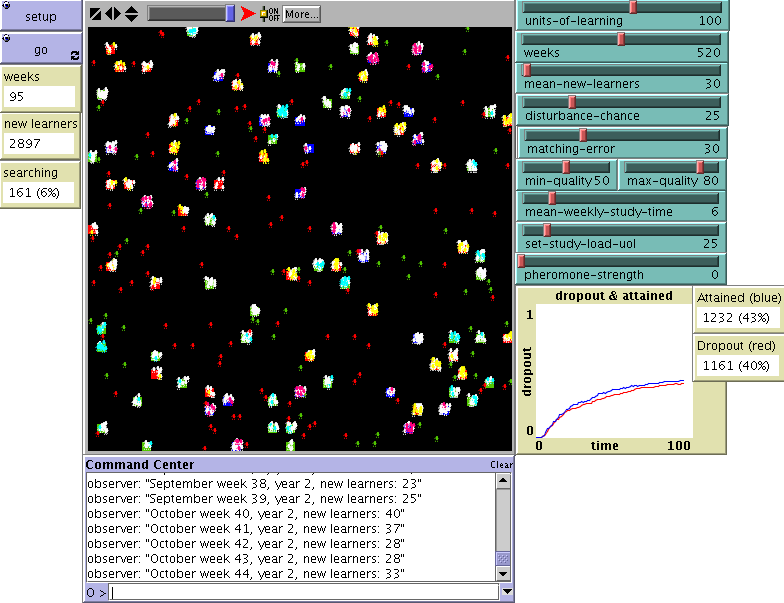
|
| Figure 3. The interface of the model in the Netlogo environment |
| Settings in user interface: |
| Units of learning: 100 |
| Weeks: 1040 (the number of 260 weeks, is controlled automatically; this setting only prevents early termination). |
| Mean-new-learners: 10 |
| Mean-weekly-study-time: 6 |
| Max-quality: 100 |
| Study-load-uol: 25 |
| Vary variables in experiment: |
| matching-error: values 0 and 100 |
| min-AN-quality: values 0 and 100 |
| disturbance-chance: values 0 and 100 |
| pheromone-strength: values 0 and 100 |
| replications: values 1, 2, 3, ... , 12 |
| Set up model with these commands: |
| setup |
| Step model with these commands: |
| go |
| Stop after this many steps: |
| 260 |
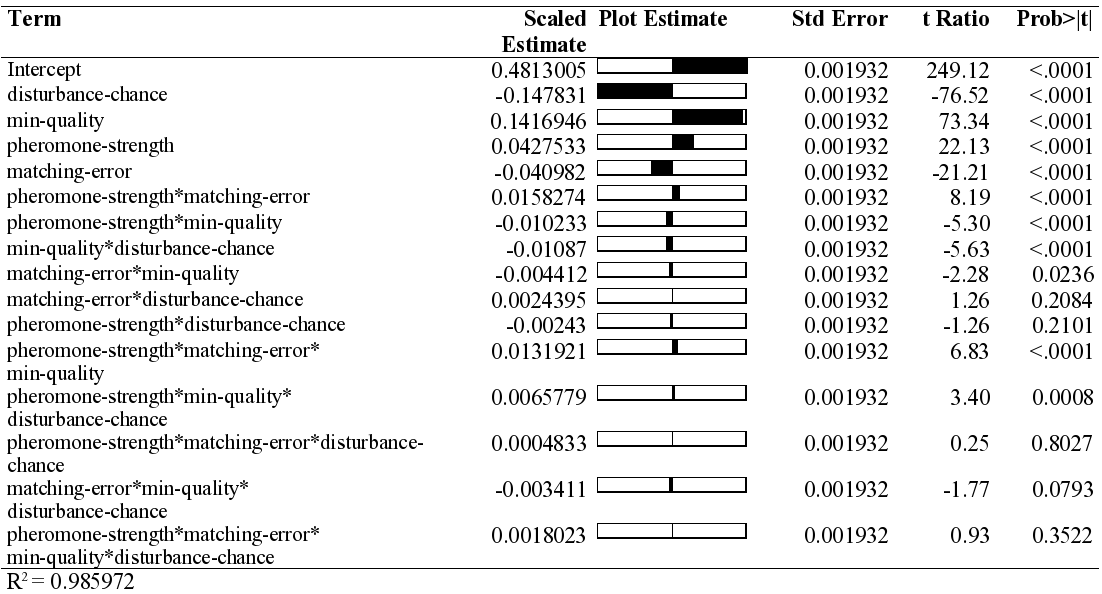
|
| Table 1. Scaled estimates for full factorial model, factors centred by mean, scaled by range/2. |
|
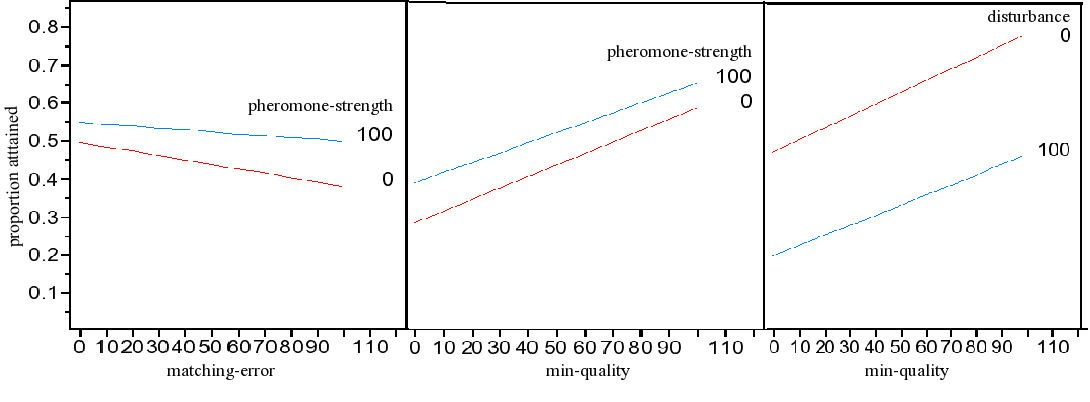
| Figure 4. The interactions in the model |
| Table 2: Attained proportion for the interaction effects | ||||
| Pheromone- strength | matching-error | min-quality | ||
| 0 | 100 | 0 | 100 | |
| 100 | 55% | 50% | 39% | 66% |
| 0 | 50% | 38% | 29% | 59% |
| difference | 5% | 12% | 10% | 7% |
disturbance | min-quality | |
| 0 | 100 | |
| 100 | 20% | 46% |
| 0 | 48% | 78% |
| -28% | -32% | |
| Table 3: The reduced model with 6 effects | ||||
| Analysis of Variance | ||||
| Source | DF | Sum of Squares | Mean Square | F Ratio |
| Model | 6 | 8.7924402 | 1.46541 | 1359.179 |
| Error | 185 | 0.1994588 | 0.00108 | Prob > F |
| C. Total | 191 | 8.9918991 | <.0001 | |
| R2= 0.977818 | ||||
| Parameter Estimates | ||||||
| Term | Estimate | Std Error | t Ratio | Prob > t | ||
| Intercept | 0.4856655 | 0.005299 | 91.66 | <.0001 | ||
| matching-error | -0.00082 | 0.000047 | -17.29 | <.0001 | ||
| min-quality | 0.0028339 | 0.000047 | 59.79 | <.0001 | ||
| disturbance-chance | -0.002957 | 0.000047 | -62.38 | <.0001 | ||
| pheromone-strength | 0.0008551 | 0.000047 | 18.04 | <.0001 | ||
| pheromone-strength × min-quality | -0.000004 | 9.479e-7 | -4.32 | <.0001 | ||
| pheromone-strength × matching-error | 0.0000063 | 9.479e-7 | 6.68 | <.0001 | ||
| ||||||||||||||||||||
| ||||||||||||||||||||
| ||||||||||||||||||||
| ||||||||||||||||||||
| ||||||||||||||||||||
| ||||||||||||||||||||
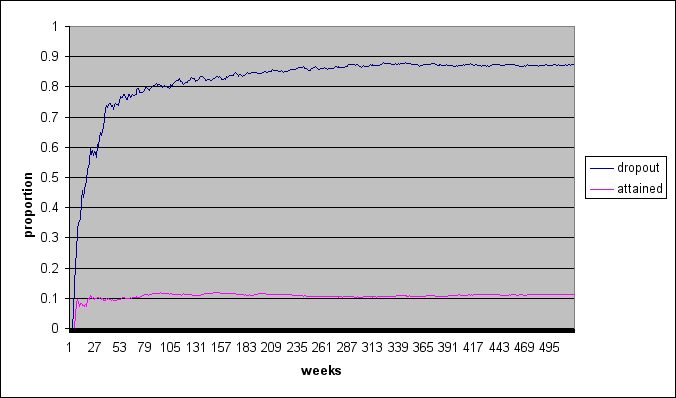
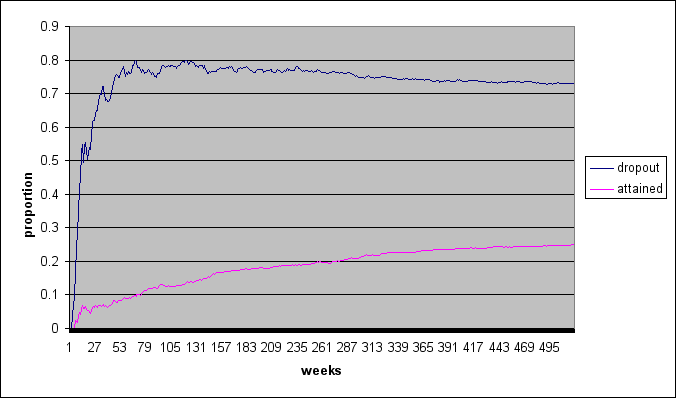
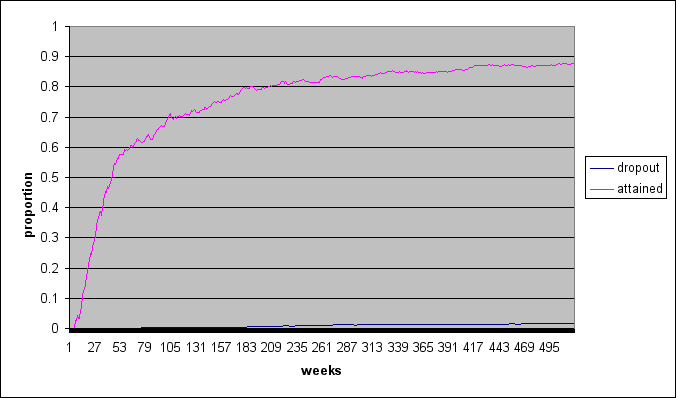
| Figure 5. Drop-out and attained proportions over 520 weeks, different settings | ||||||||||||||||||||
When comparing figure 5A with 5B, we seen that the influence of pheromones on the attained proportion continues to increase after the 260 weeks selected to compare the conditions in this study. The model itself is not expected to be influenced; however, estimates of the effect on the attained proportion depend largely on the timeframe in which the pheromones work.
BONABEAU E, Dorigo M and Theraulaz G (1999). Swarm intelligence : from natural to artificial systems. New York: Oxford University Press.
BROCKETT R G and Hiemstra R (1991) Self-direction in Adult Learning: perspectives on theory, research and practice. London: Routledge.
CANDY P C (1991) Self-direction for Lifelong Learning. San Francisco: Jossey-Bass.
DENEUBOURG J L, Goss S, Francks N, Sendove-Francks A, Detrain C and Chretien L (1991) The dynamics of collective sorting: Robot-like ants and ant-like robots. Paper presented at the Proceedings of the first international conference on simulation and adaptive behaviour.
DI MARZO SERUGENDO G, Foukia N, Hassas S, Karageorgos A, Kouadri Mostéfaoui S, Rana O, Ulieru M, Valckenaers P and Van Aart C (1998) Self-organisation: Paradigms and Applications. In Di Marzo Serugendo G, Karageorgos A, Rana O and Zambonelli F (Eds.), Engineering Self-Organising Systems. LNAI 2977, pp. 1-19. Heidelberg, Springer.
DORIGO M, Di Caro G and Gambardella L M (1999) Ant Algorithms for Discrete Optimization. Artificial Life, 5, pp. 137-172.
FIELD J (2001) Lifelong education. International Journal of Lifelong Education, 20 (1/2), pp. 3-15.
GILBERT N and Troitzsch K G (1999) Simulation for the Social Scientist. Buckingham: Open University Press.
GRASSÉ P P (1959) La construction du nid et les interactions inter-individuelles chez les bellicositermes natalenis et cubitermes sp. la théorie de la stigmergie: essai d'interprétation des termites constructeurs. Insectes Sociaux, 6, pp. 41-83.
GRIFFIN C (1999) Lifelong learning and social democracy. International Journal of Lifelong Education, 18(5), pp. 329-342.
HÄMÄLÄINEN M, Whinston A B and Vishik S (1996) Electronic Markets for Learning: Education Brokerages on the Internet. Communications of the ACM, 39(6), pp. 51-58.
KOPER E J R (1992) Studieondersteuning met behulp van de computer [computer based learner support]. Utrecht: Lemma.
KOPER E J R and Sloep P (2003) Learning Networks: connecting people, organizations, autonomous agents and learning resources to establish the emergence of effective lifelong learning (OTEC RTD Programme Plan 2003-2008). Heerlen: Open University of the Netherlands.
KOPER E J R and Olivier B (2004) Representing the Learning Design of Units of Learning. Educational Technology & Society, 7 (3), pp. 97-111. http://ifets.ieee.org/periodical/7_3/10.html
KOPER E J R and Tattersall C (2004) New directions for lifelong learning using network technologies. British Journal of Educational Technology, 35(6), pp. 689-700.
KOPER E J R, Giesbers B, Van Rosmalen P, Sloep P, Van Bruggen J, Tattersall C, et al. (in press) A Design Model for Lifelong Learning Networks. Interactive Learning Environments.
LAVE J and Wenger E (1991) Situated learning: Legitimate peripheral participation. Cambridge: Cambridge University Press.
LAW A M and Kelton W D (2000) Simulation Modeling and Analysis (third ed.). Boston: McGraw-Hill.
LOMI A and Larsen E R (Eds.) (2001). Dynamics of Organizations: computational modeling and organization theories. Cambridge: MIT Press.
LONGWORTH N (2003) Lifelong Learning in Action: Transforming Education in the 21st Century. London: Kogan Page.
MASON R (2004) ePortfolios in Lifelong Learning. British Journal of Educational Technology, Autumn, (this issue).
PASCARELLA E T and Terenzini P T (1980) Predicting freshmen persistence and voluntary drop-out decisions from a theoretical model. Journal of higher education, 51, pp. 60-75.
PYTHIAN T and Clements M (1982) Drop-out from third level math courses. Teaching at a Distance, 21, pp. 33-45.
RYAN R M and Deci E L (2000) Self-determination theory and the facilitation of intrinsic motivation, social developments and well being. American Psychologist, 55, pp. 68-78.
SHUELL T J (1992) Designing instructional computing systems for meaningful learning. In M Jones and P H Winne (Eds.), Adaptive Learning Environments. pp. 19-54. Berlin: Springer-Verlag.
SPADY W G (1970) Drop-outs from higher education: an interdisciplinary review and synthesis. Interchange, 2, pp. 38-62.
THERAULAZ G and Bonabeau E (1999) A Brief History of Stigmercy. Artificial Life, 5. pp. 97-116.
TINTO V (1975) Drop-out from higher education: a theoretical synthesis of recent research. Review of Educational Research, 45(1), pp. 89-125.
TINTO V (1982) Limits of theory and practice in student attrition. Journal of Higher Education, 53(6), pp. 687-700.
TREUER P and Jenson J D (2003) Electronic Portfolios need standards to survive. EDUCAUSE Quarterly, 2, pp. 34-42.
VINCENT S (1998) Input Data Analysis. In Banks J (Ed), Handbook of Simulation: Principles, Methodology, Advances, Applications, and Practice. pp. 55-92. New York, John Wiley.
WILENSKY U (1999) NetLogo. Center for Connected Learning and Computer-Based Modeling, Northwestern University. Evanston, IL. http://ccl.northwestern.edu/netlogo/ .
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]