André C. R. Martins (2005)
Deception and Convergence of Opinions
Journal of Artificial Societies and Social Simulation
vol. 8, no. 2
<https://www.jasss.org/8/2/3.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 10-Oct-2004 Accepted: 28-Jan-2005 Published: 31-Mar-2005
 Abstract
Abstract| q = f(Ra|p,a,b) = pa + (1 - p)(1 - b) | (1) |
| Q = f(Ra|p,e,d,a,b) = ed + (1 - e)[pa + (1 - p)(1 - b)] | (2) |
BAYES.F, as well as the subroutines, are all in the file Deception_code.zip. The priors are chosen as the discrete approximation to Beta functions with average and standard deviation chosen, favoring neither A or B. This was implemented by choosing uniform priors for both p and d. At each iteration, one article is randomly generated, with the chance of it supporting A based on the chosen true values of the parameters, that is, p = 1 and an amount of deception chosen for each simulation so that we have a total probability of observing an article supporting A given by
| q = de + (1 - e) a |
|
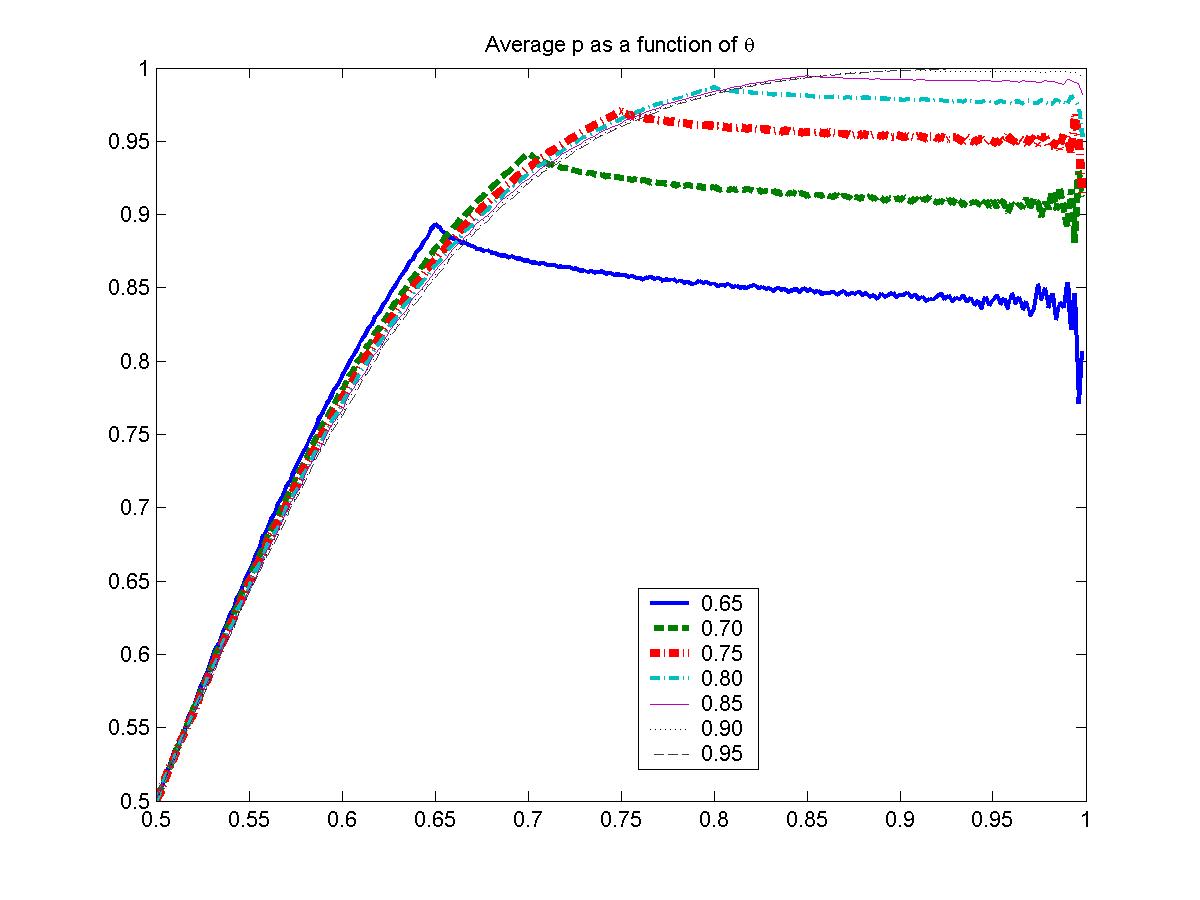
| Figure 1. Theoretical results for E[p] as a function of q, for several different values of a = b, where it was taken that E[e] = 0.2 |
|
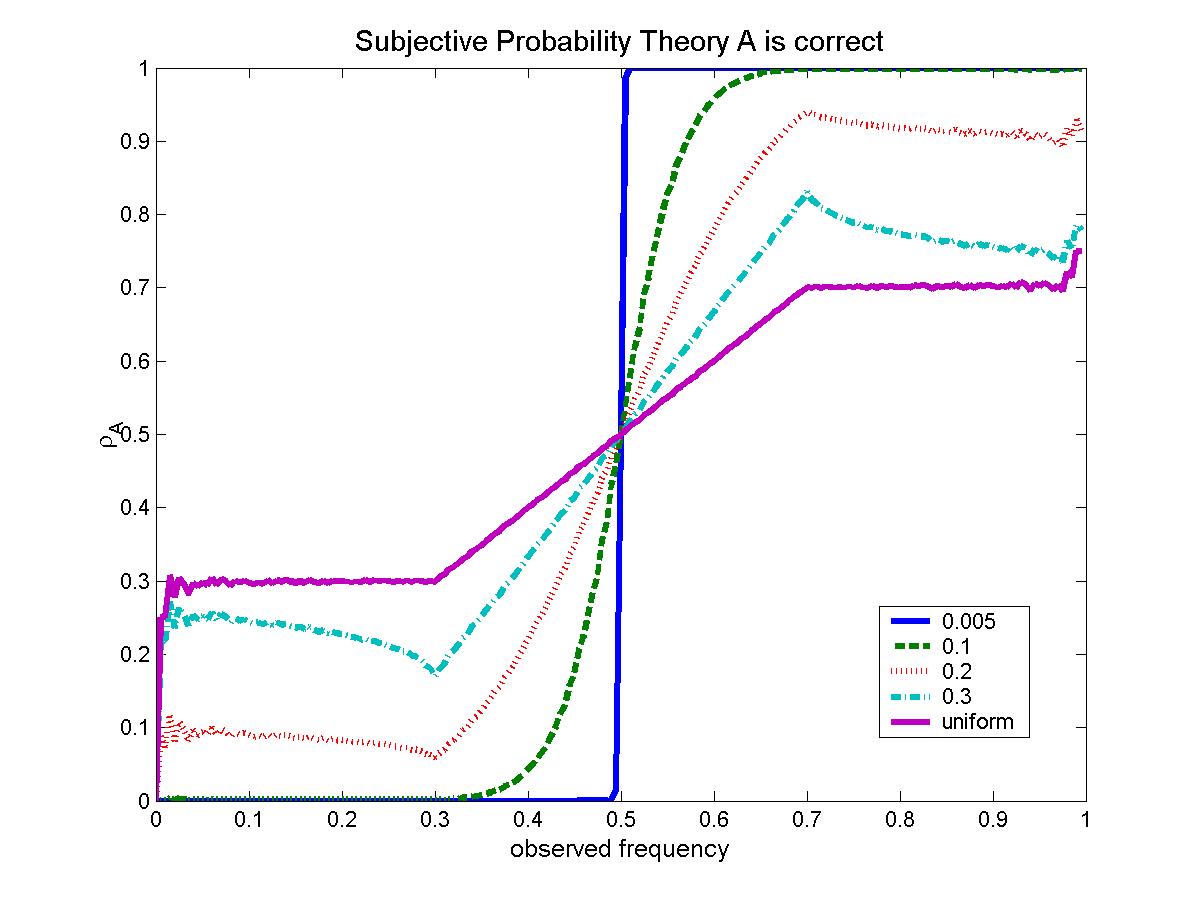
| Figure 2. Theoretical results for E[p] as a function of q for several prior distributions for the amount of deception (a = b = 0.7) |
It can be seen that, for a small amount of prior belief on deception, the reader decides which theory is correct, with certainty, based simply on the majority of articles supporting one opinion or the other. That is, the max rule studied by Lane [3] is a consequence of Bayesian analysis when there is basically no deception.
|
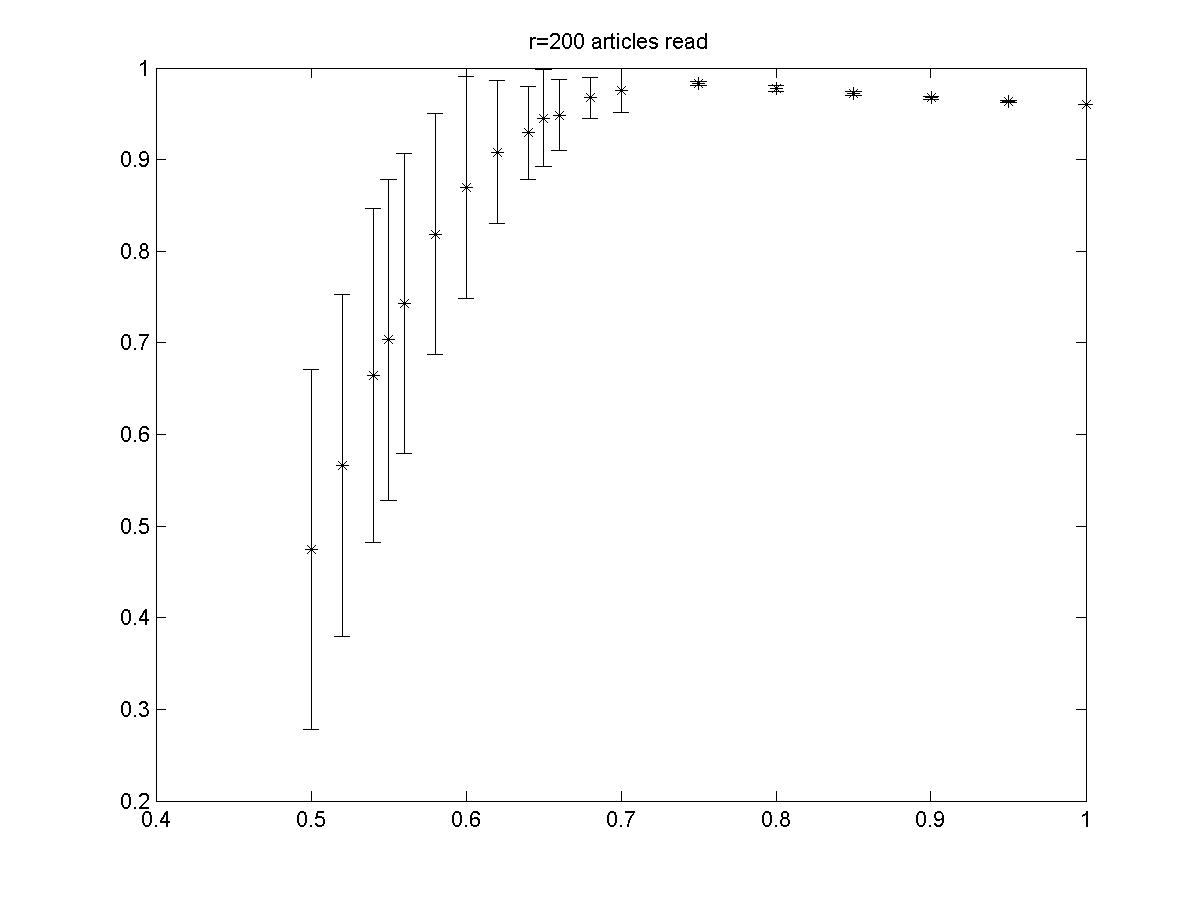
| Figure 3. E[p] as a function of q for a = b = 0.6 and r = 200 |
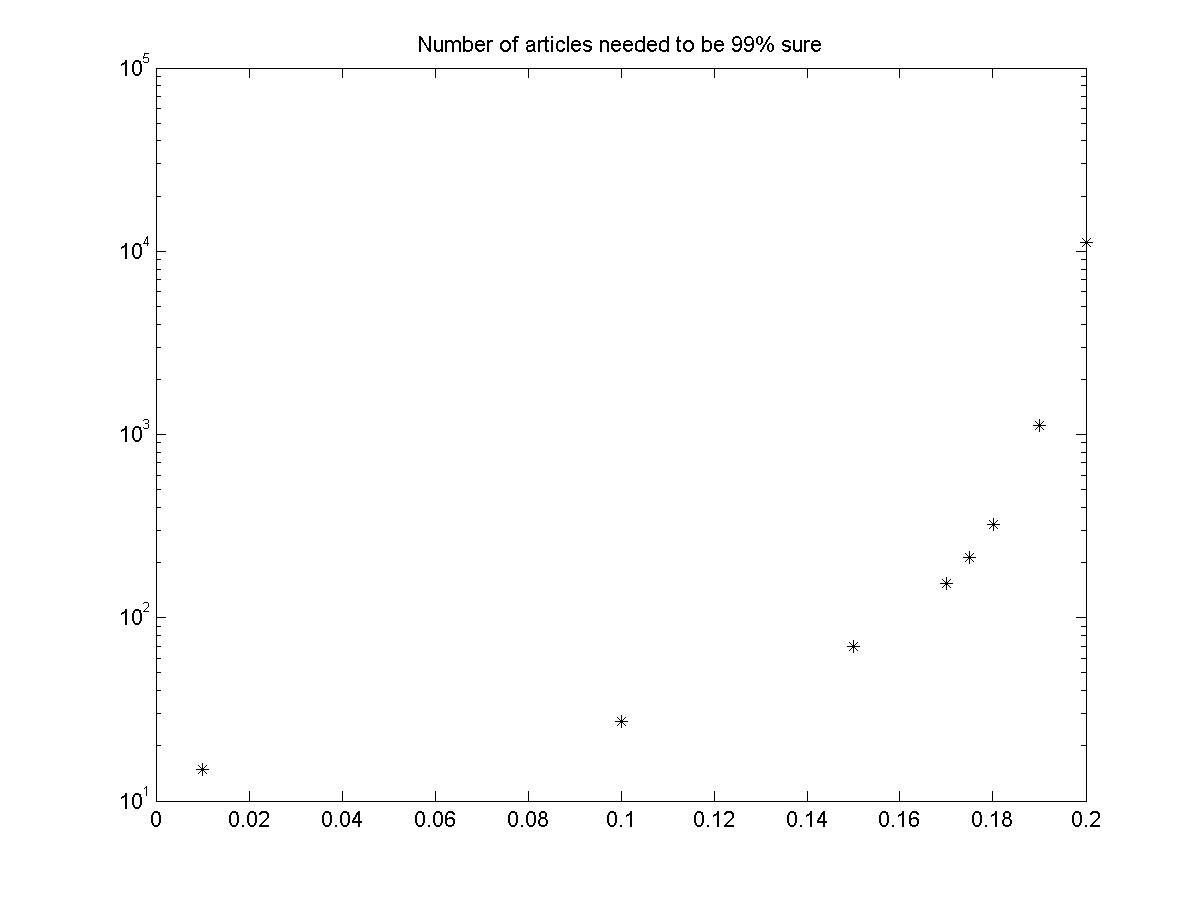
|
| Figure 4. Average number of articles one must read to be 99% sure of which theory is correct |
ELLSBERG, D. (1961) Risk, ambiguity and the Savage axioms. Quart. J. of Economics, 75, 643-669.
GIGERENZER, G., Goldstein, D. G. (1996) Reasoning the fast and frugal way: Models of bounded rationality. Psych. Rev., 103, 650-669.
HEGSELMANN, R. and Krause, U. (2002) Opinion Dynamics and Bounded Condence Models, Analysis and Simulation, Journal of Artificial Societies and Social Simulations, vol. 5, no. 3.
JAYNES, E.T. (2003) Probability Theory: The Logic of Science.Cambridge: Cambridge University Press.
LANE, D. (1997) Is What Is Good For Each Best For All? Learning From Others In The Information Contagion Model, in The Economy as an Evolving Complex System I (ed. by Arthur, W.B., Durlauf, S.N. and Lane, D.), pp. 105-127. Santa Fe: Perseus Books.
MAHER, P. (1993) Betting on Theories. Cambridge: Cambridge University Press.
MARTIGNON, L. (2001) Comparing fast and frugal heuristics and optimal models in G. Gigerenzer, R. Selten (eds.), Bounded rationality: The adaptive toolbox. Dahlem Workshop Report, 147-171. Cambridge, Mass, MIT Press.
MARTINS, A. C. R. (2005) Are Human Probabilistic Reasoning Biases Actually an Approximation to Complex Rational Behavior?, in preparation
PLOUS, S. (1993) The Psychology of Judgment and Decision Making. New York, NY: McGraw Hill, Inc.
SZNAJD-Weron, K. and Sznajd, J. (2000) Opinion Evolution in Closed Communities, Int. J. Mod. Phys. C 11, 1157.
WEIDLICH, W. (2000) Sociodynamics Amsterdam: Harwood Academic Publishers.
WEISBUCH, G. et al (2001) Interacting Agents and Continuous Opinion Dynamics, condmat0111494.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]