Hu Bin and Xia Gongcheng (2005)
Integrated Description and Qualitative Simulation Method for Group Behavior
Journal of Artificial Societies and Social Simulation
vol. 8, no. 2
<https://www.jasss.org/8/2/1.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 16-Mar-2004 Accepted: 28-Dec-2004 Published: 31-Mar-2005
 Abstract
Abstract|
|
where lk or lk+1 ∈ L, k or k+1 ∈ {1,2,...,p}, L is the quantity space of the landmark values (the values of state variables at distinguished time points). inc, std and dec represent the change direction of xi. inc means "increase", dec means "decrease" , and std means "standard" (no change).
|
|
| Figure 1. Basic causal graph |
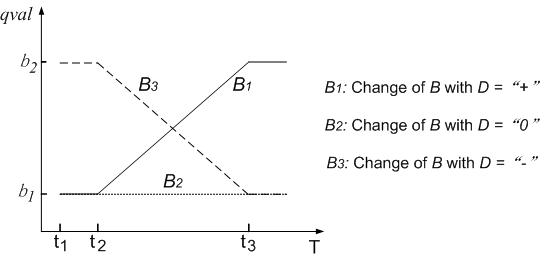
|
| Figure 2. Change of B |

|
| Figure 3. Schematic framework of an employee group system |
Before deriving the QSIM description for the above factors and their complex relationships, we give an example.
| QS(x, ti) = <qval> | (1) |
where x ∈ {X1, X2}, ti indicates that X1 or X2 changes only at a distinguished time point, ti ∈ {t0, t1, ..., tn } is a distinguished time point, qval ∈ {"-", "0", "+"}. For X1, "-", "0" or "+" indicates negative, no influence or positive, respectively. For X2, "-", "0" or "+" indicates low, moderate or high, respectively.
| QS(f, ti) or QS(f, ti, ti+1) = <qval, qdir> | (2) |
where f ∈ { G1, G2, G3, G4, G }, qval is the magnitude of f and qdir is its change direction. In qualitative simulation, the simulation clock is moved alternately to the time point and in the time interval, which are referred to as time stages. Therefore, the time stages are:
t0, (t0, t1), t1, (t1, t2), ......, ti, (ti, ti+1), ti+1, ......(tn-1, tn), tn
|
|
(3) |
where lj ={-1,0,1}. lk is the landmark value of f, and is the same as the distinguished value of f. (lk, lk+1) indicates that the value of qval is between lk and lk+1.
| qdir = {2-, -, 0, +, 2+} | (4) |
where "-", "0" and "+" refer to change directions down, no change and up, respectively. "2" indicates that the change speed of f is very high. We use "2" to indicate the degree to which the cause variable affects f. When the cause variable has a great effect (negative or positive) on f, then the state variable in qdir is "2".
|
|
(5) |
|
|
(6) |
|
| Figure 4. Causal graph used in this paper |
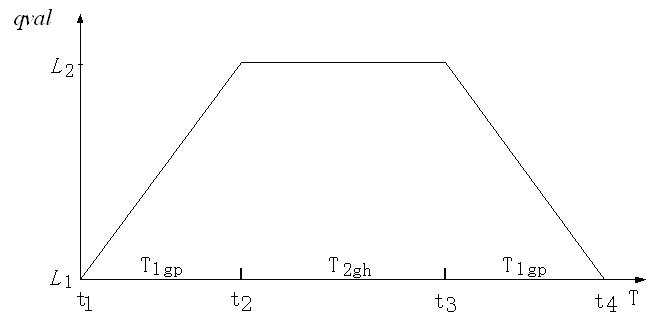
|
| Figure 5. Transition of B with D="+" |
"2" means that T2gh dictates the length of time that B stays at a landmark value (does not change). In Figure 5, time period (t2, t3) is T2gh. After B reaches L2, it remains for the length of time referred to by T2gh.
"g" represents the state variable. g ∈ {0, 1, 2, 3, 4}. "0", "1", "2", "3" and "4" indicate that B is G, G1, G2, G3 and G4, respectively. "p" represents the change speed of B. p ∈ {1, 2}. "1" means fast, "2" means slow. So in Figure 5, "1" indicates that the time period (t1, t2) or (t3, t4) is short, while "2" indicates that the period is long.
"h" represents the duration of T2gh. h ∈ {0, 1, 2, ∞}. "0" indicates that T2gh = 0 (B does not stay at L2). Once it reaches L2, it immediately returns to L1. "1" indicates the T2gh is a short period of time (B delays at L2 for a short period of time). "2" indicates that T2gh is a long period of time (B delays at L2 for a long period of time). " ∞" indicates that T2gh is an infinite period of time (B will never return to L1).
"h" can be used to refer to the organizational culture of the enterprise. When D = "+", h ="1" indicates that the group is behaving normally, with slight variations. Once the state variable reaches the new landmark value, it will stay there for a short period of time, and then, will return to its original state. h ="2" indicates that the group is behaving normally with no variations. Once the state variable reaches the new landmark value, it will stay there for a long period of time. By using "h" this way we are able to illustrate the effect of organizational culture.
.jpg)
|
| (a) |
.jpg)
|
| (b) |
| Figure 6. Transition of B with D = "-" |
|
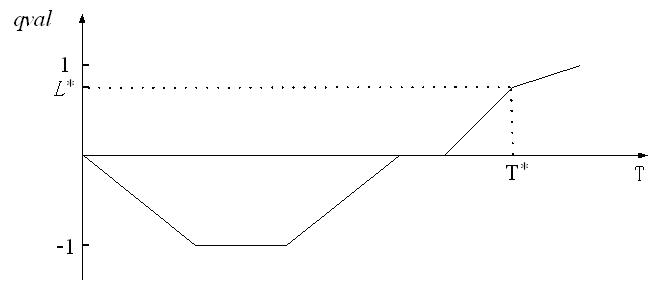
| Figure 7. The generation of the new landmark value L* |
|
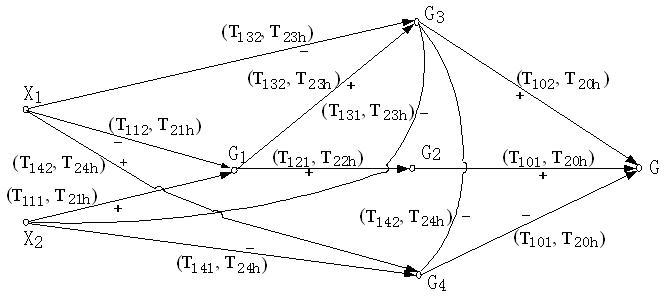
| Figure 8. Group Behavior Causality |
Figure 8 is not a generic model for all enterprises, but serves as an example for the illustration and validation of the proposed method.
Rule 2: Reasoning Sequence. In Figure 8, the reasoning sequence of variables runs from left to right. However, changes to state variables all happen at the same time and not from left to right.
Rule 3: Calculation of the change of direction of B.
Let CDB be the change of direction of B. According to Figure 4, CDB depends on D and QS(A, ti). If A is the environment or decision variable, the calculation of CDB is performed as illustrated by Table 1. For example, suppose A is X1 and QS(X1, ti) = <+>, meaning that new or updated software has been released. Suppose B is G3 (the cohesion of the informal sub-group). Therefore, if D = "-", then the CDB of G3 is "-".
If A is a state variable, the calculation of CDB is done as illustrated by Tables 2 and 3. The state variable is expressed by a 2-tuple with qval and qdir, so CDB is calculated by qval or qdir. Since the value of qdir is expressed as either "-", "0" or "+", the way we calculate CDB using qdir in Table 2 is identical to the way it is done in Table 1.
However, the value of qval is expressed in three ways: "less than 0", "0" and "greater than 0" (See Table 3). These values are represented by "-", "0" and "+" respectively. Therefore, the way to calculate CDB using qval in Table 3 is also the same as Table 1.
| Table 1: Calculation of CDB (if A is environment or decision variable) | |||
| QS(A, ti) D | - | 0 | + |
| - | + | 0 | - |
| 0 | 0 | 0 | 0 |
| + | - | 0 | + |
| Table 2: Calculation of CDB using qdir (if A is the state variable) | |||
| Qdir of QS(A, ti) D | -/2- | 0 | +/2+ |
| - | + | 0 | - |
| 0 | 0 | 0 | 0 |
| + | - | 0 | + |
| Table 3: Calculation of CDB using qval (if A is state variable) | |||||
| qval of QS(A, ti) D | -1 | (-1,0) | 0 | (0,1) | 1 |
| - | + | + | 0 | - | - |
| 0 | 0 | 0 | 0 | 0 | 0 |
| + | - | - | 0 | + | + |
Rule 4: Calculation of p.
When A is a state variable, during the change process of B, the values of p are calculated as follows:
IF qdir of A is "2+" or "2-", then p = "1"
IF qdir of A is "+" or "-", then p = "2"
IF qdir of A is "0", then B remains unaffected.
"2" indicates that the effect of A on B is great. This causes A to change quickly in the next time stage. So p = "1". If there is no "2" in qdir of A, then the effect is moderate, and p = "2".
Rule 5: State transition.
The state transitions of B are illustrated in Figure 9 according to the rules outlined above, and in which h is calculated according to the following:
IF CDB ="+" and the group is behaving normally with slight variations, then h = "1".
IF CDB ="+" and the group is behaving normally with no variations, then h = "2".
IF CDB ="-" and group morale is high, then h = "0".
IF CDB ="-" and group morale is normal, then h = "1".
IF CDB ="-" and group morale is low, then h = "2".
IF CDB ="-" and group morale is very low, then h = " ∞".
CDB = "+" shows that qval of B has increased. CDB = "-" shows that qval of B has decreased. The state transitions of B imply common group dynamics and organizational culture. Since group dynamics and organizational cultures are varied and complex, the possible ways in which B can change are varied. These possibilities are illustrated in subfigures of Figure 9.
.jpg)
|
| Figure 9a. State transitions of B when CDB = "+", p = "2", h= "2" |
Figure 9(a) illustrates a case where A has a moderate effect on B which causes the group to behave normally with no variations. This is expressed as p = "2" and h= "2". If p = "2", this indicates that B will take a long period of time to reach the landmark value L2. Since h= "2" after B reaches L2, it will stay at L2 for a long period of time.
.jpg)
|
| Figure 9b. State transitions of B when CDB = "+", p = "2", h= "1" |
Figure 9(b) illustrates a case where A has a moderate effect on B which causes the group to behave normally with slight variations. This is expressed as p = "2" and h= "1". Since h= "1" after B reaches L2, it will stay at L2 for a short period of time.
.jpg)
|
| Figure 9c. State transitions of B when CDB = "+", p = "1", h= "1" |
Figure 9(c) illustrates a case where A has a great effect on B which causes the group to behave normally with slight variations. This is expressed as p = "1" and h= "1". Since p = "1", B will take a short period of time to reach the landmark value L2.
.jpg)
|
| Figure 9d. State transitions of B when CDB = "+", p = "1", h= "2" |
Figure 9(d) illustrates a case where A has a great effect on B which causes the group to behave normally with no variations. This is expressed as p="1" and h= "2" which results in the same as above.
.jpg)
|
| Figure 9e. State transitions of B when CDB = "-", p = "2", h = "0" |
Figure 9(e) illustrates a case where A has a moderate effect on B and where group morale is high. This is expressed as p = "2" and h= "0". Since group morale is high (h= "0"), after B falls (decreases) to L2, it will immediately increase back to its original value.
.jpg)
|
| Figure 9f. State transitions of B when CDB = "-", p = "2", h= "1" |
Figure 9(f) illustrates a case where A has a moderate effect on B and where group morale is normal. This is expressed as p = "2" and h= "1". Since group morale is normal after B falls to L2, it will not increase immediately, but will do so over a short period of time.
.jpg)
|
| Figure 9g. State transitions of B when CDB = "-", p = "2", h= "2" |
Figure 9(g) illustrates a case where A has a moderate effect on B and where group morale is low. This is expressed as p = "2" and h= "2". Since group morale is low, after B falls, it will remain low for a long period of time.
.jpg)
|
| Figure 9h. State transitions of B when CDB = "-", p = "2", h= " ∞" |
Figure 9(h) illustrates a case where A has a moderate effect on B and where group morale is very low. This is expressed as p = "2" and h= " ∞". Since group morale is very low, after B falls, it will remain low indefinitely.
.jpg)
|
| Figure 9i. State transitions of B when CDB = "-", p = "1", h= "0" |
Figure 9(i) illustrates a case where A has a great effect on B and where group morale is high. This is expressed as p = "1" and h= "0".
.jpg)
|
| Figure 9j. State transitions of B when CDB = "-", p = "1", h= "1" |
Figure 9(j) illustrates a case where A has a great effect on B and where group morale is normal. This is expressed as p = "1" and h= "1".
.jpg)
|
| Figure 9k. State transitions of B when CDB = "-", p = "1", h= "2" |
Figure 9(k) illustrates a case where A has a great effect on B and where group morale is low. This is expressed as p = "1" and h= "2".
.jpg)
|
| Figure 9l. State transitions of B when CDB = "-", p = "1", h= " ∞" |
Figure 9(l) illustrates a case where A has a great effect on B and where group morale is very low. This is expressed as p = "1" and h= " ∞".
Rule 6: Time priority (the successor state filter).
When A affects B, B may have several successor states after transition. The function of this rule is to filter out anomaly successor states that do not exist in reality. This rule also determines the distinguished time point of B. The rule is as follows:
The distinguished time point of B is the time point at which a successor state reaches the landmark value first. The corresponding value on the Y-axis is the landmark value of B and all remaining successor states are filtered out. There are two variations on this rule:
Rule 7: State combination.
Following Rule 6, if the successor states of B have different qval and inconsistent qdir, then the following is applied in order to combine them.
|
|
is the number of successor states. Their mean values are:
|
|
Then the rules are:
| IF SQV<1 then B's qval = -1 | IF SQD<1 then B's qdir = 2- |
| IF SQV=-1 then B's qval = (-1, 0) | IF SQD=-1 then B's qdir = - |
| IF SQV = 0 then B's qval = 0 | IF SQD = 0 then B's qdir = 0 |
| IF SQV = 1 then B's qval = (0, 1) | IF SQD = 1 then B's qdir = + |
| IF SQV > 1 then B's qval = 1 | IF SQD > 1 then B's qdir = 2+ |

|
| Figure 10. Conceptual model of integrated qualitative simulation with inputs and outputs |
(2)G3
1)By X1, QS(G3, 0, t1)= <(-1, 0), -> where t1 = T132
2)By G1, QS(G3, 0, t1)= <(0, 1), +> where t1 = T132
3)By X2, QS(G3, 0, t1) = <(-1, 0), -> where t1 = T131
Choose X2 as the cause variable where t1 = T131.
(3)G2
By G1, QS(G2, 0, t1)= <(0, 1), +> where t1 = T121.
(4)G4
1)By X1, QS(G4, 0, t1)= <(0,1),+> where t1 = T142
2)By X2, QS(G4, 0, t1)= <(-1,0),-> where t1 = T141
3)By G3, QS(G4, 0, t1)= <(0,1),+> where t1 = T142
Choose X2 as the cause variable where t1 = T141.
(5)G
1)By G2, QS(G, 0, t1)= <(0,1),+> where t1 = T101
2)By G3, QS(G, 0, t1)= <(-1,0),-> where t1 = T102
3)By G4,QS(G, 0, t1)= <(0,1),+> where t1 = T101
Therefore combine QS(G, 0, t1)= <(0, 1), +> where t1 = T101.
We will use one example from the above to help clarify the meaning of the simulation as a whole. We will use number 1: "By X1, QS(G1, 0, t1) = <(-1, 0), ->, where, t1 = T112".
"By X1" refers to the effect had by X1 on state variable G1. "QS(G1, 0, t1) = <(-1, 0), ->" shows that the value of G1 has been affected and changed to <(-1, 0), -> ) in the time interval (0, t1) from QS(G1, t0) = <0, 0>. "T112" is a time period as is previously explained. However, it is used here to record the time of t1. It indicates that the time period from 0 to t1 is T112. Therefore t1 is a fuzzy time point. We do not know the exact duration, only that the period of time between 0 and T112 is long. We know this because p = "2".
Now t1 = T101. This indicates that the time period between 0 and t1 is T101.
According to Rule 6, because T132>T131, time point t3 = T131+T131+T131, and G3 generates a new landmark value L*31. QS(G3, t2, t3) = <(0, L*31), +> where t3 = T131+T131+T131.
Because T142>T141, time point t3 = T141+T141+T141, and G4 generates a new landmark value L*41, QS(G4, t2, t3)= <(-1, L*41), -> where t3 = T141+T141+T141.
Because T132>T131, time point t4 = T131+T131+T131+T131, and G3 generates a new landmark value L*32, QS(G3, t3, t4)= <(0, L*32), -> where t4 = T131+T131+T131.
Because T142>T141, time point t4 = T141+T141+T141+T141, and G4 generates a new landmark value L*42.
In this simulation run, T1g1, T2g1 represent a short period of time (because p = "1"). T1g2, T2g2 represent a long period of time (because p = "2"). The results are listed in table 4.
| Table 4: Simulation results | |||||
| QS(G1, t) | QS(G2, t) | QS(G3, t) | QS(G4, t) | QS(G, t) | |
| T = t0 | <0, 0> | <0, 0> | <0, 0> | <0, 0> | <0, 0> |
| T =(t0, t1) | <(0, 1), +> | <(0, 1), +> | <(-1, 0), -> | <(-1, 0), -> | <(0, 1), +> |
| T = t1 | <1, 0> | <1, 0> | <-1, 0> | <-1, 0> | <1, 0> |
| T =(t1, t2) | <1, 0> | <1, 0> | <(-1, 0), +> | <(-1, 0), +> | <1, 0> |
| T = t2 | <1, 0> | <1, 0> | <0, 0> | <0, 0> | <1, 0> |
| T =(t2, t3) | <1, 0> | <1, 0> | <(0, L*31), +> | <(-1, L*41), -> | <1, 0> |
| T = t3 | <1, 0> | <1, 0> | < L*31, 0> | <L*41, 0> | <1, 0> |
| T =(t3, t4) | <(0, 1), -> | <(0, 1), -> | <(0, L*32), -> | <(L*41, L*42), +> | <(0, 1), -> |
| T = t4 | <0, 0> | <0, 0> | <L*32, -> | < L*42, +> | <0, 0> |
.jpg)
|
.jpg)
|
|
| Figure 11. Change process of state variables |
| Table 5: Simulation results of Alternative 1 | |||||
| QS(G1, t) | QS(G2, t) | QS(G3, t) | QS(G4, t) | QS(G, t) | |
| T =(t3, t4) | < L*, 0> | < L*, 0> | <(L*31, 1), +> | <(L*41, 0), +> | < 1, 0> |
| T = t4 | < L*, 0> | < L*, 0> | <1, 0> | < 0, 0> | < 1, 0> |
| T =(t4, t5) | <( L*,1), +> | <( L*,1), +> | <1, 0> | <(L*41, 0), -> | < 1, 0> |
| T = t5 | <1, 0> | <1, 0> | <1, -> | <L*41, 0> | <1, 0> |
| T =(t5, t6) | <(0,1), -> | <(0,1), -> | <(L*32, 1), -> | <(L*41, L*42), +> | <(0,1), -> |
| T = t6 | <0, 0> | <0, 0> | <L*32, 0> | <L*42, 0> | <0, 0> |
| Table 6: Simulation results of Alternative 2 | |||||
| QS(G1, t) | QS(G2, t) | QS(G3, t) | QS(G4, t) | QS(G, t) | |
| T =(t4, t5) | <(0,1), +> | <(0,1), +> | <L*32, 0> | <L*42, +> | <(0,1), +> |
| T = t5 | <1, 0> | <1, 0> | <L*32, 0> | < 0, 0> | <1, 0> |
| T =(t5, t6) | <1, 0> | <1, 0> | <( L*32, L*31), 0> | <(L*41, 0), -> | <1, 0> |
| T = t6 | <1, 0> | <1, 0> | <L*31, 0> | <L*41, 0> | <1, 0> |
| T =(t6, t7) | <(0,1), -> | <(0,1), -> | <( L*32, L*31), -> | <(L*41, L*42), +> | <(0,1), -> |
| T = t7 | <0, 0> | <0, 0> | <L*32, -> | <L*42, 0> | <0, 0> |
.jpg) .jpg)
|
| Figure 12. Illustration of Alternative 1 |
.jpg)
.jpg)
|
| Figure 13. Illustration of Alternative 2 |
BERNDSEN R, Daniels H (1994), Causal Reasoning and Explanation in Dynamic Economic Systems. Journal of Economic Dynamics and Control, 1994,18:251-271.
BERENDS R, Romme G (1999), Simulation as a Research Tool in Management Studies. European Management Journal, 1999, 17(6):576-583.
BROOKS I (2003), Organisational behavior: individuals, groups and organization. Harlow: FT Prentice Hall, 2003.
CEM Say A C, Akyn H L (2003), Sound and complete qualitative simulation is impossible. Artificial Intelligence, 2003, 149: 251-266.
CLANCY J D, Kuipers J B (1998), Qualitative Simulation as a Temporally-extended Constraint Satisfaction Problem. Proceedings of the Fifteenth National Conference on Artificial Intelligence(AAAI-98), Cambridge, Ma: AAAI/MIT Press, 1998.
DIJKUM C, DeTombe D and Kuijk E (1999), Validation of Simulation Models. Amsterdam: SISWO (SISWO Publication 403), 1999.
GLYMOUR C (2003), Learning, prediction and causal Bayes nets. TRENDS in Cognitive Sciences, 2003, 7(1):43-48.
GUERRIN F, Dumas J (2001), Knowledge representation and qualitative simulation of salmon redd functioning Part I: qualitative modeling and simulation. BioSystems, 2001, 59:75-84.
IWASAKI Y (1988), Causal Ordering in a Mixed Structure. Proceedings of the Seventh National Conference on Artificial Intelligence(AAAI-88), St Paul, Minnesota,1988:313-318.
IWASAKIY, Y and Simon H A (1986), Causality in design behavior. Artificial Intelligence, 1986, 29(1):3-32.
KUIPERS J B (1986), Qualitative Simulation. Artificial Intelligence. 1986,29:289-338.
KUIPERS J B (1993), Qualitative Simulation: Then and Now. Artificial Intelligence, 1993, 59:133-1140.
KUIPERS J B (1993), Reasoning with qualitative models. Artificial Intelligence, 1993, 59:125-132.
KUIPERS J B (1994), Qualitative Reasoning: Modeling and Simulation with Incomplete Knowledge, Artificial Intelligence, MIT Press, Cambridge, MA, 1994.
LIN K P, Farley A M (1995), Causal reasoning in Economic Models. Decision Support Systems, 1995,15:167-177.
PEARL J (2000), Causality: Models, Reasoning, and Inference. Cambridge University Press, Cambridge, 2000.
PLATZNER M, Rinner B, Weiss R (1997), Parallel Qualitative Simulation. Simulation Practice and Theory, 1997, 5 (7-8):623-638.
PLATZNER M, Rinner B (2000), Toward Embedded Qualitative Simulation: A Specialized Computer Architecture for QSIM. IEEE Intelligent System, 2000, March/April: 62-68.
SALVANESCHI P, Cadei M, Lazzari M (1997), A Causal Modelling Framework for the Simulation and Explanation of the behavior of Structure. Artificial Intelligence in Engineering, 1997, 11:205-216.
SHEN Q and Leitch R R (1993), Fuzzy Qualitative Simulation. IEEE Trans. Syst. Man & Cybernet, 1993, 23.
WELD D (1990), Exaggeration. Artificial Intelligence, 1990, 43: 311-368.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2005]