Maria Fasli (2004)
Formal Systems ∧ Agent-Based Social Simulation = ⊥?
Journal of Artificial Societies and Social Simulation
vol. 7, no. 4
<https://www.jasss.org/7/4/7.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 16-Dec-2003 Accepted: 05-Jun-2004 Published: 31-Oct-2004
 Abstract
AbstractI(i, γ ) ⇒ B(i, γ ) D(i, γ ) ⇒ ¬B(i, ¬ γ )
succeeded( decommit ( si, sj, inevitable ◊ φ ) ) ⇒ (¬ O( si, sj, inevitable ◊ φ ) ∧ done( communicate ( si, sj, MB( si, φ ) ) ) ) ∨ (¬ O( si, sj, inevitable ◊ φ ) ∧ done( communicate( si, sj, ¬ MB( si, optional ◊ φ ) ) ) ∧ done( communicate( si, sj, ¬ O( si, sj, inevitable ◊ φ ) ) ) )
Right( sj, si, ψ ) ∧ MB( sj, ¬ O(si, sj, inevitable ◊ φ ) ) ∧ ¬ MB( sj, φ ) ⇒ optional( MI( sj, optional ◊ ψ ) )
Right( sj, si, ψ ) ∧ MB(sj, ¬ O( si, sj, inevitable ◊ φ )) ∧ ¬ MB(sj, φ ) ⇒ inevitable( MI( sj, inevitable ◊ ψ ) ) U MB( sj, ψ )
Pref(i, φ , ψ ) ⇒ B( i, optional ◊ φ ) ∧ ¬ B( i, optional ◊ ψ )
EPref( si, φ , ψ ) ≡def ∀ i ( i ∈ si) ⇒ Pref( i, φ , ψ )Then a mutual preference among the members of a social agent si is defined as:
MPref( si, φ , ψ ) ≡def EPref( si, φ , ψ ) ∧ MB( si, EPref( si, φ , ψ ) )
SCom( si, sj, φ ) ⇔ O( si, sj, φ ) ∧ Right( sj, si, ψ ) ∧ MI( si, φ ) ∧ MB( {si,sj}, (O( si, sj, φ ) ∧ MI( si, φ ) ∧ Right(sj,si, ψ ) ) )
SCom( si, sj, inevitable ◊ φ ) ⇒ inevitable( SCom( si, sj, inevitable ◊ φ ) U MB( si, φ ))
SCom( si, sj, inevitable ◊ φ ) ⇒ inevitable( SCom( si, sj, inevitable ◊ φ ) U (MB( si, φ ) ∨ ¬ MB(si, optional ◊ φ ) ) )
CCom( si, φ ) ⇔ ∀ i(i ∈ si) ⇒ SCom( i, si, φ ) ∧ MI( si, φ ) ∧ MB( si, MI( si, φ ))
RoleSCom( a, φ ) ∧ In( si, a, r) ⇒ ∃ sj,b In( sj, b, r) ∧ SCom( si, sj, φ ) ∧ ¬ (si = sj)
succeeded( droprole( si, sj, a )) ⇒ (¬ In( si, a, r ) ∧ ¬ SCom( si, sj, φ ) ∧ done( communicate( si, sj, ( ¬ In( si, a, r ) ∧ ¬ SCom( si, sj, inevitable ◊ φ ) ) ) ) ) ∨ (¬ In( si, a, r ) ∧ ¬ SCom( si, sj, φ ) ∧ done( communicate( si, sj, (¬In( si, a, r ) ∧ MB(si, φ ))))) ∨ (¬ In( si, a, r ) ∧ ¬ SCom( si, sj, φ ) ∧ done(communicate( si, sj, ( ¬ In( si, a, r ) ∧ ¬ MB( si, optional ◊ φ ))))An agent may also decide to drop a commitment which is part of its role without dropping the role itself and perhaps accepting that a form of sanction will have to be imposed.
In( J, student, r1 ), In( S, supervisor, r1 ) RoleScom( student, followadvice ) ∧ In( J, student, r1 ) ⇒ In( S, supervisor, r1 ) ∧ SCom( J, S, followadvice )
In( J, player, r2 ), In( A, team, r2 ) RoleScom( player, playgame ) ∧ In( J, player, r2 ) ⇒ In( A, team, r2 ) ∧ SCom( J, A, playgame )
SCom( J, S, writepaper ) ⇔ O( J, S, writepaper ) ∧ I( J, writepaper ) ∧ Right( S, J, inhibitprogress (S , J ) ) ∧ MB( {J,S}, O( J, S, writepaper ) ∧ I( J, writepaper ) ∧ Right( S, J, inhibitprogress( S, J) ) )
SCom( J, A, playgame ) ⇔ O( J, A, playgame ) ∧ I( J, playgame ) ∧ Right( A, J, exclude( A, J) ) ∧ MB({J,A}, O( J, A, playgame ) ∧ I( J, playgame ) ∧ Right( A, J, exclude( A, J ) ) )
Pref( J, writepaper, playgame )
Pref(J, exclude( A, J ), inhibitprogress( S, J ) )
B( J, optional ◊ writepaper ) ∧ ¬ B( J, optional ◊ playgame )
succeeded( decommit( J, A, inevitable ◊ playgame ) ) ⇒ (¬ O( si, sj, inevitable ◊ playgame ) ∧ done( communicate ( si, sj, ¬MB( si, optional ◊ playgame ))) ∧ done( communicate( si, sj, ¬ O( si, sj, inevitable ◊ playgame) ) ) )
CCom( A, wincup ) ⇔ ∀ i(i ∈ A) SCom( i, A, wincup ) ∧ MI( A, wincup ) ∧ MB( A, MI( A, wincup ) )
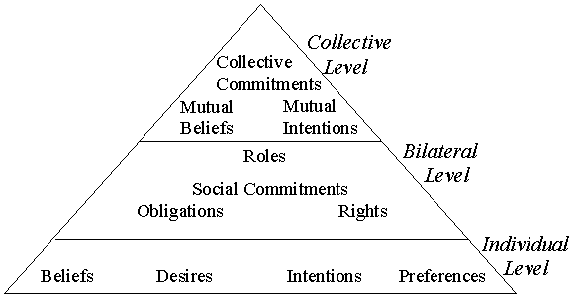
|
| Figure 1. The three levels of operators |
CASTELFRANCHI, C. (1995), "Commitments: From individual intentions to groups and organizations". In Proceedings of the First ICMAS Conference. pp. 41-48.
CAVEDON, L. and Sonenberg, L. (1998), "On social commitments, roles and preferred goals".
In Proceedings of the Third ICMAS Conference. pp. 80-87.
COHEN, P. R. and Levesque, H. J. (1991), Teamwork. Nous, 25. pp.485--512.
COHEN, P. R. and Levesque, H. J. (1990), Intention is choice with commitment. Artificial Intelligence, 42. pp. 213-261.
DENNETT, D. C. (1987), The Intentional Stance. The MIT Press.
DIGNUM, F., Kinny D. and Sonenberg L. (2002), "Motivational attitudes of agents: On desires, obligations and norms". In From Theory to Practice in Multi-Agent Systems, Proceedings of the Second International CEEMAS Workshop, Springer-Verlag. pp. 83-92.
DIGNUM, F., and Sonenberg, L. (2003), "A dialogical argument for the usefulness of logic in MAS". Available at: http://cfpm.org/logic-in-abss/papers/Dignum&Sonenberg-reply.pdf
DIGNUM, V., Meyer, J.-J. Ch., and Weigand, H. (2002), "Towards an organizational model for agent societies using contracts". In Proceedings of the First AAMAS Conference. pp. 694-695.
DUNIN-KEPLICZ, B. and Verbrugge R. (1999), "Collective motivational attitudes in cooperative problem solving". In Proceedings of the First International CEEMAS Workshop. pp. 22-41.
EDMONDS, B. (2003), "How formal logic can fail to be useful for modelling or designing MAS".
http://cfpm.org/logic-in-abss/papers/Edmonds.pdf
EDMONDS, B. (2002), "The purpose and place of formal systems in the development of science".
FAGIN, R., Halpern, J. Y., Moses, Y. and Vardi, M.Y. (1995), Reasoning about Knowledge, MIT Press, Cambridge, MA.
FASLI, M. (2000), Commodious Logics of Agents, PhD thesis, University of Essex, UK.
FASLI, M. (2003a), Heterogeneous BDI agents. Cognitive Systems Research, 4(1), pp.1-22.
FASLI, M. (2003b), Reasoning about knowledge and belief: A syntactical treatment. Logic Journal of the IGPL, 11(2), pp. 245-282.
FASLI, M. (2003c), "From social agents to multi-agent systems: Preliminary report". In Proceedings of the 2003 CEEMAS Conference. pp.111-121.
FASLI, M. (2003d), "Reasoning about the dynamics of social behaviour". In Proceedings of the AAMAS 2003 Conference. pp. 988-989.
FASLI, M. (2003e), "Social interactions in multi-agent systems: A formal approach". In Proceedings of the IEEE/WIC 2003 Intelligent Agent Technology Conference, pp. 240-246.
FERBER, J. and Gutknecht, O. (1998), "A meta-model for the analysis and design of organizations in multi-agent systems". In Proceedings of the Third ICMAS Conference, pp. 128-135.
HUGHES, G.E. and Cresswell M.J. (1968), An Introduction to Modal Logic. Methew & Co Ltd.
GROSZ, B. and Kraus, S. (1996) Collaborative plans for complex group action. Artificial Intelligence, 86(2). pp. 269-357.
KRAUS, S. and Lehmann, D. (1988), Knowledge, belief and time. Theoretical Computer Science, 58, pp.155-174.
MA, G. and Shi, C. (2000), "Modelling social agents in BDO logic". In Proceedings of the Fourth ICMAS Conference. pp. 411-412.
MCCARTHY, J. (1979), "Ascribing mental qualities to machines". In Ringle M. (Ed), Philosophical Perspectives in Artificial Intelligence. The Harvester Press Limited . pp. 161-195.
MONTAGUE, R. (1973), "The proper treatment of quantification in ordinary English". In Thomason R. (Ed), Formal Philosophy, Selected Papers of Richard Montague, Yale University Press. pp. 247-270.
RAO, A. and Georgeff, M. (1998), Decision procedures for BDI logics. Journal of Logic and Computation, 8(3). pp. 293-343.
RAO, A., Georgeff, M. and Sonenberg, E. (1992), "Social plans: A preliminary report". In Decentralised A.I.-3. pp. 57-76.
ROYAKKERS, L. and Dignum, F. (2000), "Organisations and collective obligations". In Proceedings of the Database and Expert Systems Applications Conference. pp. 302-311.
SALMON, N. and Soames, S. (1988), Propositions and Attitudes. Oxford University Press.
THOMASON, R. (1980). A note on syntactical treatments of modality. Synthese, 44. pp. 391-395.
van der HOEK, W. (1990), "Systems for knowledge and beliefs". In Proceedings of the European Workshop in Logics in Artificial Intelligence (JELIA '90), volume LNAI: 478, Springer-Verlag . pp. 267-281.
van der HOEK, W., van Linder, B. and Meyer, J.-J.Ch. (1998), "An integrated modal approach to rational agents. In Wooldridge M. and Rao A. (Eds), Foundations of Rational Agency, Applied Logic Series 14, Kluwer. pp. 133-168.
van LINDER, B., van der Hoek, W., and Meyer, J.-J.Ch. (1996), "Formalising motivational attitudes of agents: On preference, goals and commitments". In Wooldridge M., Muller J.P. and Tambe M. (Eds), Intelligent Agents II - Agent Theories, Architectures and Languages, LNAI: 1037, Springer-Verlag. pp. 17-32.
van der TORRE, L. and Tan Y.-H. (1999), "Rights, duties and commitments between agents". In Proceedings of the International Joint Conference on Artificial Intelligence (IJCAI'99). pp.1239-1244.
von WRIGHT G.H. (1963), The Logic of Preference. Edinburgh University Press, Edinburgh.
WOOLDRIDGE, M., Jennings, N.R. and Kinny, D. (2000), The Gaia methodology for agent-oriented analysis and design. Autonomous Agents and Multi-Agent Systems, 3. pp.285-312.
ZAMBONELLI, F., Jennings, N.R. and Wooldridge, M. (2001) "Organisational abstractions for the analysis and design of multi-agent systems". In Cinacarini P. and Wooldridge M. (Eds), Agent-Oriented Software Engineering. pp. 127-141.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2004]