Marie-Edith Bissey, Mauro Carini and Guido Ortona (2004)

ALEX3: a Simulation Program to Compare Electoral Systems

Journal of Artificial Societies and Social Simulation vol. 7, no. 3
<https://www.jasss.org/7/3/3.html>

To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary

Received: 05-Nov-2003    Accepted: 11-May-2004    Published: 30-Jun-2004

Abstract

The paper describes a program for comparing electoral systems based on the simulation of the preferences of the voters. The parameters requested (distribution of first preferences, district magnitude, etc) are set up by the user. The program produces the resulting Parliament under a number of electoral systems, an index of representativeness and an index of governability. The first part of the paper describes the characteristics of the program. In the second part it is used to compare eleven electoral systems in two virtual but realistic cases.

Keywords:

Electoral Systems, Electoral Simulation, Representativeness, Governability

A new program for the evaluation of electoral systems

1.1

In this first section, we describe a program for comparing electoral systems. It has been designed for the election of a (one-Chamber) Parliament, but may be used for analogous settings as well.

1.2

An electoral system affects many aspects of the political process^[1], though there is a general agreement that two of them are of paramount relevance: the efficiency of the system in representing voters' will (or representativeness, shortened as R) and its effect on the efficiency of the resulting government (or governability, shortened as G).

1.3

G and R may be evaluated through the assessment of numerical indicators, hopefully plausible but unavoidably arbitrary. We label them g and r respectively.

1.4

There should be no shyness in suggesting that electoral policies can be based on the values of indicators: this is what happens commonly in economic policing, where choices are frequently driven by changes of decimals in quite rough indicators like aggregate inflation or GNP growth rate.

1.5

The indicators are described in detail in ¶ 1.12. Briefly, g depends on the number of parties and of MPs supporting the Government, while r depends on the difference of seats attributed to parties under the system considered and under proportional representation, assumed to be the most representative system. The range of both is the interval 0-1.

Simulative assessment of electoral systems.

1.6

Consequently, we assume that electoral systems may be evaluated through their performance with reference to g and r. In order to do that, however, real data are of limited utility. The reason for this is obvious: the information collected is too poor. Among really-used systems only the single transferable vote and the approval vote provide information on second and further preferences. Only mixed-members systems provide information useful both for proportional and plurality voting. In addition, the real vote is strongly influenced by the electoral rules. For instance, usually there are few parties in first-past-the post constituencies, so there is no basis to assess the utility of a possible change to proportionality. If we want to compare, say, Condorcet voting with the majority rule or perfect proportionality, we cannot rest on reliable, comparable and generalizable real-world data.

1.7

This is why it is useful to resort to simulation. Our program, ALEX3, developed at the Laboratory for Experimental and Simulative Economics of the University of Piemonte Orientale, simulates the preferences of the voters for parties and candidates, and allows (for the moment) to compare eleven electoral systems, namely plurality, runoff majority, one-district pure proportionality, one-district threshold proportionality, multi-district pure proportionality, Condorcet, Borda, two mixed-member systems, single transferable vote and VAP. VAP is a suggested new system, described in detail in other papers (see Ortona 2000 and 2002a), presently undergoing testing at the University of Piemonte Orientale. By and large, the VAP system assigns a premium of votes (but not of seats) to the governing majority, in order to enhance governability. More on this can be found in Appendix 2^[2].

1.8

The basic features of the program are summarized in the next section, while a broader description is in Appendix 1; for a fully comprehensive description, however, you should resort to the user's guide, see Appendix 1. The remainder of this section describes the indicators and offers some suggestions for policy-making and for improving the program.

Basic features of ALEX3

1.9

The user can set up a number of characteristics, namely:

1. The size of the Parliament;
2. the number of voters;
3. the number of parties (i.e. the number of candidates in every constituency for non-proportional systems);
4. the district magnitude;
5. the share of votes of the parties;
6. the concentration of the parties across the constituencies;
7. other parameters necessary to create the voters' preference orderings for parties and candidates.

All data are requested through user-friendly windows.

1.10

The program allows to simulate realistic cases - for instance it is possible to create a "country" where there are some four medium-size parties and a cohort of small ones, with significant regional clusters, (similar to Italy today), as well as one with just two large parties and one or no minor ones, as majoritarian-system supporters like.

1.11

Once the parameters have been set up, the program creates the voters (with fully ordered preferences) and asks the user to choose the electoral systems to be employed. For each system the program produces the corresponding Parliament and the index r. Then the user can choose the parties supporting the government, and the program produces the index g.More than one parliament can be displayed on screen and the results can be saved as text files. This concludes the session, but data may be used for further elaboration, as will be suggested in section 5.

The indices.

1.12

The literature presents several indices of proportionality, like Gallagher's, Rae's, Lijphart's^[3], or Mudambi's (Mudambi 1997), which could be considered as good proxies for representativeness. However, proportionality indices are based on the difference between the share of votes and that of seats, which are both system-specific.

1.13

Therefore, those indices may be employed to compare the performance of a given electoral system across different cases, but are of no use if one aims instead to compare different electoral systems in a given case, which is the purpose of ALEX3.

1.14

The situation is slightly better for governability, where at least three indices may in principle be used, as well as sensible combinations of them^[4], i.e.,

1. Pre-election identifiability, which scores ("impressionistically", according to Shugart and Wattenberg 2000) 1 if electors may designate directly the government, 0 if they do not, 0.75 if there are two well-defined blocs but neither can be identified with a government before the election, and 0.5 when only one bloc is clearly defined.
2. Plurality enhancement, which is defined as s /0.5- v /0.5, where s is the share of seats of the largest party (or coalition), and v that of votes. A high value of the index means that "few" votes became "many" seats, thus allowing for a sounder majority.
3. Majority approximation, which scores 1 if one party (coalition) gets a majority, and s /0.5 if not, where s is the share of seats of the largest party.

1.15

These indices are not used in ALEX3 for the following reasons. Index a) is unsatisfactory, as it is too ill-defined for a quantitative analysis. Index b) again combines the share of votes with that of seats. Index c) may be used, but it may provide unrealistic results, and can be improved. For instance, the score is the same whether a party, ruling alone, has 51% or 90% of the seats. If the government is made up of a coalition of two parties, each with 40% of the seats, the value of the index is 0.8; a much weaker coalition of four parties with 42%, 3%, 3% and 3% scores more.

1.16

To sum up, there are no indices sufficiently sensible and fine-tuned to be employed in quantitative simulations in the literature. Hence we created new ones, both for representativeness and for governability. The index for representativeness draws on the basic idea of comparing votes and seats, using the votes expressed in proportional representation as indicative of the true preferences. The index for governability accepts the principle that the governability decreases with the number of the parties in the governing coalition, so it may be considered a refinement of the majority approximation index (c). For sake of clarity, both are standardized to the interval 0-1. Their description follows^[5].

1.17

Index of representativeness, r. In principle, the index for a given electoral system should be based on the difference between the distribution of seats assigned by that system and votes cast under pure proportionality. However, in a nation-wide district the share of votes and that of seats under pure proportionality may be safely assumed to be equal; hence the index is based on the difference between the distribution of seats in the system to which the index refers and in one-district pure proportionality. The formula is

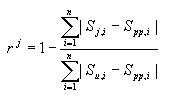
(1)

where j refers to the electoral system, n is the number of parties, S_j,i is the number of seats obtained by party i under system j, S_pp,i is the number of seats obtained by party i under perfect proportionality rule (PPR), and S_u,i is the number of seats obtained by party i if all the seats go to the largest party in system j ^[6].

1.18

The loss of representativeness incurred by party i is the (absolute) difference between the seats it would get under PPR and those actually obtained. Summing this loss across all the parties we obtain the total loss of R (first sum). In order to normalize this value, we divide it by the total possible loss of R. This maximum is obtained when the relative majority party takes all the seats (second sum). This way we got a loss of representativeness index. Subtracting it from 1 we transform it into a representativeness index.

1.19

Index r is obviously arbitrary, yet it is quite "natural", as it is simply the standardization of the sum of seats unduly lost or obtained.

1.20

Index of governability, g. It is generally assumed that governability is inversely related to the number of parties in the governing coalition. Though this assumption is subject to debate (see for example, Lijphart 1994, or Farrell 2001), it is the most important argument in favour of non-proportional systems. As a consequence, we use it as the basis for our governability index. More precisely, we assume that Governability depends mostly on m, the number of crucial parties of the governing coalition, i.e. those parties that destroy the majority if they withdraw; and secondarily on f, the number of seats of the majority. Hence, we add lexicographically the f -component, g_f, to the m-component, g_m. The range of g_f is the difference between successive values of g_m: the term in m defines a lower and an upper boundary, and the term in f specifies the value of the index between them.

1.21

g_m is equal to 1/(m + 1), hence the limits provided by its values are 1/m (upper boundary) and 1/(m + 1) (lower boundary). For instance, if the Government is supported by just one party, the range of g is between 0.5 and 1; if it supported by two (or by three and more, but with only two large enough to destroy the majority if they withdraw), g is comprised between 0.333 and 0.5, and so on. Note that the addition of new parties produces smaller and smaller decreases in g, as it should be: the loss of governability is high if we move from one to two parties in the governing coalition, whereas it is negligible if we move, say, from ten to eleven. The figure to be added to the lower boundary, g_f, depends on the lead of the majority coalition, according to the following proportion:

gf / [1/m - 1/(m+1)] = (f-t/2)/(t-t/2)

which yields

gf = [1/m - 1/(m+1)] (f-t/2)/(t/2)

where t is the total number of seats in the Parliament.

1.22

For instance, if there are 100 seats, and the governing majority is made up of one party with 59 MPs, the value of g_f is 0.09 (9/50*1/2). This value must be added to 0.5, to give a value of g equal to 0.59. Finally, the formula for g is:

g = gm +gf = 1/(m+1) + [1/m - 1/(m+1)] (f-t/2)/(t/2)

where m is the number of crucial parties supporting the Government, f is the number of seats of the majority and t is the total number of seats. The value of g reaches its maximum, 1, when a party has all the seats, and decreases with the increase of m, thus justifying the claim that the range of g is the interval (0,1].

1.23

Index g is quite natural too: it is the simplest possible index obeying three basic rules, i.e. (a) the governability is inversely related to the number of parties and to the number of seats of the governing coalition, (b) the number of parties is more relevant than the number of seats and (c) increasing the number of parties produces a declining decrease in governability, i.e. the marginal effect of the number of parties is decreasing.

Policy suggestions

1.24

The program may be used to study quite a lot of problems. The simple assessment of r and g for several systems in realistic cases is useful by itself. The effect of vote clustering on the performance of an electoral system could be assessed. It could be of interest to compare the results of pure proportionality with those of the single transferable vote, given different characteristics of the voters. One could investigate the relative performance of Condorcet and Borda, and thus put their souls to rest, as their ghosts are probably still debating somewhere in the skies. Also, it is possible to investigate experimentally the "real" occurrence of Condorcet cycles. And so on. In the second part of this paper we will see an application of the program to two realistic cases.

Future improvements

1.25

The next version of the program will include some new features^[7].

• First, we plan to include at least a power index, probably based on Banzhaf's. The analysis of the distribution of power is obviously of great interest per se; but it will also open the way to a different approach to the study of both governability and representativeness^[8]. Just to give a flavor of the problems that may be addressed: shall we desire a fair distribution of power, for the sake of representativeness, or a concentrated distribution of power for the sake of governability? Is it possible to find a system that best marries a fair distribution of power with a high level of governability - or vice-versa a concentrated power with a high level of representativeness?^[9]
• Second, we plan to introduce further indices both for G and R, in order to run a sensitivity analysis on the indices.
• Third, we plan to make the program apt to import databases of voters.
• Fourth, new voting systems will be added.
• Finally - further improvements may be suggested by the users. If you would like to be among them, please contact the author (see Appendix 1 for details).

An application: the choice of the best electoral system

Theory

2.1

Thanks to the theorems of Arrow and McKelvey, we know that the objectively best electoral system does not exist. But within the limits of our assumptions an electoral system that performs better than any other with reference to both G and R may empirically be deemed the best one (among those considered). Yet, such a system probably will not be found, as there is normally a trade-off between the two dimensions.

2.2

However, the policymaker can in principle establish a priori a relationship between R and G, in order to leave it to the electoral process to "objectively" produce the best system. Here we suggest a procedure^[10].

2.3

First, we assume that the social utility function for electoral systems is a Cobb-Douglas function in g and r, U = Ag^ar^b . This form is suitable not only for its simplicity and versatility, but also for the meaning of a and b, the partial elasticities of U with reference to g and r respectively.

2.4

Given two electoral systems, X and Y, we may write

Ux > Uy iff Agarb > AGaRb

(1)

where we write for simplicity the values of g and r for X in lower-case and those for Y in upper-case.

2.5

Now consider the ratio a/b, call it p. It may be characterized as the price in terms of a relative decrease of r that the community accepts to pay for a given relative increase of g (and 1/p the opposite). If for instance p = 2, it is worthwhile to accept a 20% reduction of r to gain a 10% increase in g^[11]. As the indifference curves are convex, this means that if G is very high it is worth paying a small increase in R with a large decrease in G, and vice-versa, as it should be.

2.6

Equation 1 reduces easily to

Ux > Uy iff (g/G)bp > (R/r)b

Hence the condition may be written as

pLn(g/G) > ln(R/r)

(2)

i.e.

p > ln(R/r)/Ln(g/G) if g > G or p < ln(R/r) / ln(g/G)

(3)

provided that g, or G, or both are < 1^[12].

2.7

The only a priori information requested is the value of p, the elasticity ratio. This ratio may be considered a proxy for the relative weight that the community assigns to relative increases in the value of g and r. If for instance a, say, 10% increase in g is valued more than the same increase in r, p > 1, and vice-versa. We argue that this parameter may actually be provided by the political system. There are several possibilities. For instance, the community may "start" with a = b, and change the ratio for the next election if the entity in charge thinks that representativeness or governability have been excessive. Another possibility is that the community order the systems according to their supposed degree of proportionality, and chooses the first one (i.e. PPR) if the value of g is above a given threshold; otherwise it moves to the second one, and so on. Under this rule, the best system is the most proportional one, provided that its governability reaches a given value (or viceversa, obviously).

Two case studies

2.8

We will consider two cases that mimic real-world ones, Italy and UK. Let's start from Italy, with reference to the 2001 election^[13]. Italy uses a mixed-member system, hence there is a proportional vote that provides the basic information. The real shares of the parties have been recomputed to exclude very small ones (accounting for less than 3%); twelve parties remaining. Once ordered from left to right, the (recomputed) share of votes were (in percentages) 5.18, 1.72, 2.23, 17.07, 14.96, 4.01, 2.46, 2.31, 3.32, 30.31, 4.06 and 12.37 respectively. All other parameters have been set at their default values (which makes this inquiry more exploratory than conclusive). We assumed, to start with, a = b, i.e. p = 1. The Chamber was supposed to have 80 seats, with 100 electors for every district and with 16 five-seat districts for proportionality and single transferable vote^[14]. To compute g, we assumed (here and below) that the majority coalition was the minimum winning coalition of adjacent parties. Results appear in Table 1.

Table 1: r and g for eleven electoral system in an Italy-like case
System [15]	r	g	rg[16]
Borda	0.303	0.687	0.208
Condorcet	0.250	0.825	0.206
Plurality	0.036	0.975	0.035
Run-off Plurality	0.303	0.787	0.238
Mixed-Member 1 °	0.337	0.755	0.254
Mixed-Member 2 °	0.339	0.762	0.258
One-district Proportionality	1	0.168	0.168
Multi-district Proportionality*	0.643	0.367	0.236
Threshold proportionality+	0.821	0.256	0.210
VAP	0.7	0.667	0.467
Single Transferable Vote*	0.661	0.362	0.239

°	25% of seats elected through one-district proportionality
*	Hare quota (simple rounding was used for one-district proportionality)
+	4% threshold (as for real)

2.9

Using Equation 2, or directly from the fourth column, it is easy to find out that VAP is by large the Condorcet winner, as could have been expected (see Appendix 2). If we rule it out to consider only systems actually in use, the Condorcet winner is Mixed-Member 2. This result is remarkable (and possibly unexpected), as Mixed-Member 2 is, in fact, the system actually employed.

2.10

The results above allow for a lot of sensitivity analysis. We report only three examples. First, threshold proportionality performs quite well, hence we attempted to increase the threshold to test whether a different value makes it possible for threshold proportionality to perform better than mixed-member 2. Second, we computed the value of p necessary to make threshold proportionality and multi-district proportionality preferable to mixed-member system 2. Finally, we looked for the Condorcet loser, i.e. for the system that performs worse than any other.

2.11

Changing the threshold does not alter the result. Threshold proportionality never beats mixed-member 2. On the contrary, a slight difference in the relevance accorded to G and R is sufficient to make threshold proportionality preferable to mixed-member 2: this happens if p < 0.811, i.e. if a, say, 10% increase in governability produces the same increase in utility as a 12.3% change in representativeness. pluri-district proportionality performs better than threshold proportionality, and a lower change in p is sufficient to make it preferable to mixed-member 2: the condition is p < 0.876. The Condorcet loser is plurality, as may be expected in a case with many parties.

2.12

It is of interest to remember that in 2000 a referendum was held to decide whether to abolish the proportional part of mixed-member voting, thus moving to plurality. The change was rejected only because participation was (very slightly) under 50%. This has probably been for good: according to our experiment, the move to plurality was worthy only for a value of a / b greater than 9.097, i.e. only if voters agreed to a reduction of more than 90% in representativeness in exchange for a 10% increase in governability, which seems quite unlikely.

2.13

Now let us consider the UK. To limit the constraints induced by the median voter principle we considered the votes cast for the election of the European Parliament (of 1999, the most recent at the time of writing). After some rearranging to exclude a cloud of minor parties (accounting for some 5% of votes), we are left with seven, i.e. (left to right), green, labour, liberals, conservatives, independence and two regional parties, one from Scotland and one from Wales, with (respectively, in that order) 6.63, 29.76, 13.44, 37.97, 7.39, 2.85 and 1.96% of the votes. The collocation of the last three on the left-right axis is quite arbitrary; but this feature affects only the distribution of further preferences, and as we kept the program's default values, it is assumed that preferences are not very dispersed^[17]. We also assumed that the two regional parties are concentrated in eight and in five districts respectively, with a concentration factor of 10 and 15. This reproduces the reality quite faithfully^[18]. Finally, the Parliament was supposed again to have 80 seats (instead of the 87 to be elected by UK voters), to allow for 16 five-seat proportional districts, with 100 voters each. Results are in table 2. All the system-specific features (here and below) are as in table 1.

Table 2: r and g for eleven electoral system in an UK-like case
System	r	g	rg
Borda	0.200	0.875	0.175
Condorcet	0.240	0.850	0.204
Plurality	0.280	0.800	0.224
Run-off Plurality	0.280	0.825	0.231
Mixed-Member 1°	0.440	0.700	0.308
Mixed-Member 2°	0.540	0.650	0.351
One-district Proportionality	1	0.337	0.337
Multi-district Proportionality	0.800	0.350	0.280
Threshold proportionality	0.920	0.346	0.318
VAP	0.781	0.618	0.483
Single Transferable Vote	0.840	0.346	0.291

2.14

The winner is, as expected, VAP, and the second is again mixed-member two. Plurality scores only ninth (eighth excluding VAP). Only if British electors accept to trade a 31.7% decrease in representativeness for a 10% increase in governability, is plurality preferable to the mixed-member 2. Noticeably, with p = 1 all proportional systems score better than plurality.

A policy suggestion: choosing the electoral system after the vote

2.15

The results of the previous section may be strongly affected by minor changes in a number of features, like the values of p, the distribution of second and further preferences of voters, the geographic clustering of votes, and so on. In addition, and obviously, they depend on the actual votes: the conclusion that VAP (or mixed-member 2) is the best system is valid only for the virtual cases considered, and possibly for the real ones they simulate, if a more profound sensitivity analysis can confirm it. Nevertheless, the fact that mixed-member 2 is the winner in both cases seems to suggest that it may be the best system in general (which, by the way, has been argued quite convincingly in the literature, see below). Is this true? In other terms: mixed-member system 2, noticeably the system adopted for real in one case, proved to be the best one in both the instances we considered. Is this result robust for plausible changes in preferences?

2.16

To answer this question, we considered the results of the 1996 election (Italian case) and of the 1994 election (UK case). In Italy, after rearranging to exclude minor parties (which again accounted for less than 3% of the votes), we are left with ten parties, with (left to right) 8.83, 2.57, 21.66, 6.98, 4.41, 5.95, 1.95, 21.15, 10.37 and 16.13 percent of votes. The resulting values of the indices appear in Table 3.

Table 3: r and g in another Italy-like case
System	r	g	rg
Borda	0.444	0.650	0.286
Condorcet	0.381	0.625	0.238
Plurality	0.413	0.346	0.143
Run-off Plurality	0.333	0.637	0.212
Mixed-Member 1	0.619	0.254	0.157
Mixed-Member 2	0.619	0.254	0.157
One-district Proportionality	1	0.205	0.205
Multi-district Proportionality	0.730	0.265	0.193
Threshold proportionality	0.921	0.252	0.232
VAP	0.624	0.719	0.449
Single Transferable Vote	0.841	0.254	0.214

2.17

The winner is again VAP. If we rule it out, the winner is Borda, followed by Condorcet. If we limit the choice to "normal" systems (no country employs Borda or Condorcet), the winner is threshold proportionality. The change is dramatic: we move from a substantially majoritarian system to a substantially proportional one. Note also that the previous winner now scores only eighth (ninth considering VAP). Plurality keeps firmly its last place.

2.18

What for the UK? The results for the 1994 election appear in Table 4^[19].

Table 4: r and g in another UK-like case
System	r	g	rg
Borda	0.545	0.700	0.381
Condorcet	0.318	0.825	0.262
Plurality	0.114	0.925	0.105
Run-off Plurality	0.114	0.938	0.107
Mixed-Member 1	0.364	0.788	0.287
Mixed-Member 2	0.432	0.738	0.319
One-district Proportionality	1	0.375	0.375
Multi-district Proportionality	0.864	0.375	0.324
Threshold proportionality	0.841	0.396	0.333
VAP	0.880	0.667	0.587
Single Transferable Vote	0.886	0.379	0.336

2.19

Ruling out VAP, this time the winner is Borda, followed by no less than one-district pure proportionality and by STV; the best system in 1999, mixed-member 2, scores only seventh (sixth excluding VAP). The good performance of proportional systems is particularly remarkable if we consider that the long-lasting tradition of plurality arguably kept the supply of parties well below the demand.

2.20

Comparing tables 3 and 4 with tables 1 and 2, the most interesting result is that (at least with p = 1) the best system changes in both cases, and in both cases changes to a quite different system. This conclusion, as the ones above, should be confirmed by further replications of the experiment in various settings. But if it is confirmed (as we may reasonably expect), it has a deep theoretical implication: the "best" electoral system, albeit on a pure empirical basis, may be a misleading notion, as it may differ according to circumstances.

2.21

This opens the way to a very interesting possibility, that of choosing the electoral system after the vote. All what is requested to choose the electoral system after the vote is a) a rule, defined a priori to choose the best system, like the one of the previous section; and b) the information necessary to assess different system, to be collected during the voting procedures, i.e. an ordering of preferences^[20]. As this is what is done wherever Single Transferable Vote is employed, we know that this is possible.

2.22

Scholars are increasingly concerned by the problem of avoiding the exploitation of the pitfalls of electoral systems by political rent-seekers. Mixed-members systems are particularly appreciated, as they force the parties to try to maximise their consensus both in a majoritarian and in a proportional environment (see for example, Shugart 2001; Shugart and Wattenberg 2000). Choosing the system after the vote would work better. It makes it possible not only to force the parties to behave that way, but also to avoid a wrong assignment of the seats to the majoritarian and proportional shares. If a mixed member is actually the better system, this rule will pinpoint it; if not (and we've just conjectured that this is possible) the rule will avoid a mistake.

2.23

To pursue further this argument is far beyond the theme of this paper. We conclude by suggesting only that accumulating broader experimental evidence will probably be very useful.

Appendix 1: The program

How to use ALEX3

A1.1

ALEX3 is written in Java. Therefore, Java (or at least Java Runtime) must be installed on the computer^[21]. The program works through user-friendly windows. The first window allows the user to set up the number of voters in each uninominal district, the number of uninominal districts, the magnitude of plurinominal districts, the number of parties, the probability to choose as the second preference the next party in the order of preferences, the probability to choose as the second preference the second next party, the probability to choose the preferred candidate in the preferred party. The first two probabilities are employed to establish the complete ordering of preferences of the voters; the third to allow the choice of candidates of parties different from the preferred for single transferable voting. In the following window, the user is requested to set up the characteristics of the political parties: their overall share of votes ("quota"), and whether they are concentrated in one or more district. At this point, the user has the possibility to save the values of the parameters in a text file.

A1.2

When all the parameters have been set up, the program starts computing the voters' preferences for the political parties and creates the uninominal districts. If plurinominal systems are requested the program will also compute the voters' preferences for the candidates of each party, and the plurinominal districts will be created by grouping the uninominal ones. When the districts have been created, the user can save in a text file the voters' preferences for parties and candidates, and the composition of uninominal and plurinominal districts. It is possible to append these results to the file created earlier.

A1.3

Next, the list of electoral systems that can be used is displayed. To see the Parliament resulting from a given system, the user simply has to click on the button next to the name of the system. A new window opens with the characteristics of the Parliament: number of seats and representativeness index. The user is requested to create a Government; the resulting governability index will appear^[22]. Some electoral systems need some extra parameters: the user will be asked to set them up via a dialog window which appears when clicking on the name of the electoral system. Other buttons are for saving the characteristics of the Parliament, or for exiting from the program. There is no limit to the number of windows one can open, so it is possible to open a window for each system in the list.

Description of the program: voters, parties and constituencies

A1.4

To assign the votes to the parties, the first n1 voters are given a first preference for party 1 (n1 corresponding to the share of votes of party 1 in the population), the next n2 voters are given a first preference for party 2 (n2 corresponding to the share of party 2 in the population), etc. Parties are ordered on a left/right scale, with party 1 being on the far-left and party n being on the far-right. Once the first preferences of the electors are known, the program creates their complete preference ordering, using the probabilities defined in the first window of the program: the probability of choosing the first next party and the probability of choosing the second next party (if the two probabilities do not sum to 1, the rest is the probability of choosing another party at random).

A1.5

More precisely, in order to choose the party at the second place in the elector's preference ordering, the program (a) removes the first preferred party from the list of parties and save it in the first place in the vector of the elector's preferences, and (b) with probability p1 chooses the party next (randomly right or left) to the preferred party, with probability p2 chooses the second next party, with probability p3 = 1 - p1- p2 chooses another party.

A1.6

This party is inserted at the second place in the elector's preference ordering and becomes the party currently preferred. To find the remainder of the preference ordering, ALEX3 proceeds in the same way, using the party currently preferred as a starting point. The procedure is duly corrected for the case when the currently preferred party is at one extremity of the list of parties.

A1.7

The districts are created after the voters' preferences for parties have been computed. Each district contains E voters, E being set by the user at the beginning of the session (hence, all districts have the same size). In the program, political parties can be concentrated in a given number of districts, to simulate regional clustering (or gerrymandering). A party that is concentrated in one or more districts is called a major party. When a party is major, it is necessary to establish the number of districts in which it is concentrated, and the coefficient of concentration T > 1, which allows the computation of the number of voters with this major party as first preference assigned to the district(s). In other words, we define (a) the number of districts in which a given party is concentrated, K, and (b) the total number of voters who have that party as first preference, F. Each district in which the party is concentrated contains T*F/K voters who have this party as first preference. Obviously, in remaining districts they are fewer than the average share, given that the overall share has been fixed.

A1.8

The plurinominal districts are created by adding the uninominal ones, grouping together the districts where a party is concentrated.

Short notes on the electoral systems

One-district Proportionality

A1.9

The districts are aggregated, and the seats in the parliament are distributed according to the shares of votes of the parties in the population. In other words, the seats represent the (rounded off) weight of the parties as inserted in the third window of the program. By construction, the value of the index of representativeness is 1.

Threshold Proportionality

A1.10

When the user clicks on the button next to this system, a dialog window appears, asking for the threshold value. All the parties who have a share of votes (strictly) smaller are excluded from the parliament. The seats are distributed proportionally among the remaining parties. Again, there is only one district.

Plurality

A1.11

The candidate (i.e. the party) with the most votes wins in each district.

Runoff majority

A1.12

In each district all parties but the two with the most votes are excluded. The second round is implemented with these two parties only and the one with the most votes wins. If after the first round the first party has at least 50% of the votes, it is elected without the need of a second round.

Mixed Member System, 1

A1.13

Part of the parliament is elected with the Plurality System, and the remainder is elected using the Proportional System. The share of seats assigned through the Proportional System is a parameter specified by the user. The program computes an entire parliament with the Plurality System, and another parliament with the Proportional System. The final parliament is produced using a weighted mean of the two temporary parliaments, the weights being determined by the value of the parameter set earlier by the user.

Mixed-Member System, 2

A1.14

Part of the parliament is elected with the Plurality System, and the remainder is elected using the Proportional System. Contrary to the mixed system above, the votes used to elect the 'plurality part' are lost for the 'Proportional part'. The share of the parliament elected with the Proportional System is decided by the user. As in the previous mixed system, the program creates first a parliament with the plurality system, then a parliament with the Proportional System, employing only the votes not used by the plurality part. Finally, the two parliaments are unified.

Borda Count

A1.15

This system uses the voters' complete preference ordering. Each elector gives points to each party, according to its position in his preference ordering. The points given correspond exactly to the position of the party in the elector's preference vector (0 for the most preferred party, N-1 for the least preferred party, where N is the total number of parties). The program sums the points for each party of each district. The party with less points wins, in each district.

Condorcet Winner

A1.16

The Condorcet winner is chosen in each district. It is the party that beats all the others when taken in pairs.

Multi-district proportionality

A1.17

The user may choose among several methods for the assignment of seats, i.e. Hare, D'Hondt, Imperiali and Sainte-Lagüe. It may be useful to remember that the most proportional system is probably the last one, at least according to Lijphart (1994) ^[23].

Single Transferable Vote

A1.18

The seats for each party, in each plurinominal district, are assigned according to a quota value. If some seats are not assigned, the votes unused by the elected candidates are transferred to the next candidate in the elector's preference ordering, and the candidates with the highest number of votes (obtained + transferred) are elected. The operation is repeated until all the seats have been assigned. If at a given round there is no assignment, the candidate with less preference is excluded, and its votes are distributed as above.

A1.19

Three methods can be used to compute the quota, i.e. N.B. [votes/(seats+1)], Droop [votes/(seats+1)+1] and Hare (votes/seats). For each elected candidate (number of votes greater than or equal to the quota), the surplus is computed as the difference between the number of votes and the quota. The surplus is transferred, starting with the largest, in the following way: (a) from the candidate's voters, a number of voters equal to the surplus to share out is extracted at random; (b) the votes of these voters are transferred to the candidate indicated as next preferred in their preference ordering, and not yet elected; and (c), if as a result a candidate's votes becomes equal to or greater than the quota, this candidate is elected and eliminated from the list of candidates available to be elected.

The VAP System

A1.20

It is described in some detail in Appendix 2 below.

How to receive the program

A1.21

The program may be obtained, for free, writing to the Professor Guido Ortona; you will only be requested to fulfil the following requirements:

1. The program must not be used for profit;
2. The program should be cited in every research paper or article that employs it;
3. A copy of the study in which the program is used should be sent to the corresponding author.

A complete user's guide (in PDF format) will be provided together with the program.

A1.22

Finally, note that the program for experiments ALEX3 is still... experimental; it may contain minor errors, and is surely susceptible of improvements. The authors apologize for the eventual errors and will be grateful to those who will suggest improvements.

Appendix 2: The VAP system

A2.1

The system is described in detail in Ortona (2002a, 2002b). Here we provide only a short summary. The system considers a "true" Parliament and a "virtual" one. The "true" Parliament is elected with pure proportionality (in ALEX3 with one overall district). The "virtual" parliament depends on the composition of the government. The major party(ies) of the governing coalition receive a prize in votes in Parliament (not in seats) such that the coalition keeps a pre-determined majority if small members defeat. The governments loses the majority only when a major party (or a relevant number of its MPs) leave the coalition. The system recalls a majority premium, with two basic difference: there will be no non-elected MPs, and, more important from our point of view, the premium is fine-tuned so to reduce Representativeness as little as requested to obtain the desired level of Governability. The prize is determined assigning a weight a (> 1) to the major parties of the governing coalition, according to the formula

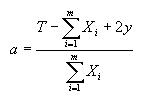
where X is the number of seats of the m largest (i.e. major) parties in the Government, and T is the total number of seats in the Parliament. This way, the Government keeps a majority of y if the small parties of the governing coalition defeat. In ALEX3 the value of y is fixed to 1, while m may be established by the experimenter through the assignment of the share of seats in the proportional system necessary to be considered major.

A2.2

Running the program, we first see a window with the "true" Parliament. In order to produce the virtual one, the user has to decide the composition of the Government. When the coalition thus formed obtains the majority, a dialog window appears, asking the user whether the government is complete. If the answer is 'no', the user can add more parties to the Government. If the answer is 'si' (yes), the virtual parliament is created, giving to each MP of the major parties a votes (or virtual seats) instead of 1. The indices are computed with reference to the virtual Parliament.

Notes

¹ See Ortona (2002a or 2002b) for a sixteen-item list taken from recent literature.

² Approval voting has been excluded as previous experiments showed that it is inferior to Condorcet voting with reference both to G and R. See Ortona (1998).

³ For a review, see Lijphart (1994, p.67).

⁴ See Shugart and Wattenberg (2000), p.30; Shugart (2001).

⁵ For a more detailed discussion of the indices, see Ortona (2002a).

⁶The value of S_u,i is the total number of seats for the largest party, and 0 for all the others. If several parties are the largest ones ex aequo, we take one at random.

⁷ ALEX3 is the third version of the program. The first one required a specific database and did not include plurinominal systems. The second is like this one, but without plurinominal systems.

⁸ An interesting discussion of power topics in is Mudambi et al. (2001).

⁹ In a previous paper, the Gini coefficient relative to the Banzhaf’s power indices was employed as an additional measure of governability; but the computing was performed outside the program. See Ortona (2002a).

¹⁰ A more detailed description of the procedure may be found in Fragnelli, Monella and Ortona (2002).

¹¹ Here is the proof.

From U = Ag^ar^b and a =pb we get dU = dg(bpAg^bp-1r^b) + dr(bAg^bpr^b-1)
If U does not change 0 = dg(bpAg^bp-1r^b) + dr(bAg^bpr^b-1)
dg(bpAg^bp-1r^b) = - dr(bAg^bpr^b-1)
dr/r = - p(dg/g)

¹² Remember that g ≤ 1. If (trivially) the value of both g and G is 1, the value of r will establish the best system.

¹³ Lower Chamber only.

¹⁴ It may be of some interest to recall that in Italy some 1,500 respondents are commonly assumed to be sufficient to provide a reliable nation-wide survey.

¹⁵ See Appendix 1 for details.

¹⁶ Assuming p = 1, i.e. a = b, the selection criterion becomes "system X is preferred to system Y iff g_x^ar_x^a > g_y^ar_y^a, i.e. g_xr_x > g_yr_y. The rank of r times g provides the rank of the electoral systems.

¹⁷ See Appendix 1 for details.

¹⁸ See again Appendix 1.

¹⁹ When parties obtained (rearranged) 3.30, 45.31, 17.16, 28.78, 1.07, 3.30 and 1.07% of votes respectively.

²⁰ Not necessarily complete.

²¹ Java Runtime 1.4 can be downloaded from http://java.sun.com.

²² To avoid the mushrooming of possible Governments, it is almost inevitable to adopt some rules concerning the coalition that will actually be chosen. A reasonable set is to suppose that (a) the Government must be supported by the majority of MPs and (b) the Government is made by a minimum winning coalition of parties adjacent on the left-right axis. The program could easily implement the conditions, thus producing automatically the government; however, we preferred to leave this task to the user, as condition (b) is not that frequent in real world, and it may be of interest to explore different possibilities.

²³ This claim could be tested through ALEX3.

References

FARRELL D M (2001) Electoral Systems: a Comparative Introduction. Houndmills, Basingstoke: Palgrave.

FRAGNELLI V, Monella G and Ortona G (2002) "Governability and Representativeness: Simulation of Concrete Voting Situations", paper presented to the Spanish Meeting on Game Theory and applications, Sevilla, July.

LIJPHART A (1994) Electoral Systems and Party Systems: a Study of Twenty-seven Democracies, 1945-1990. Oxford: Oxford University Press.

MUDAMBI R (1997) A Complete Information Index for Measuring the Proportionality of Electoral Systems. Applied Economics Letters, 4. pp. 101-104.

MUDAMBI R, Navarra P and Sobbrio G (2001) Rules, Choices and Strategy: The Political Economy of Italian Electoral Reform. Cheltenham: Edward Elgar.

ORTONA G (1998) Come funzionano i sistemi elettorali: un confronto sperimentale. Stato e mercato, 54. pp. 83-112.

ORTONA G (2000), "A weighted-voting electoral system that performs quite well", in Dardanoni V and Sobbrio G (eds.), Istituzioni politiche e finanza pubblica, Angeli, Milano; also as a working paper, Dep. of Public Choice, Università del Piemonte Orientale, 4 (1999).

ORTONA G (2002a) "Experimental Assessment of a suggested two-stage electoral system", Paper presented to the 2002 Conference of the European Public Choice Society, Belgirate (Italy), April.

ORTONA G (2002b) "Choosing the electoral system: why not simply the best one?" Working Paper, Department of Public Choice, Università del Piemonte Orientale, 32.

SHUGART M S (2001) Electoral "efficiency" and the move to mixed-member systems. Electoral Studies, 20. pp. 173-193.

SHUGART M S and Wattenberg M P Eds. (2000) Mixed-member Electoral Systems: the Best of Both Worlds? Oxford: Oxford University Press.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2004]