Luis R. Izquierdo, Nicholas M. Gotts and J. Gary Polhill (2004)
Case-Based Reasoning, Social Dilemmas, and a New Equilibrium Concept
Journal of Artificial Societies and Social Simulation
vol. 7, no. 3
<https://www.jasss.org/7/3/1.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 28-Dec-2003 Accepted: 03-Apr-2004 Published: 30-Jun-2004
 Abstract
Abstract| Though analogy is often misleading, it is the least misleading thing we have. |
| SAMUEL BUTLER |
Psychological game theory [...] overlaps behavioral game theory but focuses specifically on non-standard reasoning processes rather than other revisions of orthodox game theory such as payoff transformations. Psychological game theory seeks to modify the orthodox theory by introducing formal principles of reasoning that may help to explain empirical observations and widely shared intuitions that are left unexplained by the orthodox theory (Colman 2003)
Behavioral game theory is about what players actually do. It expands analytical theory by adding emotion, mistakes, limited foresight, doubts about how smart others are, and learning to analytical game theory. Behavioral game theory is one branch of behavioral economics, an approach to economics which uses psychological regularity to suggest ways to weaken rationality assumptions and extend theory. Camerer (2003, p.3)
| Table 1: Payoff matrix for the 2-player Prisoner's Dilemma | |||||
| Player 2 | |||||
| Cooperate | Defect | ||||
| Player 1 | Cooperate | Reward | Temptation | ||
| Reward | Sucker | ||||
| Defect | Sucker | Punishment | |||
| Temptation | Punishment | ||||
Temptation > Reward > Punishment > Sucker
In the n-player social dilemma every agent gets a reward as long as there are no more than M defectors (M < n). The Payoff that defectors get is always higher than the Payoff obtained by those who cooperate (Def-P > Coop-P). However, every player is better off if they all cooperate than if they all defect (Coop-P + Reward-P > Def-P). Table 2 shows the Payoff matrix for a particular agent:| Table 2: Payoff matrix of the "Tragedy of the Commons game" for a particular agent | |||
| Fewer than M others defect | M others defect | More than M others defect | |
| Agent cooperates | Coop-P + Reward-P | Coop-P + Reward-P | Coop-P |
| Agent defects | Def-P + Reward-P | Def-P | Def-P |
| t | dft-ml … dft-2 dft-1 | dt | pt |
| dt-ml … dt-2 dt-1 |
| dfi | is the number of defectors (excluding agent A) in time-step i, |
| di | is the decision made by Agent A in time-step i, and |
| pt | is the Payoff obtained by Agent A in time-step t. |
|
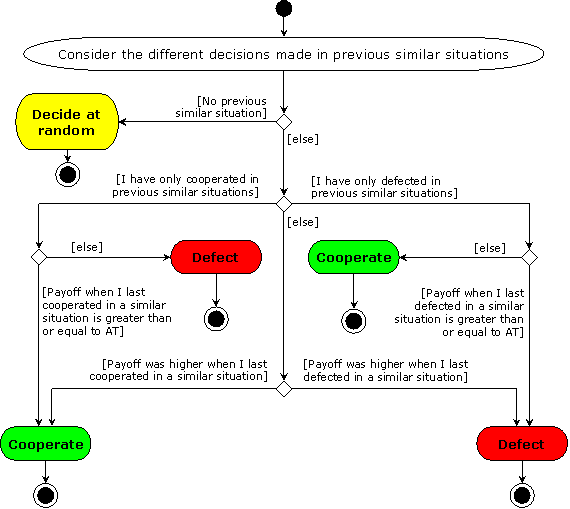
| Figure 1. UML activity diagram of the Agents' decision making algorithm in the R-model |
| Table 3: Decisions made by each of the two Agents in the PD when visiting a certain state of the world for the i-th time. In the first column, Payoffs are denoted by their initial letter. In columns 2 to 5, the first letter in each pair corresponds to the decisions of one Agent, the second letter to those of the other. C is cooperation and D is defection. The first imbalance between CC and DD for every value of AT has been shadowed. The meaning of x and y is explained in the text. The results shown in this table are independent of the Memory Length | ||||||
| Aspiration Thresholds (AT) | 1st visit (random) | 2nd visit | 3rd visit | 4th visit and onwards | x | y |
| T < AT | CC | DD | CC | CC | 1 | - |
| CD | DC | DD | DD | - | 2 | |
| DC | CD | DD | DD | - | 2 | |
| DD | CC | CC | CC | 1 | - | |
| R < AT ≤ T | CC | DD | CC | CC | 1 | - |
| CD | DD | DC | DD | - | 2 | |
| DC | DD | CD | DD | - | 2 | |
| DD | CC | CC | CC | 1 | - | |
| P < AT ≤ R | CC | CC | CC | CC | 0 | - |
| CD | DD | DC | DD | - | 2 | |
| DC | DD | CD | DD | - | 2 | |
| DD | CC | CC | CC | 1 | - | |
| S < AT ≤ P | CC | CC | CC | CC | 0 | - |
| CD | DD | DD | DD | - | 1 | |
| DC | DD | DD | DD | - | 1 | |
| DD | DD | DD | DD | - | 0 | |
| AT ≤ S | CC | CC | CC | CC | 0 | - |
| CD | CD | CD | CD | - | - | |
| DC | DC | DC | DC | - | - | |
| DD | DD | DD | DD | - | 0 | |
|
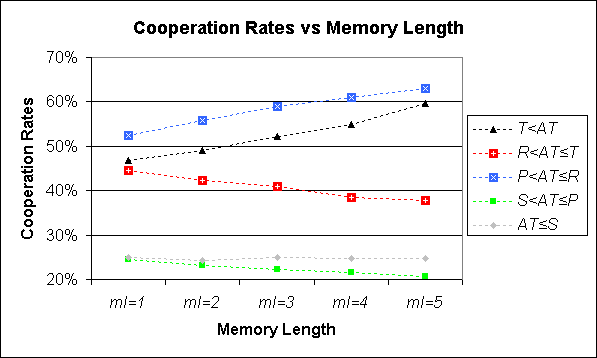
| Figure 2. Average cooperation rates when modelling two agents with Memory Length ml and Aspiration Threshold AT, playing the PD. The average cooperation rate shows the probability of finding both Agents cooperating once they have finished the learning period (i.e. when the run locks in to a cycle). The values represented for ml = 1 have been computed exactly. The rest of the values have been estimated by running the model 10,000 times with different random seeds. All standard errors are less than 0.5 % |
| Table 4: Effect on average cooperation rates of each of the two factors outlined in the text above depending on the value of AT, and results from the simulation runs | |||||
| AT ≤ S | S < AT ≤ P | P < AT ≤ R | R < AT ≤ T | T < AT | |
| Effect of Factor 1 | No bias | Bias towards cooperation | Bias towards cooperation | Bias towards cooperation | Bias towards cooperation |
| Effect of Factor 2 | No bias | Bias towards defection | Bias towards cooperation | Bias towards defection | No bias |
| ... | ... | ... | ... | ... | ... |
| Total effect | No bias | Bias towards defection | Bias towards cooperation | Bias towards defection | Bias towards cooperation |
|
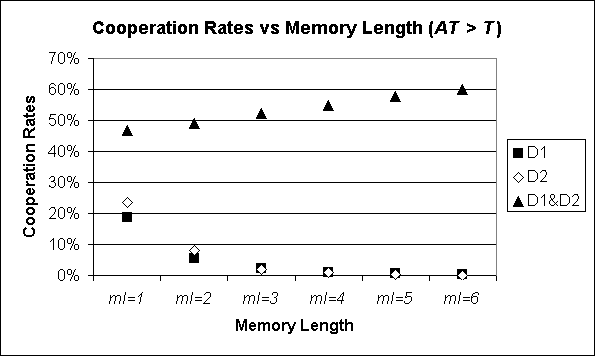
| Figure 3. Average cooperation rates when modelling two agents with Memory Length ml, Aspiration Threshold greater than Temptation, and with 3 different representations of the state of the world (D1, D2, and D1&D2), playing the PD. The values represented for ml = 1 have been computed exactly. The rest of the values have been estimated by running the model 10,000 times (ml = 2, 3, 4) or 1,000 times (ml = 5, 6) with different random seeds. All standard errors are less than 1% |
|
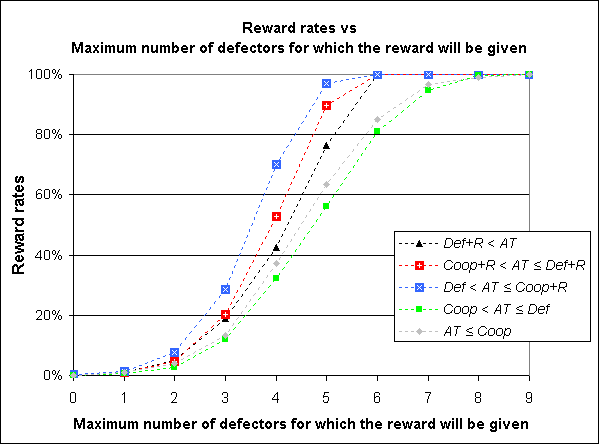
| Figure 4. Average reward rates for different values of M in the Tragedy of the Commons game played by 10 Agents with Memory Length ml = 1. Each represented value has been estimated by running the model 1,000 times. All standard errors are less than 1.5% |
|
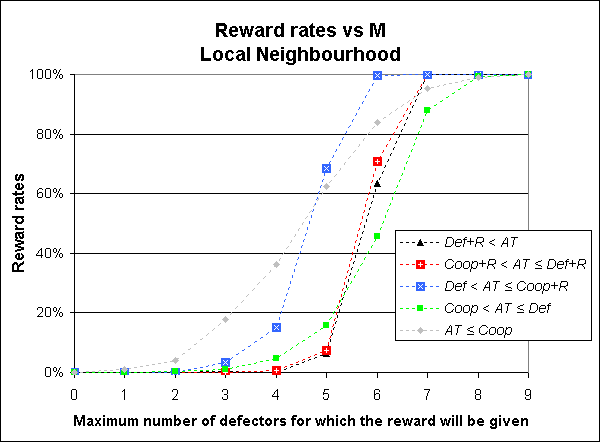
| Figure 5. Average reward rates for different values of M in the Tragedy of the Commons game played by 10 Agents with Memory Length ml = 1. Every Agent A can observe other 5 Agents only, who are the only ones that can observe Agent A. Each represented value has been estimated by running the model 1,000 times. All standard errors are less than 1.5% |
|
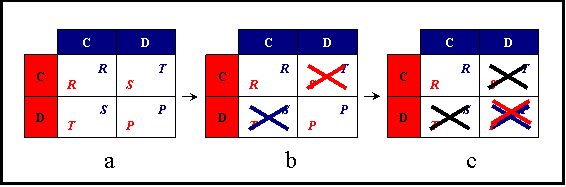
| Figure 6. Elimination of dominated outcomes. Figure b shows the remaining outcomes after having applied one step of outcome dominance. Figure c shows the remaining outcomes after having applied two steps of outcome dominance. Red crosses represent outcomes which are unacceptable for player Red (row), blue crosses represent outcomes which are unacceptable for player Blue (column), and black crosses represent outcomes eliminated in previous steps |
|
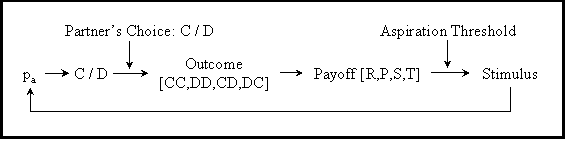
| Figure 7. Schematic model of reinforcement learning (Flache and Macy 2002). pa is the probability of making decision 'a', where 'a' can be either cooperate (C) or defect (D) |
2 For a detailed analysis of the finitely repeated Prisoner’s Dilemma, see Raub (1988).
3 The controversy concerns the effects of synchrony in the spatially embedded PD and, though fascinating, is not relevant here.
4 The word ‘Agent’ will be written starting with a capital ‘A’ when it refers to the computer implementation.
5 Universal defection is a Nash equilibrium as long as M < n-1.
6 Obviously there are always implicit assumptions in any model. Learning depends upon the contextual knowledge and the framework that the learning algorithm provides (the so-called logical, or model, bias).
7 Valid deductive arguments are those whose conclusions follow from their premisses with logical necessity (Copi 1986, p. 169).
8 Non-deductive arguments are not claimed to demonstrate the truth of their conclusions, but to support their conclusions as probable, or probably true. Arguments of this type are called inductive arguments in some textbooks (e.g. Copi 1986, p. 404, or Salmon 1984, p. 32) and should not be confused with the inference process of generalisation by induction (which is a particular type of non-deductive argument).
9 A tie is impossible in either of the two games reported in this paper.
10 This also applies to the Tragedy of the Commons Game: when Agents cannot recall any cases, they make the same decision by model design. When Agents can recall only one case in which they either cooperated or defected, they all recall the same case, and therefore they all make the same decision. Finally, when Agents can recall one case for each possible decision, those cases necessarily show a situation in which all of them cooperated or all of them defected. When given universal cooperation and universal defection as the only two possible options, they all cooperate.
11 This effect is explained in detail by Izquierdo et al. (2003).
12 If the Aspiration Threshold does not exceed Sucker, Agents repeat the same decision that they made at random the first time they visited a certain state of the world whenever they visit the same state again.
13 Or, conversely, some cycles comprise fewer different states of the world than others.
14 Except, again, for the trivial case where AT ≤ S, in which the average cooperation rate is always 25%.
15 Recall that our Agents know only whether they cooperated or defected, and how many others defected. In the TC game, the information provided to the Agents is thus not complete in the sense that they cannot identify who is defecting, as they could in the PD (since there was only one other player).
16 When the game is played by 25 Agents, average reward rates are greater than 80% if M ≥ 15 and greater than 99% if M ≥ 19, for any Aspiration Threshold.
17 Except in the case of minimally effective cooperation in the “Tragedy of the Commons” game.
18 A slightly more restrictive concept is that of an undominated outcome, in which no player can be guaranteed the same or a higher payoff by changing their decision. The concept of undominated outcome as equilibrium implies that Agents deviate from an outcome only if it is certain that they will not be worse off by doing so, whereas the strictly undominated concept implies that Agents move away from an outcome only if it is certain that they will be better off by doing so. The concept of undominated outcome as equilibrium is neither weaker nor stronger than the Nash equilibrium.
19 Probabilities might reach their natural limits in the implementation of the conceptual model due to floating-point rounding errors.
20 Bendor et al. (2003) have proved that any pure outcome of the stage game can be SRE when Aspiration Thresholds are not fixed.
21 Floating-point inaccuracies might make SRE reachable in certain implementations of the model.
22 If we consider undominated outcomes as opposed to strictly undominated outcomes, then statement a) is only true for games in which players never get the same payoff when they select different actions. In those games (e.g. the Prisoner’s Dilemma and the Tragedy of the Commons game), the two equilibrium concepts are equivalent. We find the concept of undominated outcomes more appealing than its strict version, particularly when outcome dominance is to be applied iteratively. However, in this paper we have focused on the latter because the relation of the former with the Nash equilibrium and with CBRE algorithms is not so clear.
- Boundedly rational:
- A boundedly rational agent acts as if they have consistent preferences, but limited computational capacity (compare with the definition of instrumentally rational below).
- Deficient equilibrium:
- An equilibrium is deficient if there exists another outcome which is preferred by every player.
- Common knowledge of rationality (CKR):
- CKR means that every agent assumes: (a) that all agents are instrumentally rational, and (b) that all agents are aware of other agents' rationality-related assumptions (this produces an infinite recursion of shared assumptions).
- Individually-rational outcome:
- An outcome giving each player at least the largest payoff that they can guarantee receiving regardless the opponents' moves.
- Instrumentally rational:
- An instrumentally rational agent acts as if they have consistent preferences and unlimited computational capacity.
- Maximin:
- the largest possible payoff a player can guarantee themselves. This is Punishment in the Prisoner's Dilemma and Def-P in the Tragedy of the Commons game.
- Mutual belief:
- A proposition A is mutual belief among a set of agents if each agent believes that A. Mutual belief by itself implies nothing about what, if any, beliefs anyone attributes to anyone else (Vanderschraaf 2002).
- Nash equilibrium: (Nash 1951):
- a set of strategies such that no player, knowing the strategy of the other(s), could improve their expected payoff by changing their own.
- Outcome:
- a particular combination of strategies, one for each player, and their associated payoffs. In the one-shot games studied in this paper, an outcome corresponds to a cell in the payoff matrix.
- Pareto inefficient:
- An outcome is Pareto inefficient if there is an alternative in which at least one player is better off and no player is worse off.
- Strictly dominated strategy:
- For an agent A, strategy SA is strictly dominated by strategy S*A if for each feasible combination of the other players' strategies, A's payoff from playing SA is strictly less than A's payoff from playing S*A (Gibbons 1992, p. 5).
- Tit-for-Tat (TFT):
- This is the strategy consisting of starting cooperating, and thereafter doing what the other player did on the previous move.
AUMANN R (1976) Agreeing to disagree. Annals of Statistics, no. 4, pp. 1236-1239.
AXELROD R (1984) The Evolution of Cooperation. Basic Books, USA.
BENDOR J, Diermeier D and Ting M (2003) The Predictive Power of Learning Models in Social Dilemma Research. Working Paper, Stanford University.
BRENAN G and Lomasky L (1984) Inefficient Unanimity. Journal of Applied Philosophy, 1, pp. 151-163.
CAMERER C F (2003) Behavioral Game Theory: Experiments in Strategic Interaction. Princeton University Press.
CHAVALARIAS D (2003) Human's Meta-cognitive Capacities and Endogenization of Mimetic Rules in Multi-Agents Models. Presented at the First Conference of the European Social Simulation Association, Groningen, The Netherlands, 18-21/9/03. Conference proceedings available online.
COLLINS (2000) The Collins English Dictionary. HarperCollins Publishers.
COLMAN A M (1995) Game Theory and its Applications in the Social and Biological Sciences. 2nd edition. Butterworth-Heinemann, Oxford, UK.
COLMAN A M (2003) Cooperation, psychological game theory, and limitations of rationality in social interaction. The Behavioral and Brain Sciences, 26, pp. 139-153.
CONTE R and Paolucci M (2001) Intelligent social learning. JASSS - the Journal of Artificial Societies and Social Simulation, Vol. 4, no. 1. Website publication as at 9th March 2004: https://www.jasss.org/4/1/3.html
COPI I M (1986) Introduction to Logic. Seventh Edition. Macmillan, New York.
DAWES R M (1980) Social Dilemmas. Annual Review of Psychology, pp. 161-193.
DIEKMANN A (1985) Volunteer's Dilemma. Journal of Conflict Resolution, 29, pp. 605–610.
DIEKMANN A (1986) Volunteer's Dilemma. A Social Trap without a Dominant Strategy and some Empirical Results. In Diekmann A and Mitter P (Eds.), Paradoxical Effects of Social Behavior — Essays in Honor of Anatol Rapoport, pp. 187-197. Heidelberg: Physica.
DORAN J (1997) Analogical Problem Solving. In: Bundy A (Ed.) Artificial Intelligence Techniques: A Comprehensive Catalogue. Springer-Verlag, fourth revised edition, p. 4.
EREV I and Roth A E (1998) Predicting How People Play Games: Reinforcement Learning in Experimental Games with Unique, Mixed Strategy Equilibria. American Economic Review, 88, 4, pp. 848-881.
FLACHE A and Macy M W (2002) Stochastic Collusion and the Power Law of Learning. Journal of Conflict Resolution, Vol. 46, no. 5, pp. 629-653.
FUDENBERG D and Levine D (1998) The Theory of Learning in Games. MIT Press, Cambridge, MA.
GIBBONS R (1992) A Primer in Game Theory. FT Prentice Hall, Harlow (England).
GILBOA I and Schmeidler D (1995) Case-Based Decision Theory. The Quarterly Journal of Economics, 110, pp. 605-639.
GILBOA I and Schmeidler D (2001) A Theory of Case-Based Decisions. Cambridge University Press, Cambridge, UK.
GOTTS N M, Polhill J G and Law A N R (2003) Agent-Based Simulation in the Study of Social Dilemmas. Artificial Intelligence Review, 19, pp. 3-92.
HARDIN G (1968) The Tragedy of the Commons. Science, 162, pp. 1243-1248.
IZQUIERDO L R, Gotts N M and Polhill J G (2003) Case-Based Reasoning and Social Dilemmas: an Agent-Based Simulation. Presented at the First Conference of the European Social Simulation Association, Groningen, The Netherlands, 18-21/9/03. Conference proceedings available online.
KAHNEMANN D, Slovic P and Tversky A (Eds.) (1982) Judgement Under Uncertainty: Heuristics and Biases. Cambridge University Press.
KLEIN G A and Calderwood R (1988) How Do People Use Analogues to Make Decisions?. In: Kolodner J L, (Ed.) Proceedings of the DARPA Case-Based Reasoning Workshop, Morgan Kaufmann, Calif., US.
KREPS D, Milgrom P, Roberts J and Wilson R (1982) Rational Cooperation in the Finitely Repeated Prisoners' Dilemma. Journal of Economic Theory, 27, pp. 245-252.
KUHN S (2001) Prisoner's Dilemma. The Stanford Encyclopedia of Philosophy (Winter 2001 Edition), Edward N Zalta (Ed.). Website publication as at 9th March 2004: http://plato.stanford.edu/archives/win2001/entries/prisoner-dilemma/
LEDYARD J O (1995) Public Goods: A Survey of Experimental Research. In Kagel J H, and Roth A E (Eds.), The Handbook of Experimental Economics. Princeton University Press.
LOUI R (1999) Case-Based Reasoning and Analogy. The MIT Encyclopedia of the Cognitive Sciences, Wilson R A and Keil F C (Eds.), pp. 99-101.
LUCE D and Raiffa H (1957) Games and Decisions. New York: Wiley.
MACY M W (1990) Learning Theory and the Logic of Critical Mass. American Sociological Review, Vol. 55, pp. 809-26.
MACY M W (1991) Learning to Cooperate: Stochastic and Tacit Collusion in Social Exchange. American Journal of Sociology, Vol. 97, pp. 808-43.
MACY M W (1995) PAVLOV and the Evolution of Cooperation. An Experimental Test. Social Psychology Quarterly, Vol. 58, No 2, pp. 74-87.
MACY M W (1998) Social Order in Artificial Worlds. JASSS - the Journal of Artificial Societies and Social Simulation vol. 1, no. 1. Website publication as at 9th March 2004: https://www.jasss.org/1/1/4.html
MACY M W and Flache A (2002) Learning Dynamics in Social Dilemmas. Proceedings of the National Academy of Sciences, vol. 99, Suppl. 3, pp. 7229-7236
NASH J (1951) Non-cooperative Games. Annals of Mathematics, 54, pp. 285-295.
NICOLOV N (1997) Case-based Reasoning. In: Bundy A (Ed.) Artificial Intelligence Techniques: A Comprehensive Catalogue. Springer-Verlag, fourth revised edition, 1997, pp.13-14.
NOWAK M A and May R M (1992) Evolutionary Chaos and Spatial Games. Nature, 359, pp. 826-829.
RAUB W (1988) An Analysis of the Finitely Repeated Prisoners' Dilemma. European Journal of Political Economy, 4 (3), pp. 367-380.
RAUB W and Voss T (1986) Conditions for Cooperation in Problematic Social Situations. In Diekmann A and Mitter P (Eds.), Paradoxical Effects of Social Behavior — Essays in Honor of Anatol Rapoport, pp. 85-103. Heidelberg: Physica.
REISBERG D (1999) Learning. The MIT Encyclopedia of the Cognitive Sciences, Wilson R A and Keil F C (Eds.), pp. 460-461.
ROSS B (1989) Some Psychological Results on Case-based Reasoning. In Hammond, K (Ed.), Proceedings of the Case-Based Reasoning Workshop, pp. 144-147 San Mateo. DARPA, Morgan Kaufmann, Inc.
ROTH A E (1995) Introduction to Experimental Economics. In: Kagel J H and Roth A E (Eds.), The Handbook of Experimental Economics. Princeton University Press.
ROTH A E and Erev I (1995) Learning in Extensive-Form Games: Experimental Data and Simple Dynamic Models in the Intermediate Term. Games and Economic Behavior, Special Issue: Nobel Symposium, vol. 8, pp.164-212.
SALMON M (1984) Introduction to Logic and Critical Thinking. Harcourt Brace Jovanovich.
SCHANK R (1982) Dynamic Memory: a Theory of Reminding and Learning in Computers and People. Cambridge University Press, Cambridge, UK.
SCHANK R and Abelson R P (1977) Scripts, Plans, Goals and Understanding. Lawrence Erlbaum Associates, Hillsdale, New Jersey.
SIMON H A (1957) Models of Man: Social and Rational; Mathematical Essays on Rational Human Behavior in a Social Setting, John Wiley and Sons, New York.
VAN DAMME E (1987) Stability and Perfection of Nash Equilibria. Springer Verlag, Berlin (2nd ed. 1991).
VANDERSCHRAAF P (2002) Common Knowledge. The Stanford Encyclopedia of Philosophy (Summer 2002 Edition), Edward N Zalta (ed.). Website publication as at 9th March 2004: http://plato.stanford.edu/archives/sum2002/entries/common-knowledge/
WATSON I (1997) Applying Case-Based Reasoning: Techniques for Enterprise Systems. Morgan Kaufman Publishers.
WEIBULL J W (1995) Evolutionary Game Theory. MIT Press.
WEIBULL J W (1998) Evolution, Rationality and Equilibrium in Games. European Economic Review, 42, pp. 641-649.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2004]