Piergiuseppe Morone and Richard Taylor (2004)
Small World Dynamics and The Process of Knowledge Diffusion: The Case of The Metropolitan Area of Greater Santiago De Chile
Journal of Artificial Societies and Social Simulation
vol. 7, no. 2
<https://www.jasss.org/7/2/5.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 07-Feb-2004 Accepted: 12-Feb-2004 Published: 31-Mar-2004
 Abstract
AbstractThat the advance of knowledge lies at the core of modern growth process is more than an inference from the growth accounts. It is a perception enforced by well over a century of common experience. Economists have therefore applied themselves to learning more about the ways that practical knowledge is gained and exploited. A new outlook has developed and spread. It is not yet well defined (Abramovitz 1989)
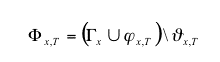
|
(1) |
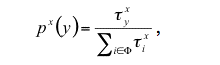
|
(2) |

|
(3) |
|
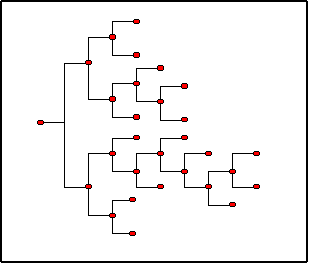
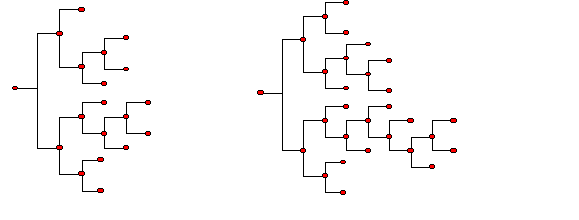
| Figure 1. Cognitive Map |
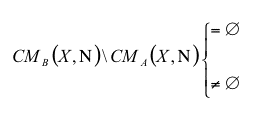
|
(4) |
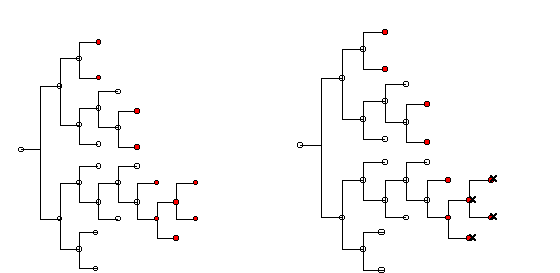
| |
| Agent A | Agent B |
| Figure 2. Comparing two Cognitive Maps | |
| |
| CMB\CMA | Learning Region |
| Figure 3. Knowledge interaction and the occurrence of learning | |
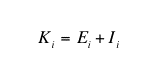
|
(5) |
where Ei was the level of education obtained by agent i through a formal process of individual learning, and Ii was the level of education of agent i obtained through the process of informal interactive learning (face-to-face interaction).
 . The knowledge function was then defined as:
. The knowledge function was then defined as:
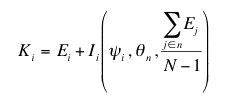
|
(6) |
| Table 1: Original database | |||||
| Variable | Number of Obs. | Mean | Std. Dev. | Min. | Max. |
| District | 7732 | 18.64602 | 10.28054 | 1 | 34 |
| Schooling | 7732 | 10.90184 | 3.892597 | 0 | 19 |
| Kind | 7732 | 2.504268 | 1.405629 | 0 | 6 |
| Computer | 7732 | 0.146275 | 0.353404 | 0 | 1 |
| Table 2: Simulation sample database | |||||
| Variable | Number of Obs. | Mean | Std. Dev. | Min. | Max. |
| District | 232 | 18.78017 | 10.45332 | 1 | 34 |
| Schooling | 232 | 11.15517 | 3.758058 | 0 | 18 |
| Kind | 232 | 2.577586 | 1.409005 | 0 | 6 |
| Computer | 232 | 0.1422414 | 0.350052 | 0 | 1 |
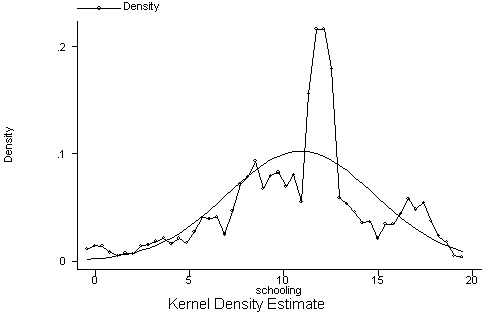
|
| Figure 4. Original database |
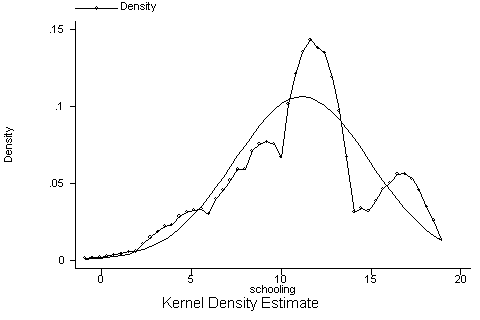
|
| Figure 5. Sample database |
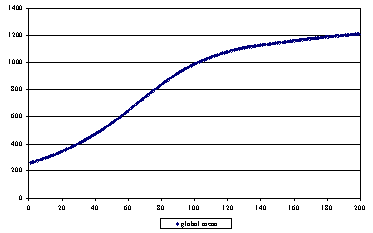
|
| Figure 6. Changes in the average level of knowledge |
|
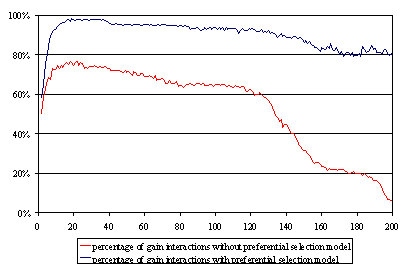
| Figure 7. Percentage of gainful interactions. Studying the efficiency of the system |
|
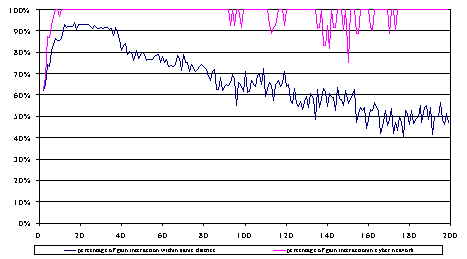
| Figure 8. Percentage of gainful interactions within districts and cyber-network |
|
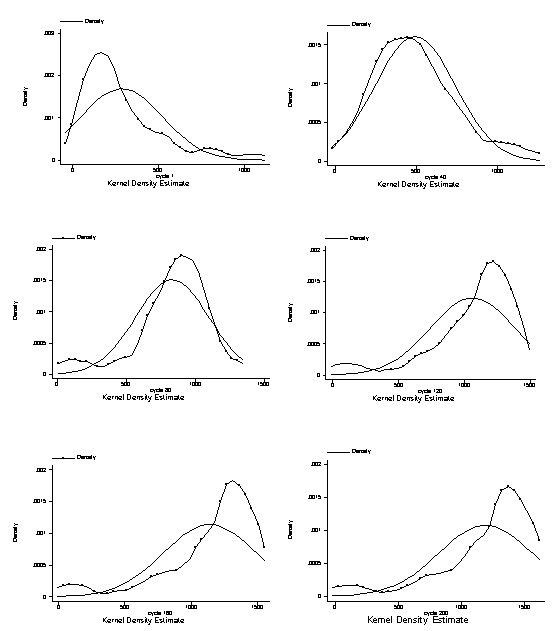
| Figure 9. Kernel density functions of knowledge and normal distribution |
|
| Figure 10. Kernel density functions of knowledge and normal distribution |
|
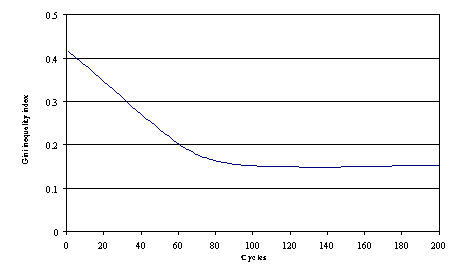
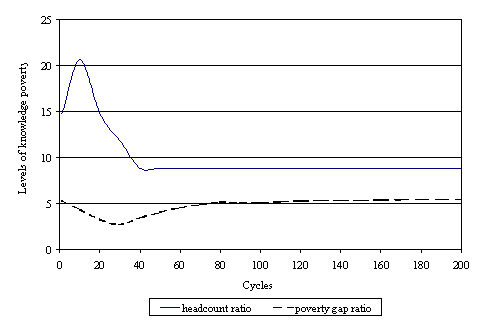
| Figure 11. Poverty measures applied to knowledge |
| |
| Variance levels by districts | Mean levels by districts |
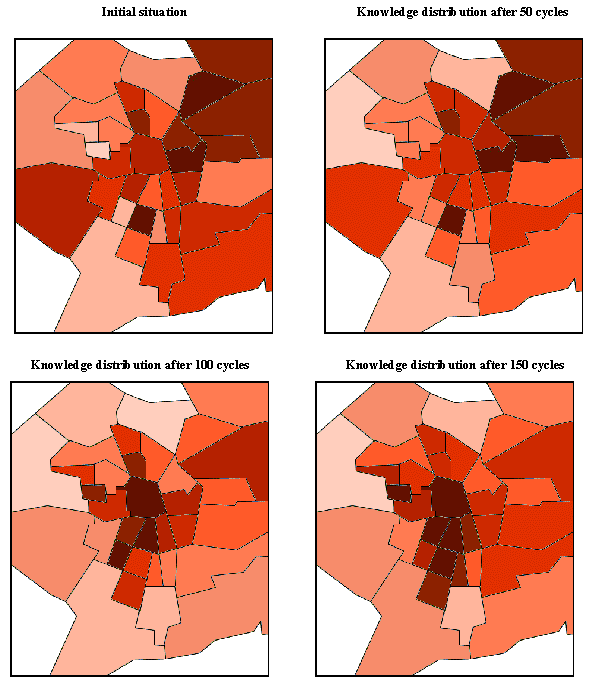
| Figure 12. Changes in knowledge average and variance by districts | |
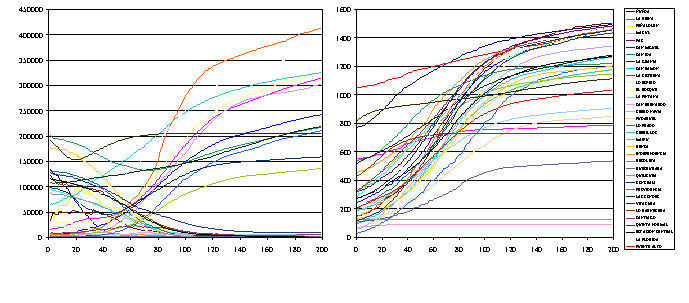
|
| Figure 13. Changes in knowledge mean by districts |
| |
| Average change in knowledge variance by districts | Average level of knowledge by districts |
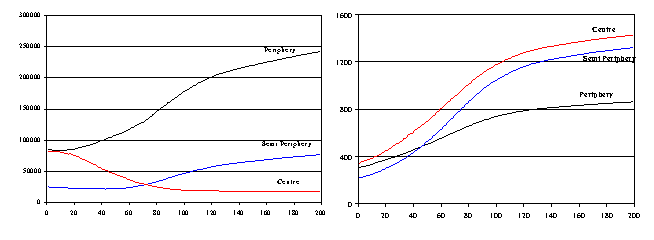
| Figure 14. Centre-Periphery dynamics | |
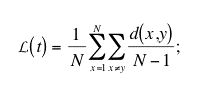
|
and the average cliquishness:
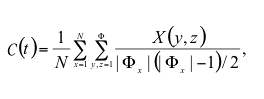
|
where X (y, z) = 1 if y and z are connected at time t (no matter whether the connection is a first generation or next generation connection), and X (y, z) = 0 otherwise.
| Table 3: Small world calculation results | |||
| C | L | ||
| Simulation Results | Cycle 1 | 0.4396 | 2.1727 |
| Cycle 50 | 0.1425 | 2.3082 | |
| Cycle 100 | 0.2661 | 2.9281 | |
| Cycle 150 | 0.2853 | 3.2699 | |
| Cycle 200 | 0.2578 | 2.9669 | |
| Random Network | Cycle 1 | 0.0388 | 2.4789 |
| Cycle 50 | 0.0345 | 2.6193 | |
| Cycle 100 | 0.0345 | 2.6193 | |
| Cycle 150 | 0.0302 | 2.7991 | |
| Cycle 200 | 0.0302 | 2.7991 | |
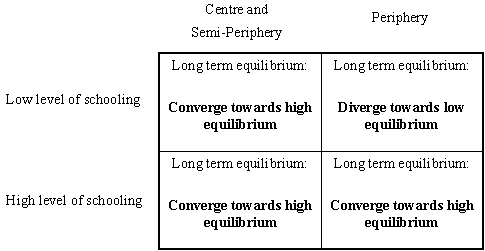
|
| Figure 15. Possible long-term equilibria |
| Table A1: Schooling distribution, original sample | |||
| Schooling | Freq. | Percent | Cum. |
| 0 | 144 | 1.86 | 1.86 |
| 1 | 26 | 0.34 | 2.2 |
| 2 | 68 | 0.88 | 3.08 |
| 3 | 134 | 1.73 | 4.81 |
| 4 | 159 | 2.06 | 6.87 |
| 5 | 127 | 1.64 | 8.51 |
| 6 | 390 | 5.04 | 13.55 |
| 7 | 157 | 2.03 | 15.58 |
| 8 | 724 | 9.36 | 24.95 |
| 9 | 553 | 7.15 | 32.1 |
| 10 | 625 | 8.08 | 40.18 |
| 11 | 480 | 6.21 | 46.39 |
| 12 | 2155 | 27.87 | 74.26 |
| 13 | 415 | 5.37 | 79.63 |
| 14 | 312 | 4.04 | 83.67 |
| 15 | 205 | 2.65 | 86.32 |
| 16 | 289 | 3.74 | 90.05 |
| 17 | 491 | 6.35 | 96.4 |
| 18 | 231 | 2.99 | 99.39 |
| 19 | 47 | 0.61 | 100 |
| Total | 7732 | 100 | |
| Table A2: Schooling distribution, simulation sample | |||
| Schooling | Freq. | Percent | Cum. |
| 0 | 1 | 0.43 | 0.43 |
| 2 | 2 | 0.86 | 1.29 |
| 3 | 2 | 0.86 | 2.16 |
| 4 | 9 | 3.88 | 6.03 |
| 5 | 5 | 2.16 | 8.19 |
| 6 | 10 | 4.31 | 12.5 |
| 7 | 6 | 2.59 | 15.09 |
| 8 | 20 | 8.62 | 23.71 |
| 9 | 16 | 6.9 | 30.6 |
| 10 | 20 | 8.62 | 39.22 |
| 11 | 11 | 4.74 | 43.97 |
| 12 | 68 | 29.31 | 73.28 |
| 13 | 12 | 5.17 | 78.45 |
| 14 | 6 | 2.59 | 81.03 |
| 15 | 5 | 2.16 | 83.19 |
| 16 | 12 | 5.17 | 88.36 |
| 17 | 19 | 8.19 | 96.55 |
| 18 | 8 | 3.45 | 100 |
| Total | 232 | 100 | |
| Table A3: Geographical distribution, original sample | |||
| District | Freq. | Percent | Cum. |
| 1 | 253 | 3.27 | 3.27 |
| 2 | 98 | 1.27 | 4.54 |
| 3 | 377 | 4.88 | 9.42 |
| 4 | 195 | 2.52 | 11.94 |
| 5 | 199 | 2.57 | 14.51 |
| 6 | 86 | 1.11 | 15.62 |
| 7 | 198 | 2.56 | 18.18 |
| 8 | 176 | 2.28 | 20.46 |
| 9 | 177 | 2.29 | 22.75 |
| 10 | 145 | 1.88 | 24.62 |
| 11 | 211 | 2.73 | 27.35 |
| 12 | 290 | 3.75 | 31.1 |
| 13 | 305 | 3.94 | 35.05 |
| 14 | 270 | 3.49 | 38.54 |
| 15 | 242 | 3.13 | 41.67 |
| 16 | 283 | 3.66 | 45.33 |
| 17 | 153 | 1.98 | 47.31 |
| 18 | 138 | 1.78 | 49.09 |
| 19 | 515 | 6.66 | 55.76 |
| 20 | 156 | 2.02 | 57.77 |
| 21 | 86 | 1.11 | 58.89 |
| 22 | 261 | 3.38 | 62.26 |
| 23 | 73 | 0.94 | 63.2 |
| 24 | 103 | 1.33 | 64.54 |
| 25 | 208 | 2.69 | 67.23 |
| 26 | 129 | 1.67 | 68.9 |
| 27 | 466 | 6.03 | 74.92 |
| 28 | 151 | 1.95 | 76.88 |
| 29 | 77 | 1 | 77.87 |
| 30 | 307 | 3.97 | 81.84 |
| 31 | 180 | 2.33 | 84.17 |
| 32 | 202 | 2.61 | 86.78 |
| 33 | 529 | 6.84 | 93.62 |
| 34 | 493 | 6.38 | 100 |
| Total | 7732 | 100 | |
| Table A4: Geographical distribution, simulation sample | |||
| District | Freq. | Percent | Cum. |
| 1 | 5 | 2.16 | 2.16 |
| 2 | 2 | 0.86 | 3.02 |
| 3 | 20 | 8.62 | 11.64 |
| 4 | 3 | 1.29 | 12.93 |
| 5 | 8 | 3.45 | 16.38 |
| 6 | 2 | 0.86 | 17.24 |
| 7 | 5 | 2.16 | 19.4 |
| 8 | 6 | 2.59 | 21.98 |
| 9 | 7 | 3.02 | 25 |
| 10 | 1 | 0.43 | 25.43 |
| 11 | 8 | 3.45 | 28.88 |
| 12 | 9 | 3.88 | 32.76 |
| 13 | 6 | 2.59 | 35.34 |
| 14 | 6 | 2.59 | 37.93 |
| 15 | 5 | 2.16 | 40.09 |
| 16 | 6 | 2.59 | 42.67 |
| 17 | 1 | 0.43 | 43.1 |
| 18 | 5 | 2.16 | 45.26 |
| 19 | 15 | 6.47 | 51.72 |
| 20 | 11 | 4.74 | 56.47 |
| 21 | 3 | 1.29 | 57.76 |
| 22 | 5 | 2.16 | 59.91 |
| 23 | 3 | 1.29 | 61.21 |
| 24 | 4 | 1.72 | 62.93 |
| 25 | 8 | 3.45 | 66.38 |
| 26 | 4 | 1.72 | 68.1 |
| 27 | 15 | 6.47 | 74.57 |
| 28 | 6 | 2.59 | 77.16 |
| 29 | 3 | 1.29 | 78.45 |
| 30 | 8 | 3.45 | 81.9 |
| 31 | 6 | 2.59 | 84.48 |
| 32 | 6 | 2.59 | 87.07 |
| 33 | 13 | 5.6 | 92.67 |
| 34 | 17 | 7.33 | 100 |
| Total | 232 | 100 | |
| Table A5: Distribution of kind of school, original sample | |||
| Kind | Freq. | Percent | Cum. |
| 0 | 139 | 1.8 | 1.8 |
| 1 | 1775 | 22.96 | 24.75 |
| 2 | 2995 | 38.74 | 63.49 |
| 3 | 1029 | 13.31 | 76.8 |
| 4 | 474 | 6.13 | 82.93 |
| 5 | 1305 | 16.88 | 99.81 |
| 6 | 15 | 0.19 | 100 |
| Total | 7732 | 100 | |
| Table A6: Distribution of kind of school, simulation sample | |||
| Kind | Freq. | Percent | Cum. |
| 0 | 1 | 0.43 | 0.43 |
| 1 | 53 | 22.84 | 23.28 |
| 2 | 89 | 38.36 | 61.64 |
| 3 | 33 | 14.22 | 75.86 |
| 4 | 13 | 5.6 | 81.47 |
| 5 | 42 | 18.1 | 99.57 |
| 6 | 1 | 0.43 | 100 |
| Total | 232 | 100 | |
| Table A7: Distribution of use of computer at work, original sample | |||
| Computer | Freq. | Percent | Cum. |
| 0 | 6601 | 85.37 | 85.37 |
| 1 | 1131 | 14.63 | 100 |
| Total | 7732 | 100 | |
| Table A8: Distribution of use of computer at work, simulation sample | |||
| Computer | Freq. | Percent | Cum. |
| 0 | 199 | 85.78 | 85.78 |
| 1 | 33 | 14.22 | 100 |
| Total | 232 | 100 | |
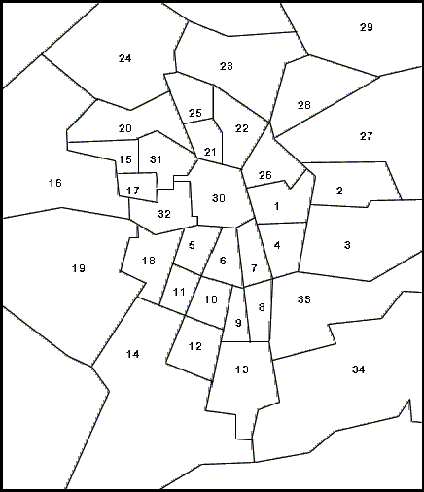
| |
| District | Code |
| ÑUÑOA | 1 |
| LA REINA | 2 |
| PEÑALOLEN | 3 |
| MACUL | 4 |
| PAC | 5 |
| SAN MIGUEL | 6 |
| SAN JOA | 7 |
| LA GRANJA | 8 |
| SAN RAMON | 9 |
| LA CISTERNA | 10 |
| LO ESPEJO | 11 |
| EL BOSQUE | 12 |
| LA PINTANA | 13 |
| SAN BERNARDO | 14 |
| CERRO NAVIA | 15 |
| PUDAHUEL | 16 |
| LO PRADO | 17 |
| CERRILLOS | 18 |
| MAIPU | 19 |
| RENCA | 20 |
| INDEPENDENCIA | 21 |
| RECOLETA | 22 |
| HUECHURABA | 23 |
| QUILICURA | 24 |
| CONCHALI | 25 |
| PROVIDENCIA | 26 |
| LAS CONDES | 27 |
| VITACURA | 28 |
| LO BARNECHEA | 29 |
| SANTIAGO | 30 |
| QUINTA NORMAL | 31 |
| ESTACION CENTRAL | 32 |
| LA FLORIDA | 33 |
| PUENTE ALTO | 34 |
| Macro-districts Composition: | |
| Centre: 1, 4, 5, 6, 7, 21, 26, 30, 31, 32; | |
| Semi-periphery: 8, 9, 10, 11, 12, 13, 15, 17, 18, 20, 22, 25; | |
| Periphery: 2, 3, 14, 16, 19, 23, 24, 27, 28, 29, 33, 34. | |
| Figure A1. Map of Greater Santiago Region and District Codes | |
2 See, among others, Ellison (1993, 2000), Anderlini and Ianni (1996), Berninghaus and Schwalbe (1996), Goyal (1996), Akerlof (1997), Watts (2001).
3 An intuitive example would be that of a student who stops interacting with her/his teacher when she/he feels that she/he has nothing to learn from the interaction, or when her/his knowledge surpasses that of her/his teacher. Another example could be that of two equally educated agents who might stop communicating when they become specialised in two very different areas, so no shared interest remains.
4 In this way we assume that agents are constrained by 'bounded rationality' in the sense that they respond to utility signals. This does not mean that they maximise utility (Katz 2001).
5 Moving from left to right, each pair of years of schooling corresponds to a complete column activated. We set the initial level of education (0 to 2 years of schooling) as three full columns activated (with the third column containing four nodes), then additional pairs of years of schooling correspond to an additional column in the cognitive map.
6 After the eighth year of schooling students choose to specialise either in humanistic-scientific general education or technical-professional education.
7 We define the cognitive map only as a function of X and N because at this stage we are not interested in the depth of knowledge.
8 In the simulation model p is set equal to 0.1.
9 We refer explicitly to the work of Cohen and Levinthal (1989) on returns from R&D. The concept of individual absorptive capacity was already developed in Morone (2001).
10 This region, called Región Metropolitana, includes 42% of the economically active national population (see: Bravo et al. 1999:7).
11 Chilean schools can be entirely funded by the government, partially funded by the government or entirely private.
12 Agents younger than 14 years old are probably engaged mainly in individual learning as schooling represent a major part of their life, while people over 65 are probably less likely to be involved in knowledge exchange processes (because they are already too wise!).
13 Given the structure of knowledge expressed by the cognitive map, we calculate changes in knowledge based on the total number of activated nodes for each agent.
14 Longer simulations show how the curve completely levels off, meaning that the system reaches a long-run stable equilibrium.
15 The only change introduced was in the preferential selection: the value τi defined in equation (3) was not updated so it remained equal to 1. No acquaintances were dropped. Apart from that the two simulations here compared are identical.
16 We studied distributional changes by means of inequality and poverty measures used typically in income distribution analysis. We did so because we are interested in studying the distributional properties of the model as well as its network and efficiency properties.
17 We call the ignorance line what is usually called the poverty line.
18 A detailed map with the district codes is reproduced in the annex.
19 A detailed description of each macro-district composition is reproduced in the annex.
AKERLOF, G. (1997), "Social Distance and Social Decisions", Econometrica, 65: 1005-1027.
ANCORI, B., A. Bureth, et al. (2000), "The Economics of Knowledge: the Debate About Codification and Tacit knowledge", Industrial and Corporate Change, 9, (2): 255-287.
ANDERLINI, L. and A. Ianni (1996), "Path Dependence and Learning from Neighbours", Games and Economic Behaviour, 13: 141-177.
BALA, V. and S. Goyal (1995), "A Theory of Learning with Heterogeneous Agents", International Economic Review, 36(2): 303-323.
BALA, V. and S. Goyal (1998), "Learning from Neighbours", Review of Economic Studies, 65: 595-621.
BÉNABOU, R. (1993), "Working of a City: Location Education and Production", Quarterly Journal of Economics, 58: 619-652.
BERNINGHAUS, S. and U. Schwalbe (1996), "Evolution, Interaction, and Nash Equilibria", Journal of Economic Behaviours and Organization, 29: 57-85.
BEYER, H.(2000), "Education and Income Inequality: A New Look", Estudios Publicos, 77.
BORGATTI,S.P., M.G. Everett, and L.C. Freeman, (1999), UCINET 5.0 Version 1.00. Natick: Analytic Technologies.
BRAVO, D., D. Contreras, Madrano (1999), "The Return to Computer in Chile: Does it Change after Controlling by Skill Bias? ", mimeo, Department of Economics, University of Chile.
BROCK, W. and S. Durlauf (1995), "Discrete Choice with Social InteractionI:Theory" NBER Working Paper, 5291.
CHWE, M. S-Y. (2000), "Communication and Coordination in Social networks", Review of Economic Studies, 67: 1-16.
COHEN, W. M. and D. A. Levinthal (1989), "Innovation and Learning: The Two Faces of R&D", The Economic Journal, 99(September): 569-596.
COWAN, R. and N. Jonard (1999), "Network Structure and the Diffusion of Knowledge", MERIT Working Papers, 99-028.
DURLAUF, S. (1996), "Neighborhood Feedbacks, Endogenous Stratification, and Income Inequality", in: W. Barnett, G. Gandolfo and C. Hillinger (ed), Dynamic Disequilibrium Modelling, Cambridge, Cambridge University Press.
ELLISON, G. (1993), "Learning, Local Interaction, and Coordination", Econometrica, 61: 1047-1071.
ELLISON, G. (2000), "Basins and Attraction, Long Run Stochastic Ability and the Speed of Step-by-Step Evolution", Review of Economic Studies, 67: 17-45.
ELLISON, G. and D. Fudenberg (1993), "Rules of Thumb of Social Learning", The Journal of Political Economy, 101(4): 612-43.
ELLISON, G. and D. Fudenberg (1995), "Word-of-Mouth Communication and Social Learning", Quarterly Journal of Economics, 110(1): 93-125.
GLAESER, E. L., B. Sacerdote, and P. Scheinkman (1996), "Crime and Social Interactions" Quarterly Journal of Economics, 111: 507-548.
GOYAL S. (1996), "Interaction Structure and Social Change", Journal of Institutional and Theoretical Economics, 152: 472-494.
JOVANOVIC, B. and R. Rob (1989), "The growth and diffusion of Knowledge", Review of Economic Studies, 56(198-9): 569-82.
KATZ, J. (2001), "Structural Reforms and Technological Behaviour. The Sources and Nature of Technological Change in Latin America in the 1990s", Research Policy, 30: 1-19.
KIEFER, N. (1989), "A Value Function Arising in Economics of Information", Journal of Economic Dynamics and Control, 7: 331-337.
MORONE P. (2001), "The Two Faces of Knowledge Diffusion: the Chilean Case", Universidad de Chile, Departamento de Economia, Working Paper, 178.
MORONE, P. and R. Taylor (2004), "Knowledge Diffusion Dynamics of Face-to-Face Interactions", Journal of Evolutionary Economics, forthcoming.
MORRIS, S. (2000), "Contagion", Review of Economic Studies, 67: 57-68.
WALLIS, S., and S. Moss (1994), Efficient Forward Chaining for Declarative Rules in a Multi-Agent Modelling Language, available online at: http://www.cpm.mmu.ac.uk/cpmreps
WATTS, A. (2001), "A Dynamic Model of Network Formation", Games and Economic Behaviours, 34: 331-341.
WATTS, D. and S. Strogatz (1998), "Collective Dynamics of Small-World Networks", Letters to Nature, 393, June: 440-442.
WILSON, R. J. and J. J. Watkins (1990), Graphs: An Introductory Approach, Wiley: New York.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2004]