Eric Darmon and Dominique Torre (2004)
Adoption and Use of Electronic Markets: Individual and Collective Learning
Journal of Artificial
Societies and Social Simulation vol. 7, no. 2
<https://www.jasss.org/7/2/2.html>
To cite articles published in the Journal of Artificial Societies and Social Simulation, reference the above information and include paragraph numbers if necessary
Received: 07-Feb-2004 Accepted: 02-Jan-2004 Published: 31-Mar-2004
 Abstract
Abstract
| ci,t= ζ where ζ is randomly drawn from a uniform distribution between 0 and y. |
(1) |
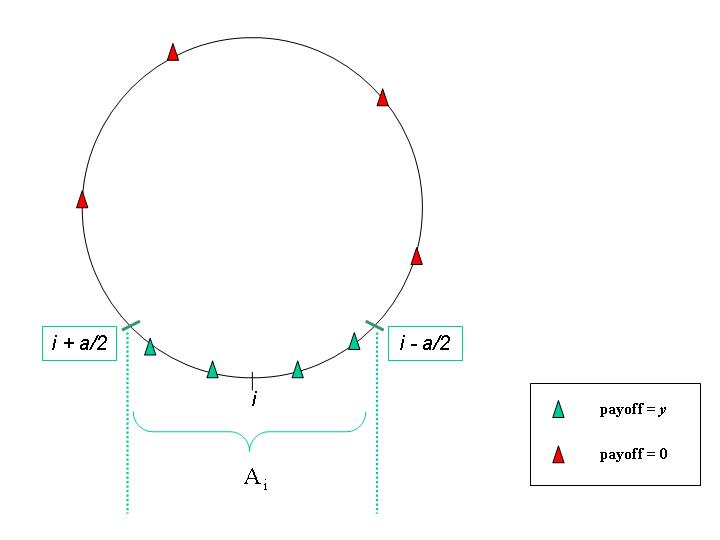 |
| Figure 1a. Agent's i preferences and payoffs |
| y if 0 if |
(2) |
| (3) |
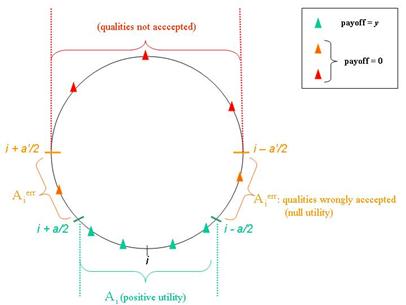 |
| Figure 1b. Agent's i errors and payoffs on the electronic market |
| (4) |
Going back to our simplified example ( N = 100; a = 0.1; a' = 0.5; choice of Agent 50), let us suppose that Agent 50 trades with Agent 57 on the electronic market. After consuming, Agent 50 can precisely assess the quality provided by Agent 57. As this quality does not fill his needs, Agent 50 will not consider the goods provided by Agent 57 during his future trades. The ex ante uncertainty about quality is then lowered and Agent 50's individual expertise is increased.
The membership of a community is ruled by an exogenous parameter: the total population is divided in two sub-populations according to the exogenous parameter μ (μ ∈ [0,1]). The first group is composed of (1 - μ) N agents who are not members of any community. These agents then learn individually as described previously. The remaining (μ) agents (uniformly distributed on the quality circle) share transaction experiences in one single community[4].
The internal working of this community is very simple: at the end of the period, each member of the community informs all other members about the quality (location) of the good traded over the electronic market. The other members incorporate this information as if they had themselves traded this quality[5].
Going back to our simplified example, let us suppose that Agents 50 and 0 are both members of the same community. If Agent 0 trades with Agent 57 on the electronic channel, he will inform Agent 50 about the characteristics of the good traded. Thanks to this description, Agent 50 finds out that the good provided by agent 57 does not fill his needs. During his future search on the electronic market, Agent 50 will then refuse to transact with Agent 57. This learning mechanism is homothetic to the individual one. The only difference is that, unlike the individual learning case, Agent 50 does not need to experience by himself the wrong good and get a null payoff.
| (6a) |
| (6b) |
| (6c) |
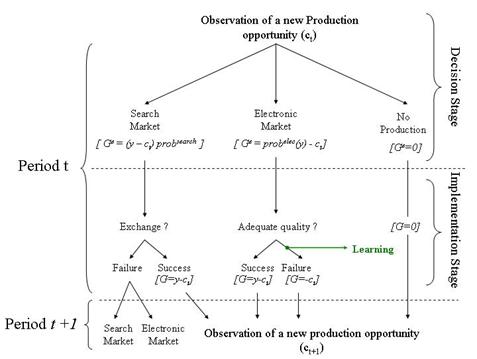 |
| Figure 2. Decision Tree of agent i at period t |
 |
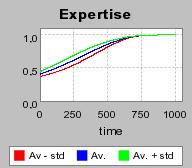 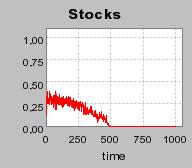 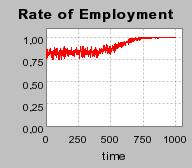 |
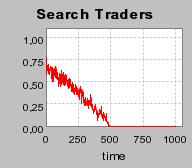
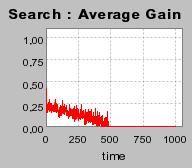
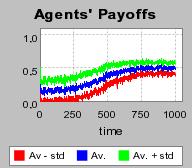
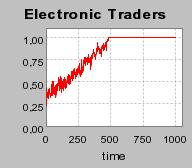
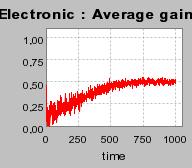
| Figure 3. Individual learning; a = 0.2 and τ = 0.8; Permanent idiosyncratic supply shocks: new production cost at each period |
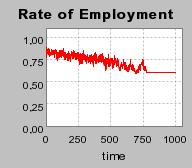 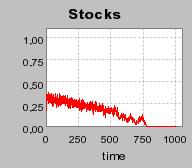
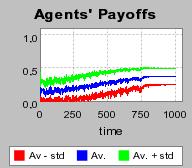 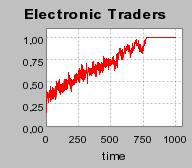 
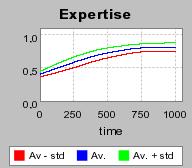 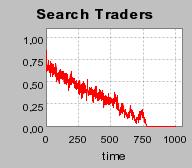 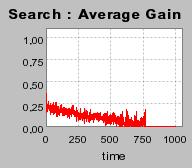 |
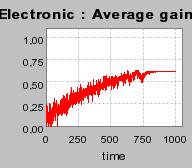
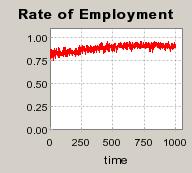
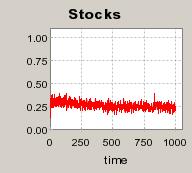
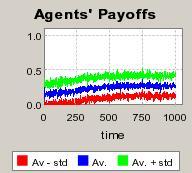
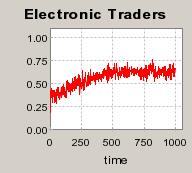
| Figure 4. Individual learning; a = 0.2 and τ = 0.8; No supply shock: heterogeneous but constant production costs |
  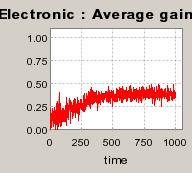
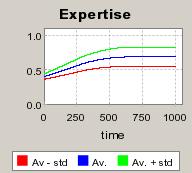 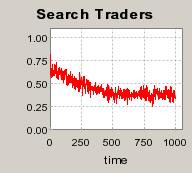 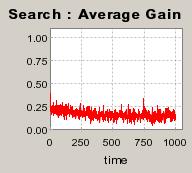 |
| Figure 5. Individual learning; f = 1%f = 1%; a = 0.2 and t = 0.8; Supply shocks: new production cost at each period |
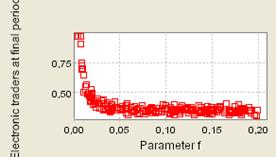 |
| Figure 6. 400 repeated iterations of the process; Supply shocks; depreciation rate f ranging from 0 to (0.2). The chart exhibits the adoption rate of the electronic channel once the economy has reached its stationary position (averaged on the last periods) |
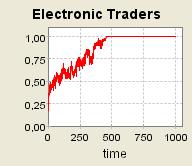 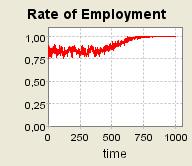 |
| Figure 7. τ = 0.8 and a = 0.2 ; 40 agents are grouped into one single community (μ= 0.2) ; Supply shocks |
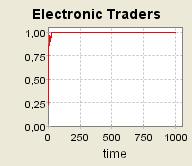  |
| Figure 8. τ = 0.8 and a = 0.2 ; 160 agents are grouped into one single community (μ= 0.8) ; Supply shocks |
Table 1: τ = 0.8 ; a = 0.2 ; Supply shocks. |
||||
| No Learning | Individual Learning | Social Learning [μ = 0.2] |
Social Learning [μ = 0.8] |
|
|
Average Employment Rate |
0.81 | 0.89 | 0.9 | 0.96 |
| Average Payoff (whole population) | 0.14 | 0.34 | 0.39 | 0.47 |
|
Average participation rate of the electronic market: |
0.37 | 0.82 | 0.85 | 0.99 |
|
Average Payoff VC |
-- | -- | 0.46 | 0.49 |
| Average Payoff
(non members of a VC) |
-- | -- | 0.34 | 0.38 |
Table 2: τ = 0.8 ; a = 0.2 ; Constant production costs. |
||||
| No Learning | Individual Learning | Social Learning [μ = 0.2 ] | Social Learning [μ = 0.8 ] | |
|
Average Employment Rate |
0.83 | 0.71 | 0.74 | 0.87 |
|
Average Payoff (whole population) |
0.16 | 0.28 | 0.32 | 0.45 |
|
Average participation rate of the electronic market: |
0.37 | 0.75 | 0.82 | 0.99 |
|
Average Payoff VC |
-- | -- | 0.42 | 0.51 |
|
Average Payoff |
-- | -- | 0.29 | 0.25 |
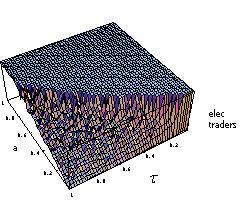 |
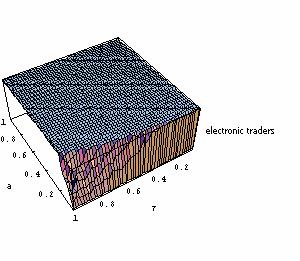
| Figure 9. Results of 2500 iterations with Parameters a and τ both ranging from 0 to 1. The chart presents the share of electronic traders (among the employed population) at Period 1000 (after convergence); No learning. |
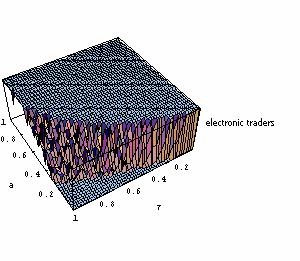 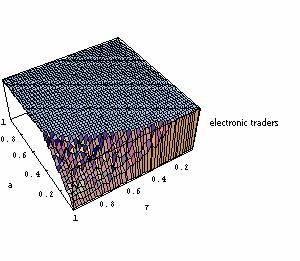 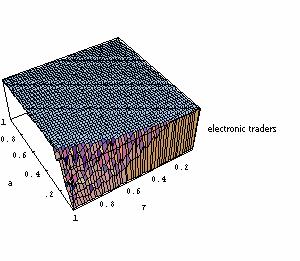  |
| Figure 10. Repartition of agents after 250 (top left), 500 (top right), 750 (bottom left) and 1000 (bottom right) periods; individual learning; production costs randomly drawn at each period |
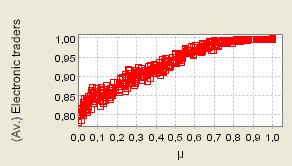  |
| Figure 11. 400 repeated iterations of the process with μ randomly selected from 0 to 1; Supply shocks (We only report here the process as production costs are renewed at each time step. The charts depicting the second case - heterogeneous but constant production costs - (available on request) are qualitatively similar) |
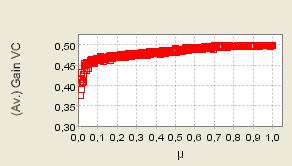 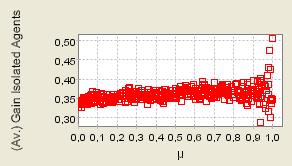 |
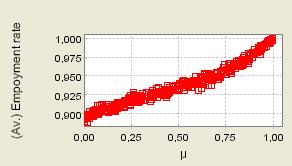
| Figure 12. 400 repeated iterations of the process with μ randomly selected from 0 to 1; Supply shocks |
[2] The term
![]() is numerically equal to
is numerically equal to
![]() where
where ![]() if agent j
chose to operate at period t on the traditional
market, 0 else.
if agent j
chose to operate at period t on the traditional
market, 0 else.
[3]
Formally, every times he trades with an ![]() -agent, agent
i will be definitely remove this
-agent, agent
i will be definitely remove this ![]() -agent from
the set
-agent from
the set ![]() . If i meets j at
period t on the electronic market:
. If i meets j at
period t on the electronic market:
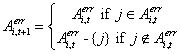 |
[5.i] |
This procedure decreases the risk of making a null-payoff
trade for the next periods. As the size of the set
![]() is
decreased, agent i's expertise mechanically
increases.
is
decreased, agent i's expertise mechanically
increases.
![]() /
/ ![]() = #
= # ![]() / #
/ # ![]() where "#" denotes the cardinal of the
set, with by definition #
where "#" denotes the cardinal of the
set, with by definition # ![]()
![]() aN.
aN.
[4] We only present here the results as agents are belongs to one single community. We have simulated other cases where agents are distributed into several communities. These results are available on request.
[5] Formally, we model a community V as a set of agents. Let k and k' be two members of this community and let us suppose that agent k has traded with agent j on the electronic market. At the end of the period, agent kupdates his own expertise according to the individual learning pattern (see equation [5.i]). He then informs all the other members belonging to his community about the quality traded. Let k' (k' ≠ k) be one of these members. Agent k' will then incorporate the delivered information in his own set of information i.e. as if he had traded himself with agent j.
Formally, this leads to an expression of the learning mechanism close to the individual one: agent k has met agent j at period τ on the electronic market, and transmits the information to agent k':
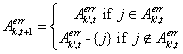 |
[5.ii] |
This process is then repeated for each members k' of the community.
[6] Technically, each piece
of information belonging to the initial interval
![]() is forgotten with probability
f. The size of the set
is forgotten with probability
f. The size of the set ![]() is then no longer
strictly decreasing with time t.
is then no longer
strictly decreasing with time t.
[7] The explanation provided in this paper focuses on the problem of the use of ICT embedded in electronic market. Of course, this factor is not exclusive from other factors mentioned in the introduction.
[8] We could further notice that, after convergence, the average payoff is not stable over time but permanently oscillates around a constant average, despite the repartition of the population among the three possible states (i.e. unemployment, traditional and electronic market) is constant. The observed fluctuations are mainly due to the random draws of a new production costs at each period: as the size of the sample of agents is finite, the inter-periodic variations has to be assimilated to some supply shocks. The average payoff fluctuates around 0.5 or equivalently (y ñ average production cost). This value is maximal when the economy has reached a full-employment state and remaining inequalities are only caused by heterogeneous producing capacities distributed among agents.
[9] This finding has to be related to what happens in the "no learning" case (see Appendix 1).
[10] We could have done differently by assuming that the most individually-expert agents participate to VC more than less expert. This new assumption would however only reinforce our conclusions.
BALASUBRAMANIAN S and Mahajan V (2001) The Economic Leverage of the Virtual Community. International Journal of Electronic Commerce, Spring 2001, pp. 103-138.
BARNATT C (1998) Virtual Communities and Financial Services - Online Business Potentials and Strategic Choice. International Journal of Bank Marketing, pp.161-169.
BUGHIN J and Hagel J (2000) The Operational Performance of Virtual Communities - Towards a Successful Business Model? Electronic Markets, pp.237-246.
DUMANS M-E (2003) Concurrence Entre Commerce Electronique Et Commerce Traditionnel (Competition between Online Retailers and Traditional Shops). Revue Economique, May 2003. pp. 687-696.
ELLIASSON G (2002) "The Macroeconomic Effects of Computer and Communications Technology." 170. Report of the Royal Institute of Technology (KTH): Stockholm
HENG S H, Creemers M and Verhagen T (2001) Some Pre-Requisites for Electronic Commerce. Vrije Universiteit WP.
KARDARAS D, Karakostas B and Papathanassiou E (2003) The Potential of Virtual Communities in the Insurance Industry in the U.K. and Greece. International Journal of Information Management, pp. 41-53.
LANGTON C S, Roghè F and Shaw M (2000) "Consumer Mass Market Online Payment Solutions" In Handbook on Electronic Commerce. M Shaw, R Blanning, T Strader and A Whinston (Eds). Heildelberg: Springer Verlag, pp. 273-288.
LEE M K O and Turban E (2001) A Trust Model for Consumer Internet Shopping. International Journal of Electronic Commerce, Fall 2001. pp. 75-91.
O.E.C.D. (2001) Electronic Commerce. Policy Brief, July 2001.
RATCHFORD B T, Talukar D and Lee M-S (2001) A Model of Consumer Choice of the Internet as an Information Source. International Journal of Electronic Commerce, Spring 2001. pp. 7-21.
ROTHAERMEL F T and Sugiyama S (2001) Virtual Internet Communities and Commercial Success: Individual and Community-Level Theory Grounded in the Atypical Case of Timezone.Com. Journal of Management, pp. 297-312.
SCHUBERT P and Ginsburg M (2000) Virtual Communities of Transaction: The Role of Personalization in Electronic Commerce. Electronic Markets, pp.
STEINMUELLER E W, Shenk I and Mansell R (2000) Net Compatible: The Economic and Social Dynamics of E-Commerce. Communications and Strategies, pp. 241-276.
STRADER T J and Shaw M J (2000) "Electronic Markets: Impact and Implications" In Handbook on Electronic Commerce. M Shaw, R Blanning, T Strader and A Whinston (Eds). Heilderberg: Springer Verlag, pp. 77-100.
WANG Y, Yu Q and Fesenmaier D R (2002) Defining the Virtual Tourist Community: Implications for Tourism Marketing. Tourism Management, pp. 407-417.
Return
to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2004]