Matthias Scheutz and Paul Schermerhorn (2004)
The Role of Signaling Action Tendencies in Conflict Resolution
Journal of Artificial Societies and Social Simulation
vol. 7, no. 1
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/7/1/4.html>
Received: 08-Jun-2003 Accepted: 14-Sep-2004 Published: 31-Jan-2004
 Abstract
Abstract| Stop | Continue | |
| Stop | (BS+CS+n×CC, BS+CS+n×CC) | (BS+CS+n×CC, BC+CC+n×CC) |
| Continue | (BC+CC+n×CC, BS+CS+n×CC) | |
where
| CC, CS < 0 < BS < BC. | (1) |
| (2) |
| (3) |
| (4) |
|
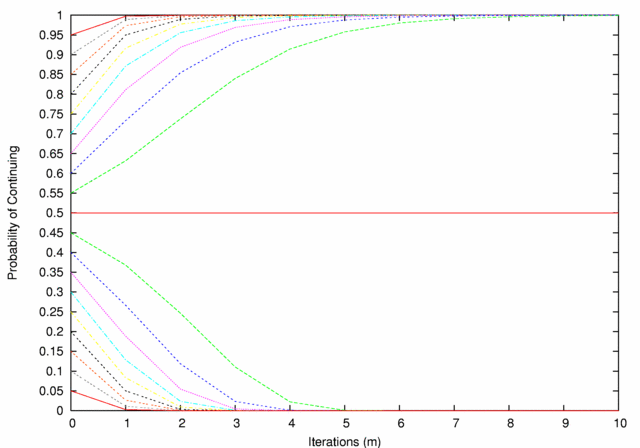
| Figure 1. Decision Mechanism Performance. Lines are paired by color, each pair representing a contest in which the two agents' D-values sum to 1. The probabilities of continuing at 0 iterations are just the original D-values; thereafter the probabilities diverge from one another (except in the (0.5,0.5) case) according to the rule described above |
|
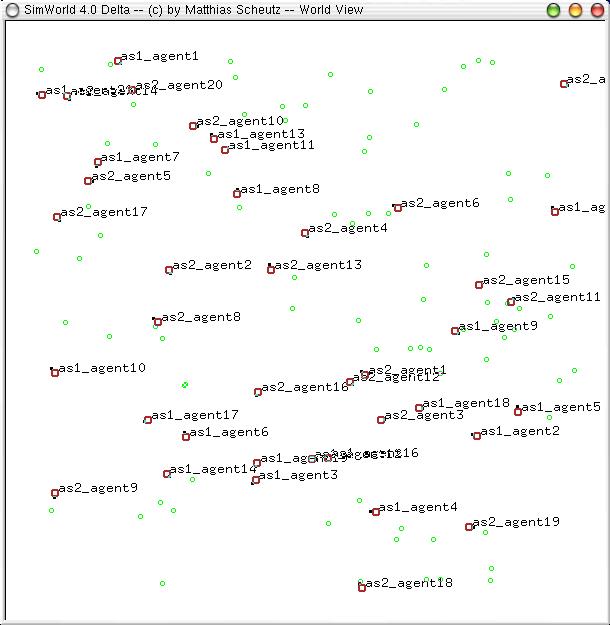
| Figure 2. The SimWorld artificial life environment (graphical mode); small green circles represent food sources and red circles represent agents, with black tics indicating agents' headings. Here, 0-social agents (labeled "as1_agent" followed by their ID number) are competing against m-social agents (labeled "as2_agent" followed by their ID number) |
;;; the loop to update one simulation cycle
foreach cycle do
generate new food resources
foreach entity in allentities do
percepts(entity) := run_sensors(entity, allentities)
endforeach
foreach entity in allentities do
actions(entity) := run_rulesystem(entity, percepts(entity))
endforeach
foreach entity in allentities do
perform actions(entity)
endforeach
remove dead agents, update agents' body representations, update counters
perform statistics
endforeach
;;; select actions based on percepts
function run_rulesystem(entity, percepts) returns action;
generate a combined force vector for the percepts
opponent := detect_opponent(percepts)
if exists(opponent) then
P := entity.tendency
if infinite-social(agent) then
if entity.tendency > opponent.display then
P := 1
else
P := 0
endif
else
for i from 1 to entity.iterations do
if P > opponent.display then
P := P + ((1 - P) / P) * (P - opponent.display)
else
P := P - (P / opponent.display) * (opponent.display - P)
endif
endfor
endif
if P ≥ random(1.0) then
action := retreat (i.e., generate force away from opponent)
else
action := fight (i.e., set force to 0)
endif
else
action := move as determined by the force vector
endif
endfunction
| motion_vector = 20 * ( ∑VF (1 / |VF|2 * VF)) - 20 * ( ∑VS (1 / |VS|2 * VS)) - 5 * ( ∑VO (1 / |VO|2 * VO)) . | (5) |
|
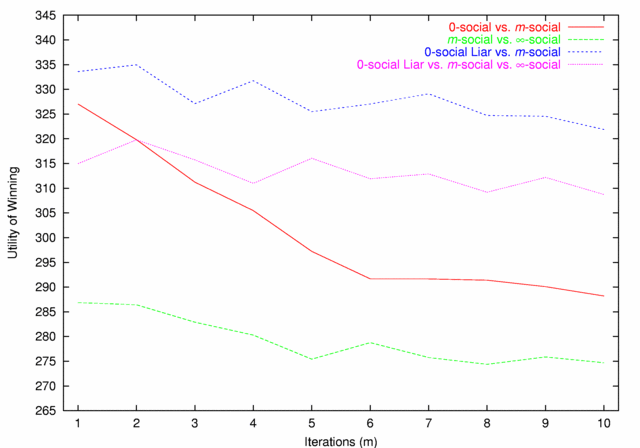
| Figure 3. Utility of Winning |
|
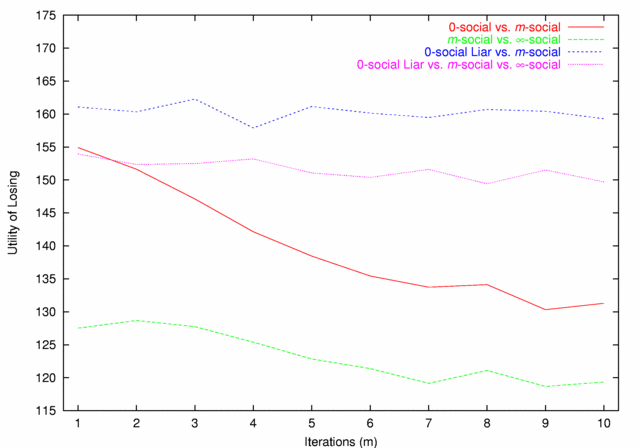
| Figure 4. Utility of Losing |
|
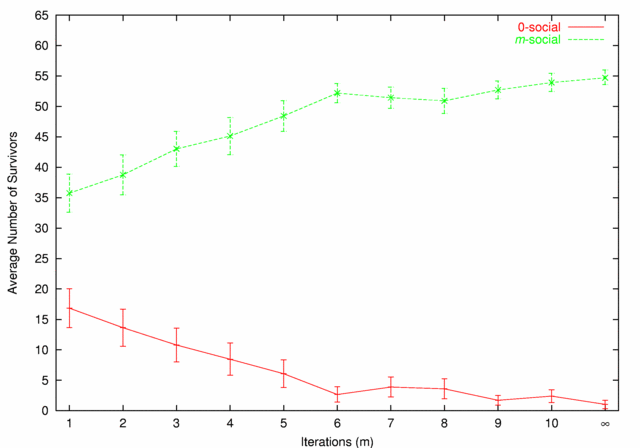
| Figure 5. 0-social vs. m-social |
|
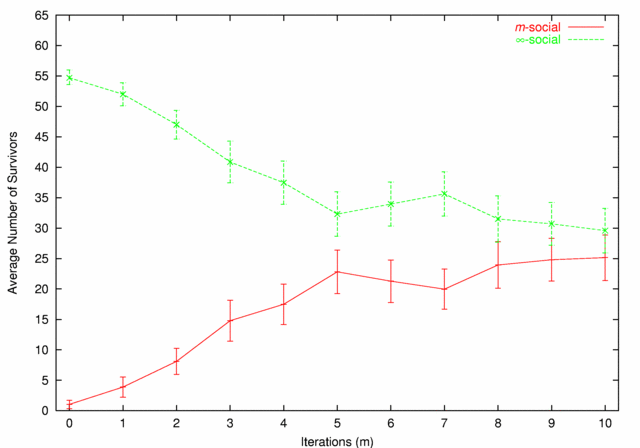
| Figure 6. m-social vs. ∞-social |
|
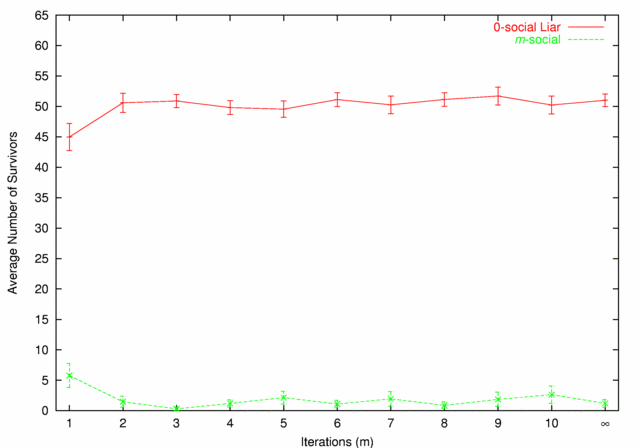
| Figure 7. 0-social Liars vs. m-social |
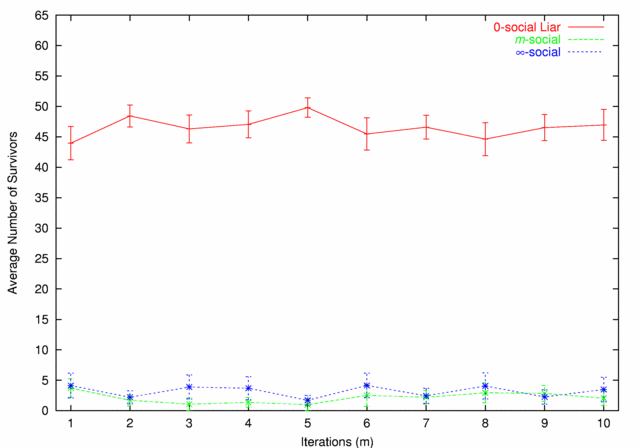
|
| Figure 8. 0-social Liars vs. m-social vs. ∞-social |
| Stop | Continue | |
| Stop | (-90 - 50×n,-90 - 50×n) | (-90 - 50×n,270 - 50×n) |
| Continue | (270 - 50×n,-90 - 50×n) | |
| (6) |
and an expected individual utility of
| PCX × (1 - PCY) × 277 + (1 - PCX) × -90 + PCX × PCY × -50 + n × -50 | (7) |
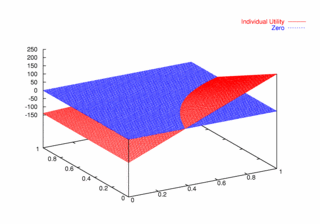
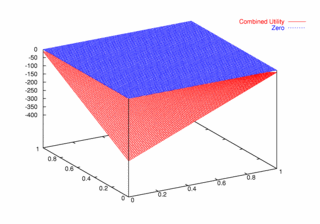
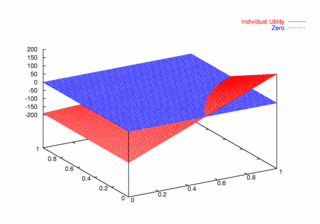
where PCX and PCY represent the probabilities of agent X and agent Y continuing, respectively. Figures 9, 10, and 11 plot these utilities for all combinations of PCX and PCY, with combined utilities on the left, individual on the right. In each of the figures, the utility is plotted against the zero plane. In Figure 9, which plots utilities for the one round game, most combinations of probabilities yield positive combined utilities. Only combinations near (0, 0) and (1,1) produce negative outcomes. Likewise, a large portion of the probability combinations yield positive individual utilities.
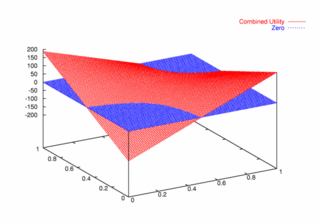
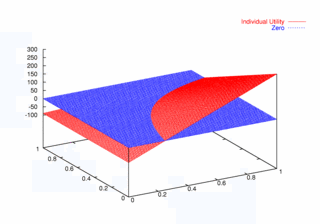
|
| Figure 9. Utility Space for One-Round Games |
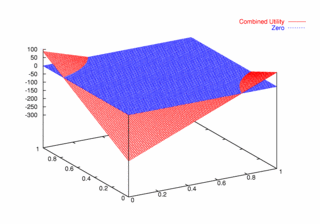
|
| Figure 10. Utility Space for Two-Round Games |
|
| Figure 11. Utility Space for Three-Round Games |
ANDERSON, C. A. and Bushman, B. J. (2002), "Human aggression." Annual Review of Psychology, 53, pp. 27-51.
BURTON, J. W. (1998), Conflict resolution: the human dimension." The International Journal of Peace Studies, 3(1). <http://www.gmu.edu/academic/ijps/vol3_1/burton.htm>.
DECOURSY, K. and Jenssen, T. (1994), "Structure and use of male territorial headbob signals by the lizard Anolis carolinensis." Animal Behavior, 47, pp. 251-262.
DE WAAL, F. B. M. (2000), "Primates--a natural heritage of conflict resolution." Science, 289, pp 586-590.
HOFMANN, H. and Schildberger, K. (2001), "Assessment of strength and willingness to fight during aggressive encounters in crickets." Animal Behavior, 62, pp. 337-348.
PAINE, R. (1969), "A note on trophic complexity and community stability." The American Naturalist, 103, pp. 91-93.
SCHEUTZ, M. (2001), "The evolution of simple affective states in multi-agent environments." In Proceedings of AAAI Fall Symposium, Falmouth, MA. 2001. <http://www.nd.edu/~airolab/publications/scheutz01aaaifs.pdf>.
SCHEUTZ, M. and Schermerhorn, P. (2002), "Steps towards a theory of possible trajectories from reactive to deliberative control systems." In Proceedings of the 8th Conference of Artificial Life, Sydney, NSW, Australia. December 9-13, 2002. <http://www.nd.edu/~airolab/publications/scheutzschermerhorn02alife8.pdf>.
SHMAYA, E. and Solan, E. (2002), "Two Player Non Zero-sum Stopping Games in Discrete Time." Center for Mathematical Studies in Economics and Management Science (Northwestern University) Discussion Paper 1347. <http://www.math.tau.ac.il/~eilons/final9.pdf>.
SHMAYA, E., Solan, E., and Vieille, N. (2003), "An Application of Ramsey Theorem to Stopping Games." Games and Economic Behavior, 42(2), pp. 300-306.
SOLAN, E. and Vieille, N. (2001), "Stopping Games--Recent Results." Les Cahiers de Recherche 744. <http://www.hec.fr/hec/fr/professeur_recherche/cahier/finance/CR744.pdf>.
SOLAN, E. and Vieille, N. (2002), "Deterministic Multi-Player Dynkin Games." Center for Mathematical Studies in Economics and Management Science (Northwestern University) Discussion Paper 1355. <http://www.math.tau.ac.il/~eilons/deterministic4.pdf>.
TOUZI, N. and Vieille, N. (2002), "Continuous-Time Dynkin Games with Mixed Strategies." SIAM J. Control Optim., 41(4), pp. 1073--1088.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2004]