Claudia Pahl-Wostl and Eva Ebenhöh (2004)
An Adaptive Toolbox Model: a pluralistic modelling approach for human behaviour based on observation
Journal of Artificial Societies and Social Simulation
vol. 7, no. 1
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/7/1/3.html>
Received: 09-May-2003 Accepted: 03-Aug-2003 Published: 31-Jan-2004
 Abstract
Abstract| Table 1: Comparison of experiments, case studies and statistical mass surveys | |||||
| Experiments | Case Studies | Statistical Mass Surveys | |||
|---|---|---|---|---|---|
| Comparability /
Control of setting |
high | low | medium to high | ||
| Representativeness | medium
(biased sample) |
medium
(unique situation) |
high | ||
| Realism /
realistical context |
low | high | medium | ||
| Repeatability | high | low | high | ||
| direct observability
of social interactions |
high | medium | low | ||
There is a small body of related research labled "Parallel Experiments with Real and Computational Agents" by Tesfatsion (2002, p.16). There are a few economical studies that deal with both, experimental settings with human subjects and parallel experiments with computational agents. However, with the exception of Duffy (2001) these do not try to capture individual human behaviour, but rather have (boundedly) rational computational agents evolve over time to show or explain the observed aggregated behaviour of the human subjects. Learning is usually implemented as a genetic algorithm. (For example see Pingle and Tesfatsion 2001, Andreoni and Miller 1995).
| Table 2: Experimental design | |||||||||||||
| Round | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Setting A | CPR P | CPR P | CPR P | CPR P | CPR P | CPR P | CPR | CPR | CPR | CPR | CPR | CPR | 5 groups of 24 subjects |
| Setting B | CPR | CPR | CPR | CPR | CPR | CPR | CPR P | CPR P | CPR P | CPR P | CPR P | CPR P | 5 groups of 24 subjects |
| Table 3: Survey of important assumptions | |
| agents' cooperativeness c | random variable between 0 and 1, normal distribution |
| agents' "inclination to be annoyed"
and "willingness to punish" |
independent random variables between 0 and 1, normal distribution |
| agents expectations about the others | expected cooperativeness
expected inclination to be annoyed expected willingness to punish |
| higher expected common investment (cooperativeness) in games with punishment | offset=0.15 (setting A)
offset=0.3 (setting B) |
| agents' strategies |
|
| strategy changes with cues |
|
exp. cooperativeness = (1 - learning rate) * exp. cooperativeness + learning rate * investment
All agents believe the general contribution to be higher in games with punishment. This offset is 3 money units in setting A and 6 money units in setting B. These values have been taken from the aggregated data.
| Table 4: Strategy implementation | ||
| Maximizing strategy |
for (0 .. numSteps) do {
decision += step
calculate outcome
for (all future games) do {
calculate expected outcome
outcome += expected outcome
}
if (outcome > maxOutcome) {
maxOutcome = outcome
remember decision
}
}
|
Note: Decisions are tried out and outcome is calculated. For this, the loop starts with an initial decision of 0 and increases it by a predefined step in this case 0.05 = 1 money unit. The last decision remembered is the decision that yields the highest expected outcome. The future games are the games that directly depend on this decision, like the "punishment game" after an "investment game". |
| Reciprocal strategy |
decision = expected cooperativeness |
|
| Cooperative strategy |
if (expected cooperativeness > 0.4) decision = 1 else decision = 0.75 |
Note: A decision value of 1 is a contribution of 20 money units and a decision of 0.75 is a contribution of 15 money units, which is the minimum that we identified as cooperative behaviour. |
| Table 5: Cues and cue values | ||
| coopIsHigher |
if (investment > (expected cooperativeness + tolerance) coopIsHigher = 1 else coopIsHigher = 0 |
|
| coopIsLower |
if (investment < expected cooperativeness - tolerance) coopIsLower = 1 else coopIsLower = 0 |
|
| noDefectors | if (number of (other) defectors = 0) noDefectors = 1 else noDefectors = 0 |
|
| numDefectors | numDefectors = number of (other) defectors |
Note: defined by investment ≤ 1 money unit |
| noCooperators | if (number of (other) cooperators = 0) noCooperators = 1 else noCooperators = 0 |
|
| numCooperators | numCooeprators = number of (other) cooperators |
Note: defined by investment ≥ 15 |
| profitIsHigher | if (profit > last rounds profit + tolerance) profitIsHigher = 1 else profitIsHigher = 0 |
|
| profitIsLower | if (profit < last rounds profit - tolerance) profitIsLower = 1 else profitIsLower = 0 |
|
| profitLtInvestment | if (profit < my investment) profitLtInvestment = 1 else profitLtInvestment = 0 |
|
| numPunishers | numPunishers = number of punishers |
Note: player agents that punished this agent with any positive number |
| punishmentIsHigher | if (punishment > expected punishment + tolerance) punishmentIsHigher = 1 else punishmentIsHigher = 0 |
|
| punishmentIsLower | if (punishment < expected punishment - tolerance) punishmentIsLower = 1 else punishmentIsLower = 0 |
|
| punishmentGtGain | if (punishment cost > this rounds gain) punishmentGtGain = 1 else punishmentGtGain = 0 |
|
| Table 5: Multipliers for the different cues according to each strategy | |||
| Maximizing | Reciprocal | Cooperative | |
| coopIsHigher | -1 | -1 | 2 |
| coopIsLower | 1 | -2 | -2 |
| noDefectors | -2 | 0 | 0 |
| numDefectors | 1 | -2 | -2 |
| noCooperators | 0 | 0 | -2 |
| numCooperators | 0 | -1 | 0.5 |
| profitIsHigher | 1 | 2 | 1 |
| profitIsLower | -1 | -1 | -2 |
| profitLtInvestment | 0 | 0 | -1 |
| numPunishers | -0.5 | 0 | 0 |
| punishmentIsHigher | -1 | 0 | 0 |
| punishmentIsLower | 1 | 0 | 0 |
| punishmentGtGain | -1 | 0 | 0 |
certainty = certainty * (1 + enforcement) * matching factor for (all cues) certainty = certainty + (cue value * corresponding parameter * certainty step) if (certainty < certainty tolerance) change strategy
| Table 7: Calculating the matching factor for strategies from agents' cooperativeness | ||
| Maximizing Strategy | 0.5 - cooperativeness | Cooperativeness below 0.5 increases and above 0.5 decreases the agent's certainty about maximizing strategy. |
| Reciprocal Strategy | if (cooperativeness < 0.5) (-0.5 + 2 * cooperativeness) else (-0.5 + 2 * (1 - cooperativeness)) |
Cooperativeness below 0.25 and above 0.75 decreases and between 0.25 and 0.72 increases the agent's certainty about reciprocal strategy. |
| Cooperative Strategy | ((-0.5) + cooperativeness) * 2 | Cooperativeness below 0.5 decreases and above 0.5 increases the agent's certainty about cooperative strategy. This is doubled because cooperative strategy seems to depend more on conviction than the other strategies. |
if (defection > 0.1) angerlevel = annoyance + defection else angerlevel = annoyance + defection - 0.8 if (randomNumber < (2 * angerlevel)) punishDecision = (punishment + defection) / 2 else punishDecision = 0 punishPoints = 10 * punishDecision
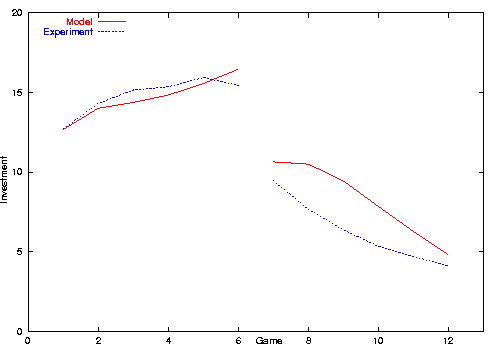
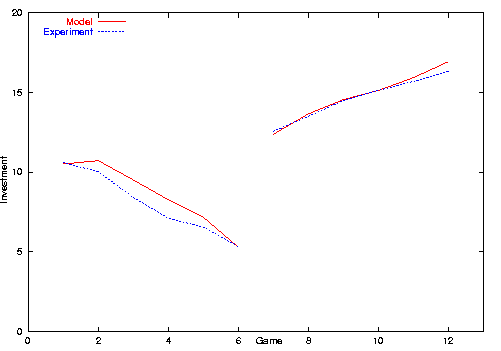
We made model runs similar to the experimental setting, model run A starts with games with punishment (see figure 1) and model run B starts with games without punishment (see figure 2). Model runs have been conducted with 1200 player agents. We did not do model runs with only 24 agents because of a strong influence of the random number generator. Even in runs with 120 players the mean investment usually deviates considerably from the mean investment of the experiment, in some cases not even the trend was reproduced. In fact, this effect is interesting and needs to be analyzed in more detail. We believe that the higher variance is due to the lack of prior knowledge of our agents compared to the experiment's participants.
|
| Figure 1. Mean investment in the experiment and model setting A |
|
| Figure 2. Mean investment in the experiment and model setting B |
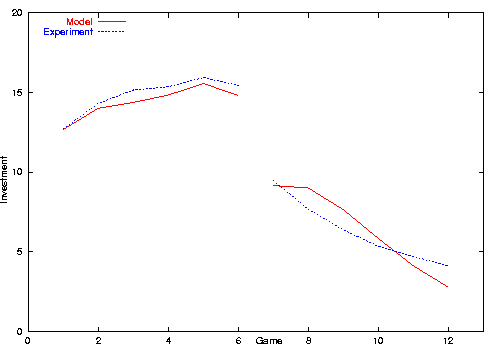
Another difference is that mean punishment in the model is higher than in the experiment (1.07 compared to 0.73 mean punishment decision in setting A). The reason for this may be that participants were more risk avers than agents.
|
| Figure 3. Mean investment in the experiment and modified model setting A |
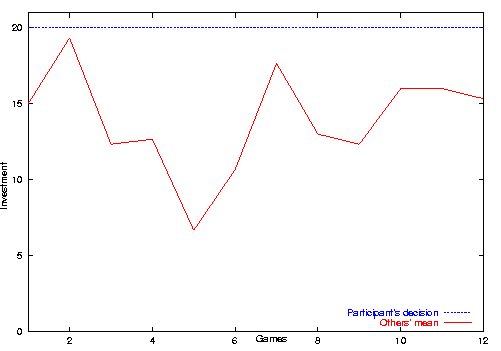
|
| Figure 4. Mean investment in the experiment and modified model setting A |
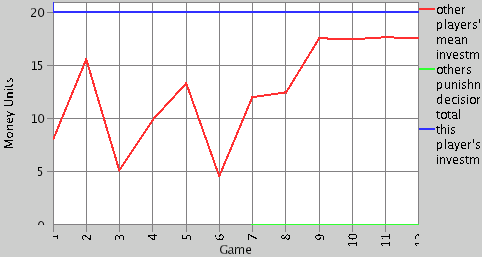
|
| Figure 5. Example of a cooperative agent from the simulation |
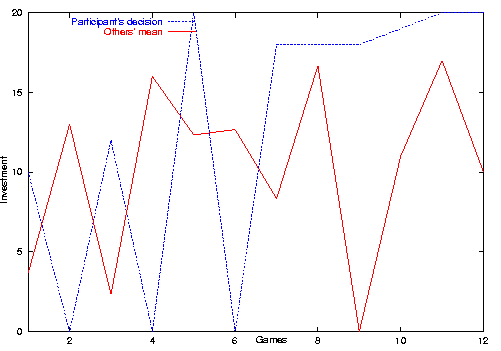
|
| Figure 6. Example of a reciprocal participant |
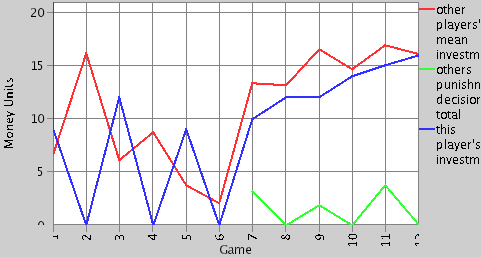
|
| Figure 7. Example of a reciprocal agent from the simulation |
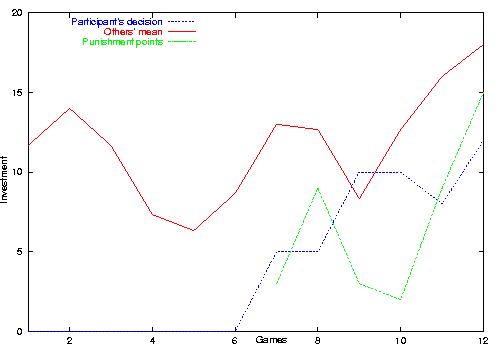
|
| Figure 8. Example of a maximizing participant of the original experiment |
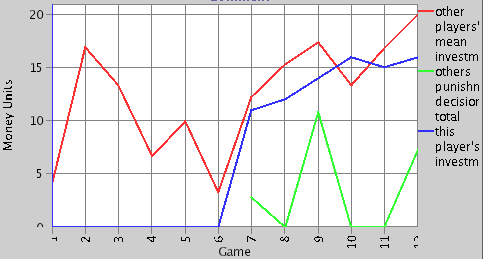
|
| Figure 9. Example of a maximizing agent from the simulation |
|
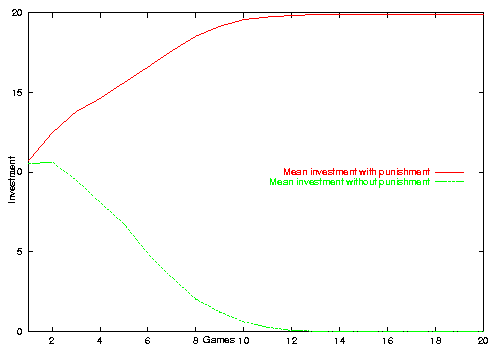
| Figure 10. Mean investment in the long run with and without punishment |
| Table 8: Sources of intentional reliability (cf. Nooteboom 2002, p. 9) | |||||
| Macro | Micro | ||||
| Egotistic | Sanctions from authority or contractual obligation with enforcement | Material advantage or self-interest | |||
| Altruistic | Ethics: values and social norms of proper conduct, moral obligations | Friendship, kinship, routines, empathy | |||
This framework is a good base to structure future observations from both empirical and modelling studies. An individual's cooperativeness determines his/her expectations about the behaviour of other players and individual and social learning effects may occur on different time scales. The work reported in this paper provides a start to compile a more comprehensive knowledge base.
ANDREONI J and Miller J H (1995) Auctions with Artifical Adaptive Agents. Games and Economic behaviour 10, pp. 39-64
ANDREONI J, Brown P M and Vesterlund L (2002) What Makes an Allocation Fair? Some Experimental Evidence. Games and Economic behaviour 40, pp. 1-24
BISSEY M-E and Ortona G (2002) The Integration of Defectors in a Cooperative Setting. Journal of Artificial Societies and Social Simulation 5, 2 https://www.jasss.org/5/2/2.html
BRENNER T (1999) Cognitive Learning in Prisoner's Dilemma Situations. Computational techniques for modelling learning in economics. Boston: Kluwer, pp. 333-361
BURNHAM T C (2000) Engineering altruism: a theoretical and experimental investigation of anonymity and gift giving. Journal of Economic behaviour & Organization 50, pp. 133-144
DEADMAN P J, Schlager E and Gimblett, R (2000) Simulating Common Pool Resource Management Experiments with Adaptive Agents Employing Alternate Communication Routines. Journal of Artificial Societies and Social Simulation 3, 2. https://www.jasss.org/3/2/2.html.
DEADMAN P J and Schlager E (2002) Models of Individual Decision Making in Agent-Based Simulation of Common-Pool-Resource Management Institutions. Integration Geographic Information Systems and Agent-Based Modelling Techniques for Simulating Social and Ecological Processes. Oxford: Oxford Univ. Press, pp. 137-169
DEFFUANT G, Amblard F, Weisbuch G, and Faure T (2002) How can extremism prevail? A study based on the relative agreement interaction model. Journal of Artificial Societies and Social Simulation 5, no. 4 <https://www.jasss.org/5/4/1.html>
DEFFUANT G, Weisbuch G, Amblard F, and Faure T (2003) 'Simple is beautiful ... and necessary' Journal of Artificial Societies and Social Simulation 6, no. 1. <https://www.jasss.org/6/1/6.html>
DIEKMANN A and Preisendörfer P (2001) Umweltsoziologie. Eine Einführung. Reinbeck: rohwolts enzyklopädie
DUFFY J (2001) Learning to speculate: Experiments with artificial and real agents. Journal of Economic Dynamics and Control 25, pp. 295-319
EPSTEIN J M and Axtell R (1995) Growing artificial societies: Social Science from the Bottom Up. Washington: Brookings Institution Press/MIT Press Cambridge, MA.
FEHR E and Gächter S (2002) Altruistic punishment in humans. Nature. 415, pp. 137-140
GIGERENZER G and Selten R (2001) Bounded Rationality. The Adaptive Toolbox. Cambridge, Massachusetts: The MIT Press.
GIGERENZER G (2001) The Adaptive Toolbox. In Gigerenzer G and Selten R Bounded Rationality. The Adaptive Toolbox. Cambridge, Massachusetts: The MIT Press, pp. 37-50
HARE M and Pahl-Wostl C. 2001. Model uncertainty derived from choice of agent rationality - a lesson for policy assessment modelling. In N. Giambiasi and C. Frydman, (eds.) Simulation in Industry: 13th European Simulation Symposium. SCS Europe Bvba, Ghent. pp 854-859.
HAYASHI N, Ostrom E, Walker J, and Yamagishi T (1999) Reciprocity, Trust and the Sense of Control: A cross-societal Study. Rationality and Society 11 pp. 27-46.
HELD M. and Nutzinger H.G. eds. (1999) Institutions shape human beings - human beings shape institutions. (in German: Institutionen prägen Menschen - Menschen prägen Institutionen). Campus Verlag, Frankfurt/Main.
HENRICH J et al. (2001) In Search of Homo Economicus: behavioural Experiments in 15 Small-Scale Societies. American Economic Review 91 pp. 73-78
JAGER W, Janssen M A, De Vries H J M, De Greef J and Vlek C A J (2000) Behaviour in commons dilemmas: Homo economicus and Homo psychologicus in an ecological-economic model. Ecological Economics 35, pp. 357-379.
JAGER W, Janssen M A (2002) Using artificial agents to understand laboratory experiments of common pool resources with real agents. In Janssen M A Complexity and Ecosystme Management. The Theory and Practice of Multi-Agent Systems Edward Elgar, Cheltenham, UK, Northampton, MA, USA, pp. 75-102
KAHNEMAN D and Tversky A eds. (2000) Choices, values and frames. Cambridge University Press, Cambridge, MA.
KOTTONAU J (2002) Simulating the Formation and Change of the Strength of Political Attitudes Diss. Eth No. 14664, Swiss Federat Institute of Technology Zurich
LINDENBERG S (1991) Die Methode der abnehmenden Abstraktion: Theoriegesteuerte Analyse und empirischer Gehalt. In Esser H and Troitzsch K (ed.) Modellierung sozialer Prozesse. Bonn: Informationszentrum Sozialwissenschaften, pp. 29-78
McCLINTOCK C and Liebrand W (1988) Role of Interdependence Structure, Individual Value Orientation, and Another's Strategy in Social Decision Making: A Transformational Analysis. Journal of Personality and Social Psychology 1988, Vol. 55, No. 3, 396-409
NEWIG J (2003) Symbolische Umweltgesetzgebung. Rechtssoziologische Untersuchungen am Beispiel des Ozongesetzes, des Kreislaufwirtschaft- und Abfallgesetzes sowie der Grofeuerungsanlagenverordnung. Schriften zur Rechtssoziologie und Rechtstatsachenforschung. Berlin, Duncker & Humblot.
NOOTEBOOM B (2002) Trust: Forms, Foundations, Functions, Failures and Figures. Edward Elgar, Cheltenham, UK.
OSTROM E (2000) Collective Action and the Evolution of Social Norms. Journal of Economic Perspectives 14, pp. 137-158.
PAHL-WOSTL C (2002) Participative and Stakeholder-based policy design, evaluation and modeling processes. Integrated Assessment 3, pp. 3-14
PINGLE M and Tesfatsion L (2001) Non-Employment Benefits and the Evolution of Worker-Employer Cooperation: Experiments with Real and Computational Agents. ISU Economic Report No. 55 <http://www.econ.iastate.edu/tesfatsi/sce2001.pdf>
TESFATSION L (2002) Agent-Based Computational Economics: Growing Economies from the Bottom Up. ISU Economics Working Paper No. 1
TODD P M and Gigerenzer G (2003) Bounding rationality to the world. Journal of Economic Psychology 24, pp. 143-165
VON RANDOW G (2003) When the center becomes radical. Journal of Artificial Societies and Social Simulation 6, no. 1. <https://www.jasss.org/6/1/5.html>
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]