Margaret Edwards, Sylvie Huet, François Goreaud and Guillaume Deffuant (2003)
Comparing an individual-based model of behaviour diffusion with its mean field aggregate approximation
Journal of Artificial Societies and Social Simulation
vol. 6, no. 4
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/6/4/9.html>
Received: 13-Jul-2003 Accepted: 13-Jul-2003 Published: 31-Oct-2003
 Abstract
Abstract|
|
(1a) |
|
|
(1b) |
where V(i,A) and V(i,B) are the number of neighbours of agent i respectively of behaviour A or B and the a,b,c,d are parameters of the model. We suppose hereafter that eiA = eiB = 0
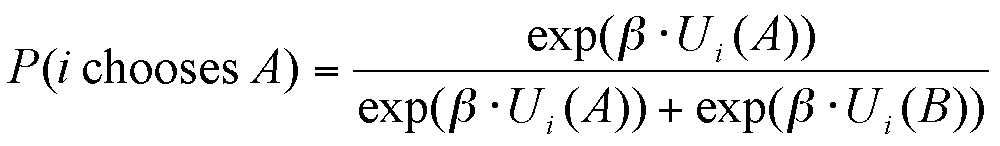
|
(2a) |
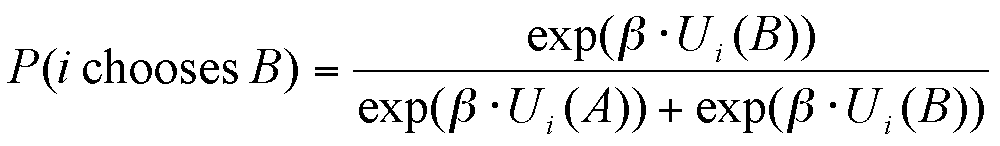
|
(2b) |
The extent of the dependence of the final choice on the social utility, which corresponds to the uncertainty in the decision, is ruled by the parameter β.
|
|
Suppose that there are nA agents of behaviour A in the population (and nB = N - nB agents with behaviour B). We approximate nA(k) as being proportional to the probability of picking k agents with behaviour A among v picked at random from the population. This probability is given by the binomial formula:
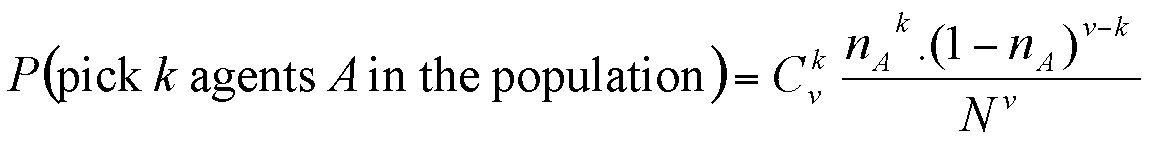
|
From which we derive:
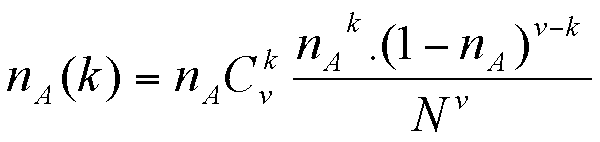
|
Similarly, we have:
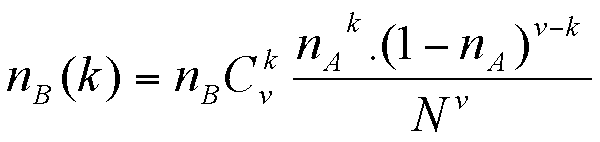
|
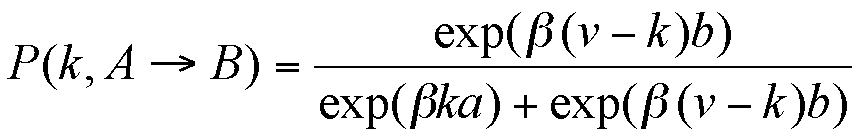
|
(3a) |
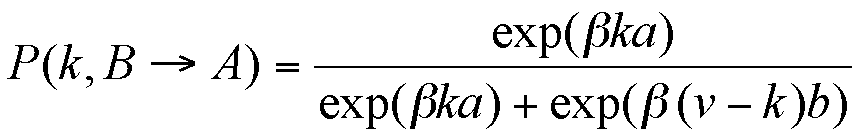
|
(3b) |
|
|
(4a) |
|
|
(4b) |
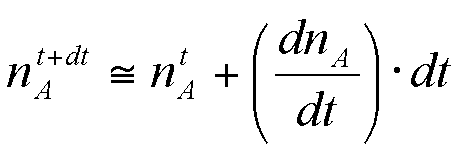
|
The derivative is expressed as
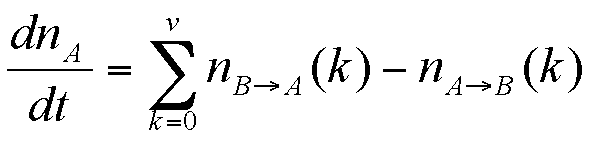
|
(5) |
So the new number of agents A becomes (for dt=1)
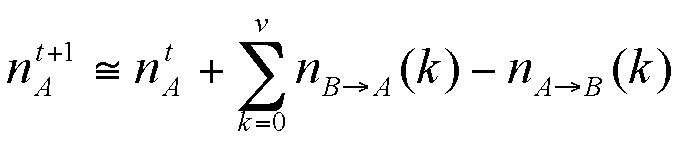
|
(6) |
Which finally leads to a deterministic equation for the evolution of our aggregate model, coherent with the individual-based model :
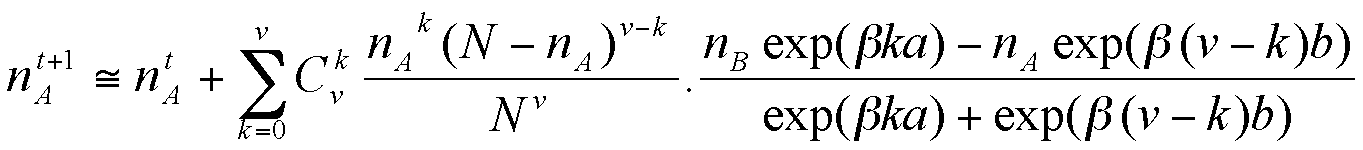
|
(7) |
This gives us the new value of nA, and we can compute the value of s(t+1), and iterate again.
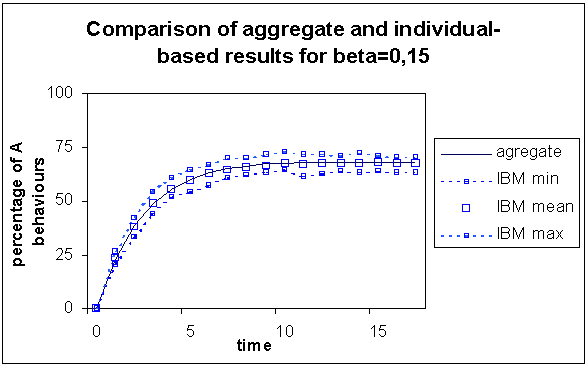
|
| Figure 1. Comparison of the results of the aggregate with the individual-based model for β = 0.15, for which out of 150 simulations are represented the minimum, the maximum and the mean values. The trends are very similar |
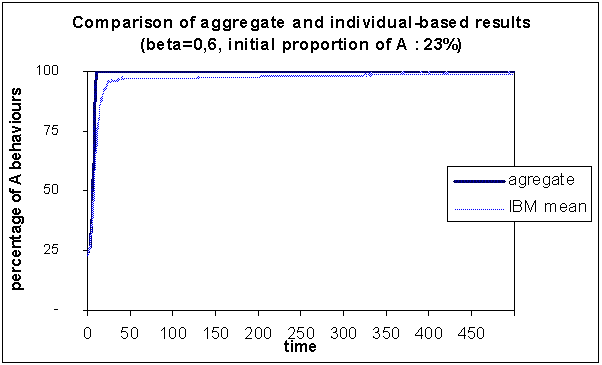
|
| Figure 2. Comparison of the results of the aggregate with the individual-based model, for which we have represented the mean over 150 simulations, for β = 0.60 and initially 23% A behaviours |
In this case, at long term the mean of the individual-based model is very similar to the result from the aggregate model, i.e. 100% A behaviours.
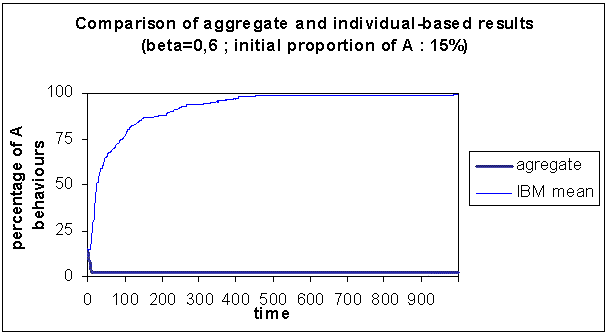
|
| Figure 3. Comparison of the results of the aggregate with the individual-based model, for which the mean out of 150 simulations is represented, for β = 0.60 and initially 15% A behaviours |
|
|
where x is the vector of choices of the individuals, and A(x) (respectively B(x)) represents the number of links between two individuals with A (respectively B) behaviours. The equilibrium states correspond to maxima of this potential. We see that all-A or all-B are local maxima, since the change in opinion of a single individual can only lead to a decrease of this potential in these cases.
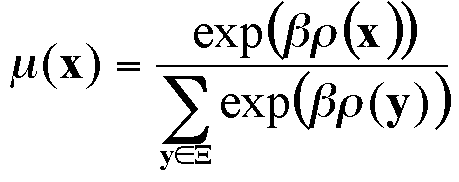
|
Therefore the most likely state x is the one that maximises the potential function ρ(x). However, note that there is a strictly positive probability for each state to appear (even though it can be very small). The mean of a set of simulation results is therefore expected to tend towards a mean of the most probable states, weighted by μ(x).
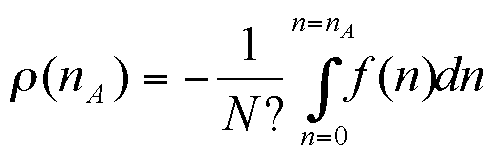
|
(8) |
A unit time step is defined as the time necessary for the re-evaluation of behaviours for the whole population, following the rules proposed by Young.
|
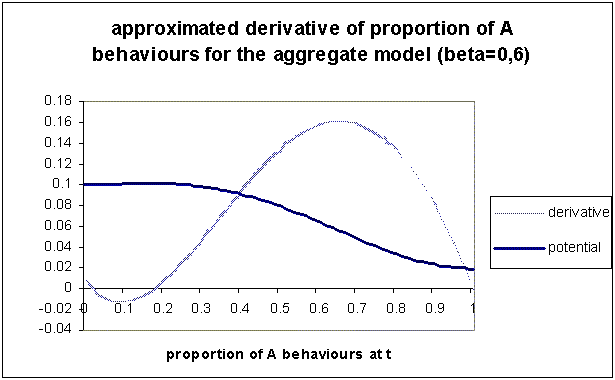
| Figure 4. Approximated derivative and associated potential, of the aggregate calculation of proportion of A (proportions between 0 and 1) for β=0.6. The minima of the potential describe the attractors of the aggregate model's dynamics. Here there are two: one for 0% A and one for 100% A |
|
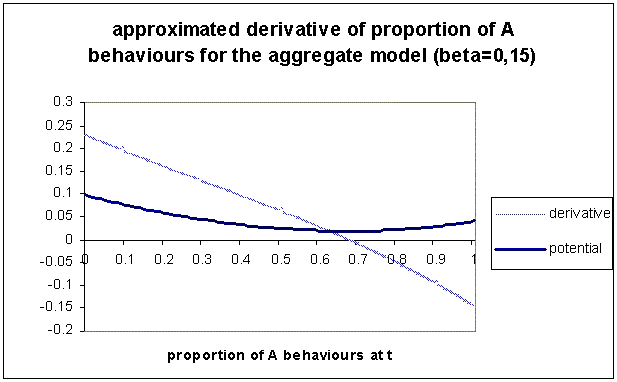
| Figure 5. Approximated derivative of the aggregate calculation of proportion of A, for β=0.15. Only one attractor corresponding to the minimum of the potential appears around 68% of A behaviours |
|
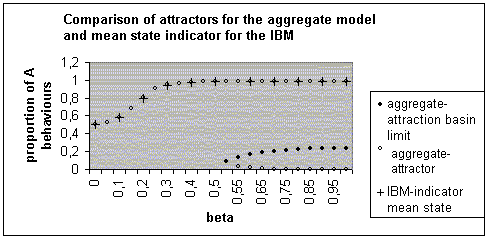
| Figure 6. Different equilibrium states for the aggregate model and mean final states for the individual-based model, for different values of β |
DUBOZ, R., Ramat, E. and Preux, P. (2002) "Scale transfer modelling : using emergent computation for coupling an ordinary differential equation system with a reactive agent model", System Analysis - Modelling - Simulation, 43(6): 793-814.
EDWARDS, M., Huet, S., Goreaud, F and Deffuant, G. (2003) "Comparaison entre un modèle individu-centré de diffusion de l'innovation et sa version agrégée dérivée par champ moyen pour des simulations à court terme", Proceedings of the workshop Modèles Formels de l'Interaction (MFI) 2003, Lille (France)
FAHSE, L., Wissel, C. and Grimm, V (1998) "Reconciling Classical and Individual-Based Approaches in Theoretical Population Ecology: A Protocol for Extracting Population Parameters from Individual-based models", The American Naturalist, vol. 152(6):838-852.
FAURE, T., Deffuant, G. and Weisbuch, G. (2002) "Dynamics of influence on continuous uncertain opinions : Evolution of the opinion probability distribution", submitted.
GILBERT, N. and Troitzsch, K. G. (1999) Simulation for the social scientist. Milton Keynes: Open University Press.
GRANOVETTER, M. (1978) "Threshold models of collective behaviour", American Journal of Sociology 83:1360-1380
GRIMM, V., (1999) "Ten years of individual-based modelling in ecology: what we have learned and what could we learn in the future?", Ecological Modelling, 115, p.129-148.
KIRKPATRICK, S., Gelatt, C.D. and Vecchi, M.P. (1983) "Optimization by Simulated Annealing,'' Science, No. 4598, 13 May.
PICARD, N. and Franc, A. (2001) "Aggregation of an individual-based space-dependant model of forest dynamics into distribution-based and space-independent models", Ecological Modelling, 145(1): 69-84.
VALENTE, T.W. (1995) Network models of the diffusion of innovations. Cresskill, New Jersey, Hampton Press.
WEIDLICH, W (2000) SocioDynamics: A Systematic Approach to Mathematical Modelling, Harwood.
YOUNG, P. (1998) Individual Strategy and social structure, Princeton University Press
YOUNG, P. (1999) "Diffusion in Social Networks", Working Paper No 2., Brookings Institution.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]