The validity of simulation results remains an open problem in multiagent-based simulation (MABS). Since such validity is based on the validation of computational models, we propose a cross-element validation method that validates computational models by investigating whether several models can produce the same results after changing an element in the agent architecture. Specifically, this paper focuses on learning mechanisms applied to agents as one of the important elements and compares three different MABSs employing either an evolutionary strategy (ES), a learning classifier system (LCS), or a reinforcement learning (RL). This type of validation is not based on the between-models addressed in conventional research but on a within-model. A comparison of the simulation results in a bargaining game, one of the fundamental examples in game theory, reveals that (1) computational models are minimally validated in the case of ES- and RL-based agents; and (2) learning mechanisms that enable agents to acquire their rational behaviors differ according to the knowledge representation (i.e., the strategies in the bargaining game) of the agents. Concretely, we found that (2-a) the ES-based agents derive the same tendency in game theory but the LCS-based agents cannot in the case of employing continuous knowledge representation; and (2-b) the same ES-based agents cannot derive the same tendency in game theory but the RL-based agents derive it in the case of employing discrete knowledge representation.

Keywords:

Bargaining Game; Comparison Of Different Learning Mechanisms; Multiagent-based Simulation; Validation

Introduction

1.1

Comparisons of different computational models are critically important for multiagent-based simulation (MABS) (Moss and Davidsson 2001). This is because such comparisons contribute to (1) validation of simulation results, (2) verification of computational models by checking program-bugs, (3) enrichment of our understanding of outcomes, and (4) replication of other models that derive effective cumulative scientific progress in the MABS research area (Takadama and Shimohara 2002). To promote such comparisons, Axtell proposed the concept of "alignment of computational models" or "docking"^[1] which asserts the importance of investigating whether two computational models can produce the same results (Axtell et al. 1996). This indicates that both computational models are minimally validated if the two results are the same. In Axtell's work, he conducted this kind of investigation by replicating culture models (Axelrod 1997) in Sugarscape (Epstein and Axtell 1996) and found many significant results. Recently, comparisons of Virtual Design Team (VDT) (Levitt et al. 1994) and ORGAHEAD (Carley and Svoboda 1996) have been made, and these studies provided useful implications (Haghshenass et al. 2002, Louie et al. 2002).

1.2

It should be noted, however, that it is not easy to replicate either computational model with the other for the following reasons: (1) it is difficult to compare different computational models under the same evaluation criteria, since they are developed according to their own purpose; (2) common parts in different computational models are very few; and (3) simulation results are sensitive to how the agents are modeled, which makes it difficult to produce the same results. These difficulties prevent replication of computational models and their fair comparisons.

1.3

To overcome these difficulties, we propose a cross-element validation method that stresses the importance of comparing the results of MABSs whose agents differ only in one element. As an example of such parts, we consider the learning mechanisms applied to agents. Precisely, this type of validation is not based on the between-models addressed in conventional research but on a within-model. The importance of this type of validation increases when addressing complex dynamics or social phenomena caused by the micro-macro loop in agent societies because simulation results are substantially affected by the difference of a single element within the model.

1.4

As the first step toward such cross-element validation for MABS, this paper starts by comparing the results of computational models that employ either of the following three learning mechanisms: (1) evolutionary strategy (ES) (Bäck et al. 1992), (2) learning classifier system (LCS) (Goldberg 1989, Holland et al. 1986), and (3) reinforcement learning (RL) (Sutton and Bart 1998). These kinds of research effort may be considered evaluations of learning mechanisms rather than validation of computational models. However, the results of such efforts are indispensable to increasing the validity of simulation results. This is because a learning mechanism is an important element that derives complex dynamics or social phenomena in MABS. We also believe that a comparison of several kinds of such elements within a model contributes to achieving a general validation for MABS. Toward this goal, we start by comparing the results of computational models employing different learning mechanisms.

1.5

This paper is organized as follows. Section 2 starts by explaining a well-known example for investigating the influence of different learning mechanisms. A concrete implementation of agents is described in Section 3. Section 4 presents computer simulations, and Section 5 discusses a comparison of the results of different computational models. Finally, our conclusions are given in Section 6.

Bargaining Game

2.1

As a concrete domain, we focus on bargaining theory (Muthoo 1999, Muthoo 2000) and employ a bargaining game (Rubinstein 1982) addressing the situation where two or more players try to reach a mutually beneficial agreement through negotiations. This game has been proposed for investigating when and what kinds of offers of an individual player can be accepted by the other players. We selected this domain for the following reasons: (1) this game is a fundamental example; and (2) since the rational behaviors of players have already been analyzed in game theory (Osborne and Rubinstein 1994), we can validate simulation results by comparing the rational behaviors of players.

2.2

To understand the bargaining game, let us give an example from Rubinstein. In his work (Rubinstein 1982), he illustrated a typical situation using the following scenario: two players, P₁ and P₂, have to reach an agreement on the partition of a "pie". For this purpose, they alternate offers describing possible divisions of the pie, such as "P₁ receives x and P₂ receives 1-x at time t", where x is any value in the interval [0,1]. When a player receives an offer, the player decides whether to accept it or not. If the player accepts the offer, the negotiation process ends, and each player receives the share of the pie determined by the concluded contract. If the player decides not to accept the offer, on the other hand, the player makes a counter-offer, and all of the above steps are repeated until a solution is reached or the process is aborted for some external reason (e.g., the number of negotiation processes is finite or one of the players leaves the process). If the negotiation process is aborted, neither player can receive any share of the pie.

2.3

Here, we consider the finite-horizon situation, where the maximum number of steps (MAX_STEP) in the game is fixed and all players know this information as common knowledge (Ståhl 1972). In the case where (MAX_STEP=1) (also known as the ultimatum game ), player P₁ makes the only offer and P₂ can accept or refuse it. If P₂ refuses the offer, both players receive nothing. Since a rational player is based on the notion of "anything is better than nothing", a rational P₁ tends to keep most of the pie to herself by offering only a minimum share to P₂. Since there are no further steps to be played in the game, a rational P₂ inevitably accepts the tiny offer.

2.4

By applying a backward induction reasoning to the situation above, it is possible to perform a simulation for MAX_STEP>1. For the same reason seen in the ultimatum game, the player who can make the last offer is better positioned to receive the larger share by offering a minimum offer (Ståhl, 1972). This is because both players know the maximum number of steps in the game as common knowledge, and therefore the player who can make the last offer can acquire a larger share with the same behavior of the ultimatum game at the last negotiation. The point of multiple-step negotiation is to investigate whether the advantageous player can continue the negotiation to the last step to acquire a larger share under the situation where each step in the negotiation process is not constrained by the previous ones. From this feature of the game, the last offer is granted to the player who does not make the first offer if MAX_STEP is even, since each player is allowed to make at most MAX_STEP/2 offers. On the other hand, the last offer is granted to the same player who makes the first offer if MAX_STEP is odd.

2.5

After this section, we use the terms "payoff" and "agent" instead of the terms "share" and "player" for their more general meanings in the bargaining game.

Modeling Agents

3.1

To implement agents in the framework of the bargaining game described in the previous section, we employ the following three learning mechanisms: (1) evolutionary strategy (ES), (2) learning classifier system (LCS), and (3) reinforcement learning (RL). We employ these mechanisms for the following reasons: (1) the ES mechanism performs well with a real number that can represent various offer values in the bargaining game; (2) the LCS architecture is implemented by modeling human beings (Holland et al., 1986), and several conventional research works employing LCS have already investigated social problems (e.g., an artificial stock market (Arthur et al. 1997)); and (3) the RL mechanism has been well studied in the context of computer science. Specifically, we employ (1) the conventional (&mu + &lambda) evolution strategies (Bäck et al. 1992) for ES, (2) a Pittsburgh-style classifier system (Smith 1983) instead of a Michigan-style classifier system (Holland 1975) for LCS, and (3) Q-Learning (Watkins and Dayan 1992) for RL.

3.2

Here, considering the strategies (defined later) of the bargaining agents, the ES and LCS mechanisms update the contents of strategies (i.e., offer values), while the RL mechanism updates the worth of strategies (i.e., the worth of offer values).^[2] From this difference, this section starts by describing the ES- and LCS-based agents and then describes the RL-based agents.

ES- and LCS-based agents

The ES- and LCS-based agents are implemented by the following components.

• Memory
  • Strategies memory in Figure 1 stores a set of strategies (the number of strategies is n) that consist of fixed numbers of pairs of offers (O) and thresholds (T). These strategies are similar to those used in Oliver's study (Oliver 1996). The offer and threshold values are encoded by floating point numbers in the interval [0, 1]. In this model, agents independently store different strategies, which are initially generated at random.
  • Selected strategy memory stores the one strategy selected to confront the strategy of an opponent agent. Figure 1 shows the situation where agent A₁selects the xth strategy while agent A₂ selects the yth strategy.
• Mechanism
  • Learning mechanism updates both offer and threshold values in order to generate good strategies that acquire a large payoff. The detailed mechanism is described later.

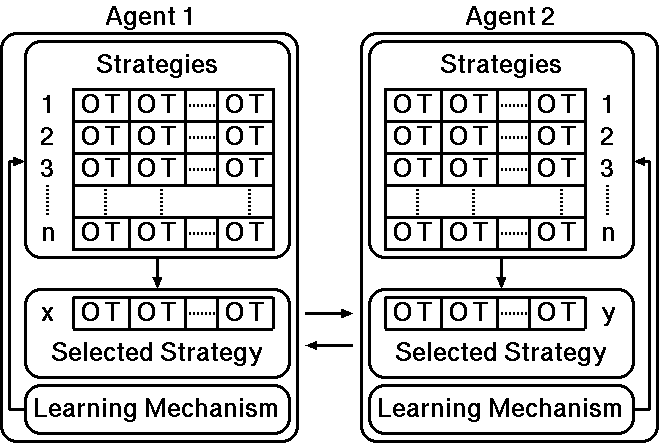
Figure 1. ES- and LCS-based agents

3.3

As a concrete negotiation process, agents proceed as follows. Defining {O,T}_i^A_{1,2}as the ith offer or threshold value of agent A₁or A₂, agent A₁starts with the first offer O₁^A₁. Here, we count one step when either agent makes an offer. Then, A₂ accepts the offer if O₁^A₁ &ge T₁^A₂; otherwise, it makes a counter-offer O₂^A₂, i.e., the offer of A₂. This cycle is continued until either agent accepts the offer of the other agent or the maximum number of steps (MAX_STEP) is reached. To understand this situation, let us consider the simple example where MAX_STEP=10, as shown in Figure 2. Following this example, A₁ starts by offering 0.1 to A₂. However, A₂ cannot accept the first offer because it does not satisfy the inequality of O₁^A₁(0.1) &ge T₁^A₂(0.9). Then, A₂ makes a counter-offer 0.1 to A₁. Since A₁cannot accept the second offer from A₂ for the same reason, this cycle is continued until A₁accepts the 10th offer from A₂, where the offer satisfies the inequality of O₁₀^A₂(0.1) &ge T₁₀^A₁(0.1). If the negotiation fails, which means that the maximum number of steps has been reached, both agents can no longer receive any payoff, i.e., they receive 0 payoff. Here, we count one confrontation when the above negotiation process ends or fails.

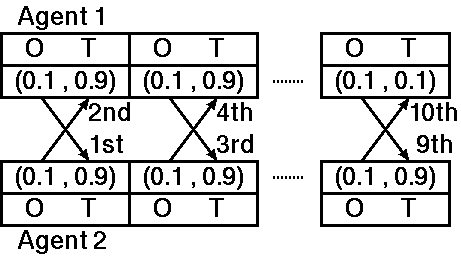
Figure 2. Example of a negotiation process (ES- and LCS-based agents)

3.4

Next, the fitness of each strategy is calculated by the average of payoffs acquired in a fixed number of confrontations ( CONFRONTATION), where the strategies of the other agents are randomly selected in each confrontation. For example, the xth strategy of A₁in Figure 1 confronts the randomly selected strategies of the other agents in the CONFRONTATION number of confrontations, and then the fitness of the xth strategy is calculated by the average of the payoffs acquired in these confrontations. Since each agent has n number of strategies, the (CONFRONTATION × n × 2) number of confrontations is required to calculate the fitness of all strategies of the two agents. Here, we count one iteration when the fitness of all strategies of the two agents is calculated.

3.5

In each iteration, the EC- and LCS-based agents update their own strategies by modifying the numerical values of the offer and threshold by the following conventional elite selection procedure (Goldberg, 1989): (1) a fixed number (&mu or GENERATION_GAP × n) of the best strategies (parents, i.e., strategies having high fitness values) remains in the set; (2) a fixed number (&lambda or GENERATION_GAP × n) of new strategies (offspring ) is produced from the set of parents by applying the mutation operation in (&mu + &lambda)-ES and the crossover, mutation, and inversion operations in the Pittsburgh-style LCS; and (3) new strategies replace the same number of strategies having low fitness values. Note that this way of updating the strategies of agents is not the same as simply applying the evolutionary operations such as crossover, mutation, and inversion to the entire population of strategies; instead, it involves applying these operations to newly generated populations to maintain elite strategies.

RL-based agents

3.6

Next, the RL-based agents are implemented by the following components.

• Memory
  • Strategies memory stores a fixed number of matrixes of offers (O) and thresholds (T) as shown in Figure 3. The RL-based agents have these matrixes because they do not have a mechanism for updating the contents of strategies (i.e., offer and threshold values) like the ES- and LCS-based agents but have a mechanism for updating the worth (Q) of strategies (precisely, the worth of pairs of offer and threshold). In this model, agents independently have different worths of strategies which are updated through learning.
  • Combined strategy memory stores one strategy by combining several pairs of offer and threshold, where each of the pairs is derived from all matrixes as shown in Figure 3. Based on this strategy, an agent confronts the strategy of the other agent.
• Mechanism
  • Learning mechanism updates the worth of pairs of offer and threshold in order to generate good strategies that acquire a large payoff. The detailed mechanism, except for the action selection (acceptance or counter-offer), is described later (Note that the learning mechanism is composed of update mechanism and action selection). The action selection of RL in this paper is based on the &epsilon-greedy method , which selects an action of the maximum worth (Q-value) at the 1-&epsilon probability, while selecting an action randomly at the &epsilon (0 &le &epsilon &le 1) probability.

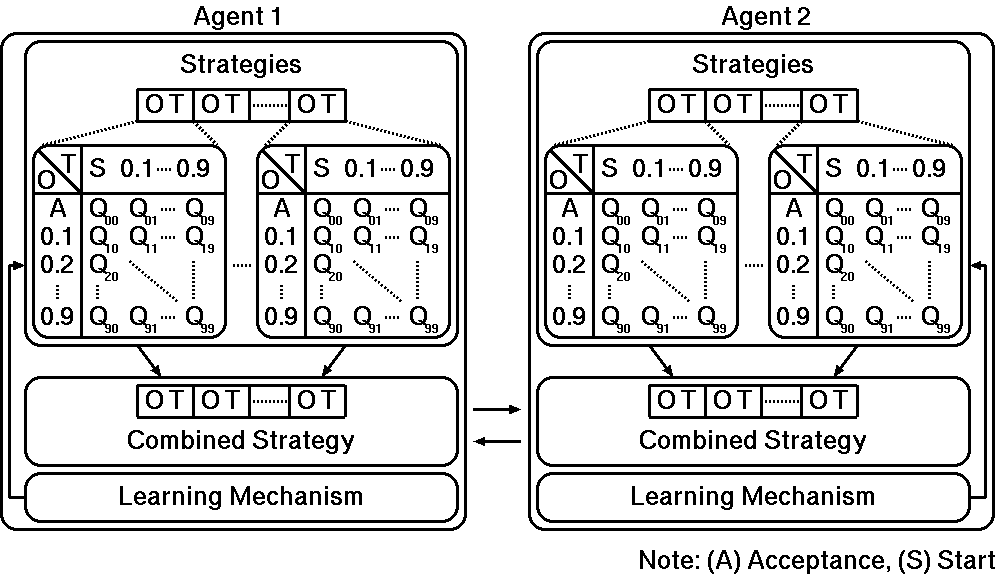
Figure 3. RL-based agents

3.7

As a concrete negotiation process, agents proceed as follows. Defining {O,T}_i^A_{1,2} as the ith offer or threshold value of agent A₁or A₂ as the same as ES- and LCS-based agents, agent A₁starts with the first offer O₁^A₁. Then, A₂ accepts the offer if the acceptance (A) in the row T₂^A₂ (=O₁^A₁) of a matrix is selected; otherwise, it makes a counter-offer O₂^A₂ determined from the same row T₂^A₂ (=O₁^A₁). This cycle is continued until either agent accepts the offer of the other agent or the maximum number of steps (MAX_STEP) is reached. To understand this situation, let's consider the simple example where MAX_STEP=10 as shown in Figure 4. Following this example, A₁starts to make an offer O₁^A₁(0.1) to A₂ by selecting one value in the row T₁^A₁(S(start)). However, A₂ does not accept the first offer because it decides to make an O₂^A₂(0.1) counter-offer selected from a value in the row T₂^A₂(0.1). In this example, the cycle is continued until A₁accepts the 10th offer from A₂ by selecting O₁₀^A₁(A(acceptance)) from a value in the row T₁₀^A₁(0.1). If the negotiation fails, which means the the maximum number of steps has been reached, both agents can no longer receive any payoff, i.e., they receive 0 payoff. Here, as in the case of the ES- and LCS-based agents, we count one confrontation when the above negotiation process ends or fails.

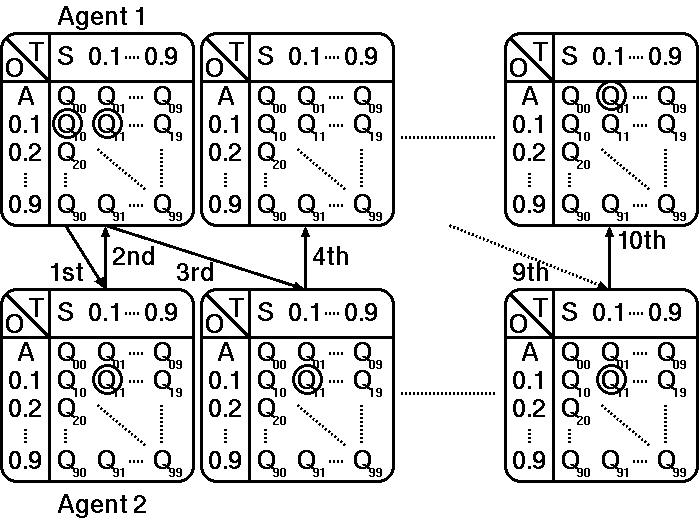
Figure 4. Example of a negotiation process (RL-based agents)

3.8

In each confrontation, the RL-based agents update the worth pairs of offer and threshold by the following conventional equation (1), where Q(t,o), Q(t',o'), r, O(t'), &alpha (0 < &alpha &le 1), and &gamma (0 &le &gamma &le 1), respectively, indicate the worth of selecting the offer (o) at threshold (t), the worth of selecting 1 step next offer (o') at 1 step next threshold (t'), the reward corresponding to the acquired payoffs, a set of possible offers at 1 step next threshold (t'), the learning rate, and the discount rate.

Q(t,o)=Q(t,o)+&alpha[r+&gamma max_{o'&isin O(t')} Q(t',o')-Q(t,o)]   ....   (1)

3.9

Finally, we count one iteration when the (CONFRONTATION × n × 2) number of confrontations is done in order to investigate the simulation results of the RL-based agents at the same level of the ES- and LCS-based agents. Note that CONFRONTATION (i.e., the number of confrontations for each strategy) and n (i.e., the number of strategies) are determined in the simulation of the ES- and LCS-based agents.

Simulation

Simulation design

4.1

The following two simulations were conducted as comparative simulations.

• ES vs. LCS: Investigation of the influence of different learning mechanisms handling continuous values for representing strategies. Both offer and threshold values in this case are represented by ordinal real numbers (e.g., 0.11, 0.234, or 0.9117).
• ES vs. RL: Investigation of the influence of different learning mechanisms handling discrete values for representing strategies. Both offer and threshold values in this case are restricted by a real number with one decimal digit (e.g., 0.1, 0.2, or 0.9) in ES, while they are represented by the discrete values in a 0.1 unit in RL as shown in Figure 3.

4.2

In each simulation, the following two cases are investigated. Note that all simulations are conducted up to 5000 iterations, and their results show average values over 10 runs.

• Case (a): Payoff
• Case (b): Average negotiation process size

As the parameter setting, the variables are set as shown in Table 1. Note that preliminary examinations found that the tendency of the results does not drastically change with the parameter setting.

Table 1. Parameters in simulations

4.3

All simulations in this paper were implemented by C language with standard libraries and were conducted in a Linux OS with Pentium 700MHz Processor. Note that the same simulation can be implemented and conducted in other compiler and platform.

Simulation results

4.4

Figure 5 shows the simulation results of both the ES- and LCS-based agents. The upper figures indicate the payoff, while the lower figures indicate the average negotiation process size. The vertical axis in the figures indicates these two cases, while the horizontal axis indicates the iterations. Specifically, the payoff of agent A₁is shown in the lower lines, while that of A₂ is shown in the upper lines. Furthermore, Figure 6 shows the simulation results of the ES-based agents restricted to a real number with one decimal digit and RL-based agents. All axes in this figure have the same meaning as those in Figure 5. From these results, we find that the difference in tendency follows the different learning mechanisms applied to the agents.

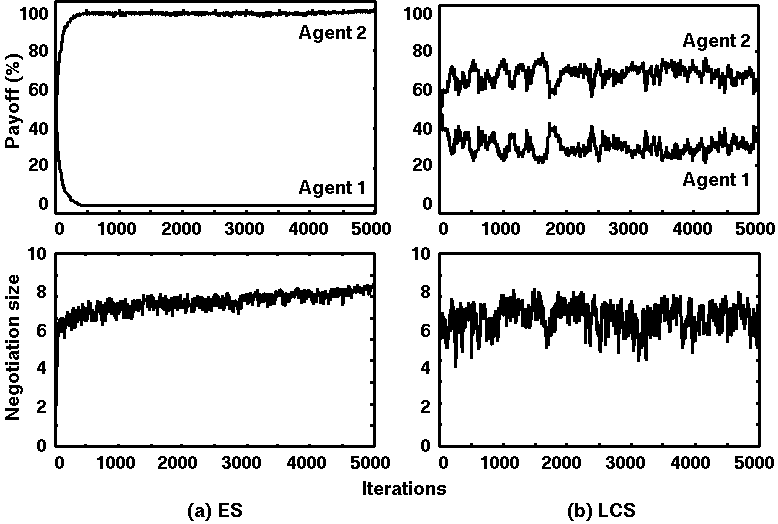
Figure 5. Simulation results of ES vs. LCS: Average values over 10 runs at 5000 iterations

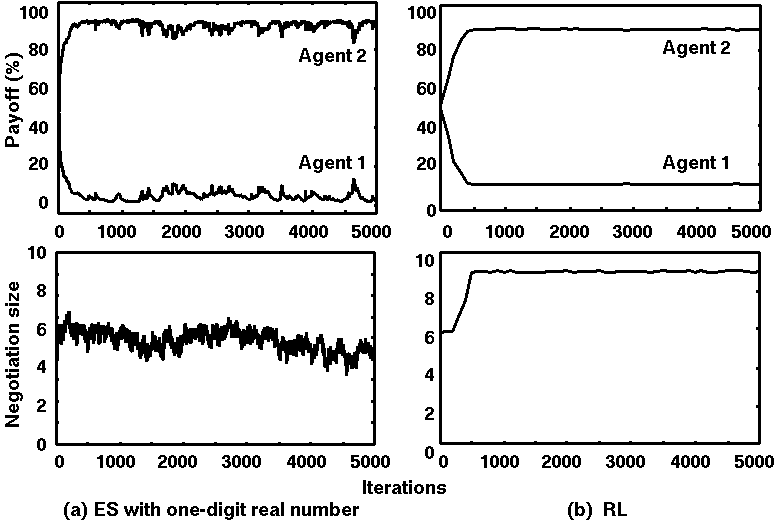
Figure 6. Simulation results of ES with one decimal digit vs. RL: Average values over 10 runs at 5000 iterations

Discussion

ES vs. LCS

5.1

First, we conduct simulations on different learning mechanisms that handle continuous values for representing the strategies shown in Figure 5. This figure shows that (1) the payoff of the ES-based agents finally converges at the mostly maximum or minimum value (i.e., 100% or 0%), while that of the LCS-based agents neither converges at a certain value nor close to the maximum or minimum value; and (2) the average negotiation size of the ES-based agents increases, while that of the LCS-based agents does not but simply oscillates.

5.2

The reasons for the above results are summarized as follows. (1) The values added to or subtracted from the offer and threshold values in ES decrease as the iterations become large, while the crossover, mutation, and inversion operations in LCS are constantly performed. Since most of these operations work as a divergent or explored factor, a decrease in this influence makes simulation results converge; otherwise, it derives an instability in the simulation results. (2) The offer and threshold values in all offspring are modified at every iteration in ES, while they are modified only by a mutation operation executed at a low probability in LCS. Furthermore, ES modifies such values in the manner of a gradient search, while LCS modifies them randomly.

5.3

Here, we consider that game theory proves that rational agents A₁ and A₂ receive the maximum and minimum payoffs in the final negotiation process, respectively. This is because A₁in our simulations has to accept any small offer proposed by A₂ at the 10th negotiation process; otherwise, A₁ cannot receive any payoff, i.e., it receives 0 payoff. Therefore, we expect the following simulation results: (1) learning agents can acquire the maximum and minimum payoffs; and (2) the average negotiation size increases if the agents learn strategies appropriately. In analyzing the simulation results according to the above two assumptions, the ES-based agents show the same tendency in game theory, but the LCS-based agents do not. Note that "the same tendency" means to show similar results given by game theory.

ES vs. RL

5.4

Next, we investigate the simulation results for different learning mechanisms handling discrete values for representing strategies as shown in Figure 6. This figure shows that (1) the payoff in the ES-based agents restricted to a real number with one decimal digit does not completely converge, while that in the RL-based agents finally converges at a value near the maximum or minimum value (i.e., 90% or 10%); and (2) the average negotiation size in the restricted ES-based agents decreases, while that in the RL-based agents increases. As for the first result, the payoff by RL-based agents does not converge at the mostly maximum or minimum value (i.e., 100% or 0%) because the action selection of the RL-based agents in this simulation is based on the &epsilon-greedy method, which means that agents behave randomly at some percentage (i.e., 0.05% in this simulation). Such random actions prevent an acquisition of rational behaviors that derive mostly a maximum or minimum payoff. In this sense, it seems that the restricted ES-based agents slightly outperforms the RL-based agents only from the viewpoint of the convergent values, but here we would stress that both values are mostly the same, and this difference can be reduced by minimizing the &epsilon value. Therefore, we do not discuss this difference in detail.

5.5

To seek the reasons for the above different results, let us move our focus on to the 10th offer in Figure 2, where the values of the offer and threshold are set as 0.11 and 0.12, respectively. In this case, the agent who receives the offer from the opponent agent cannot accept it in the normal ES because the inequality of O(0.11) &ge T(0.12) described in Section 3.1 is not satisfied. In contrast, the same agent accepts the offer in the ES that is restricted to a real number with one decimal digit because the inequality of O(0.1) &ge T(0.1) is satisfied. In RL, on the other hand, the same agents can learn to refuse the offer from the opponent agent, even though their strategies are represented by the discrete values in the 0.1 unit (not in the 0.01 unit). This is because the decision of acceptance or rejection of the offer in RL is determined not by values of offer and threshold but by the probabilities of their worth. This means that such a decision is not affected by a restriction on the explanation of values in strategies. Here, the above analysis is based on an example of the 10th offer in Figure 2, but the same holds for other steps. For this reason, agents with the restricted ES may accept unwilling (i.e., small) offers in each negotiation process size, while the normal ES or RL can learn not to accept them.

5.6

These findings indicate that (1) the restricted ES-based agents cannot show the same tendency in game theory, even through the normal ES-based agents can; and (2) in comparison with the restricted ES-based agents, the RL-based agents can show the same tendency in game theory, even though their strategies are represented by the 0.1 discrete unit.

Implications and their validity

5.7

The above analysis suggests that learning mechanisms that enable agents to acquire their rational behaviors differ according to the knowledge representation (i.e., strategies in the bargaining game) of the agents. In particular, the ES mechanism can elicit rational behaviors of agents when strategies are represented by continuous values such as an ordinal real number, while the RL mechanism can elicit the same behaviors when strategies are represented by discrete values. From these implications, we confirmed the following important lessons through cross-element validation in MABS.

• The influence of learning mechanisms: Simulation results are sensitive to the learning mechanisms as shown by the simulation results described in the previous section. Due to this impact, we should investigate the influence of the learning mechanisms before investigating complex social problems.
• The influence of knowledge representation: Some social scientists may employ discrete values to represent strategies in the bargaining game for concise representation or their easy understanding (indeed, we have met such situations). However, such decision should be carefully made only after investigating the influence of knowledge representation of agents.

5.8

The above lessons tell us where to start an investigation on the influence of modeling agents. But, it should be noted that these lessons are based on the validation of computational models. In this research, however, computational models were not validated by simply comparing both results. This is because two compared results are different from each other. However, an additional comparison of results in game theory is needed to validate the computational models in the cases of ES- and RL-based agents. For ES-based agents, the simulation results differ from those in game theory when employing discrete values, but they are the same when employing continuous values. This indicates that ES-based agents are minimally validated (the only difference is strategy representation in the bargaining game). For RL-based agents, the simulation results are the same as those in game theory, which indicates that RL-based agents are validated. Finally, LCS-based agents were not validated in this research, but they have been validated in other experiments. These validations of the three computational models support the validity of the above lessons.

Toward computational validity and future directions

5.9

In this paper, we have approached the validity of simulation results by validating the computational models via cross-element validation. However, this is limited to cross-element validation as an aspect of "alignment of computational models" or "docking". This is because the compared results may be different as with the simulation results described in Section 4. To overcome this problem, we have compared them with rational behaviors of agents investigated in game theory as an aspect of "theoretical analysis". We should note here that (1) this type of validation is based on rationality which is one aspect of validation; and (2) this validation is only valid when rational behaviors of agents can be analyzed as in the bargaining game. To address such a case, it is important to compare more than two results of different computational models. Such a direction should be conducted as an important future research project.

5.10

On the other hand, a more important direction toward the validity of simulation results is to approach it by integrating three approaches as shown in Figure 7, i.e., (1) alignment of computational models or docking, (2) theoretical analysis, and (3) a link to the real world.^[3] An example of a link to the real world is a comparison of simulation results with observed behavioral patterns of human players conducted in experimental economics (Friedman and Sunder 1994; Kagel and Roth 1995). Since rational behaviors stated by game theory are not those of real actors (Nydegger and Owen 1974; Güth et al. 1982; Neelin et al. 1988; Roth et al. 1991),^[4] it is important to compare not only results in game theory but also those of the real world toward exploring another way of validating computational models. For example, if the same computational model could produce both different results (i.e., theoretical results and real results), such a model would have a wide range of capabilities that apply to both theory and the real world. An exploration of such models would also contribute to increasing the validity of computational models.^[5]

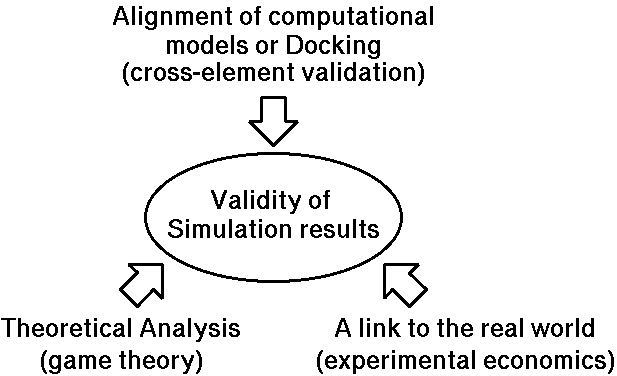
Figure 7. Three approaches to the validity of simulation results

5.11

In addition to the future research described above, the following endeavors should be pursued:

• Complex simulation: One of the significant directions is a comparison of simulation results with more than two agents in order to investigate complex systems. Since this paper only employs two players, it is actually a minimal MABS. Therefore, it is important to conduct investigation in a complex case in the validation of computational models.
• Relationship between examples and elements of computational models: Another direction is to investigate the relationship between examples (e.g., the bargaining game) to be used and elements of computational models (e.g., the learning mechanism) to be tested. Such comprehensive investigations, including many simulations in other domains and other elements, would contribute to increasing the validity of simulation results.
• Computational validity: According to Burton and Obel, computational validity is a balance of three elements: (1) the question or purpose, (2) the computational model, and (3) the experimental design (Burton and Obel 1995). Since this idea of computational validity is deeply related to our approach to validity, a final significant direction is to investigate the relationship between Burton's approach and ours.

Conclusions

6.1

Toward the validity of simulation results in MABS, this paper proposed a cross-element validation method that promotes validation of computational models by investigating whether several models can produce the same results after changing an element in the agent architecture. Specifically, we focused on learning mechanisms applied to agents as one of the important elements and compared several computational models based on different learning mechanisms. To investigate the utility of this approach, we made the following two comparisons in a bargaining game: (1) ES- vs. LCS-based agents, both handling continuous knowledge representation of agents; and (2) ES- vs. RL-based agents, both handling discrete knowledge representation. Through these comparisons, we found that (1) computational models are minimally validated in the case of ES- and RL-based agents; and (2) learning mechanisms that enable agents to acquire their rational behaviors differ according to the knowledge representation of the agents.

6.2

However, these results have only been obtained from three learning mechanisms (i.e., ES, LCS, and RL) and from one social problem (i.e., the bargaining game). Therefore, further careful qualifications and justifications, such as analyses of results using other learning mechanisms or in other domains, are needed to increase the validity of simulation results. Such important directions must be pursued in the near future in addition to the future directions described in Section 5.4. However, the following implications are suggested from the current results: (1) the ES-based agents can derive the same tendency in game theory but the LCS-based agents cannot in the case of employing continuous knowledge representation; and (2) the same ES-based agents cannot derive the same tendency in game theory but the RL-based agents can derive it in the case of employing discrete knowledge representation.

Acknowledgements

The research reported here was supported in part by a contract with the Telecommunications Advancement Organization (TAO) of Japan entitled "Research on Human Communication" and by the Okawa foundation for information and telecommunications.

Notes

¹ Carley used the term "cross-model validation" instead of "alignment of computational models" or "docking" (Carley and Gasser 1999).
² In the context of RL, worth is called "value". We select the term "worth" instead of "value" because the term "value" is used as a numerical number that represents the offer in strategies.
³ This integration for validity is derived from Deguchi's concept of an integration of simulation, theory, and real world (Deguchi 2003).
⁴ Actually, not all research in experimental economics claim that humans do not act rationally. Some research such as (Binmore et al. 1985) has reported that humans have the capability to acquire rational behaviors. Specifically, (Binmore et al. 1988) clarified that their intention in (Binmore et al. 1985) was not to show to what extend humans could act rationally but rather to verify whether humans could act rationally.
⁵ One such direction will be reported in Takadama et al. (2003).

References

ARTHUR, W. B., Holland, J. H., Palmer, R., and Tayler, P. (1997), "Asset Pricing Under Endogenous Expectations in an Artificial Stock Market," in W. B. Arthur, S. N. Durlauf, and D. A. Lane (Eds.), The Economy as an Evolving Complex System II, Addison-Wesley, pp. 15-44.

AXELROD, R. M. (1997), The Complexity of Cooperation: Agent-Based Models of Competition and Collaboration, Princeton University Press.

AXTELL, R., Axelrod, R., Epstein J., and Cohen, M. D. (1996), "Aligning Simulation Models: A Case Study and Results," Computational and Mathematical Organization Theory (CMOT), Vol. 1, No. 1, pp. 123-141.

BÄCK, T., Rudolph, G., and Schwefel, H. (1992), "Evolutionary Programming and Evolution Strategies: Similarities and Differences," The 2nd Annual Evolutionary Programming Conference, pp. 11-22.

BINMORE, K., Shaked. A., and Sutton, J. (1985), "Testing Non-cooperative Bargaining Theory: A Preliminary Study," American Economic Review, Vol. 75, No. 5, pp. 1178-1180.

BINMORE, K., Shaked, A., and Sutton, J. (1988), "A Further Test of Noncooperative Bargaining Theory: Reply," American Economic Review, Vol. 78, No. 4, pp. 837-839.

BURTON, R. M. and Obel, B. (1995), "The Validity of Computational Modes in Organization Science: From Model Realism to Purpose of the Model," Computational and Mathematical Organization Theory (CMOT), Vol. 1, No. 1, pp. 57-71.

CARLEY, K. M. and Svoboda, D. M. (1996), "Modeling Organizational Adaptation as a Simulated Annealing Process," Sociological Methods and Research, Vol. 25, No. 1, pp. 138-168.

CARLEY, K. M. and Gasser, L. (1999), "Computational and Organization Theory," in Weiss, G. (Ed.), Multiagent Systems - Modern Approach to Distributed Artificial Intelligence -, The MIT Press, pp. 299-330.

DEGUCHI, H. (2003), "Economics as Complex Systems," Springer, to appear.

EPSTEIN, J. M. and Axtell, R. (1996), Growing Artificial Societies, MIT Press.

FRIEDMAN, D. and Sunder, S. (1994), Experimental Methods: A Primer for Economists, Cambridge University Press.

GOLDBERG, D. E. (1989), Genetic Algorithms in Search, Optimization, and Machine Learning, Addison-Wesley.

GÜTH, W., Schmittberger, R., and Schwarze, B. (1982), "An Experimental Analysis of Ultimatum Bargaining," Journal of Economic Behavior and Organization, Vol. 3, pp. 367-388.

HAGHSHENASS, L., Levitt, R. E., Kunz, J. C., Mahalingam, A., and Zolin, R. (2002), "A Study on the Comparison of VDT and ORGAHEAD," The CASOS (Computational Analysis of Social and Organizational System) Conference 2002.

HOLLAND, J. H. (1975), Adaptation in Natural and Artificial Systems, University of Michigan Press.

HOLLAND, J. H., Holyoak, K. J., Nisbett, R. E., and Thagard, P. R. (1986), Induction, The MIT Press.

KAGEL, J. H. and Roth, A. E. (1995), Handbook of Experimental Economics Princeton University Press.

LEVITT, R. E., Cohen, G. P., Kunz, J. C., Nass, C. I., Chirstiansen, T. R., and Jin, Y. (1994), "The Virtual Design Team: Simulating How Organization Structure and Information Processing Tools Affect Team Performance", in K. M. Carley and J. Prietula (Eds.): Computational Organization Theory, Lawlence-Erlbaum Assoc., pp. 1-18.

LOUIE, M. A., Carley, K. M., Levitt, R. E., Kunz, J. C., and Mahalingam, A. (2002), "Docking the Virtual Design Team and ORGAHEAD," The CASOS (Computational Analysis of Social and Organizational System) Conference 2002.

MOSS, S. and Davidsson, P. (2001), Multi-Agent-Based Simulation, Lecture Notes in Artificial Intelligence, Vol. 1979, Springer-Verlag.

MUTHOO, A. (1999), Bargaining Theory with Applications , Cambridge University Press.

MUTHOO, A. (2000), "A Non-Technical Introduction to Bargaining Theory," World Economics, pp. 145-166.

NEELIN, J., Sonnenschein, H., and Spiegel, M. (1988), "A Further Test of Noncooperative Bargaining Theory: Comment," American Economic Review, Vol. 78, No. 4, pp. 824-836.

NYDEGGER, R. V. and Owen, G. (1974), "Two-Person Bargaining: An Experimental Test of the Nash Axioms," International Journal of Game Theory, Vol. 3, No. 4, pp. 239-249.

OLIVER, J. R. (1996), "On Artificial Agents for Negotiation in Electronic Commerce," Ph.D. Thesis, University of Pennsylvania.

OSBORNE, M. J. and Rubinstein, A. (1994), A Course in Game Theory, MIT Press.

ROTH, A. E., Prasnikar, V., Okuno-Fujiwara, M., and Zamir, S. (1991), "Bargaining and Market Behavior in Jerusalem, Ljubljana, Pittsburgh, and Tokyo: An Experimental Study," American Economic Review, Vol. 81, No. 5, pp. 1068-1094.

RUBINSTEIN, A. (1982), "Perfect Equilibrium in a Bargaining Model," Econometrica, Vol. 50, No. 1, pp. 97-109.

SMITH, S. F. (1983), "Flexible Learning of Problem Solving Heuristics through Adaptive Search," The 8th International Joint Conference on Artificial Intelligence (IJCAI '83), pp. 422-425.

Ståhl, I. (1972), Bargaining Theory, Economics Research Institute at the Stockholm School of Economics.

SUTTON, R. S. and Bart, A. G. (1998), Reinforcement Learning - An Introduction -, The MIT Press.

TAKADAMA, K. and Shimohara, K. (2002), "The Hare and The Tortoise - Cumulative Progress in Agent-Based Simulation -," in A. Namatame, T. Terano, and K. Kurumatani (Eds.), Agent-based Approaches in Economic and Social Complex Systems, The IOS Press, pp. 3-14.

TAKADAMA, K., Sugimoto, N., Nawa, N. E., and Shimohara, K. (2003), "Grounding to Both Theory and Real World by Agent-Based Simulation: Analyzing Learning Agents in Bargaining Game," NAACSOS (North American Association for Computational Social and Organizational Science) Conference 2003 .

WATKINS, C. J. C. H. and Dayan, P. (1992), "Technical Note: Q-Learning," Machine Learning, Vol. 8, pp. 55-68.

Return to Contents of this issue

© Copyright Journal of Artificial Societies and Social Simulation, [2003]