Bruce Edmonds and David Hales (2003)
Replication, Replication and Replication: Some Hard Lessons from Model Alignment
Journal of Artificial Societies and Social Simulation
vol. 6, no. 4
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/6/4/11.html>
Received: 13-Jul-2003 Accepted: 13-Jul-2003 Published: 31-Oct-2003
 Abstract
Abstract| Table 1: Pairings is the number of times per generation each agent has an opportunity to donate to a randomly encountered other. The donation rate is the percentage of such encounters in which the choosing agent cooperates, that is, donates b = 1.0 at a cost of c = 0.1 to itself. The average tolerance is the average over all agents and all generations. | ||
| Effect of pairings on donation rate | ||
| Parings | Donation rate (%) | Average tolerance |
| 1 | 2.1 | 0.009 |
| 2 | 4.3 | 0.007 |
| 3 | 73.6 | 0.019 |
| 4 | 76.8 | 0.021 |
| 6 | 78.7 | 0.024 |
| 8 | 79.2 | 0.025 |
| 10 | 79.2 | 0.024 |
| Table 2: The number of pairings is held at P = 3. The recipient benefit his held at b = 1 and the cost to the donor is varied as shown | ||
| Effect of cost of donating on donation rate | ||
| Cost | Donation rate (%) | Average tolerance |
| 0.05 | 73.7 | 0.019 |
| 0.1 | 73.6 | 0.019 |
| 0.2 | 73.6 | 0.018 |
| 0.3 | 73.5 | 0.018 |
| 0.4 | 60.1 | 0.011 |
| 0.5 | 24.7 | 0.007 |
| 0.6 | 2.2 | 0.005 |
|
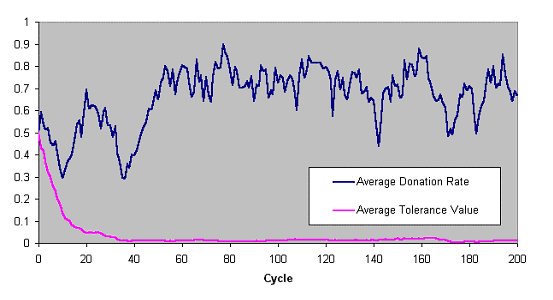
| Figure 1. The average donation rate (the proportion of parings that resulted in a donation) and the average value of the tolerances across the whole population in a typical run of the Riolo et al. model (number of pairings=3 cost=0.1) |
Strategies of donating to others who have sufficiently similar heritable tags ... can establish cooperation without reciprocity. (Riolo et al. 2001, page 443)
| Table 3: Pairings is the number of times per generation each agent has an opportunity to donate to a randomly encountered other. The donation rate is the percentage of such encounters in which the choosing agent cooperates, that is, donates b = 1.0 at a cost of c = 0.1 to itself. The average tolerance is the average over all agents and all generations. The values in brackets show the difference between these results and the original results given in table 1 | ||
Effect of pairings on donation rate | ||
| Pairings | Donation rate (%) | Average tolerance |
| 1 | 5.1 (3.0) | 0.010 (0.1) |
| 2 | 42.6 (38.3) | 0.012 (0.5) |
| 3 | 73.7 (0.1) | 0.018 (0.1) |
| 4 | 76.8 (0.0) | 0.021 (0.0) |
| 6 | 78.6 (0.1) | 0.023 (0.1) |
| 8 | 79.2 (0.0) | 0.025 (0.0) |
| 10 | 79.4 (0.2) | 0.026 (0.2) |
| Table 4: The number of pairings is held at P = 3. The recipient benefit his held at b = 1 and the cost to the donor is varied as shown. The values in brackets show the difference between these results and the original results given in table 2 | ||
| Effect of cost of donating on donation rate | ||
| Cost | Donation rate (%) | Average tolerance |
| 0.05 | 73.7 (0.0) | 0.018 (0.001) |
| 0.1 | 73.7 (0.1) | 0.018 (0.001) |
| 0.2 | 73.7 (0.1) | 0.019 (0.001) |
| 0.3 | 73.7 (0.2) | 0.018 (0.000) |
| 0.4 | 61.0 (0.9) | 0.011 (0.000) |
| 0.5 | 45.9 (21.2) | 0.008 (0.001) |
| 0.6 | 8.1 (5.9) | 0.006 (0.001) |
| Table 5: Pairings is the number of times per generation each agent has an opportunity to donate to a randomly encountered other. The donation rate is the percentage of such encounters in which the choosing agent cooperates, that is, donates b = 1.0 at a cost of c = 0.1 to itself. The average tolerance is the average over all agents and all generations. The values in brackets show the difference between these results and the initial re-implementation results given in table 3 | ||
Effect of pairings on donation rate | ||
| Parings | Donation rate (%) | Average tolerance |
| 1 | 5.2 (0.1) | 0.011 (0.1) |
| 2 | 42.6 (0.0) | 0.012 (0.0) |
| 3 | 73.3 (0.4) | 0.018 (0.0) |
| 4 | 76.6 (0.2) | 0.022 (0.1) |
| 6 | 78.6 (0.0) | 0.023 (0.0) |
|
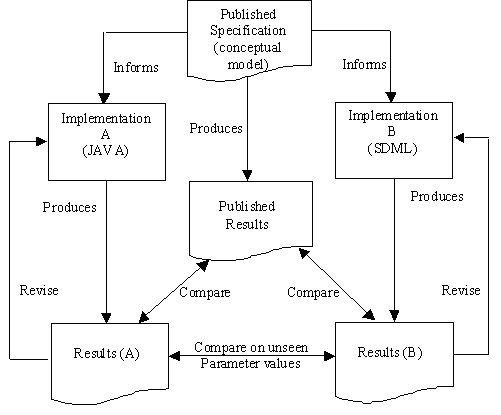
| Figure 2. Relationship of published model and two re-implementations |
After all agents have participated in all parings in a generations agents are reproduced on the basis of their score relative to others. The least fit, median fit, and most fit agents have respectively 0, 1 and 2 as the expected number of their offspring. This is accomplished by comparing each agent with another randomly chosen agent, and giving an offspring to the on with the higher score.
| Table 6: Outline pseudo-code algorithms for the three different tournament selection methods tested | ||
| Three Variants Of Tournament Selection | ||
| LOOP for each agent in population Select current agent (a) from pop Select random agent (b) from pop IF score (a) > score (b) THEN Reproduce (a) in next generation ELSE IF score (a) < score (b) THEN Reproduce (b) in next generation ELSE (a) and (b) are equal Select randomly (a) or (b) to be reproduced into next generation. END IF END LOOP | LOOP for each agent in population Select current agent (a) from pop Select random agent (b) from pop IF score (a) >= score (b) THEN Reproduce (a) in next generation ELSE score (a) < score (b) Reproduce (b) in next generation END IF END LOOP | LOOP for each agent in population Select current agent (a) from pop Select random agent (b) from pop IF score (a) <= score (b) THEN Reproduce (b) in next generation ELSE score (a) > score (b) Reproduce (a) in next generation END IF END LOOP |
| (a) No Bias | (b) Selected Bias | (c) Random Bias |
| Table 7: Here we compare the results of donation rates (Don) and average tolerances (Ave. Tol) for each of the three different tournament selection algorithms described in table 6 over different "pairings" values. We note that the "selected bias" method very closely matches the published results from the initial model (given in table 1). As before the results are calculated from 30 independent runs to 30,000 generations. | ||||||
| Results From the Three Variants of Tournament Selection | ||||||
| No Bias (a) | Selected Bias (b) | Random Bias (c) | ||||
| Pairings | Don | Ave. Tol | Don | Ave Tol | Don | Ave Tol |
| 1 | 5.1 | 0.010 | 2.1 | 0.009 | 6.0 | 0.010 |
| 2 | 42.6 | 0.012 | 4.4 | 0.007 | 49.6 | 0.013 |
| 3 | 73.7 | 0.018 | 73.7 | 0.019 | 73.7 | 0.018 |
| 4 | 76.8 | 0.021 | 76.9 | 0.021 | 76.8 | 0.021 |
| 6 | 78.6 | 0.023 | 78.6 | 0.023 | 78.7 | 0.023 |
| 8 | 79.2 | 0.025 | 79.2 | 0.025 | 79.2 | 0.025 |
| 10 | 79.4 | 0.026 | 79.4 | 0.026 | 79.4 | 0.026 |
| Table 8: Here we compare the results of donation rates (Don) and average tolerances (Ave. Tol) for each of the three different tournament selection algorithms described in table 6 over different donation cost values. We note that the "selected bias" method very closely matches the published results from the initial model (given in table 2). The results are calculated from 30 independent runs to 30,000 generations | ||||||
| Results from the Three Variants of Tournament Selection | ||||||
| No Bias (a) | Selected Bias (b) | Random Bias (c) | ||||
| Cost | Ave. Don | Ave. Tol | Ave Don | Ave Tol | Ave Don | Ave Tol |
| 0.05 | 73.7 | 0.018 | 73.6 | 0.018 | 73.7 | 0.018 |
| 0.1 | 73.7 | 0.018 | 73.7 | 0.019 | 73.7 | 0.018 |
| 0.2 | 73.7 | 0.019 | 73.7 | 0.019 | 73.7 | 0.018 |
| 0.3 | 73.7 | 0.018 | 73.6 | 0.019 | 73.7 | 0.018 |
| 0.4 | 61.0 | 0.011 | 60.5 | 0.011 | 61.0 | 0.011 |
| 0.5 | 45.9 | 0.008 | 26.2 | 0.007 | 46.7 | 0.008 |
| 0.6 | 8.1 | 0.006 | 2.1 | 0.005 | 9.9 | 0.006 |
| Table 9: Here are the results when all parameters are identical to those used in Table 1 (i.e. the original published results) except that donation only occurs when the differences in tags is strictly less than (rather than less then or equal to) tolerance. As can be seen, donation is completely wiped out | ||
Effect of pairings on donation rate (strict tolerance) | ||
| Parings | Donation rate (%) | Average tolerance |
| 1 | 0.0 | 0.000 |
| 2 | 0.0 | 0.000 |
| 3 | 0.0 | 0.000 |
| 4 | 0.0 | 0.000 |
| 6 | 0.0 | 0.000 |
| 8 | 0.0 | 0.000 |
| 10 | 0.0 | 0.000 |
| Table 10: Results obtained when all parameters are identical to those used in Table 2 (i.e. the original published results) except that donation only occurs when the differences in tags is strictly less than (rather than less then or equal to) tolerance. As can be seen, donation is completely wiped out | ||
| Effect of cost of donating on donation rate (with strict tolerance) | ||
| Cost | Donation rate (%) | Average tolerance |
| 0.05 | 0.0 | 0.000 |
| 0.1 | 0.0 | 0.000 |
| 0.2 | 0.0 | 0.000 |
| 0.3 | 0.0 | 0.000 |
| 0.4 | 0.0 | 0.000 |
| 0.5 | 0.0 | 0.000 |
| 0.6 | 0.0 | 0.000 |
|
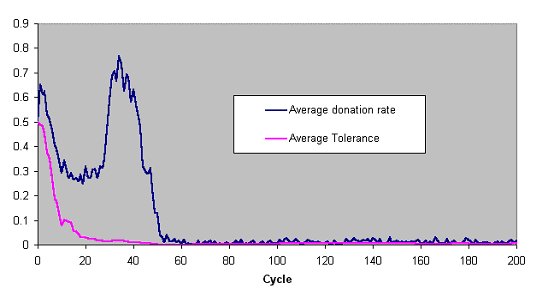
| Figure 3. The average donation rate (the proportion of pairings that resulted in a donation) and the average value of the tolerances across the whole population in a typical run of the Riolo et al. model (number of pairings=3 cost=0.1) but with strict tag comparisons. |
|
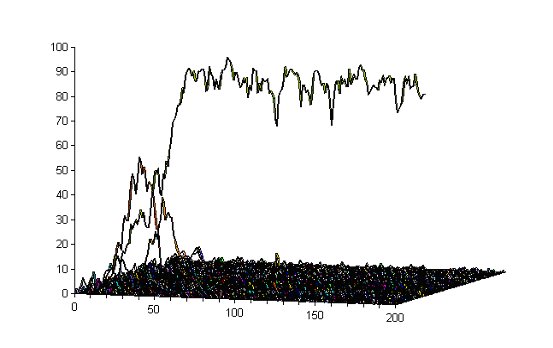
| Figure 4. The frequency histogram of each interval of 0.01 (0-0.01, 0.01-0.02 etc.) over the first 200 generations in the typical run illustrated above in Figure 1 (the Riolo et al. model with 3 pairings and cost of donation at 0.1), i.e. each 'line' shows how many individuals have a tag in that range in that generation. Significant detail from this is shown in Figure 5 immediately below |
|
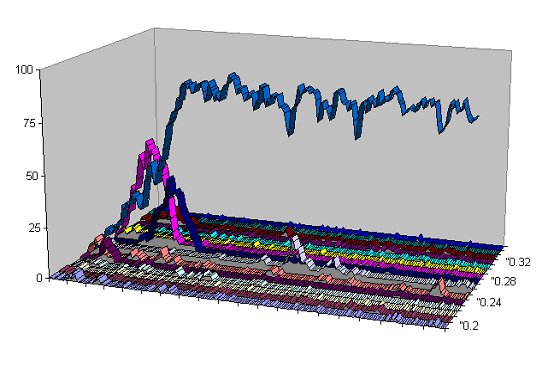
| Figure 5. Detail from Figure 4 showing the frequency of tag values over time for the intervals 0.02-0.021, 0.021-0.022, ..., 0.034-0.035 for the first 200 generations |
|
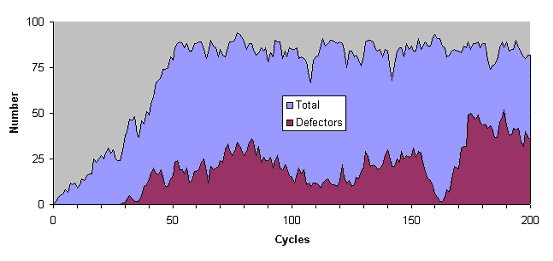
| Figure 6. The total frequency of tag values in the dominant interval and the number of these that have a zero tolerance value (called defectors here since they only donate to others with an identical tag) over the first 200 generations |
| Table 11: Results when tolerance is forced to be always zero for all agents (i.e. the tolerance mechanisms is turned-off) with all other settings as they were for the original results given in Table 7 | ||||||
| Results when tolerance set to zero for different Pairings | ||||||
| No Bias (a) | Selected Bias (b) | Random Bias (c) | ||||
| Parings | Don | Ave. Tol | Don | Ave Tol | Don | Ave Tol |
| 1 | 3.1 | 0.000 | 0.0 | 0.000 | 4.1 | 0.000 |
| 2 | 65.4 | 0.000 | 0.0 | 0.000 | 65.6 | 0.000 |
| 3 | 75.3 | 0.000 | 0.0 | 0.000 | 75.4 | 0.000 |
| 4 | 77.6 | 0.000 | 0.0 | 0.000 | 77.7 | 0.000 |
| 6 | 78.8 | 0.000 | 0.0 | 0.000 | 78.8 | 0.000 |
| 8 | 78.9 | 0.000 | 1.9 | 0.000 | 78.9 | 0.000 |
| 10 | 79.0 | 0.000 | 7.6 | 0.000 | 79.0 | 0.000 |
| Table 12: Results when tolerance is forced to be always zero for all agents (i.e. the tolerance mechanisms is turned-off) with all other settings as they were for the original results given in Table 8 | ||||||
| Results when tolerance set to zero for different Costs | ||||||
| No Bias (a) | Selected Bias (b) | Random Bias (c) | ||||
| Cost | Ave. Don | Ave. Tol | Ave Don | Ave Tol | Ave Don | Ave Tol |
| 0.05 | 75.3 | 0.000 | 0.000 | 0.000 | 75.4 | 0.000 |
| 0.1 | 75.3 | 0.000 | 0.000 | 0.000 | 75.4 | 0.000 |
| 0.2 | 75.3 | 0.000 | 0.000 | 0.000 | 75.4 | 0.000 |
| 0.3 | 75.3 | 0.000 | 0.000 | 0.000 | 75.4 | 0.000 |
| 0.4 | 66.0 | 0.000 | 0.000 | 0.000 | 66.0 | 0.000 |
| 0.5 | 59.7 | 0.000 | 0.000 | 0.000 | 59.8 | 0.000 |
| 0.6 | 17.2 | 0.000 | 0.000 | 0.000 | 20.3 | 0.000 |
Compulsory donation to others who have identical heritable tags can establish cooperation without reciprocity in situations where a group of tag clones can replicate themselves exactly- which is a somewhat less significant result that that claimed in the original paper.
| Table 13: Results when a very small level of Gaussian noise is added to the tag value during the replication process (when an agent is copied into the next generation). Notice that the donation rate drops sharply[13] (over Table 7) - this would not happen if the originally published interpretation held | ||||||
| Results when noised added to tag values on reproduction | ||||||
| No Bias (a) | Selected Bias (b) | Random Bias (c) | ||||
| Pairings | Don | Ave. Tol | Don | Ave Tol | Don | Ave Tol |
| 1 | 3.7 | 0.009 | 1.9 | 0.009 | 4.2 | 0.009 |
| 2 | 3.1 | 0.007 | 1.5 | 0.006 | 3.7 | 0.007 |
| 3 | 4.0 | 0.005 | 1.5 | 0.005 | 5.1 | 0.005 |
| 4 | 6.8 | 0.005 | 2.0 | 0.005 | 8.5 | 0.005 |
| 6 | 13.1 | 0.004 | 6.2 | 0.004 | 14.2 | 0.004 |
| 8 | 15.5 | 0.004 | 12.7 | 0.004 | 16.2 | 0.004 |
| 10 | 12.1 | 0.002 | 10.9 | 0.003 | 12.8 | 0.003 |
| Table 14: Results when a very small level of Gaussian noise is added to the tag value during the replication process (when an agent is copied into the next generation). Notice that the donation rate drops sharply (over Table 8) - this would not happen if the originally published interpretation held | ||||||
| Results when noise added to tag values on reproduction | ||||||
| No Bias (a) | Selected Bias (b) | Random Bias (c) | ||||
| Cost | Ave. Don | Ave. Tol | Ave Don | Ave Tol | Ave Don | Ave Tol |
| 0.05 | 4.0 | 0.006 | 1.5 | 0.005 | 5.1 | 0.005 |
| 0.1 | 4.0 | 0.005 | 1.5 | 0.005 | 5.1 | 0.005 |
| 0.2 | 3.9 | 0.005 | 1.4 | 0.005 | 5.0 | 0.005 |
| 0.3 | 4.0 | 0.005 | 1.4 | 0.005 | 5.2 | 0.006 |
| 0.4 | 3.2 | 0.005 | 1.3 | 0.005 | 3.8 | 0.005 |
| 0.5 | 2.7 | 0.005 | 1.3 | 0.005 | 3.2 | 0.005 |
| 0.6 | 2.5 | 0.005 | 1.2 | 0.005 | 2.9 | 0.005 |
2 Unfortunately, in many papers the conceptual model is not explicitly delineated; a causal reading might lead one to believe the simulation was directly about the observed phenomena (Edmonds 2000)
3 Of course, there could be problems with both aspects (when specifications are vague and implementations complex).
4 Several recent models and investigations have shown how "tags" (arbitrary social cues) can catalyize group level self-organisation from previously disparate individuals (Hales 2001, Hales 2002a, Hales 2002b, Hales and Edmonds 2002).
5 We say "seemingly" because not all is what it may first appear - the process of re-implementations here described uncovered some interested issues concerning the model (but more of this later).
6 Strictly speaking they are not groups but this term provides a more vivid picture of what occurs.
8 Using a (unrealistically strong) philosophical sense of "prove" here.
9 In extremely simple cases (no real numbers, no random component, no input from outside world, very simple algorithms etc.) it has been possible to effect a machine verification with respect to formal specification, but this is not possible with any simulation of the kind we are talking about.
10 Indeed further statistics recording the proportion of donation events the occur between non-tag-clone agents were collected, these were always almost zero.
11 When the model was implemented with a probabilistic roulette wheel selection algorithm (where reproductive success is probabilistically and proportionally related to fitness - or score in this case) results similar to the random bias results were produced.
12 This is in addition to the 10% chance of having the tag value reset - which remains unchanged.
13 Notice also the non-monotanicity in the donation rates - indeed further runs examining 20 and 40 awards showed even lower donation rates. This interesting phenomenon is beyond the scope of this paper and may be addressed in future papers.
14 The implemented simulation is usually a particular case of the conceptual model which is more generally applicable but less precise.
15 Even then the chaotic nature of some of the processes may mean that complete alignment is impossible. These difficulties imply that, often, it may not be possible to separate out the theory that the simulation is supposed to embody and the implementation.
16'Wrong' in the sense that, at least in some detail or other, the implementation differs from what was intended or assumed by the modeller.
The only permanent variables that change are the tag and tolerance values for each of the 100 individuals. Temporary variables (that only have effect within a generation) are the donations and the fitness scores).
In Riolo et al. (2001) only c, the donation cost, and P, the number of pairings, are varied. In this paper the following are never varied: the population, the tag range, the probability of tag or tolerance mutation; or the standard deviations of the tolerance mutation Gaussian noise.
Key algorithm options are:
For each generation For each agent, a Randomly select another different agent, b If total score of b is strictly greater than the total score of a (selected bias) Then replace a with b Else keep a Next agent For each agent, a With probability 0.1 replace its tag with a new random value in [0, 1] With probability 0.1 Add Gaussian noise (mean 0 sd 0.01) to tolerance If tolerance less 0 set to 0, if greater 1 set to 1 Reset a's score to zero Next agent For each agent, a Randomly select another different agent, b If +ve difference of (tag of a) and (tag of b) < (the tolerance of a) (strict comparison) Then add 1 to score of b and subtract c from score of a Next agent Next generation
Strategies of donating to others who have sufficiently similar heritable tags ... can establish cooperation without reciprocity.As a result of our investigations we give it a more restricted interpretation:
Compulsory donation to others who have identical heritable tags can establish cooperation without reciprocity in situations where a group of tag clones can replicate themselves exactly.
CHAKRAVARTI, Laha, and Roy, (1967), Handbook of Methods of Applied Statistics, Volume I, John Wiley and Sons, pp. 392-394.
EDMONDS, B. (1998), Social Embeddedness and Agent Development. UKMAS'98, Manchester, December1998. (available at: http://cfpm.org/cpmreps.html ).
EDMONDS, B. (1999), Syntactic Measures of Complexity. Philosophy. Manchester, University of Manchester. (available at: http://bruce.edmonds.name/thesis).
EDMONDS, B. (2000), The Use of Models - making MABS actually work. In Moss, S., Davidsson, P. (Eds.) Multi-Agent-Based Simulation. Lecture Notes in Artificial Intelligence, 1979:15-32. Berlin: Springer-Verlag.
ENGELFRIET, J. Jonker, C. and Treur, J. (1999), Compositional Verification of Multi-Agent Systems in Temporal Multi-Epistemic Logic. In Proceedings of the 5th International Workshop on Intelligent Agents V : Agent Theories, Architectures and Languages (ATAL-98), Springer. Lecture Notes in Artificial Intelligence 1555:177-194.
HALES, D. (2000), Cooperation without Space or Memory: Tags, Groups and the Prisoner's Dilemma. In Moss, S., Davidsson, P. (Eds.) Multi-Agent-Based Simulation. Lecture Notes in Artificial Intelligence, 1979:157-166. Berlin: Springer-Verlag.
HALES, D. (2001), Tag Based Cooperation in Artificial Societies. Ph.D. Thesis, Department of Computer Science, University of Essex (available at: http://www.davidhales.com/thesis).
HALES, D. (2002a), 1. Evolving Specialisation, Altruism and Group-Level Optimisation Using Tags. In Sichman, J. S., Bousquet, F. Davidsson, P. (Eds.) Multi-Agent-Based Simulation II. Lecture Notes in Artificial Intelligence 2581:26-35 Berlin: Springer-Verlag.
HALES, D. (2002b), Smart Agents Don't Need Kin - Evolving Specialisation and Cooperation with Tags. CPM Working Paper 02-89. The Centre for Policy Modelling, Manchester Metropolitan University, Manchester, UK (available at: http://cfpm.org/cpmreps.html).
HALES, D. & Edmonds, B. (2002) Evolving Social Rationality for MAS using "Tags". CPM Working Paper 02-104. The Centre for Policy Modelling, Manchester Metropolitan University, Manchester, UK (available at: http://cfpm.org/cpmreps.html).
HOLLAND, J. (1993), The Effect of Labels (Tags) on Social Interactions. SFI Working Paper 93-10-064. Santa Fe Institute, Santa Fe, NM. (available at: http://www.santafe.edu/sfi/publications/wplist/1993)
MORGAN, M. and Morrison, M. (2000) Models as Mediators, Cambridge University Press.
POPPER, K. R. (1969) Conjectures and Refutations. London: Routledge & Kegan Paul.
RIOLO 2001"> RIOLO, R. L., Cohen, M. D. and Axelrod, R (2001), Evolution of cooperation without reciprocity. Nature, 411:441-443.
SIGMUND, K. and Nowak, M. A. (2001), Evolution - Tides of tolerance. Nature 414:403.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]