Hiroshi Takahashi and Takao Terano (2003)
Agent-Based Approach to Investors' Behavior and Asset Price Fluctuation in Financial Markets
Journal of Artificial Societies and Social
Simulation
vol. 6, no. 3
To cite articles published in the Journal of Artificial Societies and Social
Simulation, please reference the above information and include paragraph
numbers if necessary
<https://www.jasss.org/6/3/3.html>
Received: 31-Oct-2002 Accepted: 1-Jun-2003 Published: 30-Jun-2003
 Abstract
Abstract Introduction
Introduction Related Work
Related Work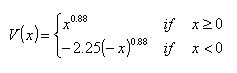
 Design of the Virtual Financial Market
Design of the Virtual Financial MarketRefer to Black (1992) for the detail of the bayes correction model[19].
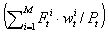 are the decreasing function of the stock price, and the total number
of the stock issued in the market (N) is constant. We derive the traded price as
are the decreasing function of the stock price, and the total number
of the stock issued in the market (N) is constant. We derive the traded price as 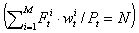 by calculating the price (Pi) where the total amount of
the stock retained by investors
by calculating the price (Pi) where the total amount of
the stock retained by investors 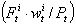 , which is the demand, meets the
total market value of the stock, which is the supply[20].
, which is the demand, meets the
total market value of the stock, which is the supply[20].
 Analyses of Price Fluctuation
Analyses of Price Fluctuation
|
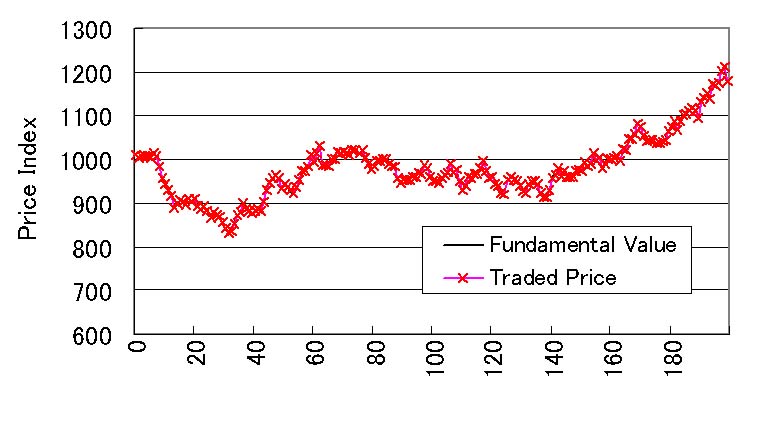
| Figure 1. Price history (when 100% of investors predict based on the fundamental value) |
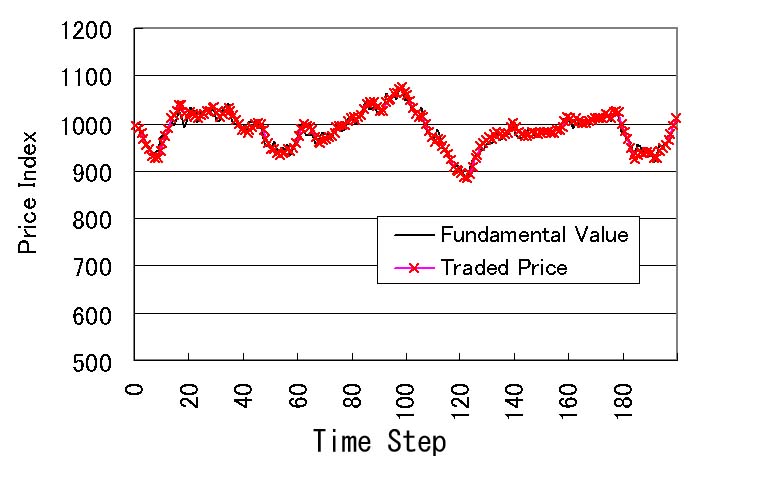 |
| Figure 2. Price history (fundamentalists : trend predictors = 500 : 500) |
|
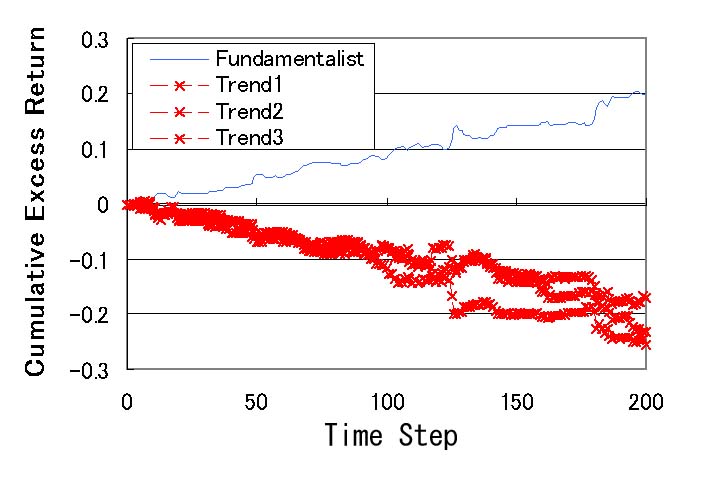
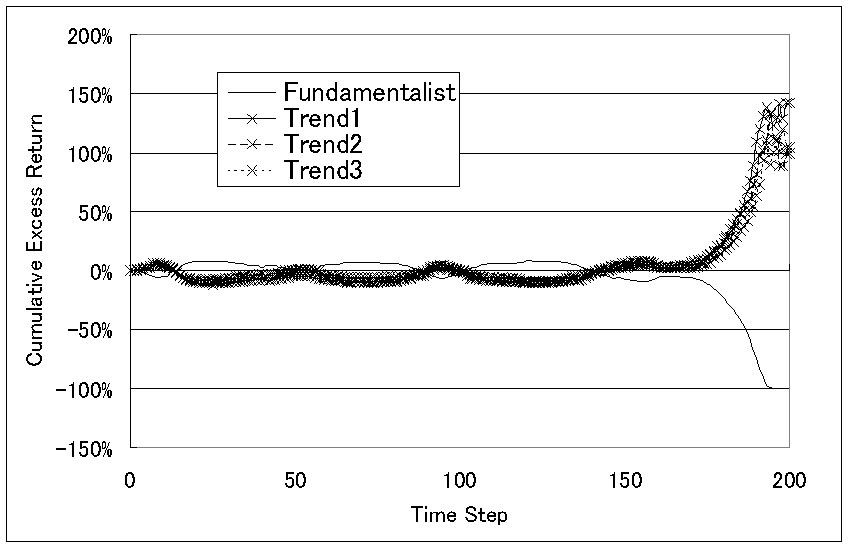
| Figure 3. Cumulative excess returns (fundamentalists : trend predictors = 500 : 500) |
|
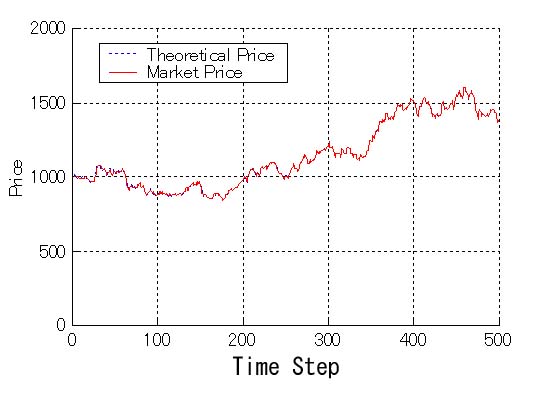
| Figure 4. Price history when natural selection works (fundamentalists : trend predictors = 500 : 500) |
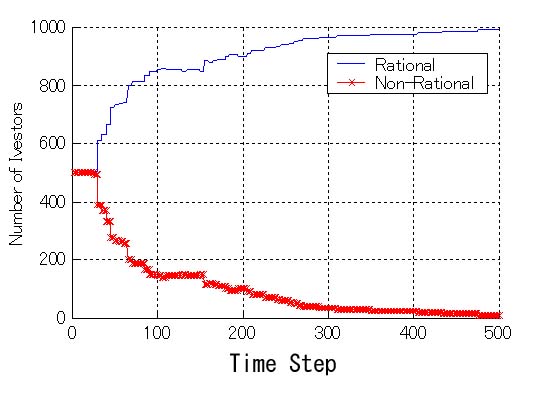 |
| Figure 5. History of the number of investors when natural selection works (fundamentalists : trend predictors = 500 : 500) |
|
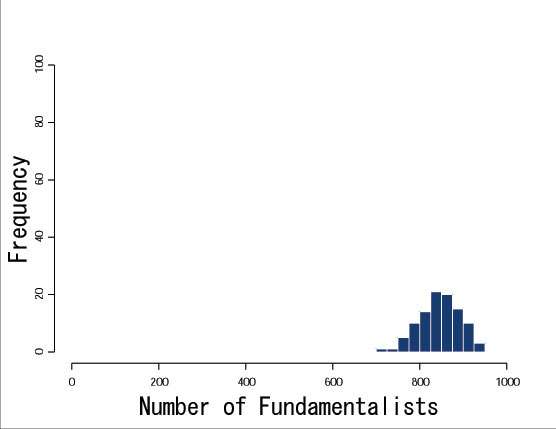
| Figure 6. Distribution of the number of fundamentalists (t=200) |
|
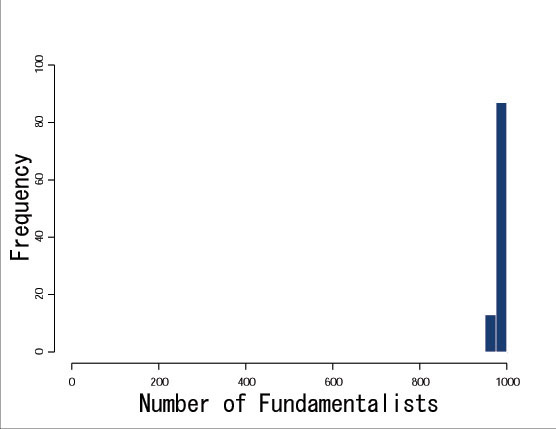
| Figure 7. Distribution of the number of fundamentalists (t=500) |
|
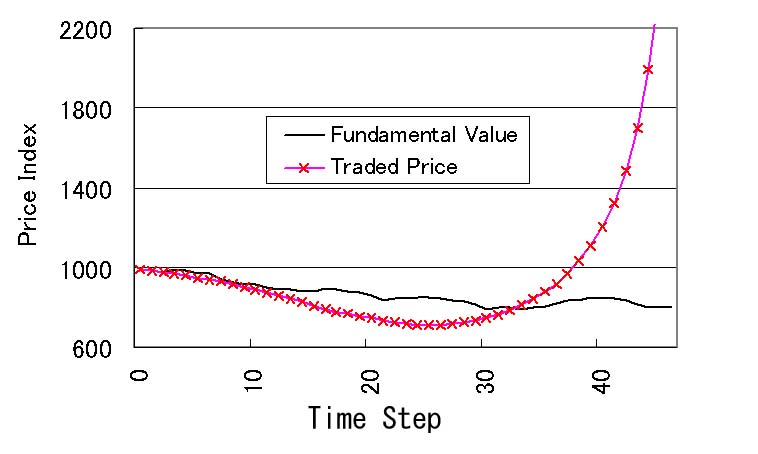
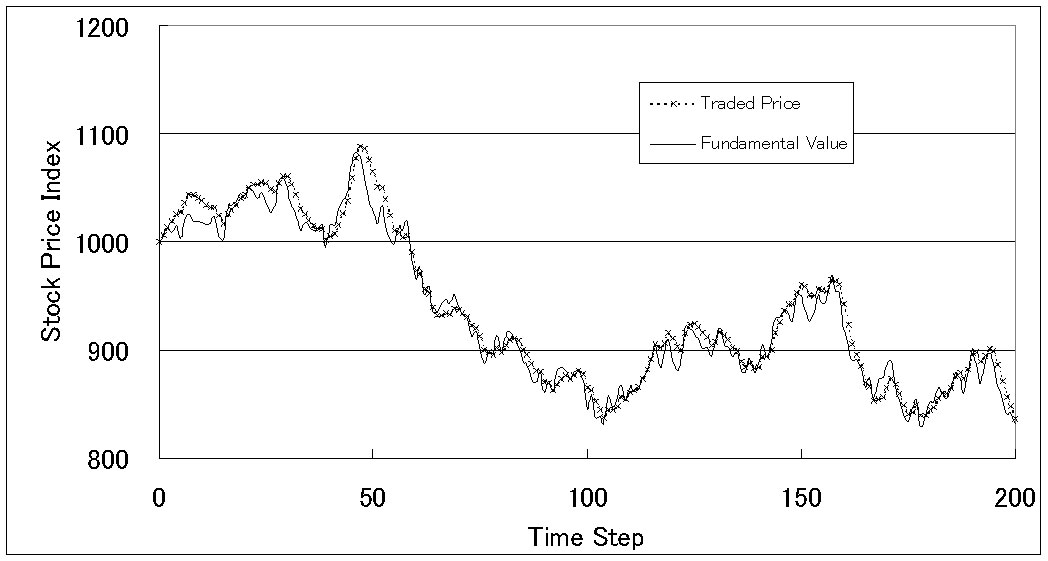
| Figure 8. Price history (fundamentalists : trend predictors = 100 : 900) |
|
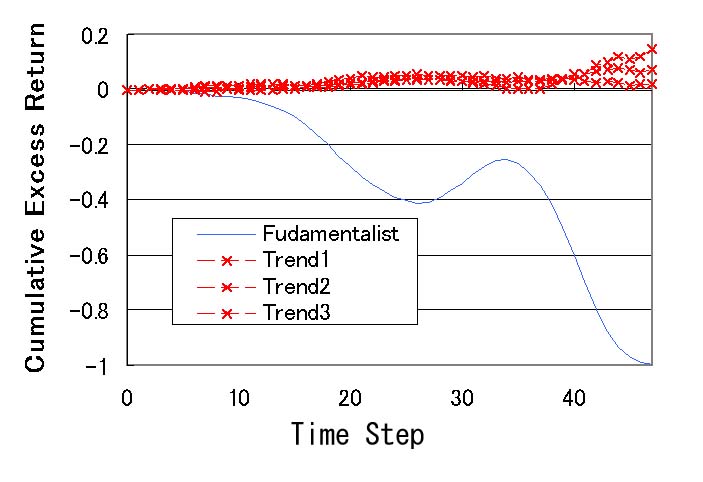
| Figure 9. Cumulative excess returns (fundamentalists : trend predictors = 100 : 900) |
|
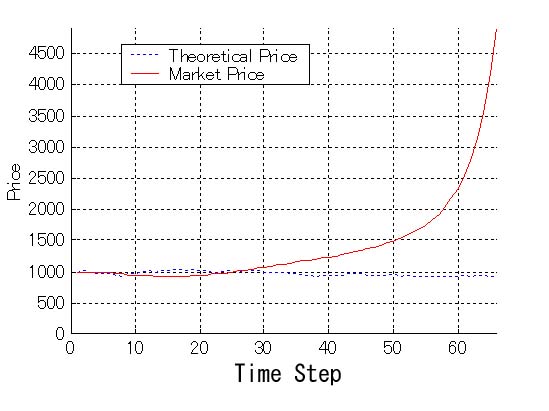
| Figure 10. Price history when natural selection works (fundamentalists : trend predictors = 100 : 900) |
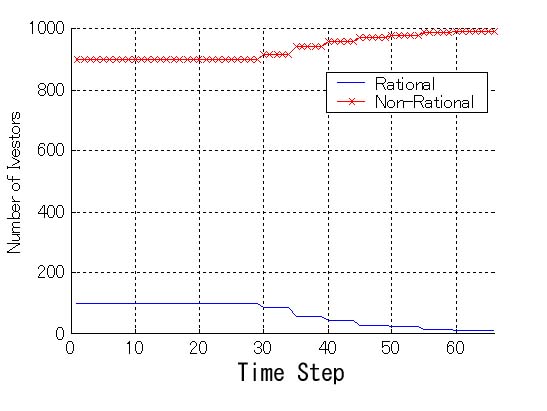 |
| Figure 11. History of the number of investors when natural selection works (fundamentalists : trend predictors = 100 : 900) |

|
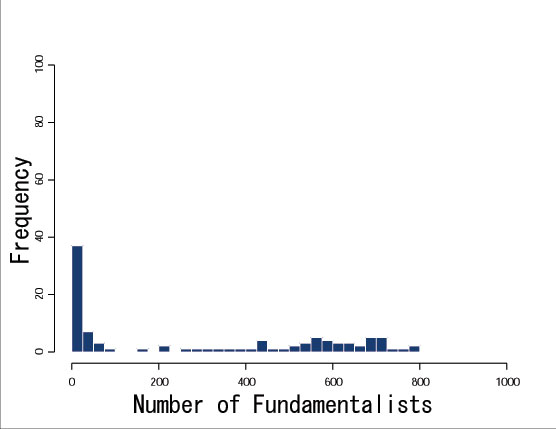
| Figure 12. Distribution of the number of fundamentalists (t=50) |
|
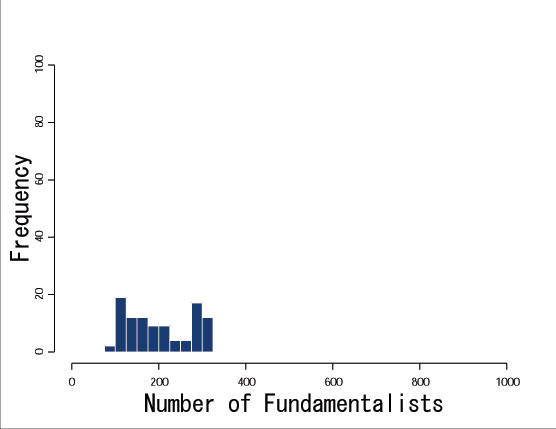
| Figure 13. Distribution of the number of fundamentalists (t=100) |
|
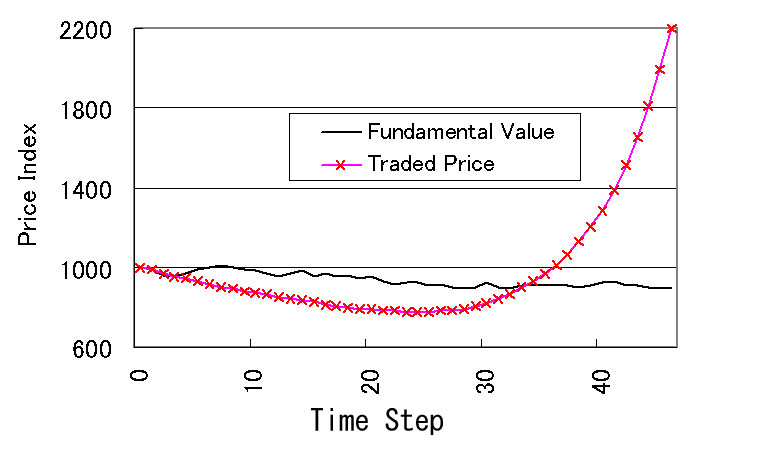
| Figure 14. Price history (with the investment restriction) |
|
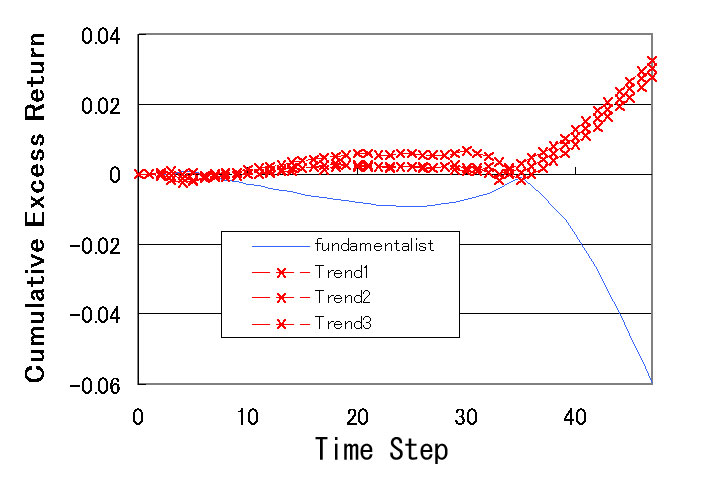
| Figure 15. Cumulative excess returns (with the investment restriction) |
|
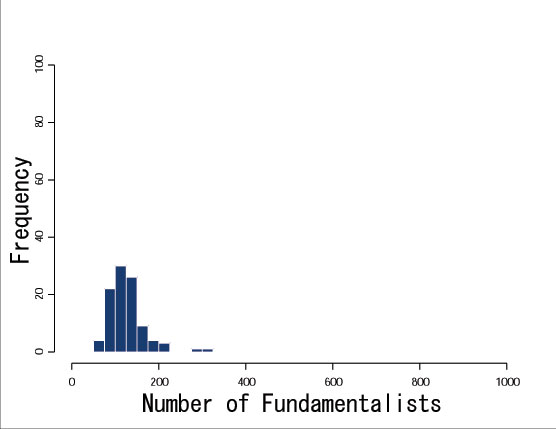
| Figure 16. Distribution of the number of fundamentalists (with the investment restriction, t=50) |
|
| Figure 17. Distribution of the number of fundamentalists (with the investment restriction, t=100) |
|
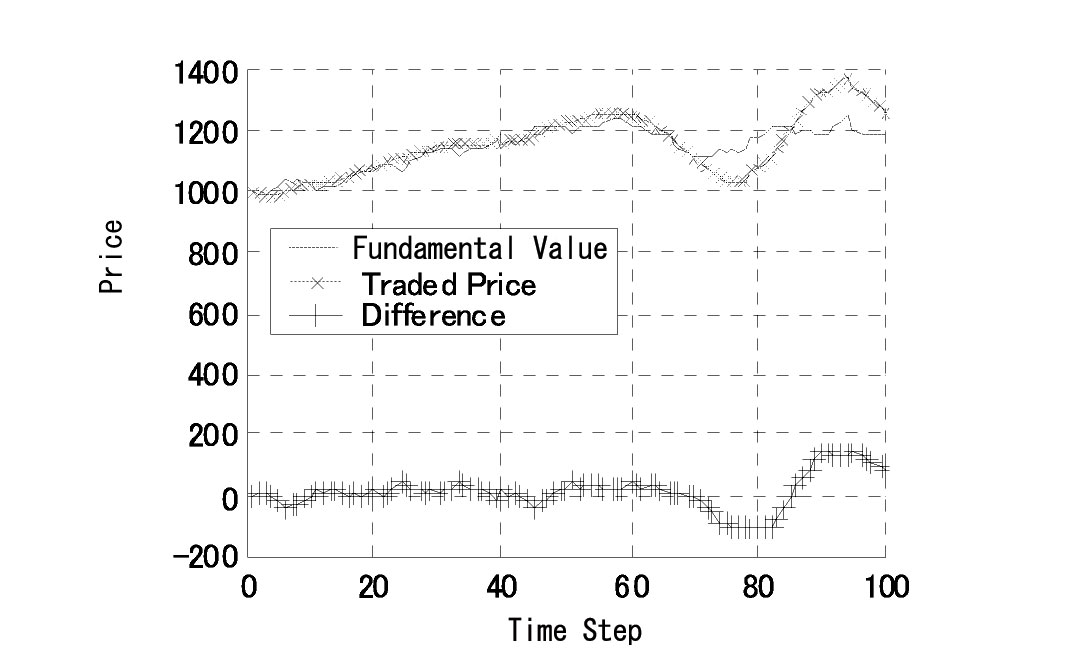
| Figure 18. Price history (when some investors have no restriction) |
|
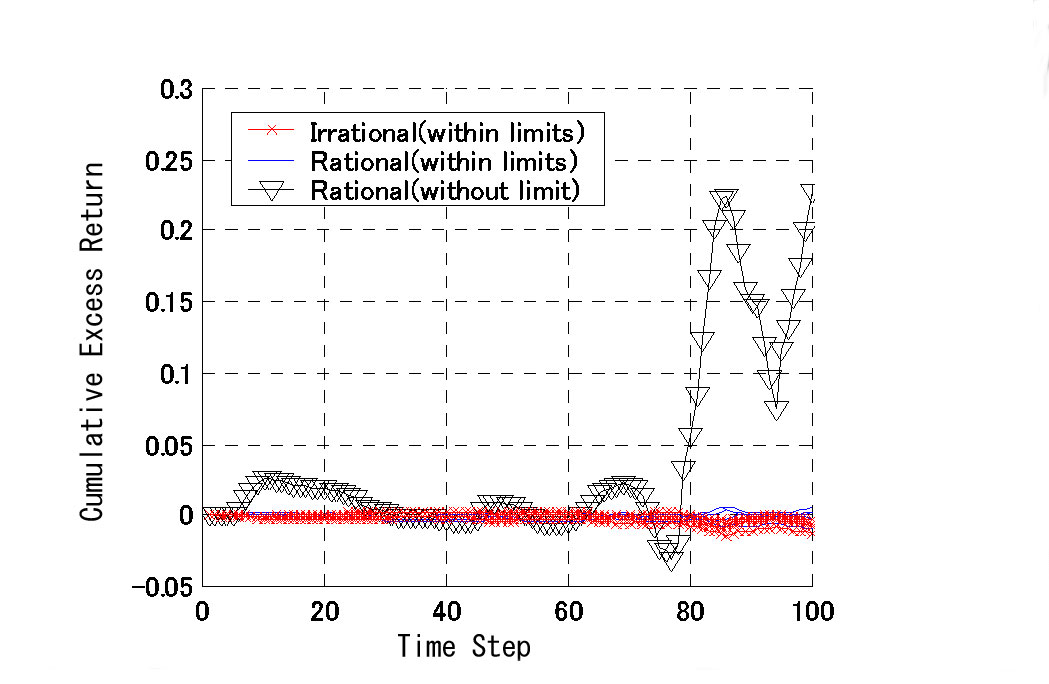
| Figure 19. Cumulative excess returns (when some investors have no restriction) |
|
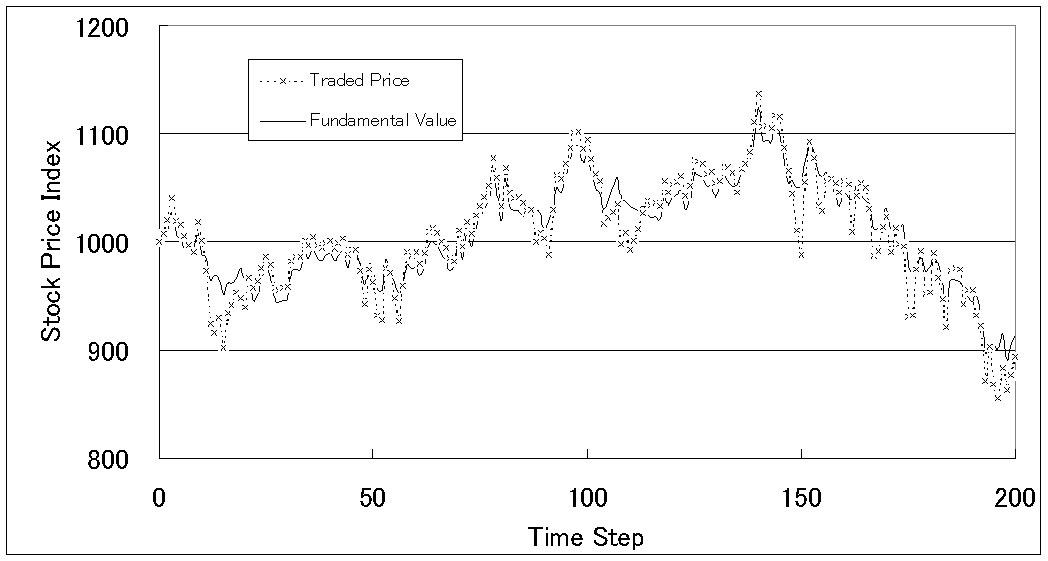
| Figure 20. Price history (when overconfident investors [k=0.9] exist) |
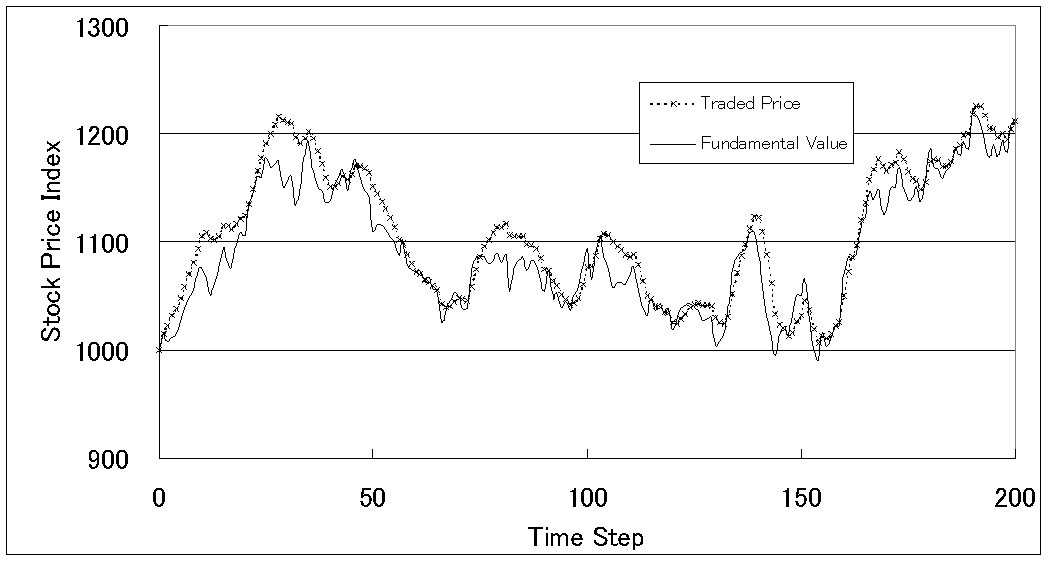
|
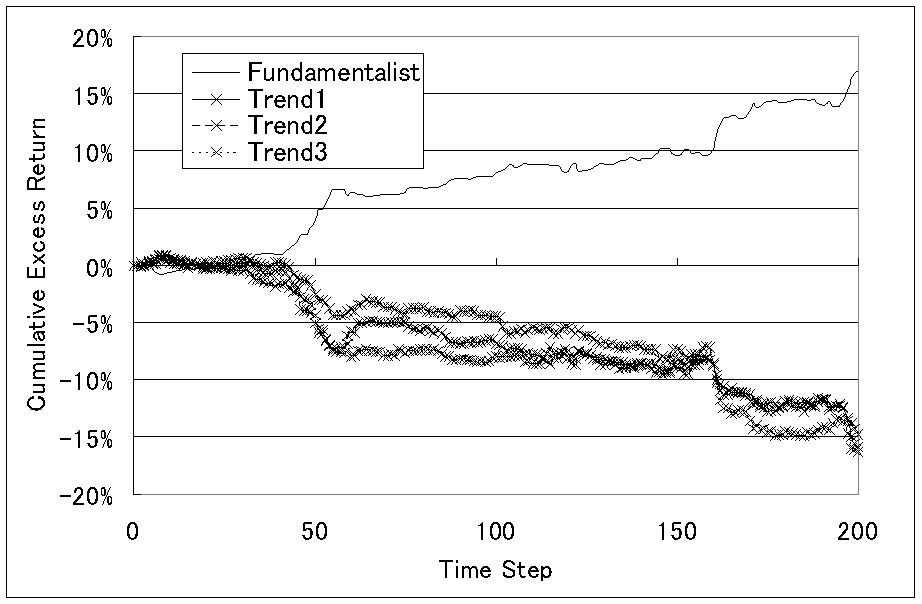
| Figure 21. Cumulative excess returns (when overconfident investors [k=0.9] exist) |
|
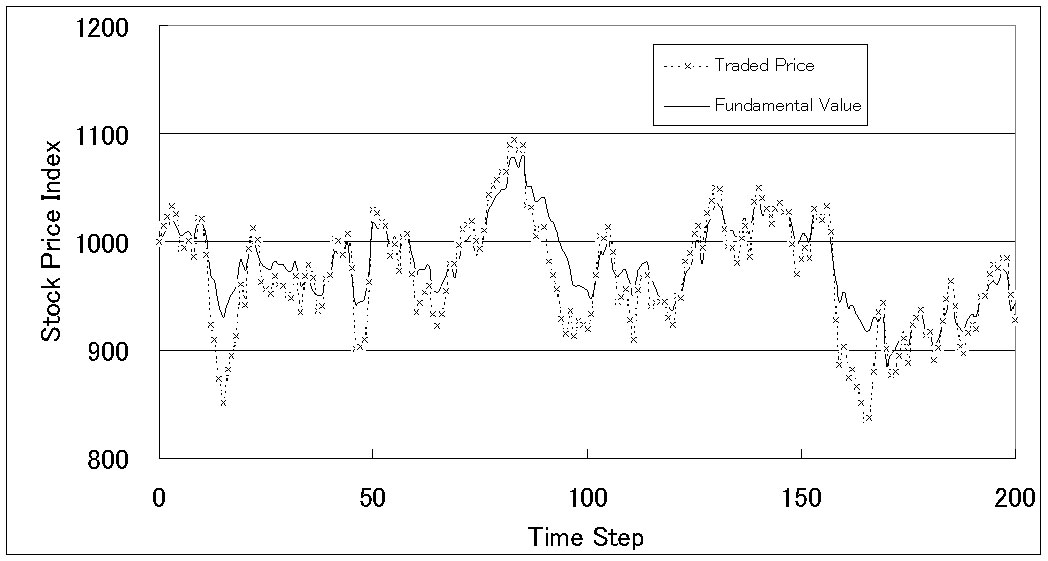
| Figure 22. Price history (when overconfident investors [k=0.8] exist) |
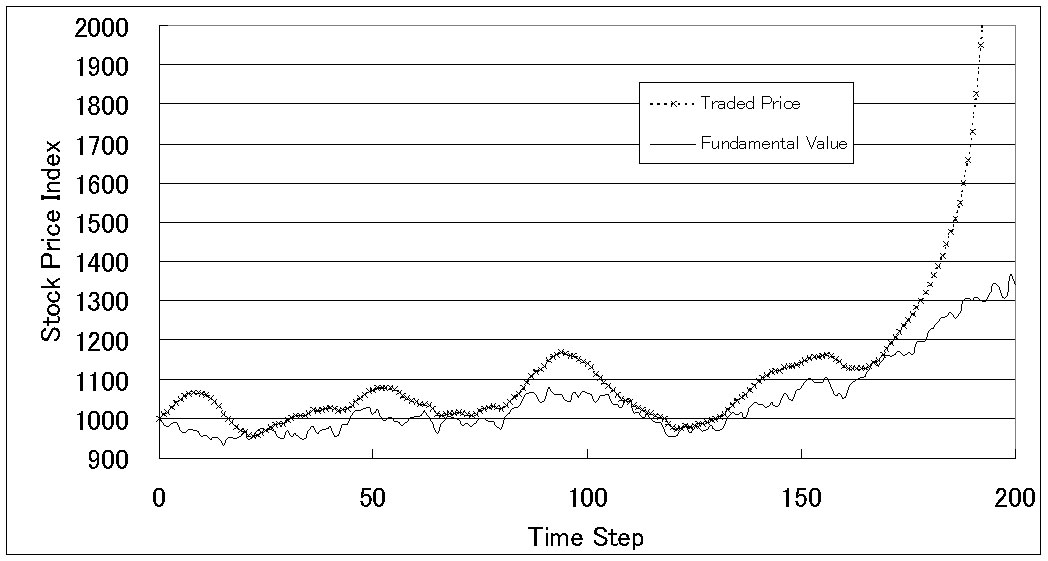
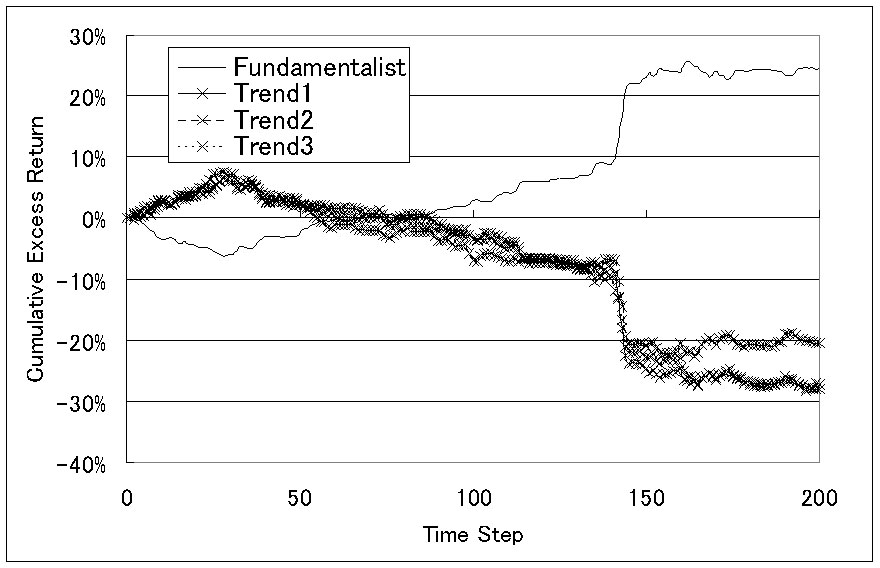 |
| Figure 23. Cumulative excess returns (when overconfident investors [k=0.8] exist) |
|
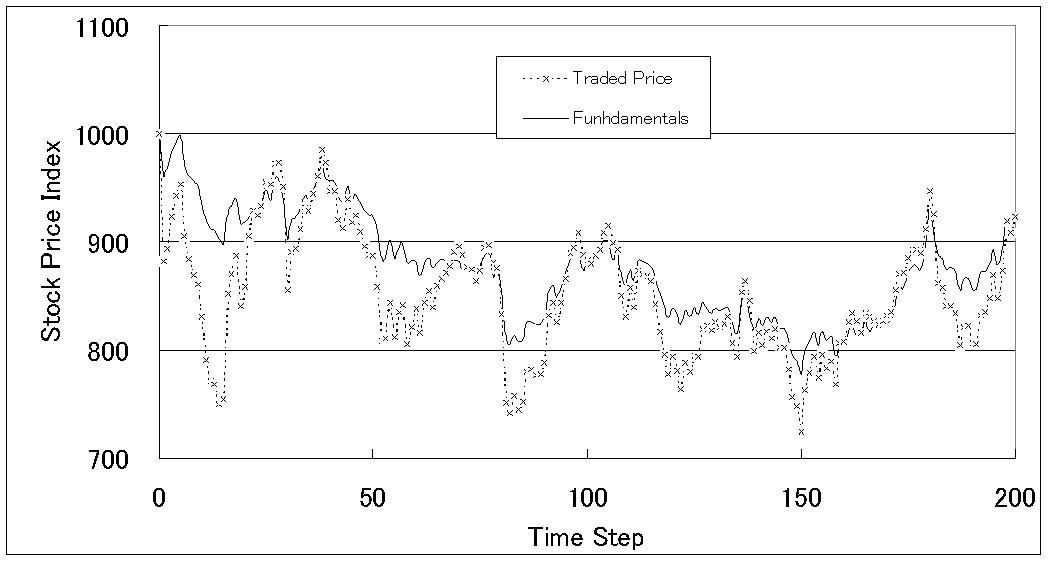
| Figure 24. Price history (when overconfident investors [k=0.6] exist) |
|
| Figure 25. Cumulative excess returns (when overconfident investors [k=0.6] exist) |
|
| Figure 26. Price history (when fundamental predictors based on Prospect Theory [10 days] exist) |
|
| Figure 27. Price history (when fundamental predictors based on Prospect Theory [max 10 days] exist) |
|
| Figure 28. Price history (when fundamental predictors based on Prospect Theory [max 20days] exist) |
|
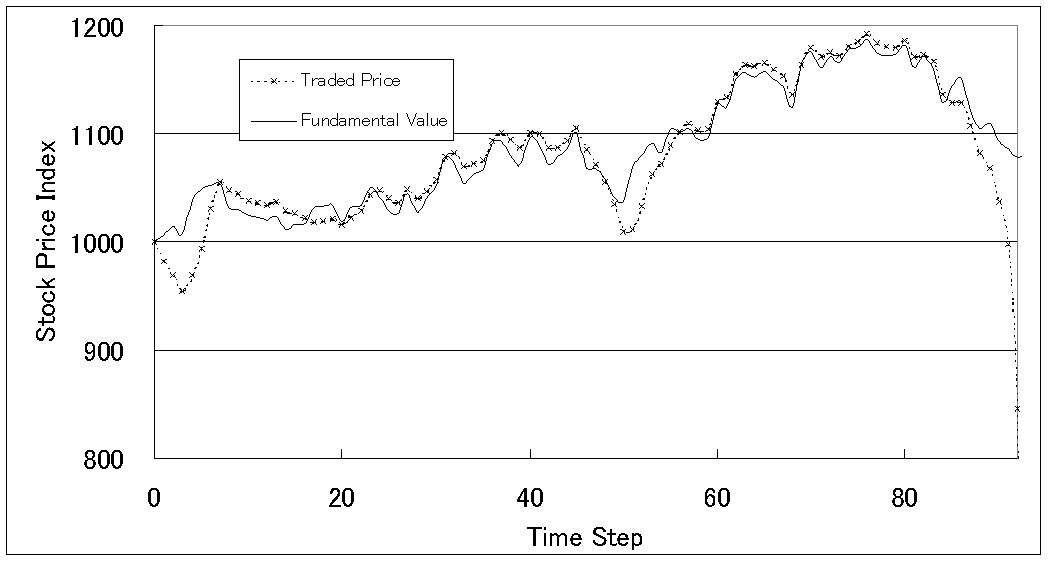
| Figure 29. Price history (when trend predictors based on Prospect Theory exist) |
 Conclusion
Conclusion2Even when CAPM was suggested, Simon already pointed that the rationality of human being is bounded (Simon 1955). However, an asset price in financial markets is considered to be priced based on the fundamental value for the reasons that "irrational investors behave random and their behaviors are canceled out" and "arbitrage transactions adjust the market price to the fundamental value". Friedman also insisted that even if the assumptions are unrealistic, the traditional finance is valid while it has enough explanation power (Friedman 1953). On the other hand, Behavioral Finance casts some doubt on the assumptions of traditional financial theories by pointing "there are good reasons to believe that the behavior of irrational investors is biased" and "the capability of arbitrage is limited".
3Hirshleifer (2001)describes how Agent-Based Approach is effective to analyze financial markets.
4Several articles including our paper analyze artificial markets in which investors change their strategies based on their own rules (Kirman and Teyssiere 2001, Lux and Marchesi 1999). Our work focuses the temporal change of the number of investors during the simulation (e.g. see fig. 5-7).
5It is also reported that rational investors adopt the optimal strategy in consideration of irrational investors' behavior. However, in the interests of simplicity, we make analyses based on the investors who do not consider other investors' behavior and always follow the pre-defined rules.
6For example, they try to derive the optimal portfolio strategy under the condition that the lending and borrowing interest rates are different.
7The investors in real markets collect the information from media and information terminals and update their belief based on it.
8Every investor adopts the same benchmark that is buy-and-hold of the portfolio consists of 1,000 CASH and 1,000 STOCK at the initial state (t=0).
9It is conventionally pointed that the typical means-variance models have a problem that "the slight difference in return makes large difference in assets allocation". The bayes correction model has resolved this problem and is closer to the investors' real behavior.
10When a loss arises as against the reference point, the investor estimates the loss larger than the actual and tends to behave more like a risk taker. This behavior vastly differs from the decision-making based on maximization of expected utility. On the other hand, when a profit arises as against the reference point, the form of the value function convexes upward, which is similar to the form of the conventional maximization of expected utility.
11The models for biases on decision-making are proposed in De Long (1990a), De Long (1990b), Barberis and Shleifer (1998), Kyle (1997), and Hong and Stein (1999). Although Behavioral Finance is sometimes considered ad hoc, it may be not in accordance with the reports that say that the emotion plays a key role in decision-making of human being (Damasio 1994, LeDoux 1996, Loewenstein 1996).
12Chiarella (1992) and Lux (1998) analyze the influences of heterogeneous investors with differential equations formulation, but the analyses lack the constraints assumptions about investors. On the other hand, agent-based approach deal with various kinds of analysis hard to analyze with differential equations. This is one of the advantages of our agent-based approach to financial market analysis.
13Behavioral finance tries to explain non-standard investors, such as trend followers, noise traders, overconfident investors, and loss avert investors from psychological view points. Several researchers have analyzed the effects of trend predictors and noise traders on asset prices with agent-based approach (Kirman and Teyssiere 2001, Lux and Marchesi 1999). In our paper, we deal with trend predictors, overconfident investors, and loss avert investors. One of the novelties of this research is to analyze the effects of overconfidence and loss aversion.
14See http://www.rr.iij4u.or.jp/~taishi/research
15We also analyze the case that the investment ratio of the risk asset is restricted (see section 4).
16For the simplicity, the investor models in this paper make investment decisions based on single period model. The analysis based on investors who consider multi- period is one of our future works. It is reported that rational investors adopt the strategy in consideration of irrational investors' behavior. However, for the simplicity, we assume that the behavior of each investor does not change according to the other investors' behavior. The analysis of the market that contains the investors who consider other investors' behavior is also one of our future works.
17Every investor adopts the same benchmark that is buy-and-hold of the portfolio consists of 1,000 cash and 1,000 stock at the initial state (t=0).
18When the most recent price is higher than the price at the reference point, the original predicted price remains as the ultimate predicted price.
19Appendix B at the end of this paper shows the outline of the bayes correction model.
20Although there are other determination methods of traded prices, we adopt the simplest method in accordance with Arthur et al. (1997). We expand traditional financial theory such as CAPM by adopting an equation based price determination because, in this paper, we will explore the limitation of conventional financial theory by Agent-Based Simulation. Elaboration of the price determination method is one of our future works. At the price determination, we change the value of (Pt) in increments of 0.1 and search the price to satisfy the equality condition. Although we adopt the simplest price determination method, consideration of other methods is also one of our future works.
21Every experiment described in this paper is repeated more than fifty times in each condition so that the reproducibility of the results is confirmed. We also analyzed the volatility of this market including the comparison of simulation data with empirical data. The detail is discussed elsewhere Takahashi and Terano (2002).
22When every investor is fundamentalist, the valuation of the asset price completely agrees among all investors. Therefore, the stock price fluctuates according to the fluctuation of the corporate profit, but the number of stock held by each investor does not change and no transaction occurs.
23As for the trend prediction investor, we have illustrated typical three trend investors (Trend1, Trend2, Trend3).
24Even if the traded price deviates from the fundamental value, it is adjusted by the fundamentalists.
25We obtain the same result even when we increase the ratio of the trend predictors up to 70%.
26At the beginning, the price fluctuation does not show the extreme trend so that the influence of fundamentalists is relatively large and the traded price fluctuates around the fundamental value. After a certain terms, however, the price fluctuation shows the extreme trend in many cases so that the traded price largely deviates from the fundamental value. Note that we abort the experiment when the traded price becomes fivefold or fifth part of the fundamental value because the computation takes too long and the extreme deviation of the prices is unrealistic.
27In this paper, every investor initially has the same amount of assets. It is also one of our future works to analyze the cases that each investor initially has different amount of assets.
28This experiment shows two types of results: one is the case the fundamentalists are eliminated and another is the case they are not. The main factor that brings different results is how the situation of excess returns was when the natural selection principle worked for the first time. For example, the fundamentalists tend to be eliminated from the market if the trend predictors obtain excess returns when the natural selection principle works for the first time.
29In the experiments on this investor ratio without the investment restriction, we have obtained the results that conform to the conventional financial theories.
30For example, if the ratio of the stock to the total market value at the term t-1 is 50%, the investment ratio of the stock at the term t must be 50%±5%. Such both over and lower risk limits are usually found in the business area of asset management of pension.
31This tendency is accelerated when the degree of overconfidence is increased.
32We set the reference point of Prospect Theory at ten days before.
33 ericum corresponds to the fitness of genetic algorithm.

|
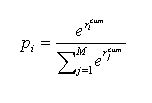
|

|
The short term expected rate of return of the investor i  is calculated from the predicted stock price
is calculated from the predicted stock price 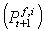 and the current stock price Pt as
and the current stock price Pt as 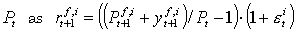 , where
, where 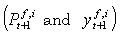 are the stock price and the
predicted return of the investor
are the stock price and the
predicted return of the investor 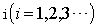 respectively. The short term expected rate of
return contains the error term
respectively. The short term expected rate of
return contains the error term 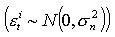 to reflect the fact that the in-depth prospects
are different even among the investors of the same prediction type.
to reflect the fact that the in-depth prospects
are different even among the investors of the same prediction type.
The expected rate of return on the stock 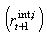 is calculated as
is calculated as
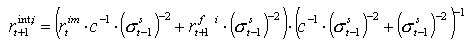 . As described above, the
expected rate of return on the stock
. As described above, the
expected rate of return on the stock 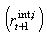 can be calculated based on the corporate profit
at the term t and the information (such as prices) available from the market at and before
the term t-1.
can be calculated based on the corporate profit
at the term t and the information (such as prices) available from the market at and before
the term t-1.








ARTHUR, W.B., HOLLAND J.H., LEBARON B., PALMER R.G. AND TAYLOR, P. (1997),"Asset Pricing under Endogenous Expectations in an Artificial Stock Market," The Economy as an Evolving Complex System II, Addison-Wesley, pp.15-44.
AXTELL, R. (2000),"Why Agents? On the Varied Motivation For Agent Computing In the Social Sciences," the Brookings Institution Center on Social and Economic Dynamics Working Paper November No.17. Barberis, N., Shleifer A. and Vishny, R. (1998),"A model of Investor sentiment, ", Journal of Financial Economics 49, pp.307-343. BARBERIS, N., HUANG, M. and SANTOS, T. (2001), "Prospect Theory and Asset Prices, " The Quarterly Journal of Economics 116, pp.1-53.
BAZERMAN, M. (1998), Judgment in Managerial Decision Making, John Wiley & Sons.
BARBERIS, N. AND SHLEIFER, A., "Style Investing, " Journal of Financial Economics forthcoming.
BERGER, J.O. (1985), Statistical Decision Theory and Bayesian Analysis, Springer.
BLACK, R., AND LITTERMAN, R. (1992), "Global Portfolio Optimization, " Financial Analysts Journal September-October, pp.28-43.
CHIARELLA, C. (1992), "The dynamics of speculative behaviour, " Annals of Operations Research, 37, pp.101-123.
DAMASIO, A.R. (1994), Descartes' Error: Emotion, Reason, and the Human Brain, New York: G.P. Putnam.
DELONG, J.B., SHLEIFER, A., SUMMERS, L. AND WALDMANN, R. (1990a), "Noise trader risk in financial markets," Journal of Political Economy 98,pp.703-738.
DELONG, J.B., SHLEIFER, A., SUMMERS, L. AND WALDMANN, R. (1990b),"Positive feedback investment strategies and destabilizing rational speculation," Journal of Finance 45, pp.375-395.
EPSTEIN, J. M. AND AXTELL, R. (1996), Growing Artificial Societies Social Science From The Bottom Up, MIT Press.
FAMA, E. (1970),"Efficient Capital Markets: A Review of Theory and Empirical Work," Journal of Finance 25,pp.383-417.
FRIEDMAN, M. (1953), Essays in Positive Economics, University of Chicago Press.
Goldberg, D. (1989), Genetic Algorithms in Search, Optimization, and Machine Learning, Addison-Wesley.
HOWSON, C. AND URBACH, P. (1993), Scientific Reasoning, Open Court Publishing Company.
INGERSOLL, J. E.(1987),Theory of Financial Decision Making, Rowman & Littlefield.
HIRSHLEIFER, D.(2001),"Investor Psychology and Asset Pricing," Journal of Finance 56,1533-1597.
HONG, H. AND STEIN, J.C. (1999),"A Unified Theory of Underreaction, Momentum Trading, and Overreaction in Asset Markets, " Journal of Finance 54,pp.2143-2184.
KAGEL, J.H. AND ROTH., A.E.(eds.) (1995), The Handbook of Experimental Economics, Princeton University Press.
KAHNEMAN, D. and TVERSKY, A. (1979), "Prospect Theory of Decisions under Risk," Econometrica 47,263-291.
KAHNEMAN, D., SLOVIC, P. AND TVERSKY, A. (1982), Judgment under uncertainty: Heuristics and biases, Cambridge University Press.
KAHNEMAN, D., AND TVERSKY, A. (1992), "Advances in. prospect Theory: Cumulative representation of Uncertainty," Journal of Risk and Uncertainty 5.
KAHNEMAN, D. AND TVERSKY, A. (2000), Choices, Values, and Frames, Cambridge University Press.
KIRMAN, A. AND TEYSSIERE, G. (2001), "Microeconomic Models for Long-Memory in the Volatility of Financial Time Series," CeNDEF Working Paper, 5a.4.
KYLE, A.S. and Wang, A. (1997),"Speculation Duopoly with Agreement to Disagree: Can Overconfidence Survive the Market Test? , "Journal of Finance 52,pp.2073-2090.
LEDOUX, J. (1996), The emotional Brain: The Mysterious Underpinnings of Emotional Life, Academic Press.
LEVY, M., LEVY, H. AND SOLOMON, S. (2000), Microscopic Simulation of Financial Markets, Academic Press.
LOEWENSTEIN, G. (1996), "Out of control: visceral influences on behavior," Organizational Behavior and Human Decision Processes 65,pp.272-292.
LUX, T. (1998), "The socio-economic dynamics of speculative markets:interacting agents, chaos, and the fat tails of return distributions," Journal of Economic Behavior & Organization, 33, pp.143-165.
LUX, T. AND MARCHESI, M. (1998), "Scaling and criticality in a stochastic multi-agent model of a financial market, " Nature, 397, pp.498-500.
O'BRIEN, P. (1988), "Analysts' Forecasts as Earnings Expectations," Journal of Accounting and Economics January, pp.53-83.
PALEPU, K.G., BERNARD, V.L. AND HEALY, P.M. (1996),Introduction to Business Analysis & Valuation, International Thomson Publishing.
RUSSEL, S.J. AND NORVIG, P. (1995), Artificial Intelligence, Prentice-Hall.
SHARPE, W.F. (1964), "Capital Asset Prices: A Theory of Market Equilibrium under condition of Risk, "The Journal of Finance 19,pp.425-442.
SHARPE, W.F. (1987), "Integrated Asset Allocation," Financial Analysts Journal September-October.
SHILLER, R.J. (2000), Irrational Exuberance, Princeton University Press.
SHLEIFER, A. (2000), Inefficient Markets, Oxford University Press.
SIMON, H.A. (1955),"A behavioral model of rational choice," Quarterly Journal of Economics 69, pp.99-118.
SIMON, H.A. (1996), The Sciences of the Artificial, MIT Press.
TAKAHASHI, H., AND TERANO, T. (2002), "Bridging GARCH Model and Prospect theory in Financial Market behaviors via Agent-Based Simulation", 8th international conference of the society for computational economics Computing in Economic and Finance.
TVERSKY, A AND KAHNEMAN, D. (1981), "The Framing Decisions and the Psychology of Choice, " Science 211, pp. 453-458.
WOLFRAM, S. (1994),Cellular Automata and Complexity, Addison Wesley.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]