Zhigang Wang and Warren Thorngate (2003)
Sentiment and social mitosis: Implications of Heider's Balance Theory
Journal of Artificial Societies and Social Simulation
vol. 6, no. 3
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/6/3/2.html>
Received: 25-Mar-2003 Accepted: 30-May-2003 Published: 30-Jun-2003
 Abstract
Abstract
| Table 1: Settings of the variables for each run of the simulation. | ||||
| Run | Group size | Positive relations | Negative relations | Null relations |
| 1 | 9 | 6 | 30 | 0 |
| 2 | 9 | 10 | 26 | 0 |
| 3 | 9 | 14 | 22 | 0 |
| 4 | 9 | 18 | 18 | 0 |
| 5 | 9 | 22 | 14 | 0 |
| 6 | 9 | 26 | 10 | 0 |
| 7 | 9 | 30 | 6 | 0 |
| 8 | 9 | 3 | 21 | 12 |
| 9 | 9 | 6 | 18 | 12 |
| 10 | 9 | 9 | 15 | 12 |
| 11 | 9 | 12 | 12 | 12 |
| 12 | 9 | 15 | 9 | 12 |
| 13 | 9 | 18 | 6 | 12 |
| 14 | 9 | 21 | 3 | 12 |
| 15 | 16 | 15 | 105 | 0 |
| 16 | 16 | 30 | 90 | 0 |
| 17 | 16 | 45 | 75 | 0 |
| 18 | 16 | 60 | 60 | 0 |
| 19 | 16 | 75 | 45 | 0 |
| 20 | 16 | 90 | 30 | 0 |
| 21 | 16 | 105 | 15 | 0 |
| 22 | 16 | 10 | 70 | 40 |
| 23 | 16 | 20 | 60 | 40 |
| 24 | 16 | 30 | 50 | 40 |
| 25 | 16 | 40 | 40 | 40 |
| 26 | 16 | 50 | 30 | 40 |
| 27 | 16 | 60 | 20 | 40 |
| 28 | 16 | 70 | 10 | 40 |
| 29 | 25 | 30 | 270 | 0 |
| 30 | 25 | 70 | 230 | 0 |
| 31 | 25 | 110 | 190 | 0 |
| 32 | 25 | 150 | 150 | 0 |
| 33 | 25 | 190 | 110 | 0 |
| 34 | 25 | 230 | 70 | 0 |
| 35 | 25 | 270 | 30 | 0 |
| 36 | 25 | 25 | 175 | 100 |
| 37 | 25 | 50 | 150 | 100 |
| 38 | 25 | 75 | 125 | 100 |
| 39 | 25 | 100 | 100 | 100 |
| 40 | 25 | 125 | 75 | 100 |
| 41 | 25 | 150 | 50 | 100 |
| 42 | 25 | 175 | 25 | 100 |
| Figure 1: . A starting nine-person matrix with 15 positive sentiment relations (+1), 11 negative sentiment relations (-1) and 10 null relations (0) randomly configured. | ||||||||
| +1 | 0 | -1 | 0 | +1 | +1 | -1 | 0 | |
| -1 | -1 | +1 | 0 | +1 | +1 | -1 | ||
| 0 | 0 | +1 | -1 | +1 | +1 | |||
| 0 | 0 | 0 | -1 | +1 | ||||
| -1 | +1 | +1 | -1 | |||||
| -1 | +1 | 0 | ||||||
| +1 | -1 | |||||||
| +1 | ||||||||
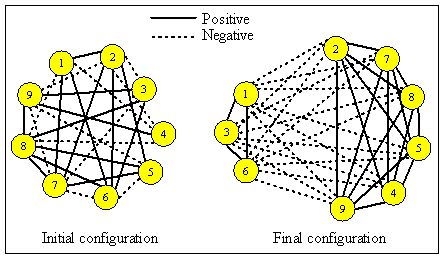
|
| Figure 2. Transformation of random positive, negative and null relations among nine people into two subgroups |
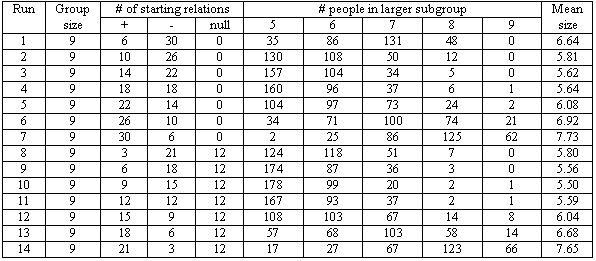
| Table 2. Number of the 300 iterations in a run when the largest subgroup of a 9-person group contained 5, 6, ..., 9 people. |
|
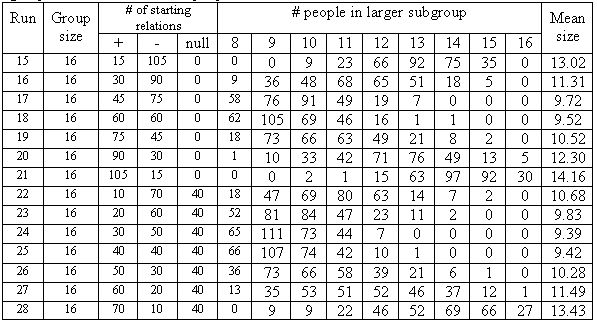
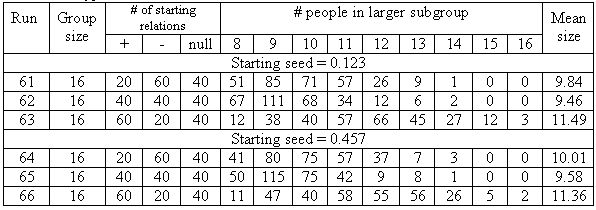
| Table 3. Number of the 300 iterations in a run when the largest subgroup of a 16-person group contained 8, 9, ..., 16 people. |
|
| Table 4. Number of the 300 iterations in a run when the largest subgroup of a 26-person group contained 13, 14, ..., 26 people. |
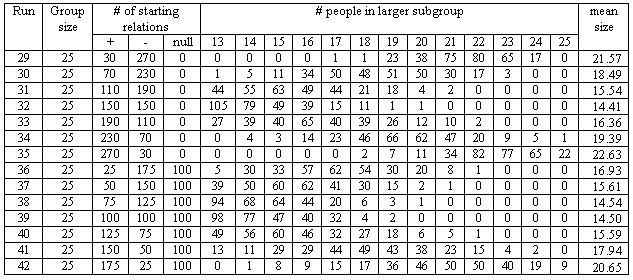
|
| Table 5a. Typical results from Same Start condition, no null relations. |
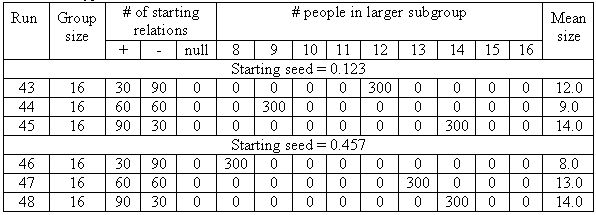
|
| Table 5b. Typical results from the Same Order condition, no null relations. |
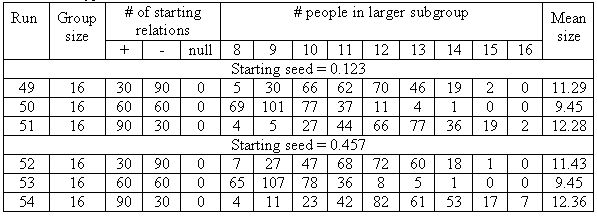
|
| Table 6a. Typical results from Same Start condition, 33% null relations. |
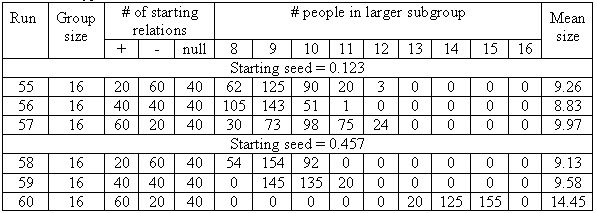
|
| Table 6b. Typical results from Same Order condition, 33% null relations. |
|
..comment ..fill(A,b,c): fills top-right corner of an AxA square matrix with b "+1s", c "-1s" and
............ (A*A-A)/2 - b - c zeros. ..nbal(A): calculates the number of balanced, imbalanced and null triads ..balance(A): runs the Heider balance simulation ..who(A): finds people in groups and counts them ..It is used for the Heider simulation ..w thorngate, 19 December 2002 ..endcomment function fill(nrc,npl,nmi) .. nrc: # of rows/columns, npl: # of + links, nmi: # of - links relations=zeros(nrc,nrc); plus=ones(1,npl); .. create a vector of npl 1s minus=-(ones(1,nmi)); .. create a vector of -1s zero=zeros(1,(nrc*nrc-nrc)/2-npl-nmi); .. create the vector of 0s y=plus | minus | zero;.. catonate the three vectors y=shuffle(y); .. randomize the order of 1s, -1s and 0s w=1; for i=1 to (nrc-1); .. loop to put the elements of y in the upper triangle of relations matrix relations(i,i+1:nrc) = y(w:w+nrc-i-1); w=w+nrc-i; end; return relations .. return the resulting relations triangle endfunction function nbal(relations) .. used only to determine how many iterations needed to reach steady state balanced=0; imbalanced=0; null=0; r=rows(relations); for i=1 to r-2; .. select all combinations of three group members for j=i+1 to r-1; for k=j+1 to r; a=relations(i,j); b=relations(i,k); c=relations(j,k); d=a*b*c; .. multiply the three links if d==1; .. if result is +1, the triad is balanced balanced=balanced+1; endif; if d==-1; .. if result is -1, the triad is imbalanced imbalanced=imbalanced+1; endif; if d==0; .. if result is 0, 1 or 2 links must be zero null=null+1; endif; end; end; end; return {balanced,imbalanced,null}; endfunction function balance(rel) relations=rel; r=1:rows(relations); for trial=1 to 100000; a=shuffle(r); b=sort(a(1:3)); first=relations(b(1),b(2)); second=relations(b(1),b(3)); third=relations(b(2),b(3)); bal=first*second*third; if bal==-1; relations(b(1),b(2))=-(relations(b(1),b(2))); endif; if ((bal==0) && (abs(first)+abs(second)+abs(third)==2)); if first==0; relations(b(1),b(2))=second * third; elseif second==0; relations(b(1),b(3))=first * third; elseif third==0; relations(b(2),b(3))=first * second; else; endif; endif; end; nbal(relations); return relations; endfunction function subgroups(relations) x=relations+relations'; .. add mirror image in bottom right triangle r=cols(x); groups=zeros(1,r); g=0; for i=1 to r-1; if groups(i)==0; .. Has current element been categorized? 0=no g=g+1; .. create next category number groups(i)=g; .. assign new category number to ith element endif; for j=i+1 to r; y=sum(x(i,:)*x(j,:)); .. test to see if i and j have equal relations to all others if y==(r-2) && groups(j)==0; .. if they do, then they are in same group groups(j)=groups(i); endif; end; end; if groups(r)==0; .. tests for condition when last element is different than all others
groups(r)=g+1; endif; g1=sum(groups==1); .. count times result = 1 group g2=sum(groups==2); .. count times result = 2 subgroups g3=sum(groups>=3); .. count times result = 3 or more subgroups return [g1 g2 g3] endfunction function doit(a,b,c) .. run a 300-iteration simulation sums=zeros(300,3); "trial:" for t=1 to 300 t .. shown on screen just to indicate how far simulation has run z=fill(a,b,c); .. fill the matrix with relations for this iteration x=balance(z); .. balance the filled matrix sums(t,:)=subgroups(x); .. record the size of the subgroups end; b=max(sums(:,1),sums(:,2))'; .. find the largest subgroups mean(b) .. show average of largest subgroups on screen result=zeros(2,a); for i=1 to a; result(1,i)= i; result(2,i)= sum(b==i); end; return result endfunction
function doit(a,b,c) .. run a 300-iteration simulation sums=zeros(300,3); "trial:" for t=1 to 300 t .. shown on screen just to indicate how far simulation has run seed(123); .. and seed(457) to produce same pseudorandom sequence z=fill(a,b,c); .. fill the matrix with relations for this iteration seed(time()); .. to produce different pseudorandom sequence for each triad sampling x=balance(z); .. balance the filled matrix sums(t,:)=subgroups(x); .. record the size of the subgroups end; b=max(sums(:,1),sums(:,2))'; .. find the largest subgroups mean(b) .. show average of largest subgroups on screen result=zeros(2,a); for i=1 to a; result(1,i)= i; result(2,i)= sum(b==i); end; return result endfunction
function doit(a,b,c); .. run a 300-iteration simulation sums=zeros(300,3); "trial:" for t=1 to 300 t .. shown on screen just to indicate how far simulation has run seed(time()); to produce different pseudorandom sequence for sentiment relations z=fill(a,b,c); .. fill the matrix with relations for this iteration seed(124); .. and seed(457) to produce same pseudorandom sequence for triad sampling x=balance(z); .. balance the filled matrix sums(t,:)=subgroups(x); .. record the size of the subgroups end; b=max(sums(:,1),sums(:,2))'; .. find the largest subgroups mean(b) .. show average of largest subgroups on screen result=zeros(2,a); for i=1 to a; result(1,i)= i; result(2,i)= sum(b==i); end; return result endfunction
AXELROD R (1997) The complexity of cooperation: agent-based models of competition and collaboration. Princeton, N.J.: Princeton University Press.
BRONFENBRENNER U (1961) The mirror-image in Soviet-American relations: A social psychologist's report. Journal of Social Issues, 17. pp. 45-56.
CARLEY K (1991) A Theory of Group Stability. American Sociological Review, 56(3). pp. 331-354.
CARROLL, M. P. (1977) A test of Newcomb's modification of balance theory. Journal of Social Psychology, 101(1). pp. 155-156.
CARTWRIGHT D and Harary F (1956) Structural Balance: A Generalization of Heider's Theory. Psychological Review, 63. pp. 277-293.
CRANO W D and Cooper R E (1973) Examination of Newcomb's extension of structural balance theory. Journal of Personality and Social Psychology, 27(3). pp. 344-353.
DOREIAN P and Mrvar A (1996) A Partitioning Approach to Structural Balance. Social Networks, 18(2). pp. 149-168.
GROTHMANN, R. (2002). The Euler programming language. Available at http://mathsrv.ku-eichstaett.de/MGF/homes/grothmann/euler/
HARARY F, Norman R, and Cartwright D (1965) Structural Models: An Introduction to the Theory of Directed Graphs. Wiley, New York.
HEIDER F (1946) Attitudes and cognitive organization. Journal of Psychology, 21. pp. 107-112.
HEIDER F (1958) The psychology of interpersonal relations. New York: John Wiley & Sons.
HUMMON N P and Doreian P (2003) Some dynamics of social balance processes: bring Heider back into balance theory. Social Networks, 25(1). pp. 17-49.
LONDON I and Thorngate W (1981) Divergent Amplification and Social Behavior: Some methodological considerations. Psychological Reports, 48. pp. 203-228.
MACY M W and Willer R (2002) From Factors to Actors. Annual Review of Sociology, 28. pp. 143-166.
MARK N (1998) Beyond Individual Differences: Social Differentiation from First Principles. American Sociological Review, 63(3). pp. 309-330.
MOORE M (1978) An international application of Heider's balance theory. European Journal of Social Psychology, 8(3). pp. 401-405.
NEWCOMB T M (1968) "Interpersonal balance". In Abelson, R. P., Aronson E, McGuire W J, Newcomb T M, Rosenberg M J, and Tannenbaum O H (Eds.). Theories of Cognitive Psychology, Chicago: Rand McNally.
NEWCOMB T M (1981) Heiderian balance as a group phenomenon. Journal of Personality and Social Psychology,40. pp. 862-867.
NOWAK M A and Vallacher R R (1998) Dynamical social psychology. The Guilford Press. New York.
OSGOOD C E and Tannenbaum P H (1955) The principle of congruity in the prediction of attitude change. Psychological Review, 62. pp. 42-55.
RAE D and Taylor M (1970) The analysis of political cleavages.New Haven, CT: Yale University Press.
ROSENBERG M and Abelson R (1960) An analysis of cognitive balancing. In Rosenberg M J (Ed.), Attitude organization and change: An analysis of consistency among attitude components, New Haven, CT: Yale University Press.
TAJFEL H (1970) Experiments in intergroup discrimination. Scientific American, 223(2). pp. 96-102.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]