H. Fort (2003)
Cooperation with random interactions and without memory or "tags"
Journal of Artificial Societies and Social Simulation
vol. 6, no. 2
To cite articles published in the Journal of Artificial Societies and Social Simulation, please reference the above information and include paragraph numbers if necessary
<https://www.jasss.org/6/2/4.html>
Received: 19/12/2002 Accepted: 16-Feb-2003 Published: 31-Mar-2003
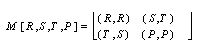
|
| T > R > P > S. | (1) |
In case one wants that universal cooperation be Pareto optimal, the additional required condition is:
| 2R > S + T. | (2) |
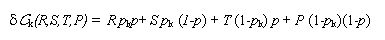
|
(3) |
where the variable pk takes only two values: 1 if k is a C-agent and 0 if k is a D-agent. It turns out that, in general, the value of p is not known by the agents. Thus a simpler estimate of the expected utilities εk is obtained by substituting p in the above expression for the per-capita-income δ Ck (R,S,T,P) by his own probability of cooperation pk[2]. In other words, agent k makes the simplest possible extrapolation and assumes that the average probability of cooperation coincides with his pk; the estimate εk corresponds to the utilities he would made by playing with himself. That is,
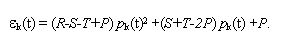
|
(4) |
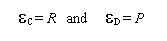
|
(5) |
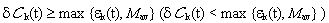 the agent assumes it is doing well (badly) and therefore his behavior (C or D) is adequate (inadequate).
the agent assumes it is doing well (badly) and therefore his behavior (C or D) is adequate (inadequate).
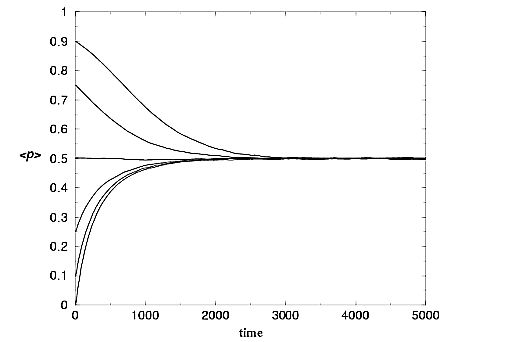
|
| Figure 1. <p> vs. time, for the canonical payoff matrix. fC0 = 0, 0.1, 0.25, 0.75 and 0.9. |
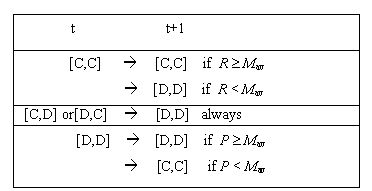
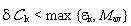 he inverts his behavior. In an encounter [C,C] both agents get δC = R which coincides with their estimate εC= R, hence they keep their behavior if
he inverts his behavior. In an encounter [C,C] both agents get δC = R which coincides with their estimate εC= R, hence they keep their behavior if 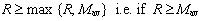 and otherwise change their behavior to D if R < Mav. On the other hand, in an encounter [D,D] both agents get δC = P which coincides with their estimate εD= P, hence they keep their behavior if
and otherwise change their behavior to D if R < Mav. On the other hand, in an encounter [D,D] both agents get δC = P which coincides with their estimate εD= P, hence they keep their behavior if  and otherwise change their behavior to C if P < Mav. Finally, In an encounter [C,D] the C-agent gets δCC = S and his estimate is εC = R and the D-agent gets δCD = T and his estimate is εCD= P. Hence, the C-agent would keep his behavior if S ≥ max {R, Mav}, but this cannot happen because S < R then he changes to D. The D-agent keeps his behavior because T = max {R,S,T,P} and then T ≥ max {P, Mav}. After the four kind of possible encounters the 2 interacting agents end with the same behavior (C or D). Table 1 summarizes the possible outcomes for payoff matrices satisfying the PD condition (1).
and otherwise change their behavior to C if P < Mav. Finally, In an encounter [C,D] the C-agent gets δCC = S and his estimate is εC = R and the D-agent gets δCD = T and his estimate is εCD= P. Hence, the C-agent would keep his behavior if S ≥ max {R, Mav}, but this cannot happen because S < R then he changes to D. The D-agent keeps his behavior because T = max {R,S,T,P} and then T ≥ max {P, Mav}. After the four kind of possible encounters the 2 interacting agents end with the same behavior (C or D). Table 1 summarizes the possible outcomes for payoff matrices satisfying the PD condition (1).
|
| Table 1. Possible outcomes for the different PD game interactions. |
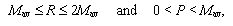
|
(6) |
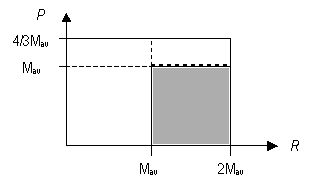
for which the proposed strategy produces cooperation (in gray), and the rest for which peq = 0.0 (in white).
|
| Figure 2. Different region in the (R,P) plane: cooperative (gray) and non-cooperative (white). |
|
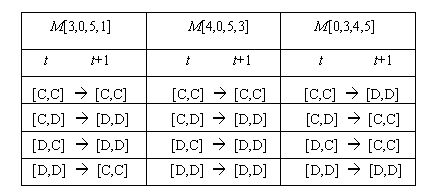
| Table 2. Transitions for payoff matrices M[3,0,5,1], M[4,0,5,3] and M[0,3,4,5] |
| 2(1-peq)2 = 2 peq(1-peq) | (7) |
one of its roots is peq=0.5 (the other root is peq=1); and for M[4,0,5,3] we have
| 0 = 2 peq(1-peq) | (8) |
one of its roots is peq=0.0 (the other root is peq=1).
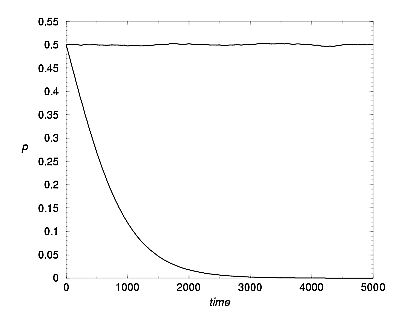
|
| Figure 3. p vs. time, for payoff matrices M[3,0,5,1] with peq=0.5 and M[4,0,5,3] with peq=0.0. |

|
(9) |
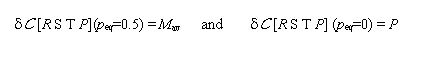
|
(10) |
2 One might consider more sophisticated agents which have "good" information (statistics, surveys, etc.) from which they can extract the average probability of cooperation in "real time" p(t) to get a better estimate of their expected utilities. However, the main results do not differ substantially from the ones obtained with these simpler agents.
3 max{A,B} stands for the maximum of A and B.
4 The choice of Mav as a reference point is quite arbitrary, indeed whether or not cooperation becomes a stable strategy depends on the fact that two payoffs are greater and the other two smaller than the reference point.
5 For instance "altruists", C-inclined independently of the costs, with payoff matrices with high values of S or "anti-social" individuals, for whom cooperation never pays, with very low values of R.
AXELROD, R. (1997), The Complexity of Cooperation, Princeton University Press.
AXELROD, R. And COHEN M. (1999), Chapter 3 of Harnessing Complexity, The Free Press.
COHEN , M. D. ,RIOLO R. L. and AXELROD R. (2001), Rationality and Society 13: 5.
FORT, H. (2002) to be published elsewhere.
HOFFMANN, R. (2000), Journal of Artificial Societies and Social Simulation 3 (2). <https://www.jasss.org/3/2/forum/1.html>
KRAINES, D. P. and KRAINES V. 1989, Theory and Decision 26 (1989): 47.
MAYNARD SMITH, J. 1982, Evolution and the Theory of Games, Cambridge University Press.
NOWAK M. A. and MAY R 1992., Nature 359: 826.
NOWAK M. A., MAY R. and SIGMUND K. 1995, Scientific American, June 1995: 76.
WEINBULL, J. W. 1995, Evolutionary Game Theory, MIT Press.
Return to Contents of this issue
© Copyright Journal of Artificial Societies and Social Simulation, [2003]